Coupling intercellular molecular signalling with multicellular deformation for simulating three-dimensional tissue morphogenesis

Abstract

During morphogenesis, three-dimensional (3D) multicellular structures emerge from biochemical and mechanical interplays among cells. In particular, by organizing their gradient within tissues, the diffusible signalling molecules play an essential role in producing the spatio-temporal patterns of cell status such as the differentiation states. Notably, this biochemical patterning can be dynamically coupled with multicellular deformations by signal-dependent cell activities such as contraction, adhesion, migration, proliferation and apoptosis. However, the mechanism by which these cellular activities mediate the interactions between multicellular deformations and patterning is still unknown. Herein, we propose a novel framework of a 3D vertex model to express molecular signalling among the mechanically deforming cells. By specifying a density of signalling molecules for each cell, we express their transport between neighbouring cells. By simulating signal-dependent epithelial growth, we found various types of tissue morphogenesis such as arrest, expansion, invagination and evagination. In the expansion phase, growth molecules were widely diffused with increasing tissue volume, which diluted the growth molecules in order to support the autonomous suppression of tissue growth. These results indicate that the proposed model successfully expresses 3D multicellular deformations dynamically coupled with biochemical patterning. We expect our proposed model to be a useful tool for predicting new phenomena emerging from mechanochemical coupling in multicellular morphogenesis.

1. Introduction

Multicellular morphogenesis is a sequential process of deformations in three-dimensional (3D) space. The coordination of 3D tissue deformations correlates with geometric cell patterns, where individual cells are characterized by their biochemical states such as protein synthesis, mRNA transcription and gene methylation. During morphogenesis, such cell patterning can be dynamically rearranged because of the regulatory nature of signalling molecules inside and outside cells. As an example, because the signalling molecules diffuse away from a localized source, they assume a distribution with a steady gradient within a tissue [1,2]. By reading the local levels of the signal concentrations, the cells determine their positions and differentiate to form the global tissue pattern. The global pattern can be robustly organized in the entire tissue by balancing molecular production and degradation [3]. Furthermore, the diffusivity of signalling molecules can be physically affected by the geometry of their passages, i.e. local cell shapes and configurations, and global tissue morphologies. Thus, based on diffusible molecular signalling, cell patterning can dynamically interact with 3D tissue deformations.

Cells have different biochemical states within their respective patterned domains. Depending on these biochemical states, cells express characteristic cell activities such as contraction, adhesion, migration, proliferation and apoptosis [4–11]. These cell activities generate mechanical forces, which induce tissue deformations. Therefore, depending on the signalling molecules, cell activities drive various tissue deformations. Moreover, global tissue deformations cause local changes in the cell mechanical states, such as cell shape, size and stress, which can trigger further molecular signalling [12]. Hence, signal-dependent cell activities mediate the interactions between the multicellular deformations and patterning. Thus, one current challenge in developmental biology is to reveal how tissue morphogenesis emerges from the mechanochemical coupling of multicellular deformations and patterning.

Cells have the characteristics of 3D structures such as apical, basal and lateral areas of epithelium, whose behaviours drastically vary from a mechanical viewpoint. For example, apical areas actively generate contractile forces by actomyosin activities [6], and basal areas passively respond to extrinsic forces in a viscoelastic manner [13]. In embryogenesis, the deformations of such 3D-structured cells are integrated into 3D tissue deformations, i.e. epithelial invagination, evagination, tubulation, elongation, torsion and branching [14]. Because of these 3D characteristics, most multicellular deformations cannot be quantitatively captured by two-dimensional (2D) approximations. Moreover, signalling molecules diffuse inside the 3D-structured tissues in order to organize 3D biochemical patterns and couple multicellular deformations and patterning in 3D space. Therefore, to understand the mechanochemical coupling in embryonic morphogenesis, it is necessary to analyse multicellular morphogenesis in 3D space.

To analyse 3D multicellular morphogenesis at the single-cell level, 3D vertex models have been proposed [15]. Vertex models have succeeded in reproducing several developmental phenomena such as blastocyst formation [16] and convergent-extension [17]. Furthermore, 3D vertex models have been improved in terms of kinematic and mechanical expressions of multicellular behaviours such as cell rearrangements [18], cell division [19] and cell viscoelasticity [20]. Hence, vertex models are gradually gaining more attention as robust tools for simulations of various multicellular morphogenesis processes at the single-cell level. Notably, recent studies have reported several findings by coupling 2D vertex models with biochemical patterning [21]. However, in 3D vertex models, biochemical patterning has not yet been considered because of the difficulty in 3D modelling. Therefore, incorporating molecular signalling into 3D vertex models will aid in the exploration of mechanochemical coupling in multicellular morphogenesis.

In this study, to model the mechanochemical coupling of multicellular morphogenesis at the single-cell level, we propose a novel framework of a 3D vertex model expressing intercellular molecular signalling. In the proposed model, molecular signalling transport is expressed between neighbouring cells. To demonstrate the applicability of the proposed model, we simulate signal-dependent epithelial growth and discuss the coupling of multicellular deformations and patterning.

2. Expressing intercellular molecular signalling on a three-dimensional vertex model framework

2.1. Expression of multicellular deformation

In tissues such as epithelium, cells aggregate by adhering to one another, as shown in figure 1a. In 3D vertex models, individual cell shapes are represented by polyhedrons, as seen in figure 1b. Polygonal faces consisting of a polyhedron are shared by neighbouring polyhedrons, and the polyhedrons' vertices and edges constitute a single network that represents the entire morphology of a cell aggregate [15]. In addition, the network is reconnectable to depict cell rearrangement [18].

Figure 1.

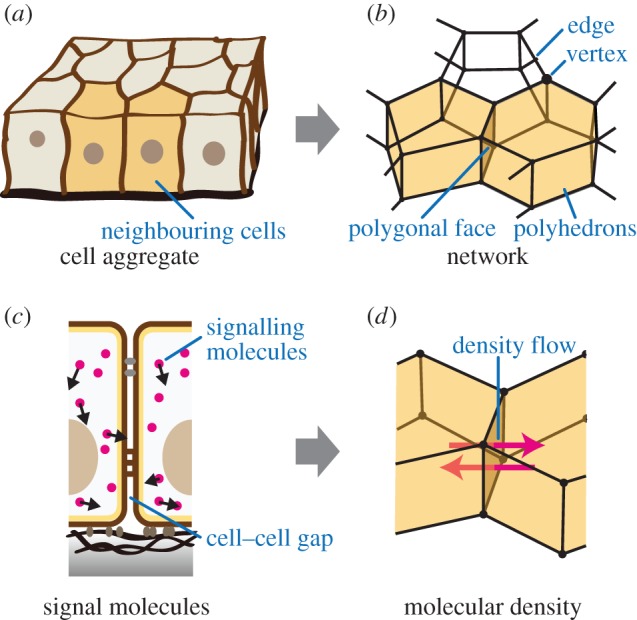
Expressing molecular signalling in the proposed model. (a) Illustration of the cell aggregate. (b) Illustration of a network comprising vertices and edges. Individual cells (two neighbouring yellow cells in (a)) are modelled by single polyhedrons (two neighbouring yellow polyhedrons in (b)), and neighbouring polyhedrons share the polygonal faces of their boundaries (brown polygonal face between neighbouring yellow cells in (b)). (c) Schematic of signalling molecules within the cell aggregate. There is a gap at the boundary between neighbouring cell surfaces. (d) Schematic of molecular signalling between neighbouring cells. (Online version in colour.)

Multicellular deformations are expressed by vertex movements. The velocity of the i^vth vertex, with the position vector represented by 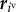, is expressed by

2.1

The left-hand side of equation (2.1) indicates a viscous frictional force exerted on the i^vth vertex, where the constant η^v is the viscous friction coefficient of the vertices. The right-hand side of equation (2.1) indicates a force acting on the i^vth vertex, where 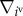is the gradient with respect to the i^vth vertex position. In equation (2.1), U is an effective energy function, which represents the active and passive cell behaviours.

2.2. Expression of intercellular molecular signalling

In cell aggregates, signalling molecules can be transported within and/or among cells, as shown in figure 1c. By supposing that molecular diffusion within cells is much more rapid than that between cells, we represent 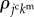as the k^mth molecular density inside the j^cth cell. Hence, based on the 3D vertex model framework, molecular signalling can be expressed by the transport of signalling molecules among individual cells, as shown in figure 1d. By representing 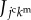as a flux of the k^mth signalling molecules toward the j^cth cell from the surrounding, flux 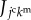can be written as

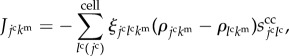2.2

where 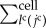is the summation for all cells neighbouring the j^cth cell. Scalar 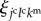is a molecular transfer coefficient of the k^mth signalling molecules between the j^cth and l^cth cells. Scalar 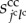is the surface area between the j^cth and l^cth cells.

Signalling molecules are transported into the cell through the cellular surface and generated and degraded inside the cell. According to the law of conservation of mass, the k^mth molecular density inside the j^cth cell 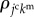satisfies the following relationship:

2.3

where 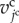is the j^cth cell volume and 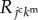is the reaction rate of the k^mth signalling molecules inside the j^cth cell. This expression of multicellular signalling enables the reproduction of multicellular patterning dependence on their deformations.

Moreover, to couple multicellular deformations and patterning, cell activities are dependent on the signalling molecules within cells. Hence, the energy function U in equation (2.1) is defined as a function of the molecular densities of cell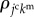s, , as

2.4

where the bracket represents a set as 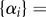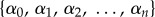and .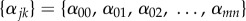

3. Computational simulation of signal-dependent epithelial growth

Organizing complicated structures of tissues and organs requires coordinating the spatial patterns of cell growth. The tissue growth is regulated by several growth molecules such as FGFs, Wnts, TGFβs and SHH [14]. These growth molecules, produced in localized source cells, diffuse within tissues. Hence, it is important to reveal the effects of the diffusivity of these growth molecules on tissue deformations. Therefore, to demonstrate the applicability of the proposed model, signal-dependent epithelial growth was simulated as a simple example.

3.1. Mathematical expression of cellular mechanochemical behaviours

3.1.1. Cell mechanical behaviours

To simulate multicellular morphogenesis driven by the biochemical and mechanical interactions, the energetic behaviour of each cell is simply expressed by the energy function U in equation (2.4), as follows:

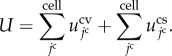3.1

In equation (3.1), function 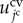is the volume elastic energy of the j^cth cell and is the surface elastic energy of the j^cth cell.

For cell volume elasticity, the current volume of the j^cth cell, 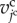, is introduced. Then, the cell volume elastic energy, 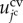, is given as follows:

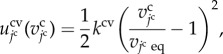3.2

where the constant k^cv is the volume elasticity. The variable is the equilibrium volume of the j^cth cell.

For cell surface elasticity, the current surface of the 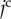th cell, 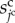, is introduced. Then, the cell surface elastic energy, 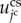, is given as follows:

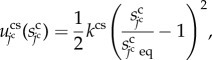3.3

where the constant k^cs is the surface elasticity. Assuming that the equilibrium state of the cell shape is spherical, variable 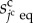is defined by

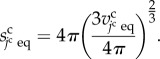3.4

Because equation (3.4) indicates a surface area of an equivalent sphere with the same volume, cell shapes tend to be spherical because of the force balance between the cell volume and surface elasticity in equations (3.2) and (3.3).

3.1.2. Expressions of cell volume growth

In general, the cell cycle is separated into four phases: G1, S, G2 and M. Cells grow according to these phases and divide in the M phase. Before entering the S phase, individual cells make the decision of whether they should divide or enter a resting phase, G0. Hence, to express the cell cycle in the model, we introduce four cell states (I, II, III and IV) as shown in figure 2a. In the model, before entering state III, the cells decide whether they should proceed to state III or pause on the basis of the density of growth molecules as

3.5

where ρ_th is the threshold density of growth molecules.

Figure 2.

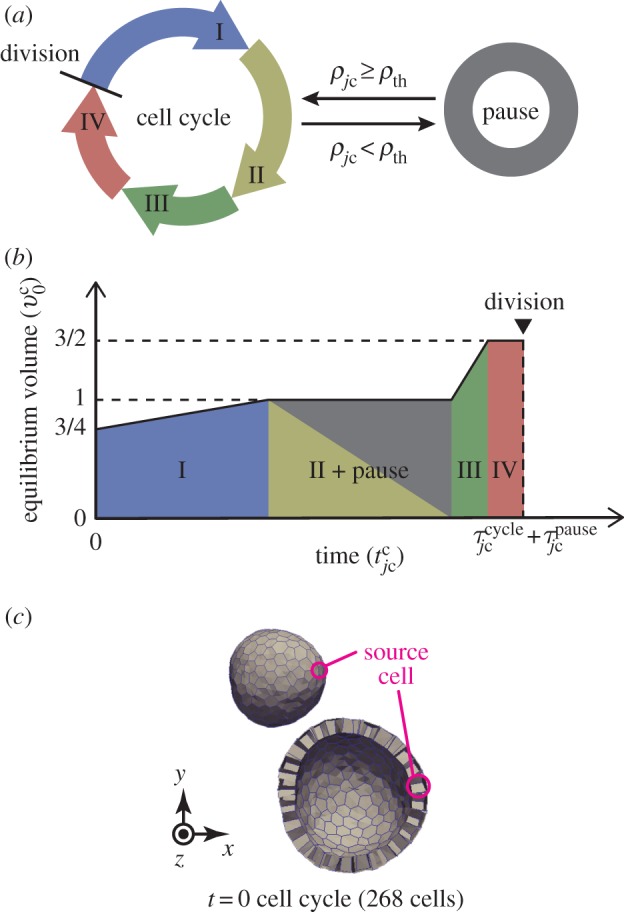
Cell growth behaviour and initial structure. (a) Illustration of the cell cycle. A divided cell grows from state I to IV successively. The cell growth pauses when its molecular density is less than the threshold ρ_th. (b) Increase in cell volume according to cell states. (c) Whole and clip views of an epithelial vesicle under initial conditions. The monolayer tissue involves a single source cell that produces growth molecules. In (c), the clip view of tissues is shown 1.5 times as large as the whole view. (Online version in colour.)

To express the shift of the cell states in the model, we define the cell time for each cell during the cell cycle, represented by 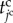. By representing the total time period within the cell cycle and the pause state by 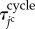and 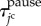, respectively, the j^c cell time 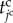passes from 0 to 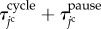. The total time period of cell cycle 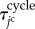is randomly determined to satisfy

3.6

3.7

where indicates the statistical average. The constants 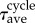and 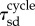indicate the average and the standard deviation of the growth times, respectively. Here, the time ratios of states I, II, III and IV within 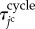were denoted by ψ^I, ψ^II, ψ^III and ψ^IV ( ≥ 0, ψ^I + ψ^II + ψ^III + ψ^IV = 1), respectively. The total time in which the j^c cell arrested in the state pause, 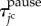, can be expressed by

3.8

where indicates the floor function.

In one cell cycle, individual cells double their volumes while the rate of growth varies depending on the four phases during cell cycle [22]. Hence, the cell volume growth is expressed by increasing the cell equilibrium volume from 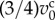to 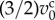with two growth periods according to cell states, as shown in figure 2b. The growth rate of the j^cth cell volume, represented by 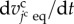, is defined as

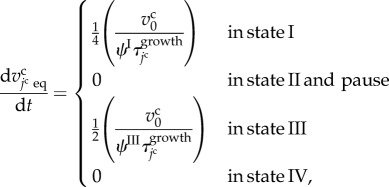3.9

where 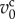is a characteristic cell volume. This function is similar to that in previous studies [19,23].

When the equilibrium volume of the j^cth cell 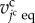exceeds , the j^cth cell is divided into two daughter cells. Cell division is expressed using a cell proliferation model [19] in which cell division is represented by dividing a single polyhedron at a plane. The direction of the dividing plane is fixed to be normal to the cell surface neighbouring the inside yolk and is also fixed to be locally oriented and normal to the longest axis of the cell shape. Details of the manner of cell division are similar to those of the local regulation used in our previous studies [19,23]. The source cell also divides into two cells, one of which is randomly selected as a new source cell.

Effective energy U in equation (2.1) depends not only on the positions of the vertices but also on time due to equation (3.9). Hence, the time derivative of U can be written as

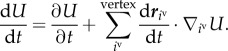3.10

Substituting equations (2.1) and (3.9) into the right-hand side of equation (3.10), the time derivative of U can be rewritten by

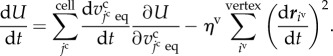3.11

In the right-hand side of equation (3.11), the first term takes an arbitrary value in the real number with respect to time and represents the effective energy change with time due to cell volume growth as an active cell behaviour. The second term takes only non-positive values and represents the effective energy decrease due to cell deformations as a passive cell behaviour.

3.1.3. Intercellular molecular behaviours

Cell growth is assumed to be regulated by the density of the growth molecules. By using equation (2.3), the transport of the growth molecules, whose density is represented by 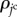, is described as

3.12

3.13

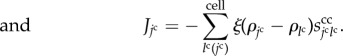3.14

In equation (3.13), the constants k^src and k^deg are the generation and degradation rates of the growth molecules. In equation (3.14), the constant ξ is a molecular transfer coefficient of the growth molecules between cells.

3.1.4. Initial condition

The morphology of epithelium under the initial conditions is simply expressed as a spherical vesicle enclosed by a monolayer cell sheet, as shown in figure 2c. The epithelial vesicle comprises 268 proliferative cells involving a single source cell. Under the initial conditions, molecular densities are set to zero within all cells. Individual cell times, 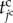, are randomly set to satisfy a uniform distribution, and individual cell volumes, 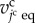, are set according to these individual cell times.

3.1.5. Parameter setting

To solve equation (2.1), parameters were normalized to unit length 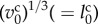, unit energy 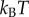, unit time 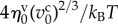(=τ) and unit molecular density 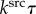. All physical parameters are shown in table 1.

Table 1.

Physical parameters.

symbol	value	description
ηv	1.0	friction coefficient of vertices
kcv	20.0	cell volume elasticity
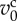	1.0	characteristic cell volume
kcs	2.56	cell surface elasticity
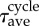	400	statistical average of cell cycle
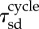	40	standard deviation of cell cycle
ψI	0.6	time ratio of state I
ψII	0.2	time ratio of state II
ψIII	0.1	time ratio of state III
ψIV	0.1	time ratio of state IV
ρth	0.368	threshold of molecular density for cell growth
ξ	0.1–10.0	transfer coefficient of growth molecules
ksrc	1.0	production rate of growth molecules
kdeg	0.002–0.24	degradation rate of growth molecules

To compare simulation results with experimental data, physical parameters in the model can be dimensioned by choosing the specified cells as follows. Assuming that cells are spherical, their volume and diameter are related by

3.15

where 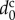is the diameter of spherical cells. Using parameter 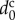, the unit of length, 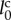, can be rewritten as

3.16

For instance, the diameter of the endothelial cells varies between 8 and 12 μm [24]. In this case, the unit value of length 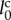is estimated to be 6–10 μm. Moreover, by supposing that the average cell cycle is 24 h, the unit value of time τ is estimated to be 3.6 min.

3.2. Numerical implementation

The simulation procedure is shown in figure 3. Time integrations of equations (2.1) and (3.9) were numerically performed using the Euler method with a time step of 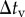. Time integration of equation (2.3) was numerically performed using the Euler method with a time step of 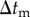. According to the reversible network reconnection model [18], local network patterns were reconnected when each edge included in the local pattern became shorter than a threshold value, 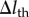. Trials for applying the reconnection rule were conducted for each edge and trigonal face for each time interval of 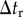. Numerical parameters are shown in table 2.

Figure 3.

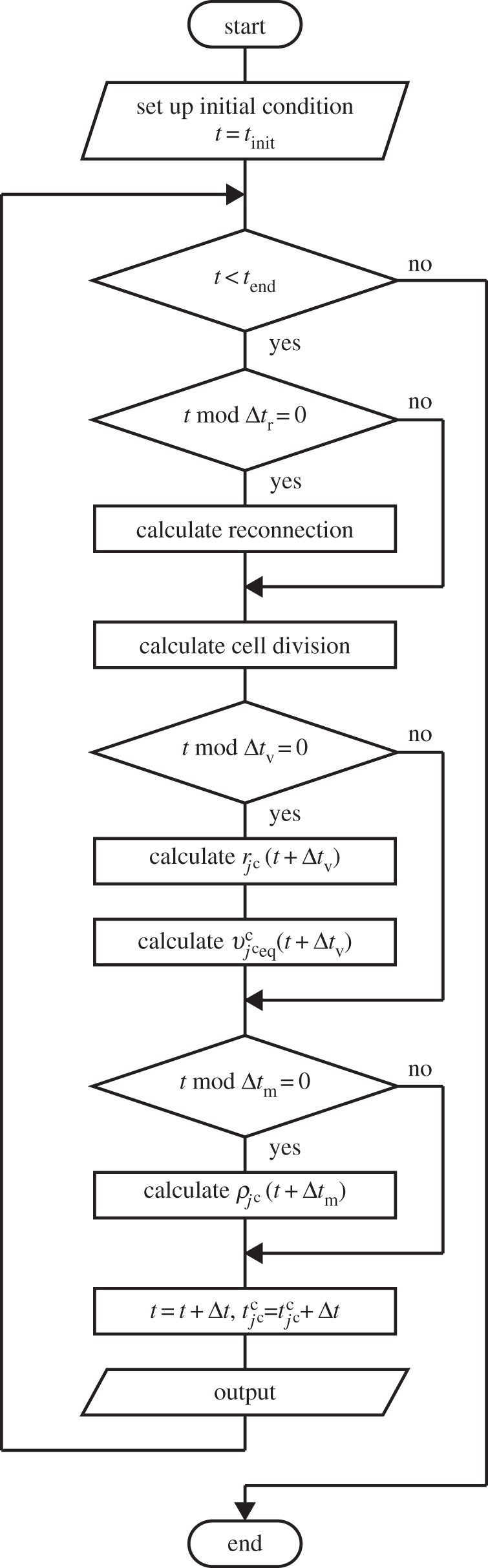
Outline of simulation procedure. The integration of time t was numerically performed with the time step of Δt from the initial t_start to the end t_end. Time step Δt is the greatest value, by which 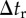, 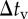and 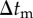can be divided into integers.

Table 2.

Numerical parameters.

symbol	value	description
Δtv	1.0 × 10−3	integration time step of vertex movements
Δtm	1.0 × 10−4	integration time step of molecular density
Δtr	2.0 × 10−3	time interval of network reconnections
Δlth	5.0 × 10−3	threshold length of network reconnections

3.3. Dependence of tissue morphogenesis on molecular diffusivity

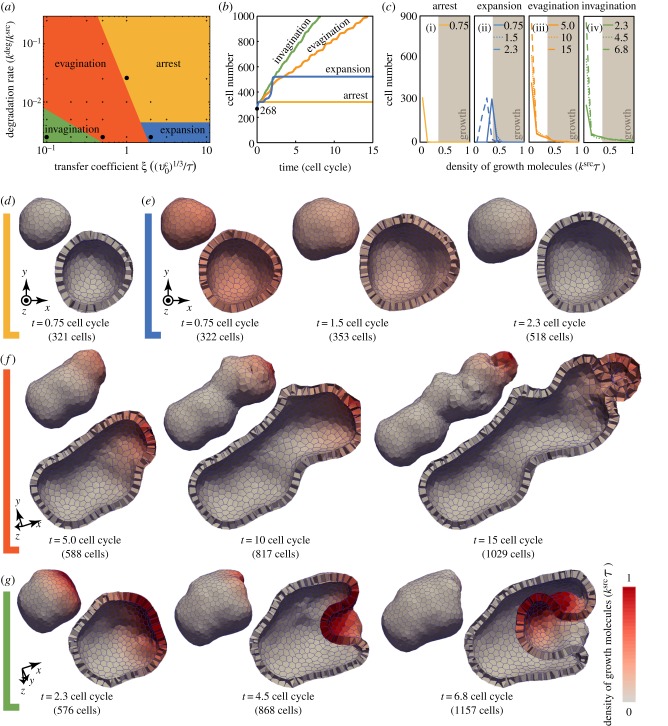
To analyse the effects of molecular diffusivity on multicellular patterning and deformations, we varied the transfer coefficient ξ and the degradation rate k^deg. For the employed parameter range, we found the epithelial morphogenesis which drastically differed depending on these parameters, as shown in the phase diagram presented in figure 4a. Within the employed time range of 15 cell cycles, the epithelial morphogenesis can be categorized into four phases: arrest, expansion, evagination and invagination. The criteria for categorizing the epithelial morphogenesis are as below.

• Arrest: All cells shifted their states to pause before one cell cycle.

• Expansion: A fraction of the cells grew for more than one cell cycle, and then all cells shifted their states to pause.

• Evagination: A fraction of the cells continues growing; the tissue grew while maintaining the convex geometry macroscopically around the growth area.

• Invagination: A fraction of the cells continues growing; the tissue grew while producing the concave geometry macroscopically around the growth area.

Figure 4.

Computational simulations of signal-dependent epithelial growth. (a) Phase diagram of the tissue morphogenesis. Morphogenesis is categorized into four phases: arrest (yellow), expansion (blue), evagination (orange) and invagination (green). (b) The number of cells composing a tissue as a function of time. Plotted colours indicate the four phases of morphogenesis marked by points in the phase diagram shown in (a): arrest (yellow), expansion (blue), evagination (orange) and invagination (green). (c) Histograms of molecular density for the four phases. Cells are sorted by their molecular densities with respect to the range of 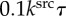. Brown areas indicate those of cell growth, where the density of growth molecules is higher than the threshold ρ_th. Individual lines in each histogram correspond to time steps shown in (d–g), respectively. (d–g) Time series images of the growing epithelial vesicles in the four phases, respectively. Colours indicate the density of the growth molecules within individual cells. In (d–g), the clip view of tissues is shown 1.5 times as large as the whole view. The deformation processes in the phases of expansion, evagination and invagination are also shown in the electronic supplementary material, movies 1, 2 and 3, respectively. (Online version in colour.)

Depending on the phase, the dynamics of the cell numbers and molecular distributions varied, as shown in figure 4b,c, respectively. In the arrest phase, the molecular densities within all cells were maintained lower than the threshold ρ_th, as shown in figure 4c(i). Hence, cell growth was continuously arrested, as shown in figure 4d. In the expansion phase, the growth area initially gradually increased with time, and, after expanding into the entire tissue, the number of growth molecules decreased throughout, as shown in figure 4c(ii). Hence, the tissue temporally expanded; the expansion was then followed by arrest, as shown in figure 4e. Here, because tissue deformations were relatively small, the tissue grew while maintaining the convex geometry macroscopically. In the evagination phase, the growth area is stably confined within the narrow area, as shown in figure 4c(iii), where the tissue continuously elongated along the narrow area, as shown in figure 4f. In the invagination phase, the growth area is also confined within a certain area, as shown in figure 4c(iv); however, the tissue elongated at first, as seen in evagination, and then suddenly invaginated, as shown in figure 4g. As shown in figure 4c(iii,iv), the growth area in invagination is larger than that in evagination. This difference in growth areas corresponds to the number of growing cells. Therefore, the diffusivity of growth molecules leads to various tissue patterns and deformations.

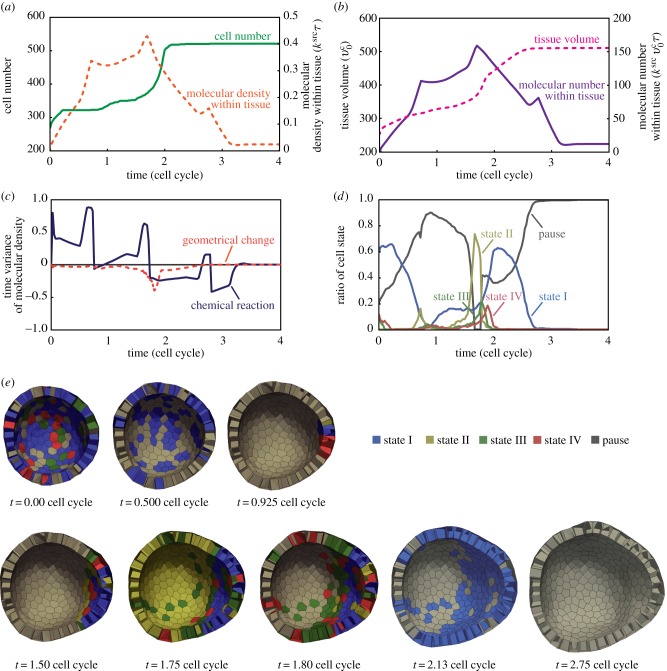
3.4. Bidirectional interaction between multicellular deformation and patterning

In the expansion phase (figure 4e), we particularly observed the bidirectional interaction between multicellular deformations and patterning. The tissue expansion was directly induced by the temporal increase in the number of cells around t = 2, as shown in figure 5a. During the expansion phase, 0 ≤ t ≤ 3, the molecular density throughout the entire tissue was temporarily increased and then decreased. The total amount of the growth molecules within the tissue also increased and decreased, as shown in figure 5b. As there was a temporal increase in growth molecules, the tissue volume increased around t = 2. Remarkably, around t = 1.6, the timing of the increase in tissue volume corresponds to the decrease in the growth molecules. These results implied the possibility that the increase in the tissue volume diluted the growth molecules in order to affect the biochemical patterning. Therefore, tissue expansion could be caused by bidirectional interaction between multicellular deformations and patterning.

Figure 5.

Molecular and cellular dynamics during tissue expansion. The tissue that is under the condition marked by the point within the blue area is shown in the phase diagram of figure 4a. (a) The number of cells (solid line) and the density of growth molecules (dotted line) as a function of time. (b) The total amount of growth molecules (solid line) and the total volume of tissue (dotted line) as a function of time. (c) Contributions of degradation (solid line) and dilution (dotted line) to molecular density as a function of time. These contributions are estimated by equation (3.17) using data in (a) and (b). (d) Ratios of cell states as a function of time. Cell states I, II, III, IV and pause are shown by blue, yellow, green, red and grey lines, respectively. (e) Time-series images of the growing epithelial vesicle in the expansion phase. Cells are coloured according to cell state: I (blue), II (yellow), III (green), IV (red) and pause (grey). The process of the cell cycle is also shown in the electronic supplementary material, movie 4. (Online version in colour.)

Notably, the density and number of the growth molecules have three peaks within the time interval of a cell cycle (figure 5a,b). This corresponds to the divisions of the source cell. Hence, tissue patterning was affected by the dynamics of the source cell.

Moreover, to clarify the bidirectional interaction, we estimated the contributions of the geometrical change and chemical reactions to molecular density. Supposing the molecular density within the whole tissue, ρ^t, is a function of the total amount of molecules, m^t, and volume, v^t, the time variance of ρ^t can be written as

3.17

The first and second terms on the right-hand side of equation (3.17) indicate contributions of the chemical reactions and the geometrical change, respectively. Here, the chemical reactions involve the effects of both molecular production and degradation, and the geometrical change indicates the changes in the entire tissue volume. Based on data shown in figure 5a,b, we estimated these contributions to ρ^t, as shown in figure 5c. Until t = 1.8, the chemical reactions mostly contributed to the increase in ρ^t and gradually contributed to the decrease in ρ^t. By contrast, the geometrical change always contributed to the decrease in ρ^t, namely the dilution of the molecules. The dilution effect temporally strengthened around t = 1.8, depending on the temporal increase in the tissue volume. Note that the dilution effect is temporarily larger than that of the degradation around t = 1.8. These results suggested that tissue expansion was certainly caused by the bidirectional interaction between multicellular deformations and patterning.

Furthermore, according to molecular and cellular dynamics, the cell states dynamically shifted, as shown in figure 5d,e. During 0 ≤ t ≤ 0.925, most cells shifted their states from state I to pausing. During the interval 0.925 ≤ t ≤ 1.8, all pausing cells gradually shifted their states to II, III and IV. In particular, the shifting of cell states to III led to a radical increase in the growth rate of the tissue volume, as shown in figure 4b; this also promotes the dilution effect, as shown in figure 4c. Around t = 2.125, most cells occupied states I, II and pause. During 2.125 ≤ t ≤ 2.75, all cells shifted their states to pausing owing to degradation. The increase in the number of the pausing cells led to the decrease in the growth rate of the tissue volume in figure 4b. These results demonstrate that tissue morphogenesis is driven by the coupling of multicellular deformations and patterning through signal-dependent cell activities.

4. Discussion

4.1. Continuous or transient growth of tissue

Computational simulations using the proposed model demonstrated signal-dependent epithelial morphogenesis in 3D space (§3). At the beginning of the tissue growth, all cells started to grow according to the cell's state under the initial conditions. In the phases of arrest and expansion (figure 4d,e), where the transfer coefficients are relatively high (figure 4a), the peak of the molecular distribution can be low within the entire tissue. The low value of the peak density makes the tissue growth transient. By contrast, in the phases of invagination and evagination (figure 4f,g), where the transfer coefficients are low, the peak of the molecular distribution can be high. The high value of the peak density causes the tissue to continue growing. Therefore, the continuity of the tissue growth depends on the peak density of the growth molecules.

4.2. Evagination or invagination

Local growth can produce either an invagination or evagination partly owing to the inclusion of the resistance by the viscous force in equation (2.1). This is because the viscous force in equation (2.1) increases linearly with the vertex velocity. As the tissues with such resistance are not explicitly included in the model, this resistance appears to be an artefact of the vertex model. In this study, because the growing tissue maintains the structure of a monolayer sheet, most of the vertices compose the surface boundary of the growing tissue. Hence, assuming that the growing tissue is embedded in external tissues with a much higher viscosity, the viscous force in equation (2.1) can be a resistance to tissue deformations as well as the viscous forces from the external tissues [20]. In this assumption, the viscous force in equation (2.1) can be regarded as those from the external tissues such as the lumen and extracellular matrix (ECM). With these considerations, the growing tissue can be expected to show either invagination or evagination depending on the size and velocity of the growth area.

Here, as the degradation rate increases, the density becomes lower throughout the entire tissue. Hence, as the degradation rate increases, the tissue growth area becomes narrower. In addition, the wider area of the tissue growth leads to the formation of a planar sheet that exhibits lower stiffness than a convex sheet. Therefore, based on the resistance force, the width of the tissue growth area determines whether invagination or evagination occurs.

Notably, the cell elasticity described by equation (3.2) includes longitudinal elasticity, but not shear elasticity. This limitation may produce a quantitative difference in the phase diagram of figure 4a, but will not change the phase diagram qualitatively. This is because the shear elasticity of the cells provides resistance to the viscous forces exerted from the surroundings during expansion. Examination of the quantitative effects of the cell mechanical properties with longitudinal and shear elasticity on multicellular deformations is challenging and will be addressed in future studies.

4.3. Mechanochemical coupling in tissue expansion

In the expansion phase, the degradation rate is lower than that in the arrest phase (see figure 4a). Hence, the peak of the molecular distribution was higher, and the tissue growth ceased later. In figure 4e, the widely diffused growth molecules increased the entire tissue volume. This increase in the tissue volume diluted the growth molecules to support the autonomous suppression of tissue growth (figure 5a–c). When this dilution effect is sufficiently strong to overcome the concentration of the growth molecules, all cells shift their states to pause to arrest the tissue after temporal growth (figure 5d,e). Otherwise, several cells around the source cell continue to grow (figure 4f,g). Hence, by balancing dilution with concentration, molecular signalling regulates the phase transition of the tissue morphogenesis.

During the cell growth expressed by equation (3.9), cell volumes mainly increase in state III, and the cell pausing occurs before entering state III. The time gap between the volume growth and pausing caused the large increase in the tissue volume around t = 2 in figure 5b. Hence, the time variation of the cell growth rate in equation (3.9) during the cell cycle is important for driving the tissue expansion. These results suggested that the tissue expansion resulted from the mechanochemical coupling, i.e. the bidirectional effect between the multicellular deformations and patterning. Thus, the proposed model successfully explains multicellular deformations dynamically coupled with biochemical patterning.

4.4. Applicability to mechanochemical coupling in various multicellular dynamics

To approach mechanochemical coupling in multicellular morphogenesis, we expressed intercellular molecular signalling on the 3D vertex model framework in this study. In this model, by defining a molecular density at each cell, molecular transport between the neighbouring cells is described (§2). This definition corresponds to that of the direct transport between neighbouring cells in the epithelium [25]. Moreover, the definition in the proposed model can be regarded as approximately describing transport through the cell–cell boundary width. If the approximation is insufficient, the proposed model can be modified by defining a molecular density for each cell–cell boundary face. Signalling molecules also diffuse through the outside of epithelium such as the lumen and ECM, where molecules could diffuse like those in fluids with flows [25]. Combining the proposed model with the immersed boundary method is one idea for obtaining molecular transport both within and outside the epithelium [26]. Therefore, the proposed model has a large potential for expressing various transport scenarios of diffusible signalling molecules among cells.

Moreover, from a spatial viewpoint, the proposed model enables the description of molecular transport at the single-cell level. The analyses at the single-cell level reproduced the molecular distributions depending on the cell shapes and configurations. Hence, the proposed model has an advantage over the continuum models while analysing molecular transport depending on the multicellular geometry. At the single-cell level, the gradient of the signalling molecules could be inhomogeneous due to the signalling noise, which could be interesting from the perspective of robustness [3,27]. The proposed model can also be applicable for analysing the effects of signalling noise on 3D tissue morphogenesis. Conversely, the applicable area of the proposed model is limited to the single-cell level. To investigate intracellular dynamics coupled with multicellular interactions, combining the proposed model with more refined models might be required. Thus, the proposed model is advantageous for expressing various biochemical signalling at the single-cell level.

To simulate signal-dependent epithelial growth, cell growth was expressed relative to cell activities. In embryogenesis, various cell activities play a role in coupling the multicellular deformations and patterning. For example, calcium transients drive tissue deformations by triggering cell constrictions [28,29]. The calcium-dependent constriction can be expressed by the tensile force along the cell circumference depending on calcium density. Therefore, by designing the energy function, the proposed model enables analysis of the mechanical effects of various cell activities coupled with the molecular signalling.

In this study, molecular behaviours were expressed simply as a diffusion process from the source to the sink. The proposed framework is also applicable for expressing the various biochemical patterns such as the reaction–diffusion system [30]. To examine the mechanisms of chemical patterning, several patterns, such as the arrangements of spots and stripes, have been numerically produced by the reaction–diffusion dynamics on a steady, plain tissue [31]. These pioneering studies have succeeded in explaining the spatio-temporal variety of biological patterning in 2D space [32]. Despite the difficulty in observing the diffusions of small molecules in vivo, the reaction–diffusion system could have an enormous impact in understanding embryonic morphogenesis. Moreover, a recent study using a continuum model has emphasized the importance of biochemical patterning coupled with tissue deformations in 3D space [33]. Hence, the next challenge is to deepen our understanding of the mechanochemical coupling at the single-cell level during large tissue deformations. The proposed model enables the implementation of the reaction–diffusion system using 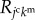in equation (2.3), and may be applicable to realistic systems with more complex cascades among multiple cells. Therefore, the proposed model has the potential to provide remarkable predictions of undiscovered phenomena, which could guide future experimental approaches.

5. Conclusion

This study proposed a novel framework of a 3D vertex model for describing intercellular molecular signalling dynamically coupled with multicellular deformations. Using the proposed model, we demonstrated the computational simulations of signal-dependent epithelial growth. The bidirectional effects of multicellular deformations and patterning led to the production of several spatio-temporal behaviours of 3D morphogenesis, namely arrest, expansion, evagination and invagination. Thus, the proposed model enables the simulation of 3D multicellular morphogenesis coupled with various molecular signalling processes among cells. Therefore, we anticipate our proposed model to be a useful tool for integrating the biochemical and mechanical underpinnings in multicellular morphogenesis. Computational exploration would suggest the elucidation of as yet undiscovered phenomena emerging from the mechanochemical coupling in multicellular morphogenesis.

Authors' contributions

S.O. developed the proposed model, participated in the design of this study and drafted the manuscript; Y.I. conceived the study, participated in its design and helped draft the manuscript; T.W. performed computational simulations and data analysis; T.A. participated in the design and coordination of the study and helped draft the manuscript. All authors discussed the results, contributed to their interpretation, and read and approved the final manuscript.

Funding statement

Part of this study was supported by Platform for Dynamic Approaches to Living System from the Ministry of Education, Culture, Sports, Science and Technology, Japan. S.O. was supported by JSPS KAKENHI (grant no. 25889070). Y.I. was supported by MEXT KAKENHI (grant no. 25127707).

Competing interests

The authors declare no competing interests.