Rate of language evolution is affected by population size

Significance

Evolutionary methods are increasingly being applied to investigating linguistic change. But does language change conform to the predictions of evolutionary theory? Here, we use data from closely related pairs of languages to show that a key prediction of evolutionary theory is met: rates of gain of new words are higher in larger populations whereas rates of word loss are greater in small populations. Our analysis provides, to our knowledge, the first statistically robust evidence of an influence of population size on rate of language change. These results demonstrate the potential for demographic factors to influence language evolution.

Abstract

The effect of population size on patterns and rates of language evolution is controversial. Do languages with larger speaker populations change faster due to a greater capacity for innovation, or do smaller populations change faster due to more efficient diffusion of innovations? Do smaller populations suffer greater loss of language elements through founder effects or drift, or do languages with more speakers lose features due to a process of simplification? Revealing the influence of population size on the tempo and mode of language evolution not only will clarify underlying mechanisms of language change but also has practical implications for the way that language data are used to reconstruct the history of human cultures. Here, we provide, to our knowledge, the first empirical, statistically robust test of the influence of population size on rates of language evolution, controlling for the evolutionary history of the populations and formally comparing the fit of different models of language evolution. We compare rates of gain and loss of cognate words for basic vocabulary in Polynesian languages, an ideal test case with a well-defined history. We demonstrate that larger populations have higher rates of gain of new words whereas smaller populations have higher rates of word loss. These results show that demographic factors can influence rates of language evolution and that rates of gain and loss are affected differently. These findings are strikingly consistent with general predictions of evolutionary models.

Population size can play a crucial role in the evolution of languages and cultures (1). However, opinions differ on both the possible mechanisms and the expected patterns (2–7). It has been suggested that larger populations will generate more innovations and are less prone to random loss of cultural elements (8–10), but may have less efficient diffusion of innovations than smaller populations (4). Alternatively, languages spoken by small isolated populations of speakers may have lower rates of loss if they maintain tighter cultural norms that improve transmission and resist change (11). Rates of change might be accelerated by founder effects when a new population is started from a small number of colonists, which could result in loss of elements from the ancestral language (11–13). Population size might also influence language complexity if small populations can develop greater linguistic complexity (11), whereas large, widespread languages that are often learned by adults may become simplified (14). Conversely, it has been suggested that the average rate of word turnover is essentially the same in all languages (15–17), or that it is determined primarily by other factors such as language contact (6, 18).

Uncovering systematic patterns of rates of language change may reveal underlying mechanisms of language evolution (13, 19). In particular, investigating rates of language change can demonstrate whether language evolution follows the predictions of population genetic models (20). Systematic variation in the rates of language change may affect attempts to reconstruct the history of human cultures from comparative language data, particularly the estimation of time (21). Theoretical modeling has been used to explore the consequences of population size on rates of language evolution; however, such models unavoidably require prior assumptions about the way language change diffuses through populations (4, 6). Tests of population size effects have so far been equivocal and have been limited by the availability of appropriate data and methodology (3, 7, 22). In particular, similarities and differences across languages cannot be compared as if they were statistically independent data points, because closely related languages are expected to be similar in many aspects. This hierarchical pattern of similarities can confound attempts to find causal correlations between aspects of human language and culture by creating spurious correlations, a methodological challenge sometimes referred to as Galton’s problem (23, 24). The comparison of rates of evolutionary change in different lineages presents additional challenges because we need to be able to infer the number of evolutionary changes that have occurred along each lineage (25, 26). Because rates are based on count data, the accuracy of rate estimates will depend not only on the amount of data compared between the languages but also on the time since their divergence (26). It is important to test these hypotheses against observations from real languages within a statistically robust framework that controls for the effect of phylogeny on covariation and explicitly deals with the effect of time of divergence on rate estimation.

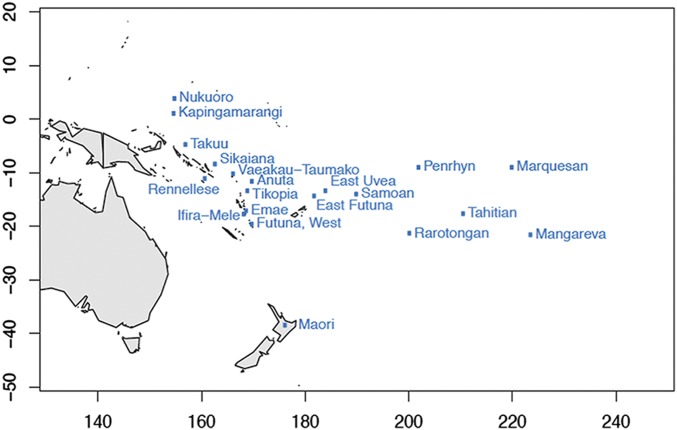
The Polynesian languages provide an excellent test case for examining the effects of population size on rates of language evolution (Fig. 1). They form a distinct lineage within the Austronesian language family, one of the largest language groups in the world, and are well-documented in comparative language databases (27, 28). They arise from a relatively recent history of colonization (29, 30), and the relationships between languages have been extensively investigated (31). Polynesian languages have well-defined areas of occupation, and establishment dates for most language groups can be derived from archaeological data (32). By comparing rates in recently established sister languages occupying similar habitats, we avoid potential confounding social and environmental variables. Due to this combination of factors, there is no better “natural experiment” to test the effect of population size on rates of language evolution. Although the Polynesian languages form only a small subset of the Austronesian language family, there are no other language groups that would allow us to control for age, area, and relationships to the extent we can with the recent Polynesian radiation.

Fig. 1.

Map of Polynesian languages included in this study.

To control for statistical nonindependence due to shared history, we based our analyses on phylogenetically independent sister pairs—that is, we considered differences between pairs of languages that are likely to be each other’s closest relatives (31, 33, 34). This approach allowed us to compare changes that have happened in each language since they split from their common ancestral language. Barring borrowing, the changes in cognate sets we counted in each language of the pair occurred independently of changes occurring in any other language in the dataset and so represent statistically independent instances of word gain and loss. However, we formally tested the phylogenetic signal in the data and also analyzed the data without the assumption of phylogenetic structure.

The sister-pairs approach is more appropriate to these data than attempting to estimate rates of change on all edges of a phylogeny. A “whole phylogeny” approach would require branch lengths that are proportional to time. Although we have good archaeological dates for the establishment of most of the populations in our study, we could not extrapolate these dates to the internal divergences in the phylogeny without making prior assumptions about the rates of language change over time (29). Similarly we have carefully selected sister pairs with known relationships, whereas a whole-tree approach would require us to make assumptions about the more distant relationships between the ancestral lineages that gave rise to these contemporary populations. We have selected only pairs of languages where the relationships are well established and there is no evidence of replacement or blending of populations, avoiding populations with complicated settlement histories. Thus, the sister-pairs approach represents a conservative approach to the data that minimizes the assumptions that we must make about the history of the languages and the mechanisms of population and language change.

Our analysis measured one specific aspect of language change, the gain and loss of cognate (homologous) words of basic vocabulary (27). We compared rates of word gain and loss in pairs of closely related languages, with estimates of current population sizes as well as historical population sizes estimated at the time of European contact. The age of each language was derived from archaeological data, and area inhabited by summing the land area of all islands on which the language is traditionally spoken. We estimated the relative number of word gains and losses in each language of each pair by comparing the presence or absence of cognate terms (words related by descent from a common ancestral form) in 210 semantic units in basic vocabulary, such as kinship terms, body parts, and numbers (27). By using cognate terms for basic vocabulary items, we could compare terms that were homologous across languages and had retained a common meaning. Restricting our analysis to basic vocabulary items helped to limit the problem of semantic shift, where cognate terms take on new meanings in some descendant languages. Basic vocabulary is considered to be relatively resistant to borrowing (35). It also helped ensure that we had comparable data for each of our language pairs: each of the languages had nearly all of the basic vocabulary items recorded but had varying amounts of general lexicon available in other databases (28). Furthermore, because rate of word change has been linked to frequency of use (19), comparing the same set of semantic units across all languages in the study helped prevent bias in rates due to word selection.

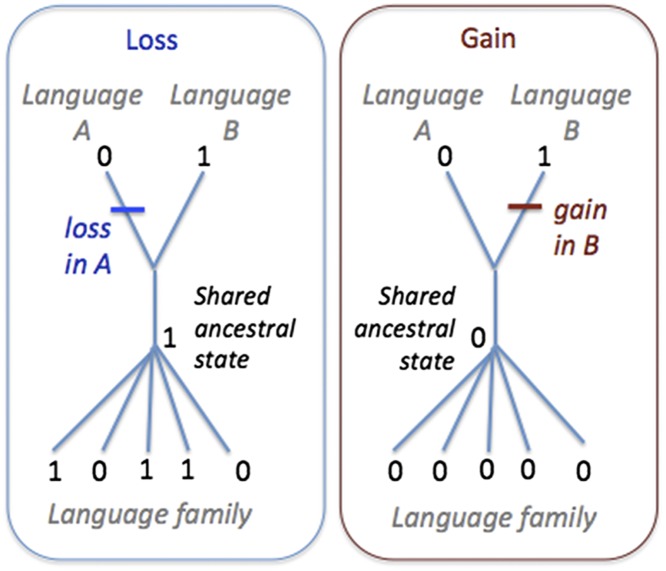
For each language, we counted as a gain any word that had no identified cognates in any other language in the database, representing adoption of a new word for one of the basic vocabulary items. Any cognate set present in one language of the pair but not the other, and which was recognized in at least one other language in the family, was considered to have been present in the common ancestor of the pair then lost in one language (Fig. 2). Gain and loss rates were estimated separately because the addition of a new word does not necessarily involve the loss of an existing word because languages can have multiple lexemes (word items) per semantic unit (basic vocabulary category). We did not include borrowed words or language pairs known to have a high rate of borrowing.

Fig. 2.

Coding scheme for counting word gains and losses in a pair of sister languages, A and B. The presence (signified by a 1) of a cognate in one member of the pair and any members of the language family indicates the presence of that cognate in the shared ancestor of the pair. Absence (signified by a 0) of that cognate in the other member of the pair is evidence that it has been lost from that language since it split from the other language. Any word (lexeme) present in one language but with no cognates in any other language in the family is considered to have been gained in that semantic category in that language since it split from the other member of the pair and so is counted as a word gain in that language.

We used Poisson regression to test the effect of population size on the rate of gain, loss, and total change (see SI Appendix for details). We modeled rates as linear functions of population size on log–log scales to confine rates to positive values (where all logs are natural logs, or log_e). Numbers of cognate gains and losses were standardized by the total number of semantic units compared in each pair of languages. We applied the Akaike information criterion with correction for small sample size (AICc) to test the fit of alternative models of language evolution to the observed data. The models varied in (i) whether the data were phylogenetically structured or not, (ii) whether new populations rapidly achieved a stable population size upon colonizing a new area, or underwent a more protracted period of growth, (iii) whether new languages formed by an allopatric process, where a parent population underwent fission to produce two daughter populations, or by a peripatric process, where the parent population gave rise to a daughter population by a process of colonization, and (iv) whether or not new languages experienced a founder effect, losing a number of words when a new population became established (Methods). We estimated the power of Poisson regression to detect the effect of population size on the rate of gain, loss, and total change, at the significance level of 0.05 (36).

Results

Our analyses revealed two significant patterns in the data: languages that had larger speaker populations tended to have higher rates of gain of new words in basic vocabulary than their smaller sister languages, and smaller populations tended to have higher rates of word loss from basic vocabulary (Table 1 and Fig. 3). Variation in population size explained about 10–20% of the variation in word gains and losses (Table 1). Because gain and loss showed opposing patterns, overall rates of change (gain plus loss) were not significantly related to population size (Table 1 and SI Appendix, Fig. S1).

Table 1.

Significance tests for the effect of population size on rate of word gain and loss

Rate	Mean	SE	Upper 95% CI	Lower 95% CI	R2	Power	Likelihood* ratio
Gain	0.29	0.064	0.435	0.145	0.144	0.68	22.8
Loss	−0.12	0.032	−0.048	−0.194	0.186	0.69	14.5
Total	−0.03	0.028	−0.092	0.033	0.010	0.08	1.2

^*Best-fitting model: phylogenetically structured analysis based on the colonization model using a pair-wise approach with 10 language pairs. Total is the sum of estimated gains and losses for each language. The mean, SE, and 95% confidence intervals (CIs) of regression coefficients, as well as R², power of the test, and likelihood ratio against a null model (where population size has no effect), are reported. The values in bold indicate a significant effect of population size on the rate of language change.

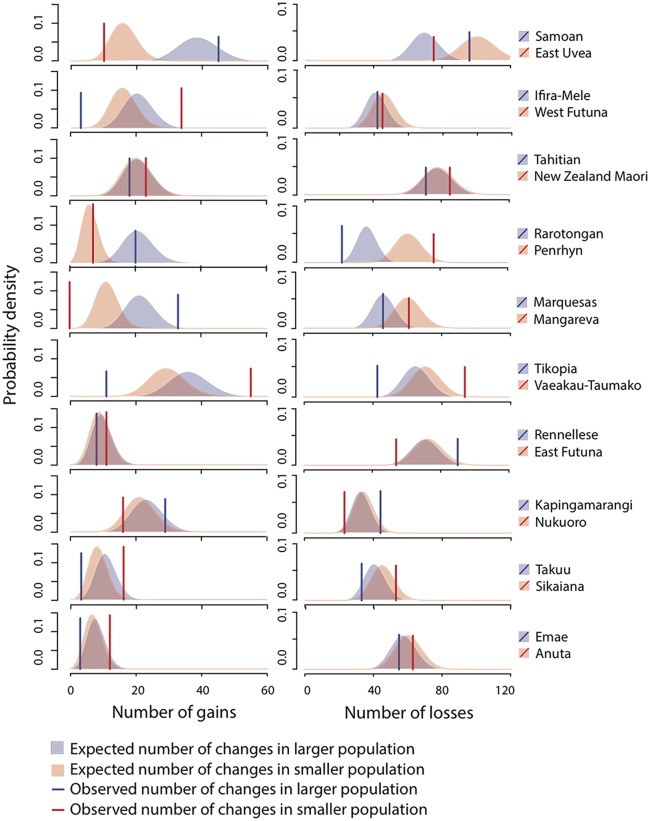
Fig. 3.

Histograms of observed and expected numbers of gains and losses of cognates from basic vocabulary in 10 language pairs under the best-fitting model (phylogenetically structured, constant population size, no founder effects). Plotted distributions show the expected probability of having a certain number of gains or losses for each language, given the model fitted to all data points. Vertical lines show the observed numbers of gains or losses in each language. The language with the larger speaker population size is colored blue whereas the language with smaller population size is colored red, and the panels are ordered from the pair with the oldest divergence at the top to the youngest at the bottom. More often than expected by chance, the smaller population has a higher rate of word loss and the larger population has a higher rate of gain, even though specific circumstances in particular languages may override this general trend.

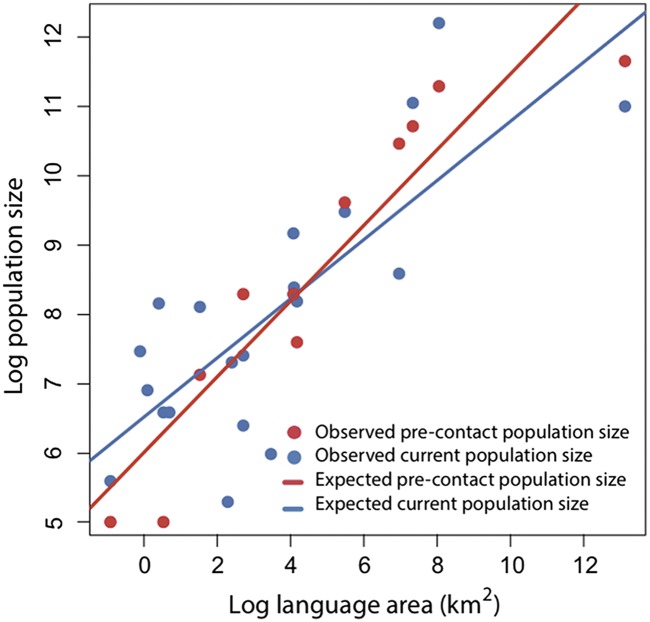
We found that both current and precontact population sizes were strongly predicted by area (Fig. 4). Accounting for phylogenetic structure provided a better fit to the data than a nonhierarchical model where each language group would be considered to be an independent data point (SI Appendix, Table S2). Allowing for a period of population growth does not provide a better fit to the data, nor does accounting for founder effects. Therefore, the results presented here are from the best-fitting model: the phylogenetically structured analysis assuming stable population size over time and no founder effect.

Fig. 4.

Relationship between log population size and log language area for the languages included in this study, where logs are the natural logs (ln, log_e), for both current population size and historical population time estimated at the time of European contact (pre-contact).

Our data suggest that the size of the speaker population of each language is determined primarily by the area available (SI Appendix, Table S3). Because we do not have all measures of population size for each language group, each analysis has different numbers of data points (for example, 11 populations have precontact population size and island size, thus 9 degrees of freedom, and 20 populations have present population size and island size, thus 18 degrees of freedom). Precontact population size is strongly correlated with language area (t₉ = 6.13, P = 1.7 × 10⁻⁴), suggesting that precontact populations were typically at a carrying capacity. Current population size is also strongly correlated with both precontact population size (t₉ = 4.84, P = 9.2 × 10⁻⁴) and island size (t₁₈ = 5.36, P = 4.3 × 10⁻⁵). The finding that population size is linked to area, together with the result that accounting for the period of population growth does not provide a better fit to the data, is consistent with evidence suggesting high rates of population growth in Polynesia, which in some cases led to the introduction of cultural mechanisms for curtailing population growth (37).

The pattern of higher rates of word gain in larger populations was confirmed when the Poisson regression analysis was repeated using only the pairs that had estimates of precontact population size (mean = 0.30, likelihood ratio = 53.3) and those that had data on current population size “in area,” not including speakers living in migrant populations on other islands (mean = 0.67, likelihood ratio = 30.2). However, these reduced datasets did not have a significantly higher rate of loss in smaller populations (precontact, mean = −0.00, likelihood ratio = 0.0; current, mean = −0.05, likelihood ratio = 3.0). Given the strong correlation between island size and population size, we also repeated the Poisson regression analysis using island size instead of current population size: these results confirmed higher rates of word gain in larger populations, but not higher rates of loss in smaller populations (SI Appendix, Table S3).

Discussion

We found that Polynesian languages with larger speaker-population sizes had higher rates of gain of new words than their smaller sister languages, consistently across all analyses. We also found that languages with a smaller number of speakers had higher rates of loss of lexemes from basic vocabulary items although this result was not always significant in the reduced datasets. Total rate of change (gain plus loss) was not significantly related to population size.

Our results have a number of important implications for the study of language evolution. Most importantly, we demonstrate that population size can influence the patterns and rates of language change. Our results do not support the hypothesis that smaller populations gain new words rapidly due to greater rate of uptake of innovation. Instead, our analyses suggest that rates of gain and loss of basic vocabulary items may, in some ways, conform to some general predictions of evolutionary models. Population genetic theory predicts that larger populations should have higher rates of adaptation because there are more individuals to generate novelty and fewer disruptive influences of random sampling on the process of fixation of new variants. The observation that rate of gain of new words is greater in larger populations is compatible with the establishment of new words by a process analogous to positive selection. An alternative explanation for this pattern is that smaller populations might have denser social networks that tend to be conservatizing, enforcing linguistic norms and resisting change (5, 11, 38).

Our finding that small populations have greater rates of word loss is compatible with the expectation from evolutionary theory that small populations are prone to loss of diversity due to the chance of incomplete sampling of variants each generation. Although lost words could be replaced by novel innovations, the lower rate of gain in smaller populations suggests that the loss of cognates in these languages is not due to higher rates of word turnover. Instead, the pattern of loss is compatible with stochastic fluctuation in frequency of lexeme use (akin to the process of genetic drift): in a small population, such fluctuations are more likely to go to zero, resulting in the loss of one lexeme for that unit of basic vocabulary (39).

These results suggest that languages with consistently small speaker populations undergo a greater rate of word loss from basic vocabulary. This process is distinct from the founder effect, which predicts loss of diversity associated with colonization events (11, 12). Although a small population of founders cannot carry all of the genetic alleles of a large parent population, it may be possible for a small number of speakers to use all of the basic vocabulary from the parent language (40). Despite the likely establishment of new Polynesian languages from relatively small colonizing populations, we do not find that a founder model describes our data better than one of gradual loss of words.

If the finding that rates of word gain are greatest in large populations is a general feature of language change, then it has implications for understanding the connection between rate of language change and the diversification of language families. Higher rate of language change has been reported in diverse language groups, based on word turnover rates (13). One possible explanation for this association is that change is highest when populations are divided. However, our results suggest that small subdivided populations may be more likely to undergo word loss than accelerated gain of new words. More work is needed to establish both the generality and causes of these patterns.

Methods

Comparisons.

Pairs of sister languages were chosen based on established relationships (31, 33, 41), ascertained using the linguistic comparative method, which uses patterns of language change, such as systematic sound correspondences, to identify language relationships (42). We did not include any comparisons between languages that are considered to have a high degree of borrowing and contact: for example, the languages of Tonga, Niue, and Pukapuka. Any undetected loan words in basic vocabulary will reduce the apparent rate of loss and gain because loan words will be counted as retentions, reducing the power of the tests to detect differences in rates. Borrowing could bias our results only if it is systematically affected by population size. For example, if smaller languages are more prone to borrowing than their larger sister languages, then we might detect fewer losses in smaller populations, if losses are replaced by reborrowing from the sister language. Borrowing should not affect the gain rate, which counts only words with no cognates recorded in any other language in the family. A plot of the number of identified loan words against population size for these languages provides no evidence that loan rate is influenced by population size (SI Appendix, Fig. S2).

Population Data.

We included several measures of population size. Contemporary population size for each language was taken from the Ethnologue (43), representing the number of speakers for each language group, estimated between 1993 and 2011 (SI Appendix, Table S1). We recorded both the total number of speakers reported in the Ethnologue and also the “in area” population of speakers found within the language area, excluding speakers in migrant communities established outside the area. We also included, where available, estimates of population size at the time of first contact with Europeans (32). These “precontact” estimates were included to represent the likely population size of each language group before changes in population size brought about by contact with Europeans (37). The languages included in our analysis ranged in population size from 200 to over 360,000 speakers.

We estimated the area of each language included in our analysis (Fig. 1) from the sum of the area of the islands on which the language was traditionally spoken (hereafter referred to as “language area”). Language area was derived primarily from published sources (32, 44), with additional information from the United Nations Environment Program (UNEP) “Island Directory” (islands.unep.ch). Distance between each pair was calculated using the “Distance Measurement Tool” function of Google Maps to estimate the shortest coast-to-coast distance. However, this distance was not found to have any explanatory power in preliminary data analyses and so was not included in final analyses.

To calculate absolute rates of change, we sought establishment dates for each language, based on archaeological evidence of settlement in each language area (30, 32, 45). Because we were concerned with the establishment of separate language groups, we took the conservative approach of taking the first evidence of permanent, continuous settlement, rather than the earliest evidence of human presence. For example, evidence of human presence on Kapingamarangi dates to 1,000 y B.P., but archaeologists suggest that the island was only sporadically occupied between 700 y B.P. and 300 y B.P., after which stabilization of the islet allowed permanent occupation (46). We therefore took 300 y B.P. as the establishment of the population of speakers of the Kapingamarangi language. We have included only language groups considered to have a continuous history in the current area, without replacement by other language groups. For this reason, we excluded languages with complicated settlement histories, such as Fiji and Rotuma.

Counting Word Gains and Losses.

For this study, we considered only word gain and loss, not other forms of language evolution such as phonological change, morpho-syntactic change, and semantic change (12, 14, 47). We used the Austronesian Basic Vocabulary Database (27), which records up to 210 basic semantic units for more than 1,100 languages spoken in the Pacific region. By using basic vocabulary, we ensured that cognate terms not only had a common history but a common meaning across language comparisons.

We considered each of the 210 identified basic vocabulary sets as semantic units. So, for example, one semantic unit is “one hundred,” which may be represented by different words in different languages (e.g., rau in Anuta, gau in Rennellese, vahiki in Vaeakau-Taumako). We used the term “cognate set” to represent a set of lexical units that are clearly related by descent and have been identified by linguists as being derived from a common ancestral word. A classic example is the word for “five,” for which many Polynesian languages share related terms, such as lima in Fijian, nima in Tongan, gima in Rennellese, ’ima in Marquesan, and rima in New Zealand Maori. In this case, the cognate set was those words that are recognizably descended from the ancestral word, reconstructed as the protoform *lima in the ancestral Proto-Malayo-Polynesian language (27). When we refer to a word in one language having a cognate in another language, we mean that both languages contain words from the same cognate set in the same semantic unit. We will refer to the particular version of the word found in each language as “lexemes.” A language might have more than one lexeme for a given semantic unit. For example, the Marquesan language has three alternative lexemes in the semantic unit “good” ('eka, meitaì, kanahau) whereas the Mangaraven language has two recorded lexemes for “good” (reka, meitetaki).

Our approach to estimating rates of language change differed from other studies of language evolution. The standard approach for investigating rates of change in historical linguistics is to calculate “retention rates” within defined lists of basic vocabulary (15). The retention rate—or the number of shared cognates—provides a useful indicator of the amount of change between a language and its ancestor (48). However, the retention rate does not distinguish between gains and losses and thus cannot allow comparison of these two processes. Another approach has been to quantify lexical distance between words using a Levenshtein distance metric to quantify how different two languages are (6). However, the Levenshtein distance does not distinguish between true homology—cognate words—and chance similarity (49). A third approach is to use computational phylogenetic methods to estimate the rate of change on the branches of a phylogeny (50, 51). Although the sister-pairs approach lets us constrain the date of origin of sister lineages, the “whole tree” approach would require us to solve dates, rates, and branch lengths simultaneously. Our approach overcame these limitations by identifying changes in homologous word sets, estimating separate rates of word gain and loss, and using independently established relationships between languages to correct for phylogenetic nonindependence. Our aim was not to establish the relationships between languages or their general levels of similarity. Instead, we considered the presence or absence of cognates on a pair-wise basis to localize the gain or loss of particular words to the history of each language.

Consider a pair of languages, A and B, that are each other’s closest relatives, such that they share a more recent common ancestor with each other than either does with any other member of the language family (Fig. 2). We want to be able to count the relative number of word gains and losses that have occurred in each language since they shared a common ancestral language. We consider that, if a lexeme present in either of these languages has a cognate in at least one other member of the language family, then it must have been retained from the ancestral language (assuming that two independent gains of the same cognate are unlikely and that borrowing has been eliminated from the database). If a cognate is present in language A but not in B, then we assume it has been retained in A but lost in B. Loan words have been removed from the database so we discount the possibility that the cognate was lost from the common ancestor and then regained in language A. Although the database may contain unidentified loan words, our analysis is based on items of basic vocabulary that are more resistant to being borrowed (52). Moreover, the most likely source of loan words is a language’s sister (2, 53), the effect of which would be to weaken the signal in our data rather than create false patterns. Simulation studies of borrowing suggest that any unidentified loan words would make the sister languages seem more similar than they actually are by masking innovations or losses (53).

If language A contains a lexeme in a semantic unit in the word list that has no identified cognates in language B or in any other language in the family, then it is considered to be a novel invention in language A after it split from language B. Although we cannot discount the possibility that it was gained in the common ancestor of the pair and then lost in B, this explanation is less parsimonious. Note that gain and loss in a given sematic unit may be either linked or unlinked: a new lexeme may be added without the loss of an existing lexeme, or it may replace an existing cognate with a new lexeme (in which case it will be counted as both a loss of one cognate and a gain of a novel word).

This approach provides two rates-informative patterns in the data: cognates present in one member of the pair and not the other (evidence of loss) and noncognate terms present in one language but not in any other language in the family (evidence of gain) (Fig. 2). This approach is somewhat similar to the Tajima test (54, 55) in that it considers patterns of shared characters in the data to compare the rate of change in each member of a pair of lineages with respect to an outgroup. We took a conservative approach to counting word changes, excluding any lexemes marked as possible borrowings or those that seemed to show cognacy with other lexemes in the same semantic unit even if not labeled as such in the database. Semantic units where one member of the pair had no recorded lexemes were recorded as “missing” and did not contribute to analysis of rates.

The number of lexemes compared varied between pairs because not all languages have the full set of 210 semantic units recorded in the Austronesian Basic Vocabulary Database (27) and languages differ in the number lexemes per semantic units. In all analyses, numbers of gains, losses, and total changes (gains plus losses) between languages in a pair were standardized by their total number of semantic units compared.

Statistical Analysis.

Because languages evolve through a process of descent with modification, we expect them to show phylogenetic signal, such that closely related languages will show similarities due to features inherited from their shared common ancestor (56). The process of descent leaves a pattern of hierarchical similarity in the data that creates statistical nonindependence in language features. Here, we accounted for phylogenetic signal by applying a pairwise approach by fitting different intercepts of language evolving rates for different pairs of languages. We refer to this approach as “pair-wise.”

However, it may be the case that the specific traits we are interested in—population size and rates of language change—do not always show hierarchical patterns of similarity. If we assume that all of the Polynesian populations included in this study have the same intrinsic population growth rate, then population size may be largely determined by the available area for each population (Fig. 4) rather than by heritable features of each cultural group. Similarly, because Polynesian languages are broadly similar in structure, the determinants of language change may be effectively independent of the state of the common ancestor and largely a function of the particular circumstances of each particular group. In this case, we might consider each language group to be an independent experiment in language evolution, triggered by the establishment of a new population on an uninhabited island. To allow for this possibility, we also analyzed by fitting a common intercept for all of the pairs. We refer to this approach as “tip-wise” because it considers each separate “tip” of the phylogeny as an independent data point.

Polynesia was largely peopled through relatively small numbers of colonists making ocean voyages and establishing new settlements on uninhabited islands (37, 57). Therefore, we expect that each language group was started by a relatively small founding population that then grew in size. However, it is not clear whether the small founder population would have a significant impact on the estimation of the overall average rate of language change (Discussion). To account for this uncertainty, we compared different models: the “constant” model assumes that the founding population rapidly grew to the carrying capacity of the area and then stabilized, and the “growth” model assumes a continuous density-dependent population growth, for which a common population growth rate and initial population size are fitted to all language pairs. Note that the constant model under the pair-wise approach does not require absolute date estimates

We considered two alternative models for the origination of a new language: “fission,” where an ancestral population splits to form two daughter populations, and “colonization,” where a small number of colonists from a parent population establish a single daughter population (SI Appendix, Fig. S3). Fission is analogous to allopatric speciation whereas colonization is analogous to peripatric speciation. Clearly, there is no clear line between fission and colonization because the difference between the two models lies in the relative change in population size from the parent population to the founder population. However, we made this distinction because the two models differed in the way we used establishment dates to estimate age of pairs. Under a fission model, we considered the older date of the two establishment dates to most closely approximate the age of the split between the two languages. However, it is likely to often be the case for this dataset that new languages are established through colonization (29, 30), and therefore the age of establishment of the parent population overestimates the date of the split between the parent and daughter populations. So under the colonization model we used the younger of the two dates to approximate the time since the two languages started accumulating differences from each other.

In addition to the gradual loss of words over time as a language evolves, there may be an initial loss of lexemes when a population is founded, if the founding population does not use all of the lexemes used in the parent language. To model this initial sampling effect on word loss, we implemented additional Poisson regressions under the founder scenario where words were lost due to sampling error. For the pair-wise approach, a single estimate of the absolute number of initial losses was fitted to all language pairs under the fission scenario, or to just the daughter population in the colonization scenario (because the parent population is assumed to undergo no founder effect at the time when its daughter population establishes). For the tip-wise approach, multiple estimates of the initial losses were fitted to each language, with each pair of languages sharing an estimate in the fission model. Details of the models of language and population change are given in SI Appendix.

We applied likelihood ratio tests with Bonferroni correction to each of the scenarios against their null models that assume no effect of population size on language-evolving rates. We applied the Akaike information criterion with correction for small sample size (AICc) to examine which scenario best fits the observed changes in language evolution. Confidence intervals of regression coefficients between population size (or island size) and rates of language change were derived from the information matrix. Effect size was calculated as the pseudo R² measures for Poisson regression (58). Statistical power was estimated using the R package asypow (36).