Significance
Social conventions shape every aspect of our lives, from how we greet each other to the languages we speak. Yet their origins have been a topic of theoretical speculation since the time of Aristotle. Most approaches assume that institutions are necessary to organize large populations, but the simplest explanation is that universally accepted conventions are the unintended consequence of individuals’ efforts to coordinate locally with one another. Although this hypothesis is compelling, it lacks conclusive empirical support. Here, we present results from controlled experiments demonstrating that changes in network connectivity can cause global social conventions to spontaneously emerge from local interactions, even though people have no knowledge about the population, or that they are coordinating at a global scale.
Keywords: social conventions, spontaneous emergence, complex systems, empirical testing, network science
Abstract
How do shared conventions emerge in complex decentralized social systems? This question engages fields as diverse as linguistics, sociology, and cognitive science. Previous empirical attempts to solve this puzzle all presuppose that formal or informal institutions, such as incentives for global agreement, coordinated leadership, or aggregated information about the population, are needed to facilitate a solution. Evolutionary theories of social conventions, by contrast, hypothesize that such institutions are not necessary in order for social conventions to form. However, empirical tests of this hypothesis have been hindered by the difficulties of evaluating the real-time creation of new collective behaviors in large decentralized populations. Here, we present experimental results—replicated at several scales—that demonstrate the spontaneous creation of universally adopted social conventions and show how simple changes in a population’s network structure can direct the dynamics of norm formation, driving human populations with no ambition for large scale coordination to rapidly evolve shared social conventions.
Social conventions are the foundation for social and economic life (1–7), However, it remains a central question in the social, behavioral, and cognitive sciences to understand how these patterns of collective behavior can emerge from seemingly arbitrary initial conditions (2–4, 8, 9). Large populations frequently manage to coordinate on shared conventions despite a continuously evolving stream of alternatives to choose from and no a priori differences in the expected value of the options (1, 3, 4, 10). For instance, populations are able to produce linguistic conventions on accepted names for children and pets (11), on common names for colors (12), and on popular terms for novel cultural artifacts, such as referring to junk email as “SPAM” (13, 14). Similarly, economic conventions, such as bartering systems (2), beliefs about fairness (3), and consensus regarding the exchangeability of goods and services (15), emerge with clear and widespread agreement within economic communities yet vary broadly across them (3, 16).
Prominent theories of social conventions suggest that institutional mechanisms—such as centralized authority (14), incentives for collective agreement (15), social leadership (16), or aggregated information (17)—can explain global coordination. However, these theories do not explain whether, or how, it is possible for conventions to emerge when social institutions are not already in place to guide the process. A compelling alternative approach comes from theories of social evolution (2, 18–20). Social evolutionary theories maintain that networks of locally interacting individuals can spontaneously self-organize to produce global coordination (21, 22). Although there is widespread interest in this approach to social norms (6, 7, 14, 18, 23–26), the complexity of the social process has prevented systematic empirical insight into the thesis that these local dynamics are sufficient to explain universally adopted conventions (27, 28).
Several difficulties have limited prior empirical research in this area. The most notable of these limitations is scale. Although compelling experiments have successfully shown the creation of new social conventions in dyadic and small group interactions (29–31), the results in small group settings can be qualitatively different from the dynamics in larger groups (Model), indicating that small group experiments are insufficient for demonstrating whether or how new conventions endogenously form in larger populations (32, 33). Important progress on this issue has been made using network-based laboratory experiments on larger groups (15, 24). However, this research has been restricted to studying coordination among players presented with two or three options with known payoffs. Natural convention formation, by contrast, is significantly complicated by the capacity of individuals to continuously innovate, which endogenously expands the “ecology” of alternatives under evaluation (23, 29, 31). Moreover, prior experimental studies have typically assumed the existence of either an explicit reward for universal coordination (15) or a mechanism that aggregates and reports the collective state of the population (17, 24), which has made it impossible to evaluate the hypothesis that global coordination is the result of purely local incentives.
More recently, data science approaches to studying norms have addressed many of these issues by analyzing behavior change in large online networks (34). However, these observational studies are limited by familiar problems of identification that arise from the inability to eliminate the confounding influences of institutional mechanisms. As a result, previous empirical research has been unable to identify the collective dynamics through which social conventions can spontaneously emerge (8, 34–36).
We addressed these issues by adopting a web-based experimental approach. We studied the effects of social network structure on the spontaneous evolution of social conventions in populations without any resources to facilitate global coordination (9, 37). Participants in our study were rewarded for coordinating locally, however they had neither incentives nor information for achieving large scale agreement. Further, to eliminate any preexisting bias in the evolutionary process, we studied the emergence of arbitrary linguistic conventions, in which none of the options had any a priori value or advantage over the others (3, 23). In particular, we considered the prototypical problem of whether purely local interactions can trigger the emergence of a universal naming convention (38, 39).
Theoretical Model
The approach used here builds on the general model of linguistic conventions proposed by Wittgenstein (39), in which repeated interaction produces collective agreement among a pair of players. Theoretical extensions of this approach have argued that myopic players interacting in social networks can unintentionally create percolating cascades of coordinated behavior (6, 10, 23, 25, 27, 40, 41). Theoretical predictions for our study are based on a derived “language game” model of convention formation (27), in which agents attempting to coordinate in pairwise interactions accrue a memory of past plays, which they use to “guess” the words that will be used by their subsequent partners (Model). Consistent with a broad range of formal approaches (5, 33, 42–44), this model predicts that the connectivity of the actors’ social networks can influence the collective dynamics of convention formation, ranging from the emergence of competing regional norms that inhibit global coordination (45) to the rapid growth of universally shared social conventions (27) (Model).
We evaluated these predictions by studying convention formation in three representative network configurations: (i) spatially embedded social topologies (i.e., one-dimensional lattices with degree 4) (45, 46, 47), (ii) randomly connected topologies (i.e., random graphs with constant degree 4) (42, 48), and (iii) homogeneously mixing populations (3, 27). Formal results show that alternative network configurations (48) fall within the range of dynamical behavior exhibited by the three topologies used here (42).
Experimental Design
Each live game, or experimental “trial,” consisted of a set of participants, a specific social network structure, and a prespecified number of rounds to play. When participants arrived to play the game, they were randomly assigned to positions within a social network. In a given round of the game, two network “neighbors” were chosen at random to play with one another. Both players simultaneously assigned names to a pictured object (i.e., a human face), blindly attempting to coordinate in the real-time exchange of naming choices (Fig. S2). If the players coordinated on a name, they were rewarded with a successful payment; if they failed, they were penalized (Materials and Methods). After a single round, the participants could see only the choices that they and their partner had made, and their cumulative pay was updated accordingly. They were then randomly assigned to play with a new neighbor in their social network, and a new round would begin. The object that participants were trying to name was the same for the entire duration of the game, and for all members of the game. Participants in the study did not have any information about the size of the population that was attempting to coordinate nor about the number of neighbors to whom they were connected.
Results
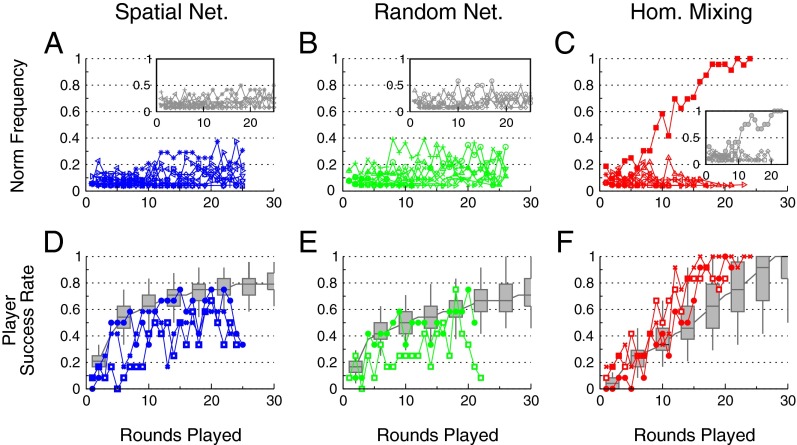
Fig. 1 (n = 24) shows that the dynamics of emergent social conventions depend decisively upon the structure of the social network. In spatial networks, populations enjoyed rapid local coordination, in some cases achieving a 50% success rate (i.e., average likelihood of matching words with a partner) as early as round 4. However, this initial success rate quickly decelerated. After 25 rounds of play, average success rates failed to reach above 75%. Throughout all of the spatial network trials, the dominant local conventions (i.e., the most popular word choices) were never used by more than 45% of the population. As shown in Fig. 2, behavior in the spatial networks evolved through a process of local coarsening (45), in which emergent regions of coordinated behavior competed with bordering local conventions (45, 49, 50). In each of the trials, these dynamics inhibited the spontaneous emergence of global coordination by creating entrenched competition between endogenously formed groups (51).
Fig. 1.
The evolution of social conventions across network topologies (n = 24). Panels indicate spatially embedded networks (A and D, blue), random networks (B and E, green), and homogeneously mixing populations (C and F, red), for eight independent trials of the study (n = 24). Panels A–C show the evolving ecology of norms for representative trials from each condition. Insets show representative model simulations. The corresponding time series (D–F) show the average level of successful matching among individual players. Model results are shown in gray (95% confidence intervals over 10,000 realizations). In spatially embedded networks (A and D), players achieved moderate success with local conventions, creating regional competition and preventing a single convention from emerging across the population. Similarly, in random networks (B and E), moderately successful local coordination produced groups in the networks, but no global consensus. By contrast, in homogeneously mixing populations (C and F), initial local failures resulted in rapid population-level learning and global coordination on a single convention.
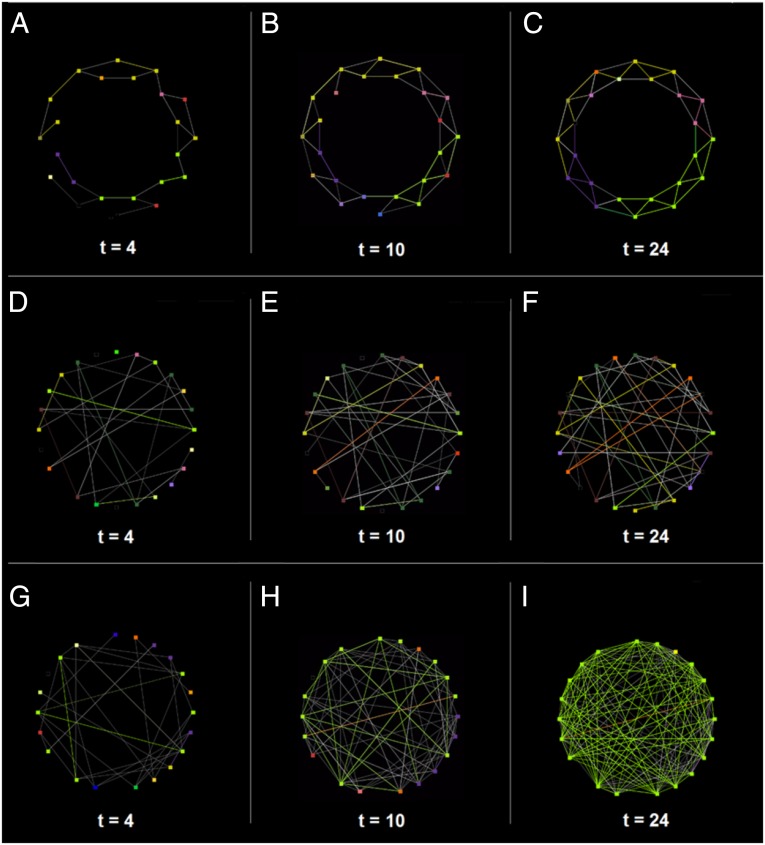
Fig. 2.
Temporal dynamics of convention formation in representative experimental trials. Panels correspond to a spatially embedded network (A–C), a random network (D–F), and a homogeneously mixing population (G–I) (n = 24). Each color corresponds to a unique name used in the trial. Node color refers to the name that was most recently used by that actor, and edge color indicates the name that the two players matched on in their most recent interaction. A white edge indicates that the two players failed to match in their most recent interaction. In the spatial network (A–C), local interactions produce clusters of coherent coordination around a shared convention, with contested border regions. A similar dynamic unfolds in the random network (D–F), where repeated interaction leads to local coordination. In the homogeneously mixing population (G–I), a single name assumes dominance, becoming the global convention.
Similar results were found in random networks, in which local groups of coordinated individuals emerged and competed for dominance (Fig. 1). Group formation in random networks was driven by repeated interactions, which created metastable boundaries between groups of neighbors despite the absence of local clustering (Fig. 2). After 25 rounds of play in randomized topologies, local groups still persisted and coordination rates never increased above 75%. In all random network trials, global social conventions never emerged. Moreover, the sizes of the dominant social conventions (i.e., the fraction of the population using the most popular word choice) were equivalent across all trials of the spatial and random networks, averaging 33% of the population. On time scales observable within our study, the dynamics of social coordination in both the spatial and random network trials were driven by local group competition, which impeded the emergence of global conventions.
Homogeneously mixing populations exhibited significantly different dynamics than those observed in the other two topologies. Initially, success rates were lower because actors did not have repeated interactions with their partners, which prevented “neighborhoods” of entrenched behavior from forming. However, local failure accelerated global coordination. In all trials with homogenously mixing populations, success rates increased to 100% well before the end of the study. Fig. 1 shows that this rapid growth in individual success corresponds to the spontaneous emergence of a global social convention. In all trials, an emergent convention grew quickly, reaching over 60% of the population by round 12, and achieving universal adoption between rounds 20 and 22. On average, by round 22, players who had never interacted with one another were all using the same convention and were able to consistently coordinate with new partners.
The speed of self-organized conventions in these networks raises the question of whether these coordination dynamics scale up as population sizes increase. There are good reasons for skepticism. As system size increases, so does the expected number of competing alternatives circulating in the population; at the same time, because interactions are limited by the number of rounds in the game, increasing system size reduces the fraction of the population with which any given individual can interact. These considerations suggest that global coordination may be much more difficult in larger populations.
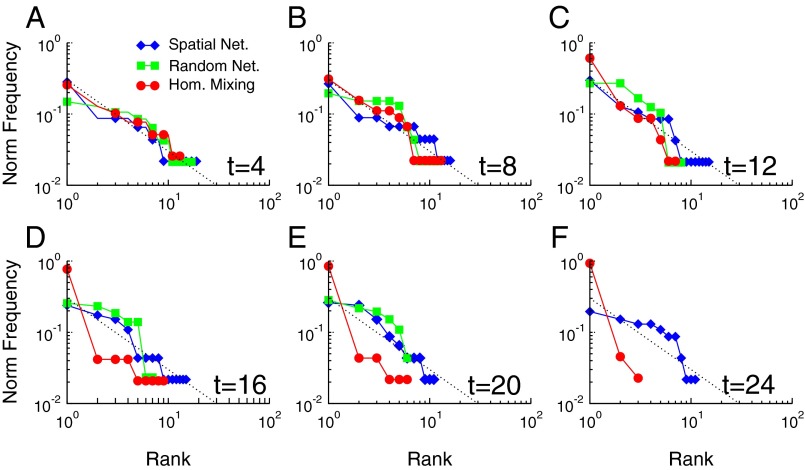
We tested this conjecture by doubling the size of the population and replicating our study. These larger trials (n = 48) permit a more detailed view of the evolving competitive landscape that constitutes the “ecology” of social conventions. Fig. 3 shows the changing distribution of popularity among the competing alternatives in all three network conditions, represented as frequency-rank plots. Early in the evolutionary process, all networks exhibited a broad distribution of active alternatives, indicating that even the least popular options had nontrivial representation within the population. However, as the ecologies evolved, the distribution of alternatives in the spatially embedded and randomly connected populations became increasingly exponential, producing an emergent “oligopoly,” in which a few entrenched local conventions eliminated all other alternatives (45, 52). Each of these conventions competed for ground against the others, but none of them assumed the majority. The ecology evolved quite differently in the homogeneously mixing populations. After the initial transient, a dominant convention rapidly emerged, breaking the symmetry with its competitors and shifting the population into a “winner take all” regime (27). Despite a large number of competing alternatives circulating in the population (Robustness), in every trial in the homogeneously mixing networks, the dynamics converged on a global convention.
Fig. 3.
The shifting distributions of conventions in diverse network topologies. Frequency-rank plots for spatially embedded networks (blue), random networks (green), and homogeneously mixing populations (red) (n = 48, single trial from each condition). In the initial rounds of the game (A–C), the fraction of the population using each name scales as a broad distribution with the overall rank of the name. The scaling is similar in all networks. However, (D) by round 16 in the homogeneously mixing population, a single name breaks the symmetry with the others, accelerating its growth and driving the other options toward extinction (E and F). Over the same time interval, the spatial network and random network exhibit much more moderate growth dynamics, producing exponential distributions with a few competing dominant groups, but without any “winner” emerging. The dashed line in all panels provides a visual guide for the Zipf distribution (slope –1). Note that for t = 24 the curve for random networks is absent due to a shorter experimental time.
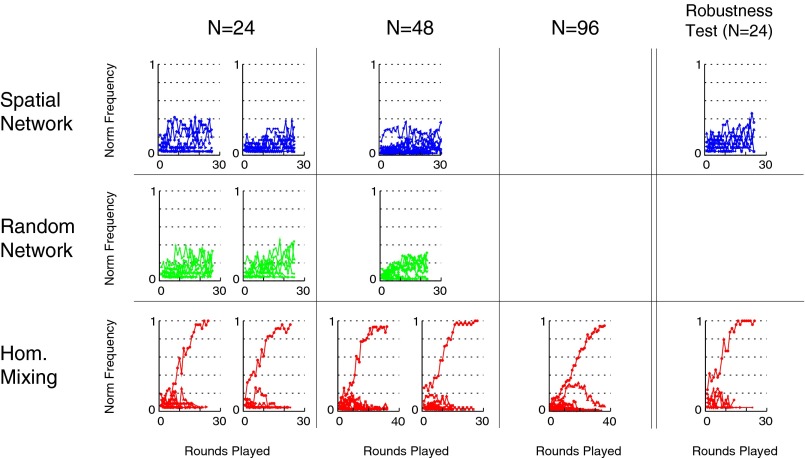
More generally, Fig. 4 shows all of the replications of our study. Consistent results were found for each of the topologies at both n = 24 and n = 48. As a final test of increasing scale, we replicated a trial of the homogenously mixing population in which the network size was again doubled (27, 33, 53). Fig. 4 shows that a shared social convention spontaneously emerged in a population of n = 96 subjects. Global coordination in the n = 96 population emerged on a time scale comparable to that of the initial trials (n = 24), despite the fact that subjects had no information about how large the coordinating population was. Within the brief time scale of the experimental observations (30 rounds of play on average), large homogenously mixing populations were significantly more likely (P < 0.01) to spontaneously create social conventions than smaller populations with less connectivity.
Fig. 4.
Size of dominant convention across conditions. The temporal evolution of the ecology of norms is reported for 13 experimental trials. Results show a significant difference in dominant convention size between locally connected networks (spatial and random networks, combined) and homogenously mixing populations (Wilcoxon Rank Sum Test, P < 0.01). In the spatial network and random network trials, the most popular convention was never used by more than 45% of the group and in most trials was well below 40%. Homogenously mixing populations, on the other hand, produced global social conventions that reached up to 100% of the population. More generally, in spatial networks the average size of the dominant convention across trials was 30% of the population (including n = 24 and n = 48), in random networks the average size was 33% (including n = 24 and n = 48), and in homogenously mixing populations the average size was 96% (including n = 24, n = 48, and n = 96).
Discussion
To ensure that our findings do not rely in any way on participants’ knowledge of the size of the population or number of interaction partners, we tested the effectiveness of the informational controls used in our experimental design by providing subjects with a postexperiment survey asking them to report (i) the most popular name in their game, (ii) the number of people in their game, and (iii) the number of people with whom they interacted. Across all network conditions and all network sizes, there were no significant differences in subjects’ responses regarding the size of their network or the number of neighbors with whom they interacted (see Fig. S5). The only difference in responses was that in all of the homogeneously mixing networks every respondent knew the norm, even though none of them knew how many people were using it.
We also evaluated the robustness of our results for possible biases in the initial distribution of conventions based on external focal points (54). To rule out the possibility that convergence may be biased by the preexisting popularity of some names, we conducted controlled experiments in which participants chose their options from among an arbitrary list of 10 names whose order was randomized at the beginning of the experiment (for each participant, to avoid implicit ranking effects). Results from these controlled experiments are indistinguishable from the results presented above (Fig. 4). Moreover, our findings are further supported by the observed levels of diversity in the emergent ecology of names in each of the other trials. In every trial of our study, the number of suggested names was larger than the size of the population (sometimes by more than a factor of 2; Fig. S4), suggesting that there were no preferred options that initially limited the set of choices in the social evolutionary process.
In sum, our findings demonstrate that social conventions can spontaneously evolve in large human populations without any institutional mechanisms to facilitate the process. Further, the results highlight the causal role played by network connectivity in the dynamics of establishing shared norms. These results contrast with prior work analyzing the effect of network structure on the speed of convergence (6, 41, 55–57). However, that work focuses on the situation where there are just two competing norms that have different payoff consequences. In our case, by contrast, the number of possible norms is not fixed in advance, and they all have identical payoff consequences. In this case, we find that increased network connectivity can accelerate the rate of convergence to a global norm. As a result, large populations without global information or incentives for collective agreement may nevertheless rapidly self-organize to produce universally shared collective beliefs and behaviors.
We anticipate that our results will be of interest to researchers investigating the effects of online connectedness on the emergence of new political, social, and economic behaviors (58). In particular, a topic of interest for future work will be to explore the practical implications of the unintended effects of increasing social connectedness on the homogenization of behaviors and beliefs among large numbers of individuals who do not even know that they are implicitly coordinating with one another.
Materials and Methods
Participants in the study were recruited at large from the World Wide Web. When participants arrived to play a game, they were randomly assigned to an experimental condition (i.e., a social network) and then randomly assigned to a position within that social network. In a given round of the game, two network neighbors were chosen at random to play with one another. Both players simultaneously assigned names to a pictured object (e.g., a human face), blindly attempting to coordinate in the real-time exchange of naming choices (Fig. S2). If the players coordinated on a name, they were rewarded with a successful payment ($0.50); if they failed, they were penalized (–$0.25). (Participants could not go into debt, so failures did not incur a penalty if a participant had a balance of $0.) After a single round, the participants could see only the choices that they and their partner had made, and their cumulative pay was updated accordingly. They were then randomly assigned to play with a new neighbor in their social network, and a new round would begin. The object that participants were trying to name was the same for the entire duration of the game and for all members of the game. An experimental trial concluded when all members completed the specified number of rounds. Participants did not have any information about the size of the population nor about the number of neighbors to whom they were connected nor even about which individuals they were interacting with in a given round. We explored the dynamics of convention formation over different network sizes (24 ≤ n ≤ 96) and degrees of social connectedness (4 ≤ Z ≤ N – 1). However, the controls within the experiment design ensured that the informational resources provided to subjects were identical across all conditions of the study.
Supplementary Material
Acknowledgments
We thank H. P. Young, A. van de Rijt, L. Dall'Asta, A. Kandler, N. Perra, R. Reagans, R. Fernandez, S. Strogatz, and B. Ribeiro for helpful comments and discussion; and A. Wagner, R. Overbey, and R. Chebeleu for website development. A.B. thanks A. Vespignani and the MoBS Laboratory at Northeastern University for support in the early stages of the study, and acknowledges support from the Research Pump-Priming Fund of City University London. This work was supported in part by a James S. McDonnell Foundation grant (to D.C.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1418838112/-/DCSupplemental.
References
- 1.Lass R. Historical Linguistics and Language Change. Cambridge Univ Press; Cambridge UK: 1997. [Google Scholar]
- 2.Lewis D. Convention: A Philosophical Study. Blackwell; Oxford UK: 1969. [Google Scholar]
- 3.Young HP. The evolution of conventions. Econometrica. 1993;61:57–84. [Google Scholar]
- 4.Barkun M. Law Without Sanctions: Order in Primitive Societies and the World Community. Yale Univ Press; New Haven, CT: 1968. [Google Scholar]
- 5.Ehrlich PR, Levin SA. The evolution of norms. PLoS Biol. 2005;3(6):e194. doi: 10.1371/journal.pbio.0030194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Young HP. Individual Strategy and Social Structure: An Evolutionary Theory of Institutions. Princeton Univ Press; Princeton, NJ: 1998. [Google Scholar]
- 7.Hechter M, Opp K-D. Social Norms. Russell Sage Foundation; New York, NY: 2001. [Google Scholar]
- 8.Zhang L, Zhao J, Xu K. 2014. Who create trends in online social media: The crowd or opinion leaders? arXiv:1409.0210.
- 9.Boyd R. Culture and the Evolutionary Process. University of Chicago Press; Chicago: 1988. [Google Scholar]
- 10.Skyrms B. Evolution of the Social Contract. Cambridge Univ Press; Cambridge UK: 1996. [Google Scholar]
- 11.Ullmann-Margalit E. The Emergence of Norms. Clarendon Press; Oxford: 1977. [Google Scholar]
- 12.Steels L, Belpaeme T. Coordinating perceptually grounded categories through language: A case study for colour. Behav Brain Sci. 2005;28(4):469–489, discussion 489–529. doi: 10.1017/S0140525X05000087. [DOI] [PubMed] [Google Scholar]
- 13.Correll SJ, Ridgeway CL. In: Expectation States Theory. Handbook of Social Psychology. DeLamater J, editor. Springer; Heidelberg: 2006. pp. 29–51. [Google Scholar]
- 14.Merton RK. Science and the social order. Philos Sci. 1938;5(3):321–337. [Google Scholar]
- 15.Kearns M, Judd S, Tan J, Wortman J. Behavioral experiments on biased voting in networks. Proc Natl Acad Sci USA. 2009;106(5):1347–1352. doi: 10.1073/pnas.0808147106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Young MW. Fighting with Food. Leadership, Values and Social Control in a Massim Society. Cambridge Univ Press; Cambridge UK: 1971. [Google Scholar]
- 17.Salganik MJ, Dodds PS, Watts DJ. Experimental study of inequality and unpredictability in an artificial cultural market. Science. 2006;311(5762):854–856. doi: 10.1126/science.1121066. [DOI] [PubMed] [Google Scholar]
- 18.Bicchieri C. The Grammar of Society: The Nature and Dynamics of Social Norms. Cambridge Univ Press; Cambridge UK: 2006. [Google Scholar]
- 19.Hayek FA. The Constitution of Liberty. Routledge; 1960. [Google Scholar]
- 20.Sugden R. Spontaneous order. J Econ Perspect. 1989;3:85–97. [Google Scholar]
- 21.Haken H. Information and Self-Organization: A Macroscopic Approach to Complex Systems. Springer; Heidelberg: 1988. [Google Scholar]
- 22.Strogatz S. Sync: The Emerging Science of Spontaneous Order. Hyperion; 2003. [Google Scholar]
- 23.Steels L. A self-organizing spatial vocabulary. Artif Life. 1995;2(3):319–332. doi: 10.1162/artl.1995.2.3.319. [DOI] [PubMed] [Google Scholar]
- 24.Judd S, Kearns M, Vorobeychik Y. Behavioral dynamics and influence in networked coloring and consensus. Proc Natl Acad Sci USA. 2010;107(34):14978–14982. doi: 10.1073/pnas.1001280107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Young HP. Social norms and economic welfare. Eur Econ Rev. 1998;42(3):821–830. [Google Scholar]
- 26.Helbing D, Yu W, Opp K-D, Rauhut H. Conditions for the emergence of shared norms in populations with incompatible preferences. PLoS ONE. 2014;9(8):e104207. doi: 10.1371/journal.pone.0104207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Baronchelli A, Felici M, Loreto V, Caglioti E, Steels L. Sharp transition towards shared vocabularies in multi-agent systems. J Stat Mech. 2006:P06014. [Google Scholar]
- 28.Durrett R, Levin SA. Can stable social groups be maintained by homophilous imitation alone? J Econ Behav Organ. 2005;57(3):267–286. [Google Scholar]
- 29.Galantucci B. An experimental study of the emergence of human communication systems. Cogn Sci. 2005;29(5):737–767. doi: 10.1207/s15516709cog0000_34. [DOI] [PubMed] [Google Scholar]
- 30.Selten R, Warglien M. The emergence of simple languages in an experimental coordination game. Proc Natl Acad Sci USA. 2007;104(18):7361–7366. doi: 10.1073/pnas.0702077104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Garrod S, Doherty G. Conversation, co-ordination and convention: An empirical investigation of how groups establish linguistic conventions. Cognition. 1994;53(3):181–215. doi: 10.1016/0010-0277(94)90048-5. [DOI] [PubMed] [Google Scholar]
- 32.Anderson PW. More is different. Science. 1972;177(4047):393–396. doi: 10.1126/science.177.4047.393. [DOI] [PubMed] [Google Scholar]
- 33.Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Rev Mod Phys. 2009;81(2):591–646. [Google Scholar]
- 34.Lehmann J, Gonçalves B, Ramasco JJ, Cattuto C. Proceedings of the 21st International Conference on World Wide Web. ACM; New York, NY: 2012. Dynamical classes of collective attention in twitter; pp. 251–260. [Google Scholar]
- 35.Kooti F, Yang H, Cha M, Gummadi PK, Mason WA. Proceedings of the Sixth International AAAI Conference on Weblogs and Social Media (ICWSM) AAAI Press, Palo Alto; California: 2012. The emergence of conventions in online social networks. [Google Scholar]
- 36.Lin Y-R, Margolin D, Keegan B, Baronchelli A, Lazer D. Proceedings of the Seventh International AAAI Conference on Weblogs and Social Media (ICWSM) AAAI Press, Palo Alto; California: 2013. #Bigbirds never die: Understanding social dynamics of emergent hashtags; pp. 370–379. [Google Scholar]
- 37.Helbing D, Yu W. The outbreak of cooperation among success-driven individuals under noisy conditions. Proc Natl Acad Sci USA. 2009;106(10):3680–3685. doi: 10.1073/pnas.0811503106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hume D. 1748. A Treatise of Human Nature (Courier Dover Publications, Mineola, NY), reprinted 2012.
- 39.Wittgenstein L. Philosophical Investigations. Blackwell; Oxford: 1958. [Google Scholar]
- 40.Blume LE. The statistical mechanics of strategic interaction. Games Econ Behav. 1993;5(3):387–424. [Google Scholar]
- 41.Kreindler GE, Young HP. Rapid innovation diffusion in social networks. Proc Natl Acad Sci USA. 2014;111(Suppl 3):10881–10888. doi: 10.1073/pnas.1400842111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dall’Asta L, Baronchelli A, Barrat A, Loreto V. Nonequilibrium dynamics of language games on complex networks. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;74(3 Pt 2):036105. doi: 10.1103/PhysRevE.74.036105. [DOI] [PubMed] [Google Scholar]
- 43.Klemm K, Eguíluz VM, Toral R, San Miguel M. Nonequilibrium transitions in complex networks: A model of social interaction. Phys Rev E Stat Nonlin Soft Matter Phys. 2003;67(2 Pt 2):026120. doi: 10.1103/PhysRevE.67.026120. [DOI] [PubMed] [Google Scholar]
- 44.Centola D, Gonzalez-Avella JC, Eguiluz VM, San Miguel M. Homophily, cultural drift, and the co-evolution of cultural groups. J Conflict Resolut. 2007;51(6):905–929. [Google Scholar]
- 45.Baronchelli A, Dall’Asta L, Barrat A, Loreto V. Topology-induced coarsening in language games. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;73(1 Pt 2):015102. doi: 10.1103/PhysRevE.73.015102. [DOI] [PubMed] [Google Scholar]
- 46.Centola D. The spread of behavior in an online social network experiment. Science. 2010;329(5996):1194–1197. doi: 10.1126/science.1185231. [DOI] [PubMed] [Google Scholar]
- 47.Centola D. An experimental study of homophily in the adoption of health behavior. Science. 2011;334:1269–72. doi: 10.1126/science.1207055. [DOI] [PubMed] [Google Scholar]
- 48.Albert R, Barabási A-L. Statistical mechanics of complex networks. Rev Mod Phys. 2002;74(1):47–97. [Google Scholar]
- 49.Barth F. Ethnic Groups and Boundaries. Universitetsforlaget; Oslo: 1969. [Google Scholar]
- 50.Axelrod R. An evolutionary approach to norms. Am Polit Sci Rev. 1986;80(04):1095–1111. [Google Scholar]
- 51.Cassidy FG. Dictionary of American Regional English. Volume I: Introduction and AC. Belknap; Cambridge, MA: 1985. [Google Scholar]
- 52.Ericson R, Pakes A. Markov-perfect industry dynamics: A framework for empirical work. Rev Econ Stud. 1995;62(1):53–82. [Google Scholar]
- 53.Jackson MO. An overview of social networks and economic applications. In: Benhabib J, Bisin A, Jackson MO, editors. The Handbook of Social Economics. North Holland; Amsterdam: 2010. pp. 511–585. [Google Scholar]
- 54.Schelling TC. Altruism, meanness, and other potentially strategic behaviors. Am Econ Rev. 1978;68(2):229–230. [Google Scholar]
- 55.Ellison G. Learning, local interaction, and coordination. Econometrica. 1993;61(5):1047–1071. [Google Scholar]
- 56.Montanari A, Saberi A. The spread of innovations in social networks. Proc Natl Acad Sci USA. 2010;107(47):20196–20201. doi: 10.1073/pnas.1004098107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Young HP. The dynamics of social innovation. Proc Natl Acad Sci USA. 2011;108(Suppl 4):21285–21291. doi: 10.1073/pnas.1100973108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Backstrom L, Huttenlocher D, Kleinberg J, Lan X. 2006. Group formation in large social networks: membership, growth, and evolution. Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (ACM, New York, NY), 44–54.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.