Matching times of leading and following suggest cooperation through direct reciprocity during V-formation flight in ibis

Significance

Cooperation in animals is an enigma because it contravenes the basic notion that evolution favors selfish genes that promote only their own well-being. Bird migration in organized V-shaped or echelon formations constitutes such a cooperation dilemma. We show that juvenile Northern bald ibis (Geronticus eremita) cooperate by taking turns and precisely matching times they spend in the advantageous trailing position and in the disadvantageous front position. This time matching is done on a pairwise level. Furthermore, we found evidence that the animals' propensity to reciprocate in leading has a substantial influence on the size and cohesion of the flight formations. This study shows that direct reciprocation can enable cooperation between animals in a natural context.

Abstract

One conspicuous feature of several larger bird species is their annual migration in V-shaped or echelon formation. When birds are flying in these formations, energy savings can be achieved by using the aerodynamic up-wash produced by the preceding bird. As the leading bird in a formation cannot profit from this up-wash, a social dilemma arises around the question of who is going to fly in front? To investigate how this dilemma is solved, we studied the flight behavior of a flock of juvenile Northern bald ibis (Geronticus eremita) during a human-guided autumn migration. We could show that the amount of time a bird is leading a formation is strongly correlated with the time it can itself profit from flying in the wake of another bird. On the dyadic level, birds match the time they spend in the wake of each other by frequent pairwise switches of the leading position. Taken together, these results suggest that bald ibis cooperate by directly taking turns in leading a formation. On the proximate level, we propose that it is mainly the high number of iterations and the immediacy of reciprocation opportunities that favor direct reciprocation. Finally, we found evidence that the animals' propensity to reciprocate in leading has a substantial influence on the size and cohesion of the flight formations.

A considerable portion of the worldwide bird population performs biannual long-distance migrations (1, 2). These journeys impose large energetic costs on the animals, and as a consequence, mortality is considerably higher during migration than at any other time of the year (3). Reasons for this increased mortality during migration include suppressed immune response, starvation, and dehydration, among others (4, 5). In greater snow geese (Chen caerulescens), for example, mortality during the autumn migration was estimated at 5% for adult birds and up to 35% for juvenile birds (6). At least a part of this increased mortality can be directly or indirectly linked to the physical exertion during migration flights. Consequently, there should be a strong selection pressure—especially on young birds during their first migration—to minimize energy expenditure during migratory flights and increase the chance of survival. Traveling in close, structured groups has been proposed as an energy-saving strategy, with savings being accrued through positive aero- or hydrodynamic interactions between members of the group (7–10). Flight in V-shaped or echelon formation by birds is perhaps the most prominent example of this. The precise aerodynamic interactions in a flock have been the subject of detailed theoretical and, more recently, empirical studies (2, 7, 11–14). During flight, high-pressure air under the wings flows around the tips to a region of low air pressure above the wings. This flow forms two vortices in the bird’s wake, produced by regions of up-wash outboard of the wings, and a central region of downwash immediately behind the bird (7, 13). This up-wash can provide a following bird with extra lift, reducing their requirements for weight support. Theoretical calculations, based on fixed-wing aerodynamic theory, suggest that by flying in this up-wash region at optimal wing-tip spacing, birds could save more than 50% of their energy costs relative to unaccompanied solo flight (7, 12, 13).

Analyses of photographs of geese formations suggested that birds fly in a position where they can potentially profit from the beneficial up-wash, although their wing-tip spacings were typically away from the optimal position, and energy savings were estimated to be between 10% and 14% only (13, 14). However, photographs taken from the ground will only provide snapshots of information from long-distance migratory flights and crucially lack information about precise positioning and height. Recent advances in bio-logging have now allowed the study of this phenomenon in greater detail. The first study to provide empirical evidence that energetic savings can be garnered from V-formation flight was done by Weimerskirch et al. (15), who demonstrated that heart rate, a proxy for energy expenditure, was lower in those birds flying in the middle of a V-formation compared with the bird positioned at the front. Studying the migratory flight pattern of a group of Northern bald ibises (Geronticus eremita), Portugal et al. (16) demonstrated that birds, when flying in formation, favored positions that allowed them to profit from the up-wash. Furthermore, the birds also coordinated their wing flaps with a phase shift mechanism such that their wingtips followed the path of the preceding bird’s wing tips through the air, allowing them to maximize the capture of beneficial up-wash through positive aerodynamic interactions.

However, not all birds in a formation can profit to the same extent. In particular, the leading individual in the front will have no energetic advantage in comparison with flying alone. Consequently, a cooperation dilemma arises around the question of who is going to fly in the front position? From an evolutionary perspective, cooperation between unrelated individuals is difficult to explain as it seems to contravene the basic notion that natural selection favors “selfish” genes that promote only their own well-being. Game theoretic models have been repeatedly applied to explain under which conditions cooperation can be an evolutionary stable strategy (17–19). Formation flight in migrating birds resembles a multiplayer volunteer’s dilemma where at least one individual in a group has to volunteer (by flying in the front position) to produce a public good, from which all other individuals can profit either directly or indirectly (by flying in the wake of the leader or another bird). For the case where individuals play mixed strategies, i.e., they volunteer with a given probability, there exists a certain probability value for volunteering which is an evolutionary stable strategy (20). That is, in a population where all individuals volunteer with a certain probability, single individuals cannot gain higher fitness by volunteering more or less frequently. The value for this probability depends on the group size and the expected benefits and costs (20, 21).

To investigate how this cooperation dilemma can be resolved, we equipped a group of juvenile Northern bald ibis with high-precision global positioning system/inertial measurement unit (GPS/IMU) data loggers (22, 23) that allowed us to monitor the flight behavior of all individuals within the flock during a human-guided autumn migration. In this study, we could, for the first time to our knowledge, determine the relative position of the birds to each other during free-flying migratory flight—a feat that was made possible due to recent advances in sensor technology. These data enable us to estimate how much time each bird spent leading a formation or trailing another bird.

Results

During the migratory flight, the birds formed a cohesive flock with a median distance to the center of mass of the flock of 5.0 m (range, 3.6–11.2 m; Fig. S1B). Summing up relative positions of the birds over the whole flight, we find a blurred V-shaped formation (Fig. S1A and Movie S1), although the overall formation shape was variable over time (16). Positions of individuals within the flock changed frequently (Fig. S2), but individuals were most often in an area where—according to aerodynamic theory—they can profit from the up-wash produced by the wings of the preceding bird (16). Based on these findings, we defined that a bird was in the wake of another bird if it was at a given time point in a rectangular area of up to 3 m behind and 1.6 m lateral to either side of the preceding bird (see SI Text and Table S1 for a discussion of this criterion). On average, birds spent 32 ± 12% of their time in the wake of another bird, although bouts of continuous flying in the wake of another bird were relatively short (median, 2 s; interquartile range, 1–4 s; maximum, 41 s), and birds frequently changed the conspecific they followed, resulting in 241 ± 74 bouts of in-wake flying per bird for a flight of 39 km.

Based on our definition of “in-wake,” we can define a formation (in contrast to a flock) as any assemblage of animals consisting of one leading bird and one or more trailing birds flying either in the wake of the leading bird or of one of the other trailing birds (Fig. 1F). Thus, although the size of the flock was constant during the flight (n = 14), formation sizes—the number of animals constituting a formation—were highly variable depending on whether individuals were flying close enough to be considered as constituting a formation. We observed pair formations consisting of only two individuals most often, making up 60.7% of all formations, whereas formations of three or four birds made up 30.8% and formations of more than four birds was 8.5%. The largest formation observed consisted of 12 birds. With a typical group size (24) of 3.00 ± 0.25 animals (n = 14; Table S2) individuals did not differ markedly in their tendency for flying in pair formations or larger formations.

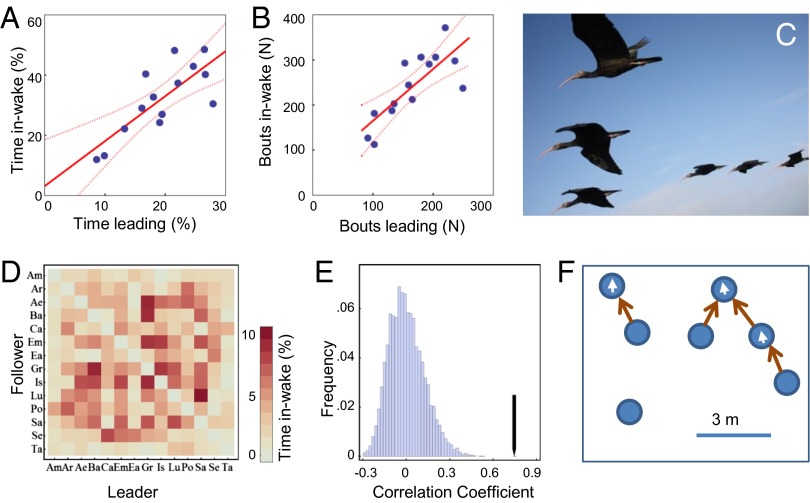
Fig. 1.

In-wake flying in Northern bald ibis. (A) Percentage of time leading a formation is plotted against the percentage of time flying in the wake of another bird. (B) Number of bouts leading a formation is plotted against the number of bouts flying in the wake of another bird. (C) Northern bald ibis (G. eremita) flying in tight formations. Image courtesy of M. Unsöld. (D) Matrix plot of the percentages of time flying in the wake of a specific bird for all 14 birds. Rows and columns give the 14 subjects (names abbreviated). (E) Histogram for the expected Pearson product moment matrix correlation coefficient assuming random associations based on 10,000 random matrix permutation and the observed value (black arrow). (F) Representation of the flock as a graph where vertices indicate individuals and a direct edge is drawn from vertex i to vertex j if bird i was in the wake of bird j, where “in the wake” is defined as being within an area of 3 m behind and 1.6 m lateral to the preceding bird. Behind and lateral are defined relative to the flight direction of the preceding bird (indicated by white arrows inside the vertices). In this hypothetical example, a flock of seven birds, consisting of one formation of four individuals (an asymmetric V-formation), a separate pair formation of two individuals (echelon formation), and an isolated bird would be represented by a graph consisting of two weakly connected components of sizes four and two, respectively, and one isolated vertex.

Comparing the time a bird was flying in the wake of another bird and the time it was leading a formation, we find a high correlation of r = 0.78 (Pearson correlation, n = 14, CI₉₅[0.42, 0.92]; Fig. 1A). A very similar picture emerges for the number of bouts of flying in the wake of another bird and leading a formation (r = 0.78, n = 14, CI₉₅[0.43, 0.93]; Fig. 1B). Fig. 1D shows the percentages of the total flight time that birds spend in the wake of each other on the dyadic level. For concordance on the dyadic level, we get a Pearson product moment correlation coefficient of r = 0.75, and a Mantel matrix permutation procedure with 10,000 permutations shows that this value is much larger (+6.1σ) than the expected value for randomized associations (Fig. 1E). That means that the time individual i spends in wake of individual j is highly correlated with the time individual j spends in wake of individual i. We found differences in the average distance that pairs of birds kept during the flight. Thus, to control for effects of spatial closeness, we added a partial matrix correlation, partialing out the average distance of the birds to each other (Methods). The partial correlation coefficient for dyadic in-wake flying, controlling for spatial distance, was slightly lower but still much higher than the expected value for random associations (r = 0.64, +6.2σ). This high correlation is even more striking considering the fact that the birds differed in body mass and physiological condition and might, consequently, have differing energetic demands.

The flock consisted of three pairs of siblings and eight genetically unrelated individuals. The birds were hand raised in four different nests, so that 12 birds each had three nest mates in the flock and two birds had one nest mate. To control for the potential influence of genetic relatedness or common rearing history, we used additional hierarchical matrix correlations where the partial correlation coefficient was calculated either only for unrelated individuals or only for non-nestmates. In both cases, we compared the observed partial correlation coefficients with expected values based on hierarchical matrix permutation procedures. Being in front of a bird was highly correlated with being in the wake of the same bird both for unrelated individuals (r = 0.67, +6.3σ) and for non-nestmates (r = 0.62, +5.5σ). Interestingly, however, the amount of time individuals fly in the wake of each other during the migration flight is not clearly correlated with their social affinity on the ground as measured with nearest-neighbor protocols (r = −0.09, σ = 1.1).

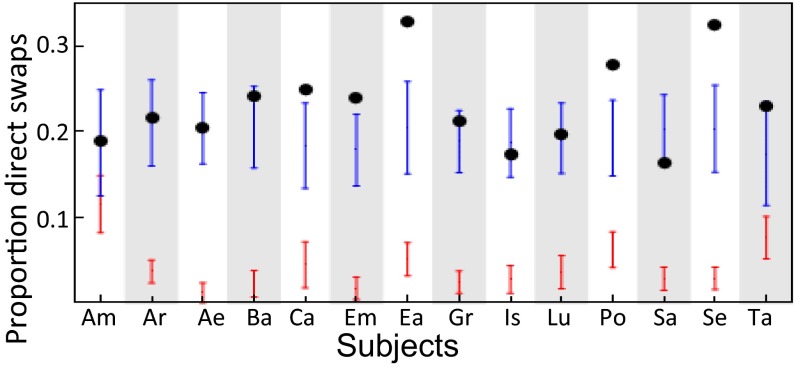
The position of individuals within a formation changes frequently. Here it is of interest whether birds tend to directly swap position on a dyadic level—that is, bird i can fly in the wake of bird j directly after bird j was flying in the wake of bird i. Such direct swaps occurred relatively frequently (median: 57 swaps per bird; interquartile range: 47–66), and the time gap between the end of the first bout and the onset of the following bout was overall very short (median, 1 s; interquartile range, 0–8 s; all dyads pooled; Fig. S3E). To see whether such direct swaps of position occur more frequently than expected due to chance alone, we compared the number of observed direct swaps with estimates for the expected numbers of direct swaps for two randomization models based on 1,000 randomly permuted data streams. For the first model, we assumed that birds have individual preferences for other birds and select them as their trailing birds with a probability proportional to their preference. As an estimate for their preference, we took the observed time of in-wake flying behind the respective bird. The observed proportions of direct swaps (0.16–0.33 of all changes) were, for all 14 birds, higher than the expected proportions (0.01–0.11) based on the randomized model, where we assumed choice of the leading bird proportional to individual preference. In all 14 cases, the difference was larger than 1.96σ, and on average the difference was 23.3σ (Fig. 2), indicating that direct swaps were, indeed, much more common as we would expect if animals chose their preceding bird according to social preference. For the second model, we assumed that birds select their trailing bird based on spatial proximity at the time of swapping. How strongly the distance influences the choice of the trailing bird was again based on estimates derived from the observed data (Methods). The predictions for the proportion of direct swaps were much closer to the observed values than those of the previous model; although the observed number of direct swaps was, on average, still 1.5σ higher than the predicted one, the observed value for direct swaps was, in only 5 of 14 cases, outside the 95% CI for the expected value, and some birds even showed a reversed trend—with fewer direct swaps as predicted (Fig. 2). Thus, overall spatial proximity at the time of swapping seems to be a better predictor for direct turn-taking than social preference for specific birds.

Fig. 2.

Direct swaps of position. Proportion of direct swaps (where a bout of in-wake flying of animal i trailing animal j is followed by a bout of animal j trailing animal i). Dots give observed values for the 14 animals and bars give the 95% parametric CI for expected values based on 1,000 random permutations of the original dataset. Red bars, model I (random choice of the leading bird); blue bars, model II (random choice of the leading bird proportional to the spatial distance at the time of swapping).

Given an overall flocking tendency, birds will occasionally find themselves in an aerodynamically advantageous area behind another bird, even if they do not actively seek out such a position. To resolve, whether the observed percentages for in-wake flying are higher than those expected to happen in a flock by chance alone, we simulated migratory flights by randomizing the observed data in a way that destroys the original spatiotemporal correlations between individuals but keeps essential characteristics of the flight behavior: the flock cohesion (measured as the birds’ distance to the center of mass of the flock), average flight speed and altitude, and the distribution of acceleration patterns (axial, lateral, and dorso-ventral; SI Text). Simulating 1,000 flights, we got expected values for times of in-wake flying of 1.01%, CI₉₅[1.0, 1.02], and an expected correlation between flying in-the wake of another bird and leading of r = 0.27, CI₉₅[−0.24, 0.68]; both are clearly lower than the observed values (32% and r = 0.78, respectively).

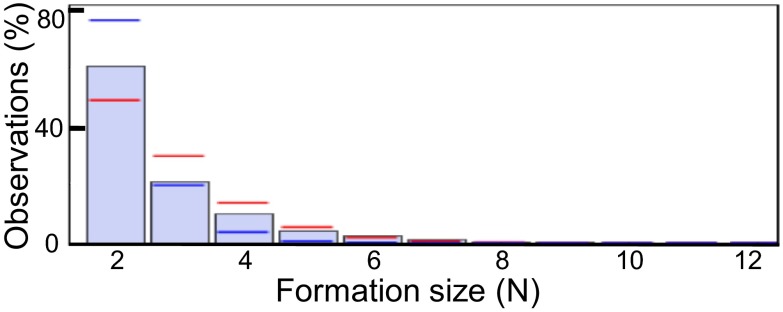
Finally, given the strong indication that in-wake flying in this group of bald ibis was primarily governed by direct dyadic reciprocation, we ought to know whether the observed formation sizes are also indicative for such a social strategy. In other words: does the distribution of observed formation sizes match with the expected distribution assuming individual preferences for flying in the wake of specific birds? For this purpose, we compared the observed distribution of formation sizes with two different models. In the first model, we calculated the distribution for expected formation sizes assuming that each individual has a certain propensity to fly in the wake of another bird. It can be seen that model I predicts the observed formation sizes reasonably well (Kolmogorov–Smirnov test for goodness of fit: g_max = 0.23, P = 0.89; Fig. 3), although it underestimates the number of pair formations while slightly overestimating the number of larger formations. In the second model, we assumed additionally that each bird differentiates between conspecifics and has a different propensity for following each individual bird. This time the model overestimates the number of pair formations and underestimates the occurrence of larger formations (g_max = 0.46, P = 0.12). This result suggests that the observed formation sizes can be largely explained by a mixture of two simple models that assumes that the birds have (i) a certain tendency to fly behind another bird and (ii) preferences for specific individuals. Additional assumptions about group coordination, communication, or other mechanisms to increase group adhesion are not required.

Fig. 3.

Observed and predicted formation sizes. Bars give the percentage of observed formation sizes at a sample interval of one second. Red lines indicate predictions based on model I assuming a general individual preference to follow any other bird. Blue lines indicate predicted values based on model II assuming individual preferences for specific birds.

Discussion

Formation flight in migrating birds is a cooperation dilemma, because only the trailing birds can profit from the beneficial up-wash produced by the leading bird. On this migration leg, all birds managed to fly in the wake of another bird for a notable proportion of the whole flight time. This finding and the high correlation on the individual level between leading a formation and flying in the wake of another bird are in line with the notion that the birds actively seek positions in the wake of other birds and that they take turns in leading. However, as a single observational study cannot deliver unequivocal proof that these findings imply cooperation based on direct reciprocity, we would like to discuss potential alternative explanations for the observed patterns before elaborating more on the evidence for direct reciprocation and its potential implications.

First, we have to consider the possibility that birds travel in flocks, where each bird is trying to stay close to the other birds, but without actively seeking to get into an aerodynamically advantageous trailing position. We used a simulation approach to generate predicted values for the proportion of in-wake flying and the correlations for leading and following that we should expect in such a case. As the observed values were much higher than the predicted ones (i.e., 32% of in-wake flying as contrasted to an expected value of 1%; Results), we argue that this assumption alone cannot sufficiently explain the reported patterns. A second possibility to consider is that the birds actively try to form formations but that they are indifferent about their position within those formations. Direct swaps of position would simply be a result of the leading bird getting exhausted and falling back. In such a case, we should expect that times of in-wake flying would be distributed more or less evenly over all dyads, but this was clearly not the case. Furthermore, if exhaustion of the leading bird was responsible for swaps of position, we should expect that (i) swaps are initiated by the leading bird by losing speed, (ii) the length of bouts should decrease with time as birds should tire, and (iii) the average time in the leading position should be correlated with the strength of the birds. We could not find support for any of these predictions (Figs. S4F and S5).

Finally, it could be the case that individuals are not cooperating but competing to be in an advantageous position. Given the high percentage of achieved in-wake flying, strong competition seems implausible; however, as we cannot make quantitative predictions for expected times of in-wake flying under competition, we cannot exclude this possibility. The short duration of bouts of in-wake flying and the high number of switches are, generally, in line with predictions for a competitive scenario. However, under strong competition, the time that a bird can stay in the favorable position should depend on its resource holding potential. As body mass is a good indicator for social dominance and energy reserves (within sex and age class), we would expect that heavier birds will be more often in the favorable position. According to aerodynamic theory, on the other hand, heavier birds should have a slightly higher optimal travel speed and might, therefore, gain less from following lighter birds. However, we could not find any evidence for either of these two opposing effects (Fig. S5).

Andersson and Wallander (25) suggested that formation flight in flocks with intermediate or low levels of relatedness could be established by birds reciprocating in taking the lead. Both theoretical and empirical studies have shown that reciprocation in a multiplayer setting is prone to defection and a rather unstable strategy, because it is based on reputation building or image scoring—that requires detailed book keeping of the actions of all other group members (26–29). Reciprocation is easier to maintain on a dyadic level (30–32). The fact that the majority of observed formations are pair formations consisting of only two individuals and the high correlation of in-wake flying on the dyadic level support the idea that direct reciprocation in terms of mutual leading is the key for solving the cooperation dilemma of formation flight in the ibis. This idea is further corroborated by the high percentage of direct swaps and the finding that the distribution of observed formation sizes closely matched the expected distribution for a model based on dyadic attraction. We must note that there might be also alternative explanations for the observed distribution of formation sizes with its high proportion of pair formations. Modeling formation flight using insights from control theory, Seiler et al. (33) argued that oscillations in the relative lateral positioning of the birds accumulate, making it inherently difficult for birds further back in the line to keep the lateral distance to the preceding bird. The strength of dyadic ties during the flight seems not to be correlated with social proximity on the ground, although this observation is in line with findings in pigeons, where social hierarchies on the ground cannot predict leader-follower relationships in the air (34).

We argue that five characteristics of the migration flight are prone to increase the success of direct reciprocation. First, the payoff structure of in-wake flying resembles the structure of a snowdrift game. In the snowdrift game, a noncooperator meeting a cooperator gains the highest payoff, but a noncooperator meeting another noncooperator earns even less from an interaction than a cooperator meeting a noncooperator (SI Text). The iterated snowdrift game is more favorable for the emergence of cooperation than the infamous iterated prisoner's dilemma (29, 35, 36). In the prisoner's dilemma, a co-operator who is exploited by a defector is worse off than a defector who cannot exploit anyone, though this is not the case in the formation flight, where defectors are effectively free riders, who do profit from co-operators but who do not incur any additional costs on them. Second, repeated bouts of in-wake flying facilitate cooperation. The more often two individuals interact in situations where they can cooperate, the higher the potential gains of mutual cooperation (32). For example, the high numbers of opportunities for cooperation have been put forward as one explanation for successful cooperation in the cleaner wrasse (37). In the Northern bald ibis, we observed between 100 and 300 bouts of following per bird during 43 min. Extrapolating these numbers we can expect several thousand* bouts of following per individual over the whole migration. As Northern bald ibis travel in small, stable groups, this gives ample opportunity for reciprocation and should constitute a high incentive for keeping up cooperation.

Third, bouts of leading and following occur close in time. In general, long delays reduce the likelihood for cooperation because long time gaps increase the risk that the interaction partner disappears and no further interactions take place. As a consequence, animals should discount the value of future interactions the more distant in time they are, and empirical studies have provided evidence that this is, indeed, the case (38, 39). Temporal closeness should, on the other hand, facilitate cooperation. The mutual grooming in impala (Aepyceros melampus) has been suggested as one example where the instant switching of the roles facilitates cooperation (40–42). Furthermore, immediate switching is cognitively less demanding as individuals do not have to memorize outcome and identities of many interactions. In fact, if switches follow instantly, a low-key mechanism like generalized reciprocity (43, 44) can be sufficient to ensure that an altruist becomes the next beneficiary. For the Northern bald ibis, the gap between one bout of in-wake flying and the following bout with reversed roles was in the majority of cases equal or less than one second—clearly a time interval short enough to facilitate reciprocation. Fourth, the potential gains from continued cooperation are high. Theoretical models predict that altruistic acts become more likely the higher the benefit for the receiver in relation to the cost for the donor of a good or service (17). One classical example where such conditions have been observed under natural conditions is food donations in vampire bats (45). At night, vampire bats forage on vertebrate blood before they return to their social roosting sites for the day. Bats that failed to feed in one night risk dying from starvation but they are helped by conspecifics that feed them with regurgitated blood. The costs for the donor of blood are high, but the benefits for the starving bat are still much higher. In migrating birds, the situation is in a way comparable: given that up to 35% of juvenile birds do not survive the first autumn migration and exhaustion plays a major role in most casualties, it can be expected that any energy savings during migration flights translate directly into increased survival probability and, hence, have a strong impact on an individual’s fitness.

Fifth, flocks of juvenile Northern bald ibis are likely to contain a noteworthy proportion of related individuals. Relatedness between individuals increases the likelihood for the evolution of cooperation due to kin selection (46), and this has been suggested as a candidate explanation for formation flight in small flocks of related individuals (25). A behavioral gene that promotes the well-being of other individuals at a cost to the carrier can still increase in frequency if the beneficiaries of the behavior carry, due to common descent, the same gene. Our study flock consisted of three pairs of siblings and eight unrelated individuals. In this respect, the group composition roughly resembles natural migration troops, where juveniles of one breeding colony, containing a certain percentage of siblings, are believed to migrate together. Although such a level of overall relatedness is not in itself sufficient to guarantee cooperation, it reduces the threshold for the cost-benefit ratio below which cooperation becomes the dominant strategy.

As the evolution of cooperation between unrelated individuals seems to be in conflict with the notion that natural selection promotes selfish genes, its existence always asks for an explanation. Although a range of alternative accounts cannot be rigorously excluded, from hypothetical aerodynamic models to speculations concerning physiology, direct reciprocation seems to be the most convincing account for our observations. In the case of migrating Northern bald ibis, it seems to be facilitated ultimately by the favorable payoff structure, an intermediate level of relatedness between group members, and potentially high gains. On the proximate level, we propose that it is mainly the high number of iterations and the immediacy of reciprocation opportunities that favor direct reciprocation. Over 40 y ago, Trivers (32) suggested reciprocal altruism as a means for maintaining mutual beneficial cooperation in social animals. However, empirical evidence for the existence of such a mechanism in natural systems remained sparse ever since. The V-formation flight of Northern bald ibis does not only provide a convincing example for reciprocal altruism in animals, but it also delivers hints for the conditions that might have favored its evolution.

Methods

Subjects.

Subjects were 14 juvenile Northern bald ibis (Geronticus eremita) that were hand-reared by human foster parents at Salzburg Zoo (Austria) and trained to follow an ultralight paraplane (powered parachute; Fig. S6) to learn a new migration route from Salzburg (Austria) to Orbetello (Italy) as part of an ongoing research and conservation program by Waldrappteam. All birds hatched in March 2011 (Table S2) and were imprinted onto human foster parents (S. Heese and D. Trobe). An extended discussion how this might influence the behavior of the birds is given in SI Text. In July, the birds began training flights behind a paraplane (Fig. S6). At the end of July, birds were equipped with leg-loop harnesses and dummy loggers to habituate them to the procedure of being equipped with loggers and carrying an additional mass (∼3.5% of the body mass of the smallest bird) during the migration. The mass of the loggers was 23 g. Given a mean body mass of 1,308 g for the birds, this was below the recommended 5% limit for flying animals (47). Experimental protocols were approved by the Royal Veterinary College (London) Ethics and Welfare Committee.

Data Collection.

The human guided migration from Salzburg (47°48′ N 13°02′ E) to Orbetello (42°26′ N 11°11′ E) started on 20 August 2011 and finished on 24 September 2011. The migration route of 1,353 km was split into six stages of 145–360 km in length, lasting between 180 and 500 min of flight. GPS loggers were attached for the first hour of the second leg from Obergrafendorf, Lower Austria (48°09′ N 15°32′ E) to Pinkafeld, Burgenland (47°22′N 16°7′E) on 24 August 2011. All 14 birds were equipped with back-mounted synchronized 23g GPS/IMU loggers, custom made at the Royal Veterinary College, London (22, 23). After 1 h of flight, the loggers were removed at a short stop-over near Altenmarkt an der Triesting (48°1′ N 15°58′ E), and the birds finished the remainder of the journey without loggers. The maximal altitude for the flight bout was roughly 700 m a.s.l. (∼400 m above ground), and the birds followed the paraplane at a distance of, on average, 147 m, typically to the left hand side. GPS was recorded at 5 Hz, and data were postprocessed differentially over a short baseline between base station and birds (Dataset S1), using Waypoint software GrafNav 8.10 (Novatel). L1 coarse/acquisition code pseudorange measurements were used to calculate the position of each bird, with velocity determined from L1 Doppler measurements (48). This approach can provide positional accuracy to 0.3 m and speed accuracy better than 0.1 m/s. The recorded flight of 46 min consisted of an initial circling phase of 3 min where the birds gained height and a phase of relatively straight flight of 43 min. The circling phase was excluded from further analysis. Three loggers showed over short periods anomalies with single readings being far out the range of possible values. These values, totaling up to 128, 43, and 12 s, respectively, were manually removed. Missing values (on average, 0.99% of all data points) were replaced by linearly interpolated position and altitude estimates between reliable values.

Data Processing.

For each time point, we calculated the relative position of each bird to every other bird in the flock. If a bird was within a rectangular area of up to 3 m behind and 1.6 m lateral (to either side) of another bird, where behind refers to 180° relative to the current flight direction of the preceding bird and lateral refers to 90° or 270°, respectively, and the difference in the altitude of the two birds was less than 1 m, then we considered the bird as flying in the wake of the preceding bird (see SI Text for a discussion of this criterion). If, based on this definition, the bird was in wake of more than one individual, we considered it as being in wake of the closest individual in the front of it. Next, we condensed the temporal resolution from 5 to 1 Hz, by splitting the data stream into time bouts of 1 s each, and considering a bird as in-wake during this second, if it was recorded as in-wake for at least three of the five sample points within that second.

Models for the Expected Formation Size and Direct Swaps.

We compare the distribution of observed formation sizes with the expected distributions for two null models. For model I, we make the assumption that individuals have given propensities to fly in the wake area of another bird. As estimates for these propensities, we take the observed frequencies of in-wake flying. For model II, we make the additional assumption that birds have individual preferences for other birds. As estimates for these preferences, we take the observed frequencies of dyadic in-wake flying. We define a direct swap as a change of position in a formation where a bird i flying in the wake of bird j is subsequently flying in front of bird j such that bird j is in the wake of bird i, without any other bird being in the wake of bird i between these bouts of in-wake flying. We compared the observed number of direct swaps with expected numbers based on two different models. For the first null model, we assumed choice of the leading individual proportional to individual preferences. For the second null model, we assumed that the choice of the leading bird is influenced by spatial proximity at the time of switching (see SI Text for details for all models).

Matrix Correlation.

For dyadic in-wake data, we calculated the Pearson product moment correlation coefficient. As dyadic data involving the same individuals are not statistically independent, we used a nonparametric matrix permutation procedure introduced by Mantel (49) to produce a null distribution for the correlation coefficient. For partialing out the effect of spatial proximity, we performed an additional partial matrix correlation (50) by calculating the partial correlation coefficient as

$$r_{xy,z}=\frac{r_{x,y}-\left(r_{x,z}\times r_{y,z}\right)}{\sqrt{1-r_{x,z}^2}\times \sqrt{1-r_{y,z}^2}},$$

where r_xy,z is the correlation between the time spent leading (x) and the time spent trailing (y) for each pair of birds with the effect of average spatial distance of the birds removed, r_x,y is the correlation between the time spent leading (x) and the time spent trailing (y) for each pair of birds, and r_x,z and r_y,z are the correlations between the average spatial distance of the birds with the time spent leading or following, respectively. To account for relatedness or common rearing environment, we made additional hierarchical matrix permutations, where the interaction matrix was rearranged as to group related individuals (or individuals with common rearing history) and permutations were made only within groups and on the group level.

Throughout the text, CI₉₅ indicates the 95% parametric CI and ± is the SD.