Droplet fragmentation: 3D imaging of a previously unidentified pore-scale process during multiphase flow in porous media

Significance

Fluid displacement processes in carbonate rocks are important because they host over 50% of the world's hydrocarbon reserves and are aquifers supplying water to one quarter of the global population. A previously unidentified pore-scale fluid displacement event, droplet fragmentation, is described that occurs during the flow of two immiscible fluids specifically in carbonate rocks. The complex, heterogeneous pore structure of carbonate rocks induces this droplet fragmentation process, which explains the increased recovery of the nonwetting phase from porous carbonates as the wetting phase injection rate is increased. The previously unidentified displacement mechanism has implications for (i) enhanced oil recovery, (ii) remediation of nonaqueous liquid contaminants in aquifers, and (iii) subsurface CO₂ storage.

Abstract

Using X-ray computed microtomography, we have visualized and quantified the in situ structure of a trapped nonwetting phase (oil) in a highly heterogeneous carbonate rock after injecting a wetting phase (brine) at low and high capillary numbers. We imaged the process of capillary desaturation in 3D and demonstrated its impacts on the trapped nonwetting phase cluster size distribution. We have identified a previously unidentified pore-scale event during capillary desaturation. This pore-scale event, described as droplet fragmentation of the nonwetting phase, occurs in larger pores. It increases volumetric production of the nonwetting phase after capillary trapping and enlarges the fluid−fluid interface, which can enhance mass transfer between the phases. Droplet fragmentation therefore has implications for a range of multiphase flow processes in natural and engineered porous media with complex heterogeneous pore spaces.

Multiphase fluid displacement processes in porous media are important for a broad range of natural and engineering applications such as transport of nonaqueous phase liquid contaminants in aquifers, oil and gas production from hydrocarbon reservoirs, subsurface CO₂ storage, or gas transport in fuel cells. Herein, capillary trapping is a fundamental mechanism that causes immobilization of a portion of the resident nonwetting phase when it is displaced by an invading wetting phase. As a result, production of the nonwetting phase is always less than 100%.

The pore-scale physics of capillary trapping are broadly understood, as the underlying mechanisms such as piston-like displacement, snap-off and film development have been observed in physical micromodel experiments and quantitative theories have been established for them (1–4). The conventional view considers such pore-scale processes to occur between multiple pores, i.e., they are interpore processes and the pores are defined as volumes connected by narrower pore throats. By contrast, intrapore processes, as presented in this paper, are not well established in the literature. During drainage (i.e., where a nonwetting phase displaces the wetting phase), the wetting phase can establish films in the corners of the pores, which results in its continuous production and hence low residual saturations of the wetting phase. During imbibition (i.e., where the wetting phase displaces a nonwetting phase), swelling of the corner wetting films causes snap-off of the nonwetting phase, which results in capillary trapping of the nonwetting phase. The trapped nonwetting phase exists as disconnected ganglia within the pore network. Numerical pore network models have been developed to include these pore-level mechanisms with the aim of predicting the macroscopic flow properties of porous materials such as the structure of the phase distributions, residual saturation, relative permeability functions, and capillary pressure curves. Some of these models, referred to as quasi-static models, assume that fluid flow is only governed by capillary forces (5–8), and hence are limited in capturing the dynamics of fluid displacements that occur under the action of both capillary and viscous forces. In another class of pore network models, referred to as dynamic models (9–11), capillary and viscous forces are considered simultaneously. Such models are more applicable in modeling the dynamics of pore-scale events controlled by both capillary and viscous forces.

The saturation distribution of two immiscible fluid phases in a porous medium is influenced by the wettability of the system, i.e., the distribution of surfaces that are preferentially water wet or preferentially wetting to a nonaqueous phase such as oil (12). It is known that a trapped nonwetting phase can be remobilized and recovered when the wetting phase is injected at capillary numbers N_c that exceed a critical level. N_c is a dimensionless ratio quantifying the relative importance of viscous to capillary forces, i.e., N_c = vµ/σ where v is the apparent velocity, µ is the viscosity of the invading phase, and σ is the interfacial tension (13). For homogeneous sandstones, remobilization typically occurs at N_c of the order of 10⁻⁵, an effect known as capillary desaturation (14).

Recent advances in X-ray computed microtomography (µCT) methods have enabled the visualization and quantitative analysis of the static distribution of fluid phases, fluid rock interactions, and the structure of wetting and nonwetting phases in porous materials (8, 15). A particular focus has been on capillary trapping (16–20). Using synchrotron X-ray μCT facilities, it has also become possible to visualize dynamic pore-scale mechanisms, including snap-off and Haines jumps (21). Most of these imaging studies have focused on relatively homogeneous pore systems such as bead packs (22), sand packs (22–26), and sandstones (8, 18, 21, 23), but less attention has been paid to carbonate rocks. However, more than 50% of the world’s remaining oil reserves are located in carbonate reservoirs (27), and carbonate aquifers supply water wholly or partially to one quarter of the global population (28). Carbonates rocks can have complex multiscale pore structures, which render the application of X-ray µCT more challenging because of the need to select a representative sample that is small enough to achieve high resolutions on µCT images but that also captures the essential heterogeneities of the pore structure (29, 30).

In this contribution, we use X-ray µCT to quantify the structure and distribution of a nonwetting phase (oil) after drainage and after its displacement by a wetting phase (brine) at low and high capillary numbers in a heterogeneous carbonate with multiple pore scales. Using image analysis, we demonstrate the effect of capillary desaturation on the cluster size distribution of the trapped oil phase. We identify a previously unidentified pore-scale event, which we refer to as droplet fragmentation. Droplet fragmentation is responsible for further production of the oil phase beyond capillary trapping. This fragmentation process occurs mainly in larger pores. It results in the production of additional oil from these large pores, contributes to a change in the structure of residual oil, and increases the oil−brine surface area. As a consequence, the trapped phase may subsequently be more difficult to mobilize after droplet fragmentation has occurred but mass transfer between the phases can increase.

Cluster Size Distribution

We have analyzed the size distributions of oil clusters after (i) injection of a mineral oil into a brine-wetted and -saturated heterogeneous carbonate core (drainage) and (ii) subsequent brine injection (imbibition). Initially, the carbonate was fully saturated with brine. During drainage, the oil saturation was established using first a slow oil injection at a rate of q = 10 μL⋅min⁻¹ (N_c = 3.95 ×10⁻⁷) followed by a fast oil injection at a rate of q = 700 μL⋅min⁻¹ (N_c = 2.77 × 10⁻⁵). Brine was subsequently injected at the same flow rates (N_c = 1.95 × 10⁻⁷, N_c = 1.37 × 10⁻⁵), respectively. At each stage, 10 pore volumes of the displacing fluid were injected. After each injection step, the flow cell was scanned using µCT under static (i.e., no flow) conditions (Table S1).

The digital volumes obtained by µCT were segmented into three binary volumes, each representing the discrete oil, brine, or rock component. The binary images of the two fluid phases were subsequently labeled such that any group of connected voxels was assigned an individual label, thus constituting a fluid cluster. To avoid artifacts from capillary end effects, the quantitative analysis presented here is based on a central 18-mm-long section of the core plug. The total length of this core plug was 44 mm. Fig. 1 shows 3D renderings of the oil phase after drainage and imbibition at the two different flow rates. The oil saturations in the central section of the sample were 0.86 and 0.69 after drainage (at q = 10 µL⋅min⁻¹ and q = 700 µL⋅min⁻¹, respectively) and 0.54 and 0.44 after imbibition (at q = 10 µL⋅min⁻¹ and q = 700 µL⋅min⁻¹, respectively). Two independent scans separated by 22 h show that the fluid saturations exhibited a considerable degree of redistribution after the 700 µL⋅min⁻¹ oil injection was ceased. Fig. 1B shows the image acquired after the fluid redistribution. This autoredistribution was caused only by the capillary forces acting at the pore level, since the density of the two phases was closely matched. Fig. 1B shows the oil clusters imaged after the redistribution.

Fig. 1.

A 3D rendering of the oil clusters after drainage (A and B) and imbibition (C and D) at high and low flow rates. Discrete clusters were rendered in different colors. Large clusters that existed after drainage were broken down to numerous smaller clusters after imbibition.

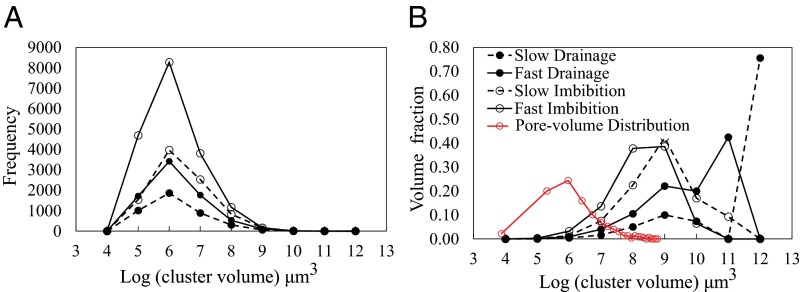
Fig. 2 shows the oil cluster size distribution after each individual injection step during drainage and imbibition. In this context, droplet refers to oil blobs smaller than the pores confining them, while cluster is a more general term describing oil ganglia saturating a number of neighboring pores, single pores, or a fraction of pores. Fig. 2A shows the cluster frequency as a function of the same cluster volumes (cubic micrometers) for each bin for the drainage and imbibition steps, e.g., for the first data point, 10³ < oil cluster volume (in cubic micrometers) < 10⁴. Fig. 2B shows the distribution of the normalized oil volume in clusters of a certain size as a function of the cluster volumes (cubic micrometers). Cluster volumes range from 10⁴ μm³ for the smallest clusters to 10¹¹ μm³ for the largest clusters. Clusters smaller than 1.42 × 10⁴ μm³ (10 voxels) were excluded to eliminate the influence of noise in the raw data. During both drainage processes, large, and probably sample-spanning, clusters existed with volumes exceeding 10¹⁰ μm³ (Fig. 1 A and B). This analysis leads to five key observations: (i) The largest oil cluster after drainage at 10 µL⋅min⁻¹ contained 76% of the total oil volume. This cluster, rendered in yellow in Fig. 1A, is clearly a percolating cluster, i.e., it connects to the inlet and outlet of the analyzed volume. At this stage, the total number of clusters was 4,142. (ii) Drainage at 700 µL⋅min⁻¹ and the subsequent fluid redistribution caused the oil saturation to reduce by 17% as a result of oil migration out of the central region of core plug. The total number of oil clusters almost doubled (i.e., increased to 7,561). (iii) After imbibition at 10 µL⋅min⁻¹, the saturation of oil was further reduced by 15%. The total number of oil clusters increased to 9,054. The volumetric cluster size distribution shows a peak at 10⁹ μm³, which is two and three orders of magnitude smaller than the two peaks recorded for the slow and fast drainage processes (at 10¹¹ and 10¹² μm³, respectively). (iv) After imbibition at 700 µL⋅min⁻¹, the oil saturation decreased by a further 10%. Further breakdown of the oil clusters occurred, doubling the total number of oil clusters present to 18,130. The continuous increase in cluster number and decrease in cluster size during both imbibition steps suggests that the oil clusters were trapped. However, additional oil was mobilized when the brine injection rate was increased. (v) The nonwetting-phase clusters are larger than the mean pore size by three to six orders of magnitude (Fig. 2B), and so oil clusters are composed of thousands of pores.

Fig. 2.

Number-based (A) and volume-based (B) cluster size distribution after the four injection steps shown in Fig. 1. Note the large oil clusters with volumes above 10¹⁰ μm³ that existed after the drainage steps. The red curve shows the pore size distribution of this rock extracted from the µCT image of the dry rock using a sphere fitting method (51). A continuous increase in number of clusters along with decrease in the cluster volumes indicates the change in oil structure during the drainage and imbibition processes.

Dominant Pore-Scale Fluid Displacement Mechanisms

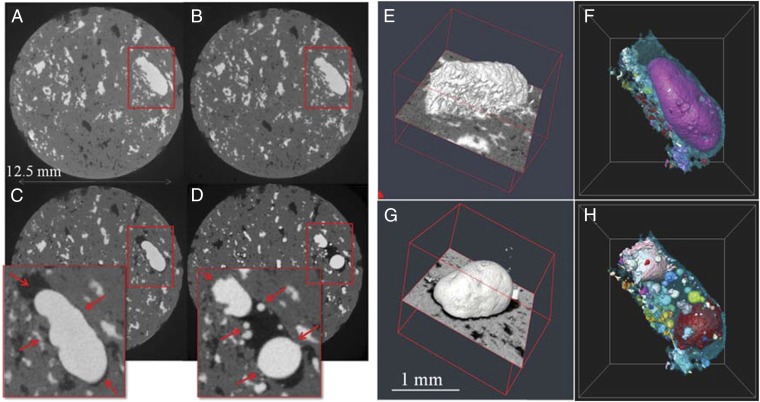
Fig. 3 A−D shows example µCT slices after each injection step. They indicate that the plug is preferentially water wet as the brine−oil contact angles (measured through brine) are below 90° (Fig. 3 C and D). Brine films in the corners of the pores after drainage cannot be resolved due to partial volume effects caused by the difference in X-ray attenuation of the two fluid phases (see Fig. S1). However, the apparent increase in the brine films’ thickness during imbibition (Fig. 3C) suggests that brine films were present.

Fig. 3.

(A−D) Example µCT slices after the four injection steps shown in Fig. 1. (E and G) A 3D rendering of the oil phase in the area highlighted in B and C, respectively. (F and H) A 3D rendering from another view point of the oil phase highlighted in C and D, respectively. The discrete oil droplets are rendered in different colors, while the blue transparent surface shows the brine phase. The large isolated oil droplet shown in C, F, and G is trapped because of a snap-off event and cannot be produced from the pore in this capillary dominated regime (N_c = 1.95 × 10⁻⁷). Red arrows indicate a visible brine film surrounding the isolated droplet of oil after snap-off (C) and fragmented droplets after fast imbibition (D).

Fig. 3 E and F shows 3D renderings of the oil phase and demonstrates how the oil phase in the largest pore in Fig. 3 B and C evolved during imbibition at 10 µL⋅min⁻¹. Before this slow imbibition process, the oil phase in this large pore was part of a well-connected cluster spanning multiple individual neighboring pores and throats (Fig. 3E). Following slow imbibition, the narrow throats in the neighborhood of the large pore were filled with brine such that the large oil cluster was broken up into 83 oil droplets trapped in the large pore and its neighbors. This observation is consistent with snap-off of oil by swelling of the corner wetting films in the pore throats. The large isolated oil droplet shown in Fig. 3 C, F, and G was trapped by the snap-off events, as it could not be displaced in this capillary-dominated flow regime. The 3D renderings of the labeled oil phase remaining after fast imbibition at 700 µL⋅min⁻¹ (Fig. 3H) show the presence of 276 oil droplets trapped in the same large pore (and in its neighbors) as shown in Fig. 3F. Of these droplets, 89% had volumes that were smaller than the volume of the original, i.e., largest, oil droplet before fast imbibition by at least two orders of magnitude (see Fig. S2). All oil droplets were in contact with the rock surface. The fragmentation of a large trapped oil droplet into many smaller droplets at high capillary numbers was observed throughout the core (see Figs. S3 and S4). The fragmentation of oil into multiple discrete droplets was most strikingly observed in the larger pores, but it also occurred in pores with volumes spanning over three orders of magnitudes, from 10⁸ µm³ to 10¹⁰ µm³ (Figs. S3 and S4). Note that the observation and quantitative analysis of this effect within pores with volumes smaller than 10⁸ µm³ was limited by image resolution.

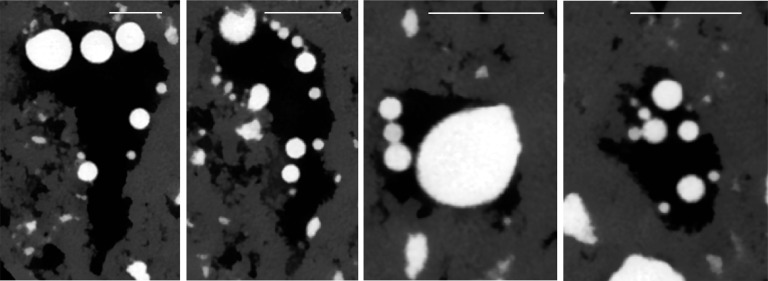
All of the instances that are reported in this manuscript as well as many more examples of droplet fragmentation have been observed in one flow experiment. Within this experiment, many tens to ∼100 fragmentation events were observed in numerous pores throughout the scanned volume (more examples are shown in Fig. 4).

Fig. 4.

Two-dimensional examples of fragmented oil droplets (white) in pores that are a few millimeters in size. The black color represents the brine phase. Droplets that appear to be in free suspension are in contact with the pore surface when viewed in 3D. (Scale bar, 1 mm.)

Cluster breakup in a relatively simple porous medium has been observed using laboratory experiments such as confocal microscope techniques (31–35) and micromodels (36). In these studies, however, the breakup of clusters occurred in the pore throats between two pore bodies. The fragmentation process that we identified is distinct because it comprises a metastable intrapore event. Droplet fragmentation has not previously been observed within sandstones or synthetic bead packs, which display simple and self-similar pore structures. It is because of the complex and multiscale pore structure inherent to this carbonate (and which is similar in many other carbonate rocks) that fragmentation was observed in this experiment. Any porous medium that displays similar characteristics, i.e., large pores with large aspect ratios (pore to throat size ratio), has the potential to accommodate droplet fragmentation.

Analysis of Fragmented Oil Droplets

Fragmentation Energy.

A suspended oil droplet forms a spherical shape to minimize its surface area (A) and thus surface free energy (σ_obA). Most fragmented droplets have shapes that are close to spherical (Fig. S5 provides a measure of the spheriodicity of the fragmented oil droplets). We assume an oil−brine (σ_ob) and oil−solid (σ_os) interfacial tension of 35 mN⋅m⁻¹ and 5 mN⋅m⁻¹ (37), respectively, and estimate the change in surface energy ΔE during fragmentation displacement as

$$\mathrm{\Delta }E=\frac{N{A}_i\left[\left(1-f\right){\sigma }_{ob}+f{\sigma }_{os}\right]-A_o{\sigma }_{ob}}{A_o{\sigma }_{ob}},$$ [1]

that is the increase in interfacial energy due to fragmentation into N droplets divided by the surface energy of the original droplet. Note that a fraction f of the fragmented oil droplets’ surface area is observed to be in contact with the rock surface. The low oil−solid interfacial tension in this fraction stabilizes the fragmented droplets. For any given droplet of arbitrary size, a minor change in incremental energy (i.e., less than 5 times the original droplet’s surface energy) is required to extensively fragment the droplet. For instance, a droplet with radius of 50 μm requires ΔE ∼5.33 × 10⁻⁹ to be fragmented into 200 smaller droplets, which is 4.85 times the original E of 1.1 ×10⁻⁹ J. This is the maximum energy required considering f = 0. The required ΔE decreases as f increases. Fig. 5 shows the additional relative energy required to fragment an oil droplet of arbitrary size into N smaller oil droplets. These calculations indicate that droplet fragmentation can occur with relatively small changes in interfacial energy.

Fig. 5.

Additional energy for fragmentation of an oil droplet of arbitrary size relative to the surface energy of the original oil droplet as a function of the number of fragments N and the fraction of the droplet’s surface that is in contact with the rock, f. The additional energy required for fragmentation is less than 5 times the original surface energy, which indicates that droplet fragmentation can occur for relatively small changes in interfacial energy that are consistent with the fluid properties used in the experiments.

The pressure−volume work of the viscous flow drives the fragmentation events. During imbibition at the high flow rate, the viscous forces exerted on oil clusters that were trapped in the pore space of the rock caused the clusters to break up into droplets. As a result of the work done, the oil−brine interface (per unit volume of oil), and hence the total interfacial energy, was increased.

Statistical Analysis of the Remaining Fragmented Droplets.

The overall increase in oil recovery due to fragmentation events is 10% of the initial oil saturation. The three pores depicted in Fig. 3 and Figs. S3 and S4 have volumes of 10¹⁰ μm³, 10⁹ μm³, and 10⁸ μm³, respectively. The volume fraction of the recovered oil as a result of fragmentation displacement is 68%, 38%, and 52%, respectively, of the oil trapped in these three pores after the slow imbibition. This change constitutes significant oil production that was initiated by fragmentation displacement and may explain published experimental observations of capillary desaturation at increasing capillary numbers (38) and, in particular, in rocks such as carbonates, which comprise a wide pore size distribution.

Stability of the Fragmented Oil Droplets.

The fragmented droplets were static in the same configuration in scans separated by over 24 h and did not move during the 3-h period of data acquisition for each scan. All fragmented oil droplets were in contact with the pore surface and stabilized by their contact with the mineral surface, relative to droplets freely dispersed in suspension. This condition of dispersed droplets attached to the mineral wall of the pore is metastable with respect to an unfragmented oil droplet, as discussed in Fragmentation Energy.

For the pore shown in Fig. 3, droplet fragmentation increased the oil−brine interfacial area as well as the oil−rock contact surface per unit volume of oil by factors of 1.62 and 4.12, respectively. The f values (per unit volume of oil) therefore increased from 0.24 to 0.43, providing more stabilization for the fragmented oil droplets. For interfacial area calculations, we refer to ref. 26. The change in interfacial energy ΔE of the oil phase was 0.73 of the initial energy of the trapped oil before fragmentation (6.4 × 10⁻⁷ J). The fragmentation energy calculations for pores with volumes 10¹⁰ μm³ and 10⁸ μm³ are presented in Table S2.

Cluster Size Analysis: Percolation Theory

Percolation theory suggests that size distribution of the trapped nonwetting phase clusters in a porous media after imbibition at infinitesimally low flow rates should scale as a power-law N(s) ∼ s^−τ (39, 40), where s is the number of pores saturated by a trapped nonwetting cluster and τ is the power-law exponent. For 3D structures, numerical simulations suggest that τ is typically larger than 2 (40−43). Values of τ larger than 2 were also observed in direct measurements of trapped cluster distributions in clastic rocks and synthetic porous media (16, 19, 20).

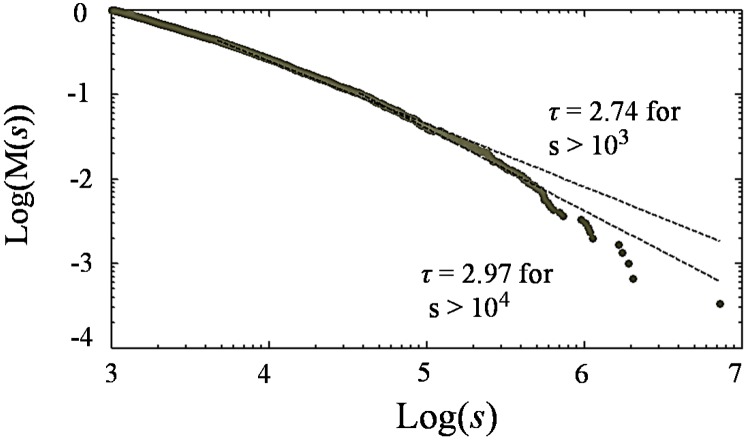
Fundamentally, percolation theory can only be applied to capillary-dominated flow with infinitesimally slow displacement rates. Therefore, here we only discuss the data obtained after the slow imbibition. It is possible to fit portions of the trapped oil “volume” distribution with a number of power-law functions such that τ ≥ 2. However, the entire range of the data does not fit a single power-law function (Fig. 6). According to percolation theory, a power-law behavior is only applicable if the cluster size is defined as the number of pores occupied and not the volume of the clusters (44). In homogeneous pore structures with narrow pore size distributions, the pore number-to-volume scaling approaches 1:1. Hence, the cluster sizes measured in volume using X-ray µCT imaging can closely replicate the number of pores occupied by the clusters. However, for heterogeneous pore systems with a wide pore size distribution, the pore number-to-volume scaling is no longer 1:1. Therefore, the number of pores occupied by clusters cannot be deduced from the volume of clusters. Further, the power-law scaling is valid only for clusters with s > 1 (44) (i.e., the bypassed oil clusters and not the clusters trapped in single pores as a result of snap-off). The power-law applies to distributions excluding the clusters that only occupy a single pore (20).

Fig. 6.

Cumulative cluster size probability distribution M(s) as a function of cluster size s, measured in voxels, calculated using a maximum likelihood estimator (52). It is possible to fit portions of the trapped oil “volume” distribution with a number of power-law functions such that τ ≥ 2. However, the entire range of the data does not fit a single power-law function.

Summary and Conclusions

Using X-ray µCT imaging and quantitative analysis of fluid phase distributions during drainage and imbibition processes (at low and high capillary numbers) in a heterogeneous carbonate core, we were able to visualize and identify features consistent with known pore-scale displacement mechanisms such as piston-like and snap-off events. In addition, we present evidence for a previously unidentified pore-scale mechanism that we term droplet fragmentation, which occurs at high capillary numbers. The experimental data suggest that droplet fragmentation significantly contributes to capillary desaturation at high capillary numbers in porous media with heterogeneous and multiscale pore systems.

Droplet fragmentation of the trapped nonwetting (i.e., oil) phase was observed in the larger pores of the carbonate, spanning at least three orders of magnitude in volume ranging between 10⁸ μm³ and 10¹⁰ μm³. The increase of viscous forces in these larger pores at higher capillary number is consistent with a small change in interfacial energy, which could cause larger trapped oil droplets to fragment into numerous smaller ones. These fragmented droplets are close to spherical shape to minimize their surface free energy.

Droplet fragmentation has a range of implications for understanding, quantifying, and modeling of multiphase fluid flow processes in a number of applications including the remediation of nonaqueous phase liquid contaminants in groundwater aquifers, subsurface CO₂ storage, and enhanced oil recovery. Droplet fragmentation changes the structure of the residual nonwetting phase, and hence increases the recovery of the nonwetting phase. Droplet fragmentation also enlarges the surface area between the wetting and nonwetting phase. The increase in surface area enhances mass transfer between both phases, which can be important for all these applications.

For example, in groundwater remediation, fragmentation displacement could not only lower the residual saturation of the trapped nonaqueous phase and mobilize this phase, it also increases the fluid−fluid surface area, which improves the effectiveness of surfactant addition and can accelerate the rate at which inorganic reagents and/or microbial treatments degrade nonaqueous phase liquids (45, 46). Similarly, during enhanced oil recovery, droplet fragmentation could reduce the residual oil saturation and enhance the rate at which chemicals and gases dissolve in oil (47). Both effects may increase oil recovery, but issues of recoalescence and mobilization remain.

The dissolution of trapped CO₂ in brine during solubility trapping is an important mechanism for secure subsurface CO₂ sequestration (48, 49). An increased CO₂−brine surface area due to droplet fragmentation can accelerate this process. Although droplet fragmentation may be limited to carbonate formations, as they normally contain a wide range of pore-sizes, it is expected that this mechanism is still of global importance considering that such formations host about 50% of the world’s hydrocarbon reserves and are a major host to the world’s groundwater resources. Droplet fragmentation is an additional mechanism that may need to be included in pore-scale models of displacement processes.

This work demonstrates that while the conventional view of pore-scale displacements mainly involves events between one or more pores or events that occur in pore throats (e.g., snap-off), processes can occur within a single pore body, both causing displacement of some of the nonwetting phase and producing a more complex fluid configuration. Hence, droplet fragmentation comprises a process that may only be represented adequately in dynamic pore-scale models.

Materials and Methods

Two-phase core flooding experiments were performed integrating µCT and a custom built X-ray transparent core holder (operating pressure to 690 kPa) to directly visualize fluid saturation distributions in a carbonate pore structure at pore scale. The carbonate sample is an outcrop Silurian dolomite (Thornton Formation) with a diameter of 12.5 mm and length of 44 mm (porosity ∼17%, permeability ∼50 milli-Darcy). More details about the rock's pore structure can be found in Figs. S6 and S7. The nonwetting phase is a mineral oil (50% 1-iododecane and 50% dodecane), the wetting phase is a 0.03 molar aqueous solution of KI. The oil and brine viscosities are 1.8 and 0.89 mPa s. This provided an excellent contrast between the two fluid phases and the rock on the acquired µCT images as well as an exact match between the densities of the two fluid phases (1.005 gr/cm³), which eliminated the potential for gravity-driven fluid redistribution during data acquisition. Image reconstructions were made using Octopus (8.5) (50), and postprocessing and quantifications were performed using Avizo Fire Versions 6.0–8.0. All tomographic data are at 11.25 µm per voxel resolution. The reader is referred to the Supporting Information for a more detailed description of the experimental procedure.