Activated germinal center B cells undergo directed migration

Abstract

Affinity maturation, the fundamental basis for adaptive immunity, is accomplished through somatic hypermutation of B-cell receptors followed by the expansion of rare mutants with higher affinity for the immunizing antigen. This process occurs over a period of weeks in unique microanatomic sites known as germinal centers. Two-photon microscopy has recently made it possible to track individual B cells moving within germinal centers in living animals. Characterizing the migration patterns of B cells within germinal centers is critical for understanding the mechanisms underlying affinity maturation. Here we present the results of two statistical approaches designed to test the hypothesis that the motion of B cells within germinal centers is random. Analysis of four different experiments shows that activated B cells move in a directed manner that sharply contrasts with the behavior of naïve B cells.

1 Introduction

The immune system operates by clonal selection (Cohn et al., 2007). When a foreign antigen finds its way into the body, it encounters a diverse repertoire of antigen receptors on T and B lymphocytes, and purely by chance, some of these receptors are capable of binding the antigen with low affinity (Murphy, Travers, and Walport, 2007). From this point onward, the immune system is adaptive, particularly in the case of B cells. B cells that initially bind to the antigen with low affinity are modified through cycles of somatic mutation of the B-cell receptor and affinity-dependent selection to produce high-affinity plasma cells, which secrete antibodies to fight infection, along with long-lived plasma cells and memory B cells, which protect the body from re-infection.

This process of affinity maturation occurs in germinal centers. These dynamic structures consist of several thousand tightly aggregated B cells and are initiated during T-cell-dependent immune responses during which antigen-activated B cells migrate to primary follicles in secondary lymphoid organs (e.g., spleen and lymph nodes). Within germinal centers, B cells proliferate rapidly and undergo somatic hypermutation (Kocks and Rajewsky, 1988). Rare mutants with increased affinity are preferentially expanded, most likely through a survival advantage whereby cells with decreased affinity have a higher death rate (Anderson et al., 2009). Germinal centers persist for approximately three weeks, and during this time, repeated cycles of mutation and selection reliably cause B-cell affinities to increase by orders of magnitude.

Despite longstanding interest in how cycles of mutation and selection enhance affinity so efficiently, the dynamic mechanisms underlying affinity maturation are incompletely understood (Kleinstein, 2008). Studying affinity maturation is challenging because the immune response is generated via interactions of cells migrating in space and through time. Several models have been proposed that ascribe functional importance to different spatial zones in the germinal center (Haberman and Schlomchik, 2003; Hauser et al., 2007; Hauser, Schlomchik, and Haberman, 2007; Kepler and Perelson, 1993; MacLennan et al., 1991; Meyer-Hermann and Maini, 2005a; Oprea and Perelson, 1997), but until very recently, it was not possible to visualize immune responses in real time in vivo. Given the dynamic nature of affinity maturation, this limitation was highly problematic. In recent years, however, we and others have visualized germinal-center cells in real time in living animals using intravital multi-photon microscopy (Allen et al., 2007; Hauser et al., 2007; Schwickert et al., 2007). This technique allows one to visualize cellular motion and other events during the immune response in real time under relatively physiologic conditions.

In order to determine how the overall structure of the germinal center contributes to the process of affinity maturation, we have been analyzing B-cell migration patterns (Hauser et al., 2007). Here we address the fundamental question of whether B-cell motion in the germinal center is random or directed (non-random). Several existing studies claim that both naïve and activated B cells undergo a random walk (Meyer-Hermann and Maini, 2005b; Miller et al., 2007; Schwickert et al., 2007), but this finding is difficult to reconcile with the distinct spatial structure of the germinal center and its dependence on various chemokines (Allen et al., 2007). Recent theoretical models have attempted to reconcile these observations (Figge et al., 2008). In contrast, our own previous work suggests that the migration of activated B cells is more directional than that of naïve cells, but we did not specifically compare B-cell motion to a random walk (Hauser et al., 2007). In this paper, we apply two statistical approaches to test the hypothesis that B cells move according to a random walk. Most previous analysis in this field was based on visual inspection of plots of squared displacement versus time (Allen et al., 2007; Schwickert et al., 2007). The methods applied here are a substantial improvement because they provide a direct, quantitative test of the random walk model. Analysis of four different two-photon experiments suggests that the migration of naïve B cells could be random but that activated B cells move in a directed manner.

2 Experimental data

We analyzed data obtained by Hauser et al. (2007), who tracked activated and naïve B cells moving within germinal centers in living mice. A full description of the experimental protocol can be found in Hauser et al. (2007). Briefly, antigen-specific B cells expressing green fluorescent protein (GFP) were transferred into GFP-tolerant mice ten days before imaging, and the mice were immunized with the antigen one day later. Two days before imaging, wild-type (naïve) B cells stained with Hoechst 33342, a blue nuclear dye, were transferred into the same mice, and an anti-CD35 antibody fragment conjugated to a red fluorochrome was injected to label follicular dendritic cells. The mice were anesthetized, and surgically exposed lymph nodes were imaged under a two-photon microscope. Three-dimensional images were acquired every 15 seconds for approximately one hour, and Volocity software was used to identify individual cells and to extract cell tracks from the images. For this paper, four mice were treated as described above. In two animals, both activated and naïve B cells were tracked. In the third mouse, only activated B cells were tracked; and in the fourth mouse, only naïve B cells were tracked. An example cell track from animal 1 is shown in light purple in Figure 1.

Figure 1.

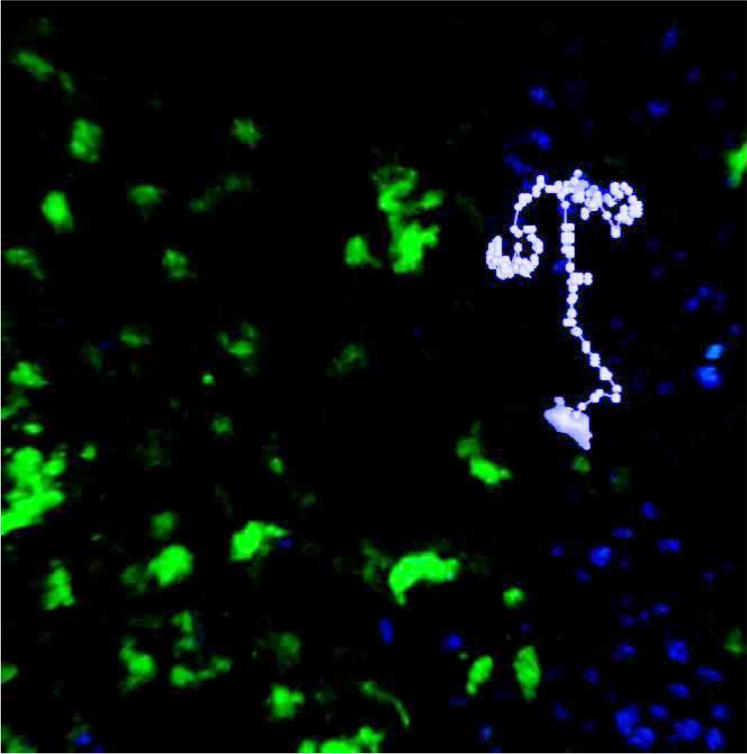
An image from a two-photon experiment overlaid with an example cell track from animal 1: Points indicate the cell centroid at 15-second imaging intervals with the entire cell shown at the beginning of the track.

We previously observed that total displacement for activated B cells is distributed according to a bimodal distribution (Hauser et al., 2007). Thus, in keeping with Hauser et al. (2007), we partitioned the activated B cells into two groups based on total displacement. Activated B cells of relatively large total displacement (>15 um) were classified as motile, and the remaining activated B cells were classified as stationary. We also analyzed the activated B cells as one group. Our data set is summarized in Table 1.

Table 1.

Number of cells tracked in each experiment

Animal Number	Motile B Cells	Stationary B Cells	Activated B Cells	Naïve B Cells
1	42	264	306	112
2	19	23	42	2784
3	74	53	127	0
4	0	0	0	5515

3 Displacement and time

The randomness of cellular motion is often assessed by analyzing the relationship between displacement and time (Allen et al., 2007; Schwickert et al., 2007). It is valuable to analyze this relationship because the variance of a random walk is always proportional to time. The variance of a random walk can be measured by calculating the mean squared displacement of a sample of cells following that random walk. If the mean squared displacement of the sample does not increase linearly with time, then one may conclude that the cells are not following a random walk.

For each set of cells in our data set, we calculated the mean squared displacement as a function of the time interval using the following formula:

$$<r^2(t)>=\frac{1}{N}{\displaystyle {\sum }_{\mathrm{k}=1}^N{|X_{\mathrm{k}}(t_{\mathrm{o}}^{\mathrm{k}}+t)-X_{\mathrm{k}}(t_{\mathrm{o}}^{\mathrm{k}})|}^2}.$$ (1)

Here, <r²(t)> is the mean squared displacement for a time interval t, N is the number of cell tracks containing t + 1 or more time points, X_k(T) is the three-dimensional position of cell k at time T, and $t_{\mathrm{o}}^{\mathrm{k}}$ is the earliest time point in cell track k. The displacement of a cell is a three-dimensional vector not necessarily equal to the total distance traveled by the cell, and the mean squared displacement is a scalar quantity. We chose not to calculate displacements relative to time points other than starting time points because we wanted to give all cell tracks equal weight regardless of their temporal length. For each set of cells, we stopped calculating the mean squared displacement when N dropped below an arbitrary lower limit of five.

For cells moving randomly in three dimensions, the relationship between mean squared displacement and time is given by

$$<r^2\left(t\right)>=6\mathit{Dt}$$ (2)

where D is the diffusion coefficient and t is the time interval (Beauchemin, Dixit, and Perelson, 2007). Taking the natural logarithm of both sides of this equation, we obtained the following:

$$\log (<r^2(t)>)=\log (6D)+\log (t).$$ (3)

Thus, if one plots the logarithm of mean squared displacement versus the logarithm of time for a group of B cells, then the plot will produce a straight line as long as mean squared displacement is proportional to some power of time. If the cells are moving randomly, then the slope of the line should be one, and if the slope of the line is not one, then the cells are probably not moving randomly. In this plot, the intercept on the displacement axis depends only on the diffusion coefficient.

We plotted the logarithm of mean squared displacement versus the logarithm of time for all the groups of B cells in our data set, and we found the slope of each line using a weighted least-squares regression. Each measurement of the logarithm of mean squared displacement was weighted according to the reciprocal of its variance, which was calculated using an error propagation formula based on the Taylor series. The plots that we obtained are presented in Figure 2. The dotted lines in each plot show the weighted least-squares fits to the experimental data. For each slope, we used a t-test to calculate a p-value for the hypothesis that the slope was equal to one.

Figure 2.

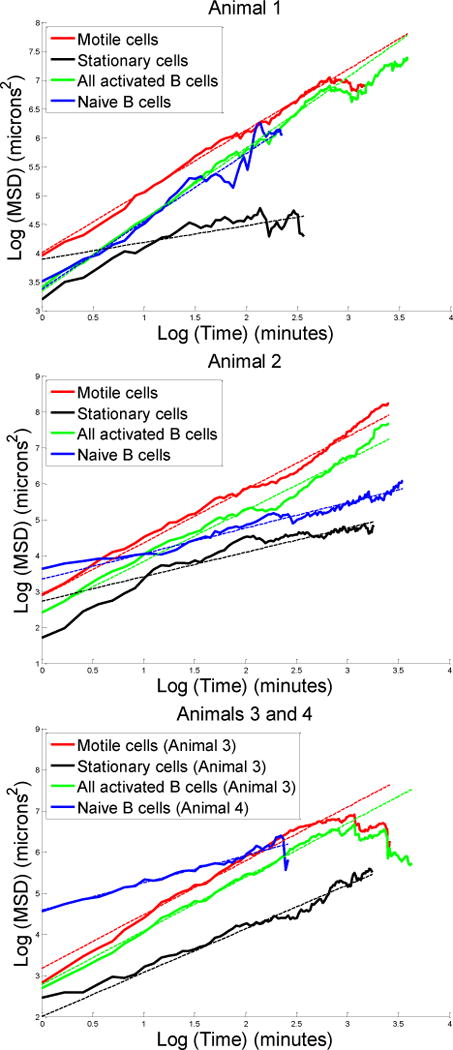
Plots of the natural logarithm of mean squared displacement (MSD) versus the natural logarithm of time

We did not use all possible data points in our regressions. We removed data points corresponding to time intervals shorter than one minute because the motion of B cells is believed to involve a lag period of approximately one minute (Figge et al., 2008). Visual inspection of the data also showed a change in slope around this time (Figure 2), consistent with altered migration behavior for time scales shorter than one minute. For all activated B cells and motile cells tracked in animals 1 and 3, we also removed data points beyond approximately fifteen minutes, after which time the mean squared displacement started to dip as the time interval increased. Although these dips could possibly be the result of physical barriers constraining the motion of activated B cells, they more likely result from B cells leaving the limited field of view. Thus, we felt it was reasonable to exclude these dips from our regressions.

The fitted slopes that we obtained are presented in Table 2. For each of three sets of activated B cells, the mean squared displacement was related to time raised to a power significantly greater than one (p<<0.01). Thus, we conclude that activated B cells move in a directed manner. As expected, the slopes for the motile cells were consistently greater than the slopes for the stationary cells. The three slopes for naïve B cells included one slope greater than one and two slopes less than one. This observation suggests that naïve B cells could be following a random walk. The peculiarities of the germinal center environment, such as dense packing, can give rise to unexpected behaviors (Beltman et al., 2007) and may violate some of the assumptions underlying our analysis. Consequently, it is perhaps most informative to compare the migration of activated and naïve B cells directly. In all experiments, we found that the slope for activated cells was greater than the slope for naïve cells, indicating that the motion of activated B cells is more directed than that of their naïve counterparts. This is especially significant given that our analysis did not exclude naïve cell tracks that move through the germinal center. These tracks may be more directed than those from naïve cells surrounding the germinal center, thus making our assessment of directionality conservative for naïve cells.

Table 2.

Estimated slopes and standard deviations

Cell Type	Animal Number	Fitted Slope	Standard Deviation
Motile cells	1	1.06	0.01
	2	1.48	0.02
	3	1.31	0.02
Stationary cells	1	0.29	0.05
	2	0.68	0.03
	3	1.06	0.02
All activated B cells	1	1.24	0.01
	2	1.41	0.02
	3	1.31	0.01
Naïve B cells	1	1.17	0.05
	2	0.71	0.02
	4	0.66	0.04

4 Incremental motion

Another important property of a random walk is that every incremental displacement is independent of all previous increments. This property implies that if one calculates every incremental displacement vector for a given cell moving in three dimensions, then these incremental displacement vectors should be distributed uniformly among the eight octants of the three-dimensional coordinate system.

For each cell track, we calculated every three-dimensional incremental displacement vector. Although the time resolution in our data set is fifteen seconds, we decided to calculate incremental displacements between data points separated by one minute because B-cell migration has been proposed to involve a directional persistence time of approximately one minute, as described earlier.

We divided the incremental displacement vectors for each individual cell track into eight bins corresponding to the eight octants of the xyz-coordinate space. We then calculated a chi-squared value T for each cell track using the following formula:

$$T={\displaystyle {\sum }_{\mathrm{k}=1}^8\frac{{(O_{\mathrm{k}}-E)}^2}{E}}.$$ (4)

Here, O_k is the number of displacements in the kth bin, and E is the expected number of displacements per bin. We set E equal to the total number of incremental displacements divided by eight because we wanted to test the hypothesis that the incremental displacements came from a uniform distribution across the bins. We obtained a p-value for each cell track by comparing its test statistic to a chi-squared distribution with seven degrees of freedom. To account for the fact that we obtained a p-value for each track, we assessed the statistical significance of each p-value at the five-percent level using a Bonferroni correction. When one uses this correction, the likelihood of obtaining one statistically significant p-value given the null hypothesis is less than five percent (Bland and Altman, 1995).

Histograms of the chi-squared values that we obtained for each type of B cell are shown in Figure 3. The dotted lines in the figure represent the thresholds of statistical significance. We obtained six statistically significant chi-squared values among the activated B cells (one stationary and five motile cells), and no statistically significant chi-squared values among the naïve B cells. To ensure that these results were not a consequence of persistence time, we doubled the assumed directional persistence time to two minutes and recalculated our results. In this case, we obtained two statistically significant chi-squared values for activated B cells, and none for naïve B cells. Similarly, using fifteen-second intervals did not significantly affect the results. Consistent with our analysis of displacement versus time, our results indicate that activated B cells undergo non-random migration whereas naïve B cells undergo migration that could be random.

Figure 3.

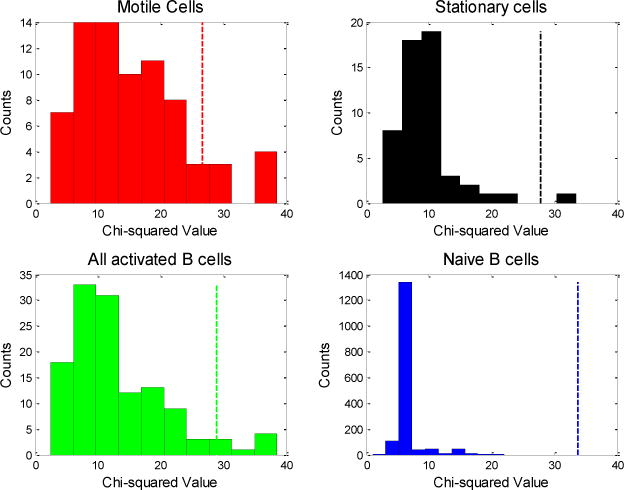
Histograms of chi-squared values for all four experiments combined: Each chi-squared value results from incremental displacement analysis of a single cell track. The dotted vertical lines indicate p-value cutoffs of 0.0004 for the motile cells, 0.0002 for stationary cells, 0.0001 for all activated B cells, and 0.00002 for naïve B cells. These are the Bonferroni corrected cutoffs corresponding to a Type I error of 0.05.

The fact that incremental displacement vectors for activated B cells are distributed non-randomly among the eight octants of our three-dimensional coordinate system does not rule out the possibility that the cells are moving randomly in a confined space of lower dimensionality. To test this hypothesis, we modified our chi-squared analysis to examine each dimension individually. For a given dimension, we binned each incremental displacement vector according to the sign of its component in that dimension; and in this manner, we calculated three chi-squared values for each cell track, one for each dimension. We used a chi-squared distribution with one degree of freedom to assess the statistical significance of each chi-squared value, and as before, we used a Bonferroni correction to correct for multiple hypothesis testing.

As expected from our previous analyses, we obtained no statistically significant chi-squared values for naïve B cells, a finding consistent with the idea that these cells move randomly. For the motile cells, we obtained statistically significant chi-squared values regardless of which plane was used to define the directionality (five significant values in the x-direction, one in the y-direction, and one in the z-direction). These results suggest that motile cells are moving non-randomly. We obtained no significant chi-squared values for the stationary cells; and when we treated all the activated B cells (motile and stationary) as one group, we once again found significant chi-squared values. The number of significant cell tracks is lower in this case compared with the motile cell analysis because of our Bonferroni correction, which resulted in a threshold of statistical significance that was higher for the set of all activated B cells than it was for the motile and stationary cells analyzed separately. The chi-squared values that we obtained for the activated and naïve B cells are presented in Figure 4. The top row of the figure represents activated B cells, and the bottom row represents naïve B cells. As one can see, all three histograms associated with the activated B cells have more values approaching statistical significance than any of the histograms associated with naïve B cells.

Figure 4.

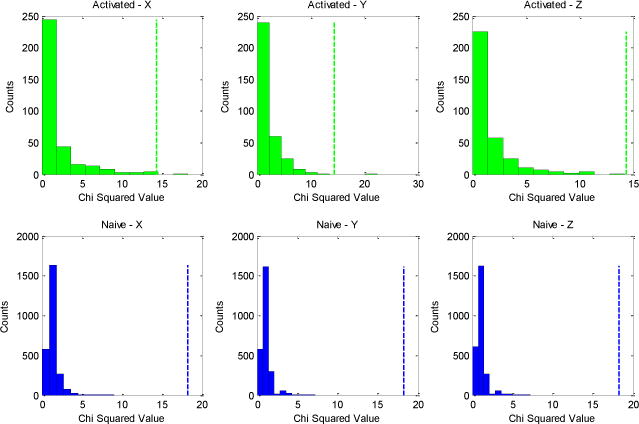
Histograms for one-dimensional chi-squared analysis: Data for activated B cells are shown in green, and data for naïve B cells are shown in blue. The vertical dotted lines represent thresholds of statistical significance corresponding to a Type I error of 0.05.

The fact that we did not find a statistically significant chi-squared value for the z-direction when we combined all the activated B cells could be related to the fact that our window for tracking cells was smaller in the z-direction than in other directions. It should also be remembered that the Bonferroni correction that we used is highly stringent. Overall, the results of this one-dimensional analysis suggest that motile B cells (and perhaps all activated B cells) move non-randomly, implying that our previous results cannot be attributed to B cells moving randomly in a lower-dimensional space.

5 Discussion

We have presented two statistical approaches for assessing the randomness of B-cell motion in germinal centers. First, by analyzing the relationship between mean squared displacement and time, we showed that the mean squared displacement is consistently related to time raised to a power significantly greater than one for activated B cells. This observation suggests that the motion of activated B cells is directed. Second, by analyzing the incremental displacement vectors of activated B cells, we showed that these displacements are not uniformly distributed and thus are not consistent with the hypothesis that all activated B cells move according to a random walk. Thus, in contrast to previous reports (Figge et al., 2008; Schwickert et al., 2007), we conclude that the motion of activated B cells is directed.

Our results suggest that directed motion (perhaps driven by chemokine gradients) could play an important role in affinity maturation. These observations provide critical constraints on models of germinal-center dynamics (Figge et al., 2008; Hauser et al., 2007; Meyer-Hermann and Maini, 2005a; Oprea and Perelson, 1997). It is worth noting that the analysis presented here did not separate cells based on location in the germinal center. Now that directed migration has been established for activated B cells, it will be important to quantify the directional drift and determine whether there are overall spatial patterns that govern cellular movement in germinal centers.

Biographies

Mark J. O’Connor received a B.S. Degree from Yale University in 2009, double majoring in Biology and Applied Mathematics, and is currently a medical student at the University of Massachusetts Medical School. His research interests include computational biology, immunology, and virology.

Anja E. Hauser, a veterinarian by training, became interested in lymphocyte trafficking during her dissertation at the DRFZ where she studied the migration of plasma cells. In 2004, she joined M. Shlomchik’s laboratory at Yale University School of Medicine, New Haven, USA, as a postdoctoral fellow and worked on B cell migration in vivo. In 2008 she returned to Germany and established her own laboratory, which focuses on the analysis of immune responses using multiphoton intravital microscopy.

Ann M. Haberman trained as a biochemist, after which she received her Ph.D. in immunology at the University of Pennsylvania, Philadelphia, USA. She is currently an Assistant Professor at the Yale School of Medicine. Her research interests include factors that promote proliferation and differentiation of germinal center B cells. Intravital two-photon laser scanning microscopy is a technique employed in her lab to visualize events during immune responses.

Steven H. Kleinstein received his B.A.S. Degree in Computer Science from the University of Pennsylvania in 1994, and his Ph.D. in Computer Science from Princeton University in 2002. He is currently an Assistant Professor in the Department of Pathology at the Yale University School of Medicine, where he is part of the Pathology Informatics division. He conducts research in the field of computational immunology, where his work combines techniques from dynamic modeling, systems biology and bioinformatics to better understand the immune response.