Fully linear reconstruction method for fluorescence yield and lifetime through inverse complex-source formulation: simulation studies

Abstract

In fluorescence imaging, both fluorescence yield and lifetime are of great importance. Traditionally, with the frequency-domain data, two parameters can be directly recovered through a nonlinear formulation. However, the reconstruction accuracy highly depends on initial guesses. To overcome this hurdle, we propose the linear scheme via an inverse complex-source formulation. Using the real and imaginary parts of the frequency-domain data, the proposed method is fully linear; it is not sensitive to initial guesses and is stable with high-level noise. Meanwhile, the algorithm is efficient, and the reconstruction takes one or a few iterations. In addition, the colocalization constraint due to the unique feature of fluorescence imaging is imposed to enhance algorithm performance. The algorithms are tested with simulated data.

Fluorescence tomography (FT) is capable of spatially resolving fluorescence yield or lifetime quantitatively. Fluorophore concentration determined from fluorescence yield provides valuable information of the location and functional status of the targeted tissue, while fluorescence lifetime provides essential microenvironment information, such as local pH, blood supply, and temperature. FT is becoming an essential in vivo molecular imaging tool for scanning small animals in recent years due to rapid advances in fluorescent probe development. Various research groups have developed small-animal FT systems for applications ranging from cancer imaging to stem cell imaging [1–7]. Although the reconstruction algorithm has been extensively examined [8–11], to date only a few studies have reported the reconstruction of lifetime [7,8]. In this Letter, we will develop techniques to improve the simultaneous reconstruction of both parameters with frequency-domain data.

Regarding the formulation of the reconstruction, a direct method was proposed to recover both fluorescence parameters, but it was nonlinear and sensitive to the initial guess [10]. In contrast, an inverse complex-source approach was suggested; however, it was not fully linear due to the use of the logarithm (log) of the amplitude and the phase of the data [11]. In this study, we adopt the complex-source formulation and make it into a fully linear scheme via the use of the real and imaginary parts of the data. Moreover, we show that the linear scheme can be further enhanced by imposing colocalization constraints.

Hereafter, we use the following coupled diffusion approximation as the forward model:

$$\begin{array}{l}-\nabla ·(D_x\nabla {\varphi }_x)+\left({\mu }_{ax}+i\frac{\omega }{c}\right){\varphi }_x=q,\\ -\nabla ·(D_m\nabla {\varphi }_m)+\left({\mu }_{am}+i\frac{\omega }{c}\right){\varphi }_m=\frac{{\mu }_{af}}{1-i\omega \tau }{\varphi }_x,\end{array}$$ (1)

where the quantities are photon density ϕ_x,m, absorption coefficient μ_ax,am, diffusion coefficient D_x,m at excitation/emission wavelength, fluorescence yield μ_af, fluorescence lifetime τ, excitation source q, modulation frequency ω, and speed of light in medium c. Let i ≤ N_s index the sources and j ≤ N_d index the detectors, with P_j representing the measuring functional, and F⃗ will be the data predicted by Eq. (1), i.e., the vector-valued function F⃗ = [P_jϕ_m,i].

Assuming that μ_ax,am and D_x,m are both known, the direct method to recover X := (μ_af, τ) for FT is through the following least-squares formulation, i.e., the minimization of the difference between the model F⃗(X) and the data Y:

$$X=\underset{X}{argmin}{\Vert \overrightarrow{F}(X)-Y\Vert }_2^2.$$ (2)

A standard method for solving Eq. (2) is through the iterative linearizations via the Born approximation. Meanwhile, Eq. (2) needs to be regularized due to its ill posedness or the data noise, for which L2 regularization is popular. That is, we iteratively solve the following with the initial guess X⁰:

$$X^{n+1}=X^n+\underset{\delta X}{argmin}[{\Vert J^n\delta X-(Y-J^n{X}^n)\Vert }_2^2+\lambda {\Vert \delta X\Vert }_2^2],$$ (3)

where Jⁿ is the Jacobian computed with the current value $X^n=({\mu }_{af}^n,{\tau }^n)$ after the nth iteration, δX is the change in X, and λ is a regularization parameter.

Notice that F⃗ is nonlinearly dependent on X and J depends on Xⁿ. Besides, Eq. (3) is only an approximation of Eq. (2). As a result, when Eq. (3) is used, both the accuracy and the stability of the reconstruction highly depend on the initial guess X⁰. When X⁰ is far from the true solution, the reconstructed solution via Eq. (3) may diverge from or converge to some local minimum instead of a true solution to Eq. (2). Fortunately, this weakness can be completely overcome through the following complex-source transformation.

In this case, the fluorescence term in Eq. (1) is treated as a complex-source pair (q_R, q_I), i.e.,

$$\frac{{\mu }_{af}}{1-i\omega \tau }=q_R+{iq}_I.$$ (4)

The formulation of Eq. (4) is intrinsic to FT due to coexistence of fluorescence yield and lifetime, which will be used again later to define colocalization constraints. With new variables X^C := (q_R, q_I) instead of X, ϕ_m,i in Eq. (1) is linear with respect to X^C.

However, the reconstruction scheme using Eq. (2) with X^C is still not fully linear yet, because P_jϕ_m,i may not linearly depend on X^C, although ϕ_m,i does. This is where our formulation deviates from the original complex-source formulation [11]. There, the use of log of the amplitude and phase of the data prevents the linear dependence of P_jϕ_m,i on X^C. In addition, the reconstruction requires nonzero initial guesses of μ_af for the execution of Eq. (3) because P_jϕ_m,i appears in the denominator of Jacobian J. As a result, one still needs to update J during iterations. Instead, we use the real and imaginary parts of the data in our algorithm, which is precisely the reason for the linear dependence of P_jϕ_m,i on X^C. Moreover, while Eq. (2) can be solved similarly through Eq. (3), Eq. (3) is exactly the same as, instead of an approximation of, Eq. (2) due to the linearity. That is, with both X^C = (q_R, q_I) and the use of the real and imaginary parts of the data, FT can be exactly solved by the following minimization problem as a counterpart of Eq. (2):

$$X^C=\underset{X^C}{argmin}{\Vert {JX}^C-Y\Vert }_2^2.$$ (5)

Notice that the Jacobian J in this formulation does not depend on X^C and, therefore, needs to be computed only once. Besides, the similar approach using Eq. (3) can be applied to regularize and solve Eq. (5) with one or a few iterations. After the reconstruction, (μ_af, τ) can be retrieved from X^C through Eq. (4).

Furthermore, the algorithm for solving Eq. (5) can be further augmented by colocalization constraints due to the aforementioned unique coexistence of fluorescence yield and lifetime in FT, which can be achieved using the following steps. Let $X^{C,n}=(q_R^n,q_I^n)$ be the solution after the nth iteration, which has not been updated yet. First, we intersect two individual supports with a threshold value ${\epsilon }_R={\sigma }_R·max(q_R^n)$ for $q_R^n$ and a threshold value ${\epsilon }_I={\sigma }_I·max(q_I^n)$ for $q_I^n$, i.e., ${\mathrm{\Omega }}_n={\mathrm{\Omega }}_{q_R^n>{\epsilon }_R}\cap {\mathrm{\Omega }}_{q_I^n>{\epsilon }_I}$. Second, we update the solution only within intersected support Ω_n through $q_R^n=q_R^{n-1}+\delta q_R^n{\chi }_{{\mathrm{\Omega }}_n}$ and $q_I^n=q_I^{n-1}+\delta q_I^n{\chi }_{{\mathrm{\Omega }}_n}$. In summary, with colocalization constraints, Eq. (5) can be solved via

$$\begin{array}{l}\delta X^{C,n}=\underset{\delta X}{argmin}[{\Vert J\delta X-(Y-{JX}^{C,n})\Vert }_2^2+\lambda {\Vert \delta X\Vert }_2^2],\\ X^{C,n+1}=X^{C,n}+\delta X^{C,n}·{\chi }_{{\mathrm{\Omega }}_n}.\end{array}$$ (6)

In theory, a single iteration of Eq. (6) should be enough due to the linearity. However, due to its ill-posed nature or the high-level noise, a few iterations are suggested with a large initial regularization parameter λ.

Last but not least, to balance the scale variation of the data, we scale Eq. (5) to minimize Σ_i|(JX^C)_i − Y_i|²/|Y_i|² instead, where i indices all source-detector pairs.

Next, we will compare the nonlinear method, Eqs. (2) and (3) (method 1), and the linear method, Eq. (5) and (6) (method 2), through various simulation studies using a 40 mm diameter synthetic phantom (Table 1). Eight sources and eight detectors are alternatively distributed around the phantom in fan-beam geometry, and the modulation frequency is set to 100 MHz. Here, the finite element method is used as a discretization method for general purposes [12], in which the photon density and reconstruction variables are discretized piecewise-linearly and -constantly, respectively. Approximately three thousand variables need to be recovered using 128 measurements.

Table 1.

Synthetic Phantom and Reconstruction Parameters^a

Case	(μaf, τ)		Noise Level	Initial Guess (μaf, τ)
	Background	Inclusions		Method 1	Method 2
1	(0, 0)	(1, 1)	1%	(0.01, 0)	(0, 0)
2	(0.5, 0.5)	(1, 1)	1%	(0.5, 0.5)	(0.5, 0.5)
3	(0.5, 0.5)	(1, 1)	1%	(0.01, 0)	(0, 0)
4	(0.5, 0.5)	(1, 1)	5%	(0.5, 0.5)	(0, 0)
5	(0.5, 0.5)	(1, 1)	10%	(0.5, 0.5)	(0, 0)

^aThe 40 mm diameter circular phantom is centered at (0, 0) with one 10 mm diameter circular inclusion centered at (0, −10) and two 4 mm diameter circular inclusions centered at (−12, 6) and (7, 7), which are located at different depths, roughly 10 mm and 6.7 mm from the boundary, respectively. Homogeneous optical background is assumed with D_x = 0.22 mm⁻¹, μ_ax = 0.01 mm⁻¹, D_m = 0.33 mm⁻¹, and μ_am = 0.015 mm⁻¹. The unit of fluorescence yield is 10⁻⁴ mm⁻¹ and that of lifetime is the nanosecond.

Five different cases were simulated. In the first case, we assumed perfect uptake, so there was no fluorophore at the background. The fluorescence yield and lifetime were set to 10⁻⁴ mm⁻¹ and 1 ns, respectively, for all inclusions (case 1). In other cases, the target-to-background contrast was set to two for both concentration and lifetime (cases 2–5). The effect of different initial guess and noise level combinations was evaluated using these cases. The reconstruction results for each case are plotted in Figs. 1–5, while the true values, initial guesses, and noise levels are specified in Table 1. In all figures and tables, the unit of fluorescence yield and lifetime is 10⁻⁴ mm⁻¹ and nanoseconds, respectively. Please note that method 1 requires nonzero initial fluorescence yield ${\mu }_{af}^0$ and that the plotted results from method 1 are post-processed through colocalization constraints similar to Eq. (6) for fair comparison.

Fig. 1.

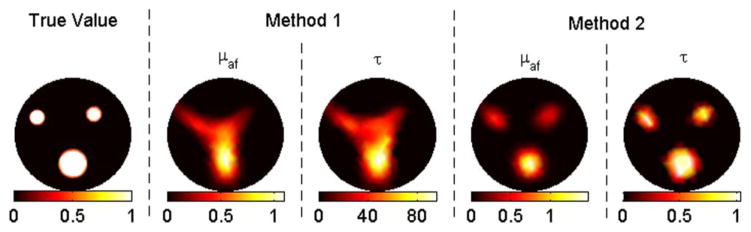
(Color online) Reconstruction results for case 1 (no background fluorescence).

Fig. 5.

(Color online) Reconstruction results for case 5 (contrast = 2) with 10% noise, correct background, and zero background as the initial guess in methods 1 and 2, respectively.

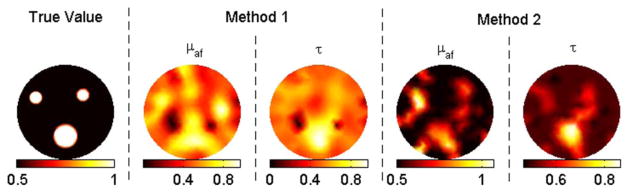
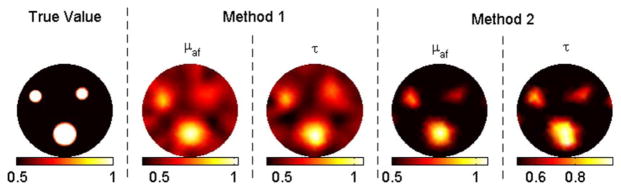
In case 1, method 1 fails to resolve the inclusions clearly, as shown in Fig. 1. Besides, the recovered mean lifetime values for inclusions are completely off, varying between 12 and 76 ns. In contrast, method 2 is able to recover the fluorescence yield of the inclusions within a 30% error. The recovered mean fluorescence yields are 1.2 × 10⁻⁴, 0.8 × 10⁻⁴, and 0.7 × 10⁻⁴ mm⁻¹, respectively. Meanwhile, this method recovers the true lifetime for each inclusion. In cases 2–5, the contrast-to-background value for each inclusion is set to two. With the correct background values as the initial guess (case 2), both methods recover the true fluorescence yield and lifetime for the big object, as shown in Fig. 2. The same parameters are recovered within 30% error again for the small objects. When the initial guess is assumed to be zero (case 3), method 2 still performs effectively, while method 1 malfunctions such that the error in the recovered fluorescence yield goes up to 60% and lifetime values for inclusions vary between 26 and 48 ns. Afterward, 5% and 10% Gaussian noise are successively added to the synthetic data, cases 4 and 5, respectively. For both cases, method 1 starts with the true background values, while method 2 starts with zeros as the initial guess. Despite the wrong values as initial guesses, method 2 produces better results than method 1, as shown in Figs. 4 and 5. For example, method 1 could only recover half of the true values for small objects for case 5 due to the high-level noise. Method 2, on the other hand, could recover both parameters within 30% error for these small objects.

Fig. 2.

(Color online) Reconstruction results for case 2 (contrast = 2) with correct background as the initial guess.

Fig. 4.

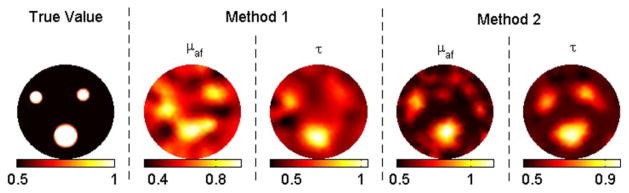
(Color online) Reconstruction results for case 4 (contrast = 2) with 5% noise, correct background, and zero background as the initial guess in methods 1 and 2, respectively.

We want to emphasize that the choice of threshold σ_R and σ_I should be task dependent: to detect the most significant object, especially with high-level noise, a large value is preferred, e.g., 20% of the maximal value; in contrast, the small threshold is able to “see” small features. Here, σ_R and σ_I are taken to be 5%, 10%, and 20%, respectively, for 1%, 5%, and 10% noise.

Fig. 3.

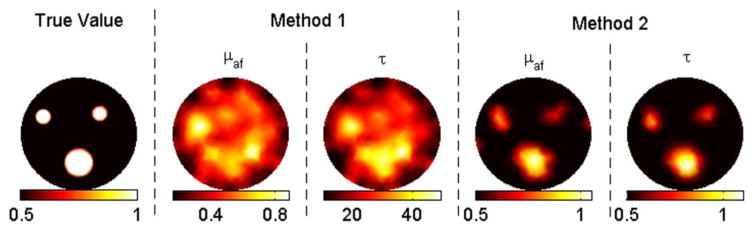
(Color online) Reconstruction results for case 3 (contrast = 2) with zero background as the initial guess.