Trait dimensionality explains widespread variation in local adaptation

Abstract

All species are locked in a continual struggle to adapt to local ecological conditions. In cases where species fail to locally adapt, they face reduced population growth rates, or even local extinction. Traditional explanations for limited local adaptation focus on maladaptive gene flow or homogeneous environmental conditions. These classical explanations have, however, failed to explain variation in the magnitude of local adaptation observed across taxa. Here we show that variable levels of local adaptation are better explained by trait dimensionality. First, we develop and analyse mathematical models that predict levels of local adaptation will increase with the number of traits experiencing spatially variable selection. Next, we test this prediction by estimating the relationship between dimensionality and local adaptation using data from 35 published reciprocal transplant studies. This analysis reveals a strong correlation between dimensionality and degree of local adaptation, and thus provides empirical support for the predictions of our model.

1. Introduction

Understanding local adaptation is a central goal of evolutionary ecology because of its important role in diversification, conservation and epidemiology [1–4]. Consequently, a large body of theory has been developed to predict the conditions under which local adaptation is expected to most readily evolve. The most robust result to emerge from this work points to the balance between gene flow and spatially heterogeneous selection as the primary determinant of local adaptation [5–8]. Specifically, if local selection pressures differ substantially among populations connected by comparatively weak gene flow, local adaptation is expected to evolve as local selection causes gene frequencies to diverge among populations. By contrast, if local selection pressures are relatively homogeneous over scales at which substantial gene flow occurs, gene flow swamps local selection and gene frequencies remain relatively homogeneous across space.

Although existing theory clearly identifies gene flow and spatially heterogeneous selection as key factors shaping local adaptation, their explanatory power appears to be relatively weak. For instance, a recent meta-analysis of studies estimating local adaptation using transplant designs in plant populations failed to identify a significant impact of spatial environmental heterogeneity, life history or mating system [9]. Similarly, another recent meta-analysis of reciprocal transplant studies found that environmental variability explained only a very small (4%) proportion of the variation in local adaptation observed across studies [10]. Although the explanatory power of these meta-analyses depends on the extent to which relevant environmental variation is included, they suggest that the extent of spatial heterogeneity in selection explains little variation in the magnitude of local adaptation. Although neither meta-analysis evaluated the importance of gene flow per se, the absence of any impact of plant life history or mating system on local adaptation suggests that gene flow may not play a particularly strong role. This view is consistent with empirical studies documenting strong local adaptation in the face of significant gene flow [11–14]. In summary, existing theory focusing on the balance between gene flow and selection does not adequately explain the abundant variation in the magnitude of local adaptation observed across reciprocal transplant studies [9,10].

One possible reason why existing theory fails to explain widespread variation in local adaptation is the common assumption that only a single trait is exposed to spatially variable selection [5,15–17]. In reality, of course, adaptation depends on a potentially very large number of traits, each of which influences an organism's performance in response to a particular environmental variable or ecological interaction. If the number of traits influencing an organism's fit to its environment differs among species, trait dimensionality could have important consequences for the widespread variation in local adaptation we observe in nature. Although some recent theory has begun to move beyond this critical assumption and integrate multiple traits [8,18,19], this theory has not focused on local adaptation as it is commonly measured empirically through the use of reciprocal transplant studies [20,21], instead focusing on the extent of trait differentiation among demes.

Here we develop and analyse a mathematical model that allows us to predict the value of local adaptation that would be detected using a reciprocal transplant study. This model allows us to explore how the number of traits exposed to spatially variable selection (trait dimensionality) influences the magnitude of local adaptation. We take two approaches to analyse this general model: first, we develop analytical approximations using classical quantitative genetic approaches in order to develop a clear set of predictions. Second, we evaluate the robustness of our analytical predictions using individual-based simulations that relax key assumptions of our analytical model. Finally, we empirically test the predictions of the models by directly estimating both dimensionality and local adaptation from reciprocal transplant data.

2. Model description and analysis

(a). Quantifying the effect of trait dimensionality on local adaptation

To investigate the impact of trait dimensionality, we developed a mathematical model that generalizes previous work on multivariate local adaptation [8,18,19]. Our model studies a species composed of a large number of populations, N, scattered across a complex and ecologically heterogeneous environment. Individuals move among these populations at some rate, m, and experience a local selective environment that favours particular trait values. Individuals that deviate from the optimal combination of trait values favoured by local selection experience reduced fitness. Consequently, natural selection drives population mean phenotypes toward their optimum local trait values [22]. Within subdivided populations, however, this process of adaptation can be counteracted by movement of individuals among populations and stochastic fluctuations in population mean phenotypes caused by random genetic drift [5,23].

The fitness of individual i from population α in environment β was determined by Gaussian stabilizing selection and is described by the function:

2.1

An individual's fitness in its own environment is given when α = β. Here, γ measures the intensity of stabilizing selection, z_i,t is the value of the individual's t^th trait. The corresponding θ_t,β is the optimal value for trait t in environment β, and n is the total number of traits exposed to spatially heterogeneous selection. Assuming stabilizing selection is relatively weak and allows us to quantify local adaptation, δ, as it is commonly measured in empirical studies using reciprocal transplant experiments [20]. Specifically, comparing population mean fitness at ‘home’ with population mean fitness ‘globally’ yields the following expression for local adaptation

2.2

where the term 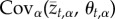measures the covariance across the metapopulation between the mean trait value of trait t in population α, and its local optimum for this trait, θ_t,α (see electronic supplementary material for a complete derivation). This expression shows that local adaptation increases with the degree of matching between population mean phenotypes and local optima and, all else being equal, with the number of traits.

To predict how local adaptation evolves, we developed a framework for studying the evolution of the critically important covariances in equation (2.2). Specifically, we employed a classical quantitative genetic approach that assumes weak selection, fixed additive genetic variance and covariance, and multivariate Gaussian phenotype distributions. With these assumptions, the change in population mean phenotype in one generation for trait t in population α is given by

2.3

where G_t,k is a matrix giving the genetic covariance between traits t and k, 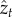is the global mean phenotype for trait t across the entire metapopulation and ε_t is a random deviation in the mean phenotype caused by genetic drift and is drawn from a multivariate normal distribution with mean zero and variance covariance matrix G/N (see electronic supplementary material for a complete derivation).

Although (2.3) can, in principle, be used to study the dynamics of local adaptation within a metapopulation, doing so requires analysing a very large system of difference equations equal to the number of traits multiplied by the number of populations. Instead, we used a change of variables that allows us to analyse any number of populations and traits by following the statistical moments describing the distribution of population mean phenotypes and local optima [5,24,25]. Remarkably, this change of variables reveals that evolution of local adaptation depends on only two variables: the covariance between the population mean value for trait t and the optimal value for this trait, 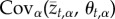, and the covariance between the population mean value for trait t and the optimal trait value for trait k, 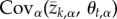. Thus, the change in the value of local adaptation that occurs over a single generation is described by the following pair of equations

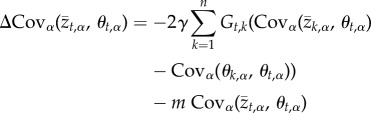2.4

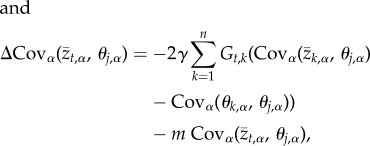2.5

where the term 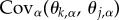measures the covariance between the optimal value of trait t and the optimal value of trait j over the metapopulation. Put differently, this term quantifies spatial variation and covariation in optimal trait values and can thus be more clearly represented as a variance–covariance matrix that we will refer to as Θ from this point forward (figure 1). Together, equations (2.4) and (2.5) fully describe the evolution of local adaptation for metapopulations of any size and, in conjunction with definition (2.2), allow us to solve for the equilibrium value of local adaptation. This equilibrium corresponds to a dynamic balance between the impacts of selection, gene flow and random genetic drift and is found by setting equations ((2.4)–(2.5)) equal to zero and solving for 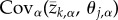and .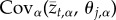

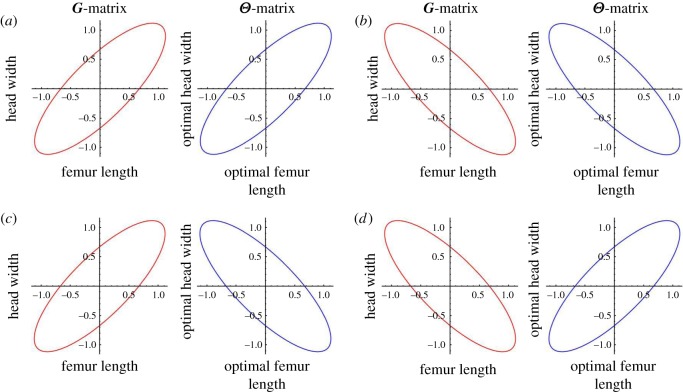
Figure 1.

Illustrating of alignment between G and Θ. Figure parts (a,b) depict alignment, (a) through positive correlations and (b) with negative correlations; (c,d) depict misalignment. (Online version in colour.)

We simplify our equilibrium solution for local adaptation by using a coordinate rotation into the principal component space of the G-matrix (electronic supplementary material). By defining a matrix A whose columns are the eigenvectors of G, we can find the two matrices G′ and Θ′ that represent the Θ and G matrices in the principal component space

2.6a

and

2.6b

where the ‘·’ indicates matrix multiplication and the superscript ‘−1’ indicates the matrix inverse. After applying this coordinate rotation, the model simplifies greatly and the equilibrium value of local adaptation is given by

2.7

This simple result shows that trait dimensionality (n) can have a significant impact on the level of local adaptation that ultimately evolves.

The simplest impact of dimensionality visible in (2.7) is similar to what we saw previously in equation (2.2), and corresponds to the simple accumulation of selection as more terms are added to the summation. Equation (2.7) also reveals, however, that the impact of dimensionality is a bit more subtle. Specifically, the rate at which local adaptation increases with dimensionality depends on the orientation of the genetic covariance matrix G relative to the environmental covariance matrix Θ (figures 1 and 2). Specifically, as the alignment between these covariance matrices decreases, the relationship between dimensionality and local adaptation weakens, potentially even becoming non-monotonic when G′ and Θ′ are strongly misaligned. Even in these cases of strong misalignment, however, local adaptation increases with dimensionality for modest numbers of traits, beginning to decrease only when trait numbers become relatively large.

Figure 2.

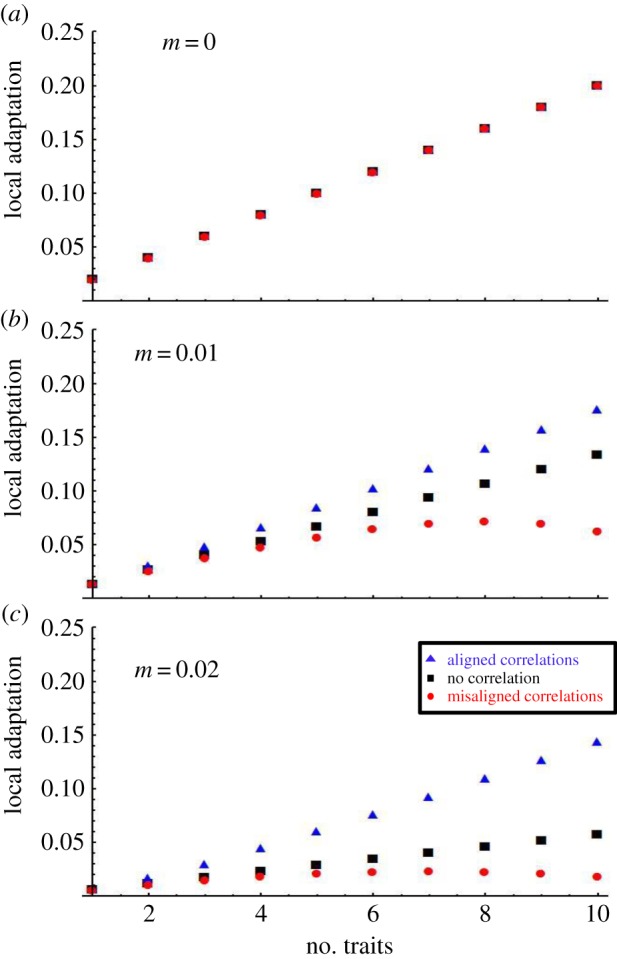
(a–c) Analytical predictions for the effect of trait dimensionality and alignment between genetic and environmental variation on local adaptation. Black squares illustrate equation (2.4) evaluated where (ρ_G = 0, ρ_Θ = 0). Similarly, the red circles are for (ρ_G = −0.09, ρ_Θ = 0.9; figure 1d) and blue triangles for (ρ_G = 0.09, ρ_Θ = 0.09; figure 1a). The phenotypic variance in each trait was 1. The strength of selection was set equal to γ = 0.01. (Online version in colour.)

In order to clarify the biological interpretation of alignment between the covariance matrices G and Θ, we provide a hypothetical example rooted in a well-studied biological system. Within the cricket species, Gryllus firmus, femur length and head width (as well as other morphological traits) have been shown to be positively genetically correlated [26]. Thus, individuals with longer than average femurs tend to produce offspring with longer than average femurs and also wider than average heads. If we now imagine that these crickets live in a metapopulation where some populations/environments select for long femurs and wide heads while others select for short femurs and narrow heads, genetic variation G and environmental variation Θ are aligned (figure 1a). If, by contrast, populations/environments where long femurs are selected for are associated with selection for narrow heads or vice versa, genetic G and environmental Θ variation would be misaligned (figure 1c). Our mathematical results suggest that, all else being equal, local adaptation would increase more rapidly with trait number in the former case than in the latter (figure 2).

3. Individual-based simulations

Our analytical approximation requires two critical assumptions: first, that selection is weak, and second, that the G-matrix is constant across space and time. Because these assumptions are known to be violated in many cases [27–30], we relax them using individual-based simulations. Simulations studied a metapopulation consisting of 200 demes, each containing 400 individuals. Selection was imposed by assuming that an individual's probability of survival to reproduction was given by equation (2.1). Gene flow occurred stochastically, with individuals moving to another randomly selected population with probability m. Reproduction occurred at the end of each generation by randomly sampling pairs of parents from the population, and creating an offspring by drawing its trait values at random from a multivariate Gaussian distribution defined by a vector of means equal to the parental means and a variance/covariance structure chosen to approximate a target G-matrix. This process was continued until an offspring population size of 400 was reached, at which point the parental population died and the life cycle repeated.

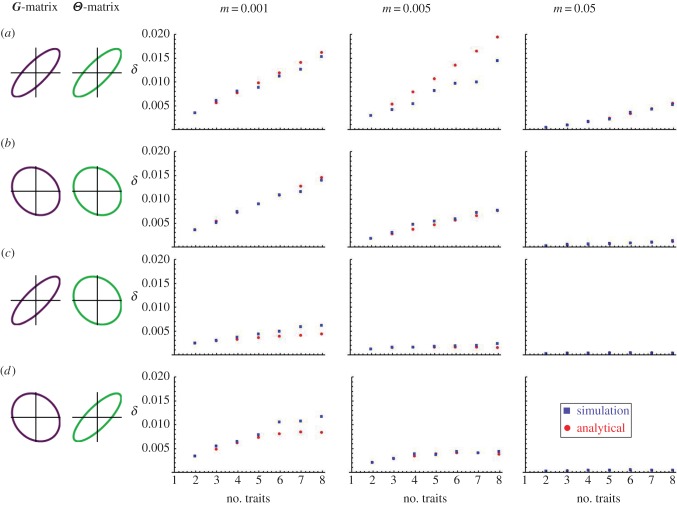
Simulations were run for three different strengths of selection and three different alignment regimes. We then compared the value of local adaptation calculated using the exact definition (2.1) and the analytical approximation (2.7) for between one and eight traits for each parameter combination. The simulations reveal that our analytical results are quantitatively robust over a broad range of parameters (figure 3; electronic supplementary material, figures S1–S9). Only when selection becomes strong does the quantitative agreement between analytical and simulation results begin to break down, and even then, qualitative predictions about the role of dimensionality and alignment between genetic and environmental variation remain quite robust. In addition to supporting our analytical predictions, simulations revealed that although increasing rates of gene flow generally decrease levels of local adaptation, they also enhance the impact of dimensionality and alignment. Finally, as expected based on our analytical results and previous research [5–7], simulations showed that stronger selection and larger amounts of genetic and environmental variation increase local adaptation.

Figure 3.

The effect of dimensionality on the extent of local adaptation produced in individual-based simulations (red squares) compared with the predicted analytical values (blue circles). Simulations were run with 200 populations, each containing 200 individuals for a time span of 1500 generations. The strength of selection for the simulations varied stochastically about γ = 0.01, while the analytical predictions were found given γ = 0.01. Traits and optima were drawn from multivariate normal distributions with unit variances and the following correlations: (a) (ρ_G = 0.9, ρ_Θ = 0.9), (b) (ρ_G = −0.1, ρ_Θ = −0.1), (c) (ρ_G = −0.9, ρ_Θ = −0.1) and (d) (ρ_G = −0.1, ρ_Θ = −0.9). (Online version in colour.)

4. Empirical test

In order to test our central theoretical prediction that local adaptation increases with dimensionality, we extended a method for estimating dimensionality originally designed for mate choice and behavioural isolation [31]. Here we apply this method to previously published reciprocal transplant data in which individuals from a set of source populations are tested in the corresponding sites, and fitness is measured for each pairwise test in the form of viability, fecundity or some composite fitness measure. The method fits points representing both population phenotypic means and local selective optima in a multidimensional space and determines the number of dimensions that best explain the data (see electronic supplementary material for more details). The technique is analogous to multidimensional scaling or principal coordinates analysis, in which the matrix of fitness measures in a reciprocal transplant experiment is treated akin to a distance matrix. However, rather than using simple Euclidean distance, the distance between the phenotypic mean of a source population and the selective optimum of a site is treated using one of two models of spatially heterogeneous stabilizing selection. This model-based approach allows us, for any dataset of fitness in a reciprocal transplant experiment, to calculate a likelihood given any particular arrangement of phenotypic means and selective optima in a d-dimensional space. We thus use maximum likelihood techniques to find the best-fit arrangement of points given each value of d, and the likelihood of this arrangement is treated as the likelihood of that value of d. The dimensionality of selection inferred from the dataset is then estimated in two ways: first using corrected Akaike Information Criterion (AICc) and related statistics to identify the most supported value of d; and second using the effective dimensionality (n_D; [32]) of the points when fit in a high-dimensional space [31]. This second metric reflects the amount of variation among phenotypic means and selective optima that is concentrated along a primary axis; for instance, a value of n_D = 3.0 means that one-third of the variation among phenotypic means and selective optima lies along a single primary axis. These estimates of dimensionality are unaffected by the identities of the populations and sites in each pairwise transplant, so that they are unbiased with respect to the metric of local adaptation used above. We verified this with both simulated datasets and random permutation of published datasets, neither of which showed any correlation between dimensionality and local adaptation (see electronic supplementary material).

We used this method to estimate trait dimensionality for 35 published reciprocal transplant datasets reviewed by Hereford [10]. All datasets contained measurements of fitness from reciprocal transplant experiments with all pairwise tests among at least three populations and sites. We then calculated local adaptation for these same datasets and regressed this value against the inferred number of dimensions from the two metrics described above. Dimensionality estimated by AICc ranged from 1 to 4, while the estimate of n_D ranged from 1.09 to 3.00. The correlation between the AICc estimate of dimensionality and local adaptation was significant (figure 4; r² = 0.20; p = 0.0071). The proportion of variance in local adaptation explained by dimensionality in this analysis (20%) is substantially higher than that explained by other factors such as degree of environmental difference (4%) or phenotypic distance (0.5%) explored in previous analyses [9,10]. The relationship between dimensionality and local adaptation held separately for datasets using viability as a fitness measure, analysed with a binomial fitness model [31], and for those using fecundity and composite fitness measures, analysed with a multivariate Gaussian fitness model (see electronic supplementary material). It was also robust to log-transformation of fecundity data and the two alternative ways of quantifying dimensionality (figure 4; electronic supplementary material, figure S10–S12), and the two metrics of dimensionality were highly correlated with each other (r² = 0.61; p < 10⁷). Finally, several of the empirical datasets come from the same published study, but were conducted in different years, on different species, or on different sets of populations, and a few actually represent different fitness metrics measured on the same reciprocal transplant experiment (figure 4; electronic supplementary material, table S2). We used a mixed linear model to account for non-independence of datasets either from the same published study or derived from the same reciprocal transplant experiment, and the relationship between the AICc estimate of dimensionality and local adaptation held in both cases (likelihood ratio tests; p = 0.0318 and p = 0.0075, respectively).

Figure 4.

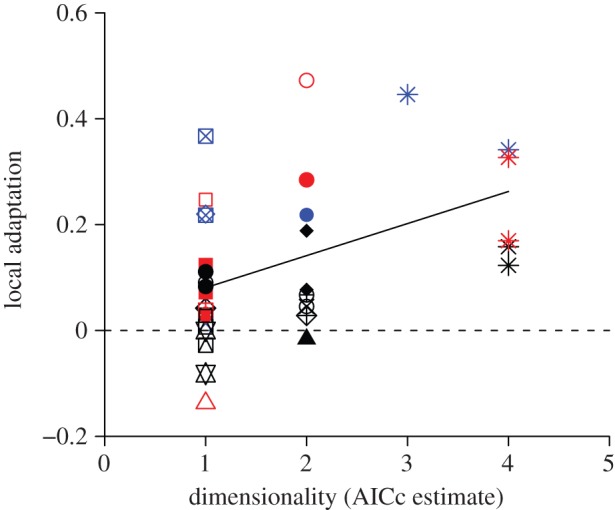
Correlation (r = 0.4472; p = 0.0071) between dimensionality estimated by AICc and local adaptation across 35 published reciprocal transplant datasets, with fitness estimated by viability (black), fecundity (red) or a composite fitness measure (blue). Symbols indicate different published studies, as several studies present results from multiple transplant experiments across different years, species or sets of populations, or using different fitness metrics (see table S2 in the electronic supplementary material). Shown are a linear regression (solid line) and no local adaptation (dashed line). (Online version in colour.)

5. Discussion

(a). Model predictions

Local adaptation quantifies the fit of an organism to its environment and has important implications for diversification, epidemiology, the persistence of metapopulations and reintroduction programs, as well as predicting the response of species to rapid climate change [2,33,34]. Although theory has long predicted that local adaptation should depend on the balance between gene flow and local selection [6,7], convincingly demonstrating this relationship at a broad taxonomic level has proven vexing. Our results point to two new causes of variation in the magnitude of local adaptation observed across organisms: trait dimensionality and alignment between genetic and environmental (co)variation. Specifically, both our analytical and simulation results reveal that local adaptation should increase as the number of traits experiencing spatially heterogeneous selection grows.

This strong linear relationship between local adaptation and dimensionality can be cast in two lights. First, as we chose to portray it, each additional trait under selection increases the total strength of selection that an individual experiences. If selection on each trait is the same as was assumed in equation (2.2), this ever increasing selection results in the strong linear relationship between dimensionality and local adaptation. Alternatively, if the total strength of selection is held constant, the relationship between dimensionality and local adaptation depends entirely on alignment between G and Θ. However, it is unlikely that the total strength of selection acting on an individual is somehow constrained or altered by the addition of new traits under selection, hence it may be more realistic that total selection does indeed increase with dimensionality. For this reason, we chose not to scale out the effect of increasing selection in equation (2.2).

In addition to the strong impact of trait dimensionality owing to increasing selection, our analytical and simulation results show that the magnitude of local adaptation depends on the alignment between genetic and environmental variation. The increase in local adaptation with dimensionality is most pronounced when genetic (co)variance aligns with the (co)variance in selective optima across populations. By contrast, when genetic and environmental variation are misaligned, local adaptation reaches a maximum at an intermediate number of traits. This occurs because adding each additional trait (moving from n to n + 1 traits) always adds only a single additional axis of selection but contributes n new sources of genetic constraint. As n increases, these additional constraints begin to outweigh the benefit of additional selection causing a decrease in local adaptation. However, owing to the constraints on the magnitude of covariances, local adaptation can never decrease below the value given by a single trait, allowing for the assertion that increased dimensionality will in general increase local adaptation.

(b). Empirical confirmation

Our analysis of 35 published studies supports the first prediction of the models, demonstrating a significant trend toward elevated levels of local adaptation in those studies characterized by greater dimensionality. This result was robust to different metrics of dimensionality and fitness, and trait dimensionality explained a much larger fraction of variance in local adaptation across datasets than previously examined factors. However, the direct effect of rates of migration on local adaptation has not been addressed in such a meta-analysis, because gene flow is often more difficult to estimate directly than local adaptation. Given the predictions of our model, we would expect that some portion of variance in local adaptation among these 35 published studies would be explained by variation in migration rates, although such an analysis is not feasible using published data.

Finding such a strong, positive relationship between local adaptation and trait dimensionality across studies suggests that the major axes of environmental and genetic variation may often be aligned within natural populations. Unfortunately, our analyses of published data do not allow us to rigorously evaluate this possibility because we lack information on the structure of environmental and genetic variation. An interesting focus for future research, and a more direct test of our theory, would involve evaluating the alignment between genetic and environmental variation using estimates of G-matrix structure within populations and estimates of environmental variation among populations. Genomic tools provide novel ways to directly estimate G-matrices in natural populations, by estimating relationship matrices directly from large numbers of markers rather than requiring a controlled breeding design [35]. Genomic data can also provide more precise estimates of migration rates [36], allowing these factors to be teased apart with empirical data.

(c). Implications for local adaptation

In addition to explaining variation in levels of local adaptation observed among studies, our results may help explain why strong local adaptation is sometimes observed in organisms with high rates of gene flow [11–14]. There are two ways in which trait dimensionality facilitates the evolution of strong local adaptation, even in the face of substantial gene flow. First, as the number of traits experiencing spatially variable selection increases, so too does the number of traits contributing to local adaptation. Thus, even if gene flow erases most phenotypic differentiation for individual traits, summing this small differentiation over many traits can produce strong local adaptation. This simple and intuitive impact of dimensionality is captured by equation (2.2). Second, and less intuitive, is the influence trait dimensionality has on the rate of adaptation within populations. This effect is most easily understood using the metaphor of the adaptive landscape. In each generation, gene flow pulls population mean phenotypes away from the summit of their adaptive peak, reducing local adaptation. Selection then acts to drive population mean phenotypes back toward the summit of their local adaptive peak, increasing local adaptation. The rate at which populations climb their adaptive peaks in response to selection can be substantially faster if the major axis of genetic variation aligns with the vector of directional selection [22]. Thus, when environmental and genetic variation are aligned, the balance between selection and gene flow is tipped in the favour of selection and local adaptation becomes more pronounced than would be expected based on a single trait.

In natural metapopulations, there may be reason to expect that genetic and environmental variation would align with one another. For example, theoretical work [27] has shown that the major axis of genetic variation (the G-matrix) on an island comes to align with the line of divergence between the island and mainland optima, as a result of migration from the mainland source, with the strength of alignment depending on mutational and selectional correlation. Here, we examine gene flow among multiple populations of equal size, so that the ‘source’ of incoming migrants to any one population is a sample from all other populations. To the extent that these other populations lie close to their respective optima, the covariance structure of incoming genetic variation should reflect the distribution of phenotypes across the metapopulation.

Together, our results identify a new and potentially important explanation for widespread variation in local adaptation. Evaluating the overall importance of trait dimensionality relative to more classical explanations based on gene flow, selection or population size will require further meta-analyses that explicitly consider these factors simultaneously. Such future studies will be essential if we wish to develop a robust understanding of the forces driving local adaptation in the wild.

Data accessibility

The work reported here is based upon mathematical theory, computer simulation and analysis of previously published data. We are happy to make the simulation data available in Dryad if appropriate.

Funding statement

Funding was provided by NSF grant nos. DEB 1118947 and DMS 0540392 (S.L.N.), National Institutes of Health grants P20RR016448 and P30GM103324 (P.A.H.), and an NSF Institutional grant in Undergraduate Mathematics and Biology (DMS-1029485).