Shape shifting predicts ontogenetic changes in metabolic scaling in diverse aquatic invertebrates

Abstract

Metabolism fuels all biological activities, and thus understanding its variation is fundamentally important. Much of this variation is related to body size, which is commonly believed to follow a 3/4-power scaling law. However, during ontogeny, many kinds of animals and plants show marked shifts in metabolic scaling that deviate from 3/4-power scaling predicted by general models. Here, we show that in diverse aquatic invertebrates, ontogenetic shifts in the scaling of routine metabolic rate from near isometry (b_R = scaling exponent approx. 1) to negative allometry (b_R < 1), or the reverse, are associated with significant changes in body shape (indexed by b_L = the scaling exponent of the relationship between body mass and body length). The observed inverse correlations between b_R and b_L are predicted by metabolic scaling theory that emphasizes resource/waste fluxes across external body surfaces, but contradict theory that emphasizes resource transport through internal networks. Geometric estimates of the scaling of surface area (SA) with body mass (b_A) further show that ontogenetic shifts in b_R and b_A are positively correlated. These results support new metabolic scaling theory based on SA influences that may be applied to ontogenetic shifts in b_R shown by many kinds of animals and plants.

1. Introduction

All living activities depend on metabolism for energy and materials. Therefore, understanding variation in metabolic rate is of fundamental importance in biology. Much of this variation is related to body size, but how and why these relationships occur remain vexing questions. General models assume that metabolic rate scales monotonically with body size according to the simple power function

1.1

where R is metabolic rate, a is the scaling coefficient (antilog of the intercept in a log–log plot), M is body mass and b (henceforth b_R) is the scaling exponent (linear slope of a log–log plot that frequently approximates 3/4) [1,2]. However, metabolic scaling often shows marked shifts during ontogeny in animals and plants (b_R varying mostly between 2/3 and 1, but also showing values outside this range) [3–7] that are not well understood. These metabolic shifts are important because they appear to be fundamentally linked to other ontogenetic changes in the physiology, growth rate, cell size, body composition, behaviour and ecology of a species [3–7].

Here, we show that ontogenetic changes in body shape and associated surface area (SA)-related resource supply predict frequently observed shifts from near isometric (b_R ∼ 1) to negatively allometric (b_R < 1) intraspecific metabolic scaling (=type III scaling [4]) in diverse aquatic invertebrates. Crucially, we also show that shape shifting predicts more rarely observed changes in metabolic scaling that occur in the opposite direction (from shallow to steep scaling). Our results demonstrate that the prediction of metabolic scaling from the body-shape-related scaling of SA applies more widely than that recently described by Hirst et al. [8]. We show here that this predictive power applies to marked variation in metabolic scaling seen not only among diverse pelagic (open water) animal taxa [8], but also during the intraspecific ontogeny of both pelagic invertebrates and those that exhibit developmental shifts from pelagic to benthic (bottom-dwelling) lifestyles. A critical assumption of our shape-shifting model is that the supply of resources or loss of wastes scales with external body surface, thus implying that exchange of materials such as respiratory gases is distributed over the body surface, which we evaluate herein. We also discuss potential implications of our findings for ontogenetic shifts in metabolic scaling observed in many other kinds of animals and plants.

2. Theoretical background

Metabolic rate may be controlled by the supply of, or demand for, resources [9–11]. Both should be considered in order to attain a comprehensive understanding of the scaling of metabolic rate with body size [4,12,13]. Here, we test opposing predictions from influential metabolic scaling theories that focus on transport of resources and waste products such as respiratory gases between the external environment and metabolizing cells. This transport may be influenced by two major steps: the exchange of materials across body surfaces and the transport of materials through internal networks. These steps are the foci for two prominent theoretical approaches to understanding and predicting biological scaling: SA theory [4,8,14,15] and resource-transport network (RTN) theory [1,2,16,17], respectively.

Although both SA and internal transport networks may be important in influencing metabolic rate and its scaling with body size, SA theory (including widely applied DEB theory, which incorporates SA theory [8,18,19]) predicts that body-shape changes should have opposite effects on the metabolic scaling exponent b_R (see equation (1.1)) than those predicted by existing RTN theory [8]. If an organism shows isomorphic growth (i.e. it grows with equal proportions in all three dimensions, so as to maintain a constant shape), SA theory (based on simple Euclidean geometry) predicts that b_R = 2/3, whereas RTN theory typically predicts that b_R = 2/3 [2,17] or 3/4 [1,2,16], depending on the physical properties of the transport network [20,21]. These predicted scaling exponents of 2/3 and 3/4 have received the most attention by biologists since the seminal studies of Rubner [14] and Kleiber [22] over 80 years ago. However, if an organism displays nearly two-dimensional growth (e.g. it grows in length and width without any significant change in depth, thus appearing increasingly flat), SA theory predicts that b_R ∼ 1 [8,15], whereas RTN models predict that b_R ∼ 1/2 [17], 5/8 [2,8] or 2/3 [16], depending on network geometry and dynamics. In addition, if an organism exhibits nearly one-dimensional growth (e.g. it grows in length without any significant change in width or depth, thus showing an increasingly elongated shape), SA theory predicts that b_R ∼ 1 [8,15], whereas RTN theory predicts that b_R ∼ 0 [17], 1/4 [2,8] or 1/2 [16], again depending on network properties. Therefore, increased elongation or flattening during ontogeny (trends towards one- or two-dimensional growth) should lead to an increase in b_R, according to SA theory, whereas RTN theory predicts the opposite—a decrease in b_R. Conversely, ontogenetic trends away from increasingly elongated one-dimensional or flattened two-dimensional growth, but towards isomorphic three-dimensional growth, reverse the changes in b_R predicted by the two theories: SA theory predicts decreasing b_R, and RTN theory increasing b_R. Studying the effects of ontogenetic shape shifting on metabolic scaling thus provides an excellent opportunity to test the relative validity of models based on two major competing theories of metabolic scaling, which is much needed for the field to advance [23,24].

3. Testing theory using animals with mixed ontogenetic metabolic scaling

Several kinds of aquatic animals with complex life cycles exhibit ontogenetic shifts in the scaling of aerobic metabolism, typically measured as the rate of oxygen consumption. In these animals, respiration scaling exponents (b_R) most often change from near 1 in larvae or young juveniles to less than 1 in older juveniles or adults [3,4,25], but reverse shifts also rarely occur [26,27]. From the literature, we collected respiratory and morphometric data on aquatic invertebrates that have complete or partial pelagic (open water) life histories to test whether and how these ontogenetic shifts in metabolic scaling are related to changes in body shape.

Unfortunately, actual measurements of body SA during ontogeny are rare [8]. Therefore, as a first-order approximation, we quantified differences in shape-related growth between life-history phases by using Euclidean geometry for smooth surfaces to deduce SA–mass scaling exponents (b_A, or the slope of log₁₀ body SA versus log₁₀ body mass). To achieve this, we first used readily available body length and mass data to obtain mass–length scaling exponents (b_L), estimated as the slopes of least-squares regressions (LSRs) of log₁₀ body mass versus log₁₀ body length (along the longest axis). Values of b_L were calculated separately for larvae, juveniles and adults [28]. Logarithmic transformation was used to permit easy detection of proportional changes [29]. If growth is occurring proportionally in three dimensions without any change in mass density, b_L should be 3, whereas if growth involves pure elongation in only one dimension (along the longest axis) or pure flattening because of size increases in only the two longest dimensions, b_L should be 1 or 2, respectively [8]. For intermediate patterns of body-shape change, involving disproportionate growth in one or two of the longest dimensions, 1 ≤ b_L ≤ 3. Values of b_L may even be more than 3, if growth in the shortest dimensions (width and/or depth) is proportionately greater than that for length along the longest axis that is used to calculate b_L (i.e. the animal is becoming relatively thicker and/or broader) [8].

Ranges of b_A values were inferred from b_L values that are less than or equal to 3 by using formulae for the extreme possibilities of different degrees of elongation (one-dimensional growth) and flattening (two-dimensional growth) [8]. The formula for different degrees of elongation is

3.1

whereas the formula for different degrees of flattening is

3.2

Equation (3.1) applies for 1 ≤ b_L ≤ 3, and equation (3.2) applies for 2 ≤ b_L ≤ 3, as represented in figure 1a,b by the left- and right-hand purple curves for b_L ≤ 3, respectively. Ranges of potential b_A values were also inferred from b_L values that are more than 3 by using formulae quantifying disproportionate thickening in one or two of the shortest dimensions. The formula for thickening of only the shortest dimension is the same as equation (3.2), whereas the formula for thickening of only the second shortest dimensions is b_A = 1 − (1/b_L) (supplementary information 1g in [8]), as represented in figure 1a,b by the bottom and top purple curves for b_L > 3, respectively. When data on the scaling of body width with body length were available, it was possible to predict a single value of b_A rather than a range (see the electronic supplementary material).

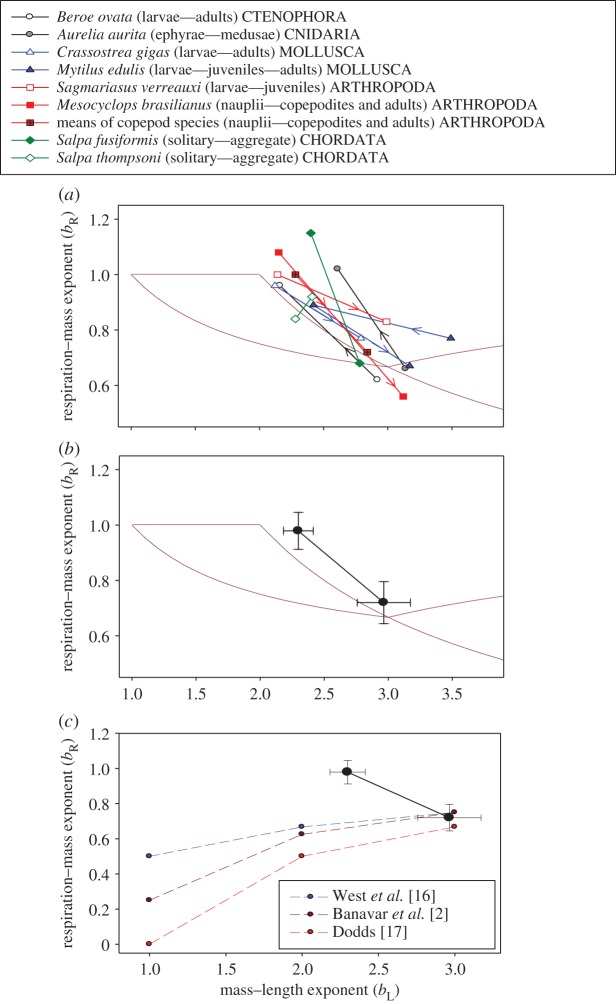
Figure 1.

Ontogenetic shifts of respiration–mass exponents (b_R) in relation to mass–length exponents (b_L) of several species of aquatic invertebrates in five different phyla (a) and for all species averaged together (b,c), where b_R is the scaling exponent for log₁₀ RMR in relation to log₁₀ body mass, and b_L is the scaling exponent for log₁₀ body mass in relation to log₁₀ total body length (data from tables 1 and 2). Multiple b values for the life-history stage of a species or group of species (copepods) were averaged. Arrows indicate the direction of ontogenetic change. In (b,c), the upper left and lower right points were calculated by averaging all of the paired b_R and b_L values that occurred in ontogenetic stages with the higher versus lower b_R, respectively. The 95% confidence limits are shown for each mean value of b_R and b_L._. Also shown in (b) are the bounded range of values of b_A (log₁₀ body SA in relation to log₁₀ body mass) in relation to b_L (depicted as light purple lines) calculated using equations (3.1) and (3.2) based on Euclidean geometry (also see [8]); and in (c) the predicted effects of body-shape changes (b_L) on b_R (depicted as dashed coloured lines) according to the RTN models of West et al. [16], Banavar et al. [2] and Dodds [17] (also see [8]). Note that in seven of eight species sampled, ontogenetic shifts in b_L are accompanied by inverse shifts in b_R, as predicted by SA scaling theory (b), but in contradiction to RTN scaling theory (c). (Online version in colour.)

The empirical b_L values and inferred b_A values were then compared to scaling exponents (b_R) for regressions of log₁₀ routine metabolic (oxygen consumption) rate (RMR) in relation to log₁₀ body mass of different ontogenetic stages both within and among several species of aquatic invertebrates.

Both b_L and b_R values were based on LSR, the method used for all of the literature scaling analyses included in our study. An alternative, often used method, reduced major axis (RMA) analysis, gave similar b values (b_RMA = b_LSR/r) to those from LSR, because reported correlation coefficients (r) were always high (more than or equal to 0.8). The r values for b_L averaged 0.97 ± 0.01 (±1 s.e., n = 15), and those for b_R averaged 0.96 ± 0.01 (n = 19) (calculated from r² values in the electronic supplementary material for table 1). As a result, b_L and b_R values based on RMA analyses averaged only approximately 3–4% higher than those based on LSR.

Table 1.

Ontogenetic scaling exponents from LSRs of log₁₀ body mass in relation to log₁₀ body length (b_L) and log₁₀ RMR in relation to log₁₀ body mass (b_R) for larvae, juveniles and/or adults of the Atlantic ctenophore Beroe ovata, moon jellyfish A. aurita, Pacific oyster C. gigas, common mussel M. edulis and spiny lobster S. verreauxi; for nauplii, copepodites and adults of the copepod M. brasilianus; and for solitary and aggregate life cycle stages of the salps (pelagic tunicates) Salpa fusiformis and S. thompsoni. Values of b_L and b_R were taken or calculated from published data in the sources listed in the electronic supplementary material, where additional data and methodological information can also be found. Values of b_A for log₁₀ body SA in relation to log₁₀ body mass were estimated from b_L values and scaling exponents of body width versus length (electronic supplementary material). When data for scaling of width versus length were not available, ranges of potential b_A values are given (based on equations (3.1) and (3.2)). Note the parallel changes in b_A and b_R values (shown in italic), regardless of whether decreases or increases in b_R were observed during ontogeny (except possibly for the transition from veliger larvae to juveniles in M. edulis; also see text). Statistically significant ontogenetic shifts in b_L and b_R values occur in all species, except for between solitary and aggregrate life stages of S. thompsoni.

species	stage	bL	bA	bR
Beroe ovata	juveniles	2.92	0.67 (0.67–0.68)	0.62
	adults	2.47	0.80 (0.70–0.81)	0.99
		2.23	0.87 (0.72–0.90)	1.04
		1.78	1.09 (0.78–1.00)	0.86
Aurelia aurita	ephyra larvae	3.14	0.64 (0.64–0.66)	0.63
				0.35
				1.01
	medusae	2.50	0.80 (0.70–0.80)	0.93
		2.72	0.74 (0.68–0.74)	1.11
				1.01
Crassostrea gigas	veliger larvae	2.12	0.95 (0.74–0.94)	0.96
	adults	2.79	0.68–0.72	0.77
Mytilus edulis	veliger larvae	3.49	0.57 (0.57–0.71)	0.90
				0.90
				0.70
				0.59
	juveniles	2.42	0.71–0.83	0.89
	adults	3.17	0.63–0.68	0.66
				0.68
Sagmariasus verreauxi	phyllosoma larvae	2.14	0.91 (0.73–0.93)	1.00
	juveniles	2.99	0.67	0.83
Mesocyclops brasilianus	nauplii	2.15	0.73–0.93	1.08
	copepodites and adults	3.12	0.64–0.68	0.56
Salpa fusiformis	solitary zooids	2.40	0.71–0.83	1.15
	aggregate zooids	2.78	0.68–0.72	0.68
Salpa thompsoni	solitary zooids	2.28	0.72–0.88	0.84
	aggregate zooids	2.41	0.71–0.83	0.92

4. Results

We compared conspecific b_L, b_R and inferred b_A values for different ontogenetic phases of a ctenophore, a scyphozoan, two bivalves, two crustaceans and two thaliaceans (table 1), as well as mean heterospecific values for the nauplii, copepodites and adults of several copepod crustaceans (table 2).

Table 2.

Mean ontogenetic scaling exponents from LSRs of log₁₀ body mass in relation to log₁₀ body length (b_L) and log₁₀ RMR in relation to log₁₀ body mass (b_R) for nauplii, copepodites and adults of several copepod species (b_L and b_R values were taken from published sources given in the electronic supplementary material, whereas the ranges of potential b_A values for log₁₀ body SA in relation to log₁₀ body mass were estimated from b_L values using equations (3.1) and (3.2) in the text). Mean scaling exponents were calculated by averaging mean conspecific values among species. The 95% CI and number of species sampled (n) are given for each scaling exponent. Note the parallel changes in b_A and b_R values (shown in italic).

stage	bL ± 95% CI (n)	bA	bR ± 95% CI (n)
nauplii	2.28 ± 0.27a (17)	0.72–0.88	1.00 ± 0.16b (4)
copepodites and adults	2.84 ± 0.20a (20)	0.68–0.70	0.72 ± 0.22b (7)

^aBased on dry mass, carbon mass or nitrogen mass.

^bBased on dry body mass.

For seven of the eight species sampled, ontogenetic shifts in the metabolic scaling exponent (b_R) are accompanied by inverse shifts in the scaling exponent of body mass in relation to length (b_L) (table 1 and figure 1a). The only exception is the pelagic tunicate Salpa thompsoni, which showed no significant difference in b_R or b_L between the solitary (oozoid) and aggregate (blastozoid) life-cycle stages (table 1 and figure 1a). Remarkably, even this exception supports a link between b_R and b_L, because both life stages of S. thompsoni have relatively high b_R values associated with relatively low b_L values, as compared with the exponents exhibited by the other species sampled (figure 1a). Furthermore, inverse shifts in b_R and b_L occurred in the other seven species sampled regardless of whether b_R showed an increase or decrease during ontogeny (table 1 and figure 1a). Inverse relationships between b_R and b_L, also seen among all of the species averaged together (figure 1b,c), follow SA theory (figure 1b), but contradict all existing RTN models (figure 1c). Although ontogenetic stages with a mean b_L ∼ 3 (2.97 ± 0.21 95% confidence interval (CI)) exhibited a mean b_R (0.72 ± 0.08) not significantly different from 2/3 or 3/4, as predicted by both SA and RTN theory, stages with a mean b_L ∼ 2.3 (2.30 ± 0.12) exhibited a mean b_R (0.98 ± 0.07) not significantly different from 1 and significantly greater than 2/3 and 3/4, as predicted by SA theory, but in contradiction to all RTN models, which predict b_R values less than 2/3 or 3/4 (figure 1b,c).

As the scaling exponent for body SA (b_A), as inferred from Euclidean geometry, is inversely related to b_L (figure 1a; equations (3.1) and (3.2)), it follows mathematically that ontogenetic shifts in b_R and b_A should be positively correlated, as observed in seven of the eight species sampled (table 1 and figure 2a). As predicted by SA theory, b_R and b_A are also positively correlated for all species averaged together (figure 2b), and when these exponents were compared pairwise among each of the ontogenetic phases of each species (figure 2c). The slope for the latter correlation (1.14) is not significantly different from 1, as expected if b_R varied in direct proportion to b_A (figure 2c).

Figure 2.

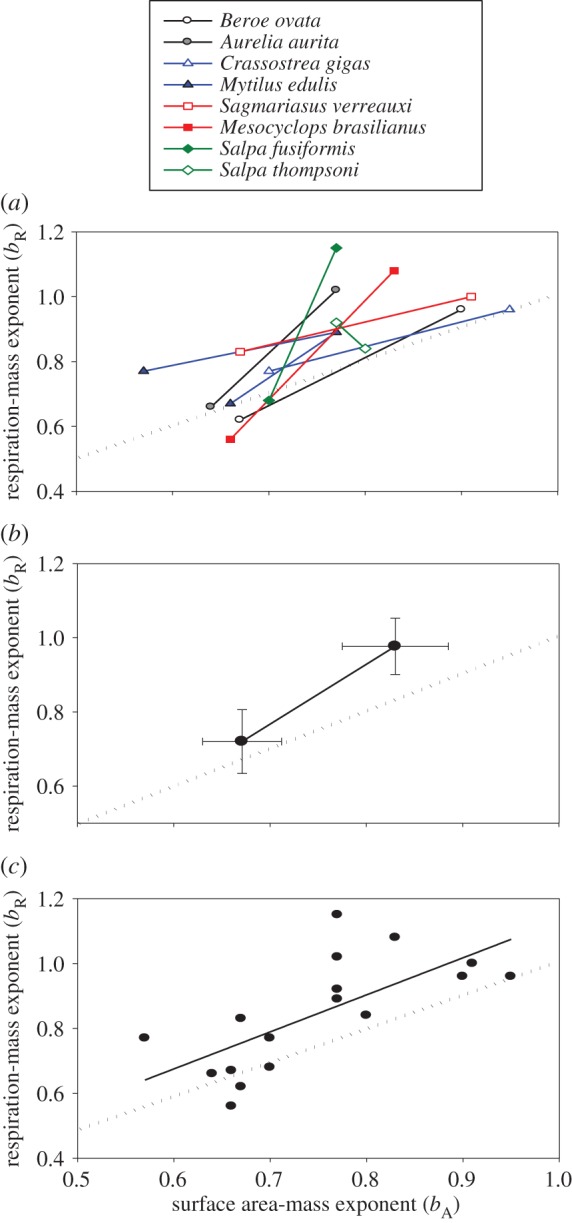
Ontogenetic shifts of respiration–mass exponents (b_R) in relation to SA–mass exponents (b_A) of several species of aquatic invertebrates (a) and for all species averaged together (b), where b_R is the scaling exponent for log₁₀ RMR in relation to log₁₀ body mass, and b_A is the scaling exponent for log₁₀ surface area in relation to log₁₀ total body length (data from table 1). Values of b_A were calculated using b_L values and additional data in the electronic supplementary material. Multiple b_R values for the life-history stage of a species were averaged, whereas the midpoint was used when only a range of b_A values was available. In (b), the lower left and upper right points were calculated by averaging all of the paired b_R and b_A values that occurred in ontogenetic stages with the lower versus higher b_R, respectively. The 95% confidence limits are shown for each mean value of b_R and b_A. As predicted by SA scaling theory (also see [8]), in seven of eight species sampled, ontogenetic shifts in b_A are accompanied by positively correlated shifts in b_R. Also shown in (c) is a significant positive correlation between b_R and b_A for each ontogenetic stage of each species. The equation for the LSR line is: b_R = 1.14 ± 0.64 (95% CI) (b_A) − 0.0092 (r² = 0.454; p = 0.0018, n = 17). In (a–c), the dotted diagonal lines represent b_R = b_A. (Online version in colour.)

Similar ontogenetic shifts are seen when b_R, b_L and b_A values are compared between nauplii and copepodites/adults averaged among several species of copepods (table 2 and figure 1a). The heterospecific, inversely related shifts in b_R and b_L almost exactly parallel those observed for the single copepod species Mesocyclops brasilianus (figure 1a).

The spiny lobster Sagmariasus verreauxi nicely exemplifies how ontogenetic changes in metabolic rate and body shape correlate. The phyllosoma larvae are very thin and flat, and show nearly two-dimensional growth, until they metamorphose into adult-looking benthic juveniles that are much thicker and show three-dimensional growth. This marked shift in growth pattern and body form is represented by an abrupt ontogenetic shift in b_L values, from 2.142 ± 0.260 (95% CI) in the phyllosoma larvae to 2.991 ± 0.037 in the juveniles (figure 3a and table 1). The phyllosoma b_L value is not significantly different from 2, whereas the juvenile b_L value is not significantly different from 3. As a result, the scaling exponents predicted for SA (b_A) from Euclidean geometry (see the electronic supplementary material) are 0.91 for the phyllosomas and 0.67 for the juveniles (table 1). Like b_A, the b_R values for RMR are also higher in the phyllosomas (1.002 ± 0.081) than in the juveniles (0.829 ± 0.157) (figure 3b and table 1). Comparisons of the 95% CI [23,32] reveal that the b_L and b_R values are both significantly different between the two life-history stages. The phyllosoma b_R value is not significantly different from 1, but is significantly greater than 1/2, 5/8, 2/3 and 3/4. By contrast, the juvenile b_R value is significantly less than 1, not significantly different from 3/4 and significantly greater than 1/2, 5/8, and just barely 2/3.

Figure 3.

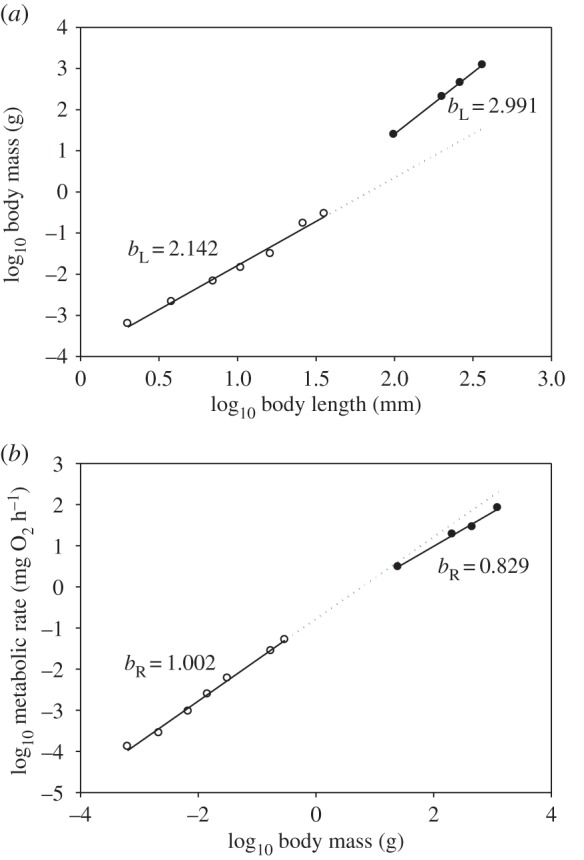
Scaling of log₁₀ wet body mass in relation to log₁₀ total body length (a) and log₁₀ RMR in relation to log₁₀ wet body mass (b) in phyllosoma larvae (open points) and juveniles (filled points) of the spiny lobster S. verreauxi maintained at 21–23°C. Each point in (a,b) is based on 4–11 replicate measurements, respectively [30,31]. The phyllosoma points represent instars 1, 3, 6, 9, 12, 15 and 17. The standard errors for each RMR value are all less than 20% of the mean. The LSR equations for the scaling lines and their coefficients of determination (r²) and significance levels (p) for phyllosoma larvae and juveniles are: (a) Y = −3.931 + 2.142 (X), r² = 0.988, p = 0.00001; Y = −4.574 + 2.991 (X), r² = 1.000, p < 0.00001; and (b) Y = −0.773 + 1.002 (X), r² = 0.995, p < 0.00001; Y = −0.673 + 0.829 (X), r² = 0.993, p = 0.00353, respectively. The number by each line is the scaling slope (exponent). Linear extrapolations of the empirical scaling lines for the phyllosoma larvae are shown as dotted lines to highlight the ontogenetic scaling shifts for both body shape (a) and metabolic rate (b).

5. Discussion

The parallel changes in the scaling exponents for RMR and inferred SA observed in seven of the eight species sampled supports the importance of SA changes in the observed ontogenetic shifts in metabolic scaling, but contradicts predictions of all current models emphasizing internal RTNs. SA theory predicts positive correlations between the scaling exponents for SA (b_A) and RMR (b_R), as observed, whereas current RTN theory incorrectly predicts negative correlations between b_A and b_R. Although RTN theory has been claimed to be universally applicable to all of life [1,16], or at least to macroscopic multicellular eukaryotes [33], RTN theory may not apply to animals without circulatory systems, or with open or incompletely closed circulatory systems [2,4,21], which are far more common taxonomically than those with completely closed circulatory systems (including only vertebrates, cephalopod molluscs, and some annelid and nemertean worms [34,35]). In fact, two of the animal species included in our study have no or very rudimentary circulatory systems (a ctenophore and scyphozoan), whereas the other six have open or incompletely closed circulatory systems (the bivalve, crustacean and thaliacean species) [35]. Nevertheless, Hirst et al. [8] have shown that the similarly steep ontogenetic scaling of both metabolic rate and SA with body mass in squids (cephalopods), which have closed circulatory systems, is also consistent with SA theory, but not with RTN theory. This additional deviation from RTN theory may be because squids use both their skin and gills for gas exchange, and also distribute resource-laden blood by means of multiple hearts found throughout the body [35], rather than from a single centralized heart or distribution centre, as assumed by the theory [1,2,16,17]. If current RTN theory does not apply to squids for these reasons, then annelid worms that use multiple hearts to pump blood [34] and nemertean worms that have no heart at all [35] may also be exceptions. Therefore, current RTN theory appears to apply to only a small subset of animals: perhaps only vertebrates with single central hearts in a completely closed vascular system. Even the application of RTN theory to vertebrates may be of limited use, because currently it cannot explain large variation in the metabolic scaling exponent observed in various vertebrate classes, which appears to be related to physiological state, ecological lifestyle or environmental conditions [12,36–39]. Perhaps next-generation resource exchange and supply theory may resolve these problems (see §6).

In any case, the positive associations between b_A and b_R observed in this study are remarkable because they occur in animals with very different body designs, including five different phyla, and furthermore they occur regardless of whether b_A increases or decreases during ontogeny. Therefore, it is unlikely that these correlations are merely side effects of b_A and b_R being independently related to other unmeasured factors associated with developmental maturation or ontogenetic age. Rather, it is more likely that shape shifting directly affects metabolic scaling via changes in SA available for resource uptake and waste excretion.

This hypothetical mechanism for how shape shifting may affect metabolic scaling seems especially applicable to the thin-skinned pelagic animals (larval or adult) that we have studied here and in a related paper [8]. Phyllosoma, veliger and other pelagic larvae of many marine animals that show biphasic or triphasic metabolic scaling appear to be ‘skin-breathers’ (i.e. they can absorb oxygen and expel dissolved waste products such as CO₂ through their thin, permeable integuments) [40,41]. Some can even absorb nutrients through their body surfaces and metabolize them in their tissues [40,42]. Remarkably, the body-mass scaling slope for metabolism in larvae of the Pacific oyster Crassostrea gigas is not significantly different from that for uptake of the amino acid alanine [40]. However, it is not known how much cutaneous absorption of nutrients contributes to the overall energy budget of these larvae and other pelagic animals under natural conditions [43]. Our findings point towards the importance of further research on integumentary material exchange by aquatic animals, as a way to better understand variation in their metabolic scaling.

Although parallel shifts in b_A and b_R values have usually been seen in this study, possible exceptions invite further scrutiny. For example, although b_A and b_R decrease in tandem in the common mussel Mytilus edulis as juveniles mature into adults, more research is needed to determine whether shifts in SA and metabolic scaling also match as veliger larvae develop into juveniles. This is because, although the inferred b_A shift from 0.57 to 0.71–0.83 parallels the shift of b_R from 0.77 (based on an average of four values) to 0.89, the individual b_R estimates for veligers are highly variable, ranging from 0.59 to 0.90 (table 1). Some of this variation appears to be related to temperature, because as temperature increases from 6°C to 18°C, b_R decreases from 0.90 to 0.59 (see the electronic supplementary material), as predicted by the metabolic-level boundaries hypothesis [12]. Sampling error may also be important because the body-size range of growing veligers is small (less than 2 orders of magnitude), thus potentially increasing variation in b_R estimates [36,44,45] relative to those of juveniles and adults with larger body-size ranges (more than 3 and 4 orders of magnitude, respectively; see the electronic supplementary material, table S1). A similar explanation may apply to the variable b_R estimates (0.35 and 1.01) for two ephyra samples of the scyphozoan Aurelia aurita that have body-size ranges less than 1.5 orders of magnitude and that deviate markedly from the inferred b_A value of 0.64 (table 1). By contrast, the b_R estimate (0.63) for a third sample of ephyra larvae, with a larger body-size range (more than 2 orders of magnitude), is very close to the estimated b_A value. Moreover, the b_R value (0.65) for ephyra larvae of A. aurita, estimated from the metabolic data of several studies taken together, is also not significantly different from the inferred b_A value of 0.64 [46]. It is also possible that our simple Euclidean estimates of SA scaling (b_A) do not adequately represent the ontogenetic SA changes occurring in a mussel veliger or an ephyra larva. A veliger's velum (foot), which has an extensive, highly permeable surface [40], can extend far beyond the measured shell length used in calculating b_L and b_A [47]. In addition, the ephyra larva shows complex changes in body shape as it grows, thus making it difficult to accurately estimate the scaling of its SA using our method based on Euclidean geometry (see footnote 7 in the electronic supplementary material, table S1).

Another major pattern evident in our results is that although b_R is significantly correlated with b_A, it is usually greater than that predicted by b_A alone (see tables 1 and 2, and figures 1a,b and 2). Two major factors may help account for these upward deviations of b_R. First, metabolically costly growth throughout ontogeny may elevate b_R values, as has been observed in other animals and plants [3–7,11,23,48]. These growth effects prompt the question: what are the relative influences of resource supply versus metabolic demand by growth and other biological processes on ontogenetic metabolic scaling [4,9–13]? For example, does the steep scaling of SA (and presumably resource uptake) of many kinds of pelagic animals (including larvae) documented here and by Hirst et al. [8] permit or even drive the steep scaling of metabolism, or is steep SA scaling a secondary adjustment to steep metabolic scaling that is driven by high resource demand (e.g. mass-specific growth rates that often continue at a high rate throughout ontogeny in pelagic animals [4,49,50])? Attempting to answer this critical question brings into focus the importance of understanding the various factors influencing all of the steps of energy flow through an organism, and their integration, as a way to improve our knowledge of how and why metabolic rate varies with body size (see also [4]).

A second major factor that may help to explain apparent upward deviations in b_R from that predicted by our SA model (figure 1a) is that we may have underestimated SA changes during ontogeny in our study species. Our geometric estimates of b_A based on b_L do not allow the detection of increases in SA related to increased convolutions (or fractal dimensionality) of the body surface, or to the development of special respiratory and nutrient-absorption structures (e.g. the velum in veligers, and the gills in other larval or juvenile forms). In addition, half of our inferred b_A values (see table 1) may have been underestimated because they were based on the midpoint of a potential range of values, whereas in most cases the upper limit of this range, which involves shape flattening, is probably closer to the actual b_A value than the lower limit, which involves shape elongation (also see §3 and [8]). This claim is supported by two observations. First, when data on both b_L and the scaling of body width versus length were available (electronic supplementary material), the inferred b_A value was almost always closer (in 9 of 10 cases) to the predicted upper limit involving mainly two-dimensional growth (flattening) than the lower limit involving mainly one-dimensional growth (elongation) (see table 1). Second, the mean empirical relationship between b_L and b_R (and by association b_A; see figure 2a–c) for all of our study species more closely parallels the slope of the upper predicted boundary involving flattening than that of the lower boundary involving elongation (figure 1b).

Other data consistent with effects of ontogenetic shifts in body shape and SA scaling on metabolic scaling include significant correlations between b_L and b_R values among diverse ‘skin-breathing’ pelagic animals, for which species-specific values also show a closer match to the upper boundary curve for predicted b_A than to the lower boundary curve [8], and parallel steep scaling of SA and metabolic rate in echinoid larvae [51] and epipelagic squid [52]. Steep (often near-isometric) scaling of metabolic rate in larval fishes may not only be related to their sustained rapid growth rates [4], but also to their ability to absorb oxygen (and possibly nutrients, though rarely observed) through their entire body surface [53,54]. In addition, shifts from isometric to negatively allometric metabolic scaling seen in plants may be related, at least in part, to decreases in their relative ‘leafiness’ (i.e. reductions in the relative contribution of high SA leaves to total biomass) as they grow [6].

6. Conclusion

Ontogenetic shifts in metabolic scaling may often be linked to developmental changes in body shape and SA scaling. Our SA model predicts that this should happen in any organism that relies heavily on body surfaces for resource uptake, such as many kinds of thin-skinned pelagic animals and leafy plants. Ontogenetic shifts in metabolic scaling in other organisms with impermeable integuments may be related to shifts in the SA scaling of specialized respiratory structures (such as occur for gills in developing fish [53] and for tracheae during moulting in insect larvae [13]) or to other metabolically demanding developmental changes unrelated to body shape (e.g. shifts from ectothermy to endothermy in developing mammals [4]). Nevertheless, evidence reported here and elsewhere (including near-2/3-power interspecific scaling of basal and cold-induced metabolic rates in birds and small mammals with closed circulatory systems [38]) suggests that the effect of external SA on metabolic scaling may often outweigh or modify the influence of RTNs [4,8,12,48,51,52], contrary to currently influential general models [1,2]. New resource-transport theory is needed that can accommodate organisms that distribute resources from external surfaces rather than from (or in addition to) internal hubs or ‘pumps’ (e.g. heart and stomach; see also [8]). More generally, our work and a recent review [48] suggest that a comprehensive explanation of the wide diversity of metabolic scaling relationships that have been observed must consider multiple mechanisms, including those related to SA, all of which have variable effects depending upon taxon, environment and physiological state.

Funding statement

D.S.G. was supported by a sabbatical leave granted by Juniata College, A.G.H. was supported by the Natural Environment Research Council and Department for Environment, Food and Rural Affairs (grant no. NE/L003279/1, Marine Ecosystems Research Programme), and D.A. was supported by a Leverhulme Trust Fellowship.