Geographical variation in mutualistic networks: similarity, turnover and partner fidelity

Abstract

Although species and their interactions in unison represent biodiversity and all the ecological and evolutionary processes associated with life, biotic interactions have, contrary to species, rarely been integrated into the concepts of spatial β-diversity. Here, we examine β-diversity of ecological networks by using pollination networks sampled across the Canary Islands. We show that adjacent and distant communities are more and less similar, respectively, in their composition of plants, pollinators and interactions than expected from random distributions. We further show that replacement of species is the major driver of interaction turnover and that this contribution increases with distance. Finally, we quantify that species-specific partner compositions (here called partner fidelity) deviate from random partner use, but vary as a result of ecological and geographical variables. In particular, breakdown of partner fidelity was facilitated by increasing geographical distance, changing abundances and changing linkage levels, but was not related to the geographical distribution of the species. This highlights the importance of space when comparing communities of interacting species and may stimulate a rethinking of the spatial interpretation of interaction networks. Moreover, geographical interaction dynamics and its causes are important in our efforts to anticipate effects of large-scale changes, such as anthropogenic disturbances.

1. Introduction

Species diversity receives considerable attention in relation to diversity gradients [1], diversity hotspots [2], relationships between regional- and local-scale diversity [3], and its human-caused decline [4]. However, focus on diversity is not restricted to the number of species per se (i.e. α-diversity within a community). Much attention is also paid to the turnover of species among communities (β-diversity) [5] and recently β-diversity was highlighted as having a dominant role in biodiversity patterns [6]. Whittaker [7] was among the first to define β-diversity, and since then it has been studied along environmental gradients and in relation to geographical distance [5]. Increasing species dissimilarity with increasing geographical distance is well documented and referred to as distance decay (e.g. [8]). Likely reasons for distance decay patterns are dispersal and colonization limitations (due to narrow niche breadths and saturated receiver habitats), and a less similar abiotic environment with increasing distance [8].

Few studies have addressed β-diversity between communities of interacting species (i.e. among ecological networks) [9–13]. Here, we focus on plant–pollinator interaction networks, where pollinator species are linked to the plant species from which they collect floral rewards. Species are a prerequisite for links, but there is no reason to assume a priori that species and interactions display identical distance decay. Moreover, distance decay of interactions may even be an important driver of species decay because biotic interactions can be essential determinants of community composition [14]. We investigated how similarity in species and interactions change with geographical distance among pollination networks from the Canary Islands, and our study scale is nearly two orders of magnitude larger than previous studies looking at mutualistic networks in relation to distance [10,11,13].

Temporal turnover of species and interactions in networks has received considerable attention [15–20], and species show strong temporal plasticity in their linkage pattern between both seasons and years [18,21]. However, the spatial turnover of species and interactions in networks and the potential drivers hereof remains poorly known. Interaction turnover between networks, whether it is temporal or spatial, is due to either rewiring (i.e. when co-occurring species interact differently over time and space) or species turnover (i.e. when gaining and losing species affect interaction composition). In other words, rewiring occurs when temporally permanent and spatially widespread species alter their interactions over time or from site to site, whereas species turnover automatically drives turnover of interactions. Tracking these two kinds of link turnover over geographical distance may provide insight into the finer mechanics of ecological complexity and the general influence of space. Indeed, Poisot et al. [9] emphasize that species and interactions may be filtered by different mechanisms and that the level of species turnover is not necessarily a reliable predictor of, for example, the level of interaction rewiring between co-occurring species.

Our data allowed us to take one step further into the dynamics of interactions and quantify interaction turnover of individual species. Low level of partner turnover can be ascribed as high partner fidelity, whereas a high level is suggestive of partner opportunism. This is of general ecological interest, as low fidelity, for example, may buffer detrimental consequences of global changes, such as disruption of interactions due to rapid reordering of phenologies [22]. However, it remains an open question whether the reported opportunism (e.g. [18,21]) translates into species actually using a random subset of the available resources or whether they have more specific requirements. Partner fidelity has been studied at the functional level [23], but an actual quantification at finer levels for all species within networks has, to our knowledge, not been performed. In order to test for partner fidelity across the Canary Islands, we compared partner composition of each species with a null model. Additionally, we related the species-specific partner fidelities with geographical (i.e. distance between networks), local ecological (i.e. number of interaction partners and abundance of species) and macroecological (i.e. species distribution) variables.

Thus, our aims were threefold. First, we wanted to characterize similarity of pollination networks across the Canarian archipelago, focusing on both species and interactions. Second, we sought to explain the pattern of dissimilarity among networks by analysing the underlying interaction turnover. To do so, we estimated the relative contribution of species-driven interaction turnover and rewiring, and related this to geographical distance in order to achieve an understanding of interaction turnover on a macroecological scale. Lastly, we quantified partner fidelity by comparing actual partner composition of individual plant and pollinator species with a random set of partners, to explore potential ecological and geographical determinants of partner fidelity.

2. Material and methods

(a). Study sites and design

The Canary Islands, situated in the Atlantic Ocean (27.62° N–29.42° N and 13.33° W–18.17° W), consist of seven major islands, and fieldwork was conducted on five of these. We sampled at one locality on El Hierro (27.8047′ N, 17.8959′ W), La Gomera (28.0398° N, 17.2267° W), Gran Canaria (27.9041° N, 15.4331° W) and Fuerteventura (28.5643° N, 13.8919° W), and at two localities on Tenerife (Teno Bajo; 28.3531° N, 16.9123° W) and Fasnia (28.2222° N, 16.4173° W)] due to its more complex geological history (see [24,25]). Furthermore, we sampled at one locality in Western Sahara (26.1610° N, 14.4222° W). The main criterion for choice of locality was presence of a large population of Euphorbia balsamifera, but the localities shared other species (e.g. Launaea arborescens, Lycium intricatum, Kleinia neriifolia, Fagonia albiflora, Periploca laevigata and Rubia fruticosa). At each locality, two sites (50–200 m apart) were sampled twice between 16 January and 28 March in 2010. At each site, and at each visit, every flowering perennial plant species was observed for flower visitors in four observation census á 15 min. For abundant plant species, randomly selected individuals were chosen within the site for each census. During observation, the identity and frequency of flower visitors touching the reproductive parts of the plants were registered and all were operationally defined as pollinators. Approximately 1300 specimens were collected and later identified by specialists (see Acknowledgements). Owing to the extreme landscape heterogeneity on the Canary Islands, we obtained abundance estimates of plant species by counting number of individuals belonging to each species along irregular transects within each site. From these numbers, relative abundance estimates were calculated. For pollinators, we used a combination of number of visits and the relative abundance of the visited plant species to obtain a weighted abundance estimate (i.e. the species-specific number of visits paid to different plant species was multiplied with the relative abundance of the visited plant species). From these weighted measures, we calculated relative abundance estimates for each pollinator at each site. For each site, we constructed an interaction matrix consisting of A pollinator species in rows and P plant species in columns, resulting in 14 spatially separated pollination networks. The two networks on each island and in Western Sahara were treated as separate networks. Data collection lasted 295 h over a period of 42 observation days, and all sites are (based on accumulation curves and Chao2 estimates [26]) equally sampled (see [25]).

(b). Community similarity

Level of pairwise similarity between networks was calculated using Sorensen similarity, β_sor = 2a/(2a + b + c), where a is shared number of species or interactions between two sites, and b and c are number of species or interactions only occurring at one of the sites [27].

Communities differing in species or interaction richness are likely to be less similar than communities of equal richness [5]. This influence of different α-diversities was mitigated by using a null model based on 1000 random assignments of species and interactions to our networks according to a probability distribution derived from their actual occurrences across the sites [5,28,29]. That is, widespread species were more likely to be drawn and assigned to a network during the random assortments, and numbers of species and interactions assigned to a random network were constrained to equal empirical numbers. Across all pairwise combinations, we calculated the empirical similarity in plant, pollinator and interaction composition (β_emperical). The deviation from randomness was measured using z-scores given as (β_emperical − 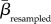)/SD_resampled, where 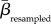and SD_resampled are the mean and standard deviation of the similarities achieved from the 1000 random assortments of species and interactions. Hence, a positive z-score suggests that two communities are more similar than expected if species or interactions were distributed randomly across the archipelago, and vice versa for a negative z-score. The significance level of each β_emperical value was obtained using the resampled values as a benchmark and all β_emperical values having z-scores larger than 1.96 or smaller than −1.96, respectively, were deemed significantly different (p < 0.05) from random.

Both the empirical Sorensen similarity values and the derived z-scores were compared to geographical distance using Mantel tests with 1000 permutations [30] performed with the vegan v. 2.0-8 package for R [31].

(c). Drivers of interaction turnover

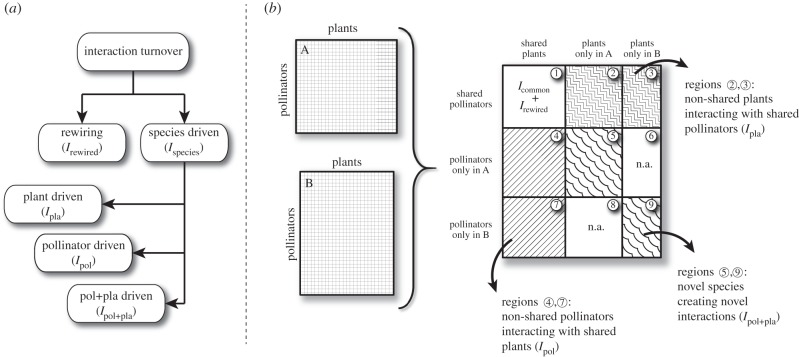
If A and B are two ecological networks, then let I_rewired be the number of interactions that change between the shared species of A and B, and let I_species be the number of interactions that change due to changes in species composition (figure 1). The total number of interactions that differ between A and B is then given by I_rewired + I_species, and the proportion of turnover that is due to rewiring and species-driven interaction turnover are rewiring = I_rewired/(I_rewired + I_species) and species-driven = I_species/(I_rewired + I_species).

Figure 1.

(a) Interaction turnover between two ecological networks can be partitioned into contributions from rewiring (i.e. when shared species alter their interactions; I_rewired) and species-driven turnover (i.e. when changing species composition change interactions; I_species), with the latter being further partitioned into pollinator-driven (I_pol), plant-driven (I_pla) and pollinator + plant-driven (I_pol+pla) interaction turnover. (b) Matrices A and B represent ecological networks, with pollinator species arranged in rows and plant species in columns, which are artificially merged into one large matrix in order to identify interactions contributing to the different categories of interaction turnover. Region 1 contains interactions between shared species, and I_common denotes interactions found in both A and B, whereas I_rewired is the sum of interactions only observed in either matrix A or B, but between shared species. Shaded areas contain interactions contributing to species-driven interaction turnover. Interactions located in regions 2 and 3 are between shared pollinators and non-shared plants (i.e. the plants are found in either matrix A or B) and represent plant-driven interaction turnover. Interactions located in regions 4 and 7 are between shared plants and non-shared pollinators comprising the pollinator-driven interaction turnover. Finally, regions 5 and 9 contain interactions between non-shared pollinators and non-shared plants and comprise the pollinator + plant-driven interaction turnover. Regions marked with n.a. do not contain any interactions due to the artificial merging of matrices A and B.

Species-driven interaction turnover (I_species) can be further partitioned into that caused by (i) pollinators only present in one of the networks but interacting with plants present in both (i.e. pollinator-driven interaction turnover), (ii) plants only present in one of the networks but interacting with pollinators present in both (i.e. plant-driven interaction turnover) or (iii) plants and pollinators only occurring in one of the communities and interacting together (i.e. a complete turnover of species and hence interactions) (figure 1). Therefore, if I_pla is number of interactions between non-shared plants and shared pollinators (regions 2 and 3 in figure 1), I_pol is number of interactions between non-shared pollinators and shared plant species (regions 4 and 7 in figure 1), and I_{pol + pla} is number of interactions between non-shared pollinators and non-shared plants (regions 5 and 9 in figure 1), then I_species = I_pol + I_pla + I_pol+pla, and the fractions of the species-driven interaction turnover that can be explained by replacement of pollinators, plants or both are T_pol = I_pol/I_species; T_pla = I_pla/I_species and T_pol+pla = I_pol+pla/I_species, respectively.

Owing to nonlinearity between geographical distance and each metric of interaction turnover, we used cubic smoothed splines. These were evaluated with confidence intervals calculated from bootstraps with replacement [32]. First, we estimated a smoothed spline for the empirical data and smoothed splines for each of 10 000 permutations of the data. Second, ‘basic bootstrap confidence intervals’ [32] were calculated as

where 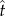represents values from the empirical spline, and 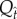is the percentile from the permutations at α = 0.05.

(d). Partner fidelity

Partner fidelity was quantified for plants and pollinators occurring at more than two sites by comparing the average of all empirical partner similarities across the archipelago with an average similarity achieved if partners were selected randomly among the available set of species at a site. First, for all plants and pollinators occurring in more than two networks, we calculated average Sorensen similarity in partner composition (Sor_emp) across all pairwise combinations of the sites at which the species occurred. This value reflects the empirical partner fidelity. Second, after selecting randomly among the available species at a site as many partners as the species originally had at that site, we again calculated average Sorensen similarity between all pairwise comparisons. This was repeated 1000 times, and z-scores (used as a proxy for deviation from randomness) were calculated for each species as (Sor_emp − Sor_rand)/Sor_SD, where Sor_rand and Sor_SD are mean and standard deviations of partner fidelities achieved from the 1000 random assortments of partners, respectively. Taxonomic resolution of partners (species, genus, family or order) probably influences level of partner similarity [23,33]. For comparison, we therefore resolved partners of plants to species, genus, family and order, and partners of pollinators to species and family. We did not resolve plant species to genus and order level due to a high level of redundancy with the partitioning into species and families, respectively.

Moreover, for each species, we had a value of partner similarity (Sorensen similarity) for each pairwise combination of the networks at which the species occurred, and each similarity value could be paired with a series of geographical and ecological variables. In this way, we assessed how partner similarities were affected by geographical distance (in km), change in abundance (difference in relative abundance of the focal species between compared networks), change in linkage level (difference in number of interaction partners of the focal species between compared networks) and geographical distribution (number of sites at which the focal species was registered). We used linear mixed-effects models, multi-modal inference and model averaging based on the bias-corrected Akaike information criterion (AICc) [34,35] with the species-specific partner similarity values for all species as a response variable (albeit separately for plants and pollinators). ‘Species’ was a random factor due to non-independence of the multiple entries of each species [36], and both random intercepts and random slopes were allowed due to the superiority compared with models only having random intercepts [37]. To obtain robust estimates and avoid model selection bias, we ran models covering all possible combinations of the fixed parameters (‘geographical distance’, ‘change in abundance’, ‘change in linkage level’ and ‘geographical distribution’) and performed a model averaging procedure of the parameter estimates using the Akaike weights [34]. Coefficients were standardized to facilitate comparisons and supplied with 95% confidence limits. Coefficients not including zero in their interval represented variables with a significant impact on partner fidelity. Additionally, in order to examine to what extent the overall community similarity influenced partner fidelities, we performed a similar modelling procedure, but instead of ‘geographical distribution’ (we omitted this variable because it did not have an effect at all, and we wanted to minimize the number of fixed parameters in order not to overstretch the modelling procedure) we used the overall similarity of the partner community as a fixed explanatory variable. That is, we used the pairwise ‘pollinator similarity’ for the whole community as a fixed variable when looking at the partner fidelity of the plant species, and pairwise ‘plant similarity’ when looking at partner fidelity of the pollinators.

Linear mixed models and model averaging were performed with the packages lme4 v. 1.0-5 and MuMIn v. 1.9.13, respectively, for R [31]. We acknowledge that the linear mixed models only account for the taxonomic non-independence (i.e. the multiple entries of each species) and not necessarily the spatial non-independence (i.e. the multiple entries of the pairwise comparisons of the networks).

3. Results

(a). Community similarity

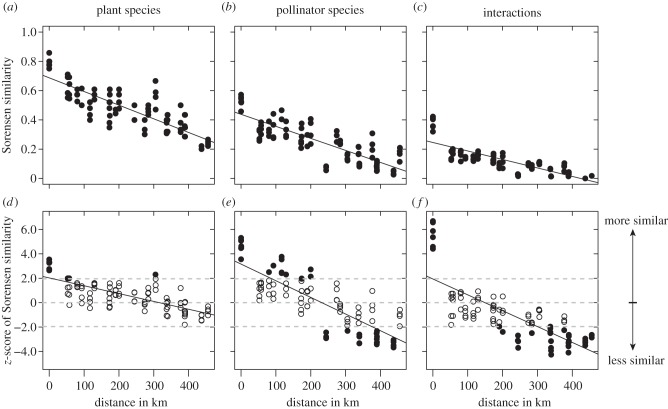
The pairwise similarity of plant (Mantel test with 1000 permutations: Sorensen: r_M = 0.841, p < 0.001), pollinator (Sorensen: r_M = 0.821, p < 0.001) and interaction composition (Sorensen: r_M = 0.824, p < 0.001) among networks decreased linearly with geographical distance (figure 2a–c). Moreover, when taking the differing α-diversities into account and instead used the z-scores, we still found a significant decrease in similarity with distance for plants (Mantel test with 1000 permutations: r_M = 0.747, p < 0.001), pollinators (r_M = 0.813, p < 0.001) and interactions (r_M = 0.759, p < 0.001) (figure 2d–f). Therefore, geographically close networks (and especially networks on the same island) were more similar in their composition than expected from a random assortment of species and interactions while distant networks were less similar than expected.

Figure 2.

(a–c) Similarity in the composition of plants, pollinators and interactions between ecological networks sampled across the Canarian archipelago as a function of geographical distance. (d–f) To reduce the effect of differing α-diversities, we calculated z-scores as a measure of deviation from randomness. z-scores were given as (β_emperical − 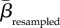)/SD_resampled, where β_emperical is the empirical similarity between two networks, and 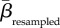and SD_resampled are the mean and standard deviation of the similarities when performing 1000 random assortments of species and interactions, respectively. Positive and negative z-scores signify higher and lower similarity, respectively, than expected from random distributions of species and interactions. Filled circles in (d–f) indicate that a given empirical pairwise comparison differed significantly from the resampled values, and grey dashed lines mark the boundary between 1.96 and −1.96.

(b). Drivers of interaction turnover

The proportional contributions of species-driven interaction turnover and rewiring varied inversely with distance due to their interdependence. While species-driven turnover increased asymptotically towards unity with increasing distance, rewiring decreased equivalently (figure 3a). Species-driven interaction turnover was further partitioned into pollinator- (T_pol), plant- (T_pla) and polliantor + plant-driven turnover (T_pol+pla) (figures 1 and 3b,c; see also Material and methods). Along the entire geographical gradient, pollinator-driven interaction turnover contributed more to the overall species-driven turnover than plant turnover (i.e. T_pol > T_pla; figure 3b). This was most pronounced at short distances. Plant-driven interaction turnover (i.e. T_pla) peaked between 100 and 130 km (see arrow in figure 3b). This peak was significant based on the bootstrap confidence bands, because the lower confidence band around the peak was higher than the upper bands at other distances. At larger distances, the overlap in both plant and pollinator composition diminished, and species-driven interaction turnover became an effect of replacement of both pollinator and plant species (i.e. T_pol+pla). In fact, T_pol+pla increased significantly (R²_adj = 0.69, F = 201, p < 0.001) and linearly along the entire geographical range of the study. At approximately 400 km, novel interactions among non-shared species accounted for 50% of the total species-driven interaction turnover (figure 3c).

Figure 3.

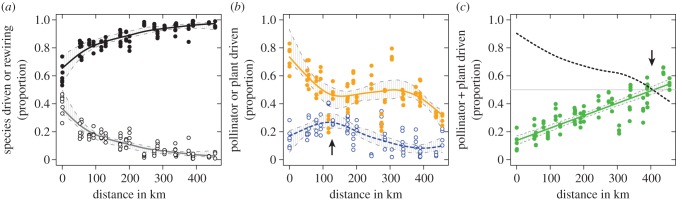
(a) The proportion of the total interaction turnover that can be labelled as either species-driven interaction turnover (black points and black line) or rewiring (open points and grey line) change in relation to geographical distance between paired networks. (b) Influence of geographical distance on the proportion of the species-driven interaction turnover that can be ascribed as pollinator-driven (closed points and line) and plant-driven (open points and dotted line). (c) Proportion of species-driven interaction turnover that is caused by a combined turnover of both plants and pollinators (pollinator + plant-driven) in relation to geographical distance (points and line). The dotted line in (c) represents the sum of the two smoothed lines in (b). Arrow in (b) highlights the peak in plant-driven turnover, whereas the arrow in (c) marks the distance at which 50% of the species-driven turnover is pollinator + plant-driven. Grey areas delimited by dotted lines are basic bootstrap confidence bands in (a,b) and normal confidence intervals in (c). (Online version in colour.)

(c). Partner fidelity

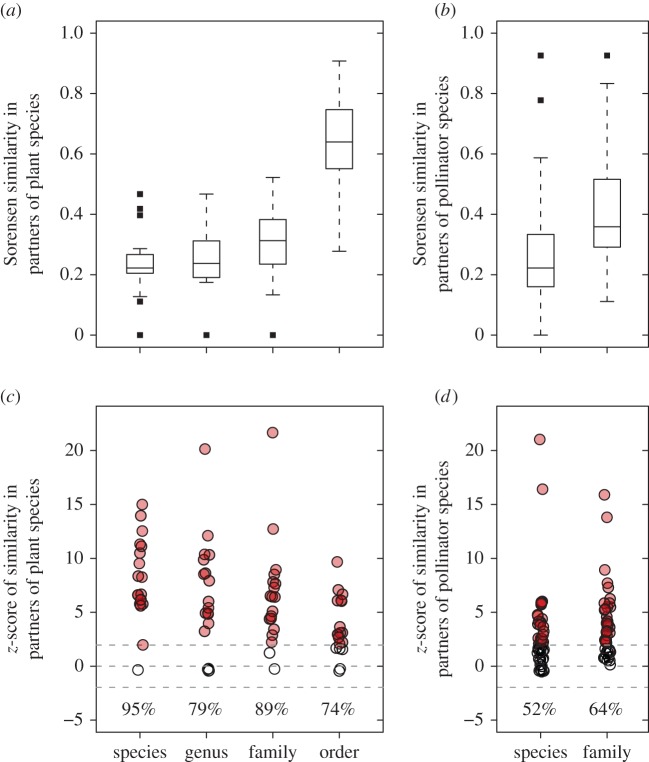
Both plant and pollinator species showed an increase in partner similarity with reduced taxonomic resolution (figure 4a,b). Eighteen out of 19 tested plant species had significantly (i.e. z-score > 1.96) higher partner fidelity than expected if partner choice was random (figure 4c). This pattern was generally independent of taxonomic resolution of partners. Approximately half (25 out of 48) of all tested pollinator species had significantly higher partner fidelity compared with random partner use (figure 4d).

Figure 4.

Averaged partner similarities of (a) plant and (b) pollinator species observed in more than two networks across the Canarian archipelago, and with the partners resolved to species, genus, family and order. Boxes represent the interquartile range (IQR), horizontal lines within the boxes represent medians, whiskers extend to 1.5 times the IQR, and outliers are plotted as squares. (c,d) The z-score measures the deviation from random and most plant species (c) and approximately half of the pollinators (d) showed significant partner fidelity (i.e. z-score ≥ 1.96). In (c,d), filled circles represent species with z-scores ≥ 1.96 and the percentage denotes the proportion of plant (n = 19) and pollinator species (n = 48) that differed significantly from random. Points in (c,d) have been jittered slightly to increase visual clarity and superimposed points results in darker colours. (Online version in colour.)

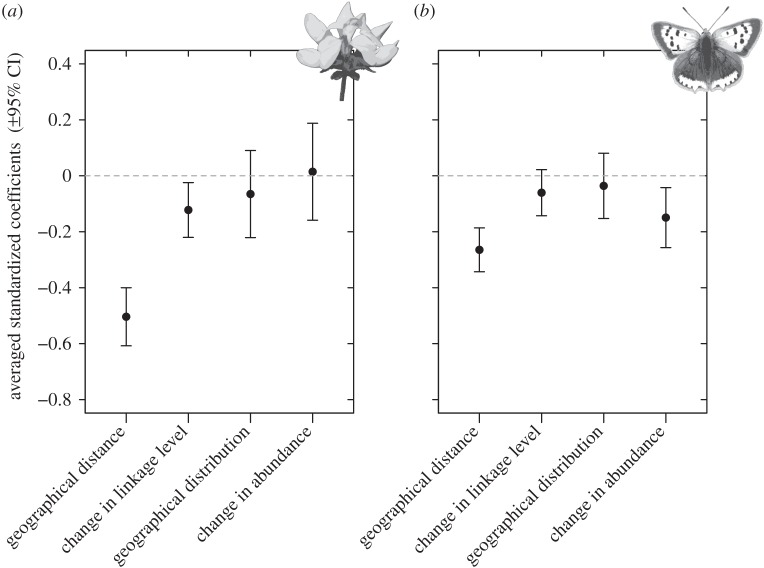
Linear mixed models (see all models and output in the electronic supplementary material, table S1), with species as random factor, revealed that partner fidelity of plant species decreased with increasing geographical distance and difference in linkage level (figure 5a). Geographical distribution and change in relative abundance of plant species had no significant impact on partner fidelity of plant species. Partner fidelity of pollinator species decreased with increasing geographical distance and difference in relative abundance, whereas geographical distribution and difference in linkage level had no effects (figure 5b). In the electronic supplementary material, figure S2, we have performed a similar modelling procedure, where we included the similarity of the entire potential partner community as an explanatory variable. These results suggest that even when taking the similarity of the entire potential partner community into account, geographical distance still had a significant negative impact upon partner fidelity of both plants and pollinators. Interestingly, the overall similarity in pollinators was more important for the partner fidelity of the plant species than the overall similarity in plants was for the partner fidelity of the pollinators. Furthermore, when taking this effect into account, ‘geographical distance’ had a more comparable impact upon partner fidelities of plants and pollinators (mainly due to a lowering of the effect on plant partner fidelity; electronic supplementary material, figure S2).

Figure 5.

Averaged standardized coefficients and their 95% CIs of fixed parameters obtained from linear mixed models applying a multi-model inference and model averaging procedure based on AICc (see Material and methods). Species-specific partner similarities of (a) plant and (b) pollinator species between two sites were the response variables, and geographical distance, change in linkage level, change in relative abundance and geographical distribution of the species were fixed effects. ‘Species’ was included as a random factor in all models due to the non-independence of the multiple entries of each species, and we allowed both random slopes and intercepts. Parameters having coefficients with confidence limits not covering zero were considered to have a significant impact on partner fidelity.

Finally, using linear mixed models with ‘change in abundance’ as an explanatory variable, ‘change in linkage level’ as a response variable and ‘species’ as a random factor (allowing both random slopes and intercepts, and fitted separately for plants and pollinators), we examined the correlation between these two variables. While ‘change in linkage level’ was positively and significantly correlated with ‘change in abundance’ for pollinators (coefficient = 0.18, p < 0.001), this was not the case for plant species (coefficient = 0.019, p = 0.93). Here, the p-values were achieved using an ANOVA test to compare the full model with a model omitting ‘change in abundance’, but retaining ‘species’ as a random factor [38].

4. Discussion

(a). Community similarity

The similarity in species and interactions among Canarian pollination networks decreased with geographical distance. Indeed, the results suggest that along the approximately 450 km, similarities in plant, pollinator and interaction composition decreased from more similar than expected to less similar than expected when compared with random assortments of species and interactions (figure 2). This is in accordance with Simberloff's [39] statement that inter-island distance affects similarity of flora and fauna between islands. That close and distant networks were more and less similar than expected, respectively, implies that some kind of assortment of species and interactions is taking place in relation to distance. Although on a spatial scale two orders of magnitude smaller, other studies have found a similar decrease in similarity for species in ant–plant mutualistic networks [11] and for plant species and interactions in plant–pollinator networks [13]. Burkle & Alarcón [10], however, found no correlation between geographical distance and the similarity in plants, pollinators or interactions along a 3 km gradient. This highlights that turnover among mutualistic networks may display system-specific patterns, and that it deserves further attention with respect to a broad range of habitats and geographical gradients. Distance decay is usually explained by decreasing environmental similarity and/or dispersal limitations [8,40]. Though both of these processes are probably at play on the Canary Islands, an additional and potentially important contributing process is speciation. Each island has many endemic species [4] that probably facilitate the high species turnover among these communities. Furthermore, the islands differ in their developmental stage (young, mature and old), which has a characteristic imprint on not only the biota [41] but also the structure of the networks [25], and this may likewise explain some of the observed dissimilarities in interactions with distance.

(b). Drivers of interaction turnover

In the Canary Islands, species-driven interaction turnover was the major driver of interaction turnover across the entire range of distances, and became the sole driver (i.e. causing more than 90% of the difference in interactions) if networks were more than 300 km apart. Others have also distinguished between species-driven interaction turnover and rewiring [9,15], but because species-driven turnover was the main contributor, we further partitioned it into pollinator-, plant- and pollinator + plant-driven (figures 1 and 3). Along the entire gradient, pollinator-driven turnover accounted for a larger fraction of the overall species-driven turnover than that of plants, which probably is an effect of (i) the initial selection of sites based on their vegetational similarity, (ii) the plant-centred sampling protocol where we observed plants for pollinators and not vice versa [42,43], (iii) the higher diversity of pollinators compared with plant species, and (iv) the perennial lifestyle of plants versus the annual lifestyle of the pollinators. Thus, pollinator species probably fluctuated more in abundance and diversity, and consequently accounted for more of the observed interaction turnover. Although selecting sites based on their floral composition could partly account for the higher pollinator-driven turnover along the entire gradient, we applied the same selection procedure to all sites, and the relative difference between the plant- and pollinator-driven component of interaction turnover in relation to geographical distance (as shown in figure 3b) should not be biased in any particular direction. That is, minimum and maximum contribution of these components along the spatial gradient should not be related to our selection criteria, and therefore display real and not apparent patterns.

Plants and pollinators in our study appear to be affected differently by distance, which resulted in plants and pollinators having separate and distinct relative contributions to the species-driven turnover. The contribution of plant-driven turnover peaked between 100 and 130 km (see arrow in figure 3b). Most neighbouring islands are within 50–100 km distance of each other, and the peak therefore reflects moving from within-island comparisons to comparisons among neighbouring islands. Mantel correlograms (electronic supplementary material, figure S3) showed that at shorter distances, spatial autocorrelation of plant species decrease quickly and plant compositions therefore already change when comparing neighbouring islands. Pollinator-driven interaction turnover dropped at 100–130 km and then stayed on a plateau until 400 km. The initial drop in pollinator-driven interaction turnover may be a result of pollinators showing spatial autocorrelation over longer distances than plants (electronic supplementary material, figure S3), which minimize the relative contribution of pollinator turnover to the total interaction turnover. Finally, pollinator + plant-driven turnover increased linearly along the entire geographical range. Thus, with increasing spatial separation, a complete substitution of both plants and pollinators accounted for an increasing fraction of the species-driven turnover, and above approximately 400 km this was the main contributor (more than 50%; see arrow in figure 3c).

Biotic interactions are a distinct and important element of diversity, and consequently receive increasing attention in conservational and biogeographic studies [44–46]. β-diversity of interactions represents a refinement in our general perception of ecological complexity, because interaction turnover reflects turnover at a higher level as it is partly driven by the dynamics of species. Indeed, spatio-temporal changes in species compositions, biotic interactions and hence the structure of ecological networks is perceived as a fruitful avenue of research, especially in relation to ongoing global changes [47,48]. The current study shows that mutualistic interactions between plants and pollinators change in a predictable way across the Canary Islands. It highlights the importance of incorporating the geographical settings (here distance) and spatial autocorrelation of the species to fully understand the variation in interaction patterns along a gradient. The presented framework represents a step towards a better understanding of the β-diversity of ecological networks on a large spatial scale and emphasize that species-driven interaction turnover (when partitioned into T_pol, T_pla and T_pol+pla) displays more complex patterns in relation to geographical distance (figure 3) than could have been deduced from the more ‘simple’ linear relationships of species β-diversity (figure 2).

(c). Partner fidelity

Fang & Huang [23] found that plants tended to interact with the same functional groups of pollinators over a 4-year period, and in a meta-analysis, Rosas-Guerrero et al. [33] found evidence for pollination syndromes—both suggestive of some level of partner fidelity at a higher hierarchical level. Working at species level, we found that 95% of the plant species and half of the pollinators showed partner fidelities (i.e. partner similarities) that were significantly higher than random (figure 4). Collectively, this suggests that species might be less plastic or opportunistic in their establishment of interactions than previously reported (e.g. [18,21,49]) and therefore susceptible to phenological mismatching caused by, for example, global warming [22,50]. The higher level of fidelity of plant species compared with pollinators (figure 4c,d) may relate to fundamental differences in their life histories. The annual and mobile behaviour of the pollinators, compared with the perennial and sedentary lifestyle of the plants, may make pollinators more opportunistic in terms of partners.

Many species, however, did not interact with the exact same partners across all sites, and therefore showed some level of plasticity. Geographical distance between sites had a negative impact on partner fidelity of both plants and pollinators. These findings are suggestive of a shift in the coevolutionary dynamics of co-occurring species when they experience increasing spatial separation [51,52]. Interactions represent selection pressures [53] and species might thus experience divergent selection regimes across the archipelago depending on their partner composition, which ultimately may lead to divergence and speciation. The assembly of sites therefore constitutes a kind of a geographical mosaic at community or network level [54]. Additionally, change in the linkage level of plants and change in abundance of pollinators also influenced partner fidelity negatively. For plants, this suggests that changes in the generalization level influence partner fidelity, whereas for pollinators, it suggests that abundances may affect partner choices, for example through interspecific competition. That is, if a pollinator is very abundant at one site it may expand its niche (i.e. visit different and potentially less preferred plant species) in order to reduce competition, which in turn would have a negative impact on the measure of fidelity.

Finally, although species and interactions vary in space and time, the global network structure (e.g. nestedness, modularity and connectance) has usually been identified as stable [11,15,16,18,23]. None of these studies have quantified the fidelity of partner compositions, and here we suggest that it may be seen as a deeper fine-scaled layer contributing to our understanding of the dynamics of global network structures. If species generally have preferences for a specific subset of partners (in both space and time), this may have a preserving effect on network topologies compared with species behaving more opportunistically. Similarly, Stouffer et al. [55] have shown that species roles (based on network motifs) tend to be spatially and phylogenetically conserved across a wide range of food webs. Therefore, the fine-scaled variability within ecological networks (i.e. choice of partners, species roles, etc.) may be more restricted and conserved than hitherto assumed.

Data accessibility

Interaction networks and geographical pairwise distances between sites can be accessed from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.76173.

Funding statement

The study was financed by Aarhus University Research Foundation (K.T.), FAPESP grant nos. 2011/22635-2 and 2014/01594-4 (D.W.C.) and the Danish Research Council FNU (J.M.O., K.T.).