How do site-specific DNA-binding proteins find their targets?

Abstract

Essentially all the biological functions of DNA depend on site-specific DNA-binding proteins finding their targets, and therefore ‘searching’ through megabases of non-target DNA. In this article, we review current understanding of how this sequence searching is done. We review how simple diffusion through solution may be unable to account for the rapid rates of association observed in experiments on some model systems, primarily the Lac repressor. We then present a simplified version of the ‘facilitated diffusion’ model of Berg, Winter and von Hippel, showing how non-specific DNA–protein interactions may account for accelerated targeting, by permitting the protein to sample many binding sites per DNA encounter. We discuss the 1-dimensional ‘sliding’ motion of protein along non-specific DNA, often proposed to be the mechanism of this multiple site sampling, and we discuss the role of short-range diffusive ‘hopping’ motions. We then derive the optimal range of sliding for a few physical situations, including simple models of chromosomes in vivo, showing that a sliding range of ∼100 bp before dissociation optimizes targeting in vivo. Going beyond first-order binding kinetics, we discuss how processivity, the interaction of a protein with two or more targets on the same DNA, can reveal the extent of sliding and we review recent experiments studying processivity using the restriction enzyme EcoRV. Finally, we discuss how single molecule techniques might be used to study the dynamics of DNA site-specific targeting of proteins.

INTRODUCTION

Essentially all of the biological functions of DNA are realized by proteins that interact with specific DNA sequences (1). Familiar examples occur at the initiation of DNA replication, during gene expression by RNA polymerase and associated transcription factors, in genome re-arrangements by site-specific recombination and transposition and in the restriction and modification of DNA by sequence-specific endonucleases and methyltransferases. For proteins that act at specific sequences, the target sites constitute a minute fraction of the cellular DNA. Yet some of these proteins locate their target sites very rapidly (2), much more rapidly than can seemingly be accounted for by diffusional collisions between the protein and the DNA molecule (3). Hence, these proteins must find their targets by ‘facilitated diffusion’, implying mechanisms that avoid fruitless searching of target-less regions of the cell or the test tube. Such mechanisms generally involve initial binding at a random DNA site via non-specific (sequence-independent) interactions, followed by intramolecular translocation to the specific binding site (4–7).

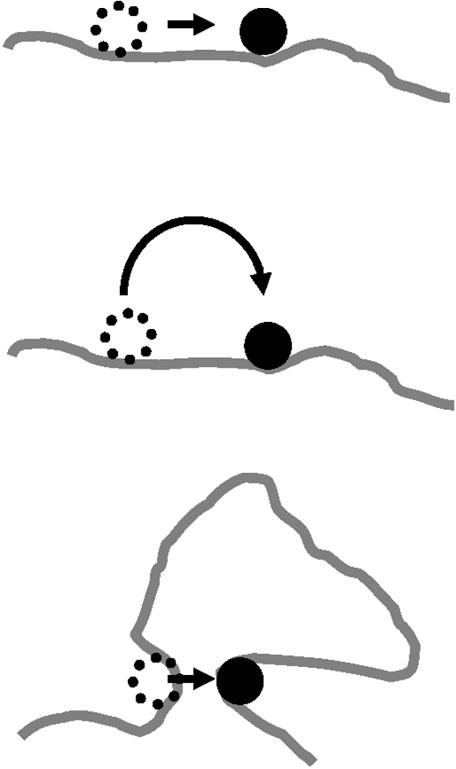
A number of proposals have been discussed for how facilitated diffusion of a protein to a target actually occurs (Fig. 1). One is that the protein moves from its initial non-specific site to its target by ‘sliding’ along the DNA, i.e. by one-dimensional (1-D) diffusion during which the protein remains in contact with the DNA for long enough periods so that appreciable diffusive motion occurs in either direction along the chain contour (8–14). Alternatively, a protein might ‘hop’ from one site to another through three-dimensional (3-D) space, by dissociating from one site and then re-associating elsewhere in the same chain. Each re-association will usually occur at a site near (in sequence) to where the protein last dissociated (15). However, occasionally a hop might occur to a sequence-distant site in the same chain. Relatively rarely, a hop may occur to a different DNA molecule (16,17).

Figure 1.

Schemes for target site location. Three commonly discussed microscopic pathways for transferring a protein from one site to another along a long DNA molecule are ‘sliding’, ‘hopping’ and ‘intersegmental transfer’. (Top) A protein might ‘slide’ along the double helix, transferring from one base pair position to the adjacent one without dissociating from the DNA. Many repeated sliding events result in 1-D diffusion of the protein along the DNA contour. (Center) If dissociation occurs, the protein might re-encounter the same DNA, but at a new contour position: we term such an event a ‘hop’. (Bottom) On scales beyond the persistence length of the DNA double helix, 150 bp (50 nm), the DNA can run into itself as a result of its random thermally excited bending. Such encounters permit the protein to move from one DNA site to another via an intermediate in which the protein is bound transiently to both sites, a process called ‘intersegmental transfer’.

In a third scenario, ‘intersegmental transfer’, the protein moves between two sites via an intermediate ‘loop’, formed by the protein binding both sites concurrently. Such transfers will, however, have a mean step size of ∼400 bp, since DNA sites are juxtaposed most readily when they are ∼400 bp apart along the contour (18,19). This distance is a consequence of the 150 bp ‘bending persistence length’, the length over which thermally excited bending occurs (20). In addition, intersegmental transfer is relevant only to proteins with two DNA-binding surfaces, such as the Lac repressor or the SfiI endonuclease (21). For many other proteins it is highly improbable that they can ever bind two DNA segments concurrently. For example, the EcoRV restriction enzyme binds either specific or non-specific DNA in a deep cleft between two protein subunits (22) and the cleft is far too narrow to accommodate two duplexes at the same time. Intersegmental transfer thus relates only to large translocations on large DNA molecules by a limited subset of DNA-binding proteins and is not discussed here further.

Berg and Blomberg (9–11) presented a theoretical analysis of how 1-D diffusion along a DNA contour can facilitate specific site targeting. This theory took into account the likely phenomenon that a protein will alternately undergo 1-D sliding and 3-D diffusive hops, with some characteristic ‘sliding length’ that is covered by 1-D diffusion. This sliding length will be determined by the lifetime of a non-specific DNA–protein interaction and by the effective 1-D diffusion constant. These ideas were further developed and applied to experiments on the Lac repressor protein by Berg et al. (12–14). By changing the salt concentration to alter the lifetime of the non-specific DNA–protein interactions, and thus to change the sliding length, Berg et al. showed that they could change the time required for the repressor to find its target in a large DNA in accord with theory. In the original study of the Lac repressor (14), the sliding length was estimated to be ∼100 bp under physiological conditions. Targeting by Lac repressor therefore occurs by a combination of 1-D and 3-D pathways.

We here present a summary of experiments and theoretical ideas on mechanisms for the transport of site-specific binding of proteins to their DNA targets. As such, this kinetic approach is an essential corollary to both thermodynamic and structural approaches to protein–DNA recognition that have been reviewed elsewhere (23–26). We start by reviewing the basic properties of non-facilitated diffusion, in order to emphasize the relatively fast rate at which site-specific binding can occur. We then present a simple analysis of 1-D and 3-D mechanisms for target site location by DNA-binding proteins. This analysis will ignore many numerical factors and other details in order to illustrate the basic concepts behind the work of Berg, Blomberg, Winter and von Hippel. While our analysis lacks the mathematical rigor of Berg and Blomberg (9–11), it permits a simple analysis of the distribution between 1-D and 3-D processes for a range of DNA conformations.

An interesting feature of facilitated diffusion by sliding, emphasized below, is that for a DNA confined to a small compartment, as in a cell, there is an optimal distance along DNA contour for 1-D sliding of ∼100 bp, which minimizes the time required for a site-specific protein to find its DNA target. If the sliding distance is shorter than optimal, time is wasted by exploration of the solution by 3-D diffusion. On the other hand, if the sliding distance is too long, time is wasted during 1-D diffusion by sampling the same DNA sites repeatedly (7).

With regard to the experimental approaches used to study the mechanisms of target site location, we discuss the traditional strategy, analysis of the kinetics of proteins binding to their target sites in long DNA chains. While this is conceptually simple, other experimental approaches can provide further information about the mechanisms of protein motion along DNA. One is the analysis of processive reactions, i.e. the interaction of a protein with two or more nearby sites along the same DNA without an intervening dissociation. This strategy is discussed below, with reference to the restriction enzyme EcoRV (27). Finally, in Conclusions and Outlook, we summarize existing experimental results and their correspondence with theoretical ideas. We also propose single molecule experiments that may permit direct observation of proteins translocating along DNA to specific sites.

THREE-DIMENSIONAL DIFFUSION-LIMITED TARGETING

Diffusion of a protein

A single protein of 10–100 kDa size has a diameter of ∼5 nm; we suppose it to move through buffer by Brownian motion (diffusion), meaning that its trajectory will be a random walk (28). The major feature of Brownian motion that we will use is that the average of the distance squared covered by a diffusing particle grows linearly with time (Fig. 2):

Figure 2.

The trajectory of a diffusing protein is a ‘random walk’. A 3-D random walk of 10⁶ steps, each of length 1, is shown here as a projection on a 2-D plane. The end-points of the walk are at (0,0) and at (–300,–300). The overall size of the random walk is roughly the square root of the number of steps, or ∼1000 steps, as expected from the mean square law R² = Dt. Although this law holds quantitatively only in statistical terms when applied to many random walks, the overall size of one random walk is usually reasonably well estimated by the mean square law. It is important to note that the random walk has many voids; it does not completely explore the 3-D region it extends through.

r² = Dt    1

where D is the diffusion constant, in units of length squared per time. We can rewrite this as r = √Dt, keeping in mind that r represents the square root of the average of the square of the distance (sometimes called the ‘root mean square displacement’). We can consider r to be the typical distance moved by our diffusing protein during the time interval t.

We can estimate the diffusion constant of a protein using Einstein’s formula for the diffusion constant of a sphere of diameter d (28):

where η is the viscosity of the buffer (for water or most aqueous buffers η = 1 × 10^–3 Pa s), and where k_BT is the amount of heat energy in one molecular degree of freedom. In the range of temperatures relevant in vivo (0–50°C) we may take k_BT = 4 × 10^–21 J (Boltzmann’s constant k_B is just the familiar gas constant divided by Avogadro’s number). The diffusion constant for a protein of diameter 5 nm is therefore roughly D = 10^–10 m²/s = 10^–6 cm²/s = 10⁸ nm²/s.

Probability of finding a nearby target by diffusion

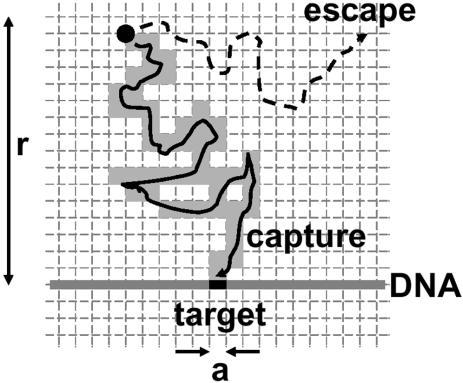
Consider a protein diffusing near a target sequence (binding site) of size a, in a large volume of buffer (Fig. 3). We suppose that when the protein approaches within a distance a of its binding site, binding becomes inevitable. We also suppose that the targets are fixed in space; since the targets are, on large, slowly diffusing DNA molecules, this is a permissible simplification, though a rigorous analysis would incorporate the segmental motion of the individual sections of the DNA chain (29). Given an initial distance r between protein and target, which must be considerably larger than either a or d (considering the nM concentrations relevant for site-specific binding reactions, it is useful to bear in mind that 1 nM corresponds to 1 molecule/µm³ or one molecule per Escherichia coli cell), what is the probability that binding will occur via simple diffusion?

Figure 3.

Probability of finding a target of size a by 3-D diffusion. The diffusing protein, at an initial distance r from the target, will either collide with the target or diffuse off into bulk solution, never finding this target. During its random walk within a distance r of the target, the protein visits a fraction a/r of the ‘voxels’ of size a (see text). The probability of encountering the target is thus a/r.

This problem can be solved by considering the trajectory of the protein, at a resolution of the binding site size a. Imagine the region near the target to be divided into volumetric pixels, or ‘voxels’, of width a. The region of size r between protein and target will be divided up into (r/a)³ voxels. The protein moves from voxel to voxel by random walk motion. According to the mean square distance law for diffusion (equation 1), each voxel is visited for a time a²/D; the region of size r is exited after a longer time, r²/D.

Thus, the total number of voxels that will be visited before the protein moves appreciably away from its target will be the ratio of these two times, (r/a)². Put another way, during the time the protein is near its target it will sample a fraction a/r of the voxels in the region near the target (Fig. 3). Thus, its probability of binding to the target is a/r, which happens to be the exact result for ‘diffusion to capture’ (28, p. 39). The typical time required for this to occur is just r²/D. Note that in this situation, binding might not occur: this occurs with a probability of 1 – a/r. In this case, the protein wanders off into empty solution, never finding its binding site.

The diffusion-limited reaction rate

The above result can be used to compute the association rate for binding, but now for targets present at concentration c. If this concentration is in units of number of molecules per volume, then the volume per target is V = 1/c. Thus, we can expect our protein to be a distance of roughly r = 1/c^1/3 from a binding site. After a time of r²/D, one of two things will have happened: with probability a/r, the protein will have bound a nearby target; otherwise, it will have diffused away from that target. However, now there are other targets, so if we wait r/a times longer, the probability of binding will be pushed up to near certainty, giving a total association time of r/a × r²/D = r³/(Da) = 1/(Dac). The association rate is the inverse of this, Dac. Finally, the association rate constant is the rate per unit concentration:

k = 4πDa.    3

The units of k are volume per time; the usual units quoted are /(mol/l)/s. The factor of 4π follows from more detailed calculations originally due to Smoluchowski (30).

Plugging in the diffusion constant (equation 2) for a protein of diameter d gives the result k = 4k_BTa/(3ηd). The factor k_BT/η = 4 × 10^–18 m³/s = 4 × 10^–15 l/s ≈ 10⁹/(mol/l)/s (below we abbreviate this unit to /M/s) gives the rough order of magnitude for the rate, but since the size of the target will be significantly smaller than our whole protein, we suppose a/d = 0.1 and obtain k ≈ 10⁸/M/s. A rate constant of this order of magnitude is often referred to as the diffusion limit (3,31): a binary reaction cannot occur at a higher rate than this if the reactants are brought together by unguided 3-D diffusion. Any additional constraints, such as a requirement for protein and target being in a precise relative orientation, will always act to reduce the association rate below the diffusive limit.

The above analysis omits, however, any contribution from electrostatic interactions between the reactants, and such interactions can lead to association rate constants that far exceed the diffusion limit. Protein–protein associations are often strongly influenced by electrostatic interactions and can occur at remarkably rapid rates even when they involve very precise alignments of the reacting partners (32). For example, the second order rate constants for the extremely specific associations of colicin nucleases with their cognate immunity proteins can exceed 1 × 10¹⁰/M/s, at least in buffers containing low salt concentrations (33,34). As expected for a process governed by electrostatics (23), raised salt concentrations reduce these rate constants to ∼1 × 10⁷/M/s, values close to the diffusion limit.

HOW FAST DO PROTEINS ACTUALLY BIND TO SPECIFIC DNA SITES?

The first measurements of the association rate of a protein to a specific DNA sequence were made with the Lac repressor binding to its operator site and these revealed remarkably large rates constants, of ≥1 × 10¹⁰/M/s (2). Several subsequent studies have provided further evidence for these enormously rapid rates and have also revealed large variations in these rate constants with the salt concentration of the binding buffer (14,35). Though electrostatic effects can, as noted above, result in association rate constants appearing to exceed the diffusion limit, this is only likely to occur in reactions at low salt concentrations. At the effective cation concentrations that will be encountered in vivo (36,37), the electrostatic effect will be negligible, as at distances exceeding a few nanometers most of the charge on both DNA and protein will be neutralized by counterions (23,24).

The initial (pre-1986) experiments on the Lac repressor are, however, open to reinterpretation. First, it was not realized at that time that the lac operon DNA used in the initial studies contained not just one binding site for the repressor but rather multiple sites (38,39). Second, it was subsequently discovered that the Lac repressor has two separate binding surfaces for its cognate DNA sequence (40; and references therein), thus resulting in a zoo of possible complexes with the native operon: individual molecules of the protein can bind to the separate sites or they can trap DNA loops by binding concurrently to two sites in the same molecule of DNA, or they can tether two DNA chains by spanning sites on different molecules of the DNA (41). Third, the initial studies on binding of the Lac repressor to its operator(s) employed a filter-binding technique, but this procedure records the total amount of DNA bound by at least one molecule of protein, so the data cannot be related directly to the occupancy of any individual site on the DNA. Moreover, the many different complexes that can be formed between the Lac protein and its operon are retained on filters with different efficiencies (42). Nevertheless, subsequent studies using a rapid footprinting procedure, which reveals directly the occupancy of individual sites, again gave rate constants close to 1 × 10¹⁰/M/s for association of the Lac repressor with its target sequence (43).

The extraordinary large rate constants for the association of the Lac repressor with its DNA have been taken to suggest that DNA-binding proteins generally bind their targets at very rapid rates (4,5). There exists, however, surprisingly little experimental evidence to justify this generalization. To date, second-order rate constants for associations with specific sites in macromolecular DNA have been measured by direct procedures for only a relatively small number of DNA-binding proteins. In recent years, most DNA–protein association rates have come from experiments, often employing fluorescence approaches, that used short synthetic duplexes of ∼20 bp as the DNA (e.g. 44,45), but facilitated diffusion cannot contribute to such rates.

At present, there probably exist more crystal structures of DNA-binding proteins (25,26) than direct measurements of the association rates of proteins with macromolecular DNA in free solution. Of these, rate constants of ≥1 × 10¹⁰/M/s were found for the Gal repressor (a relative of Lac) and for integration host factor (33,46). But very few, if any, other DNA-binding proteins have yielded association rate constants ostensibly above the diffusion limit. Instead, the majority of DNA–protein associations occur at rate constants within a factor of three of 1 × 10⁸/M/s. Examples of the latter include: RNA polymerase binding to various promoter sequences (47); the Cro and TetR repressors, the TATA binding protein and many other transcription factors binding to their respective target sites (48–50); the replication terminator Tus (51); several restriction endonucleases, some of which recognize individual sites and others pairs of sites (52,53).

[For some DNA-binding proteins, values for association rate constants have been obtained by surface plasmon resonance, a procedure that entails the capture of one of the reactants onto a solid surface (54). The rate constants measured by this technique are often several orders of magnitude smaller than the values noted above. The figures from surface plasmon resonance can be limited by either instrument response time or by the mass transport of the mobile reactant (54). We consider here only data from homogeneous systems in liquid phase. Alternatively, association rate constants have frequently been calculated from the equilibrium constant for the binding reaction and the dissociation rate constant: the latter can often be measured more readily than the association rate constant. However, this procedure is only valid if the binding reaction is a one-step process, i.e. E + S ↔ ES. In reality, most protein–ligand associations involve at least two steps, typically an initial binding followed by a structural rearrangement (31), i.e. E + S ↔ ES ↔ ES*. In these cases, the association rate constants cannot be determined from the equilibrium and the apparent dissociation rate constants, so values obtained by this procedure are also disregarded here.]

The majority of the information currently available about protein–DNA association rates has come from indirect measurements, in particular from competition experiments in which the protein is added to a mixture of two DNA molecules of different lengths: the relative rates for binding to each DNA are then assessed from the number of reactions on one DNA over the other (55–58). Of the rate constants for DNA–protein associations that have been measured directly, most fall close to the diffusion limit and only a small number of cases, principally the Lac repressor, have yielded rate constants appreciably above the limit. Though the Lac repressor is often taken as the paradigm of DNA–protein interactions in general, it is in many ways an atypical system. Nevertheless, the DNA-binding proteins that bind to specific sequences in long DNA molecules at rates close to the diffusion limit still pose a problem. Their initial encounter with the DNA chain will almost always be at a random non-specific site rather than the specific sequence so, given that the specific sequence is a very small fraction of the total DNA, the rate constant for reaching the specific site might be expected to be very much lower than the diffusional limit (4).

SIMPLE-MINDED VIEW OF FACILITATED DIFFUSION

The accepted resolution of the puzzle of how proteins associate with their targets at rates in excess of those expected for a simple diffusive search is that they undergo ‘facilitated diffusion’. The main idea is that non-specific association of proteins with DNA can reduce the time required for them to find their target sequences, essentially by restricting their motion to along the DNA contour (9–12). The association rate is increased by the non-specific DNA flanking the target, which serves to greatly increase the effective target size. To see this in the simplest quantitative way, note that the association rate increases with target size a (equation 3). Facilitated diffusion provides accelerated targeting essentially by increasing the target size, without decreasing the diffusion constant of the protein that is doing the search.

We now review how the ‘sliding’ of a protein along DNA, plus ‘hopping’ through three dimensions, can increase the association rate.

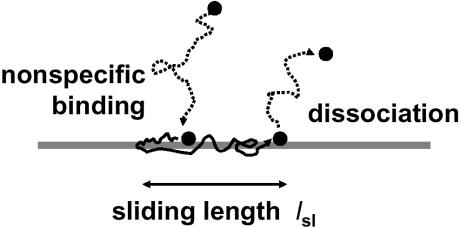
The sliding length

We consider a site-specific DNA-binding protein that can bind non-specifically and slide along the double helix (8–12). We suppose that there is a 1-D sliding diffusion constant D₁ (units of length²/time). Now, per base pair step of sliding (of contour length h = 0.34 nm), there is some (dimensionless) probability P of dissociation of the protein (Fig. 4). As discussed previously (9–14), this might require a motion of the protein to ∼1 nm away from the helix surface so as to escape the counterion ‘atmosphere’ responsible for localizing the protein, suggesting that P might be a small number.

Figure 4.

The sliding length. A protein binds non-specifically to the DNA double helix (left) and then undergoes sliding steps randomly to the left and to the right, exploring the DNA contour through 1-D diffusion. Eventually, a dissociation event occurs; the characteristic distance explored between association and dissociation events is the sliding length. Due to the random nature of 1-D diffusion, the same DNA sites will be sampled repeatedly.

Now, if N sliding steps are taken, the probability that the protein remains on the DNA is (1 – P)^N = e^{N ln(1 – P)}. The number of steps over which sliding can occur before a dissociation event is thus given by N = –1/ln (1 – P). If P << 1, then the approximation ln(1 – P) = –P is accurate, giving N = 1/P. Now, since the sliding is diffusive, the region of molecule explored by sliding will be N^1/2 = 1/P^1/2 base pairs in contour length, giving a characteristic ‘sliding length’

To obtain a long sliding length, a very small value of P is required. The time used during exploration of the sliding length is τ_sl = l_sl²/D₁; the dissociation rate is k_off = 1/τ_sl. It should be noted that the probability of dissociation per base pair slide step can be expressed in terms of the sliding diffusion constant and the dissociation rate k_off as P = k_off h²/D₁, giving the alternative formula l_sl = (D₁/k_off)^1/2 (12,59). The sliding length l_sl (Fig. 4) will be treated as a parameter below; it can be controlled experimentally by adjustment of the non-specific binding affinity, for example by varying the salt concentration (13,14,35).

During a sliding event, every DNA site visited has the same opportunity to be tested for specific binding. It is generally assumed that every site in the sliding length is actually tested (9,10,12,60).

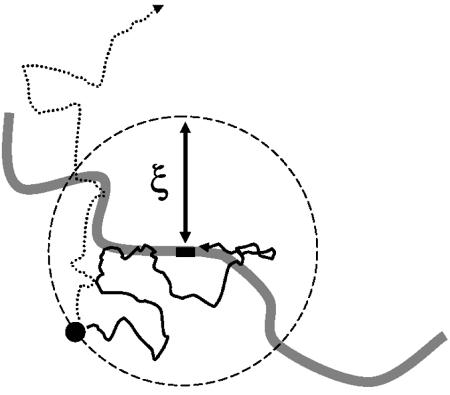
The targeting radius

If we imagine starting our protein in solution some distance from its specific binding site, there is some probability that it executes random motion leading to specific binding (Fig. 5). This capture probability should be a decreasing function of the starting distance, whatever the nature of the targeting facilitation mechanism (sliding or otherwise). It will be useful to define a ‘targeting radius’ ξ, which we take to be the initial distance for which the capture probability equals 0.5. A protein at distance ξ from its binding site thus has equal probabilities of exiting the target radius region or binding to the target (Fig. 5). The radius ξ will be useful in analysing the targeting kinetics.

Figure 5.

The targeting radius. A protein starting close to its target has a high probability of binding to the specific site; a protein starting far from its target has a low probability of binding specifically. The targeting radius ξ is the starting distance from which the probability of specific binding is 0.5. For a protein starting a distance ξ away, the two outcomes of specific binding (solid line pathway) and escape (dashed line pathway) occur with equal probability.

We can calculate ξ in terms of l_sl. We will use the mean 3-D distance between two sites along a DNA which are a contour length s apart, ρ(s). We will consider ρ(s) to be an arbitrary function, but in general it is subject to the limits

The short distance limit just expresses the fact that the DNA double helix is a straight cylinder at distances less than the persistence length of 50 nm. The long distance power law behaviour can take into account either random walk (ν = ½), self-avoiding random walk (ν = 3/5), branched self-avoiding supercoil (ν = ½), gel (ν = 1/3) or linearly folded (ν = 1) large-scale conformations (the random walk case that is relevant to unsupercoiled DNA in solution, ν = ½, will mainly be used in this report) (for more on the power law exponent ν for polymers under other circumstances see 61,62).

We can expect ρ(s) to increase with s (circular or looped structures may provide an exception to this). However, the large-scale rate of increase of ρ(s) with s[dρ(s)/ds] must be a decreasing function of s (i.e. ν < 1, the limit being the straight rod case). The constant C is defined so that it always has units of length; for the random walk case it is the statistical segment length (twice the persistence length), 100 nm for naked DNA. In general, C will also be roughly the length separating the short and long distance regimes of equation 5.

We now determine ξ, which contains some length of DNA, l. From equation 5, we have ρ(l) = ξ. We suppose that a non-specific binding event will occur whenever our protein comes within some distance b of any point on the double helix (b will be at most a few nanometres, corresponding to the thickness of the ionic atmosphere around the DNA contour). Following the approach used above, we consider the (ξ/b)³ voxels of size b inside the target radius. Whilst undergoing 3-D diffusion within the target radius, the protein visits (ξ/b)² of the sites. Thus any particular b-sized site ought to be visited with probability b/ξ during the time that the protein spends inside the target radius. The number of b-sized sites which are occupied by DNA is l/b, so the 3-D random motion of the protein can be expected to cause l/ξ non-specific interactions. The number of non-specific interactions required to find the target site is n = l/l_sl, thus we will find the target site with probability 0.5 when we have

ξ = l_sl.    6

The value of ξ does not depend on details of the conformational statistics for the DNA (equation 5), as we have only used the random walk statistics of the trajectory of the diffusing protein and the volume of the DNA inside the targeting radius. However, other quantities of interest, such as the number of sliding events during the motion inside the targeting radius, require knowledge of the conformational statistics, i.e. the exponent ν.

For short sliding distances the target radius contains a straight segment of DNA of length l_sl and only one non-specific interaction occurs before sliding to the target occurs. However, for sliding distances that are long enough to sample DNA bending we will have the situation where the targeting distance contains more than one sliding distance. For example, for the power law behaviour of equation 5, the contour length l inside the target radius will be determined by C^1–ν l^ν = ξ = l_sl, giving l = C^{1 – 1/ν} l_sl^1/ν, and the number of separate sliding events before targeting will be n = l/l_sl = (l_sl/C)^{1/ν – 1}, both of which are increasing functions of l_sl (recall ν < 1). In this situation, the trajectory inside the targeting radius will be a series of n ‘hops’ between sliding interactions; ξ is just large enough that the number of hops is equal to the number of sliding lengths worth of DNA that are inside the targeting radius.

In the case of a random coil of naked DNA (ν = ½, C = 100 nm = 300 bp), this phenomenon of hopping within the target radius occurs when the sliding length exceeds ∼100 nm = 300 bp. Note that as a DNA molecule is compacted (in equation 5, via decreasing either C or ν), ξ stays constant but the amount of hopping inside the targeting radius increases. It is worth noting that experiments have shown that compaction of the DNA by supercoiling facilitates the transfer from an initial non-specific to the final specific site (17).

We will also need to know the time required for exploration of a targeting radius region that contains DNA. This is the sum of the time needed for 3-D diffusion across the targeting radius plus the time needed to carry out n slides, or τ_ξ = ξ²/D + nτ_sl = l_sl²/D + l_sll/D₁. Since l ≥ l_sl and one expects D₁ < D (12,14), the sliding term always dominates:

The search time

We will now estimate the mean first passage time, using the statistics of the encounters between the diffusing protein and the DNA chains. We imagine that the total volume per DNA coil is V and that the coils are not strongly interpenetrating. If the DNA coils are of total contour length L, then they have a coil size R = ρ(L). Thus we consider either identical DNA molecules each containing one target in solution at number concentration c = 1/V under isolated coil conditions (R << V^1/3) or a DNA in vivo confined to a compartment of volume V. We now estimate the typical time required for the protein to find its target. This is the ‘search time’ for targeting in vivo, corresponding essentially to the time it takes for a protein to find its target in a cell of volume V. This time can also be converted to the reaction rate measured in vitro (12).

We proceed by breaking the targeting process into two stages, in the spirit of Berg et al. (12). First, the protein must diffuse through the volume V until it encounters the coil of radius R. One diffusive exploration of the volume V requires time τ_V = V^2/3/D and has a probability R/V^1/3 of the protein entering the coil (recall again the capture probability noted above). The reciprocal of the probability tells us the number of times our protein must repeatedly diffuse through the volume V to find the coil, n_V = V^1/3/R.

The second stage of targeting occurs once the protein is inside the coil. Somewhere in the coil is the targeting radius ξ = l_sl. Since we have chosen ξ so that a protein entering that region will find the target half the time and since the transport on scales larger than ξ will be random diffusion, the probability of finding the target during one diffusive exploration of the coil will be ξ/R. Thus we must revisit the coil n_C = R/ξ times to find the target.

Each coil visitation includes motion of the protein through n_ξ regions of size ξ, which happen to have DNA inside them, giving a total visitation time n_ξ τ_ξ (the 3-D diffusion through the part of the coil with no DNA in it is small compared to the 3-D diffusion through the volume V, thus we need not include it in the coil visitation time). To determine n_ξ we divide the coil region up into regions of size ξ; the random walk of the protein visits a fraction ξ/R of them during one coil exploration. The number of these sites containing DNA is L/l and, therefore, n_ξ = ξL/(R l).

To find the target therefore requires diffusion through the total volume n_Cn_V times, including n_C explorations of the coil. The total time required for this is therefore

τ = n_Cn_Vτ_V + n_Cn_ξτ_ξ.    8

Placing our results for n_C, n_V and n_ξ in equation 8 gives the result in terms of the sliding length

The coil statistics do not play a major role in the targeting time. The first term of equation 9 is the 3-D diffusion time required to come within the targeting radius of the target, while the second term is the total sliding time needed to explore the whole chain, i.e. L/l × τ_ξ.

Having this result in hand allows us to note a quick route to equation 9. We note that ignoring intermediate 1-D sliding events, the 3-D diffusion time necessary to find a target will be the time needed to find one of the target-containing regions of size l_sl (the first term). However, by the time the target region is found, 1-D exploration must have been done over a total molecular length L (the second term). The sum of these two contributions gives the total time necessary to find the target.

Reaction rate

Equation 9 can be written as a reaction rate by imagining that there are N proteins in each of the regions V that contain a single coil. The reaction time is reduced N-fold; the reaction rate per unit protein concentration (N/V) is therefore

The final term in equation 10 factors out the 3-D diffusion-limited rate (Da) and is in terms of the concentration of the target DNA, c = 1/V; the final factor thus represents the acceleration of the reaction. For fixed sliding length, the reaction acceleration goes up as the target concentration is reduced, approaching a low concentration limit of l_sl/a. Given a sliding length of ∼100 bp = 30 nm and a binding site size of ∼1 nm, the in vitro reaction rate can be accelerated by a factor of ∼30 above the 3-D diffusion limit.

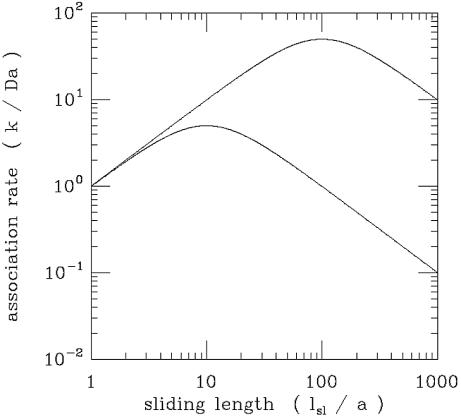
Figure 6 shows a plot of this theoretical association rate normalized to the diffusion limiting rate [i.e. k/(Da)], as a function of the sliding length normalized to the binding site size (l_sl/a). The sliding and 3-D diffusion constants are taken to be equal (D₁/D = 1) and two curves are shown; for a high target concentration (a²Lc = 0.01) and for a low target concentration (a²Lc = 10^–6). When l_sl/a = 1, there is no sliding and the diffusion limit is recovered. When some sliding occurs (l_sl/a > 1), the association rate is increased; this is the phenomenon of facilitated diffusion. However, it is important to note that it is possible to have too much of a good thing: at large values of l_sl/a, the association rate ceases to increase and starts to decline. Too long a sliding length results in 1-D diffusion oversampling the DNA contour: from the standpoint of accelerating targeting, it is preferable to periodically jump off the DNA so as to find a new region of the molecule. Only when the DNA concentration is very low can a very long sliding length result in significant acceleration of the association rate (Fig. 6).

Figure 6.

Association rate for the hopping + sliding model of Berg, Blomberg, Winter and von Hippel, normalized to the diffusion limit (k/Da), as a function of sliding length in units of the specific target size (l_sl/a). The case where sliding and 3-D diffusion occur at equal rates (D₁/D = 1) is presented. Two specific target concentration cases are shown: (upper line) low target concentration (a²Lc = 10^–6); (lower line) high target concentration (a²Lc = 10^–2). The total association rate shows a maximum at a certain optimal sliding length. For the optimal sliding length, 3-D motion keeps the protein from spending too long ‘oversampling’ any particular region of the DNA contour by 1-D diffusion. The optimal sliding length becomes shorter for higher target concentrations.

This non-monotonic behaviour was observed in seminal experiments by Winter et al. (14) as a function of the non-specific interaction strength, the latter being modulated by changing the salt concentration.

Optimization of the search time

As l_sl is increased, the first 3-D diffusion term decreases; increasing the target size reduces the time for a diffusive search. However, an increase in l_sl causes an increase in the total time spent doing 1-D sliding diffusion. The dependence of the two terms of equation 9 on l_sl causes the search time to have a minimum, and the reaction rate (equation 10, Fig. 6), to have a maximum at a special value of l_sl:

At this point, the search time has its minimum value of

Without sliding, the search would take the diffusion-limit time of V/(Da) = 1/(Dac), where a is the size of the binding site, which will be similar to the diameter of the double helix (this is just the first term inside the brackets of equation 10 with the limit that the sliding length is set to the targeting radius a). Thus sliding can speed up targeting by a factor of approximately

Since the 3-D and 1-D diffusion constants are expected to be comparable, the optimal speed up is essentially the square root of the ratio of two volumes: V, the solution volume per DNA molecule (note V = 1/c), and La², approximately the volume of the molecule itself (recall a is comparable to the double helix diameter). Both the optimal sliding distance and the maximum search speed up diverge with V since, in a large volume, the search can be hugely accelerated by disallowing dissociation of the protein from the DNA. This acceleration factor also applies to the optimal increase in reaction rate relative to the diffusion limit k = Da (see equation 10).

Search time optimized for the cell

The results of the previous section indicate that the optimal (fastest) search in dilute solution will involve a long sliding length. However, in the cell, the situation one would imagine DNA-targeting proteins to be optimized for, the DNA (or chromatin) is generally supercoiled and is confined to a small compartment: in eukaryote cells, the nucleus; in eubacteria, the nucleoid region. We now apply the results derived above to targeting inside the nucleoid/nucleus. A few caveats are in order for applications in vivo. First, we will assume that all of the genomic DNA is accessible. Of course, if the target site for a particular protein happens to be buried within a protein–DNA complex, targeting will not occur. However, our formulae still indicate the time that would have been necessary to find that site, had it been available for binding. Second, we will assume that diffusion occurs relatively freely and is the principal transport mechanism in vivo. While some proteins have been observed to diffuse relatively freely in the nucleus (16,63), this may not apply to all proteins and there may be alternative, perhaps active, mechanisms in vivo.

That said, we note that the nucleoid or nucleus is a region of highly concentrated DNA (or chromatin), with V = w²L, where the factor w is ∼30 nm [the E.coli nucleoid has V ≈ 10⁹ nm³ and L ≈ 10⁶ nm, giving w ≈ 30 nm; the human nucleus has V ≈ 10¹² nm³ and L ≈ 10⁹ nm, giving about the same value of w]. The factor w is the factor that relates genome length to nucleoid/nucleus volume and represents roughly the spacing of nearby DNA or chromatin segments.

In these terms, the optimal sliding length is

which is roughly equal to w = 30 nm (100 bp), under the assumption that D and D₁ are similar in magnitude. In this case the optimal search time is

which, given D₁ ≈ D ≈ 10⁸ nm²/s, is ∼0.3 s for the E.coli nucleoid and ∼300 s for the human nucleus. The speed up factor relative to 3-D diffusion is

which is, for a = 1 nm, a factor of ∼30.

Thus, under the crowded conditions in vivo, a sliding length of ∼100 bp optimizes the time required for a protein to find its binding site, in either the E.coli nucleoid or in the human nucleus. This short sliding length is in accord with experimental estimates of sliding distances for the Lac repressor (14) and for the EcoRV restriction enzyme (27).

PROCESSIVITY AS A PROBE FOR FACILITATED DIFFUSION

Many reports (e.g. 5) have assigned translocation of protein solely to 1-D diffusion without discussing the inevitable dissociations and diffusive motions through 3-D space. In many of these studies, an increase in association rate with increasing DNA length is taken as evidence of facilitated diffusion. However, a longer DNA always provides a larger target for the initial collision. Such studies can thus reveal whether the non-specific DNA is on the pathway to the specific site, but not in general the route taken by the protein from its initial to its final site on the DNA (55).

In an alternative strategy, the processivity of an enzyme is examined on a series of DNA substrates with two sites, with varied lengths of DNA between the sites (27). Processivity in this context is defined as the number of reactions in which the enzyme acts at both sites during one DNA-binding event relative to the total number of reactions by the enzyme. It is thus a unit-less parameter, a ratio of rates rather than an absolute rate, and, hence, simpler to analyse than total rate measurements. Moreover, in a processive reaction on a DNA with two sites separated by a known distance, the enzyme must travel along the DNA that fixed distance. In contrast, the distance travelled by a protein from an initial non-specific site to its final specific site is indeterminate: on some occasions, the initial collision may be close to the recognition site and on others far away. Consequently, the relationships between processivity and the length of DNA between the sites (27) are much simpler than those between the binding kinetics and the total length of the DNA molecule (12).

When the EcoRV restriction enzyme was tested on a series of DNA molecules with two EcoRV sites separated by varied lengths of DNA, from 50 to 750 bp, the processivity declined with increasing inter-site spacing (27). The extent of the decrease failed to match the behaviour that had been expected for translocation solely by 1-D sliding. It instead matched a model in which the translocations from one site to the other occur primarily by dissociation/reassociations through 3-D space. However, an analysis of the change in processivity with increasing site separation yielded a target size (a) of 20 nm, which is about 10 times longer than the 6 bp recognition sequence for EcoRV. Hence, it was suggested that, between each reassociation event and the next dissociation step, the DNA immediately adjacent to the new ‘landing’ site is scanned by sliding over a path length of ∼50 bp.

Several other studies have now indicated that, contrary to previous assumptions about the universality of 1-D sliding, proteins find their target sites both in vivo and in vitro mainly by transfers through 3-D space and not by remaining in continuous contact with the DNA (16,17,63–67). For example, FRAP (fluorescence recovery after photobleaching) experiments have shown that, in living cells, histone H1 transfers between its DNA-binding sites via free solution (66,67); likewise, for a repair endonuclease between sites of DNA damage (65). However, a recent analysis of sliding with dissociation concluded that the processivity of EcoRV (27) was also consistent with a model where sliding occurs over long distances, and where processivity is limited by the protein sliding off the ends of the linear DNA (59).

A further problem in 1-D sliding is posed by the many proteins that bind concurrently to two sites in DNA and loop out the intervening DNA, for example the Lac repressor itself and the SfiI restriction enzyme (21). Many of these proteins first bind one copy of the target at one DNA-binding surface and then the other copy at a second surface (68). Once the protein is fixed at one site, via one DNA-binding surface, it might seem possible for the second surface to slide along non-specific DNA until it locates its specific site. However, if the non-specific DNA continually presents the same face of the DNA helix to the second surface, the DNA has to be twisted through 360° as each helical turn (∼10.5 bp) travels past the protein. This will cause the intervening loop to become either under- or over-wound, depending, respectively, on whether the loop increases or decreases in size (69). Under-winding introduces negative supercoils and over-winding positive supercoils. Both outcomes are thermodynamically disfavoured and will soon stop any continuation of the sliding motion. It can continue only if the protein transiently dissociates from one site in the DNA, so as to release the linking number in the trapped loop and allow the loop to recover its native twist (68).

Processivity from facilitated diffusion

In a processivity experiment, one considers a protein that has just acted at one site (here acting means binding, catalysis and dissociation) and then measures the probability of it acting again at a second site in cis. The targeting distance concept permits a simple analysis of this in terms of the average inter-site distance ρ(s) (see equation 5), where s is the contour length between the two sites. For inter-site 3-D distances smaller than the targeting radius [ρ(s) < ξ = l_sl ], the processivity will be nearly constant, since ξ was defined (and then calculated) as the distance in 3-D space over which a DNA site will be found with >50% efficiency.

For inter-site 3-D distances larger than ξ, the processivity will start to decrease appreciably with increasing s. At these larger scales, the transport between sites will occur via 3-D diffusion. However, once our protein comes within a 3-D distance ξ of the second target, it will find it, again according to the definition of the targeting distance. Therefore, the processivity at large distances will just be the probability that a diffusing protein finds a target of 3-D size ξ = l_sl, which is initially a 3-D distance ρ(s) away, which is ξ/ρ(s).

In the case of a random coil DNA shorter than 100 kb, we have the limiting behaviours ρ(s) = s for s < A and ρ(s) = (2As)^1/2 for s > A, where A is the persistence length (50 nm). In the case that the sliding distance l_sl is less than A, we have three separate regimes:

In the case that l_sl ≥ A, only the first and last regimes will occur, with the boundary between them occurring for site spacing s = l = l_sl²/A. By plotting experimental data for P₂(s) versus s at fixed solution conditions, one can directly estimate the sliding distance from the range of site spacings across which little decay in processivity occurs and then check for the expected power law decay at larger inter-site spacings (27).

Processivity from sliding and dissociative loss

A recent study (59) considered an alternative model of processive DNA–protein interactions, that included sliding and dissociation and applied it to the data of Stanford et al. (27). In this model, dissociation led to irretrievable loss of the protein and different dissociation rates were assumed for the ends and for the interior regions of a linear DNA. The model was analysed exactly and it was found that the characteristic range for processive interactions was the sliding distance l_sl. For large site separations, the processivity was found to decay exponentially with increasing site spacing, approximately as a function of exp(–s/l_sl). This striking result diverges from a naïve analysis of processivity from diffusional sliding with dissociation (23), which had suggested a faster decay with increased spacing, ∼exp(–s²/l_sl²). The latter does not fit the data on EcoRV processivity (27). However, if dissociative losses at the ends of the linear DNA are large relative to those from all internal sites in the DNA chain, the resultant power law behaviour fits the experimental data well (59). It was concluded that losses of protein from the DNA ends dominate the observed decay in EcoRV processivity and that the sliding length l_sl is >1000 bp. This scheme thus requires a sliding length that is in effect infinite: this distance is longer than most of the DNA molecules used by Stanford et al. (27).

The analysis of Belotserkovskii and Zarling (59) is important because of its mathematically exact nature. Nevertheless, it assumes that the dissociation of protein results in its irretrievable loss: it neglects the possibility that a protein which dissociates from a long DNA coil can then reassociate with the same coil at a different sequence location. Moreover, it proposes that the dissociation occurs almost exclusively from the ends of the DNA chain and not from internal sites. The fit to the data of Stanford et al. (27) required a 40-fold faster dissociation rate from the ends than from internal sites. However, the EcoRV endonuclease is thought not to fall off the ends when sliding along the DNA but rather to be ‘reflected’ back towards the interior (58). Data on the dissociation rates of several other DNA-binding proteins as a function of chain length are also inconsistent with dissociation occurring primarily from linear DNA ends (14,55). The following might account for reflection from the ends: if a protein interacts with, say, 10 phosphate groups when bound to an internal site, then it should interact successively with 9, 8, 7 … 2, 1 phosphate moieties as it approaches the end of the chain. In this situation, inward steps will increase, and outward steps decrease, the number of phosphate contacts and so bias diffusion in the inward direction. However, in contrast to the EcoRI restriction enzyme (55), the dissociation rate of the EcoRI methyltransferase from linear DNA shows no variation with the length of the fragment. The methyltransferase dissociates more rapidly from a linear DNA than from the same DNA in its circular form, presumably from the ends (70).

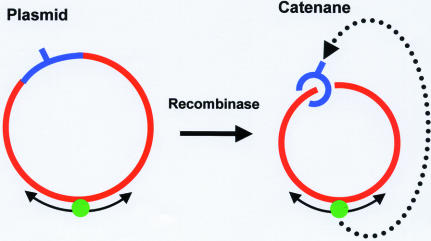
In other studies (17), target site location by EcoRV and by several other restriction enzymes was examined on either a circular DNA with one recognition site or on the same DNA after it had been converted into a catenane (Fig. 7) by the action of a recombination enzyme (many recombinases can convert a circular DNA into two circles of DNA, threaded through each other) (71). This catenane contained one large ring, of 3100 bp, that possessed only non-specific DNA sequences and one small ring, of 350 bp, that carried the recognition sequence (Fig. 7). The long segment of non-specific DNA conveyed the enzyme to the recognition site just as well when tethered to the target by catenation as when covalently contiguous with the target. Transfer of the enzyme from the non-specific circle to the specific circle must involve its dissociation from an internal site (and not from an end, as the circle has no ends) followed by its diffusion through 3-D space to the other circle and then by its binding to that circle (Fig. 7). This observation cannot be reconciled with a model (59) in which the processivity of EcoRV is due to sliding over long distances coupled to irretrievable dissociation from the ends of the DNA. The exact model of Belotserkovskii and Zarling (59) thus needs to be widened to include transfers of protein from site to site via 3-D diffusion.

Figure 7.

Plasmids and catenanes. The plasmid (on the left) contains a single recognition site (indicated with a hatchmark) within a specified segment of the circular DNA (indicated in blue). The remainder of the DNA (in red) contains only non-specific sequences. A protein (green sphere) bound to the non-specific (red) DNA can reach the recognition site by 1-D diffusion around the circle or by 3-D transfer (not shown). The plasmid is converted by a recombinase into a catenane (on the right) with two interlinked circles of DNA: a small circle (in blue) that carries the recognition sequence; a large circle (in red) with only non-specific sequences. A protein bound to the non-specific DNA in the large (red) circle cannot reach the recognition site in the small circle by 1-D diffusion but must instead dissociate from the large ring before re-associating with the small ring: since both rings are covalently continuous, the dissociation cannot occur from an end of a chain.

CONCLUSIONS AND OUTLOOK

A fundamental problem in both biology and biophysics is how DNA-binding proteins find specific sites amongst huge amounts of non-specific (chromosomal) DNA, especially under conditions where there are only a few copies of the protein in the cell. For instance, to understand the dynamics of gene regulation and thus the responses of cells and organisms to changes in their environments, it is necessary to understand how small numbers of transcription factors are transported to specific sites so as to allow reasonable response times for the activation or repression of genes (1,16). This in turn requires biochemical experiments to elucidate the mechanisms of both non-specific and sequence-specific interactions of proteins with DNA. Nevertheless, considerable gaps still exist between connecting quantitative studies of individual protein–DNA interactions to the (apparently) precisely controlled regulation systems of cells.

This review has focused on three points. First, we have outlined what experiments have been done to date to provide insight into the dynamics of DNA binding by proteins that recognize specific sequences. Second, we have discussed the theory of ‘facilitated diffusion’, where DNA sliding allows exploration of sequences around points of successive DNA encounters, in a simplified but fundamentally similar form to that presented by Berg et al. (12). Finally, we have discussed the use of experiments that probe processive interactions with more than one site along one DNA.

Association rate measurements and facilitated diffusion

To date, our experimentally based knowledge of target site location has been obtained mainly from solution phase reaction kinetics. Many experiments have followed the lines of the classic work of Winter et al. (14), where the association rate to DNA molecules of different lengths is measured directly. These types of measurements reveal how electrostatic interactions (a major contributor to most non-specific DNA–protein interactions) play huge roles in controlling reaction rates and in driving them above the ‘pure diffusion’ rates observed at relatively high salt concentrations. Association rate measurements on Lac repressor protein remain to this time one of the main supports for the facilitated diffusion theory.

Although association rate measurements are conceptually straightforward, they are experimentally challenging, and there are many potential experimental pitfalls. Perhaps most importantly, measurements of association rate do not give direct information about the spatial pathway followed by a protein to its target site. Ultimately, information about a spatial reaction pathway can only be extracted from total reaction rate measurements by the use of a model.

Processivity can reveal direct information about spatial pathways to targets

Direct information about the spatial pathway that is followed by a DNA-binding protein to its target site can, however, be obtained from a different type of solution phase kinetics, namely the analysis of processive reactions on a DNA with two or more binding sites. Experiments on restriction endonucleases have demonstrated that, by using gels to separate the reaction products cleaved at each individual site, it is possible to quantitatively measure the degree of processivity of an enzyme on DNA, i.e. to evaluate what fraction of the encounters between the enzyme and a DNA with two sites result in reactions at both sites and what fractions result in reactions at each solitary site (27,72). These measurements reveal the probability that two sites along the DNA chain are visited sequentially by the same molecule of the protein. Processivity experiments on catenated DNA molecules have provided further evidence for transfer of proteins through space from one DNA segment to a nearby one, presumably via diffusion in three dimensions (17).

The main limitations of the approaches developed with restriction enzymes are that they can be used only for enzymes that permanently modify the chemical structure of the DNA and that they are limited to analysing a small number of processive interactions, due to the necessity to resolve the products from the reactions at each individual site on a gel. Finally, it must be noted that processivity measurements can remain open to alternative interpretations (59).

Single molecule experiments on protein–DNA targeting

In the past few years, methods have been developed that might allow direct observation of the binding of a single protein to a single binding site in a large DNA. The key technology for this is the micromanipulation of single, long (tens of kilobase) DNA molecules (73,74). The basic procedure involves attaching colloidal particles of ∼1 µm diameter to the ends of the long DNA chain; these particles then act as ‘handles’ for micromanipulation. By manipulating the particles at the ends of the DNA (with laser tweezers, for example), one can move the molecule around or stretch it out to any degree desired. Magnetic particles also allow for twisting of the DNA into supercoiled configurations (75).

Even more recently, fluorescence techniques have been developed for tracking single protein molecules in solution. Although the detection of single fluorophores is still experimentally challenging, multiply labelled proteins or larger fluorescent particles (for example quantum dots or dye-impregnated colloidal particles of 10–50 nm diameter) provide easily detectable signals. By attaching such a particle to a protein, one might be able to track its progress to and along a large DNA molecule and thus directly observe its translocation path. By studying the association/dissociation processes and the apparent sliding motions on DNA molecules in different states of extension, it may be possible to directly observe the sliding length and the dissociation time. For an isolated fluorescent particle attached to a protein moving along a single well-stretched DNA it should be reasonably straightforward to determine the position of the protein (i.e. the particle) to a precision of ∼10 nm, which corresponds to ∼30 bp of DNA. This precision is routinely obtained for the location of the centres of larger, micron-sized particles, using image processing techniques (74–77).

In a number of recent experiments, single molecule approaches have been used to visualize proteins moving towards their binding sites along DNA (78–81), and the apparent translocations of the protein have been reconciled with sliding along DNA. However, to date, these types of studies have not achieved the spatial resolution of ∼1 nm needed to see whether the translocating protein remains perpetually in contact with the DNA or whether it transiently dissociates from the DNA. Nor have they achieved the time resolution of ∼1 ms that is necessary to monitor processes that may cover 10³ bp/s.

Nevertheless, such resolutions are realizable: recent experiments on the translocation of myosin and kinesin motor proteins along actin and tubulin filaments, respectively, have achieved spatial resolutions in the nanometer range and time resolutions close to 1 ms (76,77). However, the size of the steps in myosin translocation along actin, ∼17 nm, are much larger than the 0.34 nm steps that a protein would take in sliding along DNA 1 bp at a time. Moreover, each successive step in the translocation of these motor proteins occurs in the same direction, while 1-D diffusion will oscillate between different directions. Even so, in the near future protein motion along extended DNA molecules ought to be observable with resolutions close to the size of a binding site. Such experiments will perhaps allow for the first time the direct observation of the motion of a protein towards its binding site in a long DNA chain.