Acceleration and motion-correction techniques for high-resolution intravascular MRI

Abstract

Purpose

High-resolution intravascular (IV) MRI is susceptible to degradation from physiological motion and requires high frame-rates for true endoscopy. Traditional cardiac-gating techniques compromise efficiency by reducing the effective scan rate. Here we test whether compressed sensing (CS) reconstruction and ungated motion-compensation employing projection shifting, could provide faster motion-suppressed, IVMRI.

Theory and Methods

CS reconstruction is developed for under-sampled Cartesian and radial imaging using a new IVMRI-specific cost function to effectively increase imaging speed. A new motion correction method is presented wherein individual IVMRI projections are shifted based on the IVMRI detector's intrinsic amplitude and phase properties. The methods are tested at 3T in fruit, human vessel specimens, and a rabbit aorta in vivo. Images are compared using Structural-Similarity and ‘Spokal-Variation’ indices.

Results

Although some residual artifacts persisted, CS acceleration and radial motion compensation strategies reduced motion artefact in vitro and in vivo, allowing effective accelerations of up to eightfold at 200-300μm resolution.

Conclusion

3T IVMRI detectors are well-suited to CS and motion correction strategies based on their intrinsic radially-sparse sensitivity profiles and high signal-to-noise ratios. While benefits of faster free-breathing high-resolution IVMRI and reduced motion sensitivity are realized, there are costs to spatial resolution, and some motion artifacts may persist.

Introduction

Unlike conventional magnetic resonance imaging (MRI) with external detector coils, intravascular (IV) MRI receives the signal using tiny internal detectors (1-6). At field strengths of 3T, these can afford high signal-to-noise ratios (SNR) that permit 80-300μm resolution imaging of vessel walls and associated pathology as fast as several frames per second (fps) (7,8). With suitably modified sensitivity profiles, transmit/receive IVMRI probes can also provide high-resolution images from the probe's point-of-view (9), analogous to optical endoscopy, IV Ultrasound, and Optical Coherence Tomography. Nevertheless, while excelling in soft-tissue contrast, 3T IV MRI still lags behind these other modalities in speed.

Factors contributing to IVMRI's slowness include the physics of spatially encoding the MRI data, and the delays required to accommodate spin relaxation. MRI uses linear magnetic field gradients that encode the object in the spatial frequency domain (k-space). The encoding scheme is ordinarily subject to the Nyquist criterion which requires that sufficient k-space be filled to avoid aliasing errors upon reconstruction. Satisfying Nyquist ordinarily contributes directly to the long acquisition times. MRI scan-times can be reduced using recent ‘compressed sensing’ (CS) reconstruction techniques (10,11) which permit image reconstruction with a limited subset of k-space. Successful CS implementation requires ‘sparse’ data with sufficient SNR, and has been used in several conventional MRI settings including neurological, cardiac and dynamic visualization applications (10-14). However, to date CS has not been applied to IVMRI whose intrinsically high local SNR, spatial sparsity and need for speed, make it an ideal application.

Slow scan speeds are endemic to ultra-high resolution MRI, and also render IVMRI susceptible to the effects of rigid and non-rigid physiological motion—blood flow and respiration, as well as motion during probe advancement. Conventional cardiac- and breath-gating techniques reduce motion-sensitivity, but typically restrict speed and scan-time, depending on the period or incidence of the corresponding motion. While ungated acquisitions could allow frame-rates limited only by the SNR (or spatial resolution), their implementation would require other strategies for motion compensation. In past, several strategies for correcting conventional projection-reconstruction (PR) images for motion have employed data consistency criteria based on the zeroth and/or higher-order moments of each image projection (15-17) or projections of internal loop detectors (18). These methods are easily affected by intensity variations and can fail in high-resolution IVMRI where differences of the order of a millimeter can translate to ten or more pixels. Motion correction has also been reported using tiny external (19) or internal coils (20,21) deployed as tracking markers for conventional imaging. However high-resolution IVMRI requires high-resolution tracking information, and the use of external micro-coils to sense motion may offer limited value when they are remote from the microscopic field-of-view (FOV) of an internal imaging probe. Adding internal tracking coils may also make the IVMRI probe larger and more complex, and a minimally-invasive procedure less so.

In the present work we first address the speed limitation by developing CS reconstruction techniques for under-sampled IVMRI. We use these to test effective frame-rate acceleration factors of up to eight-fold. Second, we present a motion-correction method for ungated PR IVMRI based on the intrinsic amplitude and phase properties of the IVMRI detector's sensitivity profile. Third, the motion-correction method is applied to radially under-sampled data sets to test its efficacy in generating faster motion-corrected IV images. The methods are investigated in fruit, human vessel specimens, and a rabbit aorta in vivo.

Theory

A. Accelerating image acquisition

In two-dimensional (2D) Cartesian MRI, data are acquired to fill a 2D rectilinear grid in k-space and the images are reconstructed by 2D Fourier Transformation (FT). On the other hand, the PR method fills k-space along radial spokes, and the FT of each radial spoke in k-space corresponds to a projection in image space through the object at an angle perpendicular to the direction of the spoke. This direct relationship permits image reconstruction in either domain, by regridding the radial k-space data onto a rectangular grid followed by 2D FT using a Non-Uniform fast FT (NUFFT) algorithm, or using filtered back-projection techniques in image space, as in Computed Tomography. The two methods are equivalent, so we limit the description to the former approach, implemented here with an open-source NUFFT algorithm (22).

For alias-free reconstruction, both Cartesian and PR acquisition schemes ordinarily require sufficient k-space samples to satisfy the Nyquist criterion. Under-sampling in Cartesian MRI results in ‘ghost’ artefacts that appear as replicates of the original image displaced in the under-sampled dimension. Under-sampling artefacts in PR acquisitions are manifest as hyper-intense radial lines or ‘streaking’ (23). CS reconstruction ameliorates these artefacts by tailoring the under-sampling scheme so that the artefacts appear ‘noise-like’, and uses an iterative reconstruction that incorporates penalties to suppress the noise in the final image. In Cartesian acquisitions, the central k-space is fully-sampled but outer k-space is randomly sampled (11). For PR, k-space is under-sampled with a uniform angular distribution (10). All unsampled k-space data points are zero-filled.

For CS, image reconstruction is set up as a constrained minimization problem, where a functional, Φ(x), is minimized:

$$\mathrm{\Phi }(\mathbf{x})={\Vert A\mathbf{x}-\mathbf{y}\Vert }_2+\sum _n{\lambda }_n{R}_n(\mathbf{x})$$ [1]

Here y is the measured k-space complex data from all (PR) spokes or (Cartesian) lines stacked to form a vector, x is the image vector to be estimated, Aevaluates the image's FT in under-sampled k-space, the ℓ² vector norm is denoted ${\Vert \mathbf{z}\Vert }_2={({\sum }_i{\left|z_i\right|}^2)}^{1/2}$, and there are n penalty functions R(x) with weighting factors λ to constrain the resultant image based on a priori knowledge.

Suitable penalty functions that minimize the coefficients of the underlying image in a sparse transform space such as the Wavelet Transform (WT) or spatial finite-differences (minimizing Total Variation, TV), have been described earlier (10,11). The WT is a multi-scale representation of the image with coarse- and fine-scale wavelet coefficients representing low- and high-resolution image components, respectively. The TV constraint assumes that the underlying image consists of areas with constant (or mildly varying) intensity. The penalty functions using these transforms are

$$R_{\text{WT}}(\mathbf{x})={\Vert \mathrm{\Psi }\left(\mathbf{x}\right)\Vert }_1$$ [2]

$$R_{\text{TV}}(\mathbf{x})={\sum }_i|D_{\mathrm{x}}(x_i)|+|D_{\mathrm{Y}}(x_i)|$$ [3]

where Ψ is the WT and the ℓ¹ vector norm ‖z‖₁ = Σ_i|z_i|, D_x, D_Y denote the derivatives in X and Y direction, respectively.

Here, an additional penalty function was designed for PR-IVMRI based on the field profile of the probes. For a loopless antenna oriented parallel to the main field (z-axis), the trans-axial RF-field, B_1,Φ in cylindrical co-ordinates, was approximated by that of a long conductor with current I (24):

$$B_{1,\varphi }=\frac{\mu I}{2\pi r}$$ [4]

where ϕ is the azimuthal angle, r is the radial distance from the probe, and μ is the permeability of the medium. Even when the probe is not parallel to the z-axis, B_ϕ ∝ 1/r still holds (because MRI is only sensitive to the transverse B₁ component) causing hyper-intensity at the probe location (Figs. 1 a, b). Under-sampling leads to streaking artefacts with spokes emanating from the probe location (Fig. 1c). The streaking is manifest in variations of the azimuthal amplitude with the probe as centre. The new penalty function smears the variation between the spokes (thereby reducing ‘spokal variation’, SV) for a more uniform image. We divided the image pixels into concentric annular sectors, computed complex pixel-sums, determined differences between azimuthally adjacent sectors, and summed the absolute differences over all sectors. (Fig. 1d):

Fig.1.

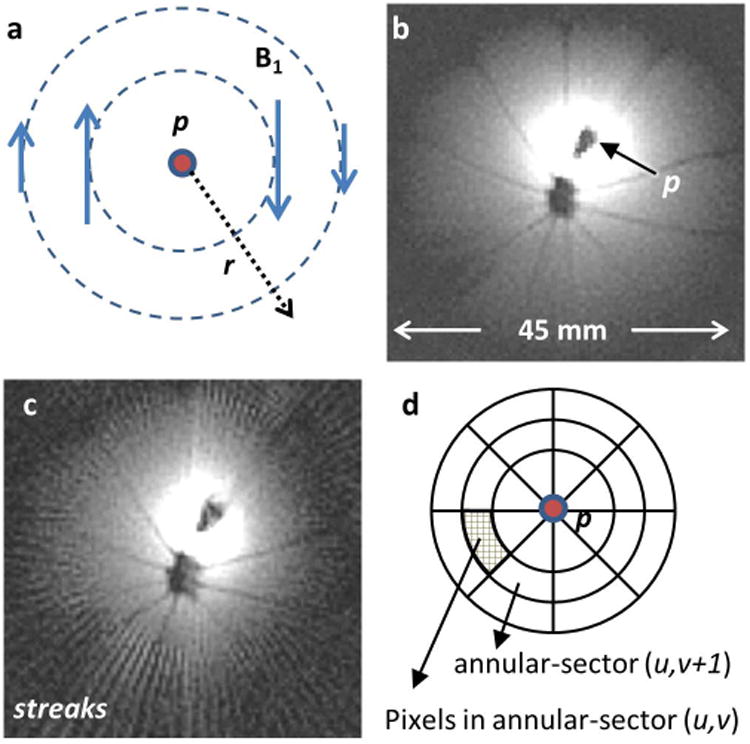
(a) The transverse field of a loopless antenna detector p showing decreasing B₁ with r and azimuthal variation in phase. (b) Typical IVMRI image of an orange obtained from probe p, showing intense bright region closest to the probe. (c) Four-fold under-sampling of the image in (b) and conventional FT reconstruction showing streaking. The r^-1 intensity filter has not been applied to (b) or (c). (d) Template used to calculate the Spokal Variation (SV) from adjacent annular sectors as explained in the text. The center of the template is placed on p.

$$\text{SV}(u,v)=\sum x(u,v+1)-\sum x(u,v)$$ [5]

$$R_{\text{SV}}(\mathbf{x})={\sum }_{u,v}|\text{SV}(u,v)|$$ [6]

where x(u, v) denotes the pixels in the u^th annulus and v^th sector.

With the penalty functions of Eqs. [2], [3] and [6], the functional in Eq. [1] becomes

$$\mathrm{\Phi }(\mathbf{x})={\Vert A\mathbf{x}-\mathbf{y}\Vert }_2+[{\lambda }_{\text{WT}}{R}_{\text{WT}}(\mathbf{x})]+[{\lambda }_{\text{TV}}{R}_{\text{TV}}(\mathbf{x})]+[{\lambda }_{\text{SV}}{R}_{\text{SV}}(\mathbf{x})]$$ [7]

This functional was minimized using iterative CS algorithms as noted below {IRGNTV (10,25), GRASP (26), SPARSE-MRI (11)}. These algorithms involved searching for minima using Gauss-Newton and/or conjugate gradient methods by sequentially varying each of the three λ terms in Eq. [7]. Optimum values of λ were selected by comparing sample datasets from the under-sampled and the fully-sampled datasets using: (a) the ratio of SV values (Eq. 6), SV_ratio = SV_A/SV_B, wherein a smaller ratio indicates less streaking in image A with respect to image B or; (b) the Structural Similarity index {SSIM (27)},

$$\mathit{\text{SSIM}}(A,B)=\frac{4{\mu }_A{\mu }_B{\sigma }_{AB}}{({\mu }_{\mathrm{A}}^2+{\mu }_B^2)({\sigma }_{\mathrm{A}}^2+{\sigma }_B^2)}$$ [8]

where A and B are the images being compared, σ_AB is their cross-correlation, μ and σ are the mean and standard deviation of the pixel intensities (if A=B, SSIM = 1). Reconstruction artefacts were analyzed using the point-spread-function (PSF) of the under-sampled trajectory. The width at which the Cartesian PSF drops to 2/π (≈ 64%, the Rayleigh criterion for distinguishing objects), and the location/amplitude of the radial PSF side-lobe were used as metrics (28).

B. Motion Correction

In-plane motion

Since the IVMRI probe is embedded within the body, in-plane body motion could cause the location of the probe to vary within the imaging plane. Assuming only rigid-body motion, if the probe location could be determined in each projection of a PR-MRI acquisition, then shifting or aligning each projection at the probe location should ameliorate the effect of the motion. To detect the probe in each projection, it can be seen from Eq. [4] and Figs. 1(a, b) that: (i) the field strength falls rapidly with distance r from the probe; and (ii) the detection phase varies azimuthally around the probe and reverses direction at the probe in every projection. In addition, (iii) the probe itself is metallic and does not contribute any MRI signal. Thus, each projection in image-space has a volcano-like signal intensity maximum close to the probe, a dip or ‘crater’ in intensity at the probe location (Fig. 2a, top), and a phase reversal at the exact location of the probe (Fig. 2a, bottom). A combination of both amplitude and phase detection provided the most robust means of detecting the probe. The center-of-mass (COM) of each projection served as the starting point. Note that the COM often differs from the probe location due to skewed intensity profiles (Fig. 2a, red diamond). Given the known physical dimensions of the probe and the image resolution, the width in pixels of the crater was determined and then used as a priori knowledge in a peak-fitting algorithm to find the crater. The probe's location was then refined using the phase information. The zero-crossing point of the phase-reversal was found using a level detection algorithm and/or maximum slew-rate detection. Once the probe's location was detected, each projection was shifted to the center of the image FOV, and all projections were aligned based on the location of the probe (Figs. 2b, c). The image was then reconstructed with the probe at its center.

Fig.2.

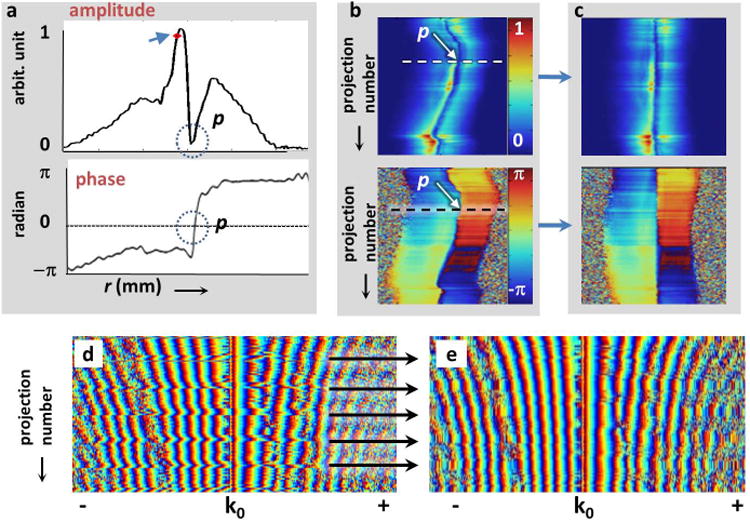
(a) Typical experimental projections from the semi-rigid loopless antenna in an orange. The amplitude of the projection (top) shows a ‘crater’ at the probe location (p, circled). The center-of-mass of the projection (arrowhead) is displaced from the probe-location. The phase (bottom) of each projection reverses at p (circled). (b) The probe's location (arrow) appears as a meandering anomaly in the stack of 200 projections (top, amplitude; bottom, phase), each acquired sequentially at 0.9° azimuthal increments. Each projection spans the FOV; the stack spans a circle. The projection in (a) is annotated (dashes). (c) Motion correction consists of re-aligning every projection based on p. A stack of phase plots of in vivo k-space projections from a rabbit acquired with a nitinol loopless antenna are shown in parts (d) and (e). Periodic aberrations (arrows) evident in (d), are replaced by the average of preceding and successive projections (e), to yield images with reduced streaking.

A further refinement to this method was implemented at high-resolution, where the shifting process was observed to be sensitive to intra-pixel jitter, which contributed to residual radial streaking. This involved comparing the detected probe location from one projection to its location in previously acquired projections, and determining the pixel-shift in image-space. If large positional deviations from the preceding, or an average of both preceding and succeeding projections were detected, a corresponding phase-shift in k-space was computed from the inverse FT of the pixel-shift (i.e. if $f(x)\stackrel{\text{FT}}{\leftrightarrow }F(\omega )$ then $f(x-n)\stackrel{\text{FT}}{\leftrightarrow }{e}^{-j\omega n}F(\omega )$). This ‘corrected’ phase-shift was then applied to the motion-corrupted projection in k-space, prior to reconstruction. In this way, only those few projections that were corrupted by motion were processed and subject to potential jitter introduced by the detection algorithm. Images reconstructed using this refinement do not necessarily have the probe at the center of the FOV, but because the probe was already located in preceding steps, a simple image translation was applied to shift it to the FOV center post-reconstruction as described previously (8).

Through-plane motion

Through-plane motion, especially from respiration, is a source of artefacts in vivo, in general. Conventionally, respiration artefacts are overcome by navigator echoes placed on the lung-diaphragm interface (29). In the absence of external navigators, we observed that when stacked, radial k-space projections exhibit a pattern of aberrant jumps (Fig. 2d) that correlate with breathing (every ∼2s for a rabbit, or approximately every 10^th projection with repetition time TR = 200ms). These projections served as ‘internal navigators’ that signified motion-corrupted projections that could be discarded, as in traditional navigator-gating. Alternatively, because in PR-MRI successive projections are highly correlated, the aberrant projections were replaced by an average of the preceding and succeeding projections (Fig. 2e). This process corrected aberrant projections from other periodic or sporadic sources as well.

C. Under-sampled motion-corrected reconstruction

Since the motion-correction methods outlined above act on each projection, they can also be applied to radially under-sampled data sets, as illustrated in Fig. 3. The motion-corrected under-sampled data were iteratively reconstructed to produce an effectively faster motion-corrected image. These were compared both visually and using the SSIM (Eq. 8) in vitro, and using the SV_ratio in vivo where motion-free images were unavailable for comparison.

Fig.3.

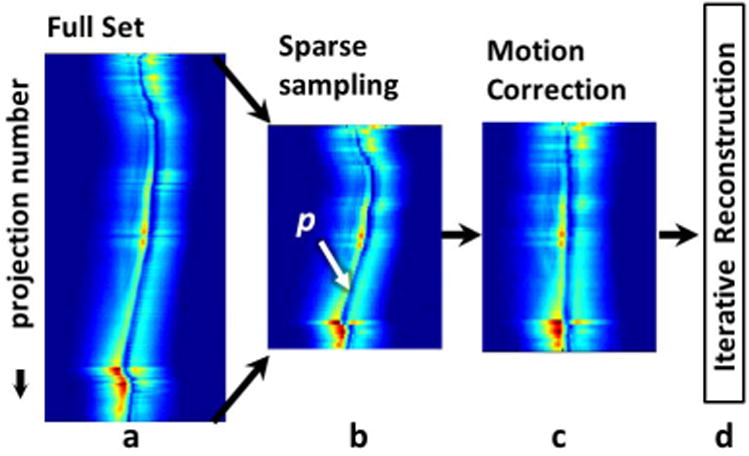
Acceleration and motion correction method showing: (a) azimuthal projection amplitudes; and (b) under-sampling of projections to a reduced dataset. (c) Motion correction consists of detecting probe p in each projection (signal void) and re-aligning every azimuthal projection on p and/or eliminating projections with excessive motion. (d) Images from the sparsely sampled motion-corrected projections are reconstructed using iterative techniques.

Methods

First, CS methods were applied to data acquired employing Cartesian encoding and a 5-turn transmit/receive loop IVMRI endoscope (8,9). The loop antenna was 2.3 mm in diameter at its widest, tuned with a 91pF micro-capacitor, and connected to an 0.8mm nitinol cable. The cable was connected to a single channel transmit/receive interface with a switchable PIN diode to decouple the receiver during conventional MRI, as described previously (9).

CS and motion-corrected radial PR-MRI were performed in a Philips 3T Achieva whole-body MRI scanner using internal loopless antennae (1) for signal reception and the scanner's body-coil for excitation (7). The loopless-antenna was either a 2.75mm outer-diameter (OD) 400mm-long semi-rigid copper coaxial cable with the inner conductor extended 42 mm to form the whip, or a 0.8mm OD biocompatible super-elastic nitinol coaxial cable with a 42mm whip suitable for IVMRI applications (7).

Data are presented from fruit, human vessel specimens in vitro, and rabbits in vivo. The first study was performed with the semi-rigid loopless antenna in an orange that was manually shaken (∼± 3mm in-plane, randomly) during MRI. For comparison, projection-shifting was compared with the first-order moment correction method implemented as described elsewhere (15). The in vitro blood vessel study was performed with the semi-rigid loopless antenna in human iliac artery specimens immersed in saline. To mimic physiologically relevant motion, the container was placed on the abdomen of a free-breathing volunteer during MRI: in-plane motion due to respiration was ∼± 4mm. In vivo studies approved by our Institutional Animal Care and Use Committee were performed on 3 healthy New Zealand white rabbits. The rabbits were sedated with intramuscular acepromazine (1 mg/kg) and ketamine (40 mg/kg), induced with intravenous sodium thiopental, and intubated to maintain an open airway. The loopless antenna was advanced into the descending aorta to the renal bifurcation via a femoral incision, as confirmed by contrast-enhanced X-ray C-arm CT prior to transfer to MRI. The loop antenna was inserted in the descending aorta via a surgical cut-down just inferior to the renal arteries. Probes were fixed in place with surgical ties.

Scout MRI was performed to locate the probe, prescribe the imaging plane, and to ‘volume shim’ the vicinity of the internal probe. IVMRI was performed with and without cardiac gating using radial and/or Cartesian gradient echoes (spoiled or balanced). For radial acquisitions, each readout was symmetric about the echo with alternating direction reversals (‘even/odd flyback’), and azimuthal angles were incremented sequentially to span the entire circle. All processing was performed off-line on ‘raw’ k-space data using scripts written in MATLAB^® (Mathworks, Nattick USA). IV images were weighted by the receiver sensitivity using an r^-1 image intensity filter centered on the probe location (Fig. 5a, b) (1,7), except where noted. Since the probe location was already determined by the motion correction algorithm, this step was relatively trivial.

Fig.5.

MRI of an orange from a semi-rigid loopless antenna p as in Fig. 1(b) without (a), and with (b) the r^-1 intensity filter (zoomed-in) applied. These images were acquired in the absence of motion and reconstructed from all 200 projections. (c) Four-fold radially under-sampled CS reconstruction of the same image data shown in part (b) (SSIM vs. 5b =0.52). (d) Conventional NUFFT reconstruction of the image data in part (c), shows streaking (arrow; SSIM vs. 5b = 0.44). (e) MRI of the same orange as in part (b), but shaken ± 3mm. The motion artefacts are debilitating (SSIM vs. 5b =0.28). (f) Motion-correction applied to image in part (e) using the COM algorithm (15) (SSIM vs. 5b =0.35). (g) Motion correction with the projection-shifting method shows reduced blurring vs parts (e) and (f) (arrows; SSIM vs. 5b =0.56). (h) Combined four-fold acceleration and motion correction with projection shifting, as applied to the data in part (e)(SSIM vs. 5b = 0.5).

All reconstruction was performed on a standard DELL XPS L502X laptop (Intel Core i7-2760QM 2.40GHz processor; 8 GB RAM; Windows 7 Professional 64-bit operating system). Freely available CS implementations {IRGNTV (25), GRASP (26), SPARSE-MRI (11)} were adapted for reconstruction. Even and odd k-space trajectories were handled separately for motion correction and recombined for reconstruction, except where noted. Motion correction was done using either projection shifting alone (for phantom and in vitro data), or with the averaging of aberrant k-space projections (in vivo data). For calculating SV in Eq. [5], the annular rings were confined to 1.5-3.5cm from the probe. The scan parameters, CS software and reconstruction penalties are summarized in Table 1. SSIM and SV_ratio indices are reported in the figure captions for the corresponding images.

Table 1.

Acquisition parameters (acquisition time, T_acq); CS software used (IRGNTV, SPARSE-MRI or GRASP); reconstruction parameters, λ where applicable; and reconstruction times (T_rec) using conventional (NUFFT) or CS reconstruction in each of the figures.

Fig.	Image details
1b	2D radial GRE; 200 spokes; 250μm in-plane resolution; TR/TE=15/6 ms. Tacq = 3s.
1c	Data from 1(b) undersampled to 50 spokes. NUFFT reconstruction, Trec ∼ 100 ms.
4a	Cardiac gated 3D Cartesian GRE; TR/TE=250/12 ms; in-plane resolution 80μm; Tacq = 3.1 min/5 contiguous slices. Center slice shown.
4b	Data from 4(a) undersampled three-fold. CS reconstruction using SPARSE-MRI. λWT = 0.09; λTV = 0.01; λSV = 0. Trec = 2 mins.
4c	Data from 4(b). Regular FFT reconstruction, Trec ∼ 10 ms.
5a	Same as 1(b).
5b	Data from 1(b) with r-1 intensity filter and zoomed.
5c	Data from 1(c). CS reconstruction using IRGNTV. λWT = 0; λTV = 2, 0.2, 0.02, 0.05 … (reduced every iteration); λSV = 0. Trec = 4 mins.
5d	Data from 1(c) with r-1 intensity filter and zoomed.
5e	Acquisition parameters same as 1(b) but with motion.
5f	Data from 5(e), motion-corrected using COM. NUFFT reconstruction, Trec ∼ 100 ms.
5g	Data from 5(e), motion-corrected using projection shift. NUFFT reconstruction, Trec ∼ 100 ms.
5h	Data from 5(g) undersampled to 50 spokes. CS reconstruction using IRGNTV, λ same as 5(c). Trec = 17mins.
7a	2D radial GRE; 0.3×0.3×2mm3 voxel; TR/TE=150/6 ms, 1000 spokes, 20mm FOV shown.
7b	Acquisition parameters same as 7(a) above, but with motion.
7c	Data from 7(b), motion-corrected. NUFFT reconstruction, Trec ∼ 100 ms.
7d	Data from 7(c) undersampled to 250 spokes. CS reconstruction using IRGNTV, λ same as 5(c). Trec = 18mins.
7e	Data from 7(d). NUFFT reconstruction, Trec ∼ 100 ms.
8a	Ungated, 0.2×0.2×5mm3 voxel, 2D Cartesian Balanced GRE, FA 90°, TR/TE 700/16ms, 25mm FOV. Tacq = 1.5 mins.
8b	Ungated, 0.2×0.2×5mm3 voxel, 200 spokes (odd) balanced radial 2D GRE, FA 90°, TR/TE = 700/6ms, 50mm FOV shown. Effective Tacq = 2.5 mins.
8c	Data from 8(b), motion-corrected. NUFFT reconstruction, Trec ∼ 100 ms.
8d	Cardiac gated, 0.2×0.2×5mm3 voxel, 400 spokes spoiled 2D radial GRE, FA 40°, TE 6ms, 40mm FOV. Tacq = 7 mins.
8e	Data from 8(c) undersampled to 50 spokes. CS reconstruction using GRASP. λWT = 0; λTV = 0.1 ; λSV = 0.0005. Trec = 7 mins.
8f	Data from 8(e). NUFFT reconstruction, Trec ∼ 100 ms.
9a	Ungated, 0.2×0.2×5mm3 voxel, 400 spokes (even+odd) balanced radial 2D GRE, FA 90°, TR/TE = 700/6ms, 15mm FOV shown. Tacq = 5 mins.
9b	Data from 9(a) undersampled to 100 spokes. CS reconstruction using IRGNTV, λ same as 5(c). Trec = 10 mins.
9c	Data from 9(a), but using only odd spokes (200 total) and motion-corrected. NUFFT reconstruction, Trec ∼ 500 ms.
9d	Data from 9(c) undersampled to 50 spokes. CS reconstruction using IRGNTV, λ same as 5(c). Trec = 25 mins.
9e	Ungated, 0.3×0.3×5mm3 voxel, Cartesian Balanced 2D GRE, FA 90°, TR/TE 9/4ms, 15mm FOV. Tacq = 0.5 secs.
9f	Data from 9(e) undersampled two-fold. CS reconstruction using SPARSE-MRI. λWT = 0.09; λTV = 0.01; λSV = 0. Trec = 3 mins.

Results

The effect of CS reconstruction of three-fold undersampled in vivo Cartesian data acquired from a loop-coil IV MRI endoscope with conventional cardiac-gating is shown in Fig. 4b. Traditional NUFFT reconstruction using the same k-space data as in Fig. 4(b) shows under-sampling artefacts especially in the high-SNR regions surrounding the probe (Fig. 4c). The effective speed-up factor in Figs. 4(b, c) vs Fig. 4(a) is 3-fold; the effects on the PSF and resolution are discussed later.

Fig.4.

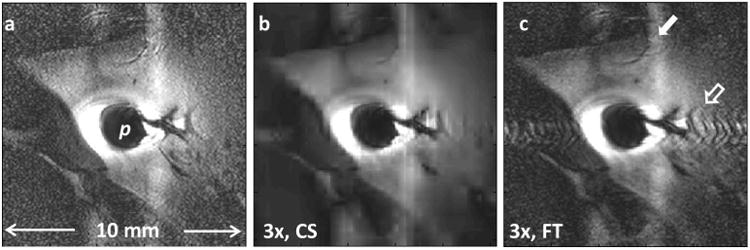
(a) Regular Cartesian in vivo MRI endoscopy of a rabbit aorta acquired with a transmit/receive loop coil (8). (b) Three-fold under-sampling using CS reconstruction (SSIM vs. 4a =0.53). (c) The under-sampled k-space from (b), when conventionally reconstructed, shows strong artefacts (hollow arrow) near the probe. The vertical bright band (arrow) is likely due to motion which cannot be corrected in this Cartesian acquisition (SSIM vs. 4a =0.69).

Structures revealed in an IVMRI of a stationary orange acquired with a loopless antenna (Fig. 5b) are retained in a four-fold under-sampled radial CS reconstruction (Fig. 5c). Some blurring of the septa between the fruit segments is evident, but not the streaking artefacts seen in a conventional under-sampled NUFFT reconstruction (Fig. 5d). Motion of the shaken orange obliterated virtually all structure in the PR image (Fig. 5e). Motion-correction of the same data set as (e) using the COM algorithm (15,16) substantially restores gross structure but shows some streaking (Fig. 5f; arrow). The projection-shifting algorithm offers further improvement, as evident in the fruit's central void and septal regions (Fig. 5g) as compared to Fig. 5(f) as well as to the source data, Fig. 5(e). This is reflected in a higher SSIM (see caption). Application of the combined algorithm comprising motion-correction and 4-fold under-sampling (Fig. 5h), reveals morphology albeit with some deterioration in resolution of the septa, as compared to Fig. 5(g). Both these images offer a dramatic improvement over the original motion-corrupted source image data in Fig. 5(e).

The effect of the undersampling in Figs. 4 and 5 is illustrated by plots of the PSF in Fig. 6. The 3-fold Cartesian under-sampling in Fig. 4(b) results in a near doubling of the PSF main-lobe width, as compared to the fully-sampled case (∼2 pixels vs. 1 pixel, see Fig. 6a). For the 4-fold under-sampled radial images in Fig. 5(c), the PSF side-lobe is about four times larger and four times closer to the main lobe, as compared to the fully sampled case (see Fig. 6b).

Fig.6.

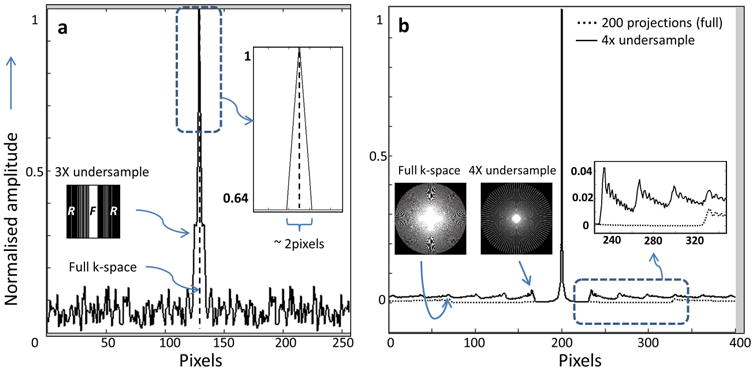
(a) PSF (solid line) of the under-sampled Cartesian image k-space used for Fig. 4(b) (inset left, bar-graph, F = fully sampled, R = randomly sampled regions), as compared to the ideal delta-function PSF from sampling all of k-space (dashed line). The width of the under-sampled PSF is almost double (inset right, zoomed) at 64% of the amplitude. (b) PSF of four-fold under-sampled radial k-space of Fig. 5(c) (solid-line). The under-sampled PSF has ∼4 times larger side-lobes that occur at ∼¼ the distance from the main lobe as the fully sampled PSF from Fig. 5(b) acquired with 200 projections (dashed-line; inset right). Inset images (left) depict k-space trajectories.

The effect of physiological motion of an iliac vessel specimen in a saline tank placed on the abdomen of a free-breathing volunteer is debilitating, with most structure lost in this example (Fig. 7b vs. 7a). Motion correction of the corrupted source data in Fig. 7(b) removes most of the radial streaking to reveal the underlying vessel wall structure in Fig. 7c (vs. Fig. 7b). Remaining vertical artefacts are attributable to residual motion. Vessel structure is also largely retained following a four-fold under-sampled CS reconstruction of the same image, shown in Fig. 7(d). Furthermore, the CS image is less noisy than a NUFFT reconstruction of the undersampled and motion-corrected data shown in Fig. 7(e).

Fig.7.

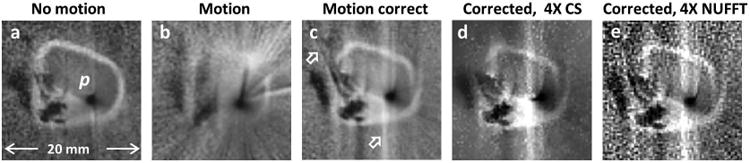
(a) IVMRI of a human iliac specimen in vitro using a semi-rigid loopless antenna with no motion. (b) IVMRI from the sample mounted on the abdomen of a free-breathing volunteer to simulate physiological motion (SSIM vs. 7a =0.1). (c) Motion correction removes radial streaking, revealing much of the specimen's underlying structure, though some vertical artefacts remain (arrow; SSIM vs. 7a =0.4). (d) Four-fold under-sampled CS reconstruction of image in part (c) (SSIM vs. 7c =0.5). (e) NUFFT reconstruction of the under-sampled motion-corrected data (SSIM vs. 7c =0.4).

Without cardiac or any other gating, in vivo images acquired with the loopless antenna at 200μm resolution in the rabbit aorta can exhibit intense ghost and radial streak artefacts in Cartesian-and radially-encoded acquisitions respectively (Figs. 8a, b). Motion correction by projection-shifting and k-space averaging of the ungated radial data shows a decrease in radial streak artefact intensity in Fig. 8(c), as compared to Fig. 8(b). A cardiac-gated image acquired separately from approximately the same location but requiring a longer scan time, is shown in Fig. 8(d). CS reconstruction applied to 1/4th of the motion-corrected data, although somewhat patchy, retains overall structure (Fig. 8e), whereas conventional NUFFT reconstruction of the same under-sampled data is overwhelmed by streaking artefacts (Fig. 8f). Zooming in on the aorta, we see that radial compressed sensing with only 1/4th of the original data (Fig.9b) provides comparable rendition vs the original (Fig. 9a), with streaking artefacts reduced by the motion correction (Fig. 9c). CS reconstruction applied to 1/8th of the motion-corrected data, provides an effectively eight-fold faster motion-suppressed in vivo image (Fig. 9d). Ungated acquisition affords imaging speeds of up to 2 fps (Fig.9e) and CS reconstruction using 1/2 the data (effectively 4 fps) faithfully renders the aorta but with some loss of detail in low-SNR regions (Fig. 9f).

Fig.8.

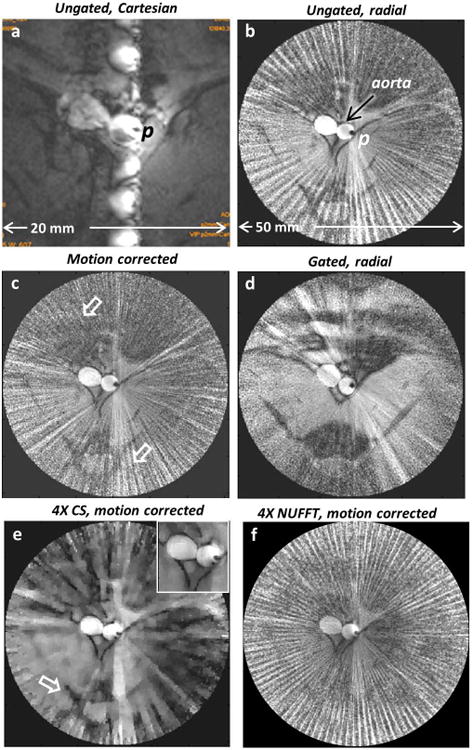
An in vivo rabbit aorta image acquired with a nitinol-based loopless antenna detector p and without any cardiac gating showing (a) ghost artefacts in Cartesian-encoded image and (b) streaking in radial-encoded image (with odd spokes) arising from physiological motion. (c) Motion-correction applied to image in part (b) reduces the streaking (arrows; SV_ratio vs. 8b =0.69). (d) Cardiac-gated in vivo IVMRI at approximately the same location reveals similar vessel structure as (c) (SV_ratio vs. 8c =1.01). (e) Four-fold speedup of (c) retains overall morphology including aorta (inset; SV_ratio vs. 8c =0.31). The tissue structure (arrow) is retained, whereas in (f) which is the conventional FT reconstruction of the same dataset as in part (e), it is swamped by streaking (SV_ratio vs. 8c =1.36).

Fig.9.

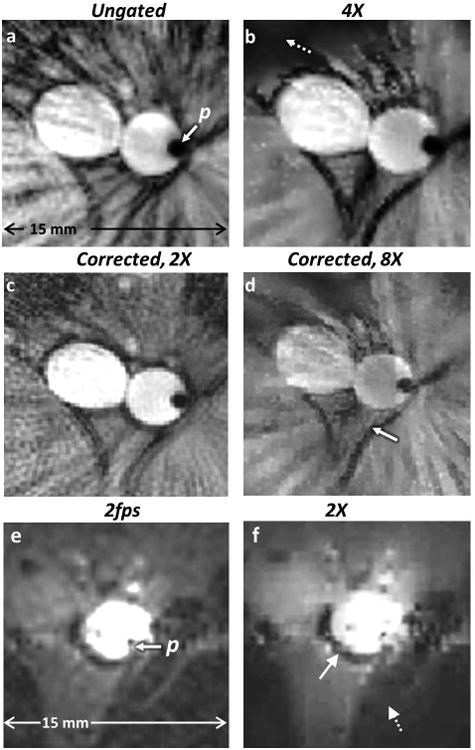
(a) Ungated radial IVMRI (zoomed anatomy of Fig. 8b) with conventional scanner reconstruction using even and odd spokes shows streaking near the aorta and surrounding tissue. (b) Tissue morphology is retained in a 4-fold under-sampled CS reconstruction of part (a) albeit with some loss of signal in regions of low SNR (dashed arrow; SV_ratio vs. 9a =0.9). (c) Motion-correction applied to half the data (using only odd spokes) in part (a) with conventional NUFFT reconstruction reduces streaking (SV_ratio vs. 9a =0.95). (d) Eight-fold under-sampling of part (a) using only odd spokes, retains morphology of the aorta and surrounding tissue (solid arrow), although the intensity of the blood signal is reduced (SV_ratio vs. 9c =1.1). (e) IVMR images from a rabbit aorta in vivo, acquired at 2fps without any cardiac gating. (f) Two-fold under-sampled CS reconstruction without any motion correction retains overall morphology (aorta, solid arrow), but some detail is lost in low SNR regions (dashed arrow). The r^-1 intensity filter has not been applied to (e) or (f) (SSIM of 9f vs. 9e =0.82).

CS reconstruction times depend significantly on the image resolution, FOV and iterative reconstruction parameters, ranging from 2 to 25 minutes, whereas the corresponding FFT and NUFFT based reconstruction was of the order of milliseconds (Table 1). The SSIM of all the corrected and/or undersampled CS reconstructed images was ≥ 0.4 and SV_ratio of corrected images was ≤ 0.95 (see figure captions).

Discussion

This paper presented strategies for accelerating image acquisition and suppressing motion artefacts in IVMRI, and demonstrated results in fruit for testing motion effects, vessel specimens in vitro (mounted on a volunteer to simulate physiological motion), and in rabbit aorta in vivo. CS reconstruction has been widely studied for MRI applications in the past, and our implementation was based on freely available open-source CS implementations. We extended previously used penalties with a new IVMRI-specific constraint (SV). As far as we are aware, this is the first application of CS reconstruction to IVMRI applications (30). Additional smoothing functions may be incorporated (10) to avoid some of the CS associated ‘patchiness’. The TV and SV constraints within the CS reconstruction favor smooth areas, blurring some areas with low contrast-to-noise ratios, while better preserving sharper edge morphology. As in any under-sampling scheme, there is some SNR loss. A possible remedy is 7T IVMRI which potentially offers a quadratic SNR improvement with field strength (31). In quantifying reconstruction artefacts, the simple PSF analysis presented here closely approximates the more sophisticated analysis of nonlinear CS reconstruction reported elsewhere (28). CS reconstruction takes significantly longer than conventional FT reconstruction (minutes vs. milliseconds), so that further software and hardware optimization, for example employing graphics processing units (32), would likely be required for practical use. Finally, the benefits of CS reconstruction are likely to grow as the dimensionality of the data is increased from the present 2D case (11).

Motion correction strategies based on PR have been used in the past in conventional MRI settings (15-17). Moment-based methods can yield erroneous results when applied to IVMRI projections wherein intensity profiles are highly skewed towards the coil (Fig. 2a, Fig. 5f). Our new method used explicit probe localization based on the amplitude and phase profiles of IVMRI detectors. Moreover, in high-resolution IVMRI applications, there are dynamic changes in projections such that corrections based on a sampling of central k-space or assumptions of a constant spin-density (17) were ineffective in our studies. All of our radial acquisitions employed gradient echoes, which was the standard radial sequence provided by the scanner manufacturer. Use of radial spin-echo sequences could offer improved immunity to field-inhomogeneity (T₂*) effects and suppress signals from flowing blood for vessel wall imaging. Experimentally compensating for view-dependent gradient timing errors (33) may reduce artefacts as well. On the other hand, the reader should also be advised that in vivo IVMRI can often exhibit little motion artefact (e.g., Fig 9e, and the cine rabbit data in Ref. 8), lest the focus here on the effects of motion and its correction unduly create the impression of an overwhelming problem.

We showed that motion correction using projection shifting and averaging of aberrant k-space projections was useful in correcting rigid-body motion in vitro, and was moderately effective in dealing with respiration and sporadic motion that occurred in relatively short periods (1-2 TRs) in vivo. When the motion lasts for a significant fraction of the imaging time, traditional cardiac and respiratory gating and/or repeat imaging may be necessary. All these correction methods have limitations in compensating for the following sources of motion. First, probe motion with respect to the body due to natural physiological motion could cause position-dependent amplitude or phase variations, although here, the tensile properties of the in vivo nitinol probe tended to hold it against the vessel wall. In any case, this motion should have affected the cardiac-gated images (Fig. 8d) which were relatively free of such artefacts. Second, object rotation can cause a mismatch between the nominal acquisition angle and the actual projection. To correct this in high-resolution images, the motion could potentially be modeled based on fast low-resolution acquisitions. Third, pulsatile blood flow causes the vessel to expand and contract during image acquisition, affecting the surrounding tissue to a lesser extent. We did explore a correction method wherein each projection was dilated/compressed to account for the radial tissue expansion/contraction, but found it difficult to reliably model the non-linear changes.

Our motion correction algorithm is applied at the TR of each projection prior to reconstruction, and is therefore amenable to real-time application to the data stream, including MRI endoscopy (9). Applying the algorithm in real-time would permit a sliding window reconstruction strategy wherein the latest projection replaces the oldest, resulting in an image-stream that updates at the TR rate. The intent is to make fast lower-resolution (200-300μm) images in real-time followed by slower high-resolution (≤100μm) images at sites where pathology is suspected (7,8) or therapy is to be delivered. When the azimuthal angle increment in PR is small, the cross-correlation between successive projections can be used for probe detection, but can introduce a delay between acquisition and motion-correction. This will be larger when non-sequential angle increments are employed. Using the amplitude and phase profiles alone, automated detection was achieved for phantom and in vitro data, but some manual processing was required for in vivo data when spurious phase wraps occurred. Transmit/receive loop probes as in MR endoscopy (9) do not exhibit phase variations so that probe detection would have to rely solely on the near-field radial sensitivity profile.

We conclude that 3T IVMRI detectors are amenable to CS reconstruction due to their sparsely-localized sensitivity profiles and intense, yet localized SNR. For radial IVMRI, projection-shifting ameliorates motion artifacts based on the probe's intrinsic radial sensitivity profile. While there is a cost to using CS both in terms of spatial resolution and reconstruction time, and some motion artifacts are likely to persist, these techniques should nevertheless offer tangible benefits for faster high-resolution IVMRI in vivo.