Monitoring local heating around an interventional MRI antenna with RF radiometry

Abstract

Purpose:

Radiofrequency (RF) radiometry uses thermal noise detected by an antenna to measure the temperature of objects independent of medical imaging technologies such as magnetic resonance imaging (MRI). Here, an active interventional MRI antenna can be deployed as a RF radiometer to measure local heating, as a possible new method of monitoring device safety and thermal therapy.

Methods:

A 128 MHz radiometer receiver was fabricated to measure the RF noise voltage from an interventional 3 T MRI loopless antenna and calibrated for temperature in a uniformly heated bioanalogous gel phantom. Local heating (ΔT) was induced using the antenna for RF transmission and measured by RF radiometry, fiber-optic thermal sensors, and MRI thermometry. The spatial thermal sensitivity of the antenna radiometer was numerically computed using a method-of-moment electric field analyses. The gel’s thermal conductivity was measured by MRI thermometry, and the localized time-dependent ΔT distribution computed from the bioheat transfer equation and compared with radiometry measurements. A “H-factor” relating the 1 g-averaged ΔT to the radiometric temperature was introduced to estimate peak temperature rise in the antenna’s sensitive region.

Results:

The loopless antenna radiometer linearly tracked temperature inside a thermally equilibrated phantom up to 73 °C to within ±0.3 °C at a 2 Hz sample rate. Computed and MRI thermometric measures of peak ΔT agreed within 13%. The peak 1 g-average temperature was H = 1.36 ± 0.02 times higher than the radiometric temperature for any media with a thermal conductivity of 0.15–0.50 (W/m)/K, indicating that the radiometer can measure peak 1 g-averaged ΔT in physiologically relevant tissue within ±0.4 °C.

Conclusions:

Active internal MRI detectors can serve as RF radiometers at the MRI frequency to provide accurate independent measures of local and peak temperature without the artifacts that can accompany MRI thermometry or the extra space needed to accommodate alternative thermal transducers. A RF radiometer could be integrated in a MRI scanner to permit “self-monitoring” for assuring device safety and/or monitoring delivery of thermal therapy.

1. INTRODUCTION

Radiometry is the science of measuring the emission of electromagnetic (EM) radiation at microwave and radiofrequencies (RFs). Black-body (BB) radiation is defined as the thermal EM radiation within or surrounding a nonreflective body that is in thermal equilibrium with its surrounds. It arises from the thermal motion of charged entities present in the body, which depend only on absolute temperature.^1–3 The relationship between the EM emissions and temperature, first noted in the 1920s,^1,2 led to the routine use of microwave radiometry for environmental and astronomical applications based on noise-power measurements performed with focused antennae operating in the gigahertz range.³ Microwave radiometry has also been used to measure temperature increases in biological tissue associated with fast-growing breast tumors^4,5 and human carotid atherosclerotic plaques, using external microwave antennae.⁶ As a passive detection method, radiometry uses no applied radiation of any form and therefore presents no radiation hazard.

Although radiometry is most often performed at microwave frequencies, the thermal irradiation extends over the whole EM spectrum, including that used for magnetic resonance imaging (MRI). In fact, with the sensitive receivers and fine bandwidths routinely used in MRI, the human body typically represents the dominant RF noise contributor to the scanner’s signal-to-noise ratio.^7–9 Thus, independent of MRI, the MRI coil is entirely capable of directly detecting the (nonreflected) thermal EM noise from the sample. Indeed, scanner noise figures (NFs) are commonly measured from the ratio of the root-mean-squared (rms) RF noise voltages recorded from a standard (50 Ω) load at two temperatures.^9,10

Based on this inherent sensitivity of the MRI scanner to thermal noise from the sample, a radiometer operating at the relatively low RF of a 64 MHz 1.5 Tesla (T) MRI scanner was introduced for measuring sample temperature using a regular external MRI loop coil as a transducer.¹¹ The MRI coil’s spatial sensitivity to thermal noise coincides with the spatial distribution of its received signal power which, by the principle of reciprocity,⁹ is the same as the power distribution that results from exciting it with unit current. Thus, the thermal sensitivity of the radiometer extends deep into the tissue lying within the coil’s sensitive volume and could be used to independently monitor sample heating during MRI.¹¹

Interventional MRI (iMRI) employing active small-diameter catheters, guidewires, needles, etc., as MRI detectors is an application of MRI technology that poses potential safety risks due to RF heating close to the conducting elements.^12–15 This is compounded when the internal device is used for both MRI transmission and reception in intravascular applications^16,17 and at ultrahigh magnetic field strengths (B₀ > 3 T)^17,18 where RF penetration effects may limit MRI access to deep tissue.^19–21 In addition, when MRI devices are used for targeted thermal therapy, for example, to enhance gene therapy,²² or for RF ablation as a treatment for cardiac arrhythmias,²³ or for tumor ablation,²⁴ having an independent means of measuring local temperature for assessing safety and titrating thermal therapy in real-time is key.

Fiber-optic temperature probes offer one option for packaging with a MRI device that avoids the confounding effect of added heating from an extra conductor.^25,26 However, their local sensitivity is limited to a few mg of tissue²⁶ so that precise placement is critical. Also, although fiber diameters are small, after adding them to an existing iMRI device, the increase in size may still limit interventional applications such as catheter deployment over a MRI guidewire in tight vessels. Clearly, there would be more space if the MRI device itself could independently monitor temperature without having to add any other thermal sensor.

Of all the MRI devices in use, the loopless antenna, formed simply from a coaxial line whose center conductor is extended by approximately a 1/4-wavelength (λ/4), is ideal as an imaging guidewire in narrow vessels and offers spatial resolution of 80 μm or better at 3–7 T.^16,25,27 The losses in a loopless antenna are primarily attributable to the electric field (E-field) distribution in the tissue between the whip and the distal end of the cable.^25,27 We therefore posit that, in addition to high-resolution MRI, a loopless antenna could also provide radiometric measures of the local temperature distribution within its sensitive volume. In particular, for devices used for both transmission and reception (again invoking the principle of reciprocity²⁸), any heating caused during transmission will have the same distribution as the antenna’s radiometric thermal sensitivity profile, at least until thermal conductivity in the tissue kicks in.

In this work, we report as a proof-of-principle, the development and testing of a superheterodyne RF radiometer (receiver) for an interventional loopless MRI antenna²⁹ operating at a 3 T MRI frequency (128 MHz) to monitor local and peak internal temperature near the device. Radiometry experiments were performed with the probe in a uniformly heated gel phantom, and also with RF power applied directly to the loopless antenna, to simulate a thermal ablation. The radiometer’s experimental performance was compared with numerical computations of the power sensitivity with the effects of thermal diffusion included, and with results from MRI thermometry studies. We determined the conversion factor for obtaining the local peak 1 g-averaged temperature rise (ΔT) at the antenna from a radiometric temperature reading.

2. THEORY

2.A. Spatial sensitivity of radiometric temperature measurements

A lossy medium at an absolute temperature T (Kelvin) emits EM radiation associated with the thermal motion of its molecules and ionic moieties according to Nyquist’s formula,²

$${\displaystyle P_n=\frac{〈V_n^2〉}{4R}=kTB.}$$ (1)

Here, P_n is the available relative noise power, $〈V_n^2〉$ is the variance of the thermal (open-circuit) noise voltage, R is the real part of the equivalent resistance of the medium, K is Boltzmann’s constant, and B is the bandwidth of the receiver. Equation (1) is also the Rayleigh-Jeans approximation of Planck’s law for black-body radiation used in microwave radiometry.³ The equation enables the absolute temperature of a medium to be estimated from the average noise power measured by a radiometer comprised of a receiving antenna, high-gain receiver electronics, and a voltage or power measuring device.

The signal reported by the RF radiometer (S_radio) is proportional to the sensitivity-weighted volume integral of the temperature inside the medium,^30,31

$${\displaystyle S_{\text{radio}}\sim \frac{{\int }_{V}T\left(r\right)\sigma \left(r\right){\left|E\left(r\right)\right|}^{2}dr}{{\int }_V\sigma \left(r\right){\left|E\left(r\right)\right|}^{2}dr}.}$$ (2)

Here, r denotes the spatial coordinates, σ is the electrical con ductivity of the medium which may vary both spatially and with temperature, and E is the E-field distribution of the antenna for unit current excitation. The antenna power receiving pattern (P_d) inside the medium is given by

$${\displaystyle P_d\left(r\right)=\sigma \left(r\right){\left|E\left(r\right)\right|}^2.}$$ (3)

For a loopless antenna, the sensitivity is highest near the cable-whip junction and the conductor, decaying rapidly with radial distance from the device.¹⁷ Therefore, the radiometric temperature measured by the loopless antenna is expected to be most sensitive to temperature changes at locations with high P_d that lie nearest the cable-whip junction. We introduce a “H-factor,” H(r), defined as the coefficient relating the local ΔT at an arbitrary location to the measured radiometric temperature rise, ΔT_radiometer. If the H-factor at a certain location is known, then the actual temperature rise, ΔT_a(r), at that location can be determined via

$${\displaystyle \mathrm{\Delta }{T}_a\left(r\right)=\mathrm{\Delta }{T}_{\text{radiometer}}H\left(r\right).}$$ (4)

The H-factor can be computed from the spatial distribution ΔT(ΔT_m) and P_d as follows:

$${\displaystyle H\left(r\right)=\mathrm{\Delta }{T}_m\left(r\right)\frac{{\int }_V{P}_d\left(r\right)dr}{{\int }_V\mathrm{\Delta }{T}_m\left(r\right)P_d\left(r\right)dr},}$$ (5)

where the integration is performed over the entire volume of the medium. We define the peak H-factor, H_peak, as the H-factor coefficient where the highest ΔT occurs. H_peak can be used as a metric for determining the maximum expected temperature rise inside the medium based on a radiometry measurement. It is worth noting that the temporal (time, t) thermal response generally must also be considered. We characterize H(r, t) using numerically computed P_d and ΔT_m distributions and compared the results with experimental data.

2.B. Effect of sample load and impedance matching

MRI detectors are usually matched to a range of input impedances for which the NF of the MRI system’s preamplifier is minimal (e.g., 25–75 Ω). We show that impedance transformation does not affect the antenna’s ability to detect radiometric temperature change. In accordance with Eq. (1), a tuned antenna with a load resistance R generates a white Gaussian thermal noise voltage V(t) with an expected value of $\sqrt{4\text{kTRB}}$ and available noise power over a bandwidth B,

$${\displaystyle \int P\left(\omega \right)d\omega ={\int }_{{\omega }_0-\raisebox{1ex}{$B$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{{\omega }_0+\raisebox{1ex}{$B$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\frac{〈V\left(\omega \right)V^{*}\left(\omega \right)〉}{4R}\approx kTB,}$$ (6)

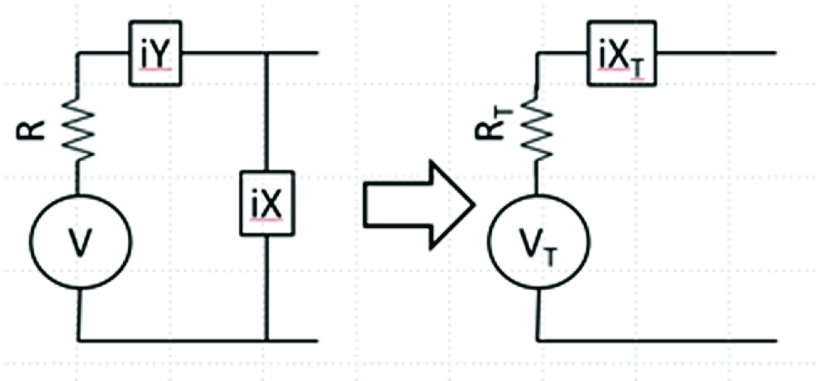
where V(ω) is the Fourier transform (FT) of V(t), and P(ω) is the power spectral density about the MRI angular frequency, ω. The final approximation in Eq. (6) becomes true when B is small compared to any variation in the noise spectrum. As shown in Fig. 1, a circuit that is lossless or whose losses are much less than those detected by the antenna may be comprised of inductors and capacitors with reactances iY and iX that transform R to a set value (e.g., match to 50 Ω). The AC Thevenin equivalent circuit can be calculated as

$${\displaystyle V_T\left(\omega \right)=\frac{iX\left(\omega \right)}{R+i(X\left(\omega \right)+Y\left(\omega \right))}V\left(\omega \right),}$$ (7a)

$${\displaystyle R_T\left(\omega \right)=\frac{RX{\left(\omega \right)}^2}{R^2+{(Y\left(\omega \right)+X\left(\omega \right))}^2},}$$ (7b)

and

$${\displaystyle X_T\left(\omega \right)=\frac{X\left(\omega \right)(R^2+Y{\left(\omega \right)}^2+X\left(\omega \right)Y\left(\omega \right))}{R^2+{(Y\left(\omega \right)+X\left(\omega \right))}^2}.}$$ (7c)

FIG. 1.

Impedance matching circuit (left) comprising lossless reactive elements (inductors and capacitors) iY and iX connected to an antenna with resistance R generating thermal noise voltage V and its Thevenin AC circuit equivalent (right). The transformed voltage, resistance, and reactance are V_t, R_t, and iX_t, respectively.

The expected variance of the noise voltage is

$${\displaystyle 〈V_T\left(\omega \right)V_T^{*}\left(\omega \right)〉=\frac{X{\left(\omega \right)}^2}{R^2+{\left(X\left(\omega \right)+Y\left(\omega \right)\right)}^2}〈V_T\left(\omega \right)V_T^{*}\left(\omega \right)〉=4kT\frac{X{\left(\omega \right)}^2}{R^2+{\left(X\left(\omega \right)+Y\left(\omega \right)\right)}^2}=4kT{R}_T\left(\omega \right).}$$ (8)

Therefore, after transformation, the expected noise variance is associated with the equivalent real resistance of the transformation relative to the original, modified only by the effect of the transforming elements on the transducer’s bandwidth. Note that if X = − 1/ωC is a parallel capacitor, C, and Y = 0, then

$${\displaystyle V_T\left(\omega \right)=\frac{1}{1+i\omega CR}V\left(\omega \right),R_T=\frac{R}{1+{\left(\omega CR\right)}^2},}$$

and

$${\displaystyle 〈V_T\left(\omega \right)V_T^{*}\left(\omega \right)〉=4kT\frac{R}{1+{\left(\omega CR\right)}^2}=4kT{R}_T\left(\omega \right)}$$ (9)

consistent with the original paper by Johnson.^1,32 Ordinarily, the bandwidth of the MRI receiver is much less than that afforded by the coil quality factor, Q, of tuned loaded MRI detectors, and the Q’s of internal coils are even lower. Thus, over a small bandwidth (e.g., ±200 KHz at 128 MHz), the expected noise variance is essentially constant, with

$${\displaystyle {\int }_{{\omega }_0-\raisebox{1ex}{$B$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{{\omega }_0+\raisebox{1ex}{$B$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}〈V\left(\omega \right)V^{*}\left(\omega \right)〉\approx 4kT{R}_{T}B.}$$ (10)

Thus, impedance matching to a fixed R_T yields the maximum available power, kTB, which is only a function of temperature,¹ and can alleviate measurement errors resulting from changes in loading.

3. METHODS

3.A. Loopless antenna and the experimental phantom

An experimental loopless antenna was fabricated from a λ/4 (40 cm) 2.2 mm diameter UT-85C semirigid coaxial cable (Micro-coax, Inc., Pottstown, PA) with an uninsulated inner conductor extended by 39 mm to form a resonant whip at the 3 T MRI frequency (128 MHz) as described previously.^25,33 The end of the antenna cable was connected to the front-end of the radiometry receiver via a cable with two bazooka baluns tuned to 128 MHz.³⁴

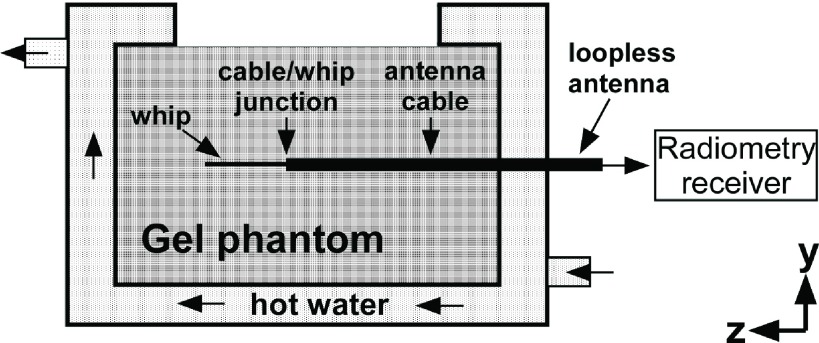
An experimental phantom was built from two concentric cylindrical chambers that were sealed from each other. A 20 cm long, 12 cm diameter inner chamber was placed at the isocenter of a cylindrical outer chamber (Fig. 2). The inner chamber was filled with a uniform gel solution (15 g/L polyacrylic acid, 0.8 g/L salt)²¹ whose electrical properties matched those used in numerical simulations (dielectric constant ε = 80; σ = 0.6 S/m) and approximated the average of those of biological tissue.³⁵ The loopless antenna was inserted inside the inner chamber of the phantom to a depth of 10 cm and connected to the radiometer’s RF receiver chain described below. At the 3 T MRI frequency, the tuned loopless antenna had a resistance of 32 Ω in the sample at the junction. As shown above, this can be matched to a desired impedance [e.g., 50 Ω (Ref. 25)] while preserving radiometric functionality.

FIG. 2.

Side-view of the cylindrical experimental phantom and the placement of the loopless antenna inside the gel.

The outer chamber of the phantom was filled with water and connected to an adjustable temperature water pump (VWR International LLC, Radnor, PA). Hot water was circulated inside the outer chamber of the phantom to uniformly heat the gel in the phantom’s inner chamber (Fig. 2). The phantom and the loopless antenna were placed inside a RF-shielded room (measured shielding factor >100 dB at the RF used) to minimize external RF interference. The water pump was located outside the room and water was conveyed to the phantom through hoses passing through the room’s waveguides. The temperature inside the gel was independently monitored at 1 Hz using fiber-optic temperature sensors (Neoptix, Inc., Quebec, Canada) placed at the cable-whip junction of the antenna and at other reference locations. These were used to verify temperature distributions and thermal equilibrium. The temperature sensors had a diameter of 1.6 mm and their sensitive volumes were assumed to occupy a cube with dimensions of 1.6 mm³, corresponding to 4.1 mg of gel weight.

3.B. The radiometry receiver

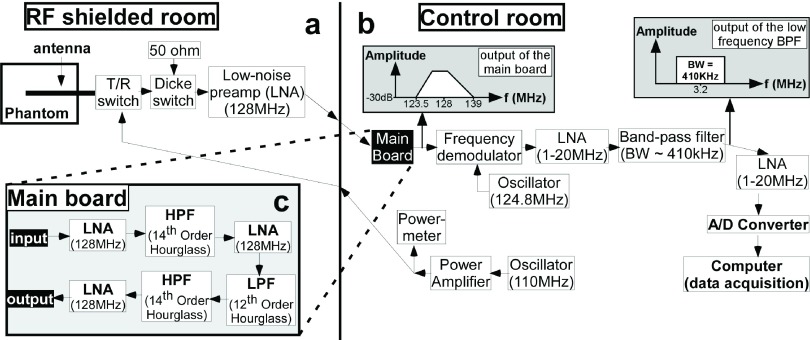
A superheterodyne receiver tuned to 128 MHz with a bandwidth of 410 KHz was designed and built for the radiometric measurements (Fig. 3). The front-end of the receiver had two MRI transmit/receive (T/R) switches. The distal T/R switch was used to switch between radiometry for measuring temperature and a RF power transmission mode for local heating or ablation of the gel by the antenna (or MRI), during which time the sensitive receiver electronics must be protected.

FIG. 3.

Block diagram of the radiometry receiver components. (a) The phantom with the loopless antenna, switches, and first preamplifier stage are placed inside the RF-shielded room. (b) The rest of the RF receiver and power delivery components are located outside the shielded room. (c) RF components in the main board include three preamplifier stages and an anti-aliasing band-pass filter consisting of a low-pass and two high-pass filters.

The second switch is a Dicke switch, placed between the first T/R switch and the receiver electronics. The third port of the Dicke switch is terminated with a 50 Ω load that is kept at a constant temperature for calibrating the radiometer’s receiver gain. The main purpose of the Dicke switch is to transition between the loopless antenna and the 50 Ω load to acquire either radiometry data or calibration data.³⁶ During the RF power transmission (or MRI) mode, the Dicke switch provides additional protection for the receiver electronics (Fig. 4). For bench testing outside of the MRI scanner, we substituted two 12 V relays (OMRON, Kyoto, Japan) with >60 dB isolation at 128 MHz, for the T/R switches. The Dicke switch is connected to a low-noise preamplifier (LNA) (Wantcom, Inc., Chanhassen, MN, Gain = 28 dB; NF = 0.4 dB) and the signal from the LNA conveyed outside the room via a long coaxial cable incorporating several solenoidal and bazooka baluns that maintain signal integrity and minimize interference.

FIG. 4.

Radiometry front-end switches (top) enable transition between three possible states (radiometry, gain calibration, local heating; below) during the experiments.

The remaining receiver electronics is kept in a monitoring room, outside the RF shield. This includes a “main board” housing three further LNA stages and an anti-aliasing band-pass filter (BPF) tuned to 128 MHz to restrict the noise bandwidth prior to demodulation [Fig. 3(c)]. The BPF consists of two 14th-order “hourglass” high-pass and a 12th-order hourglass low-pass filter stages, designed using Filter Solutions software (Nuhertz Technologies LLC, Phoenix, AZ). The BPF provides >35 dB attenuation for frequencies <123 MHz to eliminate potential signal interference from sidebands that could wrap into the bandwidth of interest (127.7–128.3 MHz) after demodulation. The filtered output signal from the main board [Fig. 3(b)] is downconverted to 3.2 MHz with a quadrature demodulator (Polyphase Microwave, Inc., Bloomington, IN) fed by a 124.8 MHz local oscillator signal provided by a frequency synthesizer (Programmed Test Sources, Inc., Littleton, MA).

The 3.2 MHz base-band signal is further boosted by two 20 dB preamplifiers (Advanced Receiver Research, Burlington, CT; NF = 2.5 dB) and filtered with lumped element BPFs designed using the Filter Solutions software. The BPFs are tuned to 3.2 MHz with bandwidths varying from 410 to 900 KHz. The signal output of the RF receiver chain [Fig. 3(b)] is connected to a DT9832A, Data Translation, Inc. (Marlboro, MA) data acquisition module (DAQ) for analog-to-digital conversion, sampled at a 2 MHz sample rate. Although the radiometry signal is above the Nyquist sampling limit, it is not attenuated by the DAQ whose 3 dB bandwidth is >10 MHz. The DAQ is connected via USB to a 2.67 GHz dual-core laptop computer (8 GB working memory) and the signals processed using matlab (Mathworks, Inc., Natick, MA).

Radiometry data were acquired continuously for 5 s, followed by a 5 s pause during which the data were stored and the average noise power determined at 0.5 s intervals (10 readings/acquisition period) from the mean-square value of the acquired samples, using the matlab timer function. Receiver gain calibration data were acquired at ≤1 min intervals using the Dicke switch to switch between the 50 Ω termination and the loopless antenna.

3.C. Experimental setup

Calibration factors for converting noise power to temperature were determined from the average rms noise from entire 5 s acquisitions in the uniformly heated phantom experiments. The noise-power measurements were corrected for system and gain variations based on contemporaneous Dicke-switched 50 Ω load measurements and compared to the Neoptix thermal sensor measurements as the standard. In the calibration experiment, the temperature of the gel phantom was increased uniformly from 25 °C to 73 °C and radiometry data acquired throughout. The radiometric temperature (T_radio) was calculated from radiometer readings (S_radio) using

$${\displaystyle T_{\text{radio}}=\psi S_{\text{radio}}+\beta ,}$$ (11)

where the linear calibration factors ψ and β were determined by plotting the temperature measured by a Neoptix sensor placed at the junction (Fig. 2) against S_radio.

After the radiometer was calibrated based on measurements with the phantom at thermal equilibrium, local heating was induced by exciting the antenna with RF power at 110 MHz. The T/R and Dicke switches connected a continuous wave RF power amplifier (Tomco, Inc., BT00250, Stepney, SA, Australia) to the loopless antenna (Fig. 4), with the 110 MHz signal supplied by the frequency synthesizer. The amplitude of the output of the power amplifier was monitored with a RF power meter (LadyBug Technologies, Santa Rosa, CA). The power loss between the power amplifier and the loopless antenna was measured as 0.33 dB (7.3%), using a network analyzer (4395A, Agilent Technologies, Santa Clara, CA). Intervals of radiometric measurement and RF exposure were interleaved, albeit with a 2 s latency delay for radiometry after RF exposure ceased.

RF exposure was repeated with different power levels and durations according to Table I. The radiometric temperature was determined using the calibration factors from Eq. (11). The temperature readings from both the radiometer and the fiber-optic sensors reflecting temporal heating and cooling were best-fitted empirically to smooth (double-exponential) curves. The experimental H-factors (H_e) at temperature sensor locations experiencing temperature increases ΔT > 2 °C was determined from

$${\displaystyle H_e=\frac{\mathrm{\Delta }{T}_{\text{sensor}}}{\mathrm{\Delta }{T}_{\text{radiometer}}}.}$$ (12)

TABLE I.

RF exposure parameters employed during radiometry experiments.

Exposure #	1	2	3	4	5	6	7
Average RF power (W)	4	4	8	8	13	16	15
RF duration (s)	123	119	60	35	31	19	57
Pause duration before the excitation (s)	n/a	342	377	217	180	223	138

3.D. MRI thermometry

MRI thermometry experiments were conducted on a 20 cm-long, 15 cm diameter cylindrical gel phantom placed in the transmit/receive head coil of a Philips Achieva 3 T scanner (Philips Healthcare, Cleveland, OH). The loopless antenna was inserted in the phantom to a depth of 10 cm. The antenna’s cable end was connected to the common port of a manual coaxial switch (CX210N, Diamond Antenna, San Marco, CA) with a slave port connected to a short to decouple the antenna during MRI excitation. The switch’s other slave port was connected to the Tomco RF power amplifier setup outside the scanner room to provide RF power at 110 MHz to induce local heating in the phantom. The applied power was monitored at the amplifier’s output with the power meter and the cable losses (=1.05 dB or 21.4%) measured with the network analyzer. MRI thermometry was interleaved with RF exposure with a ∼5 s latency delay for starting the MRI thermometry sequence after RF exposure ended.

A two-dimensional (2D) gradient-echo (GRE) sequence with repetition time/echo time (TR/TE) of 50/25 ms was used to acquire MRI thermometry data. The field-of-view (FOV) was set to 12 × 12 cm² with a 100 × 100 matrix size and a coronal slice-thickness of 1.2 mm (1 mm below the antenna). The scan duration was 5 s, repeated 60 times to generate a time-series dataset. The scanner’s reconstructed phase images were used to calculate the temperature using the proton (¹H) resonance frequency (PRF) shift method, unwrapping the phase using the smoothness property of temperature distributions to eliminate the singularities at multiples of 360°,³⁷

$${\displaystyle \mathrm{\Delta }{T}_i=\frac{{\varphi }_i-{\varphi }_0}{\gamma \alpha B_{0}TE}.}$$ (13)

Here, ΔT_i is the calculated temperature difference map, ϕ_i is the phase map at the ith time frame, ϕ₀ is the reference phase map, γ is the ¹H gyromagnetic ratio, and α (−0.01 ppm/°C) is the PRF change coefficient at B₀.

3.E. Determining the thermal conductivity of the gel

In the phantom in the absence of perfusion, the heat transfer equation^38,39 is

$${\displaystyle {\rho }_t{\mathit{C}}_t\frac{\partial T(r,t)}{\partial t}={\mathit{k}}_t{\nabla }^{2}T\left(r,t\right)+P_d(r,t),}$$ (14)

where ρ_t (kg/m³) is the gel density, C_t [(J/g)/K] is its thermal heat capacity, and k_t [(W/m)/K] is the thermal conductivity. The local RF heating from the loopless antenna dissipates radially away from the source. Therefore, the thermal conductivity of the gel surrounding the loopless antenna can be calculated from the spatial properties of the temperature distribution during thermal washout as measured by MRI thermometry.⁴⁰

The thermal conductivity (k_t) of the gel was measured from 2D transverse MRI thermometry data acquired at the antenna’s cable-whip junction at 5, 10, 15, and 20 s following RF exposure. The temperature images were fitted with 2D Gaussian distributions whose full-width half-maximum (FWHM) values were squared and linearly fitted to obtain a slope, m, from which k_t was derived via⁴⁰

$${\displaystyle k_t=\frac{4m}{{\rho }_t{C}_t}.}$$ (15)

The measured k_t value was used for all numerical simulations of the temperature distribution around the loopless antenna.

3.F. Numerical computations

EM field simulations were performed using full-wave method-of-moments analysis in FEKO software (FEKO, Inc., Stellenbosch, South Africa). The loopless antenna was modeled the same as the experimental 2.2 mm diameter cable with 39 mm resonant whip at 128 MHz. The model antenna was inserted 10 cm into a uniform cylinder with σ = 0.6 S/m and ε = 80, consistent with the phantom studies. A unit current source was placed at the distal end of the cable which was excited at 110 and 128 MHz.^25,27 The E-field distribution was computed on the coronal antenna plane at a 100 μm in-plane resolution. The power sensitivity (P_d) distribution was computed at each point using

$${\displaystyle {\mathit{P}}_d\left(r\right)=\frac{\sigma \left[E_X^2\left(r\right)+E_Y^2\left(r\right)+E_Z^2\left(r\right)\right]}{2{\rho }_t},}$$ (16)

where E_X, E_Y, and E_Z are the Cartesian E-field components. The P_d distribution of the loopless antenna is circularly symmetric about the antenna’s long axis. The three-dimensional (3D) P_d map was therefore calculated by rotating the 2D P_d distribution about the antenna axis and regridding the result to a Cartesian coordinate system. The voxel size along the z-axis was downsampled to 400 μm (voxel size: 0.1 × 0.1 × 0.4 mm³). The FOV of the 3D matrix centered at the antenna was cropped to 5 × 5 × 20 cm³ (matrix size: 501 × 501 × 501) to reduce the computation time.

The theoretical ΔT distribution inside the gel phantom at various RF exposures (accounting for RF power losses) was computed by solving Eq. (14).³⁸ The gel parameters ρ_t, C_t, and k_t were assumed to be spatially and temporally uniform inside the phantom and constant over the temperature range studied. The gel’s density (ρ_t = 1000 kg/m³) and heat capacity [C_t = 4.18 (J/g)/K] were assumed to be the same as water, with the k_t as measured above (Sec. 3.E). Ignoring the presence of the antenna, Eq. (14) was solved in the spatial frequency domain using⁴¹

$${\displaystyle T^{*}\left(v,t\right)=T_{\text{init}}^{*}\left(v,t\right)e^{-\frac{4{\pi }^2{\nu }^2{k}_{t}t}{{\rho }_t{C}_t}}+\frac{P_d^{*}\left(v\right)}{4{\pi }^2{\nu }^2{k}_t}\left(1-e^{-\frac{4{\pi }^2{\nu }^2{k}_{t}t}{{\rho }_t{C}_t}}\right),}$$ (17)

where the asterisk denotes a FT operation, ν denotes the coordinates in the spatial frequency domain, and the initial temperature distribution, T_init, was set to zero. Taking the inverse FT of Eq. (17) yielded the ΔT distribution inside the phantom. The temperature distribution following RF exposure was calculated at 5 s intervals for a 5-min cool-down period.

Three sets of temperature distributions were numerically computed for (a) RF exposure parameters used in the MRI thermometry experiment, (b) RF exposure parameters used in the radiometry experiments (Table I), and (c) a fixed 100 s RF exposure of 4–16 W (average), wherein the thermal conductivity of the medium was varied from 0.15 to 0.5 (W/m)/K to mimic the human physiological range.⁴² Because the RF heating was applied at 110 MHz and the radiometer operated at 128 MHz, the ΔT distribution (ΔT₁₁₀) was calculated from the P_d distribution of the loopless antenna at 110 MHz, and the radiometric ΔT(ΔT_radio) was calculated from the P_d distribution at 128 MHz ($P_d^{128}$),

$${\displaystyle \mathrm{\Delta }{T}_{\text{radio}}=\frac{{\int }_V\mathrm{\Delta }{T}_{110}\left(r\right)P_d^{128}\left(r\right)dr}{{\int }_V{P}_d^{128}\left(r\right)dr}.}$$ (18)

Theoretical H-factors were calculated using

$${\displaystyle H\left(r\right)=\frac{\mathrm{\Delta }{T}_{110}\left(r\right)}{\mathrm{\Delta }{T}_{\text{radio}}}}$$ (19)

to compare with the experimental values. The numerically calculated H-factor map has a voxel size of 0.1 × 0.1 × 0.4 mm³ corresponding to 4 μg of gel. This was spatially averaged to increase the mass of each voxel to 4.1 mg (1.6 × 1.6 × 1.6 mm³) to match the assumed sensitive volume of the fiber-optic temperature sensors which was based on their size. The peak 1 g-averaged H-factor (a regulatory metric) was calculated by averaging the values in a 1 × 1 × 1 cm³ cube centered at the whip 2 mm away from the junction.

4. RESULTS

4.A. Hardware

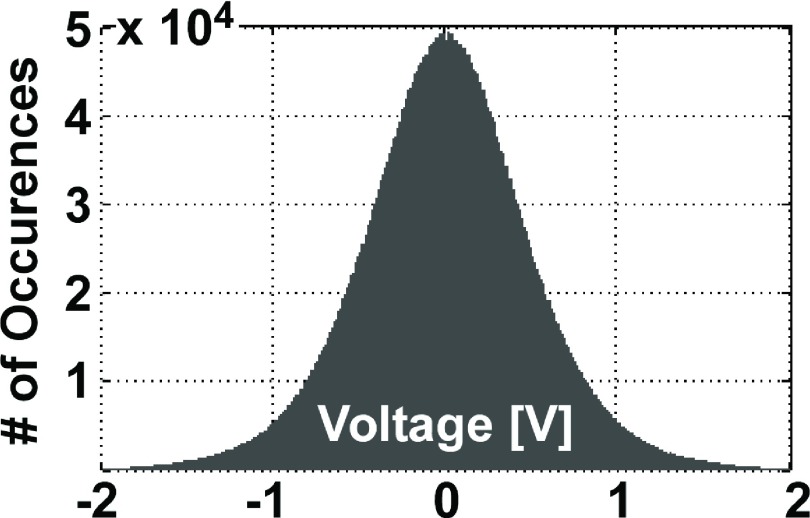
The 100–160 MHz frequency range is cluttered, which necessitated isolation of the radiometry measurements and the first LNA stage inside the RF-shielded room, analogous to the situation with MRI. The main board and the rest of the receiver electronics were located outside the screened room to avoid feedback. The NF and gain for the system measured at the output of the second LNA stage were 0.40 and 56 dB, respectively. The overall gain of the receiver was 105–110 dB. The available noise power (P_n) at 37 °C for a bandwidth of 410 KHz at 128 MHz numerically computed from Eq. (1) for the model antenna was −117.8 dBm. A histogram of a 0.5 s-long signal acquisition (10⁶ samples) is plotted in Fig. 5 and shows that the noise distribution is Gaussian, with a negligible mean value (−18 mV).

FIG. 5.

Histogram of the received samples over a 0.5 s period. The distribution is Gaussian.

4.B. Calibration with a uniform temperature distribution

The raw radiometer readings were linearly proportional to the temperature measured at the sensor located at the cable-whip junction of the loopless antenna in the thermally equilibrated gel phantom, at least up to 73 °C. The radiometer was calibrated at two different temperatures of 38 °C and 73 °C. The standard deviation (SD) of the radiometric temperature readings was ±0.24 °C sampled at two measurements/second. The calibration factors ψ and β were dependent on the radiometer gain and/or load impedance.

Initially, we encountered a problem with temporal variations in the receiver gain, which necessitated rescaling the calibration based on the noise power from the 50 Ω termination (see Figs. 3 and 4). The SD of the absolute error during a 5 h experiment increased from ±0.3 °C to ±1 °C. However, with improvements to the RF chain including better cables and baluns, gain variations were reduced to ±0.3 °C with, and ±0.4 °C without, the 50 Ω calibration rescaling over a 90 min run. Nevertheless, all reported radiometric temperature readings were cross-calibrated against the 50 Ω load. Future improvements in power supply regulation could further improve accuracy.

The temperature of the gel inside the phantom was increased uniformly to 73 °C by circulating hot water around the phantom and the radiometer signal acquired continuously. After two-point calibration, the radiometric temperature precisely tracked the temperature sensor over the entire course of the experiment (Fig. 6).

FIG. 6.

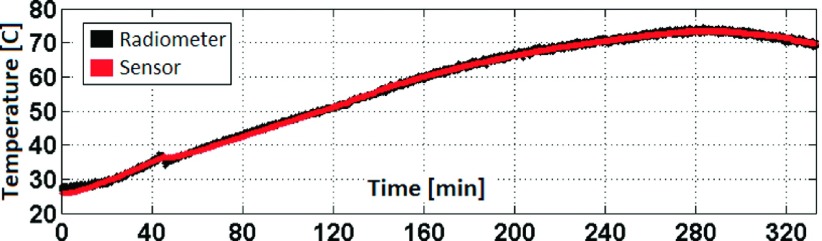
The linearly calibrated radiometric temperature tracks the sensor values during a uniform heating experiment. The accuracy of the radiometric measurement is ±0.24 °C.

4.C. Measuring the thermal conductivity of the gel

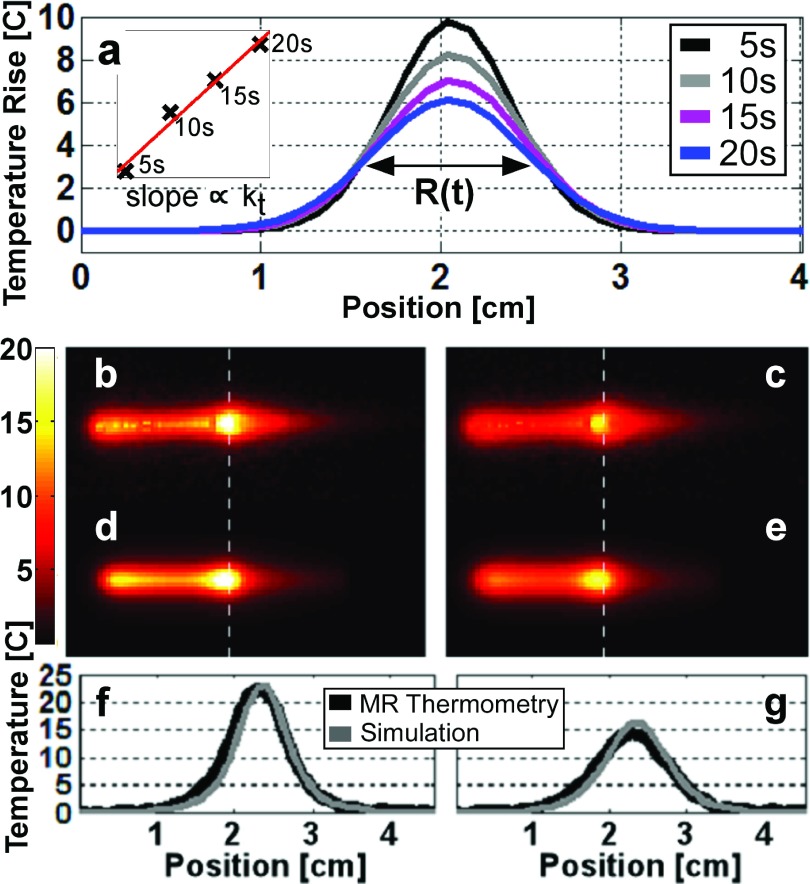
The Gaussian-fitted temperature profiles through the junction of the loopless antenna obtained from 2D MRI thermometry are shown during cool down in Fig. 7(a). A linear plot of the square of the FWHMs of the Gaussian curves [inset, top-left, Fig. 7(a)] yields k_t = 0.16 (W/m)/K for the gel, from Eq. (15).

FIG. 7.

(a) Gaussian fits to the MRI thermometry data during a 5–20 s cool-down period. The FWHMs of the Gaussian fits are squared and marked with symbol “x” on the inset (upper left) and fitted using the line plotted in red. The slope of the line is proportional to the thermal conductivity (k_t) of the gel medium. Parts (b) and (c) show the temperature rise distributions measured by MRI thermometry 5 and 20 s after the end of the RF exposure, respectively. Parts (d) and (e) show the numerically computed temperature rise at the same intervals. Parts (f) and (g) show computed (gray) and MRI thermometry (black) temperature profiles across the dashed white lines in (b)–(e). The computed and measured peak temperatures agree within 13% of each other.

4.D. MR thermometry and numerically computed temperature rise (ΔT)

The sensitivity of ΔT measured by 2D coronal MRI thermometry was ±0.25 °C. The MRI temperature distributions at 5 and 20 s following a 40 s-long 16.5 W RF exposure are shown in Figs. 7(b) and 7(c), respectively. The temperature distributions computed numerically assuming identical RF exposure conditions are shown in Figs. 7(d) and 7(e). The temperature profiles along the white dashed lines in the images are plotted below in Figs. 7(f) and 7(g) at the two times. The difference between the measured and computed peak temperatures is <13%. The FWHM of the measured and computed temperature profiles also agree within 13% of each other. These results suggest that numerical computations can adequately predict the spatial distribution of ΔT around a loopless antenna in a gel phantom. As expected, heating primarily occurs along the whip, peaking at the cable-whip junction, and decreasing along the cable.

4.E. Measuring peak temperature at the loopless antenna

Radiometric and fiber-optic temperature readings recorded at the junction during the radiometry experiment with local heating are shown in Fig. 8(a). The radiometric temperature follows the sensors closely. The computed and radiometric ΔTs are compared in Fig. 8(b). Again, the numerical computations track the measurements closely. The computed radiometric temperature predicted the peak ΔT with an average absolute error of 6.6%. The 14% error in estimating the peak temperature rise following the 8th (final) RF exposure was due to an error in monitoring the average applied RF power during the exposure. Note also that the gel’s thermal properties may vary locally with repeated heating and cooling that could affect the correlation between the radiometric and computed temperature. Therefore, only the first two RF exposures were used for the purpose of comparing simulated H-factors.

FIG. 8.

(a) Radiometric (black) and measured temperature values from the nonuniform temperature radiometry experiment. (b) Fitted experimental and computed (black) radiometric temperature rise during the RF heating experiments. The average absolute error in the simulations is 6.6%.

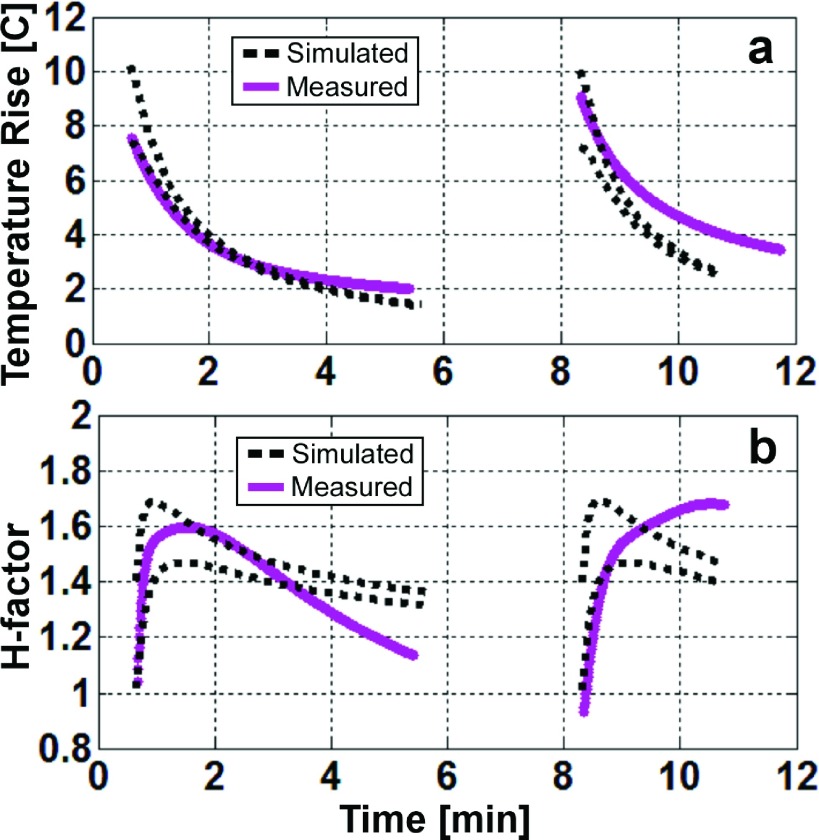
Computed and measured ΔT values for the 4.1 mg-average thermal sensor volume 1.5 mm from the cable-whip junction are plotted in Fig. 9 for the cool-down periods following the first two RF exposures. The radiometric temperatures were best-fitted to the biexponential curve with a rms error of ±0.47 °C. These curves were used for the H-factor calculations. In Fig. 9(b), the experimental H-factors (solid lines) are plotted against the minimum and maximum of the computed H-factors (dashed line). The measured absolute ΔT lies between the dashed lines immediately after the end of the RF exposure, but as time progresses, the measured ΔT deviates, decaying slower than the simulated ΔT. Similarly, the calculated H-factors match the measured H-factor at the beginning of the cool-down period but deviate as time progresses, reflecting thermal diffusion and possible changes in the local gel medium due to the extensive local heating.

FIG. 9.

(a) Minimum and maximum values of the simulated (black dashed lines) and experimental (continuous lines) temperature rise in a 1 × 1.2 mm² rectangle centered 1.5 mm away from the junction. (b) The H-factor inside the same region in dashed lines. Only the cool-down periods following the first two RF exposures are displayed.

4.F. Analyzing different medium parameters

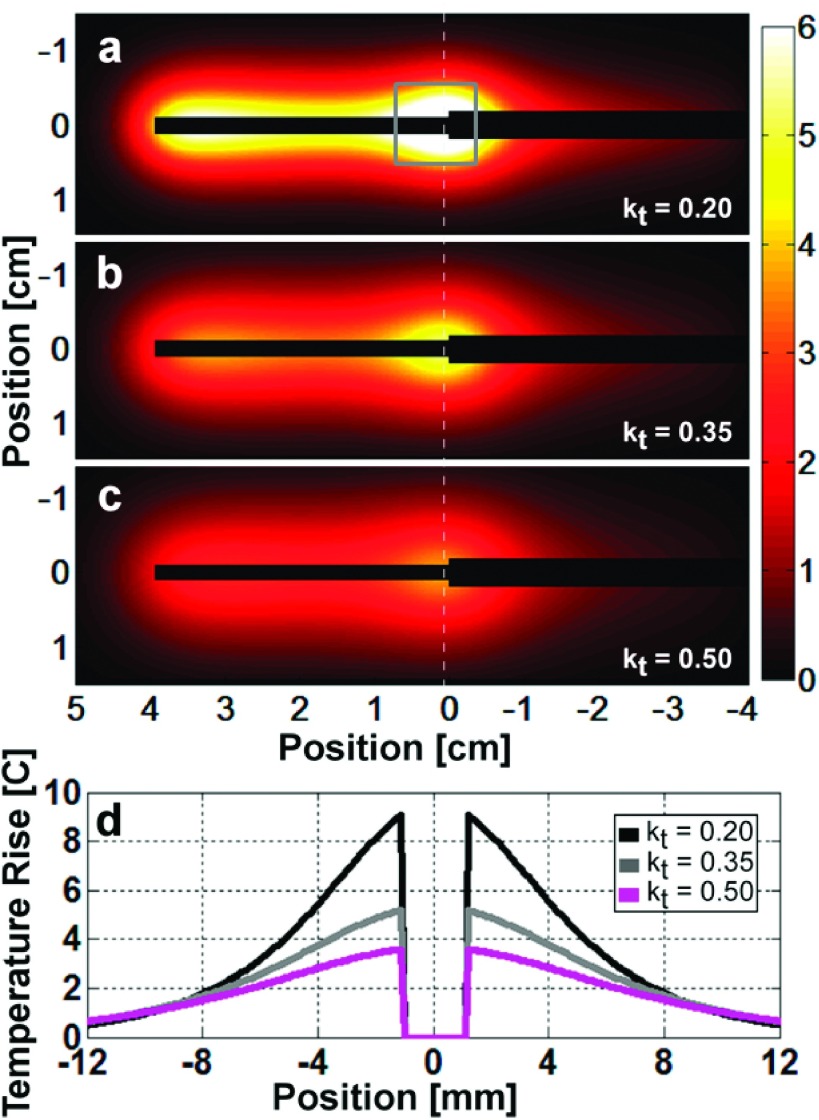
Figure 10 shows the theoretical 4.1 mg-averaged ΔT distribution calculated in the coronal plane intersecting the antenna after a 100 s-long 4 W RF exposure, for media with thermal conductivities of 0.20, 0.35, and 0.50 (W/m)/K. The profiles for ΔT along the vertical dashed line through the junction show that ΔT is highest for the medium with lowest k_t [Fig. 10(d)]. Thus, lowering the thermal conductivity tends to concentrate heating around the whip-cable junction, which is where the loopless antenna has its highest sensitivity. Consequently, the peak radiometric temperature readings are highest when thermal conductivity is low and lower in media with high thermal conductivity that can rapidly and uniformly disperse temperature differences.

FIG. 10.

Simulated 4.1 mg-averaged temperature rise 10 s after a 4 W 100 s-long RF exposure for thermal conductivity values of (a) 0.20, (b) 0.35, and (c) 0.50 (W/m)/K. (d) The temperature profiles along the white dashed lines show that as the thermal conductivity decreases, the peak temperature rise increases, and the distribution is more tightly confined about the junction. The gray annotated square in (a) represents the volume used to calculate the peak 1 g-averaged temperature rises and H-factors.

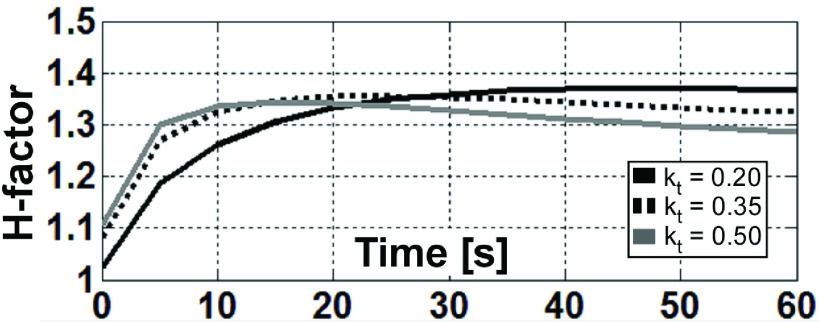
The numerically computed (spatial and temporal) peak radiometric ΔT and the peak 1 g- and 4.1 mg-averaged H-factors are listed in Table II. The peak 1 g-averaged ΔT is calculated by averaging the pixels inside the cube centered at the antenna plane as shown in Fig. 10(a). The mean computed peak 1 g-averaged H-factor for the thermal conductivity range simulated is 1.36, and the variation of individual numbers is less than 1.2%. Because the peak 1 g-averaged H-factor is robust to changes in the simulated physiological thermal conductivity range, the peak 1 g-averaged ΔT near an interventional loopless antenna can be reasonably estimated from the radiometry measurements, even though the thermal properties of the surrounding medium may not be exactly known. However, the peak 1 g-averaged H-factor is reached faster after RF exposure for media with higher thermal conductivity, while lower conductivity media retains a higher H-factor for a longer time (Fig. 11).

TABLE II.

Numerically computed peak radiometric temperature rise and peak 1 g- and 4.1 mg-averaged H-factors following a 100 s-long RF exposure in media with different physiologically relevant thermal conductivities.

Thermal conductivity[(W/m)/K]	RF power (W)	Peak radiometric ΔT (°C)	Peak 1 g-ave H-factor	Peak 4.1 mg-ave H-factor
0.15	4	6.99	1.37	2.69
0.20	4	5.86	1.37	2.59
0.25	4	5.09	1.36	2.51
0.30	4	4.53	1.36	2.45
0.30	8	9.06	1.36	2.45
0.30	16	18.11	1.36	2.45
0.35	4	4.09	1.36	2.40
0.40	4	3.74	1.35	2.36
0.45	4	3.46	1.35	2.33
0.50	4	3.21	1.34	2.30

FIG. 11.

The computed peak 1 g-averaged H-factor depends on the time duration after the end of the RF exposure and the thermal conductivity of the medium.

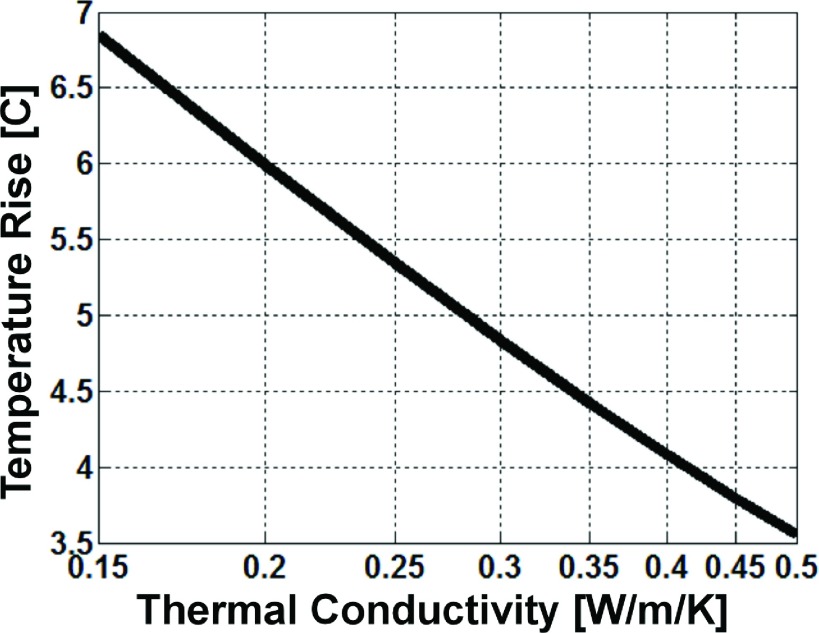
Reducing the averaging volume from 1 g to 4.1 mg in the calculations in order to match the experimental sampling volume to that of the thermal sensors increased the peak ΔT and H-factors due to the antenna’s highly concentrated thermal distribution around the whip-cable junction (Table II). The computed H-factors are independent of the average RF power level, while the ΔT values scale linearly with applied power. Finally, note that for a homogeneous medium, the radiometric ΔT is inversely proportional to the logarithm of the thermal conductivity (Fig. 12). This means that the thermal conductivity can be estimated solely by RF radiometry for a known RF (or thermal) exposure.

FIG. 12.

The numerically computed radiometric temperature rise following a 4 W 100 s-long RF exposure is inversely proportional to the logarithm of the medium’s thermal conductivity.

5. DISCUSSION

Here, we have developed a bench-top RF radiometer receiver that operates at the 3 T MRI scanner frequency of 128 MHz with a bandwidth of 410 kHz. When connected to an interventional MRI loopless antenna, the radiometer could directly measure and monitor the local temperature in the sensitive region of the antenna based on the amplitude of the RF noise detected between regular MRI scanning, thereby eliminating the need for any other thermometric devices. Moreover, due to the reciprocity principle, the loopless antenna radiometer is most sensitive to temperature in the region that heats the most: that near the cable-whip junction.¹⁷ It is indeed surprising that the peak 1 g average local temperature in the sample at the antenna is only 1.36 times the temperature measured by the radiometer from the entire antenna, as given by the peak H-factor introduced herein. This attests to the sensitivity of the radiometer for detecting local peak temperature changes associated with the presence of the antenna and provides a potential “self-monitoring” function that could be used for routine assessment of device safety. Note that because high SAR gradients can occur close to the conductor, the peak local antenna-associated heating is quite sensitive to the size chosen for the thermal sampling volume.²⁶ Reducing the sample size from 1 g to 4.1 mg to match the size of the fiber-optic sensors, for example, increased the peak H-factor to 2.7.

Importantly, the radiometer uses the existing internal MRI antenna and therefore requires no space either on the lead or the antenna for additional wires, cables, or transducers that would be required for conventional thermal sensors, other than what already exists. The radiometer is sensitive to the intrinsic thermal EM noise detected by the antenna at the MRI frequency, but does not require MRI, and is thus independent of the B₀, the applied RF field, the pulse sequence settings, etc. Nevertheless, the system’s electronics includes components that are common to those of a MRI receiver, and therefore, the radiometer could be integrated into a MRI scanner with potentially higher bandwidths. When calibrated in a thermally equilibrated homogeneous gel phantom whose electrical and thermal properties were analogous to tissue, the loopless antenna radiometer readings tracked linearly with temperature up to 73 °C with an accuracy within ±0.3 °C at two measurements/second (Fig. 6). Since the technology is based on radiometry whose noise power varies linearly with temperature [Eq. (1)], we expect this linear relationship to continue above 73 °C, which in our experiments was limited by the time to establish thermal equilibrium and the melting temperature of the gel, which was used to inhibit convection for measuring peak local heating around the antenna. The use of the Dicke switch with a 50 Ω reference load sufficed to control for gain variations but could conceivably be adjusted for other impedances.

Indeed, while sample resistance and temperature are independent parameters,^9,10 changes in the medium that alter the RF resistance of the antenna may in general affect the noise power and radiometric temperature if the sample resistance is assumed constant. As shown in Sec. 2.B, this can be overcome by matching the antenna load to a fixed impedance which can be done automatically.^11,43,44 Matching also maintains constant, the operating characteristics of the receiver chain. Alternatively, changes in the medium could be accommodated by extending the thermal calibration as a function of the RF load resistance, which can be quickly measured during MRI. In our studies, we used saline whose RF electrical characteristics approximate the average of those of biological tissue.³⁵ For intravascular applications^25,32 wherein the device is always in blood, the load is constant inasmuch as its thermal sensitivity is highly localized about the antenna junction.

The numerical simulations closely matched the MRI thermometry and radiometry experiments following the first two RF exposures. Results after subsequent exposures tended to deviate from the experimental results due to sensor localization errors and possibly changes in the thermal properties of the heated medium. In addition, computations assumed a uniform medium that did not account for the thermal conductivity of the loopless antenna itself. The accuracy of the thermal computations during cool down could thus be improved by modeling the antenna’s presence inside the medium and solving the bioheat equation via finite-difference time-domain (FDTD) based methods.^45,46

The electrical properties of the medium and tissue heterogeneity may also affect the spatial distribution of the noise power and sensitivity profile of the radiometer. Initial computations of the effect on thermal radiometry measurements of a heterogeneous RF impedance produced by extravascular muscle (with σ = 0.72 S/m and ε = 63)⁴² on an antenna placed in a blood vessel (σ = 1.25 S/m and ε = 73) suggest that within about 1 cm of the probe, the antenna’s resistance would change by <0.5%. This would affect radiometric temperature measurements by <2°, assuming the resistance change was not redressed by retuning or the resistance-based calibration noted above, which is advised. Only variations in electrical properties that occur near the cable-whip junction can have much effect.

Radiometric measurements appear less sensitive to heterogeneity in thermal conductivity, as evidenced by the peak 1 g-averaged H-factor at 128 MHz varying <1.2% over the threefold range of k_t parameters for human biological tissue⁴² (Table II). Thus, heterogeneity in thermal conductivity should not be problematic for estimating power in interventional applications with the antenna radiometer. For example, if the Food and Drug Administration (FDA) local peak exposure guideline of 8 W/kg over 5 min in any 1 g tissue during MRI (Ref. 47) was assumed for the loopless antenna in the absence of thermal perfusion or conduction, the 8 W/kg exposure would result in a ΔT of 0.6 °C in 5 min. Temperature measured by the antenna radiometer could thus aid regulatory compliance with respect to either peak local SAR or peak ΔT during an interventional procedure.

Since the 1-g peak H-factor is 1.36 and the temperature detection sensitivity in a uniform phantom is better than ±0.3 °C, the peak 1 g-averaged temperature can be determined to within ±0.41 °C at 2 Hz with the apparatus described. The radiometer’s sensitivity could be improved by increasing the receiver bandwidth and/or signal averaging, albeit at the expense of slower temperature measurements. Note also that because the radiometer readings effectively interrogate a larger volume of sensitivity, they can conceivably report peak temperatures that might otherwise be missed by the misplacement or movement of temperature sensors that have more highly localized temperature sensitivity. This may be advantageous for interventional applications.

The thermal washout rate is correlated with the thermal conductivity and perfusion rate in the surrounding medium.^40,48,49 Perfusion and k_t might be useful factors for distinguishing tumor from normal tissue or the stage of a tumor.^49,50 Tumor perfusion and k_t tend to increase in more advanced stages and decline with tumor necrosis.⁵⁰ Given that the radiometric temperature is inversely proportional to the logarithm of the thermal conductivity of a homogeneous medium (Fig. 12), it might be possible to use local RF radiometry measurements to estimate the k_t in tumors that surrounded the detector’s sensitive volume.

In conclusion, the intent of the present work was to demonstrate a proof-of-concept of deploying an internal imaging MRI antenna for the purpose of providing localized thermal measurements based on the principles of RF radiometry, thus augmenting its imaging capabilities with a potentially useful MRI-independent method of measuring and monitoring peak local temperature. This may not only improve the safe use of these devices during MRI but also aid the thermal monitoring of therapies such as ablation of tumors and other pathologies,^51,52 without the artifacts that can accompany MRI thermometry. Indeed, the radiometer could be used as an internal reference for MRI thermometry measurements.