A likelihood-based approach for computing the operating characteristics of the 3+3 phase I clinical trial design with extensions to other A+B designs

Abstract

Background

In phase I clinical trials, the ‘3+3’ algorithmic design has been unparalleled in its popularity. The statistical properties of the ‘3+3’ design have been studied in the literature either in comparison with other methods or by deriving exact formulae of statistical quantities. However, there is still much to be known about its capabilities of describing and accounting for uncertainties in the observed data.

Purpose

The objective of this study is to provide a probabilistic support for analyzing the heuristic performance of the ‘3+3’ design. The operating characteristics of the algorithm are computed under different hypotheses, levels of evidence, and true (or best guessed) toxicity rates. The dose-finding rules are further compared with those generated by the modified toxicity probability interval (mTPI) design, and generalized for implementation in all ‘A+B’ designs.

Methods

Our likelihood method is based on the evidential paradigm. Two hypotheses are chosen to correspond to two hypothesized dose limiting toxicity (DLT) rates, e.g., H₁ - unsafe vs. H₂ - acceptable. Given observed toxicities per dose, the likelihood-ratio is calculated and compared to a certain k threshold (level of evidence). Under various true toxicities, the probabilities of weak evidence, favoring H₁, and favoring H₂ were computed under four sets of hypotheses and several k thresholds.

Results

For scenarios where the midpoint of the two hypothesized DLT rates is around 0.30, and for a threshold of k = 2, the ‘3+3’ design has a reduced probability (≈0.50) of identifying unsafe doses, but high chances of identifying acceptable doses. For more extreme scenarios targeting a relatively high or relatively low DLT rate, the ‘3+3’ design has no probabilistic support, and therefore it should not be used. In our comparisons, the likelihood method is in agreement with the mTPI design for the majority of hypothesized scenarios. Even so, based on the evidential paradigm, a ‘3+3’ design is often incapable of providing sufficient levels of evidence of acceptability for doses under reasonable scenarios.

Limitations

Given the small sample size per dose, the levels of evidence are limited in their ability to provide strong evidence favoring either of the hypotheses.

Conclusions

In many situations, the ‘3+3’ design does not treat enough patients per dose to have confidence in correct dose selection, and the safety of the selected/unselected doses. This likelihood method allows consistent inferences to be made at each dose level, and evidence to be quantified regardless of cohort size. The approach can be used in phase I studies for identifying acceptably safe doses, but also for defining stopping rules in other types of dose-finding designs.

Introduction

In oncology and other life threatening diseases, dose-finding studies most often aim to identify the maximum tolerated dose (MTD), defined as a dose whose probability of toxicity is closest to some acceptable, prespecified target, also known as the dose limiting toxicity (DLT) rate.

Despite considerable efforts to encourage the use of model-based dose-finding designs, such as variants of the Continual Reassessment Method (CRM)^1-6 and Escalation with Overdose Control (EWOC),^7,8 the most common approach for dose-finding remains an ‘Up-and-Down’ algorithm. These methods assign patients sequentially based on prespecified decision rules; they are easy to implement, with no pre-specification of the underlying dose-toxicity model. There are a multitude of ad-hoc ‘Up-and-Down’ methods, with the majority falling within the range of ‘A+B’ designs.^9,10

The ‘A+B’ designs assign patients to dose levels according to prespecified criteria based on observations of target events (e.g., the DLT). Typically, the largest dose that produces a DLT in a limited proportion of patients is considered the MTD. At first, patients are enrolled in a cohort of size A receiving the same initial dose. Consider n_A the number of DLTs in cohort A. If n_A ≤ a_E patients (‘E’- escalate), the next cohort will be assigned to the next highest dose. If n_A ≥ a_T patients (‘T’- terminate), the trial is stopped with MTD declared as the dose below the current assignment.

If a_E <n_A <a_T (a_T −a_E ≥ 2), an additional cohort B is enrolled at the same dose. Consider n_B the number of DLTs in cohort B. If n_B ≤ b_E patients, the next cohort will be assigned to the next highest dose. If n_B ≥ b_T patients, the trial is stopped with MTD declared as the dose below the current assignment. The most famous ‘A+B’ design is known as ‘3+3’ where A = 3, B = 3, a_E = b_E = 0, a_T = 2, and b_T = 1.

The ‘3+3’ popularity is due mainly to its practical simplicity, with no required computer-generated operating characteristics.¹¹ However, important limitations have been raised over time; among these the algorithm's short memory (i.e., decision rules are based on outcomes from the most recent cohort) and slow dose escalation, leading to excessive treatment at dose levels less likely to be efficacious.^1,3,11 Reiner et al.¹² concluded that this design has high error rates and frequently leads to incorrect decisions. Relying more on empirical reasoning than mathematical modeling, the ‘3+3’ has limited capabilities of describing and accounting for uncertainties in the observed data. Still, despite the noted limitations, 98% of the dose-finding cancer trials conducted between 1991 and 2006 implemented variations of the ‘3+3’ algorithm.¹³

The statistical properties of the ‘3+3’ design have been studied in the literature, either in comparison with other methods or by deriving exact formulae for specific statistical quantities.¹¹ The objective of this study is not to encourage the use of algorithmic designs, but to provide a probabilistic support for analyzing their heuristic performance. Intended for any ‘A+B’ design, our likelihood-based method can be used to compute the operating characteristics and compare the design behavior under different hypotheses, levels of evidence, and true (or best guessed) toxicity rates. Such information could be used to determine whether the statistical properties of the ‘3+3’ or another algorithmic design support trial implementation. The method is based on the evidential paradigm that uses observed data to compute the likelihood-ratio (LR) and then classify the level of evidence as: 1) weak evidence or 2) strong evidence in favor of one of the proposed hypotheses (denoted here as H₁ and H₂). We illustrate the implementation of our evidential approach to the specific case of the ‘3+3’ and the modified toxicity probability interval (mTPI) designs,¹⁴ and suggest possible applications in other types of dose-finding designs.

The evidential paradigm

The concept of Likelihoodism was first introduced by Hacking in 1965 by stating the formal expression of the Law of Likelihood¹⁵ and using the likelihood-ratio (LR) for comparing two simple hypotheses, such as H₁ : θ = θ₁ and H₂ :θ = θ₂ for a parameter θ, under the assumption that a background model is true. The evidential paradigm provides the LR of the two hypotheses, LR = L(θ₂; x) / L(θ₁; x), as an objective measure of the strength of evidence. Strong evidence supporting θ₂ over θ₁ exists if for a large k, LR ≥ k. Similarly, strong evidence supporting θ₁ over θ₂ exists if LR ≤ 1/ k. Weak evidence occurs when 1/ k < LR < k, with no strong support for either hypothesis.

Error probabilities in the evidential paradigm

Misleading evidence is defined as strong evidence in favor of the incorrect hypothesis. Given two simple hypotheses and x = (x₁, x₂,…, x_n) i.i.d. observations, the probabilities of observing misleading evidence can be calculated as follows:

$$\begin{array}{c}{M}_1(n,k)=P_1(\frac{L({\theta }_2;\mathbf{x})}{L({\theta }_1;\mathbf{x})}\ge k|H_1\text{true})\\ M_2(n,k)=P_2(\frac{L({\theta }_2;\mathbf{x})}{L({\theta }_1;\mathbf{x})}\le \frac{1}{k}|H_2\text{true}),\text{for fixed}k.\end{array}$$

Following the definition above, M₁(n, k) represents the evidential analog to a type I error. It has been shown that for any fixed sample size n and any pair of hypotheses, the probability of misleading evidence satisfies the universal bound and cannot exceed 1/ k, regardless of the number of interim looks (with a similar bound under H₂).^{16, 17}

The probability of observing weak evidence is defined as the probability that an experiment will not produce strong evidence for either hypothesis, calculated under each true hypothesis:

$$\begin{array}{c}{W}_1(n,k)=P_1(\frac{1}{k}<\frac{L({\theta }_2;\mathbf{x})}{L({\theta }_1;\mathbf{x})}<k|H_1\text{true})\\ W_2(n,k)=P_2(\frac{1}{k}<\frac{L({\theta }_2;\mathbf{x})}{L({\theta }_1;\mathbf{x})}<k|H_2\text{true}),\text{for fixed}k.\end{array}$$

In the context of experimental design, Blume¹⁸ shows that both probabilities of misleading and weak evidence converge to zero as the sample size increases.

Choice of k

Royall and Blume^16,18 proposed benchmarks of 8 and 32, representing “weak” (1 < LR < 8), “fairly strong” (8 < LR < 32), and “strong” (LR > 32) levels of evidence, derived to provide levels of evidence similar to type I and II error rates of 0.05 and 0.20, respectively, in the phase III context. Phase I trials do not require such strict error control, and the limited sample sizes will seldom generate likelihood-ratios larger than 8 (or less than 1/8), suggesting that the proposed benchmark of 8 may be setting too high a bar for early studies. Figure 1 shows the relationship between levels of k and significance levels (based on a frequentist approach). Because the probability of misleading evidence is bounded by $\mathrm{\Phi }(-\sqrt{2log\left(k\right)})$ regardless of the choice of sample size,^{17, 18} the relationship between values of k and type I/II error can be determined by equating the probability of misleading evidence to rejecting the null when it is true (or, similarly, the probability of failing to reject the null when it is false). Based on this figure, it seems sensible to propose that k = 4 would provide adequate evidence in a phase I trial (which is on par with one-sided alpha level of 0.05). Even k = 2 would be considered a reasonable level of evidence in this phase of research, which is consistent with a one-sided alpha of 0.12. Attempting to achieve k = 8 is similar to setting the one-sided alpha level to 0.02, considerably more stringent than one would see even in a phase II study.

Figure 1.

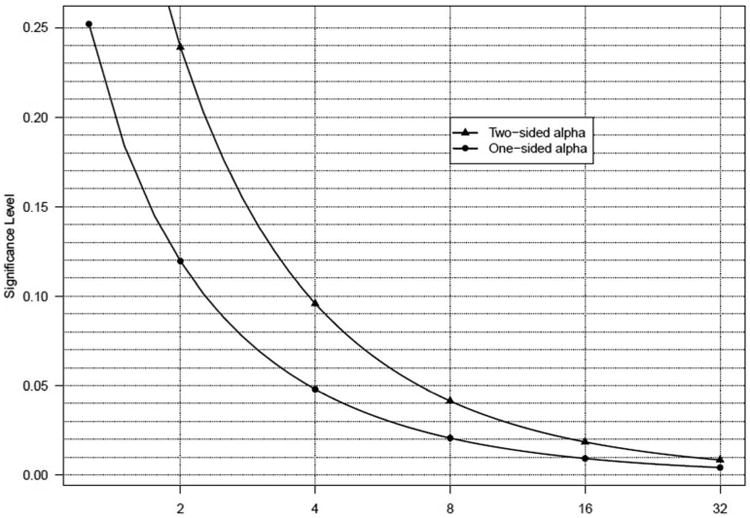
Illustration of the relationship between k thresholds (evidential paradigm) and significance (alpha) levels (frequentist approach).

Methods

The likelihood method can be used either in the preparatory phase of the trial for determining whether or not the ‘3+3’ can provide a dose with an acceptable DLT rate, or after completion, for evaluating the operating characteristics at each dose level. As shown later, it can also provide guiding principles for ascertaining toxicity of a dose when the cohort size is beyond the standard number of 3 or 6 patients used by the ‘3+3’ algorithm, and thus be extended to any ‘A+B’ design.

In our proposed method, all the statistical properties are calculated per each dose level, based on observed toxicities. Let d_j, j = 1, 2, …, D, be the set of ordered dose levels, and y_j be the corresponding number of observed toxicities at the j^th dose. Let n_j be the number of patients per dose and P(DLT | dose = d_j) = p_j be the true probability of DLT.

Consider the following where P(DLT | dose = d_j) = p₁ and P(DLT | dose = d_j) = p₂ are the two hypothesized DLT rates at dose d _j:

$$\begin{array}{c}{H}_1^j:p_j=p_1(\text{unsafe dose})\\ H_2^j:p_j=p_2(\text{acceptable dose})\end{array}$$

For a choice of p₁ and p₂ established a priori, we calculate the likelihood-ratio (LR) for each dose:

$${\mathit{\text{LR}}}_j={\left(\frac{p_2}{p_1}\right)}^{y_j}{\left(\frac{1-p_2}{1-p_1}\right)}^{n_j-y_j},j=1,2,\dots ,D.$$

For a certain benchmark k, the strength of evidence is quantified and interpreted as follows:

1. Weak evidence (supporting neither hypothesis), if $\frac{1}{k}<{\mathit{\text{LR}}}_j<k$

2. Evidence in favor of H₂, if LR_j ≥ k (acceptable dose)

3. Evidence in favor of H₁, if ${\mathit{\text{LR}}}_j\le \frac{1}{k}$ (unsafe dose)

As mentioned previously, small cohorts per dose (e.g., 6 patients for ‘3+3’) can produce only relatively modest likelihood-ratios, and thus, selecting a k > 4 is not feasible.

In the results section, we illustrate the likelihood methodology presented above for the ‘3+3’ algorithm and the mTPI approach.¹⁴ Implemented in a Bayesian framework, the mTPI design uses posterior probabilities to establish the dose-escalation rules based on three dosing intervals: ‘underdosing’ – escalate to next dose, ‘proper dosing’ – stay at the same dose, and ‘overdosing’ – de-escalate the dose. Even though the mTPI is a model-based design, the dose-finding rules can be summarized in an algorithmic fashion suitable for implementing our likelihood method. Since the mTPI has been proven to be superior to the ‘3+3’ (fewer patients treated above the true MTD, higher probabilities of identifying the true MTD), a comparison between the two would only emphasize the utility and generalizability of our likelihood approach.

Operating characteristics: simulation set-up

Via simulation study, we calculated the operating characteristics of the ‘3+3’design using the proposed likelihood method. For each dose, H₁(p₁) specifies a DLT rate that is too high (unsafe), and H₂ (p₂) specifies an acceptable DLT rate. Data were simulated under a wide range of true DLT rates (from 0.05 to 0.70) with the following performance characteristics considered:

• Probability of weak evidence

• Probability of favoring H₁

• Probability of favoring H₂

These probabilities were compared to the probabilities of escalation and non-escalation based on the algorithmic rules. For any dose d_j, let y_j1 be the count of DLTs in the first cohort of 3 patients, and let y_j2 be the count of DLTs in the second cohort of 3 patients. Then, y_j1 and y_j2 are independent binomial random variables, with n_j =3 and P(DLT | dose = d_j) = p_j, j = 1, 2, …, D. Thus, for any given p_j, the following probabilities hold true:

$$\begin{gathered} P(\mathit{\text{escalation}}|d_j)=P((y_{j1}=0)\cup (y_{j1}=1,y_{j2}=0)) \\ =P(y_{j1}=0)+P(y_{j1}=1)·P(y_{j2}=0) \\ ={(1-p_j)}^3+3p_j{(1-p_j)}^5 \end{gathered}$$

$$P(\mathit{\text{non-escalation}}|d_j)=1-P(\mathit{\text{escalation}}|d_j).$$

Note that this does not consider the expansion to six patients if zero patients has a DLT in the first three patients. The simulation results (shown in figures) are presented for benchmarks of k = 2 and 4 that displayed the most distinctive behavior for classifying levels of evidence. All simulation scenarios were conducted with 10,000 trials each using the statistical software R.¹⁹

Numerous hypotheses (p₁, p₂) were tested and compared in terms of operating characteristics; four of the most interesting and relevant sets of hypotheses are presented here. In scenarios (A) (p₁ = 0.40, p₂ = 0.15) and (B) (p₁ = 0.30, p₂ = 0.05), the midpoint of the two hypotheses is close to 0.27 and 0.17, respectively, which is consistent with the true DLT target rate of the ‘3+3’ design.

Scenarios: (C)(p₁ = 0.15, p₂ = 0.05) and (D)(p₁ = 0.50, p₂ = 0.30) were selected to demonstrate the poor behavior of the ‘3+3’ design in selecting the MTD when both hypotheses are either below or above a DLT rate of 0.20. These scenarios can be very well encountered in practice. For agents where lethal or life threatening toxicities are expected (e.g., cytotoxic agents), investigators might be only willing to accept relatively low DLT rates. Contrarily, the target DLT probability can be set high when toxicities are transient and nonfatal. This may be the case for biologic agents used in immunotherapy, such as vaccines or adoptive cell therapy, where a higher DLT rate (greater than 0.25-0.30) for certain adverse events might be considered tolerable.

The dose-finding rules for the mTPI were established using a target toxicity probability p_T equal to the midpoint of each set of hypotheses with the associated equivalence interval (EI) (p_T − ε₁, p_T + ε₂). Since Ji et al.¹⁴ showed that the mTPI design is robust to the specification of ε values, our choices of ε₁ = ε₂ vary from 0.05 to 0.125, depending on the pair of hypotheses and the corresponding midpoint.

The operating characteristics described above were not computed for the mTPI design. Since the mTPI uses posterior probabilities to construct the dosing intervals (‘underdosing’, ‘proper dosing’, ‘overdosing’), it is rather difficult to find equivalents for the likelihood probabilities of favoring H₁, H₂ or neither (weak). Still, in the discussion section we have included a brief comparison of the two approaches based on the probability of selecting the true MTD.

Results

Levels of evidence

Tables 1 - 4 show the likelihood-ratios (LR) and the corresponding decisions regarding dose safety, in parallel with the decision rules generated under the ‘3+3’ algorithm and the mTPI design. For each dose one of the following decisions is made: “acceptable dose”, “toxic dose” or “weak evidence”. Out of several k values considered, we present the results for k = 1, 2, and 4 that mark a significant change in the level of evidence. Note that there is a row included for 0 DLTs in 6 patients; in practice, many ‘3+3’ designs require that 6 patients be treated at the MTD so that the definition of the MTD is highest dose at which 0 or 1 of 6 patients experiences a DLT. However, in other ‘3+3’ implementations, the highest dose with 0 DLTs in 3 patients is acceptable as an MTD definition.

Table 1. Likelihood-ratios and decision rules for ‘3+3’ and mTPI designs (per dose level) for scenario A.

			(A) H1: p=0.40 vs H2: p=0.15
DLT(n)a	‘3+3’ rule	mTPI ruleb	L(p2)/L(p1)	Evidencec
				k=1	k=2	k=4
0(3)	acceptable (E)	acceptable (E)	LR=2.84	acceptable	acceptable	weak
0(3)+0(3)	acceptable (E)	acceptable (E)	LR=8.08	acceptable	acceptable	acceptable
1(3)+0(3)	acceptable (E)	acceptable (S)	LR=2.14	acceptable	acceptable	weak
2(3)	toxic (D)	toxic (D)	LR=0.20	toxic	toxic	toxic
3(3)	toxic (D)	toxic (D)	LR=0.05	toxic	toxic	toxic
1(3)+1(3)	toxic (D)	acceptable (S)	LR=0.57	toxic	weak	weak
1(3)+2(3)	toxic (D)	toxic (D)	LR=0.15	toxic	toxic	toxic
1(3)+3(3)	toxic (D)	toxic (D)	LR=0.04	toxic	toxic	toxic

Abbreviations: D: de-escalation; S: stay at same dose; E: escalation;

^aDose limiting toxicities (cohort size)

^bmTPI: modified toxicity probability interval with p_T = 0.275 and ε₁= ε₂=0.125

^cAcceptable: LR ≥ k; Toxic: LR ≤ 1 / k; Weak evidence (favors neither hypothesis): 1 / k < LR < k

Table 4. Likelihood-ratios and decision rules for ‘3+3’ and mTPI designs (per dose level) for scenario D.

			(D) H1: p=0.50 vs H2: p=0.30
DLT(n)a	‘3+3’ rule	mTPI ruleb	L(p2)/L(p1)	Evidencec
				k=1	k=2	k=4
0(3)	acceptable (E)	acceptable (E)	LR=2.74	acceptable	acceptable	weak
0(3)+0(3)	acceptable (E)	acceptable (E)	LR=7.53	acceptable	acceptable	acceptable
1(3)+0(3)	acceptable (E)	acceptable (E)	LR=3.23	acceptable	acceptable	weak
2(3)	toxic (D)	toxic (D)	LR=0.50	toxic	toxic	weak
3(3)	toxic (D)	toxic (D)	LR=0.22	toxic	toxic	toxic
1(3)+1(3)	toxic (D)	acceptable (S)	LR=1.38	acceptable	weak	weak
1(3)+2(3)	toxic (D)	acceptable (S)	LR=0.59	toxic	weak	weak
1(3)+3(3)	toxic (D)	toxic (D)	LR=0.25	toxic	toxic	toxic

Abbreviations: D: de-escalation; S: stay at same dose; E: escalation;

^aDose limiting toxicities (cohort size)

^bmTPI: modified toxicity probability interval with p_T = 0.40 and ε₁= ε₂=0.10

^cAcceptable: LR ≥ k; Toxic: LR ≤ 1 / k; Weak evidence (favors neither hypothesis): 1 / k < LR < k

Table 1 illustrates scenario (A) (p₁ = 0.40, p₂ = 0.15). For k =1, the weak evidence category is eliminated, and the likelihood approach generates the same inferences as the ‘3+3’ algorithm. For k = 2, the only weak evidence conclusion follows 2 out of 6 DLTs. If we treat the weak category as insufficient to conclude toxicity and continue enrolling patients, then for this scenario, the likelihood inferences are in perfect agreement with the mTPI rules. Weak levels of evidence are common when 0 out of 3, 1 out of 6 and 2 out of 3 DLTs occur under k = 4. This highlights the fact that the ‘3+3’ design does not provide sufficient information for concluding that certain doses are toxic or acceptably safe. For example, 1 out of 6 DLTs is considered the MTD definition in most implementations of the ‘3+3’. Hence, when a dose is taken forward with 1 DLT in 6 patients, the LR is only 2.14, indicating a low evidence of acceptability.

Table 2 displays scenario (B)(p₁ = 0.30, p₂ = 0.05). Compared to (A), the frequency of weak evidence under k = 4 is smaller, suggesting a stronger level of evidence. However, under k = 4, a dose is only considered acceptable for 0 DLTs in 6 patients: all other conclusions lead to weak or toxic conclusions for the dose. Also, the 2 out of 6 DLTs category is concluded toxic by the likelihood approach and the ‘3+3’ algorithm, whereas the mTPI recommends staying at the same dose.

Table 2. Likelihood-ratios and decision rules for ‘3+3’ and mTPI designs (per dose level) for scenario B.

			(B) H1: p=0.30 vs H2: p=0.05
DLT(n)a	‘3+3’ rule	mTPI ruleb	L(p2)/L(p1)	Evidencec
				k=1	k=2	k=4
0(3)	acceptable (E)	acceptable (E)	LR=2.50	acceptable	acceptable	weak
0(3)+0(3)	acceptable (E)	acceptable (E)	LR=6.25	acceptable	acceptable	acceptable
1(3)+0(3)	acceptable (E)	acceptable (S)	LR=0.77	toxic	weak	weak
2(3)	toxic (D)	toxic (D)	LR=0.04	toxic	toxic	toxic
3(3)	toxic (D)	toxic (D)	LR=0.001	toxic	toxic	toxic
1(3)+1(3)	toxic (D)	acceptable (S)	LR=0.09	toxic	toxic	toxic
1(3)+2(3)	toxic (D)	toxic (D)	LR=0.01	toxic	toxic	toxic
1(3)+3(3)	toxic (D)	toxic (D)	LR=0.001	toxic	toxic	toxic

Abbreviations: D: de-escalation; S: stay at same dose; E: escalation;

^aDose limiting toxicities (cohort size)

^bmTPI: modified toxicity probability interval with p_T = 0.175 and ε₁= ε₂=0.125

^cAcceptable: LR ≥ k; Toxic: LR ≤ 1 / k; Weak evidence (favors neither hypothesis): 1 / k < LR < k

For the low toxicity scenario (C)(p₁ = 0.15, p₂ = 0.05), the likelihood method disagrees with the other two designs only for 1 out of 6 DLTs and k = 1 (Table 3). For k = 2 and 4, 1 out of 6 and 0 out of 3 DLTs are classified as weak evidence, instead of acceptable as in the case of ‘3+3’ and mTPI designs. In the high toxicity scenario (D) (p₁ = 0.50, p₂ = 0.30) a k = 2 generates likelihood decisions in good agreement with the mTPI rules. For k = 4, all categories are classified as weak evidence, except if 4 DLTs are observed in 6 patients (toxic), or 0 DLTs in 6 patients (acceptable) (Table 4). This high likelihood of weak evidence for scenario (D) suggests that the ‘3+3’ design is particularly poor when a high DLT rate (e.g., 30%) is considered acceptable, and that the cohort size is too small to allow for valid inferences.

Table 3. Likelihood-ratios and decision rules for ‘3+3’ and mTPI designs (per dose level) for scenario C.

			(C) H1: p=0.15 vs H2: p=0.05
DLT(n)a	‘3+3’ rule	mTPI ruleb	L(p2)/L(p1)	Evidencec
				k=1	k=2	k=4
0(3)	acceptable (E)	acceptable (E)	LR=1.40	acceptable	weak	weak
0(3)+0(3)	acceptable (E)	acceptable (E)	LR=1.95	acceptable	weak	weak
1(3)+0(3)	acceptable (E)	acceptable (S)	LR=0.58	toxic	weak	weak
2(3)	toxic (D)	toxic (D)	LR=0.12	toxic	toxic	toxic
3(3)	toxic (D)	toxic (D)	LR=0.04	toxic	toxic	toxic
1(3)+1(3)	toxic (D)	toxic (D)	LR=0.17	toxic	toxic	toxic
1(3)+2(3)	toxic (D)	toxic (D)	LR=0.05	toxic	toxic	toxic
1(3)+3(3)	toxic (D)	toxic (D)	LR=0.02	toxic	toxic	toxic

Abbreviations: D: de-escalation; S: stay at same dose; E: escalation;

^aDose limiting toxicities (cohort size)

^bmTPI: modified toxicity probability interval with p_T = 0.10 and ε₁= ε₂=0.05

^cAcceptable: LR ≥ k; Toxic: LR ≤ 1 / k; Weak evidence (favors neither hypothesis): 1 / k < LR < k

Operating characteristics

The operating characteristics of the likelihood method under k = 2 and k = 4 were further evaluated by computing the following probabilities over a range of true DLT rates: P(weak evidence supporting neither hypothesis), P(favors H₁), P(favors H₂), and comparing them to the operating characteristics of the ‘3+3’ design. In Figures 2 and 3, the solid lines mark the probabilities of favoring H₂ (black) and favoring H₁ (gray) generated by the likelihood method. Using the same coloristic, the dashed lines represent the analogous probabilities derived from the ‘3+3’ algorithm: probability of escalation (black) and probability of non-escalation (gray). The gray dotted line marks the level of weak evidence for the likelihood method.

Figure 2.

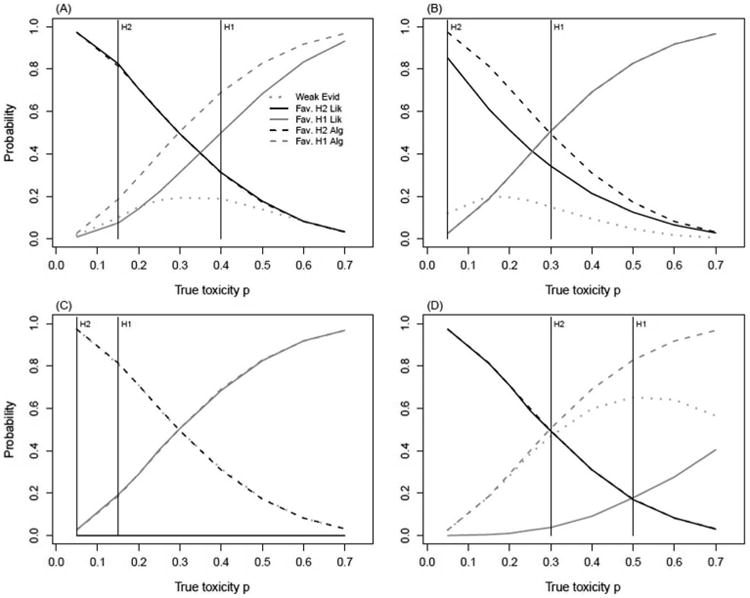
Comparison of operating characteristics computed via likelihood method and ‘3+3’ derived probabilities. Likelihood probabilities are calculated for k = 2, under hypotheses H₁(p₁) : unsafe dose; H₂(p₂) : acceptable dose.

Likelihood Method: Weak Evid: P(weak evidence | true DLT);

Fav. H2 Lik: P(favors H₂ | true DLT); Fav. H1 Lik: P(favors H₁ | true DLT).

Algorithm: Fav. H2 Alg: P(escalation | true DLT); Fav. H1 Alg: P(non-escalation | true DLT).

(A): p₁ = 0.40, p₂ = 0.15 (B): p₁ = 0.30, p₂ = 0.05

(C): p₁ = 0.15, p₂ = 0.05 (D): p₁ = 0.50, p₂ = 0.30

Figure 3.

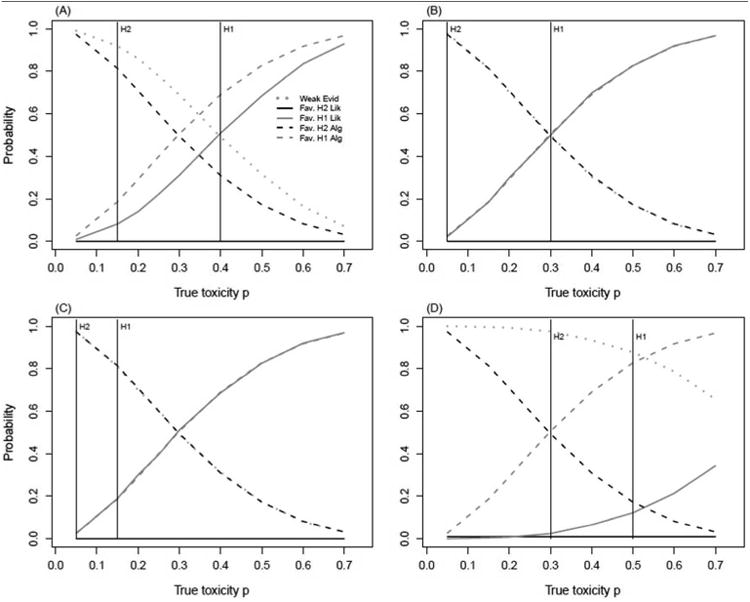
Comparison of operating characteristics computed via likelihood method and ‘3+3’derived probabilities. Likelihood probabilities are calculated for k = 4, under hypotheses H₁(p₁) : unsafe dose; H₂(p₂) : acceptable dose.

Likelihood Method: Weak Evid: P(weak evidence | true DLT);

Fav. H2 Lik: P(favors H₂ | true DLT); Fav. H1 Lik: P(favors H₁ | true DLT).

Algorithm: Fav. H2 Alg: P(escalation | true DLT); Fav. H1 Alg: P(non-escalation | true DLT).

(A): p₁ = 0.40, p₂ = 0.15 (B): p₁ = 0.30, p₂ = 0.05

(C): p₁ = 0.15, p₂ = 0.05 (D): p₁ = 0.50, p₂ = 0.30

For k = 2, the probability of weak evidence in scenarios (A) and (B) peaks at 0.19 between the two hypotheses for true toxicity values of 0.30 and 0.15, respectively (Figures 2A and 2B). In scenario (A), the likelihood method and the ‘3+3’ algorithm match in identifying an acceptable dose (favor H₂), whereas for scenario (B), the two methods identify an unsafe dose (favor H₁) with similar probabilities of over 0.50. Hypotheses (C)(p₁ = 0.15, p₂ = 0.05) produce a probability of weak evidence of 0.98 for k = 2 under a true DLT of 0.05 (Figure 2C). Surprisingly, this probability is almost the same as the probability of escalation from the ‘3+3’ design. For scenario (D) (p₁ = 0.50, p₂ = 0.30), the most notable difference in statistical properties regards the probability of correctly declaring the dose unsafe. For a true DLT rate of 0.50, this probability is 0.65 lower for the likelihood method, compared to the ‘3+3’ (Figure 2D).

For k = 4, the likelihood method never favors H₂ for any set of hypotheses. Instead, the evidence supporting dose safety is considered weak with a probability of over 95% in all scenarios (Figure 3). In addition, the probability of declaring a dose unsafe falls under 20% for scenarios (C) and (D). This dramatic behavior can have serious implications in a dose-finding trial, and we caution against using a k ≥ 4 due to the small level of evidence that can be accumulated with small cohorts.

Since the category of weak evidence does not offer any clear guidance in making a decision, its interpretation is subjective. One option would be to assume a dose is acceptable until there is sufficient evidence to prove otherwise; this would combine weak evidence with evidence in favor of H₂ (safe dose). Due to space limitations, these results are not included, but can be inferred from Figures 2 and 3 by adding the heights of the dotted gray line with the solid black line, or these are available upon request.

Using the likelihood method in other dose-finding trials

The likelihood-ratio method with a fixed k and pre-stated hypotheses for the DLT rates allows consistent inferences to be made and evidence to be quantified regardless of cohort size. Table 5 illustrates the likelihood inferences for up to 9 patients per dose, for hypotheses (A)(p₁ = 0.40, p₂ = 0.15), with cell colors indicating decisions based on thresholds of k = 2 or k = 4. In the same manner, one can experiment with different hypotheses and k values and have decision rules in place for any unexpected situations. This table helps to demonstrate the strength of conclusions that can be reached under scenario (A) for different numbers of patients treated at each dose level. This also brings up the possible conclusion that a dose should not be considered “guilty” of being toxic until there is strong evidence of toxicity. In our phase I setting, this suggests that folding weak evidence in with a conclusion of acceptable is a way to proceed. Another consideration is to set different k thresholds for “toxic” and “acceptable”; this would be consistent with the practice in phase III trials of allowing type II errors to be rather large (e.g., 20%) with tighter control on the type I error (≤ 5%). For example, a dose may considered acceptable if LR ≥ 2 and toxic if LR ≤ 1/4, narrowing the range of weak evidence. Consequently, the escalation and de-escalations rules would be established using the same pre-defined k thresholds.

Table 5.

Levels of evidence for determining if a dose is acceptable or toxic based on (p₁ = 0.40, p₂ = 0.15) and k = 2, 4. Numbers in cells are likelihood-ratios with colors indicating level of evidence. Dark/light green cells indicate evidence of acceptable dose; red/pink cells indicate evidence of toxic dose; gray cells indicate weak evidence. Dark green cells: LR ≥ 4; light green cells: 2 ≤ LR < 4; gray cells: 1/2 < LR < 2; pink cells: 1/4 < LR ≤ 1/2; red cells: LR ≤ 1/4.

	Number of patients treated at dose j
Number of toxicities at dose j		1	2	3	4	5	6	7	8	9
	0	1.42	2.01	2.84	4.03	5.71	8.08	11.45	16.22	22.98
	1	0.38	0.53	0.75	1.07	1.51	2.14	3.03	4.29	6.08
	2		0.14	0.20	0.28	0.40	0.57	0.80	1.14	1.61
	3			0.05	0.07	0.11	0.15	0.21	0.30	0.43
	4				0.02	0.03	0.04	0.06	0.08	0.11
	5					0.01	0.01	0.01	0.02	0.03
	6						<0.01	<0.01	0.01	0.01

Our interest in the likelihood approach for identifying doses as too toxic arose from the setting of dose-finding with two outcomes: a continuous efficacy outcome and a binary toxicity outcome. Our goal was to choose doses in a model-based design using the efficacy outcome, while constantly monitoring safety. This method provides a framework for declaring dose levels too toxic and hence removing them from the set of acceptable doses for subsequent patients. Even so, our approach can be used for any ‘A+B’ designs.

Discussion

In this paper we propose a likelihood-based method for analyzing the behavior of any rule-based algorithm or design using algorithmic dose-finding rules (e.g., mTPI) under different sets of hypotheses, levels of evidence, and true toxicity rates. We also propose using the method in other settings, where dose-finding may include other (efficacy) outcomes. The approach is illustrated for the specific case of the ‘3+3’ design, and compared in terms of decision rules with the mTPI design. With comprehensive R functions available upon request, the likelihood method can be useful to any investigator that intends to implement a dose-finding design and wishes to analyze the performance characteristics under different conditions/scenarios.

The method is based on the evidential paradigm which is an ideal setting for monitoring clinical trials with likelihood inference and is similar in spirit to the Sequential Probability Ratio Test (SPRT).²⁰ The strength of evidence is quantified solely by the likelihood-ratio and is amenable to sequential evaluation of the data. In our simulation study we presented three likelihood-ratio thresholds: k = 1, 2, and 4. For the four sets of hypotheses considered, k = 4 leads to more outcomes of weak evidence, demonstrating that the ‘3+3’ design is not able to provide conclusions regarding safety of doses with high confidence.

On the other hand, a cutoff of k = 1 marks the lowest level of evidence and we do not recommend its use in practice. For k = 2 and two sets of hypotheses: (p₁ = 0.30, p₂ = 0.05) and(p₁ = 0.15, p₂ = 0.05), the likelihood method and ‘3+3’ design have similar operating characteristics, i.e., high probabilities of correctly identifying acceptable doses, but low probabilities of declaring unsafe doses. This suggests that the ‘3+3’ design is consistent with these sets of hypotheses and, according to our Figure 1, a one-sided significance level of about 0.12. In general, for hypotheses with a midpoint close to 0.30, the ‘3+3’ design has some probabilistic support, with better chances of choosing a safe dose rather than a toxic one. For all the other scenarios considered here, the algorithm has very poor performance in identifying a toxic dose and thus should not be used.

Regarding the mTPI design, the likelihood method with k = 2 supports the majority of the decisions rules, even for the high toxicity scenario (D) (p₁ = 0.50, p₂ = 0.30). A further comparison with the mTPI included the probability of selecting the MTD. Two toxicity scenarios for six dose levels were considered: scenario 1 = (0.05, 0.10, 0.30, 0.50, 0.55, 0.60) and scenario 2 = (0.05, 0.10, 0.15, 0.25, 0.30, 0.40). For this purpose, hypotheses (p₁ = 0.40, p₂ = 0.15) with a midpoint of.275 were thought to be in accordance with the targeted probability of toxicity of 0.30 used in mTPI. For a sample size of 20 patients, the likelihood probability of selecting the true MTD was of 0.37 (vs. 0.60 mTPI) under scenario 1, and of 0.40 (vs. 0.22 mTPI) under scenario 2. The discrepancy between the two methods is understandable considering the fact that the likelihood method is more intended for identifying a set of acceptable doses, rather than the MTD.

We note that comparisons between the ‘3+3’ designs and the continual reassessment method (CRM) are popular in the literature. In this paper, we focus mainly on characterizing algorithmic designs and models where dose-finding rules can be expressed in an algorithmic fashion. We do not argue that algorithmic designs would be preferred. However, given their prominence, it is important to understand their weaknesses but also situations in which their behavior is reasonable. It should also be emphasized that there is a growing number of dose-finding designs in oncology research where the optimal dose is not defined solely by a toxicity endpoint. We believe our approach can be a useful addition for monitoring toxicity of doses while allowing dose-finding models to target optimal doses based on efficacy or mechanistic (e.g. pharmacodynamics) endpoints.