Abstract
Filoviruses Ebolavirus (EBOV) and Marburgvirus (MARV) cause haemorrhagic fevers with high mortality rates, posing significant threats to public health. To understand transmission into human populations, filovirus dynamics within reservoir host populations must be understood. Studies have directly linked filoviruses to bats, but the mechanisms allowing viral persistence within bat populations are poorly understood. Theory suggests seasonal birthing may decrease the probability of pathogen persistence within populations, but data suggest MARV may persist within colonies of seasonally breeding Egyptian fruit bats, Rousettus aegyptiacus. I synthesize available filovirus and bat data in a stochastic compartmental model to explore fundamental questions relating to filovirus ecology: can filoviruses persist within isolated bat colonies; do critical community sizes exist; and how do host–pathogen relationships affect spillover transmission potential? Synchronous annual breeding and shorter incubation periods did not allow filovirus persistence, whereas bi-annual breeding and longer incubation periods, such as reported for Egyptian fruit bats and EBOV in experimental studies, allowed persistence in colony sizes often found in nature. Serological data support the findings, with bats from species with two annual birth pulses more likely to be seropositive (odds ratio (OR) 4.4, 95% confidence interval (CI) 2.5–8.7) than those with one, suggesting that biannual birthing is necessary for filovirus persistence.
Keywords: bats, critical community size, Ebola, filovirus, Marburg, seasonality
1. Introduction
Pioneers of the application of mathematics to infectious disease biology posed three interrelated questions about infectious disease dynamics: can we predict and explain the size and periodicity of epidemics, how does the flow of susceptible individuals affect endemic persistence and do critical community sizes (CCSs) exist? [1–4]. Those pioneers applied their models to human infectious diseases. However, most emerging infectious diseases are zoonoses from wildlife hosts [5]. Thus, today disease ecologists often aim to address the same questions in wildlife systems.
Bats (order Chiroptera) are unique among mammals, of which they number around 20% of extant species, because they are capable of flight. However, recent analyses suggest that bats are also special with respect to their capacity to host zoonotic viruses when compared with the most speciose mammalian order, the rodents (Rodentia) [6]. Filoviruses, including Ebola and Marburg viruses, are a significant public health and conservation problem, because they cause episodic human and primate disease outbreaks with high mortality rates and with human-to-human transmission. An unprecedented ongoing Ebolavirus (EBOV) outbreak in West Africa demonstrates the high case fatality rate, with 50% (4484/8973) of cases dying [7]. The two largest Marburg virus (MARV) outbreaks caused the deaths of 83% (128/154, Democratic Republic of Congo (DRC), 1998–2000) and 90% (227/252, Angola, 2004–2005) of patients [8]. Like some other filovirus outbreaks, the DRC MARV epidemic was epidemiologically linked to bats, in this case through mining [9]. Experimentally, Zaire ebolavirus (Z-EBOV) was shown to replicate without disease in three bat species and could be isolated from faeces 21 days following infection [10]. However, despite decades of investigations and epidemiological studies suggesting bats may be a source of filovirus infection, it was only in 2005 that the first direct evidence from field studies reported that bats were naturally infected with EBOV [11].
The evidence for bats playing a role in the maintenance, transmission and evolution of filoviruses has been rapidly increasing since the study by Leroy et al. [11]. Antibodies against EBOV antigen have been detected in a number of African bat species [12]. Paweska et al. [13] demonstrated that MARV could be detected in tissues 2 to 9 days post-infection. In both this MARV study and the EBOV challenge study [10], antibody could be detected post experimental infection challenge and post viremia. Outside of Africa, antibodies reactive with Reston ebolavirus (R-EBOV) and Z-EBOV antigen have been detected in bats from the Philippines, China and Bangladesh [14–16], and a novel filovirus, Lloviu virus, has been sequenced from a European insectivorous bat [17]. With increasing evidence suggesting that bats are the reservoir hosts for filoviruses comes the opportunity to understand the mechanisms that allow persistence of infections within and emergence of infection from bat populations [12,18].
Bats are long-lived mammals, usually with highly synchronous birthing, and they invest substantial energy reserves in their offspring [19]. Host traits, such as maternally derived antibody [20,21] and seasonal birthing [22,23], can affect infection dynamics within populations. Theoretical studies using stochastic epidemiological models with a seasonal birth pulse suggest that increased birthing synchrony increases the necessary population size required for infection persistence (CCS) [23]. Thus, seasonal birthing may decrease the probability of pathogens persisting in a colony, but lead to periods of increased infection prevalence following birthing. Amman et al. [24] were the first to report that birthing may increase infection prevalence and ultimately spillover for MARV in bats. Infection prevalence of other viruses, including coronaviruses and rabies, shows seasonal dynamics in bats [25–27]. The increase in susceptible hosts and contact rates during and following the birthing period may drive infection dynamics [28], though overwinter hibernation has also been shown to be important in temperate bat systems for rabies [29]. Amman et al. [24] identified MARV in Rousettus aegyptiacus bats in a cave in Uganda by using polymerase chain reaction (PCR) and viral isolation, and discovered that the disease occurred in pulses in older juvenile bats (approx. six months old) corresponding to twice-yearly birthing seasons. Whether this is true of all filoviruses is unclear and further field studies are necessary to understand the role of host ecology in infection dynamics [12,18].
However, there is now enough data to begin to explore the effects of synchronous birthing, coloniality (as shown by R. aegyptiacus) and other factors that drive infection dynamics, within a modelling framework. Modelling studies can be used to increase understanding regarding the infection transmission processes, including if the virus(es) can persist within specific populations or species alone. These studies can highlight which aspects of host and virus biology may be important and require further study through the use of sensitivity analyses [30].
In this study, I return to the questions posed by Kermack, McKendrick and Bartlett for human infections and use currently known or estimated demographic and virological parameters to explore if (i) filovirus infections can persist within African fruit bat populations, and if so, (ii) what might CCSs be and (iii) which host and virological parameters are most important for pathogen persistence. Finally, I analyse data from serological surveys to test whether my model findings are supported by field data.
2. Model structure
Models comprised of susceptible (S), infectious (I) and immune (R) classes (SIR), using ordinary differential equations (ODE) have been used for human filovirus outbreaks, but none has attempted to address potential reservoir host dynamics [31–33].
There are few studies that report within-host filovirus dynamics, though a number of key studies [10,11,13] suggest that the processes may be represented by the classical SIR compartment classes [28]. As filoviruses are negative-strand RNA viruses and no data suggest otherwise, I followed this approach. Infection of bats with MARV has demonstrated that MARV is detectable in multiple tissues 2 to 9 days post-infection after direct inoculation [13]. Data supporting the SIR model structure are provided by some experimentally infected bats that are also seroconverting, but with none showing signs of ill-health or gross pathology, suggesting recovery with an adaptive immune response [10,13]. Further support for recovery following infection in the wild is provided by the discovery of anti-EBOV antibody-positive bats that are not PCR-positive and vice versa [11], the widespread antibody-positive bats found among bat species in the absence of disease [12], and the 13-month survival of an EBOV-seropositive bat [34]. It was demonstrated in experimental infection studies that EBOV in bats could be isolated from faeces 21 days after infection [10], giving an indication of a possible incubation period, and thus I added an exposed (E) category to make the model structure an SEIR-type model.
I assumed that transmission was density-dependent, because although some bats (e.g. Eidolon helvum and R. aegyptiacus) can roost at high densities [24,35] somewhat independent of colony size increases, if filoviruses are transmitted through contact with fluids, such as urine and faeces, it may be assumed that transmission is not necessarily independent of density within an area, and thus following [36], I modelled transmission as density-dependent. Therefore, susceptible (S) individuals become infected at the rate (β SI). Bats incubate (E) the infection for time (1/σ), the incubation period, and become infected and infectious (I) before recovery (seroconversion) at rate τ, 1/(infectious period) and survive as immune (R) for life. To determine how synchronous birthing affects the infection dynamics, an age-structured model of the bat population was used. The age-structure allows all adults (Na) to breed, but not juveniles (j) in their first year of life [35,37]. Juveniles age after 1 year (at rate ɛ) to become breeding adults in their second year of life [35]. I included a carrying capacity (K) allowing density-dependent mortality with different juvenile (δ) and adult (μ) rates [35] and assumed that density-dependent mortality occurs in all classes of the population (N). Births (b, see below) were not density-dependent, as pregnancy rates estimated from field studies of at least one African fruit bat species approach 100% [35,37]. Those born to immune adults (Ra) are assumed to have no maternally derived immunity and thus are born susceptible. The ODE model structure is therefore
 |
2.1 |
Birthing in most bats is seasonally pulsed. The use of a periodic Gaussian function (PGF) that allows births to be pulsed over a period and ensures that no births occur outside the birthing season has previously been described [23]. The function looks like
| 2.2 |
where s controls the width of birth peaks (‘synchrony’), ω the number of pulses per year, φ the offset during the year and κ is a scaling parameter. A full exploration of the function and general effects of synchronous birthing on infection maintenance is described elsewhere [23].
Because demographic stochasticity exists in the system and I wished to understand infection persistence and perform a sensitivity analysis to understand how host and pathogen traits affect persistence, I implemented a stochastic version of the model. The stochastic model was implemented as a continuous Markov process in the ‘pomp’ R package [38], coded in native C code. Births were modelled as a Poisson process and the remaining processes with Euler multinomial processes. Thus, as N individuals face a constant hazard to leave their class in k ways, at rates r1, r2, … , rn, then during a Δt time interval, the number of individuals is multinomially distributed
 |
2.3 |
where Δni is the number of individuals leaving in way i over the time interval and the probability of remaining is
 |
2.4 |
and of leaving in way j is
 |
2.5 |
For full details, see [38]. Initial conditions for all simulations were a juvenile and adult infection prevalence of 2.5% and a juvenile and adult antibody prevalence of 25%, with initial population sizes of 40 000 bats.
For all analyses, 500 simulations for each parameter set were run for 25 years. All analyses were performed in R [39].
3. Parameter estimation
I assumed that bats shared common life-history traits other than the number of birthing pulses. To estimate the parameters for the birth pulse function, I used data from Mutere (tables 1 and 2 within [37]) of monthly numbers of female E. helvum pregnant throughout the year to calculate the rate of change of pregnancy for each month. I fit the PGF using the Nelder and Mead optimization function optim in R [40] and fixed the shape parameters to estimate κ, such that the integral of the PGF (the annual birth rate) equalled the birth rate of approximately one young per year per female reported for E. helvum [35], with either one or two birth pulses per year [24,41]. The parameters values for the PGF birth pulse function parameters (ω) are in table 1, the PGF functions in electronic supplementary material, figure S1.
Table 1.
Model parameters. PRCC results from the sensitivity analysis results and the range of parameters used in the PRCC analysis are shown.
| parameter | symbol | value | unit | reference | range used in sensitivity analysis | PRCC (p-value) |
|---|---|---|---|---|---|---|
| transmission rate (density-dependent/frequency-dependent) | β | 0.0045 | per capita per day/per day | this study | 0.00045–0.045 | −0.03 (0.51) |
| juvenile mortality rate | δ | 2.31 × 10−3 | per capita per day | [35] | 2.31 × 10−4 to 2.31 × 10−2 | −0.01 (0.8) |
| adult mortality rate | μ | 5.1 × 10-4 | per capita per day | [35] | 5.1 × 10−5 to 5.1 × 10−3 | −0.05 (0.24) |
| rate of aging from juvenile to sexually mature adult | ɛ | 2.7 × 10−3 | per capita per day | [35] | n.a. | n.a. |
| incubation rate (or 1/incubation period) | σ | 1/7 or 1/21 | per capita per day | [10,13] | 4.7 × 10−3 to 0.47 | −0.47 (<0.001) |
| rate of seroconversion (or 1/infectious period) | τ | 0.14 | per capita per day | [10,13] | 0.014–1 | −0.22 (<0.001) |
| parameter to control timing of births | ϕ | 0 | — | this study | 0–1 | −0.07 (0.1) |
| annual birth pulses | ω | 1 or 2 | per year | [35,36] | 2 | n.a. |
| scalar to control birth rate | κ | 4.1 × 10−3 | per female per day | this study | 4.1 × 10−4 to 4.1 × 10−2 | 0.12 (0.006) |
| annual birth synchrony | s | 14.35 | — | this study | 1.435 to 143.5 | −0.16 (<0.001) |
| carrying capacity | K | 1 × 105 | — | [24,42] | 1 × 104 to 1 × 106 | 0.04 (0.33) |
Annual survival probability from capture–recapture data for E. helvum from the Accra colony has been estimated and showed that an exponential function with constant survival across ages was the best model [35], which I assumed was similar across bat species. This probability was transformed to an annual survival rate, μ, by using
| 3.1 |
where S is the apparent annual survival probability and t time [43,44]. See table 1 for the results.
For the unknown parameter value, β (the transmission coefficient), I made several simplifying assumptions that would enable me to estimate approximate values. First, I assumed that infection dynamics were simple SIR dynamics with no age structure, that there was a constant force of infection across age classes and that infection was at dynamic equilibrium (∞). I assumed that birth rates equalled overall adult mortality, and thus the population was stable, and the proportion of individuals in the susceptible (s) and infected (i) classes was ds(t)/dt = di(t)/dt = 0 [28,45]. This allowed β to be estimated from available data by rearranging the simplified SIR model
| 3.2 |
so that
| 3.3 |
The full derivation of equation (3.2) is found in [45] and the electronic supplementary material. The infection-related data for MARV in R. aegyptiacus [24] and estimated μ above were then used to estimate β using equation (3.3) (table 1). Importantly, the effect of altering β is explored in the sensitivity analysis below and the assumptions of this simplification discussed. Infectious periods and incubation periods were taken from experimental studies [10,13] (table 1).
4. Pathogen persistence
Using parameters estimated from the literature for African fruit bats and filoviruses (table 1), I was able to model filovirus persistence within simulated populations of bats. However, models with one or two birth pulses using two different incubation periods (7 and 21 days) led to decidedly different results. Infection either persisted in almost all 500 simulations with two pulses and a 21-day incubation period, or none with a single pulse or the shorter 7-day incubation period.
The dynamics of infectious individuals (figure 1) within populations with two birth pulses suggests why the pathogen may have failed to persist in the alternative scenarios (a single pulse of young, or shorter incubation periods; electronic supplementary material, figure S2), because the number of infected individuals drops very low between birth pulses.
Figure 1.
The effect of biannual birth pulses on filovirus persistence in simulated bat populations. (a) Number of susceptible and infected juveniles and infected adults over the final years for 500 stochastic simulations of a 25-year simulation model of filovirus–bat-infection dynamics. This model has biannual birth pulses, with the synchrony parameter (s) 14.3, a birth rate of 0.98 per female per year and an incubation period (1/σ) of 21 days. (b) The effect of altering s to model seasonal births. A fixed birth rate of 0.98 per female per year, with s from 1.43 (low synchrony) to 14.3 (high synchrony) is shown. The threshold at which births occur continuously throughout the year (s ≈ 4.29, orange solid line) is shown. (c) The effect of altering infection incubation period (1/σ) and s on pathogen persistence (z-axis, panel). Persistence was estimated as the proportion of 500 simulations for which filovirus infection was present after 25 years. Incubation periods used include those from time to detection of filoviruses in experimentally infected bat tissues post-inoculation, to time to detection of virus shedding. Synchrony values are from those estimates from field data (s = 14.3) through to continuous birthing throughout the year (threshold s ≈ 4.29, orange). Remaining parameters not specified are in table 1.
To explore the effect of population size on infection persistence, I varied the carrying capacity (K) from very small (100) to large (200 000), while keeping the other parameters except the incubation period the same. Only by including two birth pulses and an incubation period of 21 days did the model predict pathogen persistence, and only in colonies of bats over approximately 20 000 bats. Near-universal persistence occurred in populations of around 40 000 bats (electronic supplementary material, figure S2).
The two-birth-pulse 21-day incubation period model predicts infection prevalence well compared with field studies [24], with infection prevalence predicted to be very low (less than 2%, electronic supplementary material, figure S3). However, for the population size (40 000) from which the best data are available as estimated from capture–recapture studies, the model predicts a much higher seroprevalence, approaching 100%, compared with approximately 16% [24].
5. Sensitivity analysis
To examine the relative importance of different aspects of the system and effects of varying parameters, such as β, I performed a multi-parameter, global sensitivity analysis [46] on model parameters relating to both infection and host demography with the number of birth pulses fixed at two per year. I used 500 parameter sets obtained from stratified random samples from uniform distributions spanning a range of potential values for the nine parameters of interest using Latin hypercube sampling (LHS; lhs package in R [47], table 1). The rate of aging of young to adults and the number of birth pulses per year were fixed. The parameter range for LHS sampling was determined by increasing and decreasing the ‘default’ parameter value by an order of magnitude. Partial-rank correlation coefficients (PRCCs) between each parameter and model output determined the relative importance of each parameter, and the PRCC method details are in the electronic supplementary material. The model output measured was the proportion of 500 model simulations for which the virus persisted after the 25-year simulation period.
The PRCC sensitivity analysis results suggest that filovirus persistence is significantly positively affected by increasing the incubation period (1/σ), infectious period (1/τ) and birth rate (κ), and negatively by increasing synchrony (s) of the birth pulse (table 1; electronic supplementary material, figure S4).
Further exploration of the effect of birthing synchrony on persistence for differing incubation periods from 2 to 21 days demonstrates that even when synchrony is strong and before birthing occurs year-round (s ≈ 4), filoviruses are predicted to persist in over 25-year periods with incubation periods of less than 21 days (figure 1). An additional exploration of the parameter space relating to the incubation (1/σ) and infectious (1/τ) periods was performed for the two birth pulse model only for a range of values at 1-day increments for 7–21-day and 1–20-day periods, respectively. This analysis gives the intuitive results that longer incubation and/or infectious periods increase persistence when other parameters are fixed (electronic supplementary material, figure S5).
6. Data analysis
To test the predictions of the model, I collated data from publications reporting the serological findings for studies of bats and filoviruses. I used the reports of serological data only, because (i) there were substantially more reports in the literature of serological surveys than virus isolation or molecular based studies, and (ii) the findings relating to serological results may reflect the species being part of a viral reservoir system, as we may predict that infection circulates widely enough and without disease-induced mortality for anti-filovirus antibody-positive bats to be found. Once collated, I searched the literature for reports of the number of birth pulses per year for each bat species. The numbers of anti-filovirus antibody-positive and -negative animals were combined and bats were categorized as species having either one annual birth pulse, or more than one pulse. The data are in electronic supplementary material, table S1. Serological findings were reported in 12 studies for three different virus genera (MARV, Z-EBOV and R-EBOV) for 40 bat species for 8530 individual bats. Because most bat species with biannual birth pulses were fruit bats, I ran a logistic regression using the glm function in R with binomial and, adjusting for overdispersion, quasi-binomial errors. I included the interaction term between being a fruit bat and having two or more birth pulses, with the response variable being the proportion seropositive for the species. If two or more reports for the same virus were found for a single species, these data were combined. The relationship between the number of birth pulses and phylogeny (being a fruit bat of the Pteropodidae family) was examined using the Fisher's exact test, because two contingency table variable numbers were fewer than five.
The results of the statistical analyses show that if a bat is from a species that has two birth pulses (or more), it is statistically more likely to be serologically positive for antibodies against filoviruses than those that have one birth pulse with an odds ratio (OR) of 4.45 (95% CI 2.51–8.7, p-value < 0.0001). To ensure that this was not a sampling artefact nor due to the species-specific effects of R. aegyptiacus, which has been most intensively studied, I removed this species and reanalysed the results. The effect of two birth pulses or more remained statistically significant, with bats from those species still more likely to be seropositive (OR 2.73, 95% CI 1.52–5.39, p-value 0.0002). The serological data, with 95% CI for each species, are shown in electronic supplementary material, figure S6. Most bat species with biannual birth pulses, however, were fruit bats (14/16, 90%, OR 122, 95% CI 11–6775, p-value < 0.0001).
The logistic regression using a full model, with being a fruit bat species interacting with having two or more birth pulses compared with there being no interaction between them, suggested the interaction term was not significant (F-test = 1.5, p-value = 0.2, d.f. = 41). In the model with no interaction term, having two or more births (coefficient (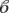 )birth = 2.6, s.e. = 0.7, z-value = 3.6, p-value = 0.0003) and being a fruit bat (
)birth = 2.6, s.e. = 0.7, z-value = 3.6, p-value = 0.0003) and being a fruit bat (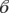 bat = −1.5, s.e. = 0.8, z-value = −2, p-value = 0.045) were both significant factors in predicting the proportion seropositive for a species. However, by taking into account overdispersion using the quasi-binomial error and F-test, this significance was removed (births:
bat = −1.5, s.e. = 0.8, z-value = −2, p-value = 0.045) were both significant factors in predicting the proportion seropositive for a species. However, by taking into account overdispersion using the quasi-binomial error and F-test, this significance was removed (births:  birth = 2.6, s.e. = 2, z-value = 1.3, p-value = 0.2; being a fruit bat:
birth = 2.6, s.e. = 2, z-value = 1.3, p-value = 0.2; being a fruit bat:  bat = −1.5, s.e. = 2.1, z-value = −0.7, p-value = 0.48).
bat = −1.5, s.e. = 2.1, z-value = −0.7, p-value = 0.48).
7. Discussion
Here, I used available data and knowledge regarding filoviruses and their bat hosts to help understand the ecology of filoviruses within their putative reservoir host populations. My simple model predicts that filoviruses may not persist in large populations of bats if birthing is highly synchronous in a single pulse each year (electronic supplementary material, figure S2). When there are two highly synchronous birth pulses, without births throughout the entire year (figure 1b; electronic supplementary material, S1 and S2), the model predicts that the incubation period required for persistence must be longer (figure 1c; electronic supplementary material, S2). However, longer infectious periods can also increase the likelihood of persistence (electronic supplementary material, figure S5), and biannual seasonal birthing can lead to persistence with shorter incubation periods if the seasonality is less strong than that estimated for E. helvum (figure 1c). The results of these simulations are supported by field data, with species with two or more birth pulses significantly more likely to be seropositive with antibodies to filoviruses than those with single synchronous birthing periods (electronic supplementary material, figure S6).
Biannual birthing in populations was mostly found in fruit bats of the family Pteropodidae (electronic supplementary material, table S1). It has been proposed elsewhere that the differences between seroprevalence (and presumably infection prevalence) against EBOV and other viruses (e.g. henipaviruses and lyssaviruses) in the African species, E. helvum, compared to other bats in the same locations [34,41,48,49] and R. aegyptiacus [24], could be owing to either ecological differences or underlying genetic host restrictions [12]. Though genetic differences likely affect host traits, the genetic host restrictions here refer to those relating to infection susceptibility (e.g. different host cell receptors or innate immune responses). Rousettus aegyptiacus and those species with the higher seroprevalence against EBOV (e.g. Hypsignathus monstrosus and Epomops franqueti) have two synchronous birth pulses, whereas E. helvum has only single, highly synchronous birth pulse each year. Ecological differences, therefore, may be a simple explanatory factor as to why E. helvum may not be a reservoir host despite being sympatric with ‘reservoir’ species, as it may not have the ecological traits that allow persistence of acute, immunizing infections. Whether it is host genetics or ecological traits that explains the field data requires further analysis, but this model would suggest that host traits may be sufficient alone. The ecological host trait hypothesis may explain the lack of evidence for MARV in Hipposideros species, insectivorous bats with a single annual birth pulse, which roost in the same cave as R. aegyptiacus [50]. Support for this ecological host trait hypothesis can be found in experimental work [10]. Two insectivorous Tadarida bat species (Tadarida condylura and T. pumila), distantly related to Pteropodidae bats, were both able to be infected with EBOV and recover, suggesting that insectivorous bats are susceptible to infection and that genetic differences relating to infection susceptibility between Pteropodiae fruit bats and insectivorous bats are less likely to explain the different findings.
Most human MARV infections (83%, 54/65) occurred at the same times each year as the seasonal birth period and high prevalence of MARV infection within R. aegyptiacus [24]. Other bat-infection studies suggest that RNA virus shedding may be linked to host ecology and seasonality, though the details differ among systems [26,29,51,52]. Together, these studies suggest that as births increase population size and contact rates, the influx of susceptible juveniles may be a central driver of bat-infection dynamics, which may itself drive spillover dynamics to humans. My model results and the field observations suggest that targeting younger bats with two or more seasonal births during or after those birthing periods might be fruitful for virological studies. However, additional sampling of other species is necessary to further test the results of this study.
Shorter incubation periods, such as those reported in [13], can lead to infection persistence with 7-day infectious periods if two pulses occur annually in this model, but only when they are less synchronous than estimated for E. helvum (figure 1). However, not only is it unclear how synchronous birthing is in most bats, it is unclear whether experimental studies reflect natural infection [53]. Viruses used in experimental systems are often highly passaged prior to infection and challenge doses and routes may not be appropriately similar to natural settings. In the EBOV challenge study, the only bat found to shed virus did so 21 days after infection, despite virus being detected in infected bat tissues prior to that eight days post-inoculation [10]. The sensitivity analyses suggest that shorter incubation and infectious periods, and increased synchrony, lead to lower infection persistence (table 1; electronic supplementary material, figures S4–S7). Additional experiments to determine within-host dynamics may be informative [54]; however, capture–recapture studies of wild bats may be most informative of the infection dynamics with natural settings.
In the model, filoviruses persisted within colonies of around 20 000 and above, when biannual birthing and 21-day incubation periods were modelled. With shorter incubation periods, less synchronous birthing was required for persistence (figure 1). These results suggest that meta-population dynamics will be necessary for filovirus persistence if colony sizes are smaller or infectious periods shorter than these and birthing highly synchronous. Meta-population dynamics, therefore, may play a key role in filovirus ecology. Amman et al. [24] provide evidence of direct movement between caves for R. aegyptiacus and genetic similarity between viruses in geographically distant locations. This may be evidence that MARV circulates within R. aegyptiacus with meta-population-like dynamics. Whether this is true meta-population dynamics, with virus extinction within colonies and then re-infection, is unknown. However, my model results suggest that meta-population dynamics may not be necessary for persistence of MARV within R. aegyptiacus colonies if colony sizes are large enough, birthing not very tightly synchronized and/or incubation times long enough. Of interest here is whether populations of R. aegyptiacus in the Middle East and Europe that appear to be less mobile are ever infected with MARV. My model predictions suggest that many colonies, such as those in Cyprus [55], may not be large enough to maintain MARV infection.
My model of filovirus–bat dynamics assumes that single species act as reservoirs. There is evidence for filovirus infection in multiple bat species, many with overlapping geographical ranges [12], for four filoviruses (MARV, Z-EBOV, R-EBOV and Lluvio virus; electronic supplementary material, table S1; [12]), suggesting multiple bat species could act as reservoirs for filoviruses. Numerous genetics studies have suggested that similar, and congeneric species, are highly vagile and panmictic across large areas [56–61], facilitating viral transmission. Multiple circulating pathogens within multiple species populations could maintain infection at the landscape level. However, multiple, genetically divergent MARV strains have been discovered within single, large R. aegyptiacus roosts [24,50], suggesting persistence within populations of gregarious R. aegyptiacus, which has biannual birthing. The results of my study may explain why anti-EBOV antibody-positive bats have been so hard to find, if infections cannot be maintained in local, less dense bat populations of other species. Leroy et al. [11] reported anti-EBOV antibodies in three fruit bat species: H. monstrosus (24%, 4/17), E. franqueti (7%, 8/117) and Myonycteris torquata (7%, 4/58), from a sample of 679 bats. These species all have two birth pulses, but their local population densities may not be sufficient to maintain infection within a locale, perhaps explaining the ephemeral nature of EBOV findings in bat populations.
Further studies, including the integration of models and data such as I started here, are necessary to understand filovirus persistence and filovirus spillover to humans. I used ‘generic’ parameters, and species-specific studies will be possible as more data become available. Substantially lower seroprevalence values (less than 3%) have been reported from large colonies (perhaps 100 000) of R. aegyptiacus [50] than my model predicts. There are many problems in interpreting serological data in wildlife [62], however, the lack of seroconversion in all bats following experimental challenge [10] may explain the difference in seroprevalence between my model and field data. Other factors include waning antibody titres with or without waning immunity. Furthermore, age-specific seroprevalence values may alter dramatically, with the probability of being seropositive varying from approximately 0.2 for 1-year-old animals to approximately 0.8 for 14-year-old animals for another RNA virus in E. helvum [41], and my model will not capture this. Also, I made simplifying assumptions, including that infection was at equilibrium within the R. aegyptiacus colonies, to estimate the transmission coefficient, β, and so further studies are necessary to estimate this parameter. However, the sensitivity analyses suggest that β may matter less than other parameters, as viral persistence results were not sensitive to 10-fold increases and decreases in the estimated β (table 1). Additional work is also required to understand bat–bat transmission. Viral antigen has been detected in female reproductive tracts [13], and thus some frequency-dependent transmission may also occur. Frequency-dependent transmission may also be more likely for species that consistently roost at high densities independent of colony size [36]. Finally, as above, additional variations of my model could include multi-species and meta-population models. These models could be developed to understand further the effects of host connectivity on filovirus persistence and the incorporation of additional complexity may provide additional insights into filovirus ecology.
The current and ongoing outbreaks of EBOV in W. Africa [63] and DRC [64] and MARV in Uganda [65] highlight the need for better understanding of the viral dynamics within their hosts. The epidemiological links between bats and human filovirus infection are sporadic, though increasing. Though filovirus ecology remains an emerging area of research, frameworks exist for multi-disciplinary, process-based approaches that integrate ecological and evolutionary dynamics [12,18,30,66,67]. By multi-disciplinary research, including models that integrate different data sources such as this, additional insights may be made that are important to inform disease management options. Returning to the questions posed by the early mathematical biologists, how then has this modelling exercise informed our understanding of filovirus biology? The results of this study can perhaps explain the periodicity of infection prevalence within the host, supporting field study data and suggest that filovirus peak prevalences may be found in juvenile bats and be seasonally peaked. The ‘flow’ of susceptible young in seasonal pulses may have to be biannual to allow endemic disease. And we have learned that given current knowledge we might expect colony sizes of tens of thousands of bat for filovirus persistence, given the periodicity of births and infection prevalence. The results of this study provide a useful framework for future studies and offer insights into filovirus ecology that can be used to guide fieldwork, experimental studies and emerging infectious disease management.
Supplementary Material
Acknowledgements
Thanks to my Research and Policy for Infectious Disease Dynamics (RAPIDD), Cambridge Infectious Diseases Consortium (CIDC), Webb Lab at Colorado State University, and Ecology and Evolution of Infectious Diseases ecology workshop (2011, 2012) colleagues for useful discussions that led to this work. Also to Nigel French and Jonathan Marshall (Massey University) and two anonymous reviewers for comments on an early draft, and Michael Buhnerkempe (UCLA) for the PRCC code.
Funding statement
Funding was partially provided by the RAPIDD programme of the Science and Technology Directorate, Department of Homeland Security and Fogarty International Center, National Institutes of Health.
References
- 1.Kermack WO, McKendrick AG. 1927. Contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A 115, 700–721. ( 10.1098/rspa.1927.0118) [DOI] [Google Scholar]
- 2.Kermack WO, McKendrick AG. 1932. Contributions to the mathematical theory of epidemics II—The problem of endemicity. Proc. R. Soc. Lond. A 138, 55–83. ( 10.1098/rspa.1932.0171) [DOI] [Google Scholar]
- 3.Kermack WO, McKendrick AG. 1933. Contributions to the mathematical theory of epidemics III—Further studies of this problem of endemicity. Proc. R. Soc. Lond. A 141, 94–122. ( 10.1098/rspa.1933.0106) [DOI] [Google Scholar]
- 4.Bartlett MS. 1957. Mealses periodicity and community size. J. R. Stat. Soc. A 120, 48–70. ( 10.2307/2342553) [DOI] [Google Scholar]
- 5.Jones KE, Patel NG, Levy MA, Storeygard A, Balk D, Gittleman JL, Daszak P. 2008. Global trends in emerging infectious diseases. Nature 451, 990–993. ( 10.1038/nature06536) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Luis AD, et al. 2013. A comparison of bats and rodents as reservoirs of zoonotic viruses: are bats special? Proc. R. Soc. B 280, 20122753 ( 10.1098/rspb.2012.2753) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.World Health Organization. 2014. Situation reports: Ebola response roadmap. See http://apps.who.int/iris/bitstream/10665/136508/1/roadmapsitrep15Oct2014.pdf?ua=1. [Google Scholar]
- 8.Brauburger K, Hume AJ, Muhlberger E, Olejnik J. 2012. Forty-five years of Marburg virus research. Viruses Basel 4, 1878–1927. ( 10.3390/v4101878) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bausch DG, et al. 2003. Risk factors for Marburg hemorrhagic fever, Democratic Republic of the Congo. Emerg. Infect. Dis 9, 1531–1537. ( 10.3201/eid0912.030355) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Swanepoel R, Leman PA, Burt FJ, Zachariades NA, Braack LE, Ksiazek TG, Rollin PE, Zaki SR, Peters CJ. 1996. Experimental inoculation of plants and animals with Ebola virus. Emerg. Infect. Dis. 2, 321–325. ( 10.3201/eid0204.960407) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Leroy EM, et al. 2005. Fruit bats as reservoirs of Ebola virus. Nature 438, 575–576. ( 10.1038/438575a) [DOI] [PubMed] [Google Scholar]
- 12.Olival KJ, Hayman DT. 2014. Filoviruses in bats: current knowledge and future directions. Viruses 6, 1759–1788. ( 10.3390/v6041759) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Paweska JT, Jansen van Vuren P, Masumu J, Leman PA, Grobbelaar AA, Birkhead M, Clift S, Swanepoel R, Kemp A. 2012. Virological and serological findings in Rousettus aegyptiacus experimentally inoculated with vero cells-adapted hogan strain of Marburg virus. PLoS ONE 7, e45479 ( 10.1371/journal.pone.0045479) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Taniguchi S, et al. 2011. Reston Ebolavirus antibodies in bats, the Philippines. Emerg. Infect. Dis. 17, 1559–1560. ( 10.3201/eid1708.101693) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Olival KJ, et al. 2013. Ebola virus antibodies in fruit bats, Bangladesh. Emerg. Infect. Dis. 19, 270–273. ( 10.3201/eid1902.120524) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yuan JF, Zhang YJ, Li JL, Zhang YZ, Wang LF, Shi ZL. 2012. Serological evidence of ebolavirus infection in bats, China. Virol. J. 9, 236 ( 10.1186/1743-422x-9-236) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Negredo A, et al. 2011. Discovery of an Ebolavirus-like Filovirus in Europe. PLoS Pathog. 7, e1002304 ( 10.1371/journal.ppat.1002304) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hayman DT, Bowen RA, Cryan PM, McCracken GF, O'Shea TJ, Peel AJ, Gilbert A, Webb CT, Wood JL. 2013. Ecology of zoonotic infectious diseases in bats: current knowledge and future directions. Zoonoses Public Health 60, 2–21. ( 10.1111/zph.12000) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Barcley RMR, Harder LD. 2003. Life histories of bats: life in the slow lane. In Bat ecology (eds Kunz TH, Fenton MB.), pp. 209–256. Chicago, IL: The University of Chicago Press. [Google Scholar]
- 20.Kallio ER, Begon M, Henttonen H, Koskela E, Mappes T, Vaheri A, Vapalahti O. 2010. Hantavirus infections in fluctuating host populations: the role of maternal antibodies. Proc. R. Soc. B 277, 3783–3791. ( 10.1098/rspb.2010.1022) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Garnier R, Ramos R, Staszewski V, Militao T, Lobato E, Gonzalez-Solis J, Boulinier T. 2012. Maternal antibody persistence: a neglected life-history trait with implications from albatross conservation to comparative immunology. Proc. R. Soc. B 279, 2033–2041. ( 10.1098/rspb.2011.2277) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Altizer S, Dobson A, Hosseini P, Hudson P, Pascual M, Rohani P. 2006. Seasonality and the dynamics of infectious diseases. Ecol. Lett. 9, 467–484. ( 10.1111/j.1461-0248.2005.00879.x) [DOI] [PubMed] [Google Scholar]
- 23.Peel AJ, Pulliam JRC, Luis AD, Plowright RK, O'Shea TJ, Hayman DTS, Wood JLN, Webb CT, Restif O. 2014. The effect of seasonal birth pulses on pathogen persistence in wild mammal populations. Proc. R. Soc. B 281, 20132962 ( 10.1098/rspb.2013.2962) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Amman BR, et al. 2012. Seasonal pulses of Marburg virus circulation in juvenile Rousettus aegyptiacus bats coincide with periods of increased risk of human infection. PLoS Pathog. 8, e1002877 ( 10.1371/journal.ppat.1002877) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mondul AM, Krebs JW, Childs JE. 2003. Trends in national surveillance for rabies among bats in the United States (1993–2000). J. Am. Vet. Med. Assoc. 222, 633–639. ( 10.2460/javma.2003.222.633) [DOI] [PubMed] [Google Scholar]
- 26.Drexler JF, Corman VM, Wegner T, Tateno AF, Zerbinati RM, Gloza-Rausch F, Seebens A, Muller MA, Drosten C. 2011. Amplification of emerging viruses in a bat colony. Emerg. Infect. Dis. 17, 449–456. ( 10.3201/eid1703.100526) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Patyk K, Turmelle A, Blanton JD, Rupprecht CE. 2012. Trends in national surveillance data for bat rabies in the United States: 2001–2009. Vector Borne Zoonotic Dis. 12, 666–673. ( 10.1089/vbz.2011.0839) [DOI] [PubMed] [Google Scholar]
- 28.Anderson RM, May RM. 1979. Population biology of infectious diseases: part I. Nature 280, 361–367. ( 10.1038/280361a0) [DOI] [PubMed] [Google Scholar]
- 29.George DB, Webb CT, Farnsworth ML, O'Shea TJ, Bowen RA, Smith DL, Stanley TR, Ellison LE, Rupprecht CE. 2011. Host and viral ecology determine bat rabies seasonality and maintenance. Proc. Natl Acad. Sci. USA 108, 10 208–10 213. ( 10.1073/pnas.1010875108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Restif O, et al. 2012. Model-guided fieldwork: practical guidelines for multidisciplinary research on wildlife ecological and epidemiological dynamics. Ecol. Lett. 15, 1083–1094. ( 10.1111/j.1461-0248.2012.01836.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lekone PE, Finkenstadt BF. 2006. Statistical inference in a stochastic epidemic SEIR model with control intervention: Ebola as a case study. Biometrics 62, 1170–1177. ( 10.1111/j.1541-0420.2006.00609.x) [DOI] [PubMed] [Google Scholar]
- 32.Legrand J, Grais RF, Boelle PY, Valleron AJ, Flahault A. 2007. Understanding the dynamics of Ebola epidemics. Epidemiol. Infect. 135, 610–621. ( 10.1017/S0950268806007217) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chowell G, Hengartner NW, Castillo-Chavez C, Fenimore PW, Hyman JM. 2004. The basic reproductive number of Ebola and the effects of public health measures: the cases of Congo and Uganda. J. Theor. Biol. 229, 119–126. ( 10.1016/j.jtbi.2004.03.006) [DOI] [PubMed] [Google Scholar]
- 34.Hayman DTS, Emmerich P, Yu M, Wang LF, Suu-Ire R, Fooks AR, Cunningham AA, Wood JLN. 2010. Long-term survival of an urban fruit bat seropositive for Ebola and Lagos bat viruses. PLoS ONE 5, e11978 ( 10.1371/journal.pone.0011978) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hayman DTS, McCrea R, Restif O, Suu-Ire R, Fooks AR, Wood JLN, Cunningham AA, Rowcliffe JM. 2012. Demography of straw-colored fruit bats in Ghana. J. Mammal. 93, 1393–1404. ( 10.1644/11-MAMM-A-270.1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Begon M, Bennett M, Bowers RG, French NP, Hazel SM, Turner J. 2002. A clarification of transmission terms in host–microparasite models: numbers, densities and areas. Epidemiol. Infect. 129, 147–153. ( 10.1017/S0950268802007148) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mutere FA. 1967. The breeding biology of equatorial vertebrates; reproduction in the fruit bat Eidolon helvum, at latitude 0°20′N. J. Zool. 153, 153–161. ( 10.1111/j.1469-7998.1967.tb04058.x) [DOI] [Google Scholar]
- 38.King AA, Ionides EL, Breto CM, Ellner S, Kendall B. 2009. pomp: statistical inference for partially observed Markov processes. See http://pomp.r-forge.r-rproject.org.
- 39.R Development Core Team. 2012. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- 40.Nelder JA, Mead R. 1965. A simplex algorithm for function minimization. Comput. J. 7, 308–313. ( 10.1093/comjnl/7.4.308) [DOI] [Google Scholar]
- 41.Hayman DT, et al. 2012. Endemic Lagos bat virus infection in Eidolon helvum. Epidemiol. Infect. 140, 2163–2171. ( 10.1017/S0950268812000167) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Towner JS, et al. 2007. Marburg virus infection detected in a common African bat. PLoS ONE 2, e764 ( 10.1371/journal.pone.0000764) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Cox DR, Oakes D. 1984. Analysis of survival data. London, UK: Chapman and Hall. [Google Scholar]
- 44.Collett D. 1994. Modelling survival data in medical research. London, UK: Chapman and Hall. [Google Scholar]
- 45.Hens N, Shkedy Z, Aerts M, Faes C, Van Damme P, Beutels P. 2012. Modeling infectious disease parameters based on serological and social contact data. New York, NY: Springer. [Google Scholar]
- 46.Blower SM, Dowlatabadi H. 1994. Sensitivity and uncertainty analysis of complex-models of disease transmission—an HIV model, as an example. Int Stat. Rev. 62, 229–243. ( 10.2307/1403510) [DOI] [Google Scholar]
- 47.Carnell R. 2009. lhs: Latin hypercube samples. R package version 0.10. http://CRAN.R-project.org/package=lhs.
- 48.Hayman DT, Suu-Ire R, Breed AC, McEachern JA, Wang L, Wood JL, Cunningham AA. 2008. Evidence of henipavirus infection in West African fruit bats. PLoS ONE 3, e2739 ( 10.1371/journal.pone.0002739) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hayman DT, Yu M, Crameri G, Wang LF, Suu-Ire R, Wood JL, Cunningham AA. 2012. Ebola virus antibodies in fruit bats, Ghana, West Africa. Emerg. Infect. Dis. 18, 1207–1209. ( 10.3201/eid1807.111654) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Towner JS, et al. 2009. Isolation of genetically diverse Marburg viruses from Egyptian fruit bats. PLoS Pathog. 5, e1000536 ( 10.1371/journal.ppat.1000536) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Wacharapluesadee S, Boongird K, Wanghongsa S, Ratanasetyuth N, Supavonwong P, Saengsen D, Gongal GN, Hemachudha T. 2010. A longitudinal study of the prevalence of Nipah virus in Pteropus lylei bats in Thailand: evidence for seasonal preference in disease transmission. Vector Borne Zoonotic Dis. 10, 183–190. ( 10.1089/vbz.2008.0105) [DOI] [PubMed] [Google Scholar]
- 52.Plowright RK, Foley P, Field HE, Dobson AP, Foley JE, Eby P, Daszak P. 2011. Urban habituation, ecological connectivity and epidemic dampening: the emergence of Hendra virus from flying foxes (Pteropus spp.). Proc. R. Soc. B 278, 3703–3712. ( 10.1098/rspb.2011.0522) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Albarino CG, Uebelhoer LS, Vincent JP, Khristova ML, Chakrabarti AK, McElroy A, Nichol ST, Towner JS. 2013. Development of a reverse genetics system to generate recombinant Marburg virus derived from a bat isolate. Virology 446, 230–237. ( 10.1016/j.virol.2013.07.038) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Towner JS. 2013. Bats as reservoirs of filoviruses (data from recent challenges). Bat Res. News54, Abstracts of papers presented at the 16th International Bat Research Conference and the 43rd Annual Meeting of the North American Society for Bat Research, San Jose, Costa Rica, pp. 71–226. [Google Scholar]
- 55.Hadjisterkotis E. 2006. The destruction and conservation of the Egyptian Fruit bat Rousettus aegyptiacus in Cyprus: a historic review. Eur. J. Wildl. Res. 52, 282–287. ( 10.1007/s10344-006-0041-7) [DOI] [Google Scholar]
- 56.Chen JP, Rossiter SJ, Flanders JR, Sun YH, Hua PY, Miller-Butterworth C, Liu XS, Rajan KE, Zhang SY. 2010. Contrasting genetic structure in two co-distributed species of Old World fruit bat. PLoS ONE 5, e13903 ( 10.1371/journal.pone.0013903) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Epstein JH, et al. 2009. Pteropus vampyrus, a hunted migratory species with a multinational home-range and a need for regional management. J. Appl. Ecol. 46, 991–1002. ( 10.1111/j.1365-2664.2009.01699.x) [DOI] [Google Scholar]
- 58.Olival KJ. 2008. Population genetic structure and phylogeography of Southeast Asian flying foxes: implications for conservation and disease ecology. New York, NY: Columbia University. [Google Scholar]
- 59.Rahman SA, et al. 2010. Characterization of Nipah virus from naturally infected Pteropus vampyrus bats, Malaysia. Emerg. Infect. Dis. 16, 1990–1993. ( 10.3201/eid1612.091790) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Olival KJ, Dick CW, Simmons NB, Morales JC, Melnick DJ, Dittmar K, Perkins SL, Daszak P, Desalle R. 2013. Lack of population genetic structure and host specificity in the bat fly, Cyclopodia horsfieldi, across species of Pteropus bats in Southeast Asia. Parasites Vectors 6, 231 ( 10.1186/1756-3305-6-231) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Peel AJ, et al. 2013. Continent-wide panmixia of an African fruit bat facilitates transmission of potentially zoonotic viruses. Nat. Commun. 4, 2770 ( 10.1038/ncomms3770) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Gilbert AT, et al. 2013. Deciphering serology to understand the ecology of infectious diseases in wildlife. EcoHealth 10, 298–313. ( 10.1007/s10393-013-0856-0) [DOI] [PubMed] [Google Scholar]
- 63.World Health Organization. 2014. Ebola Haemorrhagic Fever, Guinea (Situation as of 27 March 2014) See http://www.afro.who.int/en/clusters-a-programmes/dpc/epidemic-a-pandemic-alert-and-response/outbreak-news/4069-ebola-haemorrhagic-fever-guinea-27-march-2014.html.
- 64.World Health Organization. 2014. Ebola virus disease outbreak—Democratic Republic of the Congo—update 10 September 2014 See http://www.afro.who.int/en/clusters-a-programmes/dpc/epidemic-a-pandemic-alert-and-response/outbreak-news/4272-ebola-virus-disease-outbreak-drc-10-september-2014.html.
- 65.World Health Organization. 2014. Marburg virus disease—Uganda See http://www.afro.who.int/en/clusters-a-programmes/dpc/epidemic-a-pandemic-alert-and-response/outbreak-news/4272-ebola-virus-disease-outbreak-drc-10-september-2014.html.
- 66.Pybus OG, Fraser C, Rambaut A. 2013. Evolutionary epidemiology: preparing for an age of genomic plenty. Phil. Trans. R. Soc. B 368, 20120193 ( 10.1098/rstb.2012.0193) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Wood JL, et al. 2012. A framework for the study of zoonotic disease emergence and its drivers: spillover of bat pathogens as a case study. Phil. Trans. R. Soc. B 367, 2881–2892. ( 10.1098/rstb.2012.0228) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


