Investigating cell mechanics with atomic force microscopy

Abstract

Transmission of mechanical force is crucial for normal cell development and functioning. However, the process of mechanotransduction cannot be studied in isolation from cell mechanics. Thus, in order to understand how cells ‘feel’, we must first understand how they deform and recover from physical perturbations. Owing to its versatility, atomic force microscopy (AFM) has become a popular tool to study intrinsic cellular mechanical properties. Used to directly manipulate and examine whole and subcellular reactions, AFM allows for top-down and reconstitutive approaches to mechanical characterization. These studies show that the responses of cells and their components are complex, and largely depend on the magnitude and time scale of loading. In this review, we generally describe the mechanotransductive process through discussion of well-known mechanosensors. We then focus on discussion of recent examples where AFM is used to specifically probe the elastic and inelastic responses of single cells undergoing deformation. We present a brief overview of classical and current models often used to characterize observed cellular phenomena in response to force. Both simple mechanistic models and complex nonlinear models have been used to describe the observed cellular behaviours, however a unifying description of cell mechanics has not yet been resolved.

1. Introduction

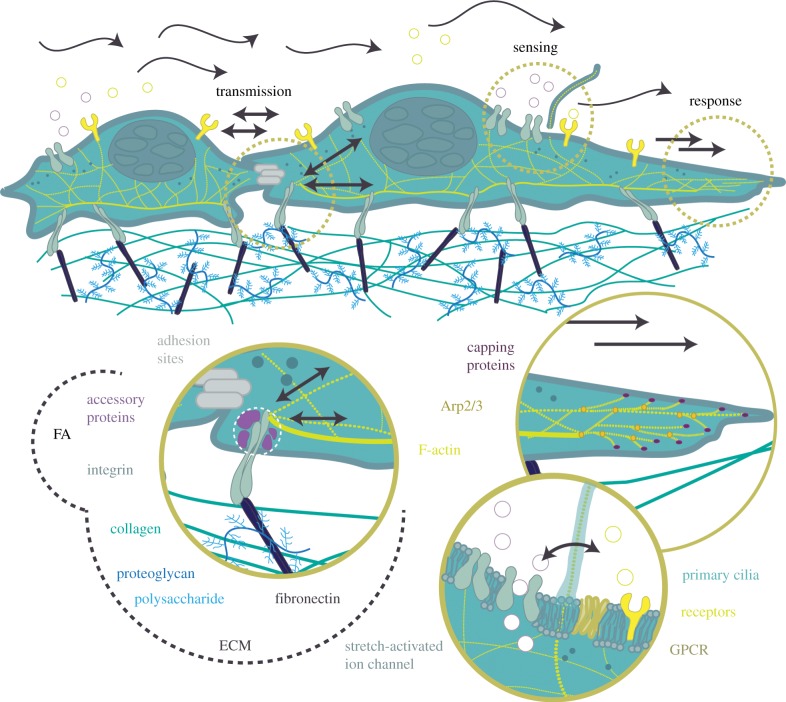
Cells are exposed to and must respond to a variety of mechanical loads in vivo [1–3]. Primary examples include: shear fluid forces on endothelial cells [4], compressive forces on bone cells [5] and highly dynamic tensile forces experienced by epithelial cells [6]. Cells are able to deform rapidly, leading to subsequent changes in their biochemistry. They ‘feel’ neighbouring cells, as well as respond to changes in their underlying extracellular matrix. Cells exposed to substrate stretch, for example, have been shown to realign in the direction of minimal deformation (perpendicular to the axis of strain) [7], whereas cells exposed to fluid shear stresses align in the direction of flow [8]. The response to mechanical stimuli is complex and depends on both force magnitude [9] and rate [10]. Strain rate, in particular, has been shown to affect stretch-induced remodelling of F-actin [11–13]. External forces transmitted through the plasma membrane and focal adhesions (FAs) are conveyed to internal load-bearing structures of the cytoskeleton, influencing nuclear deformations, transcription processes and gene expression [14,15]. Internal forces generated via molecular motors [16] and actin polymerization [17,18] are transmitted to the substrate in order to facilitate migration [19], undergo mitosis [20] and communicate with neighbouring cells [21]. This continual process of sensing, transmission and response is known as mechanotransduction and is essential for maintenance of normal cell functioning and development (figure 1).

Figure 1.

Mechanotransduction—a process of force sensing, transmission and response. Forces, such as tension/compression, and shear flow from the microenvironment are sensed by membrane surface receptors, such as primary cilia, stretch-activated ion channels and G-protein-coupled receptors (GPCRs). Meanwhile, forces from the ECM are sensed through focal adhesions (FAs) and transmitted to the inner actin cytoskeleton. Force is also transferred between adjacent cells through cell–cell junctions. Mechanical cues have been shown to elicit a variety of cellular responses, from biochemical signalling to directed migration. (Online version in colour.)

This review focuses on the role atomic force microscopy (AFM) plays in examining the mechanics of cells. In particular, we focus on non-specialized single animal cells since specialized mechanoreceptors, such as those on human skin and those that constitute the intricate architecture of the auditory system, have been studied in great detail [22,23]. Although some of the key mechanosensors, such as stretch-activated ion channels [24], integrins [25] and primary cilia [26], have been identified, how they configure themselves within the cell and how they respond to a myriad of mechanical cues has yet to be well characterized [27]. In order to understand the inner workings of mechanotransduction, we must first aim to understand the complex nature of cell mechanics. Generally, either top-down approaches involving cellular manipulation techniques or reconstitutive methods including biochemical and single biopolymer studies are employed. AFM can be used in both approaches and has become a popular tool to probe the mechanical response of cells [9,28,29]. AFM has been used to measure both elastic [30–32] and viscous [10,33–37] cellular responses, from which a number of models have been proposed in an attempt to characterize observed cellular behaviours. Although some models fit experimental data quite well, most do not fully describe all of the observed behaviour, and many appear contrasting in their predictions [38].

In this review, we aim to provide an overview of our current understanding of mechanotransduction, in the context of mechanosensing and force generation within cells. First, we will discuss some of the key players identified in mechanotransductive processes. As well, we will take a look at how cells respond to mechanical stimuli. We will then provide a concise overview of some of the classical and more current models used to describe cellular mechanics. A generalized model of cell mechanics remains elusive, and so characterization of cell mechanics lends important clues in our understanding of cell behaviours. Direct cell deformation experiments, such as those performed using AFM, are valuable in order to characterize cell deformation and recovery responses. Therefore, the main focus of this review involves a discussion of recent articles where AFM is used to directly probe the response of whole cells as well as their subcellular components.

2. Multiple mechanosensors are at play

Herein, we briefly discuss some of the main regulators of mechanotransduction—those involved in sensing, and transmission throughout the cell. Major contributors in this process include: the extracellular matrix (ECM), adhesion sites (cell–cell and cell–ECM), the cytoskeleton, surface-membrane molecules, as well as nuclear components. While providing structural support, the ECM acts as an external cell-signalling region and allows for the integration and adhesion of specific cell types. The mechanical properties of the ECM have long been known to influence cell behaviour, such as motility [39], and fate, as demonstrated by the influence of substrate stiffness on differentiation [40,41]. Sites of ECM–cell adhesion (FAs) [42], as well as cell–cell adhesion (cadherins) [43], are also directly affected by ECM composition and are known regions of force sensing and transmission. Classically, a mechanosensor was defined as a transmembrane ion channel linked via tethered networks to both intra- and extracellular anchors [44]. As a primary example, stretch-activated ion channels are driven open by membrane and cytoskeletal tension, altering the permeability of cells to specific ions [45]. These mechanosensitive channels have been proposed to act as sensors to indicate where the cytoskeleton, which absorbs and transmits most structural loads within the cell, should be reinforced [24].

Acting as a hub, FAs direct signalling molecules towards integrins—transmembrane proteins that link the extra- and intracellular microenvironments and direct many cellular responses (reviewed in [46]). External mechanical forces applied to the cell have a crucial impact on the formation and size of FAs [47]. Interestingly, focal complexes (FCs) (precursors to mature FAs) are not reliant upon mechanical tension in order to assemble [44]. Moreover, the formation of mature FAs is highly transient with disassembly occurring upon loss of mechanical stimuli, as demonstrated by loss of actomyosin contractility [48,49]. In vitro studies have shown that mechanical activation of both integrin signalling and FA assembly results from substrate stretch [11–13] and induced fluid shear stress [50], demonstrating simultaneous activation of mechanosensors.

The cytoskeleton spans the entirety of eukaryotic cells, providing structural support and integral tension, therefore its key role in mechanotransduction processes is unsurprising. Composed of actin, intermediate filaments as well as microtubules, the cytoskeleton provides a dense meshwork of polymers wherein intracellular transport occurs and local forces are widely distributed [51]. Actin, in particular, has long been known to respond to external forces through deformation and rearrangement [9,52–57]. As the most profuse protein within the cell, globular actin (G-actin) binds to adenosine triphosphate (ATP), polymerizing to form filamentous actin (F-actin). F-actin and microtubules, unlike intermediate filaments, are highly polarized. Deformation of these filaments occurs through a dynamic process of assembly and disassembly—a process that influences mechanical loading. Mechanical cues directly affect actin formation and alignment, and changes in the chemical make-up of the filament [58]. The phenomenon of F-actin re-alignment in the direction of shear flow is dependent on tyrosine kinase activity, intracellular calcium (Ca²⁺) and intact microtubules [8]. The cytoskeleton is also coupled with the plasma membrane via the actin cortex (reviewed in [59]). Proteins such as ezrin, radixin and moesin (ERM) form links between the cortex and membrane, providing a direct interface for mechanical force transduction between the extracellular and intracellular environments [60]. This interplay between the plasma membrane and underlying actin cortex has been shown to influence both cell shape and function [61,62]. Of course, intermediate filaments (reviewed in [63]), and compression-resistant microtubules also play a role in maintaining cell shape [64], in addition to sensing and trafficking signals to the nucleus [65].

The individual role of the plasma membrane in mechanotransduction has gained recent attention. Acting as a dynamic barrier between the external and internal environments of the cell, the plasma membrane mediates transport across lipid bilayers via passive diffusion for selective ions, active transport across transmembrane channels, as well as endocytosis and exocytosis. The plasma membrane is host to a number of ligand–receptor binding sites and is coated by a number of proteins that encompass the glycocalyx—which itself has been recognized as a mechanosensor (reviewed in [66]). The plasma membrane of endothelial cells is coated in a number of proteoglycans and glycosaminoglycans (GAGs) which have been shown to play a role in white blood cell rolling [67], red blood cell motion and transendothelial transport [68]. Shear stresses arising from fluid flow may affect the structure of molecular components of the glycocalyx or may alter the activation of enzymes. For example, nitric oxide (NO) production is activated in response to shear stress, acting as a homeostatic regulator of endothelial cells and the cardiovascular system [69]. In a seminal paper, Weinbaum et al. [70] demonstrated that the dynamics of GAGs due to shear flow effects can be described by a quasi-periodic fibre matrix model. The bending rigidity (EI = 700 pn nm²) of this brush-like structure was reasoned to be adequate to act as a molecular filter for plasma membrane molecules, as well as for transducing shear forces to the underlying cytoskeleton. This coincides with observation of fibres of the order of 10–12 nm, spaced approximately 20 nm apart in a mesh-like network, which suggests that glycocalyx organization is driven by connections with the underlying cortex [71]. Besides the glycocalyx, other membrane microdomains such as caveolae and lipid rafts [72,73], and membrane-bound organelles such as the primary cilia [74], have also been shown to play a role in mechanotransduction.

In discussing mechanotransduction, the importance of the nucleus, the largest cellular organelle, cannot be overlooked (reviewed in [75]). As gene host and regulator, the nucleus must respond to mechanical forces that arise from both the extra- and intracellular microenvironments. Transmission of forces to and from the nucleus occurs via the linker of nucleoskeleton and cytoskeleton (LINC) complex—a physical tie between SUN and nesprin proteins [76]. This mesh of transmembrane proteins connects the nuclear envelope (inner and outer nuclear membranes and lamina) with the actin cytoskeleton. Inner and outer nuclear membranes are coupled by nuclear pore complexes, wherein ion transport occurs. The nuclear lamina resides on the inner membrane and is mainly composed of lamins connecting the membranes to inner chromatins, among other nuclear components [75]. Despite the existence of these structural proteins, whether a force-bearing matrix exists within the inner nucleus remains controversial among researchers [77,78]. Mutations in nuclear envelope proteins, particularly lamins, result in altered transcription leading to a number of disease pathologies (laminopathies). For example, mutations of the LMNA (lamin A/C) encoding gene results in the development of muscular dystrophy. Malfunctioning of LMNA also results in abnormal nuclear and chromatin structures, with loss of A-type lamins leading to reduced nuclear stiffness [79]. Thus, it is not surprising that mechanically high-stressed tissues will result in cell death and ultimate failure in the absence of lamins. Interestingly, nuclear shape is highly correlated to expression of lamins. Human embryonic stem cells, which do not express lamin A and possess dynamic chromatin, have a very round nucleus. Only upon differentiation do these cells express notable levels of lamin A [80]. Moreover, specialized cells such as neutrophils have irregularly shaped nuclei—lobes connected by chromatin, which are the result of reduced lamin A/C and overexpression of lamin B proteins.

Although we only have discussed the most well-known mechanotransduction constituents, many others have been documented. Despite their identification, many open questions surround exactly how mechanosensors actually sense mechanical stimuli. It is possible that applied force alters the position of molecules allowing for incorporation of other extracellular molecules. Or perhaps protein configuration is altered; proteins associated with FAs such as vinculin, ERM and fibronectin, for example, all exist in dual states of inactivity or activity [44]. Altered conformations may expose new binding sites where molecular interactions can occur. Of course, mechanical stimuli such as substrate stretch and fluid shear stresses may activate more than one response from more than one mechanosensor—and so sensors such as FAs or ion channels are likely to act in unison.

3. Forces generated within the cell

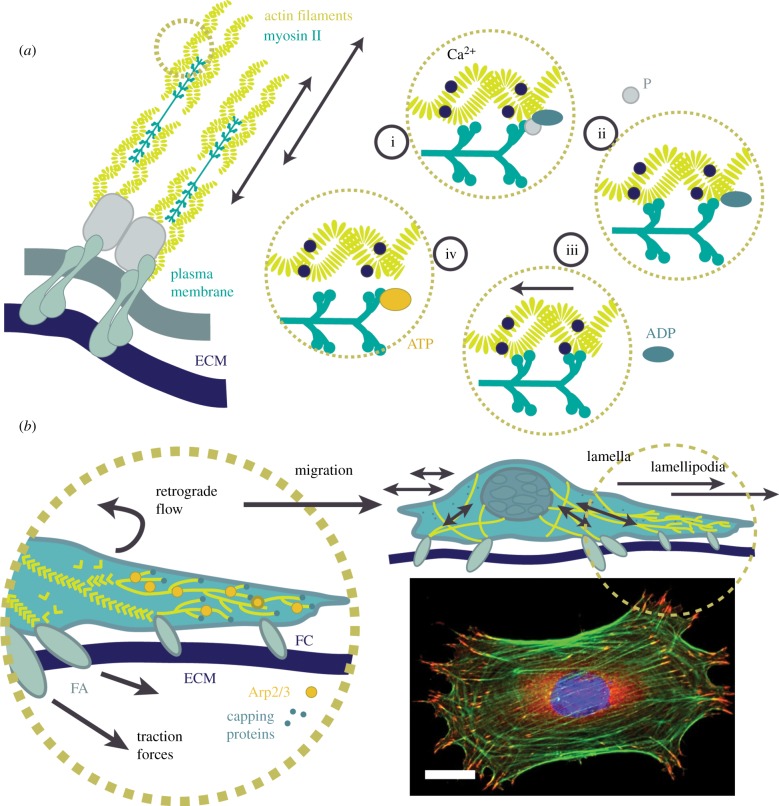
Although extracellular forces have long been known to affect cell behaviour, recent studies also implicate intracellular forces in the regulation of cell and tissue fate [58,81,82]. Often, forces generated within the cell are responsible for the dynamics involved in morphological changes, adhesion processes and motility. One mechanism of intracellular force generation is through ATP-driven sliding of molecular motors (figure 2a). Hydrolysis of ATP is required for movement of the cell's molecular motors, such as myosin II. This energy release allows molecular motors to slide along actin filaments, initiating cell contraction and expansion. Contractile forces are transmitted from the actin cytoskeleton to the ECM via FAs—mechanosensors of force from both the inner and external cellular microenvironments [47]. The magnitude of contractility is coupled with ECM stiffness, as demonstrated through observations using traction force microscopy (approx. 1–10 kPa, with increased traction forces on stiffer substrates [84]). Increased substrate stiffness results in increased FA assembly that drives increased actomyosin contractility. Increased actomyosin contractility also leads to increased FA signalling. This force-balancing act drives shape change and cell proliferation through adaptive cell adhesion. Molecular motors and their expenditure of ATP is not the only force-generating mechanism in the cell's repertoire; actin filament polymerization also directs forces along the cell membrane.

Figure 2.

Force generation within the cell. (a) Actomyosin contractility, as proposed by Huxley & Simmons [83], generates forces transmitted through FAs towards integrins and the ECM. (i) In the presence of intracellular calcium (Ca²⁺), myosin heads hydrolyse ATP before firmly attaching to actin filaments. (ii) Myosin binds to actin and forms cross-bridges. (iii) Force is generated by a ‘power stroke’ as myosin cross-bridges reorient towards the sarcomere centre. (iv) ATP binds to the myosin head and it releases from the actin bundle. (b) Propulsive forces. Actin in the lamellipodia pushes against the plasma membrane in the direction of motion through actin branching and binding of Arp2/3. Capping proteins limit the length of polymerization. Forces are not required for the formation of FCs but do develop across mature FAs in the lamella. Bottom right shows an immunofluorescent image of a C2C12 mouse myoblast cell stained for actin (green, fibres), an FA protein—vinculin (red, localized at ends of fibres)—and DNA (blue). Scale bar, 10 μm. (Online version in colour.)

Actin polymerization is a polarized process involving continual acquisition and deposition of free monomeric polymers (G-actin). This active assembly/disassembly process generates a dynamic linear polymeric chain (F-actin), in a process known as treadmilling (figure 2b). Formation of protrusions and their subsequent attachment to the underlying ECM are the driving factors involved in cellular motility. In motile cells, forces (approx. 45 pN) are generated by branching of dendritic actin networks close to the cell's periphery [85]. These forces result in protrusions at the leading edge, which must be stiff enough to withstand significant compression and tension of the plasma membrane [86]. This highly anisotropic network of actin fibres is formed by a repetitive sequence, wherein surface-membrane proteins are activated, triggering the Arp2/3 complex which is involved in recruitment of G-actin monomers to F-actin filaments, thereby creating filament branches [87]. The flow of actin towards the periphery is directed by the short effective radius of membrane-bound activating proteins. Capping proteins that diffuse throughout the cytoplasm are the limiting factor in actin filament elongation. Microtubules also contribute to the polarization process and have been shown to direct migration by activating Rac1 leading to subsequent actin polymerization in lamellipodia [88]. This repetitive process of initiation, branching and elongation, which depends on this highly anisotropic network, is what drives the cell forward.

While providing integral support, actin undergoes continual remodelling of key cellular features, such as lamellipodia, filopodia and stress fibres. Actin dynamics have long been investigated in a variety of species and cell types [89]. A seminal paper by Theriot & Mitchison [90] demonstrated that actin turnover in goldfish epithelial keratocytes is of the order of approximately 23 s. Measurements were made in the lamellipodia of these highly motile cells, and so it is unsurprising that actin turnover was found to be less rapid in a subsequent study involving slower moving fibroblasts [91]. Differences in actin polymerization rates among cells have been hypothesized to be the result of diverse localization of ADF/cofilin, which is known to induce phosphate release [92]. The rate at which individual actin filaments elongate is of the order of approximately 0.3 µm s⁻¹. Although actin turnover is rapid in motile cells, actin filaments have been observed to remain stable between hours and days in striated muscle, as ADF/cofilin binding is inhibited by tropomyosin [93]. Similarly, stable stress fibres have been observed in non-muscle cells (reviewed in [92]). While a variety of actin-binding proteins influence the polymerization/dissociation rates, mechanical forces also influence actin network organization and its mechanical properties.

The integration of mechanical forces and cellular mechanics dictates cellular shape and function. The interactions between actin and microtubules, for example, play a role in dictating locomotion, cell division, wound healing and cortical flow [94]. During migration of vertebrate tissue cells, the retrograde flow of actin at the leading edge has been directly linked to microtubule translocation to the rear of the cell. The integration of these two cytoskeletal networks has been hypothesized to direct movement through their physical links and activation of a Rho GTPase gradient [95]. Microtubule growth at the leading edge is countered by de-polymerization at the rear of the lamellum, a region where actin converges and myosin-generated contractility is high. Polarized polymerization/growth interactions between actin and microtubules have been hypothesized to stimulate Rac/RhoA activation [95], direct signalling or membrane molecules during lamellipodia protrusions [96], or regulate FAs [97]. The coupled response between cellular components is of course cell-type dependent. For instance, myosin-generated pressure gradients in the rear of fish epithelial keratocytes have been shown to promote forward motion [98]. Intracellular forces arising from cytosolic fluid flow or changes in hydrostatic and osmotic pressure also influence cell shape and volume, which are dynamically regulated by animal cells. A primary example is evidenced during mitosis, wherein actomyosin contractility, in concert with osmotic pressure, actively controls cell volume and shape. Intracellular pressure increases during prometaphase and reaches a maximum in metaphase, with a rounding pressure of 0.14 ± 0.04 nN μm⁻² (measured force of a mitotic cell on an atomic force microscope cantilever, normalized by cell area) [99]. This increase in pressure is driven by increased contractility of the cortex, which results in cell rounding and a reduction in volume. Similarly, cells have also been shown to adapt to osmotic shock conditions in vitro by altering cortical tension, water permeation and ion transport [33,100]. Moreover, cells are able to adapt to local changes in hydrostatic pressure, which has been shown to result in cellular blebs (small protrusions of membrane that detach from the cortex), to relieve tension [101]. It is quite clear from these examples that the actomyosin network coupled with mechanosensitive channels and pumps regulate the flux of water and ions across the plasma membrane to dynamically control cell volume and shape.

As discussed, cells experience a multitude of external forces that are transmitted between the outer and inner microenvironments via the cytoskeleton to inner cellular organelles, such as the nucleus. Moreover, cells themselves also generate force, through actomyosin contractility and actin branching. Although many components involved in mechanosensing have been identified, many questions still remain surrounding their exact mechanisms and function. For this reason, tools, such as AFM, have been used to probe the cellular response to force.

4. Nanomechanics using atomic force microscopy

Nanomechanics has become a popular research area, with tools such as AFM often employed to measure bulk cellular rheological properties, typically Young's (elastic) (E), or shear (G) modulus. AFM can be used to directly apply and simultaneously measure cellular forces, and so is a key tool in this emergent field. Its advantage is its versatility, as AFM can be used for imaging as well as force transmission and measurement. By altering tip geometry or chemistry, a multitude of both local and whole-cell studies can be performed on living cells in their native environments (figure 3). Studies of this nature have been shown to induce a rapid response of cells through shape change, remodelling of the cytoskeleton and calcium signalling, which all depend on frequency, duration, magnitude and location of applied force [9,29,37,102]. In the following sections, we discuss the role of AFM in measuring the mechanical properties of cells, particularly cell stiffness and viscous properties. As well, we highlight commonly observed cell behaviours in response to mechanical loading, including changes in cell geometry and internal organization. Finally, we outline some of the current techniques involving both localized and global stimulation of cell mechanics using modified cantilevers.

Figure 3.

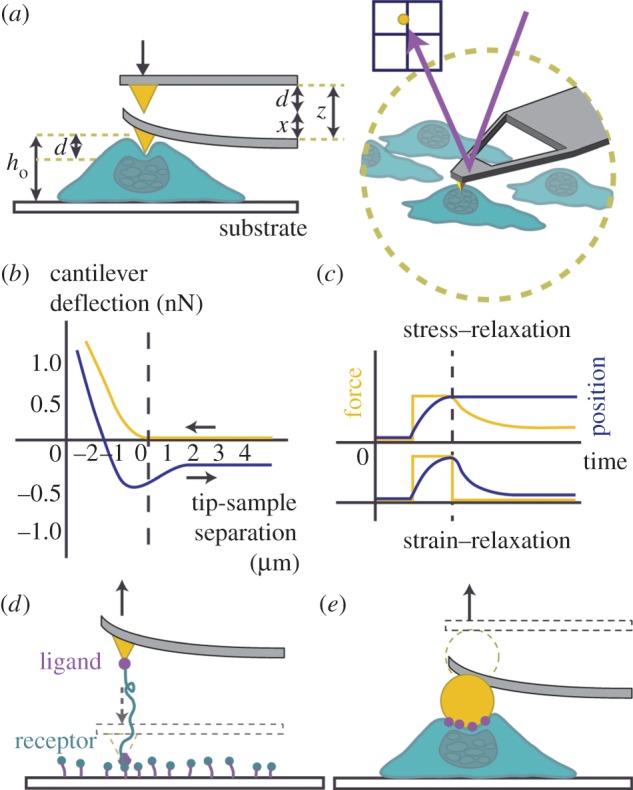
AFM modes of measurement. (a) AFM can be used to precisely apply compressive strains apically to cells within their aqueous environment. A laser deflected on the back of an atomic force microscope cantilever is measured by a photo sensitive detector (PSD). This allows for measurements of cantilever deflection to be recorded. (b) AFM force-indentation curves are often used to measure cellular elasticity, by fitting the approach curve (yellow, ←) to the Hertz model of contact mechanics. The retract curve (blue, →) often shows a hysteresis and can be used to analyse adhesion. (c) Stress and strain relaxation curves are often used to measure time-dependent cellular behaviours. Following an applied strain on a cell, the cantilever can be kept at a constant height, and measurements of cellular force onto the cantilever can be measured. On the other hand, following strain, the height of the cantilever as the cell relaxes can be measured. Modified cantilevers are also useful for measuring binding/unbinding forces between ligands and receptors. (d) Functionalized atomic force microscope tips are often employed for single-molecule interaction experiments. (e) Spherical tips or other physical modifications to atomic force microscope cantilevers can also be used to measure distributed forces. This can be combined with functionalization techniques, as shown. (Online version in colour.)

4.1. Apparent cell stiffness

The deformability of cells has been shown to affect a number of cell functions, with increased cell stiffness correlating with differentiation [40], ageing and diseased states [30,103]. Commonly, AFM is used to measure the local elastic response of cell membranes and the underlying cytoskeleton by fitting force-indentation curves to contact models such as those of Hertz [104] and Sneddon [105]. Details on these methods [106] as well as Young's moduli of a variety of cell types are listed in [35]. Apparent stiffness of mammalian cells, as measured with AFM, typically ranges between 1 and 100's of kPa [9,107,108]. Apparent cell stiffness is highly correlated with the stiffness of the actin cytoskeleton, the structure and mechanics of which are directly influenced by mechanical forces including tension/compression [109,110], hydrostatic and osmotic forces [31,99]. Studies have directly demonstrated drastic reductions in stiffness with the use of actin depolymerizers, but not with depolymerizers of microtubules [29,111,112]. Interestingly, the elastic moduli of purified filament networks are orders of magnitude lower than whole-cell measurements, with reports of E ≈ 1 Pa. While marginal increases in stiffness have been reported when crosslinkers are employed (1–100 Pa), there still remains a significant difference between the apparent stiffness of reconstituted networks and that of whole cells, probably because of the coupled nature of actomyosin contractility and hydrostatic pressure [113]. As mechanical cues largely dictate actin organization and growth, it is unsurprising that cells exposed to constant cyclic mechanical load (cardiac and muscle cells) are stiffer than endothelial cells [114].

It has become increasingly common to characterize and identify diseased and healthy cells using stiffness measurements [103,115–117]. Combined AFM imaging and local force-indentation measurements have demonstrated significant differences between healthy and diseased erythrocytes [103]. Erythrocytes from patients with type 2 diabetes demonstrated significant aggregation of surface proteins, increased tip-cell adhesion, as well as increased stiffness in comparison with healthy cells [103]. Cancer cells typically appear with a rounded morphology when cultured ex vivo [116]; however, it is difficult to compare between a malignant and benign cell type by differences in the cytoskeleton alone. For example, metastatic cancer cells have a dense actin meshwork stemming from their overexpression of key actin regulatory proteins such as Wiskott–Aldrich syndrome protein, Arp2/3, LIM-kinase, cofilin and cortactin [118]. Overexpression of these proteins drastically alters the actin structure of the lamellipodia and promotes the formation of invadopodia and podosomes (enzyme-containing actin structures that degrade the ECM). As an alternative to identification through morphology, cell stiffness has been proposed as a candidate for cancer cell detection, as cancerous cells are considerably softer (upwards of 70%) than healthy cells [36,115,116,119]. Softness associated with cancerous cells has been linked to the deformability of the cytoskeleton, which has long been known to play a role in metastasis [120]. Lekka et al. [115] have shown that this type of characterization can also be used directly with cells from tumours and surrounding tissue samples taken from patients. In comparison with normal cells, cancerous cells have been shown to have a dense elongated cellular brush, consisting of the glycocalyx and pericellular layer [119]. This brush may interfere with fitting of force curves using typical pyramidal atomic force microscope tips. Stringent statistical tests must be carried out in order for AFM analysis to be used as an effective cancer diagnostic method [115], as both substrate effects [107] and incorrect fitting of force-indentation curves can lead to deleterious reports of absolute Young's moduli.

Varied reports of cellular elasticities in the literature are in part due to the highly non-uniform cell surface. AFM-generated force maps have revealed local variations in cell height and stiffness (usually several kPa) due to the presence of internal components, such as actin bundles [108,111] and the nucleus [37]. Moreover, stiffness measurements depend not only on cell type, but also on probe geometry, rate of force application and force magnitude [35,121]. Typical high aspect ratio conical atomic force microscope tips have radii less than 30 nm and generate high local stresses which might penetrate the membrane during large magnitude force application [122]. Thus, to avoid damage and operate within the elastic deformation regime, Young's modulus measurements are generally made using low forces, in the range of 0.1 to several nanonewtons. Nawaz et al. [121] have recently shown that only at extremely low forces (less than 30 pN) and low deformations (0.2 μm) do fibroblast cells present ideal linear elastic behaviour. They used an optical trap method to apply these low forces, as the atomic force microscope is limited by thermal noise at forces nearing 20 pN in liquid. Other techniques such as magnetic twisting cytometry, optical stretching and force-modulation AFM mode have been used to apply sub-micrometre deformations to measure cell stiffness at low deformations [123]; however, these methods are beyond the scope of this review. At higher forces (more than 30 pN) delivered by an atomic force microscope in contact mode, viscoelastic behaviour was observed, as indicated by hysteresis between the force approach–retract curves. Importantly, their work demonstrated that, at very small deformations, the elastic response was rate independent and reliant upon the cortex. Considering the limited thickness of the plasma membrane (approx. 10 nm), it is unsurprising that the underlying cortex (approx. 200 nm) will largely resist the deformation [124].

Apparent stiffness, which is generally measured using AFM, is based on the assumption that the cell behaves as an isotropic purely elastic material. Dynamic AFM experiments, on the other hand, suggest that stiffness (k) increases with increasing frequency (f) and can be described by a weak power law (k(f) ∼ f^α) at higher deformations. Although power laws have often been used to describe frequency-dependent rheology, there remains variability in reports of exponents (α). Elasticity measurements of this nature are generally only comparable if all experimental conditions are kept constant. To circumvent these concerns, stiffness measurements are often used in a relative manner rather than as absolute values [111]. The heterogeneous nature of the cell, as well as influence from the underlying substrate, makes obtaining the cell's intrinsic apparent stiffness difficult to quantify. Applying shallow indentations [114] and using modified contact mechanics models [107,125] can however alleviate these issues.

4.2. Stress–strain relationships

Although a cell's apparent elasticity directly influences its deformability, it does not fully account for the complex behaviours observed following mechanical perturbation. Cells respond to abrupt external perturbations in a highly nonlinear, time-dependent manner [126]. Many AFM studies have revealed the viscoelastic nature of cells, as witnessed by creeping deformation and relaxation behaviour following loading [10,33–37]. The actin cytoskeleton alone has been shown to exhibit viscoelastic behaviours [127]. Cellular viscoelasticity is influenced by a hierarchical structure—the membrane, cortex and cytoplasm (among other subcellular components) all contribute to the cell's mechanical properties. The cortex and actomyosin in particular play key roles in maintaining cell shape and function [112,128,129]. Organization of actin significantly impacts the cellular response to force, as seen during recruitment to the cortex which provides resistance to external forces. The plasma membrane also resists deformations, as it possesses a relatively high elastic modulus [130] and a low shear modulus [131] (as shown in erythrocytes), and a bending modulus highly influenced by the underlying cytoskeleton. The membrane relieves tension through increased intermolecular separation and relieving of undulations [132]. The mechanics of the membrane and cortex are physically linked, and so the properties of both inherently influence one another. Recently, contributions of cytosolic flow have been shown to influence the response to deformation [33]. Moreover, the large-volume nucleus clearly plays a part in defining overall cell properties, which, until recently [133–135], has been mostly described as isotropic [136,137]. Clearly, the complex shape and structure of the cell's inner components play a role in defining cell mechanics. With these considerations in mind, many researchers have used AFM as a cell nano-indenter to quantify cell viscoelastic properties in the time and frequency domains [28,35,138–141].

A large number of studies have employed both pyramidal and spherical tips to directly deform cells (figure 4a) which have been shown to withstand relatively large forces (within 10–20 nN) in vitro [143,144]. These deformations of the membrane and underlying cytoskeleton result in viscoelastic behaviours. Cellular creep and relaxation experiments, measured using AFM, have been used to determine apparent viscosity and relaxation behaviours generally associated with simple models and a discrete number of time constants [10,33–37,145]. Time constants are linked to an elastic deformation regime, and exponentially increasing viscous creep (figure 3c). During constant stress experiments, creep, J, can be measured as a ratio of time-dependent strain over stress: J(t) = ɛ(t)/σ₀. On the other hand, by maintaining a constant cantilever displacement (while straining the cell), force feedback on the cantilever can be measured as a function of time. This type of experiment results in stress relaxation curves, from which apparent cell viscosity can be measured by fits to a time-dependent modification of the Hertz model [112]. The relaxation behaviour of the cell is treated as a standard linear solid model (a Maxwell model in parallel with a spring). Use of this method has shown that actin, not microtubules, is the primary influence of a cell's apparent viscosity in mouse ovarian surface epithelial cells [112].

Figure 4.

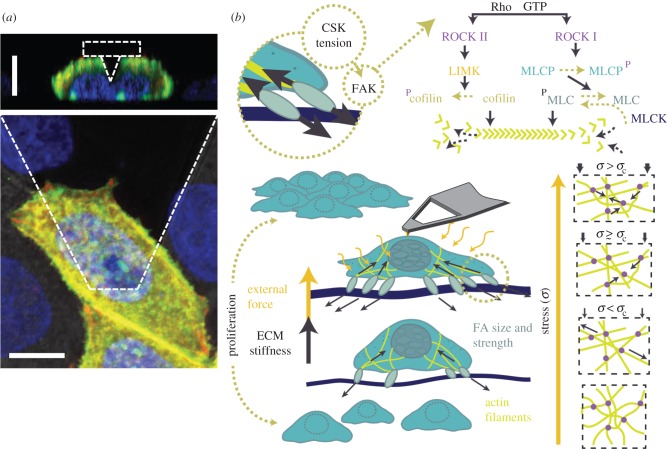
Cellular response to mechanical cues. (a) Confocal projection image of a living HeLa cell as it is being deformed by a pyramidal atomic force microscope tip (approx. 10 nN). Shown is the deformation in the orthogonal x–z direction. HeLa cells shown were transfected with EGFP—phospholipase-C-δ (a membrane marker in green)—and an actin RFP—LifeAct Ruby (an actin marker shown in red); nuclei were dyed with Hoescht (blue). Scale bars, 10 μm. (b) Both the mechanical properties of the ECM and externally applied forces, such as those from an atomic force microscope tip, have been shown to increase cell spreading, traction force magnitude and proliferation. Tension between the ECM and cytoskeleton (CSK) activates focal adhesion kinase (FAK), which has been shown to directly activate the Rho family of GTPases. Through different pathways, Rho-associated protein kinase (ROCK) has been shown to lead to both polymerization and depolymerization of actin stress fibres. Mechanical forces have also been shown to stimulate both a stress-stiffening and softening response of actin networks. One hypothetical model explaining this paradox is shown, as in [142]. With increasing stress actin filaments elongate due to tension (stiffening), until a critical stress (σ_c) is reached, following which filaments begin to buckle (apparent softening). (Online version in colour.)

Cellular rheology is best described by the mechanics observed across a wide range of frequencies, as well as force magnitudes. For this reason, many have used AFM in a dynamic mode, allowing for determination of the complex elastic or shear moduli of cells [146]. By operating in a high-frequency (50–300 Hz), low-amplitude (2–5 nm) oscillatory manner, the frequency-dependent viscoelastic behaviour of NIH 3T3 fibroblasts was examined by Mahaffy et al. [125]. Elastic storage and loss moduli of living fibroblast cells were detected by measuring the amplitude and phase shifts, and extending the Hertz model to include frequency-dependent behaviour [125]. Both elastic and adhesive properties of the cell can be examined in this oscillatory mode; however, it is necessary to include appropriate models to incorporate the deformation of soft samples of finite thickness. By taking into account tip-cell contact geometry, as well as viscous drag effects of the aqueous sample, researchers have used this dynamic mode to measure the complex shear modulus G*(ω) of cells at a range of frequencies and load magnitudes [147]. Generally, the observation that prevails is power-law behaviour. At low frequencies (less than 10 Hz), both the storage G′(ω) (elastic component) and loss moduli G″(ω) (viscous component) follow the same behaviour; however, at higher frequencies the power-law exponent of the loss modulus is progressively increased. Power-law behaviour suggests that cells may not be described by distinct time constants after all [148–151]. While experimental observations do appear to follow power-law behaviour, measurements are often only performed over millisecond- to second-long time scales. Limitations of static and dynamic methods must be taken into consideration, including possible interactions within the cell which may lead to remodelling events and unknown binding geometries [152]. Moreover, the cell is not an inert material, the cytoskeleton undergoes constant remodelling within time scales relevant to these experiments, making overall cell mechanical properties difficult to obtain.

4.3. Cellular response to force

In addition to characterizing strains, AFM deformation studies have elicited a plethora of cellular responses in vitro (figure 4b depicts several of these responses). Cell signalling, in particular, has been demonstrated in response to forces applied using AFM. One example demonstrated that vertically applied strains result in transient increases in intracellular calcium in osteoblast cells—a response transmitted to neighbouring cells [29]. Importantly, compressive forces applied to cell nuclei have been shown to result in altered gene expression [15,75]. As the cell actively senses and responds to changes in the surrounding environment, it is not surprising that mechanical tension directs the formation and remodelling of FAs in vitro. Cells are particularly sensitive to changes in stiffness and actively tune the magnitude of traction forces they generate upon their substrate, as regulated by Rho, Rac and CDC 42 GTPases [153]. Recently, AFM stiffness measurements of wild-type and mutant mouse embryo fibroblasts demonstrated that focal adhesion kinase and Cas stimulate Rac activity, promoting intracellular stiffness and a mechanosensitive feedback loop in response to ECM stiffness [154]. Compressive forces may also stimulate this feedback mechanism. Combined AFM and traction force microscopy demonstrated that external forces and substrate stiffness both direct FA size and strength [84].

Mechanisms of actin-based force generation and growth have also been investigated using nano-indenters [142,155,156]. By functionalizing (biochemically modifying) the surface of an atomic force microscope cantilever with ActA (Listeria nucleation promotion factor), and immersing it within a liquid cytoplasmic cell extract, the Arp 2/3 complex can be activated, resulting in the growth of a network of actin [155]. Force-feedback measurements have revealed three growth regimes: a development phase, a load-independent phase and load-dependent cessation of network lengthening. Surprisingly, a decreased load applied to the network resulted in an increased growth velocity demonstrating a load-history-dependent response [155]. In vitro studies have also shown that apically applied compressive forces result in highly localized non-isotropic deformations of stress fibres [9]. Myoblasts and alveolar epithelial cells are constantly exposed to quick bursts of stretch in vivo; however, in vitro experimentation has shown a complex mechanical response to cyclic forces. The response to stretch and compression results in a paradox: both cytoskeletal reinforcement and fluidization have been reported [56,157]. The same is true for reconstituted dendritic actin networks formed by a nucleating surface (an atomic force microscope cantilever). In response to a sinusoidal load, stress stiffening was observed, followed by reversible softening [142]. This behaviour has been attributed to entropic elasticity as filaments are extended, leading to a stress-stiffening regime and reversible buckling of actin filaments at higher loads [142] (figure 4b). The large elastic modulus of these anisotropically organized filaments is primed for resistance to compression—as is necessary at the leading edge of motile cells. This stress-stiffening behaviour has been observed during relatively small (less than 10 nN) cyclic forces applied at a constant height from an atomic force microscope to attached cells [158]. Initial increases in local tension were followed by a subsequent decrease (explained by stress relaxation of the cortical cytoskeleton), and long-term slow increase in tension as the cycles persist (likely diffusion-limited, as in the recruitment of myosin II). Considering that tension recovery-associated factors (such as myosin II here) are recruited during each tension–compression cycle, it is not surprising that the tension recovery slows with each cycle, as binding sites are filled, and there may be less motor proteins in the vicinity. Inhibiting of actin polymerization and myosin II contractility with the use of cytochalasin D and blebbistatin, respectively, verified that the actomyosin network is responsible for the observed tension recovery following cyclical loading [158]. This study importantly shows that cells have ‘memory’—they initially stiffen with regard to an external force, but then become increasingly insensitive to repeated perturbations, thus responding in an adaptive, and probably protective, manner.

4.4. Modified cantilevers

Biochemically modified cantilevers are often used in order to probe adhesion of whole cells, localized regions and specific molecules (reviewed in [159]). Coatings, such as poly-l-lysine, have been used to strengthen bonds between the tip and cell allowing for membrane tethering and retraction curve analysis [160]. By microinjecting biotinylated cadherin-expressing cells onto an atomic force microscope tip coated with streptavidin, single cells can be used to form adhesions with other cells in culture [161]. Using this method, researchers have shown that the specificities of E- and N-cadherins are distinct (preferring homophilic bonds), alongside producing different adhesive and compliant bonding forces. Similarly, ligand binding to atomic force microscope tips allows for examination of specific cellular molecules and their interactions [162]. Recently, biotin/streptavidin functionalization has shown that tension regulates actin depolymerization [163]. This technique has also been used in conjunction with force-mapping methods in order to spatially locate receptors of specific antibodies bound to the tip. For example, a specific tyrosine kinase antibody (anti-Flk-1) was used to demonstrate that clusters of vascular endothelial growth factor (VEGF) receptors exist. VEGF is known to play a role in altering permeability to extracellular macromolecules in endothelial cells, which aids in their growth. These clusters were shown to drastically reduce local elastic moduli, potentially caused by their reorganization of underlying cytoskeletal filaments in the promotion of cell growth [164]. This is a good example demonstrating the influence of local composition and structure on cellular mechanics.

Besides biochemical functionalization, modifications to tip geometry have also resulted in numerous interesting applications. For example, ion beams have been used to etch the cantilever's tip into a thin needle-like rod (200–300 nm in diameter) which researchers have used to perform cellular nano-surgery [165]. Sharp tips have been shown to penetrate both the outer plasma membrane and inner nuclear membrane, as demonstrated by recorded spikes in force-indentation curves. This technique has allowed for delivery of proteins and chemicals to the inner cell nuclei [165], enabling single-cell transfections [122]. Rather than decrease the size of the tip, others have attached spherical beads of a relatively large diameter (more than 20 μm) to atomic force microscope cantilevers. This approach allows for a more even distribution of compressive forces to be exerted upon cells and is often applied to adherent cells to gain a better approximation of whole-cell rheological properties. Often tip modifications are used in unison with optical microscopy techniques. For example, Stewart et al. [166] tracked the force feedback on a spherical tipped atomic force microscope cantilever and simultaneously tracked the cross-sectional area of a cell undergoing mitosis. Cell pressure was shown to increase dramatically (threefold in 10 min) alongside a small volume change, suggesting that osmotic pressures and the actin cortex largely contribute to morphological changes in the cell [166]. Tipless cantilevers have also been employed as parallel plate compression devices by adding a wedge to the end of the cantilever to correct for the mounting angle (usually 10–12°) [167].

Combining AFM with traditional microscopy methods has become quite conventional, as it provides a means for simultaneous application of external forces, quantitative measurements and direct visualization of the perturbed cells. A major limitation of these combined methods is that compressive forces on the apical surface of the cell create deformations in the orthogonal planes. To visualize deformations in the axis of loading, Chaudhuri et al. [168] developed a method using a coverslip and second CCD camera used in the lateral plane. Using this method, they were able to examine adhesive forces between leucocytes and endothelial cells. An atomic force microscope tip coated with concavalin-A was contacted with a leucocyte forming a strong bond, after which the sample surface was moved steadily away from the cantilever causing a tension on the tip-attached leucocyte and underlying endothelial cell. Large adhesive rupture forces, attributed to delamination of the cortex and membrane, were recorded as the cells were separated followed by small non-zero rupture forces as membrane tethers (visualized by their side-view method) that had formed between the two cells came apart. AFM has also been combined with other known optical techniques, such as total internal reflection microscopy (TIRF). TIRF allows for observation of the dynamics in the basal membrane of cells, all while undergoing compression from an atomic force microscope cantilever. This technique has been used to demonstrate nonlinear stress-stiffening behaviour of the cytoskeleton in the basal membrane of L929 fibroblast cells following compression [169]. Importantly, TIRF images showed that actin is responsible for force transmission throughout the cell. Although we do not discuss AFM imaging in this review, this technique has many important applications in cell mechanics. For example, it has been used to identify various membrane proteins and intracellular microfilaments [170,171]; a good review can be found in [172].

Mechanics at the mesoscale should also be considered, as embryonic development, morphogenesis and tumour progression, for example, are highly dependent on cellular organization. Techniques such as modified traction force microscopy [173] and stretching devices [174,175] have recently been used to examine coordinated cell migration and stretch, respectively. Integrated mechanical properties have been shown to supersede those of single cells [174], demonstrating the importance of characterization of multicellular mechanics. While the precision of the atomic force microscope is currently primed for single-cell studies, novel atomic force microscope modifications may prove useful for future multicellular-scale studies. Integration of single-cell and multicellular studies will be necessary for a comprehensive understanding of mesoscale mechanics.

5. Models of the cell

In an attempt to describe the observed cellular behaviours discussed, a number of models have emerged over the years (figure 5). Simple mechanical models are often used to characterize the mechanical properties of cells in the time domain. These models generally comprise one or more elastic and viscous elements, often denoted by springs and dashpots, respectively (figure 5a). The downside to this simplistic approach is that reported time constants vary widely in the literature. Discrepancies are often attributed to varying time scales and frequencies of experiments. Contrary to simple mechanical models, many researchers have reported power-law behaviour to describe the creep function of cells following an applied step-stress [148,149], which implies a large number of continuous time constants. Universality in rheological exponents appears to exist among the power-law form of cells' frequency-dependent behaviour, but not in its amplitude, as demonstrated during controlled changes of physical properties. This is particularly apparent during chemical perturbation. For example, actin depolymerization results in decreased elastic moduli of cells, however the range of values reported is quite large (100–1000's kPa). In cases of non-universality, researchers have proposed that cells were nearing a phase change, better represented by soft glassy rheology (SGR) [176,178]. Whether or not these discrepancies are due to altered interactions with the measurement probes remains an active area of research. A number of other classical models have been used to describe cellular mechanics over the years. These include, but are not limited to, the sol-gel hypothesis, tensegrity and models of active cross-linked gels, a detailed discussion of which can be found in [38]. Several models have been derived from both constitutive and global approaches to examining cell mechanics.

Figure 5.

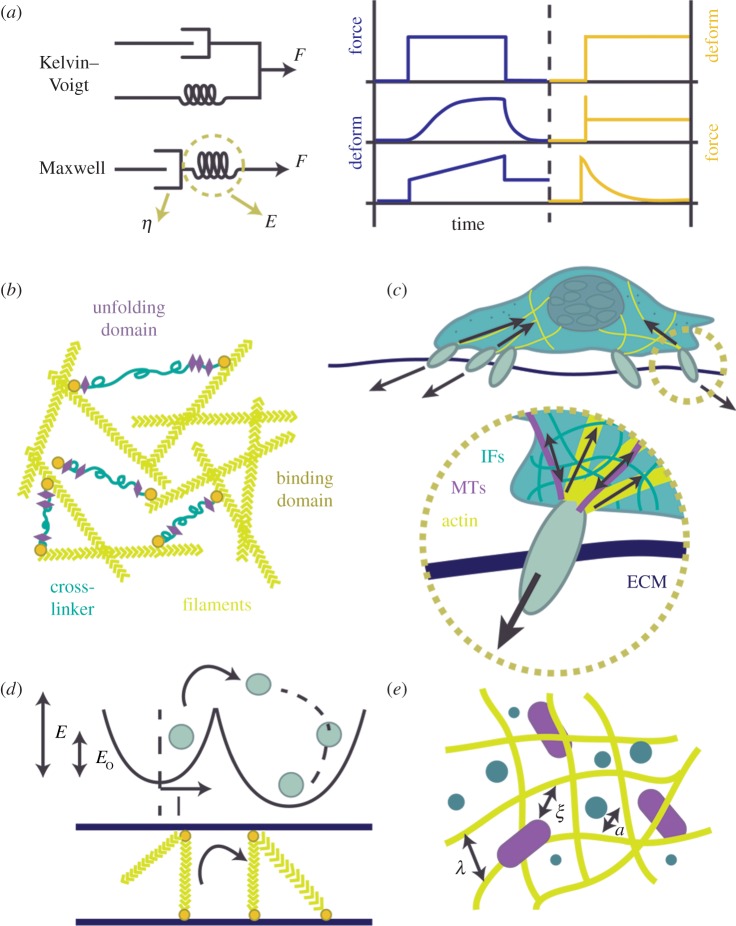
Models of cell mechanics. (a) Commonly employed viscoelastic models. The Maxwell and Kelvin–Voigt models are shown as simple combinations of springs and dashpots, representing elastic and viscous components, respectively. Shown are the stress/strain relaxation curves for each of the models. (b) Active cross-linked polymer networks. (c) Tensegrity model, as shown by force balancing between the cytoskeletal components and ECM. IF, intermediate filament; MT, microtubule. (d) SGR is shown through an image of a dynamic trap, wherein elements (myosin motors) hop between different quadratic wells or binding energies: E = 1/2kl². If attachment of a filament occurs at a length (l), then a force kl is generated (k is the spring constant) which results in sliding of the filament until equilibrium is reached. (Adapted from [176,177].) (e) Poroelastic model of cytosol flowing through a solid meshwork of filaments. The rate of flow is limited by filament size, and size of the macromolecules, a, and entanglement length of filaments, λ, and ξ, hydraulic pore size. (Adapted from [33].) (Online version in colour.)

At their most basic uncoupled state, purified polymer networks have provided a great deal of insight into the mechanics of subcellular cytoskeletal components [87]. Models based on entangled polymer networks, such as the sol-gel hypothesis, involve the transformation of a solution (sol) of monomers into a biphasic gel or network of flexible polymers (figure 5b). These biphasic polymer networks are comparable to the cytoskeletal filaments contained within the cytoplasm of the cell. Treated as an elastic continuum, these networks deform under shear, but are incompressible to hydrostatic forces. Networks of short filaments and a low concentration of crosslinkers behave as a fluid when exposed to stress (the sol state), whereas a high concentration of crosslinkers or lengthened filaments exhibit elasticity (the gel state). Traditional sol/gel states are only reliant upon thermal fluctuations; however, in the context of cells more complex ATP-driven mechanics are at play. Similarly, continuum models of active cross-linked gels have been proposed to describe the behaviours of reconstituted isotropic actomyosin networks [179–181]. By altering protein and crosslinker concentrations in vitro, self-assembly dynamics can be studied at different length, time and force scales. Under tension, models employing purified actinin and filamin, as passive crosslinkers, demonstrate power-law behaviours similar to cells. Similar to the contradictory findings in whole cells, both strain hardening and softening have been observed in reconstituted polymer networks [142,182]. Protein unfolding/unbinding has been proposed to explain these behaviours, with unbinding dominating at low pulling rates, and unfolding of crosslinkers dominating at faster rates.

Discrete models have also been used to describe whole-cell behaviour (figure 5c). First proposed by Ingber [183], the tensegrity model equates the cytoskeleton to pre-stressed structural components that act in unison to provide structural integrity to the cell. In particular, the actomyosin network is thought to generate pre-stress within the cytoskeleton, while extracellular tension is generated through cadherins or FAs. Actin and intermediate filaments have been shown to generate and sustain tension, whereas microtubules and FAs bear internal compressions of the cell. Moreover, pre-stress in cytoskeletal components has been shown to be linearly related to overall cell stiffness. While useful for describing macroscopic deformations, tensegrity does not describe cellular phenomena related to frequency dependence, thermal and non-thermal fluctuations, or localized mechanical properties. Although cell stiffening has been shown in response to externally applied forces in vitro, strain hardening might better describe such occurrences [182].

As previously mentioned, a model proposed by Sollich [177], SGR, has also been used to describe various cellular mechanical phenomena [176]. Using this model, a phase transition (ageing) is brought about by a structural rearrangement within cells that probably relies on ATP or mechanical stress (figure 5e). Promotion/inhibition of actin polymerization and myosin contractility both produce conflicting results in the literature. In contrast to the strain-hardening behaviour predicted by the tensegrity model, SGR predicts strain-softening will occur when cells undergo application of large forces. Although the application of SGR is widespread for describing the physical phenomena observed in many cellular dynamics experiments [55,147,149], it is best used to describe only the contractile actomyosin network.

Recently, poroelasticity has been used to describe the dynamic behaviour of whole cells undergoing deformation [33,99]. The premise of poroelasticity is based on deformations of soft gels [184]. As the material undergoes deformations, the fluid phase flows through a solid mesh, thus a material's ‘poroelasticity’ or deformability is limited by the pore size of the solid mesh (figure 5e). Within the framework of a cell, the cytosol is characterized by the fluid component and the dense network of filaments and proteins composes the solid mesh network. Moeendarbary et al. [33] have recently shown that cell relaxation following mechanical perturbation (with a spherical indenter) can be described using this model. Immediately following cessation of the external perturbation, the cell recovers quickly—and is attributed to the flow of cytosol through the filamentous cytoskeleton. By exposing cells to hypo-osmotic and hyperosmotic conditions, the authors demonstrate that the rate of flow of cytosol through the mesh is directly related to its pore size. Cytoplasm is the largest cellular component by volume, and its rheology in the context of cellular mechanics is likely to be dominant. While useful, poroelasticity does not describe long-duration recovery processes which are likely to be dominated by cytoskeletal remodelling.

Mechanical manipulation of cells has led to significant insight into their mechanics; however, a general mechanical model has not yet been reached. Much of the observed cellular phenomena are difficult to quantify, a complexity magnified by a structural hierarchy undergoing constant protein and structural turnover. It is probable that reported power-law exponents and master curves represent an average of multiple structures, where one structure may dominate. Alternative models to the classical ones incorporate nonlinear effects which have been proposed to describe phenomena such as cell fluidization [185]; however, they too are incomplete. Moreover, although protein unfolding/unbinding processes have been implicated in the mechanotransduction process, individual highly sensitive mechanosensors remain largely unknown. It is possible that molecules on the brink of a conformational change act as sensors within a network of cross-linked biopolymers. Considering the number of cross-linking proteins within a given cell, it is likely that the sensing occurs by multiple proteins simultaneously, as in FAs. Studies involving whole-cell mechanics as well as single-polymer studies both have their drawbacks. An all-encompassing theory of cell rheology may rely intrinsically on a coarse-grained picture of the cell. However, measurements of bulk elastic and viscoelastic properties of the cell may only be useful in limiting cases. In an illuminating review on active biological materials, Fletcher & Geissler [87] discuss how current theories involving linear and scaling-law rheological models only fit a small fraction of detail in the big picture of cell mechanics. Difficulties include simultaneous deformation of a variety of cellular structures, probe interactions and the use of non-specific inhibitors which can result in a myriad of other cellular changes. With these cautionary statements in mind, we note that only through careful examination of cellular mechanics will we be able to develop a clear understanding of the inner workings of cell mechanotransduction.

6. Conclusion

The cellular response to mechanical force is consequent upon both its structure and mechanical properties. Understanding and characterizing the cellular response to force is critical given that cell mechanics and extracellular forces themselves direct many important cellular processes, including differentiation, morphogenesis and gene expression. Exactly how these forces are sensed and transferred into biochemical cues is still an area of intense investigation. It has been proposed that mechanotransduction occurs through a force-balancing act [186], wherein extra- and intracellular generated forces contribute to mechanosensory feedback mechanisms, largely controlled by actomyosin contractility [57,109,187]. Conformational changes in key proteins are likely to account for one avenue of direct conversion of mechanical signals into biochemical responses [188,189].

Over recent decades, AFM has become a frequently employed tool used to examine the deformation response and rheological properties of cells. Apparent stiffness measurements generated from force-indentation curves have become useful for characterization and identification of normal and diseased cells. Moreover, force-feedback techniques are valuable for characterization of their viscoelastic properties. While useful, models used to interpret the observed cellular responses vary widely in the literature. A clear description of how cells respond to a variety of forces will provide insight into the mechanisms involved in many cellular functions. However, the complex interactions between many active components make it extremely difficult to obtain an overall picture of the cell. While the cytoskeleton, particularly the actin network and cortex, is particularly important in defining the elasticity of the cell, we now know that actin assembly and dynamics are largely influenced by extracellular mechanical cues, particularly from the substrate of adherent cells. Linear and scaling-law rheological models, while useful, do not fully describe non-equilibrium cell mechanics [87]. Nonlinear theories will be required to describe the full range of cell behaviours; however, they will certainly be complex. Therefore, describing specific observed phenomena, such as actin growth at the leading edge or contractility consequent of molecular motors, with simpler models that relate to the length and time scales of experiments remains beneficial.