Automated segmentation of the lamina cribrosa using Frangi's filter: a novel approach for rapid identification of tissue volume fraction and beam orientation in a trabeculated structure in the eye

Abstract

The lamina cribrosa (LC) is a tissue in the posterior eye with a complex trabecular microstructure. This tissue is of great research interest, as it is likely the initial site of retinal ganglion cell axonal damage in glaucoma. Unfortunately, the LC is difficult to access experimentally, and thus imaging techniques in tandem with image processing have emerged as powerful tools to study the microstructure and biomechanics of this tissue. Here, we present a staining approach to enhance the contrast of the microstructure in micro-computed tomography (micro-CT) imaging as well as a comparison between tissues imaged with micro-CT and second harmonic generation (SHG) microscopy. We then apply a modified version of Frangi's vesselness filter to automatically segment the connective tissue beams of the LC and determine the orientation of each beam. This approach successfully segmented the beams of a porcine optic nerve head from micro-CT in three dimensions and SHG microscopy in two dimensions. As an application of this filter, we present finite-element modelling of the posterior eye that suggests that connective tissue volume fraction is the major driving factor of LC biomechanics. We conclude that segmentation with Frangi's filter is a powerful tool for future image-driven studies of LC biomechanics.

1. Introduction

The lamina cribrosa (LC) is a mesh-like structure in the posterior eye where retinal ganglion cell (RGC) axons carrying visual information from the retina to the brain traverse the sclera. It is formed by a complex, mesh-like array of interlocking ‘beams', each of which is essentially a collagen-rich connective tissue sheath surrounding a capillary [1,2]. Together, the beams form an intricate porous structure, through which the RGC axons pass and join together to form the optic nerve. The biomechanics of this region are extremely complex. The sclera provides most of the mechanical support of the posterior eye against intraocular pressure (IOP), and the porous LC, with its lower density of connective tissue, effectively creates a region of stress concentration surrounding the delicate neural tissue of the RGC axons [3]. The LC is also the site where RGC axon damage occurs in glaucoma [4], and it has been hypothesized that axonal damage in this common eye disease is incited by mechanical deformation of the LC [5,6], potentially leading to activation of the surrounding mechanosensitive astrocytes [7], constriction of blood flow through the capillaries [8,9] or even direct blockage of retrograde and anterograde axonal transport [10]. Therefore, a better characterization of LC biomechanics is a topic of great clinical interest towards our understanding of the mechanisms leading to vision loss in glaucoma.

Unfortunately, the biomechanics of the LC are not well understood, given the extremely complex microstructure of the LC beams and also because of the difficulty of accessing the tissue experimentally. The LC is, on average, less than 400 µm thick [11], and pores can be as small as 10–50 µm in diameter [1]. It is surrounded by the delicate neural tissue of the retina and optic nerve to the anterior and posterior, respectively, and it is embedded in the tough, pressurized spherical wall of the sclera on all sides, making it very challenging to interrogate mechanically in vivo.

For this reason, imaging technologies in tandem with computer modelling have emerged as an alternative approach for studying the biomechanics of the LC, particularly its deformation response to various magnitudes of IOP. To date, a number of groups have attempted to model the biomechanics of the posterior eye, but most have treated the LC as a homogeneous, isotropic structure (ignoring the anisotropy inherent in the collagenous beams) [12–14]. There have also been several attempts to model a few individual beams comprising a subset of the LC, including employing orientation information [15–17]. Using contrast enhancement staining techniques in tandem with micro-computed tomography (micro-CT) or in second harmonic generation (SHG) confocal microscopy without contrast enhancement, we are able to image the beams of the entire LC in three dimensions at high resolution, providing an important dataset to investigate the biomechanics of this complex structure.

To study the role of LC microstructure in mediating IOP insults, we first need to extract beam locations and orientations from these image datasets. Groups have attempted to obtain this information either through time- and labour-intensive reconstruction of the three-dimensional tissue geometry from serial histology [18,19] or via complex, multi-step image processing approaches that may not work on multiple imaging modalities. Here, we present a fast and robust method for deriving both beam locations and orientations via a novel application of Frangi's vesselness filter, an image processing technique originally developed for angiogram segmentation [20]. Using a modified formulation of the filter from Antiga [21] to detect higher-order structures like plates (figure 1) that more accurately represent the structure of the LC, we can rapidly segment two- and three-dimensional image datasets of the LC from contrast enhanced micro-CT and confocal microscopy. In this paper, we demonstrate the efficacy of this filter to study a tissue of great relevance to visual function as well as one application of the technique, namely finite-element modelling of LC biomechanics.

Figure 1.

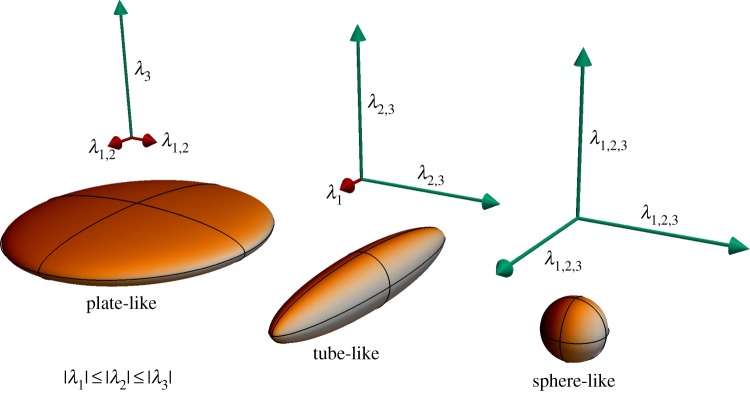
Schematic of Frangi's filter detection principle. The modified version of Frangi's filter can detect plate-like, tube-like and sphere-like objects by comparing the relative sizes of the eigenvalues of the Hessian matrix of an image dataset. Larger eigenvalues suggest that local image brightness is not aligned in the direction of the corresponding eigenvector. (Online version in colour.)

2. Methods

2.1. Micro-computed tomography

We used micro-CT imaging to visualize the LC in a porcine eye (eye A) obtained from a local abattoir. The eye was transported packed on ice and immediately dissected upon return to the laboratory. A square of tissue containing the optic nerve head and surrounding sclera was dissected free from the eye, fixed in 4% paraformaldehyde for 72 h, and then immersed in a contrast agent, 0.5% (w/v) phosphotungstic acid in 70% ethanol, for 21 days. The phosphotungstic acid binds to collagenous tissues to provide greater micro-CT contrast between LC beams and neural tissues in the LC. After staining, the eye was micro-CT scanned using an HMXST 225 CT system (Nikon Metrology, Tring, UK). The X-rays were generated from a molybdenum target using a voltage and current of 180 kV and 200 μA, respectively. A total of 3142 angular projections were collected at 0.1146° intervals in a single 360° rotation. The radial projections were reconstructed into a three-dimensional matrix of with 5 μm cubic voxels using the software package CT-Pro (version 2.0, Metris X-Tek, Tring, UK). Three-dimensional volumetric data were exported in DICOM format.

2.2. Comparison of micro-CT contrast enhancement protocols

To determine whether contrast could be improved with alternative staining protocols and to reduce the total staining time, we obtained three additional porcine eyes from an abattoir and exposed each to a different staining protocol (figure 2) [22]. One eye (eye B) was incubated in 2% phosphotungstic acid in water under 15 mm Hg hydrostatic pressure overnight, a significant reduction in time from the 21 days used to stain the original eye. In the next eye (eye C), we made a solution of 2% iodine (w/v) in water (Sigma-Aldrich) and incubated the eye for 3 days on a laboratory shaker. In the final eye (eye D), we created a solution of 1% (w/v) iodine metal with 2% (w/v) potassium iodide (known as an IKI solution; reagents from Sigma-Aldrich) in water and incubated the tissue for 3 days. Eyes B–D were scanned using identical settings using a Scanco µCT 50 scanner with a voltage of 90 keV and a current of 200 µA. We reconstructed 1300 angular projections with a 1 s exposure time and a 4 µm isotropic resolution, and specimens were placed in a 34 mm diameter sample tube.

Figure 2.

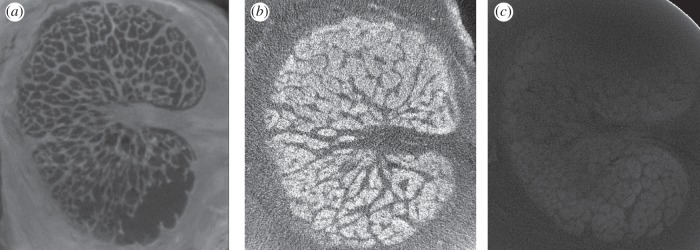
Comparison of micro-CT contrast staining techniques. Porcine LCs were exposed to various micro-CT contrast enhancing agents in an attempt to distinguish between connective tissue and neural tissue. We obtained the best contrast using a solution of 2% phosphotungstic acid in water under 15 mm Hg pressure overnight (a). Providing less effective contrast was a 2% iodine solution, in which the eye was incubated for 3 days (b), and a 1% iodine metal with 2% potassium iodide (IKI) solution (c), also with a 3 day incubation. All three images were obtained using the same micro-CT scan settings (Scanco μCT 50, 1300 projections, 1 s exposure time, 90 keV, 200 μA).

2.3. Second harmonic generation confocal microscopy

We used SHG confocal microscopy to image the LC of a different porcine eye (eye E), also obtained from a local abattoir. The fresh eye was dissected to isolate the optic nerve head, which was then embedded in Tissue-Tek optimal cutting temperature medium (Sakura Finetek) and chilled. We cryo-sectioned a 180 µm-thick slice of the optic nerve located 300 µm from the posterior scleral surface, which contained the LC. This section was placed on a glass slide and imaged with SHG microscopy using a Zeiss LSM 710 NLO microscope with an 800 nm laser to extract the collagen signal. A z-stack of 58 slices was obtained using a 10× objective, and a 7 × 7 tiling of subimages within each slice was montaged for a total in-plane resolution of 3584 × 3584 pixels. In-plane voxel resolution was 1.186 × 1.186 µm, and through-plane voxel resolution was 1.136 µm. SHG signal dropped off with tissue depth, so for this analysis, we selected a single planar slice close to the anterior face of the LC with strong contrast between collagenous beams and neural tissue.

2.4. Comparison of micro-CT with second harmonic generation confocal microscopy

Because micro-CT and SHG confocal microscopy image tissues based on different principles (micro-CT detects differential absorption of X-rays whereas SHG confocal microscopy detects photons of a specific wavelength emitted after passing through collagenous structures), we compared images of a porcine LC using both imaging methodologies to look for agreement in beam size and location. We obtained one porcine LC (eye F) and immersed it in phosphotungstic acid under 15 mm Hg pressure as above. This slice was then imaged with the Scanco micro-CT scanner using the same settings as above. Upon completion of this scan, the tissue was cryo-sectioned and mounted on a glass microscope slide for imaging with SHG confocal microscopy. We compared the structure of the LC beams from the two imaging technologies both visually and using the Matlab function imshowpair.

2.5. Image processing

We segmented the LC of a porcine eye in three dimensions from our micro-CT image stack (eye A) and a different porcine eye (eye E) in two dimensions from SHG microscopy to determine the location and orientation of beams using Antiga's modification of Frangi's filter [20,21]. Using Matlab R2014b (Mathworks), our image processing code was created by modifying existing code for Frangi's filter provided on the Matlab file exchange [23]. Our forked version of the original Matlab code by Kroon is available at https://www.github.com/iancampbell-gt/objectness3d and enables the identification of M-dimensional objects in N-dimensional images, where M < N.

We empirically determined appropriate scale ranges and filter constants by measuring the size (in pixels) of the smallest and largest beams we hoped to identify, setting α = 0.05 (its term does not contribute when M = N − 1), setting β close to 1, and setting γ close to the maximum brightness of neural tissue. Parameters were then manually iterated as needed to improve the quality of segmentation, as judged visually by one author with understanding of LC structure (I.C.C.). To segment the 16-bit greyscale porcine LC in three dimensions, settings were N = 3, M = 2 (enhancement of planes), scale range = [0.1 2] pixels in steps of 0.2 pixels, α = 0.05, β = 1, γ = 250. To segment the 16-bit greyscale porcine LC in two dimensions, settings were N = 2, M = 1 (enhancement of tubes), scale range = [10 24] pixels in steps of two pixels, α = 0.05, β = 1, γ = 1000.

2.6. Finite-element analysis

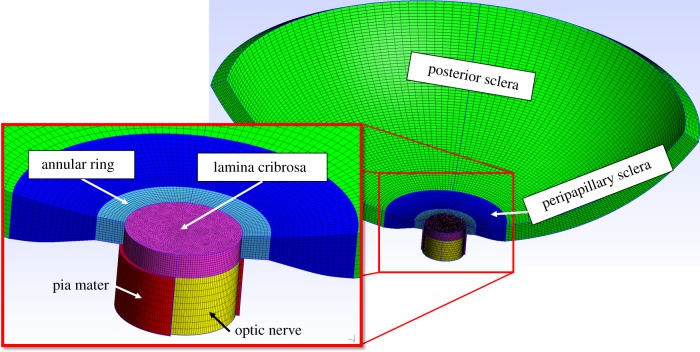
To demonstrate the utility of the segmentation described above, we built a three-dimensional finite-element model of the posterior eye to study the effects of LC beam anisotropy on LC biomechanics (figure 3). We meshed the posterior eye in Gmsh 2.8.4 software [24] according to the dimensions reported by Sigal et al. [12], specifically delineating the peripapillary sclera (a region where collagen fibres become increasingly aligned) [25] and the annular ring (a region immediately surrounding the scleral canal where collagen fibres are highly circumferentially aligned) [26]. To apply subject-specific LC material properties to our finite-element model, we meshed a cylindrical region containing the LC and manually registered it to our image stack (eye A), so that the boundaries of the LC were oriented axially with the cylinder (figure 4). We manually traced the boundaries separating the sclera and the LC and also separating the retina from the LC in the micro-CT image stack to delineate tissue regions not delineated by Frangi's filter.

Figure 3.

Finite-element model of posterior eye. We meshed the spherical posterior sclera (green) and peripapillary sclera (dark blue) where the scleral thickness tapers. The annular ring (cyan) was specifically delineated as a region with circumferentially aligned fibres centred concentrically about the axis of the optic nerve, and a cylindrical region (magenta) where we can apply subject-specific LC material properties. Posterior to the LC, the optic nerve (yellow) was modelled surrounded by a sheath of pia mater (red, cut away to show optic nerve). The model is shown cut away to aid visualization, but the complete circumference of the posterior eye was included in the model. Nodes forming the anterior inner edge of the posterior sclera were fixed in displacement.

Figure 4.

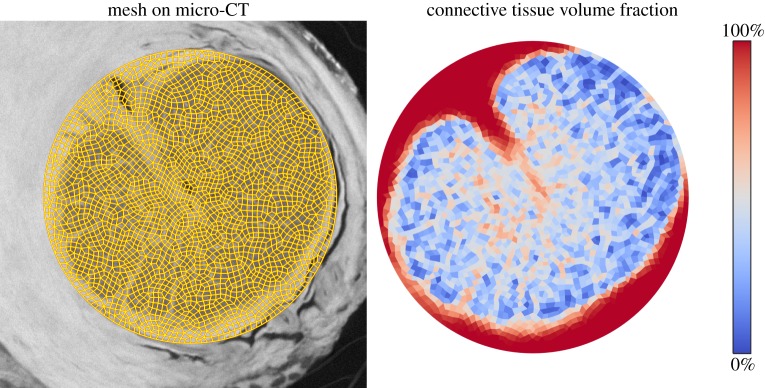
Determination of tissue volume fraction. The finite-element mesh of the LC (figure 3, magenta region) was registered to the micro-CT image stack (eye A, left). Based upon segmentation using Frangi's filter, we computed the local tissue volume fraction on an element-by-element basis (right). All tissue in the LC was assumed to be either connective or neural tissue.

For every element within the cylindrical region, we computed the tissue volume fraction (VF) of neural and connective tissue by binarizing the output of Frangi's filter. We used a binarization voxel value threshold of 0.2, empirically determined to segment beam borders in agreement with the micro-CT image. We assumed that every voxel was either neural or connective tissue and computed VF by counting the percentage of positive voxels within the convex hull of each element. Simultaneously, we also determined LC beam orientation by averaging the eigenvectors of the Hessian used in Frangi's filter (sorted by size of corresponding eigenvalue from smallest to largest) for each voxel.

We modelled inflation of the spherical posterior eye using FEBio v. 1.8.0 software [27] to 30 mm Hg, an IOP appropriate for a glaucomatous eye. Most of the tissues of the eye were modelled as a transversely isotropic Mooney–Rivlin solid with an embedded matrix of fibres following an exponential power law and the von Mises distribution [28]. Connective tissue material properties were determined by fitting the stretch–strain relationship obtained in an inflation test of human sclera from Coudrillier et al. [29] to this material model, giving the following coefficients:

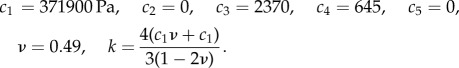The fibre plane was assumed to be tangent to the sphere formed by the ocular globe and circumferentially aligned about the LC. In the posterior sclera, we prescribed the von Mises distribution with k_f = 0 (planar isotropic distribution of fibres), in the peripapillary sclera k_f = 0.8, and in the annular ring k_f = 2 [29]. The optic nerve was modelled as a linear elastic, isotropic material with E = 30 kPa and ν = 0.49 [12], and the pia mater was also treated as linearly elastic and isotropic with E = 6c₁ and ν = 0.49. Nodes around the anterior, inner edge of the posterior sclera were fixed in displacement.

In the cylinder containing the LC, we applied different material properties in two regions, as the LC imaged with micro-CT is not perfectly cylindrical. In elements lying outside the manually contoured borders of the LC in the image stack, we applied identical material properties to the annular ring, with fibres aligned tangent to the edge of the LC border as determined by dilating the contour of the edge. Inside the LC, we computed an effective value of c₁ and c₃ on an element-by-element basis based on the volume fraction (VF) of neural and connective tissue:

Here, c_{l−connective} = 371 900 Pa as in the sclera and c_1−neural = E/6 = 5000 Pa. The element's fibre plane was determined by the two eigenvectors corresponding to the Hessian's two smallest eigenvalues.

To determine the importance of connective tissue VF and orientation, we compared strains in this subject-informed finite-element model (model 1) with those in a model constructed with a homogeneous, isotropic LC (model 2). To ensure a consistent comparison, we manually iterated the value of the Mooney–Rivlin coefficient c₁ (applied to elements within the manually contoured LC border) to enforce the constraint that the total displacement of the centre of the posterior face of cylinder containing the LC was equal between the two models, obtaining c₁ = 228 000 Pa, c₂ = 0. To further explore the role of VF in isolation of tissue anisotropy, we also created a third model (model 3) identical to the previous two, except the LC was modelled as a Mooney–Rivlin solid with

where c_{1−connective−effective} was determined to be 576 500 Pa by again manually iterating this coefficient until the displacement of the posterior face was equal to that of the subject-informed model (model 1).

3. Results

3.1. Micro-CT contrast enhancement

We obtained very good contrast between connective and neural tissue in the LC using phosphotungstic acid (eye B; figure 2), which binds to collagenous tissues to provide bright beams and dark neural tissue. Conversely, both iodine-based contrast agents brightened the neural tissue, leaving a silhouette of the mesh-like connective tissue in the LC (eyes C–D). Although beams could be resolved using all three staining approaches upon visual inspection, the phosphotungstic acid technique produced the best enhancement of structures of interest with the lowest noise levels in images of the LC. We did not observe any significant difference in staining quality between the initial porcine LC that was stained for 21 days at atmospheric pressure in an ethanol-based solution and the porcine eye pressure-stained at 15 mm Hg overnight in a water-based solution. Eyes stained with 2% iodine and with the IKI solution were not used in further analysis because of the unsatisfactory quality of staining.

3.2. Comparison of micro-CT and microscopy images

When comparing micro-CT images enhanced with phosphotungstic acid to SHG confocal microscopy images (eye F), we were able to resolve beam structures of comparable branching morphology and diameter in both sets of images. The thick, collagenous ventral groove characteristic of the porcine LC was observed on the posterior edge of LCs with both imaging technologies, and a ring of collagen surrounding the central retinal artery more anterior in the LC was also observed. We also compared one porcine LC scanned with both micro-CT and SHG. While an exact pixel-to-pixel match was not obtained, likely owing to orientation differences in the imaging plane of the tissue and to distortion of the LC between imaging modalities (loading in the micro-CT cylinder versus mounting on a glass microscope slide for SHG), inspection revealed that the same beams could be observed in both micro-CT and SHG confocal microscopy images. The phosphotungstic acid appeared to degrade the SHG signal, but beams were still visible and appeared co-localized between imaging modalities.

3.3. Beam identification with Frangi's filter

We successfully used the modified version of Frangi's filter to segment the connective tissue elements in the LC of a porcine eye in three dimensions (eye A; figure 5) and a different porcine LC in two dimensions (eye E; figure 6). In the three-dimensional porcine eye scan, the mean connective tissue VF within the boundaries of the LC was 37.7%. The settings used to filter each image stack were tuned to enhance the beams of the LC and performed optimally within the region of interest. Outside this region, where features of different thicknesses were located, artefacts were observed. In the porcine eye, the ventral groove, a thick protrusion into the LC [30] that appears bright in the micro-CT images, was not enhanced through its entire thickness using the filter's pixel range described in the methods. Attempts to filter a range of larger pixel sizes resulted in incorrect segmentation of smaller pores and thus were not used. Similarly, the central retinal artery, visible just below the tip of the ventral groove in figure 5a, introduced a local brightness gradient enhanced by the image filter that was indistinguishable from a beam using this technique. In the two-dimensional filter, small point-like dark spots in the sclera possibly caused by laser burns when setting up the second harmonic-generation imaging were enhanced as gaps in the sclera segmentation (figure 6a). These too were located outside the region of interest for which the segmentation parameters were tuned.

Figure 5.

Frangi's filter identifies beam location and orientation in micro-CT images. We applied a modified version of Frangi's filter to enhance plate-like objects in this three-dimensional image stack (eye A). (a) An example slice yields (b) a probability map that each voxel is a member of a beam, which can then be (c) binarized to segment the beams. Simultaneously, the eigenvectors of the Hessian matrix provide (d,e) information on beam orientation in three dimensions, where blue vectors correspond to the smallest eigenvalue and orange vectors correspond to the second-largest. Shown here is a two-dimensional projection of three-dimensional vectors that are orthogonal. For a three-dimensional rendering of these vectors, see the electronic supplementary video. Scale bar, 1.0 mm.

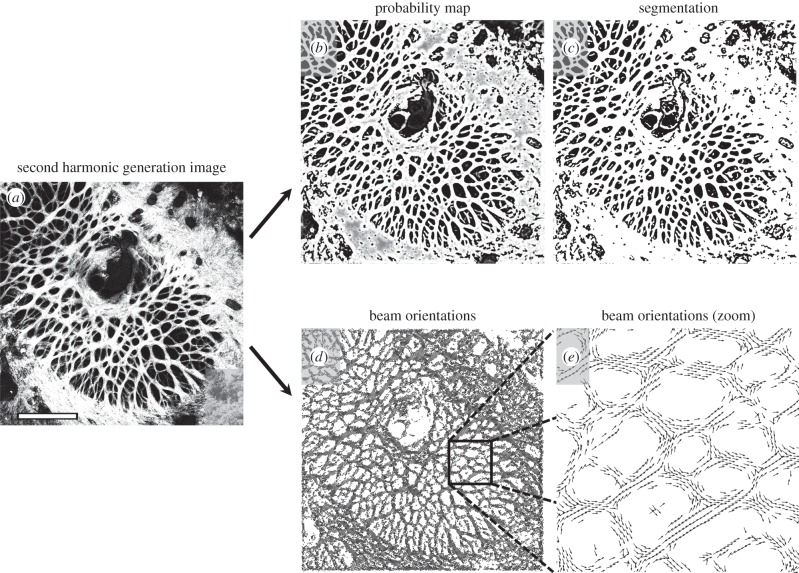
Figure 6.

Frangi's filter identifies beam location and orientation in confocal microscopy images. Similar to figure 5, we used Frangi's filter to enhance beam-like objects in this two-dimensional image (eye E). (a) The original image yields (b) a probability map that each voxel is a member of a beam, which can then be (c) binarized to segment the beams. Simultaneously, the eigenvectors of the Hessian matrix provide (d,e) information on local beam orientation. These vectors correspond to the smallest eigenvalue. In this visualization, only every 150th vector is shown due to the high resolution of the image. White scale bar, 1.0 mm.

3.4. Finite-element analysis

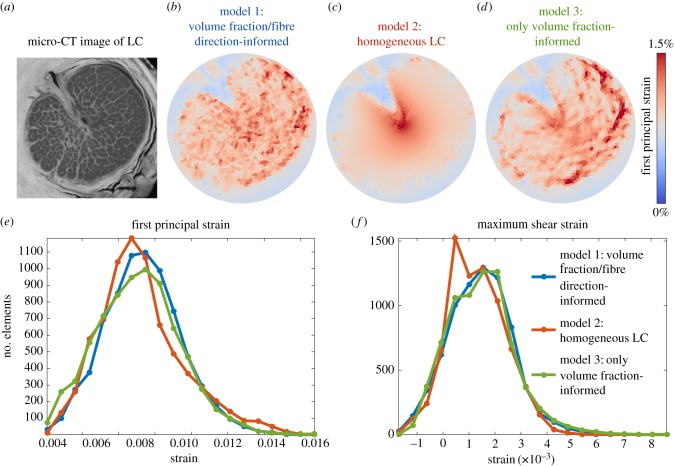
In comparisons of the subject-informed finite-element model employing beam orientation information (model 1) with the homogeneous LC (model 2), we found that the distribution of strains was considerably more uniform in the subject-informed model, whereas the homogeneous LC exhibited high strains in the centre of the LC and low strains around the periphery (figure 7). Averaging just the elements within the manually contoured boundary of the LC, first principal strain was on average 6.7% higher in the subject-informed model, second principal strain was 1.1% lower and maximum shear strain was 17.8% higher in model 1. Comparing the subject-informed model (model 1) with the model only informed by only VF (model 3), we see that the relative spatial distributions of high and low strains are similar: the subject-informed model had 1.5% higher first principal and second principal strains on average, although the maximum shear strain was 31.2% higher.

Figure 7.

Finite-element modelling of the LC. These maps of the distribution of first principal strain in a slice through the LC (b–d) demonstrate that the simplifying assumption of a homogeneous, isotropic LC produces a considerably different distribution of mechanical strains across the face of the LC, whereas removing fibre orientation information but preserving spatially resolved tissue volume fraction information has less effect on computed strains. Histogram analysis (e,f) confirms this finding, as the homogeneous model has more elements experiencing lower strains, whereas the two models informed by volume fraction have very similar strain histograms.

4. Discussion

Antiga's modification of Frangi's filter provides a robust method for segmentation of the LC that simultaneously provides information on beam location and orientation. It is currently implemented in Matlab software and can be used on any two- or three-dimensional greyscale image dataset. It is fast, easy to implement and returns results with single-voxel spatial resolution, an advantage over traditional fibre network orientation measurement methods [31]. Here, we have demonstrated its efficacy on micro-CT and SHG confocal microscopy datasets, and we have also used it successfully on a fluorescently labelled single channel from a confocal microscopy image of the LC (data not shown). This technique should presumably work well on LC data from other imaging modalities such as optical coherence tomography, ultrasound or magnetic resonance imaging, although the technique requires isotropic voxels, so datasets with anisotropic voxels would need to be resampled. In our porcine LC, we detected a connective tissue VF of 37.7%, a result lower than the 55.2–56.0% VF reported by Dandona et al. in humans [32] and higher than the VF of 21–27% reported by Roberts et al. in monkeys [16].

This technique only provides information on beam orientation, not on individual collagen fibre orientation. Here, we assume that collagen fibres are oriented along the local direction of beams, but this technique cannot provide any information on collagen fibre orientation in regions without beam-like structures, such as the sclera. In regions without beams, microstructure analysis must be performed using more traditional imaging techniques such as electron microscopy [33], small-angle light scattering [34,35] or wide-angle X-ray scattering [25].

Users of this technique may require a multi-pass segmentation approach if the images of interest contain features of widely ranging length scales. As shown in figure 5b,c, the ventral groove of the porcine eye could not be segmented using the chosen filter parameters. We produced local enhancement of the edges of the groove, but tissue in the centre of the structure was not enhanced. We found that by running the filter with a larger pixel range, we could fully enhance the ventral groove, but some of the smaller pores were not properly segmented. In our case, we overcame this limitation using manual masking of the region of interest, but users interested in segmenting both large and small structures simultaneously could easily overcome this limitation by running Frangi's filter multiple times using different filter settings then combining the results by manually masking out regions of interest in each filter output.

In this study, we have demonstrated an effective approach to image the LC with micro-CT using phosphotungstic acid as a contrast agent, as well as two iodine-based contrast agents that less effectively enhanced the tissue. We have also directly compared contrast enhanced micro-CT imaging of the LC with SHG confocal microscopy of the same tissue. While we obtained very similar results with both imaging technologies, there are several important technical considerations that will dictate which approach is most useful in future studies. Confocal microscopy provides a higher-resolution final image; however, micro-CT provides enough voxels in the cross section of each beam to effectively identify their position, and it is not clear that the additional resolution of SHG microscopy is beneficial for studies of beam location and direction. Both techniques are fully three-dimensional, but confocal microscopy suffers from signal loss with increased tissue thickness. Increasing the laser power can improve penetration depth, but sufficiently high laser intensity can actually burn the beams of the LC, whereas micro-CT uses X-rays that do not affect the tissue at the energy levels in this study. SHG microscopy produces a signal as a result of natural frequency doubling by collagen and requires no contrast agents, whereas contrast enhancement is essential to resolve connective tissue from neural tissue in the LC using conventional micro-CT. Such contrast enhancement could distort the tissue and change some of its physical properties, but micro-CT can also image large pieces of tissue without need for sectioning. We are also currently developing methods to image the LC using phase-contrast micro-CT, which does not require use of a staining agent. Clearly, no single LC imaging approach is superior to the other in all situations.

One important limitation to note is that because the phosphotungstic acid staining solution used to derive the beam structure, orientation and density for our finite-element models was ethanol-based, there is possibility that tissue shrinkage occurred owing to dehydration. If there were differential magnitudes of shrinkage between collagenous beams and surrounding neural tissue, our overall estimates of tissue VF could be skewed. Unfortunately, because tissue samples treated with phosphotungstic acid had degraded SHG signal and also because of the need to trim and mount microscopy samples on a glass slide, obtaining registered before-and-after SHG images of tissue treated with phosphotungstic acid is prohibitively difficult. We predict that tissue shrinkage, if significant, is mostly due to the ethanol in the solution, not the phosphotungstic acid. Therefore, for investigators concerned about this effect, we recommend using aqueous phosphotungstic acid solutions, noting that absorption of aqueous solutions takes orders of magnitude longer than ethanol-based solutions.

Here, we have also demonstrated the utility of our image processing approach by developing a finite-element model of the LC to explore the effects of LC composition and orientation in biomechanics of the tissue. Although these finite-element results are preliminary, they demonstrate that mechanical strains in a subject-informed LC were more uniformly distributed throughout the tissue, whereas in a simplified LC modelled as a homogeneous structure, strains were distributed by radius from the centre of the structure. We note that this effect of including the LC beams is consistent with a potential physiological role distributing strains evenly throughout the tissue, as it seems evolutionarily disadvantageous to have axons of the optic nerve subjected to considerably different magnitudes of strain based on position within the LC. Furthermore, the similarity of results between our two models informed by spatially resolved beam locations suggests that LC connective tissue VF may be a major driving factor in biomechanics of the region. These findings are consistent with previous modelling studies by Roberts et al., who also found that connective tissue VF strongly influenced optic nerve head stress and strain [16]. This finding is particularly important for our understanding of how the eye changes in processes like glaucoma, where there is evidence in animal models that connective tissue density changes over the course of the disease [36].

Our finite-element analysis technique has several limitations, which must be considered when interpreting the results. First, our element size is larger than individual beams, and thus each element represents an average of the surrounding tissue. While single-voxel element size would be most optimal when building image-driven finite-element models, such a model would be computationally infeasible with present hardware. Second, we have here modelled the LC of a porcine eye, which anatomically differs somewhat from a human LC in that its structure is more plate-like than beam-like (somewhat resembling a honeycomb) [30]. Future studies employing scans of a human LC should be performed to confirm the findings of this study. Finally, we cannot easily validate our finite-element results, as the exact deformation of the porcine LC in response to pressure is not known, and the imaging techniques employed in this study are destructive (the phosphotungstic acid used for micro-CT contrast enhancement considerably stiffens the tissue, preventing subject-specific deformation measurements). While the exact magnitudes of strain in this finite-element computer model cannot be precisely validated in vivo, this finding regarding the importance of connective tissue VF drives the sort of experimental evidence investigators should strive to collect in future studies of the biomechanics of the LC.

The settings to use with Frangi's filter depend on image brightness, contrast, intensity and the size of the beams one is trying to detect. Therefore, while some general guidelines have been provided here, users of this algorithm may need to empirically determine parameters that work for each individual dataset. Overall, this technique is robust and rapid, requires no manual segmentation or skeletonization of image datasets, and it works in three dimensions.

Data accessibility

Our modified version of Frangi's vesselness filter is available online at https://github.com/iancampbell-gt/objectness3d.

Funding statement

This work was supported by funds from the Georgia Research Alliance (CRE).