Lateral assembly of N-cadherin drives tissue integrity by stabilizing adherens junctions

Abstract

Cadherin interactions ensure the correct registry and anchorage of cells during tissue formation. Along the plasma membrane, cadherins form inter-junctional lattices via cis- and trans-dimerization. While structural studies have provided models for cadherin interactions, the molecular nature of cadherin binding in vivo remains unexplored. We undertook a multi-disciplinary approach combining live cell imaging of three-dimensional cell assemblies (spheroids) with a computational model to study the dynamics of N-cadherin interactions. Using a loss-of-function strategy, we demonstrate that each N-cadherin interface plays a distinct role in spheroid formation. We found that cis-dimerization is not a prerequisite for trans-interactions, but rather modulates trans-interfaces to ensure tissue stability. Using a model of N-cadherin junction dynamics, we show that the absence of cis-interactions results in low junction stability and loss of tissue integrity. By quantifying the binding and unbinding dynamics of the N-cadherin binding interfaces, we determined that mutating either interface results in a 10-fold increase in the dissociation constant. These findings provide new quantitative information on the steps driving cadherin intercellular adhesion and demonstrate the role of cis-interactions in junction stability.

1. Introduction

Cadherins are calcium-dependent adhesion molecules that play an important role in cell–cell junction formation, contribute to cell-type specificity and thus organize structural and functional tissue integrity in multicellular organisms. Since cadherins are essential during embryo development and throughout adulthood, many diseases are related to cadherin dysfunction (reviewed by Becker et al. [1]).

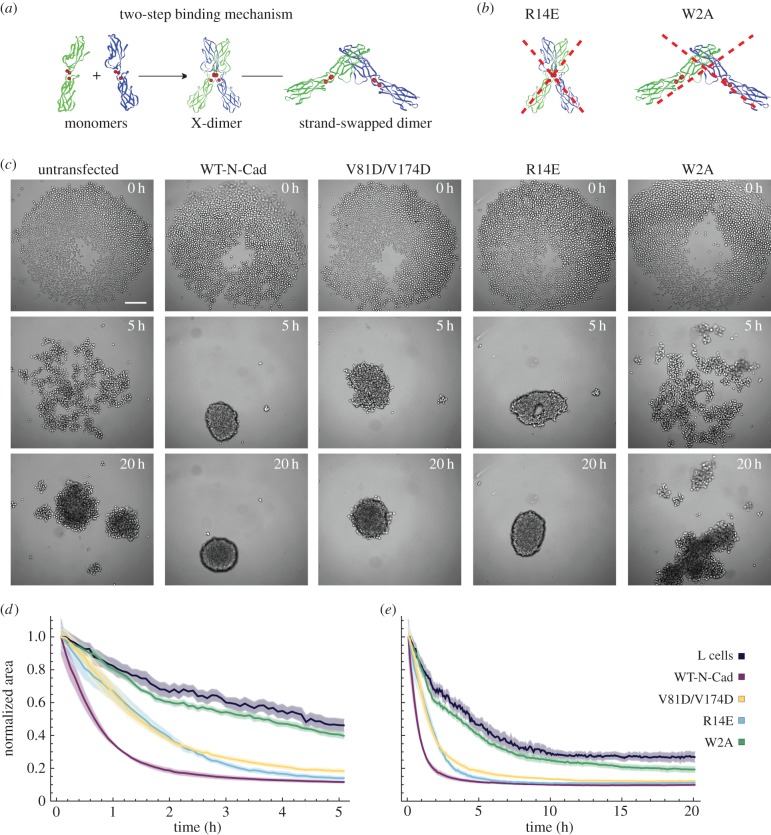
Type I classical cadherins are a subpopulation of the cadherin superfamily that consist of five extracellular (EC) domains, a single transmembrane domain and a cytoplasmic tail [2]. Binding sites for up to three Ca²⁺ are located in between each of the EC domains. Upon Ca²⁺ binding, the entire EC domain forms a rigid, rod-like structure, which facilitates dimerization and stabilization of the cadherin molecules [3]. Structural studies of E-cadherin suggest that classical cadherins form inter-junctional lattices via both cis- and trans-dimerization [4]. Cis-interactions arrange the EC domains of cadherins into linear arrays, while trans-interactions connect cadherins from neighbouring cells via a two-step binding mechanism (figure 1a). In the first step, cadherin monomers are proposed to form an ‘X-dimer’, in which the outermost EC domains of the cadherin molecules are closely aligned. The X-dimer has been proposed to facilitate the formation of a ‘strand-swapped’ dimer, where cadherin molecules insert a conserved N-terminal side chain into a hydrophobic pocket located on the partner molecule [5].

Figure 1.

Cadherin-dependent spheroid formation of L cells. (a) Scheme of the two-step binding mechanism for cadherin trans-interactions. (b) Illustration of the effects of the R14E and W2A mutations. The R14E mutation inhibits the formation of the X-dimer; the W2A mutation prevents strand-swap dimerization. (c) Images of spheroid formation at various time points for untransfected L cells and L cells expressing WT-N-cadherin or different cadherin mutants (V81D/V174D, R14E or W2A). The seed number was 2000 cells per well. Microscope: Zeiss CellObserver; objective lens: CZ 5×/N.A. 0.13; scale bar, 200 µm. (d,e) Dynamics of the area occupied by the cells from individual cell lines normalized to the area at time 0 h, plotted with two different time scales. (d) 0–5 h (highlighting the initial dynamics) and (e) 0–20 h. Shaded regions represent the standard error of the mean (s.e.m.). Note that in some cases, due to the small error, the shaded region is not visible. Number (n) of independent experiments: L cells: n = 11; WT-N-Cad: n = 11; V81D/V174D: n = 10; R14E: n = 11; W2A: n = 10. Further statistical analyses of the data are presented in the electronic supplementary material, figure S1.

N-cadherin is a member of the type I classical cadherin subfamily. Depending on the cell type, the expression of N-cadherin can lead to different cellular behaviour through the activation of different signalling pathways [6]. During metastatic cancer, for example, N-cadherin expression enables migration, whereas in the neural tube and the heart N-cadherin interactions form the scaffolding of adherens junctions resulting in cell–cell adhesion and tissue integrity. In this work, we focus on the adhesive properties of N-cadherin in a tissue-like environment.

Cells change their adhesive, migratory and proliferative properties [7,8] and lose their original tissue-associated properties [9] when cultured in a two-dimensional environment. To examine the behaviour of cadherins in a setting that resembles the situation in vivo with respect to cell morphology, migration, proliferation and adhesion more closely than cellular monolayers, we used multicellular spheroids as a model system. Spheroids exhibit the three-dimensional cellular arrangement of tissues and offer simplicity when compared with a whole organism, allowing well-controlled experimental conditions and thus providing an alternative approach to study cellular processes in a more physiologically relevant context.

In a kind of ab initio approach to study cellular assembly dynamics, we used L cells, which are mouse fibroblasts that lack endogenous cadherin molecules [10], and thus are well suited to express different cadherin molecules to study cellular assembly dynamics. We used different L-cell lines, in which either WT-N-cadherin or N-cadherin with distinct mutations that affect the different binding interactions in cis- and trans-dimerization, tagged with the Venus fluorophore, were stably expressed [11,12] (figure 1a,b). The cis-dimerization was prevented by a double mutation of valine at positions 81 and 174 to aspartic acid. In order to abolish the formation of the structural intermediate state, the X-dimer, the arginine at position 14 was mutated to glutamic acid (R14E) (figure 1b). To disrupt the trans-dimerization of cadherins, the formation of a strand-swapped dimer was prevented by mutating the tryptophan at position 2 to an alanine (W2A) (figure 1b).

To understand the influence of the various binding interfaces on intercellular adhesion and spheroid formation, we complemented our experimental analyses with a physical–computational model. Several three-dimensional cell-based modelling approaches for cellular spheroids or tumours have been developed that investigate the properties of the final cell aggregate and assume it evolves from a single cell through cell division [13–16]. Only a few models address the initial phase of spheroid formation as an aggregation of many individual cells. One approach uses a Smulochwsky-like rate equation to study the process by analysing the number of clusters of a certain size over time [17,18]. In a second model, the cells and the medium are represented as a one-dimensional two-phase mixture adhering to a deformable layer of EC matrix [19]. The principles of mass and momentum conservation govern the behaviour of this system while its cell aggregation potential is investigated.

While previous models have provided interesting ideas, none of them represents the experimental systems used in either biological or translational research. Therefore, based on our own experimental data and accepted physical principles, we developed a three-dimensional agent-based approach that treats the initial spheroid as an aggregate of individual cells. The model was validated by a comparison with 370 experimental datasets generated by analysing the spheroid formation of untransfected L cells and L cells expressing either WT-N-cadherin or one of the three cadherin mutants (V81D/V174D, R14E, W2A). We determined how spheroid formation and the structural properties of the final spheroid relate to the function of different N-cadherin binding interfaces. In particular, we predict that cis-interactions are essential for tissue integrity and were able to confirm this experimentally. By linking the results obtained with our simulations to the individual junction binding dynamics, we found that the different mutations affect junction formation very distinctly. The initial formation of a bond was similar for V81D/V174D, the cis mutant and WT-N-cadherin. However, the stability of the bond formed by V81D/V174D was much lower than the stability of a bond formed by WT-N-cadherin, which indicates that the cis-interface is essential for junction stability. Furthermore, the junctions formed by the X-dimer mutant (R14E) were relatively unstable, suggesting that the X-dimer also provides junction stability. The strand-swap mutant (W2A), on the other hand, was highly unlikely to form junctions. Together with our estimates for the dissociation constants of cadherin trans-dimers, we find that mutation of the strand-swap interface has the most severe effect on junction binding dynamics, followed by the cis-interface mutant and the X-dimer interface mutant.

2. Results

2.1. Dynamics of spheroid formation

We monitored spheroid formation in five different cell lines: (i) untransfected L cells, (ii) L cells expressing WT-N-cadherin, (iii) L cells expressing the cis-interface mutant (V81D/V174D), (iv) L cells expressing the X-dimer mutant (R14E), and (v) L cells expressing the strand-swap mutant (W2A) (figure 1c). The formation of spheroids was monitored using long-term live cell imaging where the same number of cells of untransfected L cells, L cells expressing WT-N-cadherin or one of the cadherin mutants were plated in a 96-well plate, and images were acquired every 5 min for 48 h. In untransfected L cells, we found that the cells form several loose lumps within 20 h (figure 1c) but failed to form a spheroid, characterized by a compact single structure with a clear outline. By contrast, L cells expressing WT-N-cadherin rapidly (within 5 h) formed a single round cluster with features characteristic of a spheroid in which margins formed by individual cells were barely visible. The cis-interaction mutant V81D/V174D showed slower aggregation dynamics than WT-N-cadherin cells and, although the cluster was round after 20 h, it had a less well-defined edge. Mutation of a residue involved in trans-interactions (R14E; block of X-dimer formation) led to similar aggregation dynamics to V81D/V174D. However, R14E cells formed a compact round cluster. Finally, the strand-swap mutant W2A exhibited the most severe phenotype of the mutants examined. It failed to form a spheroid and instead formed loose cellular aggregates similar to untransfected L cells. These differences in aggregation dynamics are primarily due to the mutations in N-cadherin, as the protein expression levels for WT-N-cadherin and the three cadherin mutants are comparable (electronic supplementary material, figure S1a), and the protein localization at the plasma membrane as well as the levels of expression are equivalent, as seen by immunostaining with an anti-Venus antibody (electronic supplementary material, figure S1b [11]).

To analyse the behaviour of the cells transfected with the WT-cadherin molecule and the cadherin mutants, we measured the area occupied by the group of cells as a function of time (electronic supplementary material, figure S1d) and normalized it by the initial value to quantify the changes in area associated with cell aggregation (figure 1d,e; electronic supplementary material, figure S1c). By examining the early (less than 5 h) kinetics, we found three different speeds of cell aggregation dynamics. The first type is exemplified by WT-N-cadherin, which exhibited the fastest cell aggregation, the second type comprises V81D/V174D and R14E, which exhibited an intermediate (about half as fast as WT-N-cadherin) aggregation speed, while the last type includes W2A and untransfected L cells with the slowest rates of cellular aggregation. These data indicate that WT-N-cadherin expression facilitates cellular aggregation and that any mutation of the molecule leads to a diminished capacity for cellular aggregation. Although the initial rate of decrease in area was slower for V81D/V174D and R14E than for WT-N-cadherin, indicating a slower aggregation, the final area occupied by WT-N-cadherin, V81D/V174D and R14E cells was similar. The clusters formed by untransfected L cells and W2A encompassed a significantly larger area than WT-N-cadherin cells after 5 h and even after 20 h (electronic supplementary material, figure S1c). We further examined the morphology of the aggregates after 72 h using digital scanned laser light-sheet microscopy [20] and confirmed the differences between the groups with three-dimensional datasets (electronic supplementary material, figure S1e).

Our results indicate that the different binding sites play distinct roles in spheroid formation and hence in the final structure of the spheroid. To gain further insights into the mechanisms underlying these different behaviours, we developed a computational model to describe the behaviour of the cells using physiological data obtained from the above experiments.

2.2. Computational model for spheroid formation

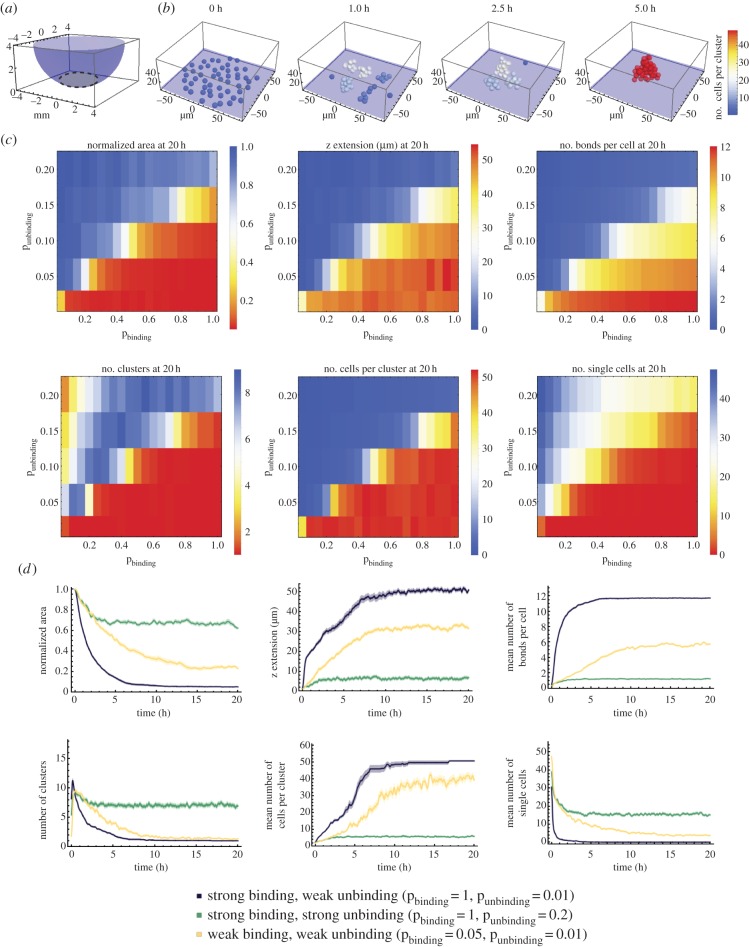
Based on our experimental results, we reasoned that cell movement and/or cell–cell adhesion are the likely primary physical mechanisms involved in spheroid formation. To determine which of these drive the process, we developed a three-dimensional agent-based computational model. We assume that cells are spheres with a radius of 5 µm and that they move within a well with non-adhesive walls. Cells in close proximity are able to adhere to one another. They form a bond with a certain probability that is described by a binding constant within a range of 0.05–1. In addition, bonds between cells can break with a certain probability that is described by an unbinding constant with a range of 0.01–1. In preliminary simulations, we observed that unbinding constants greater than 0.2 did not result in cell aggregation. Therefore, a value of 0.2 was regarded as the maximum value for all further investigations. The movement of the cells or the clusters is described by physical properties: (i) the cells move randomly, as defined by a diffusion parameter; (ii) they sink, as described by the buoyancy, which is proportional to the difference in the density of the cells relative to the medium, with a range of 2–25 mg ml⁻¹; (iii) they do not overlap due to volume exclusion; and (iv) they adhere once connected via a bond. The shape of the well defines the boundary for the random movements (figure 2a).

Figure 2.

Computational model of spheroid formation. (a) Initially, cells are distributed at the bottom (grey-shaded region) of a well (purple). (b) Exemplary simulation of spheroid formation for 50 cells with a binding probability p_binding = 1, unbinding probability p_unbinding = 0.01 and a density difference of the cells relative to the medium of 6 mg ml⁻¹. (c) Parameter scan for the binding and unbinding probabilities and cell-to-medium density difference of 6 mg ml⁻¹. Each matrix represents the mean values for a measurement based on 25 simulations. The colour code indicates the quality of the spheroid formation from successful in red to unsuccessful in blue. A successfully formed spheroid has a low normalized area, a high z extension, a large number of bonds per cell, one cluster with a large number of cells and a minimal number of single/unclustered cells (table 1). The binding probability p_binding ranges between 0.05 and 1 with increments of 0.05, while the unbinding probability p_unbinding is varied from 0.01 to 0.20 with increments of 0.05. Unbinding probability values above 0.2 yielded no cell aggregation and thus were not tested further. (d) Measurements based on 25 simulations are plotted over a period of 20 h. The density difference between cells and medium is 6 mg ml⁻¹ and three different parameter combinations for the binding and unbinding probabilities were considered. The curves were smoothed with a mean filter with a range of 5 min. Shaded regions represent the s.e.m. Owing to the small error, some shaded regions are not visible.

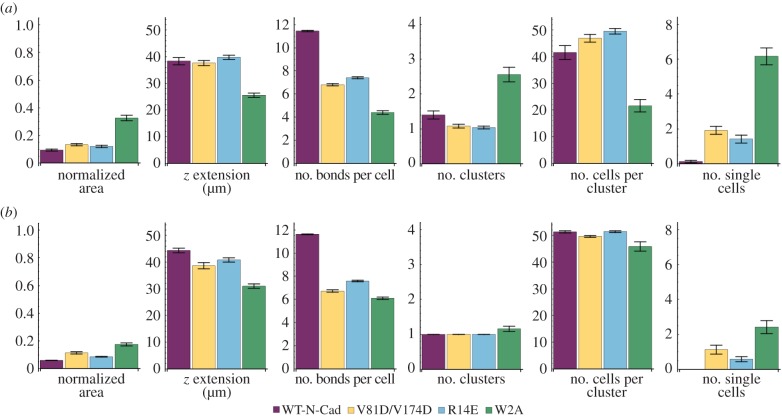
At the beginning of the simulation, the cells were randomly distributed at the bottom of the well. Figure 2b shows excerpts of a spheroid formation simulation using a binding constant of 1, an unbinding constant of 0.01 and a density difference between cell and medium of 6 mg ml⁻¹. In our simulations, we observed that single cells initially come together to form several small clusters, which then aggregate to form fewer but larger clusters. Ultimately, a single large cluster develops. The position of every cell and the number of bonds between all cells are known at every time point. Thus, we can extract a large number of measurements from the simulations, which include the number of single cells, the number of clusters, the number of cells per cluster, the number of bonds per cell, the extension in z of the whole cluster and the projected area (figure 2c,d). The projected area measured in the simulations can be directly compared with the experimental data shown in figure 1.

The phase diagrams in figure 2c depict the various measurements that were obtained from the simulations. In each diagram, two distinct regions of final cellular arrangement are separable by a virtual diagonal. Successfully formed spheroids, which have a small normalized area, a high z extension, a large number of bonds per cell, one cluster with a large number of cells and no single cells (table 1) are represented in red and lie in the lower right half of the phase diagrams (figure 2c). The predominantly blue region in the upper left half indicates an unsuccessful spheroid formation process: the cells are widely distributed, form at most three clusters containing very few cells, are weakly connected by a few bonds and do not exhibit z-axis extension. Exemplary curves for the different measurements over time for three extreme binding conditions: (i) strong binding and weak unbinding, (ii) strong binding and strong unbinding, and, finally, (iii) weak binding and weak unbinding reveal the effects of binding and unbinding probabilities on the dynamics of spheroid formation (figure 2d). Strong binding and weak unbinding led to a rapid decrease in the normalized projected area, number of clusters and single cells, while a sharp increase was found in the z extension, the number of bonds per cell and the number of cells per cluster; taken together, these parameters strongly predict successful spheroid formation (table 1). Strong binding and strong unbinding, however, led to cells with on average only a single bond. Cellular aggregation for weak binding and weak unbinding occurred at an intermediate rate compared with cases (i) and (ii) and eventually led to the formation of one cluster and a few single cells (figure 2d). Manipulating the buoyancy affected the initial rate of spheroid formation during the first 5–7 h but did not change the final fate of spheroid formation (electronic supplementary material, figure S2).

Table 1.

Characteristics of successful or unsuccessful spheroid formation.

	spheroid formation
properties	successful	unsuccessful
normalized area	small	large
z extension	high	low
number of bonds per cell	large	small
number of clusters	small (approx. 1)	large
number of cells per cluster	large	small
number of single cells	low (approx. none)	high

These results show that our model robustly generates spheroids by aggregation of single cells in the time frame comparable to our experimental data.

2.3. Computational model reproduces experimental data

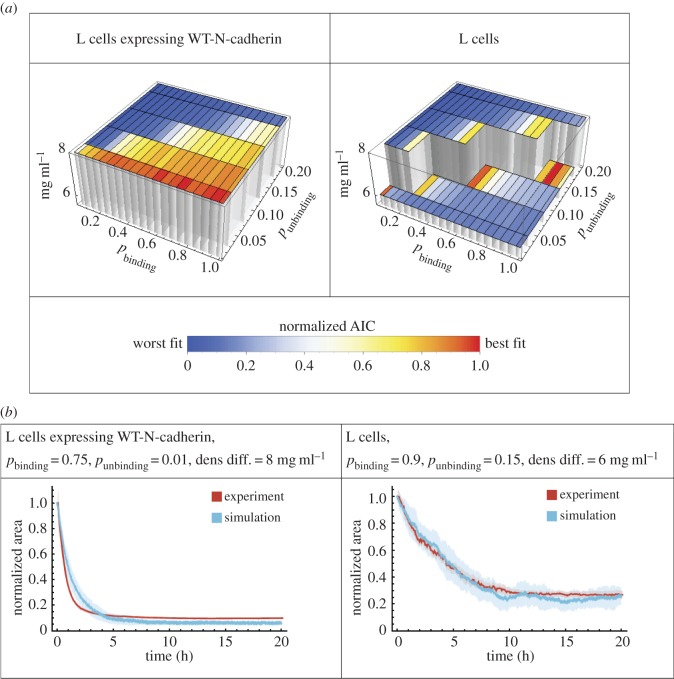
To examine directly how well the model captured the experimental data, we fitted the simulated normalized area from the model to the area obtained in the experiments (figure 1d,e). We fitted our model to the two control cases—L cells expressing WT-N-cadherin and untransfected L cells (figure 3). We performed a parameter scan for the binding and unbinding probabilities as well as the density difference between a cell and the medium and determined the goodness of fit with the Akaike information criterion (AIC). For both experimental conditions (WT-N-cadherin and untransfected), we found a range of parameter values, in which the model fitted the data well. WT-N-cadherin cells are best fitted by relatively high binding and low unbinding probability, which corresponds to our previously determined region of successful spheroid formation. Binding probabilities on the diagonal of our phase diagram best fitted the untransfected L cells (figure 3a). The best-fit parameters for the density difference between a cell and the medium for WT-N-cadherin cells and untransfected L cells are similar, indicating that the major difference between the aggregation dynamics of the two groups arises from the differences in binding or unbinding properties. An overlay of the best-fit curves and the experimental data shows that the fit is reasonable for both untransfected L cells and WT-N-cadherin (figure 3b).

Figure 3.

Fitting the model to experimental data for L cells expressing WT-N-cadherin and untransfected L cells, i.e. expressing no cadherins. (a) Three-dimensional bar graphs representing the results from fitting the model to the data by varying the cell-to-medium density difference as indicated by the height and the binding and unbinding probabilities. The goodness of the fit is shown by the normalized AIC values for fitting of the model to data from L cells expressing WT-N-cadherin (left) or untransfected L cells (right), where blue is the worst fit while red is the best fit. (b) The best-fit curves according to the model (blue, mean of 25 simulations) and the experimental data curves (red, mean of 11 experiments) for L cells expressing WT-N-cadherin (left) or untransfected L cells (right) for the normalized area over time. Shaded regions represent the s.e.m. Owing to the small error, some shaded regions are not visible. In both cases, the best-fit parameters are shown in the heading.

2.4. Calcium-dependent changes in spheroid formation dynamics

Given that cadherin structure and adhesion are calcium sensitive, we conducted experiments with L cells expressing either WT-N-cadherin or one of the cadherin mutations (V81D/V174D, R14E, W2A) to monitor cell aggregation dynamics in media that contained different EC Ca²⁺ concentrations (0, 0.4, 0.8, 1.3 or 2.1 mM Ca²⁺).

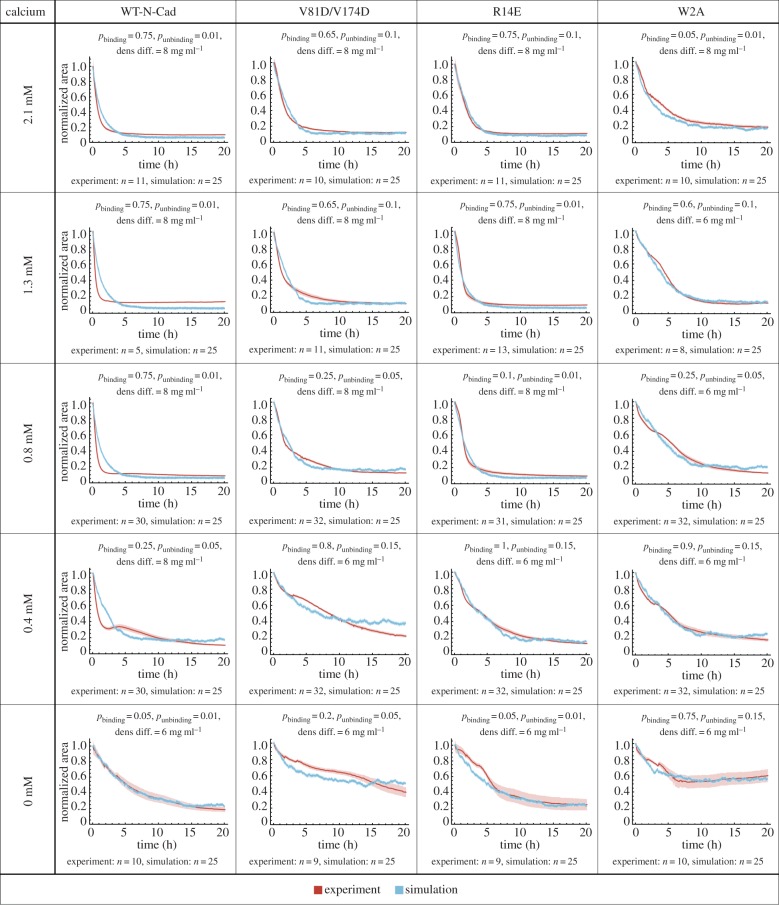
In figure 4, we compare the experimental data and the simulations for the area occupied by the WT-N-cadherin cells or cells expressing one of the N-cadherin mutants (four different groups), measured at five different EC Ca²⁺ concentrations (resulting in 20 different groups for both experiment and simulation). In each panel, the experimental data, shown in red, represents the normalized area of each experimental group (WT-N-cadherin, V81D/V174D, R14E and W2A) over time in different Ca²⁺ concentrations.

Figure 4.

Fitting the model to experimental data for L cells expressing WT-N-cadherin or a cadherin mutant for various calcium concentrations in the medium. Spheroids were formed from L cells expressing WT-N-cadherin or a cadherin mutant (V81D/V174D, R14E or W2A) at varying EC calcium concentrations (0, 0.4, 0.8, 1.3 and 2.1 mM). The mean measured normalized area (red) and mean simulated normalized area (blue) was plotted over time. Shaded regions represent the s.e.m. Note that in some cases, due to the small error, the shaded region is not visible. In all cases, the number of simulations is 25, the number of experiments is at least 5 and is indicated for the various conditions individually. For each case, the best-fit parameters are shown in the heading.

WT-N-cadherin cells showed an increase in the speed of cellular aggregation even upon decreasing the calcium concentration to 0.8 mM. As previously reported, to abolish spheroid formation, a complete depletion of Ca²⁺ was required [11]. Both V81D/V174D- and R14E-expressing cells exhibited similar sensitivities to Ca²⁺, where an effect on the cellular aggregation dynamics was observed only when the Ca²⁺ concentration was decreased below 0.8 mM, hence twice as much as for WT-N-cadherin. Varying the Ca²⁺ concentration did not rescue the low cellular aggregation exhibited by W2A-expressing cells.

The blue line in each panel of figure 4 depicts the simulation data that best fit the experimental data (see Material and methods). The binding, unbinding and density difference values used in the best-fit simulation are indicated at the top of each panel. We find that the model fits the experimental data for all 20 cases well. For WT-N-cadherin, the best-fit parameter values are the same for Ca²⁺ concentrations of 2.1, 1.3 and 0.8 mM. In the simulations, the parameter values for WT-N-cadherin at 2.1 mM (p_binding = 0.75, p_unbinding = 0.01, density difference = 8 mg ml⁻¹) result in the steepest possible decrease. Therefore, even though the experimental data result in steeper curves for WT-N-cadherin at Ca²⁺ concentrations of 1.3 and 0.8 mM, the parameter values remain the same. For 0.4 and 0 mM, junction formation is reduced, as indicated by a decreased binding probability and an increased unbinding probability. Furthermore, the best-fit parameter values for the density difference between the cells and the medium for 0 mM are decreased. This indicates a significant decrease in the speed of cell aggregation (electronic supplementary material, figure S2), which correlates with the lack of spheroid formation previously reported in [11]. For V81D/V174D cells, the best-fit parameter values are the same for 2.1 and 1.3 mM. For 0.8 mM and below, the binding and unbinding parameter values indicate less junction formation and for 0.4 and 0 mM the density difference is also decreased. Similar to WT-N-cadherin, the aggregation speed of R14E cells increases for the 1.3 mM Ca²⁺ concentration compared with 2.1 mM, which is further emphasized by an increase in junction formation due to a decrease in the unbinding probability. The binding and unbinding parameter values for the 0.8, 0.4 and 0 mM Ca²⁺ concentrations indicate less junction formation and for 0.4 and 0 mM the density difference also decreased to the lower level. This shows a significant decrease in cell aggregation for Ca²⁺ concentrations of 0.4 mM and below. For W2A cells, the best-fit parameter values for binding and unbinding indicate little junction formation at all five Ca²⁺ concentrations considered. The drop in the density difference value occurs between 2.1 and 1.3 mM. These results correlate with our previous findings of the calcium sensitivity of WT-N-cadherin and the different cadherin mutants [11].

Given that in vivo the EC Ca²⁺ concentration ranges within 1.2–2 mM, the best-fit parameters for 2.1 mM Ca²⁺ show the effects of the mutations on the binding and unbinding probabilities for a physiologically relevant condition. For the cis-interface mutant (V81D/V174D), the behaviour of the cells was best simulated by a slight decrease in binding probability and a large increase in unbinding probability when compared with WT-N-cadherin. The lack of X-dimerization (R14E) was simulated by changing the unbinding probability, which increased compared with WT-N-cadherin, whereas the ablation of strand-swapping (W2A) reduced the binding probability while the unbinding probability remained the same as for WT-N-cadherin.

These results show that our model can reproduce cellular aggregation dynamics for a variety of different experimental conditions. Hence, it is valid and can be used to further investigate how different binding sites affect spheroid formation and spheroid structure.

2.5. Effects of N-cadherin mutations on spheroid properties

Above, we measured the dynamics of spheroid formation experimentally in live cells by quantifying the area of the projection of the whole aggregate (figure 1). In order to better understand the dynamics at the level of interactions between individual cells, we used the model to extract cluster formation dynamics. For the best-fit parameters for WT-N-cadherin, V81D/V174D, R14E and W2A at 2.1 mM EC Ca²⁺, we obtained several properties of cellular aggregates from the simulations at 5 h and 20 h of spheroid formation, namely the normalized area (figure 1), z extension, number of bonds per cell, number of clusters, number of cells per cluster and number of single cells (figure 5). Since the best-fit parameters were obtained from fitting the model to the normalized area from the experiments, the normalized area from the simulation for WT-N-cadherin and its mutants reflects the experimental results and serves as a reference.

Figure 5.

Properties of the best-fit simulations for WT-N-cadherin, V81D/V174D, R14E and W2A. Measurements of geometrical and cluster formation properties of the cellular aggregates from 25 simulations for the best-fit parameters for WT-N-cadherin, V81D/V174D, R14E and W2A at (a) 5 h and (b) 20 h. The error bars indicate the s.e.m. Results of pairwise comparisons are shown in the electronic supplementary material, figure S4.

After 5 h, simulations for the WT-N-cadherin cells lead to the formation of two clusters that occupy a small normalized area and have a high z extension. Furthermore, each cluster has a high number of bonds per cell and no single cells remain (figure 5a). At 20 h, we get optimal spheroid properties with a small normalized area, a large z extension, a high number of bonds per cell, one cluster with a large number of cells and no single cells (figure 5b). This reflects the position of the best-fit parameter values for WT-N-cadherin in the region of successful spheroid formation as described in figure 3a (table 1).

In the simulations, at 5 h, V81D/V174D cells cover a larger area than WT-N-cadherin cells and one cluster occurs with a z extension and a number of cells per cluster that is comparable to the mean values for clusters of WT-N-cadherin cells. However, several cells are unbound and the number of bonds per cell is significantly lower than for WT-N-cadherin simulations (figure 5a and electronic supplementary material, figure S4a). After 20 h, simulations for V81D/V174D cells yield clusters with a larger normalized area and a smaller z extension than WT-N-cadherin. Furthermore, the cells are less connected since there are fewer bonds per cell and a higher number of single cells in the V81D/V174D simulations than in the WT-N-cadherin simulations (figure 5b and electronic supplementary material, figure S4b).

After 5 h, in the simulations, the R14E cells also cover a larger area, show an increase in the z extension and have a number of cells per cluster that is comparable to WT-N-cadherin. R14E cells form one cluster after 5 h; however, the number of single cells is significantly larger than that of WT-N-cadherin while the number of bonds per cell for R14E is significantly lower than WT-N-cadherin, and there are more unbound R14E cells than WT-N-cadherin (figure 5a and electronic supplementary material, figure S4a). At 20 h, the simulations for R14E still show a higher normalized area and a lower z extension than WT-N-cadherin, but the number of clusters and the number of cells per cluster are comparable with WT-N-cadherin. The cells in the simulations are still less connected than WT-N-cadherin, as indicated by the lower number of bonds per cell and the higher number of unbound cells.

Although R14E and V81D/V174D simulations exhibit similar dynamics for z extension and the number of single cells, they show differences in terms of their cluster formation properties. Both at 5 h and at 20 h, V81D/V174D simulations have fewer cells per cluster that are connected via fewer bonds versus R14E simulations (figure 5 and electronic supplementary material, figure S4). This suggests that, although V81D/V174D and R14E cells aggregate at a similar speed, the final V81D/V174D aggregate is less connected than the R14E aggregate.

W2A simulations indicate slow aggregation dynamics since after 5 h the cells cover a large normalized area, a large number of clusters containing few cells are formed and several cells are unbound (figure 5a). At 5 h, all properties of W2A simulations are significantly different from WT-N-cadherin as well as the cadherin mutants V81D/V174D and R14E (electronic supplementary material, figure S4a). After 20 h, the number of clusters for W2A decreased to a level comparable to the other three genotypes. However, the cells still cover a larger area, have a smaller z extension, formed fewer bonds per cell and more cells remain unbound than for WT-N-cadherin, R14E and V81D/V174D. Furthermore, at 20 h in the simulations, W2A has fewer cells per cluster than WT-N-cadherin and R14E.

In summary, the measurements suggest that the differences in the speed of area reduction correlate with the differences in the number of bonds per cell, hence the cell connectivity. Our simulations indicate that WT-N-cadherin cells form the best-connected cluster with optimal spheroid properties. Simulations of all the cadherin mutants show reduced cellular connectivity compared with WT-N-cadherin and among the mutants connectivity decreases in the following order: R14E, then V81D/V174D and W2A cells are the least connected. This raises the question of how much connectivity is sufficient to form a coherent tissue.

2.6. Effects of N-cadherin mutations on tissue coherence

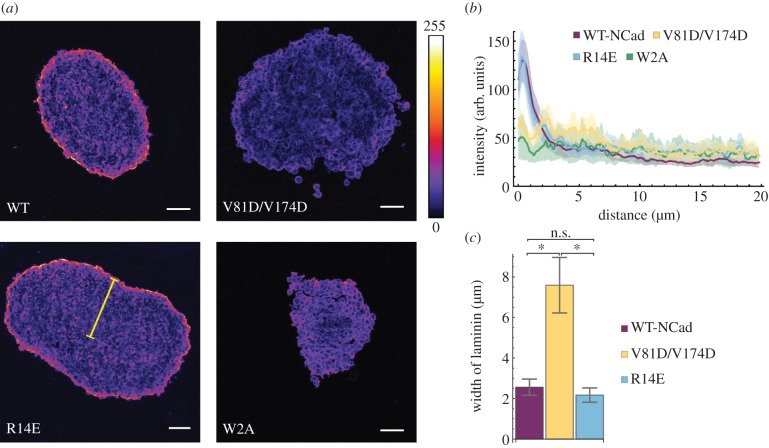
To test the predictions of the model concerning the cellular connectivity and to determine whether any of the mutants can form a coherent tissue, we immunostained the spheroids with an anti-laminin antibody. Laminin is a component of the EC matrix. It has been demonstrated previously that cells in spheroids secrete EC matrix components such as fibronectin, laminin and collagen to form an EC matrix around the outside of the spheroid [21]. Therefore, we prepared cryo-sections of the cellular aggregates 72 h post formation and examined the level and location of laminin using an antibody (figure 6a). We observed that, in WT-N-cadherin and R14E cells, laminin staining was evident on the periphery of the aggregates; however, in W2A and V81D/V174D a positive laminin signal occurred around individual cells present on the edge of the cluster. This supports the observation that WT-N-cadherin and R14E form compact spheroids while W2A and V81D/V174D form loose clusters with compromised integrity. We quantified the fluorescence intensity of the laminin staining from the edge of the spheroid to the centre (figure 6b). Since a discrete ring of laminin signal was present around the WT-N-cadherin and R14E aggregates, a distinct fluorescence intensity peak was observed within the first few micrometres from the edge of the section. On the other hand, much broader intensity profiles were observed for W2A and V81D/V174D sections. To compare the different intensity profiles, the curves were normalized to the maximum intensity of each image, and the distance from the perimeter at which the laminin fluorescence intensity was reduced by 60% (see Material and methods) was measured (figure 6c). For W2A, a decrease in intensity could not be detected, confirming that these cells are the least connected. The remaining results show a significant difference between V81D/V174D and both R14E and WT-N-cadherin. These results are further supported by immunostaining with an anti-β-catenin antibody, which revealed that L cells expressing both WT-N-cadherin and R14E formed compact clusters, while V81D/V174D and W2A cells did not, as demonstrated by the presence or the absence of β-catenin staining, respectively (electronic supplementary material, figure S5).

Figure 6.

Laminin intensity around spheroids. (a) Example images for laminin stained cryo-sections of 72 h old spheroids formed by seeding 2000 cells. Microscope: LSM780; objective lens: CZ 20×/N.A. 0.8; ex: 561 nm; em: 565–630 nm; scale bars: 50 µm. (b) Intensity profile of laminin along a line from the edge of the spheroid section to the centre for L cells expressing WT-N-cadherin or one of the cadherin mutants (V81D/V174D, R14E or W2A). In (a) an example of such a line is shown in yellow. For details of the analysis, see Material and methods. Mean ± s.e.m. are shown. (c) Bars show the mean distance (±s.e.m.) from the edge of a spheroid section to the location at which the laminin intensity dropped by 60% of its maximum value. For details of the analysis, see Material and methods. Asterisks indicate significant differences (*p < 0.05). The details of the test are provided in the Material and methods. In (b,c), the number of spheroids n are WT-N-Cad: n = 8; V81D/V174D: n = 6; R14E: n = 7; W2A: n = 5.

Our results show that WT-N-cadherin cells form spheroids, in which the cells are well connected. Interfering with trans-dimerization by abolishing X-dimerization with the R14E mutation reduces the cellular connectivity but spheroid formation still occurs. On the other hand, abolishing N-cadherin cis-interactions through the V81D/V174D mutation or interfering with N-cadherin trans-interactions by abolishing strand-swap dimerization through the W2A mutation disrupts cellular connectivity to such an extent that cellular aggregation does not lead to coherent spheroids but loose aggregates.

These results confirm the predictions from the model regarding cellular connectivity. Hence, the structures of the aggregates after 72 h can be predicted from the aggregation dynamics during the first 20 h of formation. Therefore, the differences in spheroid coherence are likely to be mainly due to differences in the formation of intercellular junctions. But how do these results relate to the role that the different binding interfaces play in the N-cadherin binding interactions? The cis-interactions organize the cadherin molecules laterally on the surface of the cell [4] and in two-dimensional cell cultures the cis mutants are still able to form junctions through trans-dimerization [11]. The cellular aggregate formed by the cis mutant, however, is not well connected. On the other hand, both R14E and W2A mutations affect trans-dimerization, and while R14E cells form spheroids, in W2A aggregates cell connectivity is severely impaired. Hence, whether or not correct trans-dimerization is possible is not sufficient to explain aggregation in living cells. Therefore, as a next step we investigate the properties of the intercellular junctions formed by WT-N-cadherin and the different cadherin mutants.

2.7. Effects of N-cadherin mutations on junction dynamics

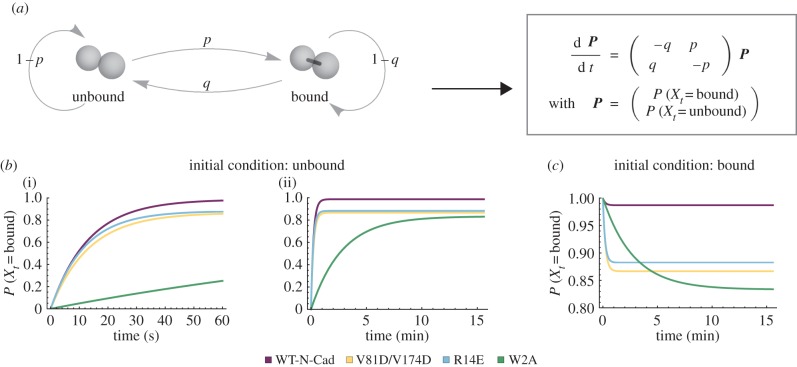
To investigate the effect of the N-cadherin mutations on the dynamics of intercellular junctions, we developed a simple model motivated by Tabdili et al. [22] to represent junction (or bond) formation between two cells (figure 7a). The two cells can either be connected by a bond or unbound. Bond formation occurs with a probability p and a bond breaks with a probability q. Hence, the probability to remain in the unbound state is described by 1 − p and the probability to remain in the bound state is described by 1 − q. The cells can cycle between the bound and unbound states. Using this method, we were able to calculate the probability of a bond between two cells at a given time point as well as over time for the two possible initial conditions: either the two cells are unbound or they are bound. For p and q, we consider the parameter values p_binding and p_unbinding that were determined by fitting the agent-based computational model to the experimental data for WT-N-cadherin and the cadherin mutants (figure 4). If the cells are unbound initially, the probability of bond formation over time for WT-N-cadherin and the cadherin mutants displays a distinct profile with an initial fast rise followed by a limiting plateau (figure 7b). This binding probability profile is in agreement with previous reports where micropipette measurements were used to quantify the binding probability for homophilic N-cadherin adhesion as a function of cell–cell contact time [22].

Figure 7.

Junction dynamics. (a) Illustration and differential equations for a simple model, which represents junction formation between two cells. The cells can be either bound or unbound. The transition from the unbound state to the bound state has probability p and from the bound state to the unbound state probability q. (b) Probability of the bound state over time if the cells are initially unbound at two different time scales ((i) 60 s; (ii) 15 min). (c) Probability of the bound state over time if the cells are initially bound. (b,c) The curves represent the solutions of the differential equations for the parameters p and q, which are determined by the best-fit parameters for spheroid formation of L cells expressing WT-N-cadherin (p = 0.75, q = 0.01), V81D/V174D (p = 0.65, q = 0.1), R14E (p = 0.75, q = 0.1) and W2A (p = 0.05, q = 0.01) (see also figure 4).

Interestingly, during the first minute of the simulation, the probability of a bond between two WT-N-cadherin cells, two V81D/V174D cells or two R14E cells is very similar (figure 7b(i)) while W2A has a much lower probability of bond formation. Although they exhibit a similar initial rise in binding probability, the steady state of V81D/V174D and R14E is significantly lower than that of WT-N-cadherin (figure 7b(ii)). This led us to ask whether the bonds formed by V81D/V174D and R14E L cells were stable. To answer this, we investigated the probability of the bound state over time given that the two cells are bound initially. V81D/V174D exhibits a fast decline in the bond probability (figure 7c), indicating unstable junctions. Eliminating the X-dimer formation (R14E) leads to a similar fast decrease in bond probability, albeit with a slightly higher steady-state value than for the cis mutant. This suggests that the X-dimer is also essential in providing stability to cadherin interactions. The steady decline in bond probability for W2A cells and the much lower steady-state value compared with the other three genotypes again shows that formation of a new bond is decreased relative to WT-N-cadherin as well as the cis and X-dimer mutant.

To relate the dynamics of junction formation to cadherin binding kinetics, we describe the cadherin dimerization as a reaction equation and compare the steady-state probability of the junction formation model to the steady-state probability for the reaction equation. Thereby, we obtain the dissociation constant for cadherin dimerization.

In detail, for the steady-state probability for the bound state for the junction formation model, we obtain

2.1

where p and q are the best-fit parameter values for the binding and unbinding probabilities, respectively, from the computational model (figure 4).

For the reaction equation of cadherin dimerization,

2.2

the steady-state probability for the bound state is given as

2.3

where K_d is the dissociation constant. Combining (2.1) and (2.3) and solving for K_d we get

2.4

Assuming that the cadherin monomer concentration is the same in all L cells expressing WT-N-cadherin and any of the cadherin mutants, we obtain conservative estimates of the K_d values as shown in table 2 in units of monomer concentration. We find that WT-N-cadherin has the lowest dissociation constant with a value of 0.01, whereas the K_d values of all cadherin binding interface mutants exhibit at least a 10-fold increase when compared with WT-N-cadherin. Although all three cadherin mutants have K_d values within the same order of magnitude, the strand-swap mutant W2A has the highest K_d value of 0.2, indicating the least N-cadherin dimerization.

Table 2.

Dissociation constant values of WT-N-cadherin and the cadherin mutants.

mutant name	description	Kd value ([monomer])
WT-N-cadherin	wild-type N-cadherin	0.01
V81D/V174D	cis-interaction mutant	0.15
R14E	X-dimer mutant	0.13
W2A	strand-swap mutant	0.2

3. Discussion

Much of our knowledge about N-cadherin binding has been obtained by X-ray crystallography. Although these studies have contributed to our understanding, the dynamics of cadherin binding in living cells remain a poorly understood, largely unexplored area. We used a multi-disciplinary approach combining long-term live cell imaging, quantitative image analysis and physical–computational modelling to study the dynamics of intercellular adhesion and spheroid formation for different N-cadherin binding interfaces. We found that, in living cells in a tissue-like context, cis-interactions do not precede trans-interactions. Furthermore, junctions formed by the strand-swap mutant form significantly slower than WT junctions while junctions formed by the cis mutant and the X-dimer mutant are less stable. Nevertheless, cells with the X-dimer mutation result in spheroids comparable to WT-N-cadherin. However the cis and strand-swap mutations lead to a loss in tissue integrity and these cells fail to form spheroids and, in consequence, to function correctly in tissue.

3.1. Intercellular binding-dependent spheroid formation

We found that, in our system, N-cadherin interactions influence spheroid formation. Long-term live cell imaging showed that the expression of N-cadherin led to an increase in the rate of cell aggregation compared with untransfected L cells. The increase in the rate of spheroid formation depended on the binding of N-cadherin. Mutations within any binding interface led to a delay in cellular aggregation. Previous work on human hepatoma cells had shown that the initial phase of spheroid formation (less than 16 h) involves integrin–ECM interactions and only in the later stages—after 20 h—are cadherin interactions considered to contribute to the process [23]. However, these results could be cell-type specific. In breast carcinoma cells, Ivascu & Kubbies [24] have demonstrated integrin-independent spheroid formation. In our system, cadherin interactions were important for all stages of spheroid formation, including the initial phase as cells expressing WT-N-cadherin formed a compact aggregate within the first 5 h (figure 1c).

In order to dissect the kinetic processes involved in spheroid formation, we developed a physical–computational model. Investigating the parameter space for the binding and unbinding probabilities we found, as expected, that a relatively high binding probability and low unbinding probability resulted in successful spheroid formation and a low binding probability and high unbinding probability prevented spheroid formation. The two regions of the parameter space of successful or unsuccessful spheroid formation are separated by a clear boundary (figure 2c). Fitting the model to the experimental data for untransfected L cells and L cells expressing WT-N-cadherin, we found, predictably, that the difference in aggregation dynamics can be mostly accounted for by a difference in the binding and unbinding probabilities (figure 3). Thus, intercellular binding is a key mechanism that determines both the formation and final structural properties of cellular aggregates. Furthermore, the best-fit parameters for untransfected L cells and WT-N-cadherin occupy different regions of our spheroid phase space (figure 3a). While untransfected L cells lay on the diagonal that separates the regions of spheroid formation from the region of no aggregation, WT-N-cadherin is located in the bottom right region of high binding and low unbinding probabilities, hence indicating successful spheroid formation. A binding probability of 0.75 (figure 3b) for WT-N-cadherin further suggests that cell adhesion need not occur every time two cells meet. Our findings are in agreement with previous findings where it has been shown that cell aggregation depends on the adhesive properties of a cell rather than the collision frequency of the cells due to diffusion [17]. Thus, the process of spheroid formation is reaction controlled rather than diffusion controlled. It remains an open question as to how the dynamics of spheroid formation rely on the N-cadherin expression levels. The results from the calcium assay indicate that a moderate decrease in calcium concentration, hence a decrease in the levels of N-cadherin molecules with binding potential, slightly increases the aggregation speed. Therefore, for a moderate increase in N-cadherin expression levels we would expect no change or, at most, a minimal decrease in the aggregation speed.

3.2. Binding-dependent dynamics of N-cadherin

Although, overall, the model fits our experimental data very well, minor discrepancies suggest that the expression of WT-N-cadherin leads to further downstream mechanisms in L cells that are not accounted for in the present form of the model. The spheroid formation dynamics of WT-N-cadherin cells and the untransfected L cells were best fitted by varying the density difference between the cells and the medium. Even so, the simulations for WT-N-cadherin spheroid formation dynamics did not provide a perfect match to the experimental dynamics. There is abundant evidence suggesting that the levels of cadherin synthesis and trafficking are correlated with morphogenesis and adhesion requirements in both heterologous cells [25] and neurons [26,27]. A study conducted in dissociated hippocampal neurons found that, at basal rates, N-cadherin had a surprisingly high turnover rate; upon stimulation of N-methyl-d-aspartate receptors, the endocytosis of N-cadherin was reduced, leading to accumulation of surface N-cadherin molecules [28]. Based on our results and previous work, we propose that in heterologous cells, too, an additional pathway exists that is activated once cadherin molecules bind, which leads to the further trafficking and accumulation of cadherin molecules at the site of binding thereby resulting in faster spheroid formation dynamics. Such a feedback mechanism could account for the difference in aggregation dynamics between model and experiment for WT-N-cadherin as well as the differences in the cell versus medium density values.

Compared with previously published dynamics of spheroid formation for human hepatoma cells [23], the spheroid formation of L cells expressing WT-N-cadherin occurs at a much faster rate. However, in another study comparing well- and poorly differentiated human prostate cancer cells, Enmon et al. [18] have observed similar differences in the rates of spheroid formation. They found that the increased rate in spheroid formation was correlated with an increased expression level of E-cadherins. Considering that our cells are stably transfected to express N-cadherins, it is possible that in our system there is a higher density of adhesion molecules expressed on the surface, facilitating spheroid formation.

3.3. Functional role of N-cadherin binding interfaces

The slower spheroid formation dynamics observed in all of the cadherin mutants highlights the physiological importance of the various binding interfaces. In the R14E mutant, the aggregation was delayed relative to WT-N-cadherin-expressing cells. Ultimately, however, the R14E-expressing cells still formed a spheroid as indicated by the laminin staining which showed a compact, coherent cluster with a layer of EC matrix surrounding it. This is in contrast to the previous reports that used a two-dimensional aggregation assay to show that R14E cells did not aggregate even after 24 h [5,29], highlighting the importance of three-dimensional cell culture approaches. These data suggest the possibility of an additional junction formation pathway that bypasses the X-dimer leading to strand-swapped dimer formation. This pathway, however, leads to a decrease in bond survival probability suggesting that the X-dimer is essential to provide stability to cadherin–cadherin interactions. Provided cells rearrange within clusters during aggregation [30,31], this finding is in agreement with previous work showing that the R14E mutant forms slip bonds that, as the name suggests, slip apart and have a reduced lifetime in the presence of mechanical stress [32].

Our study revealed that, although the reduction in the area occupied by R14E and V81D/V174D cells showed similar dynamics, the cis (V81D/V174D) mutation still failed to ultimately form a spheroid. Fitting the model to the experimental data, we obtained a slightly lower binding and a 10-fold increase in the unbinding probability for the cis mutation compared with WT-N-cadherin. For the R14E mutant, the unbinding probability showed the same increase as for the cis mutant, while the binding probability did not change with respect to WT-N-cadherin. These results indicate a positive but minor effect of the cis binding interface to junction formation. This is in contrast to the major positive contribution of the cis binding interface to the probability of a trans-interaction as shown in Zhang et al. [33]. However, mutations of the cis and X-dimer binding interfaces mainly affect the stability of intercellular junctions. The main differences observed between the R14E and V81D/V174D mutants, from our analysis, were in the number of cells per cluster and the number of bonds per cell. One consequence of these differences was the less coherent structure of the V81D/V174D clusters compared with the R14E clusters, which we confirmed by staining for a component of the EC matrix. We further showed that mutating the cis-interface led to relatively rapid unbinding, suggesting that the delay in spheroid formation was due to the instability of the junctions formed. These results are in agreement with what we observed in two-dimensional experiments [11] and expand on what has previously been reported by Harrison et al., who showed that the residence time of cis mutants in cadherin clusters was much lower than that of WT-cadherins [4].

The W2A mutation led to the most dramatic effect, yielding aggregation dynamics comparable to those of untransfected L cells and a loose final aggregate indicated by laminin staining around individual cells, rather than the entire cluster. These results are consistent with previous studies demonstrating that cadherin adhesiveness is mediated via strand-swapping of the tryptophan residue located at position 2 (Trp2) [34]. Our results for the junction dynamics of the W2A mutant suggest that this is due to a low bond formation probability compared with WT-N-cadherin.

Our findings for the dissociation constant values indicate a 10-fold decrease in cadherin dimerization when any binding interface is mutated. The estimates for the K_d values shown in table 2 are based on a conservative assumption that the monomer concentration at equilibrium does not differ between the various genotypes. Considering our experimental and modelling data on the cadherin mutant binding properties, we would expect, however, that the cadherin mutants have a much higher monomer concentration at equilibrium than WT-N-cadherin. According to equation (2.4), the K_d value is directly proportional to the monomer concentration at equilibrium. Therefore, we expect that considering the real monomer concentration would lead to more dramatic increases in the K_d values for the cadherin mutants with respect to WT-N-cadherin. Nevertheless, the dimerization for the cadherin mutants would decrease in the same order as our conservative estimate (table 2), which is in agreement with previous measurements [5,35]. These results indicate that mutating the cadherin binding interfaces affects junction formation to varying degrees.

Based on our results for cellular connectivity, junction dynamics and binding kinetics, we rank the tissue formation ability of the different L cell lines in the following order, where WT-N-cadherin forms the most coherent spheroid, followed by the X-dimer mutant (R14E), the cis-interface mutant (V81D/V174D) and the strand-swap mutant (W2A).

3.4. Cooperativity between cis- and trans-interactions

Our results directly address the question of whether cis-interactions precede or follow trans-dimerization in N-cadherin. Our data show that in living cells both WT-N-cadherin and the cis mutant (V81D/V174D) have similar initial bond formation probabilities, suggesting that cis-interactions do not precede trans-dimerization. A previous study based on Monte Carlo simulations on a two-dimensional lattice had suggested that the formation of a junction is a cooperative process involving both cis- and trans-dimerization [36]. In our study using living cells, this result was confirmed for the very first time. We demonstrate that, although trans-dimers can form in the absence of cis-interactions, lateral dimerization of the cadherin molecules is necessary for providing stability to the entire junction since the lack of this interface leads to a lower probability of bond survival, thus resulting in volatile junctions.

3.5. Conclusion

Although crystallography studies have advanced our understanding of cadherin interactions, studying the dynamics of cadherin binding in living cells is indispensable for understanding cadherin function in living organisms. In vivo, cadherins are restricted by the plasma membrane as well as by their intracellular binding partners such as β-catenin [37], which may influence their binding dynamics.

Consistent with previous studies for junction dynamics in living cells [38], we find that the X-dimer is not necessary to form junctions but the formation of junctions is delayed compared with WT-N-cadherin. Our data, however, provide new insights on the junction stability of the strand-swap and the X-dimer mutants, which stand in strong contrast to this study. While Hong et al. [38] had concluded that the W2A mutation decreases junction stability, our results show that it affects the probability of junction formation while the stability remains the same as for WT-N-cadherin. The same study [38] had suggested that the junction stability of the X-dimer mutant is increased, while our results show that the junction stability of the X-dimer mutant is decreased. These discrepancies could be due to the fact that cell adhesion molecules change their properties when cells are cultured in two dimensions [7] as well as the lack of cadherin intracellular binding domain in the constructs used by Hong et al. [38]. Thus, our results signify the importance of a three-dimensional aggregation assay, which represents a close to in vivo approach to study cadherin binding dynamics.

Three-dimensional aggregation assays have been used extensively to investigate intercellular adhesion (e.g. [39]). However, these studies have only considered the properties of the final aggregate. Our results show that, to comprehensively understand the process of cell adhesion and particularly to distinguish the process of cell assembly between WT-N-cadherin, the cis mutant and the X-dimer mutant, it is paramount to understand the dynamics of aggregation.

Contrary to previous mathematical models for spheroid growth that form a spheroid from a single cell, our model represents spheroid formation as aggregation and therefore corresponds very closely to experimental conditions. This is supported by the good fit between our model and 20 different experimental conditions. The analysis of the aggregation data with our model revealed that, in contrast to our previous data [11], the cis mutation affects tissue integrity and these cells do not form a spheroid. Combining this tissue and cell-level analysis with an approach to study the junction dynamics highlights the effects of the various binding interfaces and their importance in tissue formation and junction stability. Our results unambiguously show that the decrease in tissue integrity for the cis mutant is due to junction instability.

Altogether, our results highlight the importance of three-dimensional dynamic studies to achieve a physiological understanding of intercellular adhesion and its impact on tissue organization. Furthermore, we provide new quantitative information on the steps of intercellular adhesion. These data will stimulate future research in a variety of areas in cell and developmental biology including cancer metastasis and cardiac development.

4. Material and methods

4.1. Three-dimensional cell culture, imaging and data analysis

To form spheroids, untransfected L cells and those expressing the various cadherin mutants were split and then counted. Two thousand cells were added to a well in a HydroCell 96-U well dish (Nunc) (coated to prevent cells from sticking to the well). Normal growth Dulbecco's modified Eagle's medium (DMEM) (supplemented with 10% fetal calf serum, 1% sodium pyruvate and 600 μg ml⁻¹ G418) was used for spheroid formation. For the Ca²⁺ assay, Ca²⁺-free DMEM (including all the other supplements) was used. The Ca²⁺ concentration was adjusted using CaCl₂ and including the background Ca²⁺ concentration from the serum the final Ca²⁺ concentrations of the medium were: 0.4, 0.8, 1.3 or 2.1 mM. For the 0 mM Ca²⁺ concentration, the Ca²⁺-free DMEM was supplemented with Ca²⁺-free serum (Labtech Ltd.) to avoid effects that background Ca²⁺ may have on spheroid formation. The dish was centrifuged for 2 min at 300g to position all cells in the centre of the well and was then placed on the Cell Observer (Carl Zeiss, Inc.) within a humidified incubator set at 37°C and 5% CO₂. After programming the position of each well, image acquisition commenced. Images were captured every 5 min for 48 h using a 5× 0.16 N.A. plan-Apochromat objective lens (Carl Zeiss, Inc.), transmitted light and an AxioCam MRm (Carl Zeiss, Inc.). The position of the well was updated periodically if a spheroid moved out of the field of view.

Only those experiments in which a spheroid remained in the field of view for the entire stack were used for data analyses. To determine the area occupied by the cells, an automated pipeline was developed in CellProfiler [40]. After loading in the images, the ‘classify pixels' module was used to perform pixel classification using Ilastik [41]. The Ilastik classifier was used to segment the images. Two classes were defined—spheroid or background—and the classifier was trained on a small set of images before applying it to the large dataset. After pixel segmentation based on the probability of a pixel representing a spheroid, objects were detected based on size with a typical diameter between 150 and 100 000 spheroid-classified pixels. A manual intensity threshold of 0.3 was applied on the probability maps and the size and shape of the objects were measured. The area of each object was measured and statistical analysis was conducted using GraphPad Prism 6 and R.

4.2. Cryo-sectioning, imaging and data analysis

Spheroids were formed for 48 h, after which they were fixed with 4% paraformaldehyde (PFA), left overnight in 30% sucrose solution and then embedded in freezing medium. Ten micrometre thin cryo-sections were collected and immuno-labelled using anti-laminin (Sigma) following a standard protocol. The slides were coverslipped and imaged on an LSM 780 (Carl Zeiss, Inc.) using a 20× 0.8 N.A. plan-Apochromat objective (Carl Zeiss, Inc.). The images were analysed using NIH ImageJ, where a 20 pixel wide line was drawn from the edge to the centre of the section and the intensity profile was plotted within the first 20 μm. All the profiles were normalized to their maximum intensity and by investigating individual profiles for WT-N-cadherin and the cadherin mutants the point at which the curves reached a baseline was determined. This point of intersection was found to be at 40% of the maximum intensity. Therefore, the distance where the fluorescence intensity reduced by 60% was measured using Mathematica 9.01 (Wolfram Research). W2A was not used for this analysis as the fluorescence intensity did not decrease significantly in the first 20 μm of any section.

4.3. Light-sheet-based fluorescence microscopy

Seventy-two hours post spheroid formation, the spheroids were fixed in freshly prepared 4% PFA in phosphate-buffered saline (PBS) at 4°C for 30 min. The cell nuclei were stained with DRAQ5 (Cell Signaling) for 2 h at room temperature. The spheroids were then embedded in 1% low-melting agarose and drawn into a 20 μl Brand intra MARK micropipette according to previously described methods [9]. The micropipettes were placed in a suitable sample holder and mounted vertically into a digital scanned laser light-sheet microscope [9] in a designated perfusion chamber filled with 1× PBS (Gibco). Prior to imaging, the spheroid surrounded by agarose was extruded from the micropipette. The samples were illuminated by a 2.5× 0.06 N.A. Epiplan-Neofluar air objective (Carl Zeiss, Inc.) and emitted light was detected by a 10× 0.3 N.A. water immersion N-Achroplan objective (Carl Zeiss, Inc.) using the Andor Clara camera (Andor Technology PLC). The sample was excited using a 561 nm laser line (Omnicron GmbH) for DRAQ5. Three-dimensional recordings were generated by moving the sample along the z-axis—towards the detection lens [42]. A maximum intensity projection of the images was created using NIH ImageJ.

4.4. Agent-based model

To investigate in detail the process of spheroid formation, a three-dimensional agent-based approach was used. The smallest entity in the system is a cell. The cells move in a convex well and accumulate to form clusters. Cluster formation occurs through cell–cell binding, cell–cluster binding and cluster–cluster binding.

Based on experimental observations, a cell is assumed to be spherical. The movement of the cells is based on a set of rules. The cells move randomly as described by a Wiener process

4.1

where D is the diffusion parameter and dW is a random increment drawn from a normal distribution with mean 0 and standard deviation 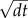. Furthermore, buoyancy determines the sinking of the cells. Cell movement is restricted by the shape of the well, which is represented by a half-sphere.

Cluster formation occurs through cells forming bonds. Two cells can form a bond with a binding probability p_binding if their centroids are closer than twice their radius r and both cells had fewer than 12 bonds in the previous time step, which is the maximal number of bonds assuming three-dimensional hexagonal packing. Bonds can break with an unbinding probability p_unbinding.

The interactions of cells are determined by a friction coefficient γ, volume exclusion between neighbouring cells and an adhesive force for each bond that connects a given cell to its neighbours. Based on experimental data for cell adhesion forces [43] and previous modelling work on multicellular tissues [44] the volume exclusion force F_excl and adhesion force F_adh are derived from Lennard-Jones potentials through 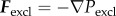and 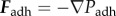. Choosing dist as the Euclidean distance between two cells, n as the normalized vector pointing along the line connecting the two cells and r as the cell radius, the forces are given by

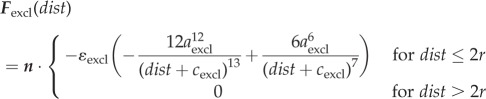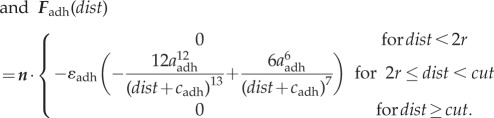Assuming that the magnitudes of the forces between two cells are zero if the distance between two cells is 2r, we get ; hence, assuming that c_excl and c_adh are positive, we get 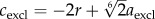and 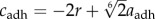. The electronic supplementary material, figure S6a,b, shows the graphs for the parameter values given in table 3.

Table 3.

Parameter values used in the physical–computational model for spheroid formation.

parameter values		source
movement
radius of a cell r	5 µm	measured in images
viscosity of the medium ηmedium	0.97 cP	fluxion technical note (http://info.fluxionbio.com/files/PDF_PUBLIC/bioflux_system/technical_notes/bioflux_viscosity_technote-1038-01.pdf)
time step	10 s
diffusion coefficient	0.05 µm² s−1	estimated by Stokes–Einstein equation (at 37°C)
density difference cell–medium	6 mg ml−1	parameter scan
volume exclusion aexcl	39 µm	chosen to balance diffusion and adhesion
volume exclusion ɛexcl	6.5 g µm² s−²	chosen to balance diffusion and adhesion
adhesion aadh	11 µm	chosen to match curve in [43]
adhesion ɛadh	0.8 mg µm² s−²	chosen to match curve in [43]
adhesion cut	30 µm	chosen to match curve in [43]
boundary conditions
centre of the well	(0, 0, 4000) µm	measurements of a well
radius of the well	4000 µm	measurements of a well
bond formation and removal
binding probability pbinding	1	parameter scan
unbinding probability punbinding	0.01	parameter scan
maximum number of bonds per cell	12	assuming hexagonal packing

To obtain cellular aggregation in the model, the sinking of the cells has to dominate over diffusion. In this case, however, the cells settle at the bottom of the well and do not form a three-dimensional aggregate. Hence, an upward movement is necessary to obtain a spheroid. We implemented this by assuming that, if a cell has a total overlap with all its surrounding cells of more than 60% of the cellular diameter, the cell moves up by 80% of its diameter.

4.5. Initial conditions

In the experiments, at the initial time point the cells were distributed in a disc-like shape at the bottom of the well due to centrifugation. The initial distribution of the cells in the model was chosen to match the distribution of the cells in the experiments. Therefore, the cells were segmented in the images for the first time point and the distances between each cell and its neighbours were calculated (electronic supplementary material, figure S6c). The six closest cells were chosen as potential neighbours of a cell. To prevent false neighbour detection at the boundaries, the mean distance between the potential neighbours and the given cell was calculated and cells that were closer than the mean distance plus 1 s.d. were accepted as neighbours.

In the model, the initial conditions are set up by random perturbation of a hexagonal packing of spheres in a circle at the bottom of the well (electronic supplementary material, figure S6d). Analysing the distances between neighbouring cells in the same manner as for the experiments showed that the distribution of distances between the model and the experiments is similar (electronic supplementary material, figure S6e).

4.6. Simulations

Simulations were performed in Mathematica v. 9.01 (Wolfram Research). Each iteration consisted of two steps. First, the solution of equation (4.1) together with cell sinking and cell adhesion were approximated with the Euler–Maruyama method (reviewed in [45]), and then the remaining actions were conducted in the following order: volume exclusion, reflection from the well wall, upward squeezing, bond formation and bond removal. The code for the simulations is provided as a package in the electronic supplementary material together with a test notebook. Both can be viewed with the Wolfram CDF player (http://www.wolfram.com/cdf-player/).

All simulations were performed for 50 cells. The remaining parameter values are shown in table 3.

The size of the time step was chosen such that the typical distance a cell moves due to diffusion during one time step is sufficiently small compared with the diameter of the cell. For our choice of parameter values, the mean distance moved by a cell is 1.5 ± 0.6 µm and the cell diameter is 10 µm.

To ensure the accuracy of the numerical method, we tested whether the error converged with decreasing time-step size. For the purpose of the test, to reduce the stochastic elements in the model to the diffusion term in equation (4.1), a cluster of 50 cells was used and an unbinding probability of 0 as well as no upward squeezing. The error was calculated as the difference between a reference solution for a time step of size 10/2⁸ and 10 realizations of eight time steps of size 10/2ⁱ for i = 0, … , 7. The electronic supplementary material, figure S6F, shows that the error decreases with a slope of 0.53, which is consistent with the expected order of convergence [45].

4.7. Measurements from the model

Since the simulations provide the details of the clusters and the positions of each cell at every time point, we can extract several measurements that describe the properties of the system (figure 2c). The normalized area is calculated as the area of the convex hull of the cell coordinates projected to the x–y-plane. The z extension is given by the difference between the maximum z coordinate and the minimum z coordinate of the cells at a given time point. The number of bonds is counted per cell. A cluster contains at least two cells, hence single cells are not considered for the calculation of the number of clusters and the number of cells per cluster. If, at a given time point, there are no clusters the number of cells per cluster is set to zero.

4.8. Fitting the model to experimental data

To fit the model to the data, we compared the normalized area over time which we obtained from the parameter scan (figure 2) with the experimental data (figure 1). The goodness of fit was quantified by the AIC, a widely accepted measure of the validity of nonlinear models. It combines the log-likelihood of the estimated model with a correction term for the number of parameters used for the fitting and is given by

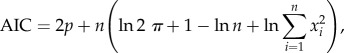where p is the number of parameters and x_i for i = 1, … , n are the residuals [46]. Note that in the figures we plot the AIC normalized for each experimental condition individually. Hence, 1 denotes the best fit and 0 the worst fit.

4.9. Statistical analysis

All hypothesis testing was performed in R [47] using a Wilcoxon rank sum test with Holm correction for multiple testing. For figure S2c in the electronic supplementary material, all the properties for all parameter values for the difference in the cell and the medium density shown in figure S2b in the electronic supplementary material were compared. This resulted in four tests with 15 comparisons each. Note that for a better overview in figure S2c in the electronic supplementary material, we only show the results for the range of the density difference between the cells and the medium relevant for fitting the experimental data in figure 1. In the electronic supplementary material, figure S4, each property was compared between the different genotypes, so six tests with 10 comparisons each were performed.

4.10. Model of junction dynamics

The model for the probability of a bond in figure 7a was motivated by a micropipette assay for studying adhesion between two cells [22]. Assuming two cells are not connected by a bond, the cells can either form a bond, which is given by a probability p, or they can remain unbound, given by 1 − p. Once a bond is formed, it can either break, determined by a probability q, or the bond can remain bound, given by the probability for survival of a bond 1 − q. Thus, for a stochastic process with random variables X_t, where 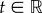, we get 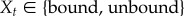. This yields the Master equation

and

and for the limit we obtain

4.2

Assuming initially there is no bond between the cells, i.e. the initial condition 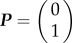, the solution of (4.2) is

Substituting the best-fit parameters for p_binding and p_unbinding from the computational model (figure 4) for p and q we obtain the solutions displayed in figure 7b.

Considering the initial condition in which the cells are bound, i.e. 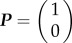, equation (4.2) is solved by

Figure 7c shows the solutions we obtain by substituting the best-fit parameters for p_binding and p_unbinding from the computational model (figure 4) for p and q.

Author contribution

The experiments and models were conceived and designed by: S.G., S.C.F., E.M.S., E.H.K.S. The experiments were performed and the data were analysed was by: S.G. Model development and implementation was by: S.C.F. The manuscript was written by: S.G., S.C.F., E.M.S., E.H.K.S.

Funding statement

We thank the Deutsche Forschungsgemeinschaft (DFG) and the Cluster of Excellence Frankfurt for Macromolecular Complexes (CEF-MC II, EXC115) for the financial support.

Conflict of interest

The authors declare no conflict of interest.