Many hepatitis C reinfections that spontaneously clear may be undetected: Markov-chain Monte Carlo analysis of observational study data

Abstract

Hepatitis C virus (HCV) reinfection rates are probably underestimated due to reinfection episodes occurring between study visits. A Markov model of HCV reinfection and spontaneous clearance was fitted to empirical data. Bayesian post-estimation was used to project reinfection rates, reinfection spontaneous clearance probability and duration of reinfection. Uniform prior probability distributions were assumed for reinfection rate (more than 0), spontaneous clearance probability (0–1) and duration (0.25–6.00 months). Model estimates were 104 per 100 person-years (95% CrI: 21–344), 0.84 (95% CrI: 0.59–0.98) and 1.3 months (95% CrI: 0.3–4.1) for reinfection rate, spontaneous clearance probability and duration, respectively. Simulation studies were used to assess model validity, demonstrating that the Bayesian model estimates provided useful information about the possible sources and magnitude of bias in epidemiological estimates of reinfection rates, probability of reinfection clearance and duration or reinfection. The quality of the Bayesian estimates improved for larger samples and shorter test intervals. Uncertainty in model estimates notwithstanding, findings suggest that HCV reinfections frequently and quickly result in spontaneous clearance, with many reinfection events going unobserved.

1. Introduction

The hepatitis C virus (HCV) infects an estimated 185 million people worldwide and is a significant cause of morbidity and mortality [1]. In high-income countries, people who inject drugs (PWIDs) are the subgroup at greatest risk of HCV infection [2]. Although approximately 25% will spontaneously clear their infection [3] and there have been major advances in HCV antiviral treatment [4], there is still no vaccine for HCV.

Naturally acquired immunity to HCV is complex. Previous infection with HCV appears to confer only partial immunity from future HCV infection. In individuals who were re-exposed to HCV after successfully clearing an initial infection (primary infection), further infections (reinfection) have been documented. Reinfection with a new HCV infection can be distinguished from viral relapse of the initial HCV infection by viral sequencing [5–11]. HCV reinfection has been observed in two main population groups, both of which are characterized by repeated exposures to HCV: PWIDs [5–10,12–16] and human immunodeficiency virus (HIV)-infected men who have sex with men who engage in high-risk sexual behaviour [11,17,18].

Longitudinal studies of HCV reinfection among PWIDs are relevant for HCV vaccine development, because they give insights into acquired natural immunity to HCV. In particular, if it were possible to identify people in whom naturally acquired immunity enabled spontaneous clearance after reinfection, the mechanism could be investigated and potentially mimicked in a vaccine [19]. To date, results from reinfection studies have varied considerably. Reinfection rates that are lower and higher than primary infection rates in the same populations have been reported [5,7–10,12–15,20]. Furthermore, a broad range of spontaneous clearance probabilities have been reported (minimum reported value: 0.3; maximum reported value: 1.0) [7,8,10,12–15,20]. Although variations between populations in the rate of reinfection are expected (depending on the frequency of exposure to HCV), the probability of spontaneous clearance after reinfection is likely to be dependent on the natural immune response to HCV, and not only the frequency of exposure, and can therefore be expected to be more consistent between populations.

We recently showed that variation in the study testing interval may account for much of the observed variation in HCV reinfection studies [21]. This is because reinfections that spontaneously clear can go undetected if the duration of the reinfection is shorter than the testing interval [22]. Ideally, short testing intervals (potentially shorter than one month) would be used to generate more reliable estimates of reinfection incidence and spontaneous clearance probability. However, it is challenging to follow PWIDs frequently. As a result, in this paper we explore an analytical method (Bayesian post-estimation) for estimating the reinfection rate, reinfection duration and probability of reinfection spontaneous clearance given study data that were collected at wider than optimal testing intervals. Data were from the Networks 2 prospective cohort study of PWIDs, which was a community-based study undertaken in Melbourne, Australia, from 2005 to 2010 and had a median three-monthly testing interval [5,15,23].

Estimation of key quantities associated with reinfection occurrence and clearance is challenging given typical observational data. In the context of data with test intervals that are on average greater than the duration of spontaneously clearing reinfection, the parameters to be estimated are intimately linked. For example, it is possible that the observed data correspond with a relatively high reinfection rate and short duration of reinfection or a lower reinfection rate and a longer duration of reinfection. This makes it difficult to estimate all three parameters simultaneously. In this paper, in addition to investigating how precisely the parameter values can be estimated given the sparseness of available data, we also use simulation studies to test the method and investigate how short the testing interval would need to be in order to generate precise and accurate estimates for the parameters of interest: reinfection rate, reinfection duration and clearance probability.

2. Material and methods

2.1. Participants and data collection

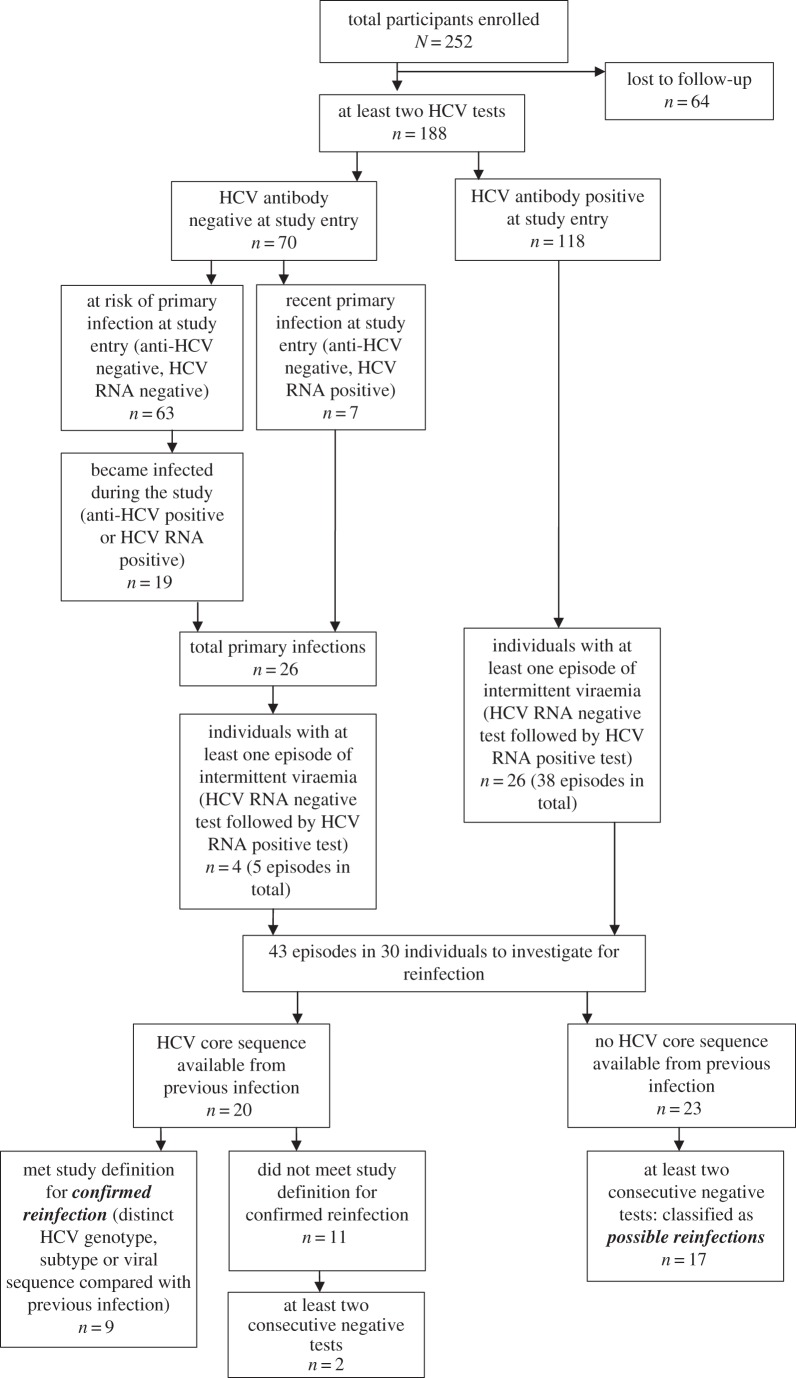
The Networks 2 study was an observational cohort study of PWIDs in Melbourne, Australia [23]. Study participants were recruited from street illicit drug markets, as reported in detail elsewhere [23]. The main recruitment period was 2005–2006 and participants were followed until 2010. Participants were followed every three months. Participation was voluntary, and informed consent was obtained from each participant in writing. At each study visit, participants were bled and tested for anti-HCV antibodies and HCV RNA among other things. Study participants who did not report receiving HCV antiviral treatment and who were classified as being susceptible to reinfection (defined below) and then had at least one subsequent HCV RNA test at any point during the study were eligible for inclusion in these analyses. In total, 252 participants were enrolled in the study, 25% (n = 64) were lost to follow-up and, of the remaining 188 participants, 46 were susceptible to reinfection (figure 1). Laboratory methods are described in the electronic supplementary material, appendix.

Figure 1.

Flowchart of reinfection classifications.

2.2. Study definitions

2.2.1. HCV infection and clearance

HCV infection and clearance classifications are illustrated in figure 1. Participants who tested positive for HCV RNA were classified as being infected with HCV, regardless of anti-HCV status. Primary infection was defined by anti-HCV seroconversion. Participants were classified as susceptible to reinfection if they had evidence of spontaneous clearance of HCV infection. This was defined as either testing anti-HCV antibody positive and HCV RNA negative at two consecutive study visits (at least 28 days apart) or, after testing HCV RNA positive, testing HCV RNA negative and then HCV RNA positive where the second appearance of viraemia was genetically distinct from the first. Among those susceptible to reinfection, occurrences of intermittent viraemia—defined as at least one HCV RNA negative test followed by an HCV RNA positive test—were identified. Where possible, HCV viral sequence analysis was used to determine whether the new viraemia was genetically distinct from previous infections (detailed methods in the electronic supplementary material, appendix). A confirmed reinfection was classified as a new episode of HCV viraemia that was genetically distinct from the previous infection (detailed methods in the electronic supplementary material, appendix). Where it was not possible to assess whether the two instances of viraemia were genetically distinct because no sequencing data were available on the initial infection, the term possible reinfection was used. A possible reinfection was classified as a new episode of viraemia that occurred after at least two consecutive negative tests (at least 28 days apart to confirm spontaneous clearance) and was not possible to assess as being genetically distinct from the previous infection. All analyses were performed for confirmed reinfections only and confirmed and possible reinfections combined.

2.2.2. Date of first susceptibility to reinfection

Data were included in these analyses from the first time that the participant was classified as susceptible to reinfection. For participants who were susceptible at study entry, this was the date of the baseline visit. For participants who were not susceptible at study entry, this was the first spontaneous clearance date (defined as the midpoint between the last HCV RNA positive test and the first HCV RNA negative test). For analyses that were limited to confirmed HCV reinfections, participants only became susceptible after clearing an infection where it was possible to sequence virus from the first infection. This meant that fewer participants were included in the confirmed reinfection analyses than in the possible reinfection analyses.

2.3. Estimates for parameter values calculated using a simple epidemiological approach

The following are simple methods for estimating the parameter values that have commonly been used in epidemiological studies. The date of reinfection was defined as the midpoint between the date of the first HCV RNA positive test and the previous HCV RNA negative test. The date of spontaneous clearance was defined as the midpoint between the last HCV RNA positive test and the first HCV RNA negative test. Reinfection rates were taken as the total number of reinfection episodes observed (in some cases there were multiple episodes per participant) divided by the number of person-years (PY) that participants were susceptible to reinfection. Clearance probability was estimated by taking the proportion of reinfection episodes with at least two follow-up tests after the estimated date of reinfection that resulted in spontaneous clearance. Duration of infection was estimated based on those reinfection episodes that resulted in spontaneous clearance. In this study, the estimates computed using this approach were used as a comparison for the model-based estimates.

2.4. Model description and assumptions

HCV reinfection and spontaneous clearance were modelled as a homogeneous Markov process consisting of three main states: susceptible (S), acute infection (I_A) and chronic infection (I_C) (figure 2). Because there is no blood test to distinguish acute from chronic infection, the transition between acute and chronic states was modelled as a hidden Markov process. The model was adapted from our previous probabilistic individual-based model of HCV reinfection and clearance [21]. Participants were classified as susceptible to reinfection if they had evidence of having previously cleared a HCV infection. Because the observational data were collected over a short time-frame (5 years), it was assumed that those in the susceptible state became reinfected at a constant rate (α). Once reinfected participants moved to the acute infection state (I_A). From the acute infection state, it was assumed that participants could spontaneously clear (with probability β), thereby returning to the susceptible state, or their infection could progress to chronicity, state I_C. The duration of a state with a constant exit rate is distributed exponentially. In order to ensure a plausible distribution for the duration of acute reinfection (γ), acute infection was divided into two states (I_A1 and I_A2) and participants left each of these states at constant rates (2/γ); thus, while the duration of each of the two acute infection states followed an exponential distribution, the combination of the two member states effectively implements a realistic gamma-distributed acute infection duration [24].

Figure 2.

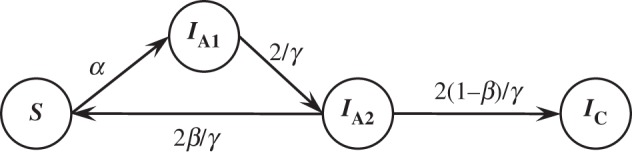
Model diagram. S: susceptible to reinfection; I_A1 and I_A2: acute reinfection; I_C: chronic reinfection. α: per-month probability of reinfection = rate of reinfection in reinfections per person-month; β: probability that a reinfection will result in spontaneous clearance; γ: average duration of acute reinfection.

Thus, the per-month rate of spontaneous clearance was defined as the product of the spontaneous clearance probability and the per-month rate of leaving the second of these acute infection states (2β/γ), whereas the per-month rate of an infection progressing from the acute infection state to the chronic infection state was defined as the product of the chronic infection probability and the per-month rate of leaving the second of these acute infection states (2(1 − β)/γ). Those with chronic infection (state I_C) were assumed to remain in that state indefinitely. Because it is not possible to distinguish acute infection from chronic infection based on laboratory data alone, the probability of being in the acute or chronic infection state given that a participant has evidence of infection was determined probabilistically (details in the electronic supplementary material, appendix). The per-month rates of reinfection and clearance were assumed to remain constant throughout and not to be dependent on the number of previous reinfections.

The model is a continuous-time deterministic ordinary differential equation model. The instantaneous rates of change between states i and j are summarized in the following instantaneous rate matrix, Q_ij:

The instantaneous rate matrix, Q, has the property that 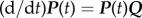, which can then be solved to provide an equation for P(t), the transition probability matrix at time, t: P(t) = e^tQ.

2.5. Model-based parameter estimation

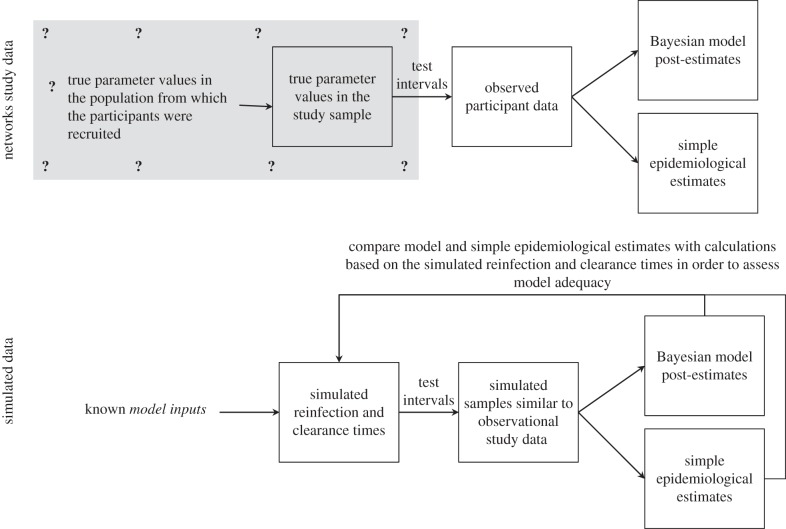
A Bayesian approach was used to estimate the unknown parameter values (reinfection rate, average duration of acute reinfection and probability that a reinfection results in spontaneous clearance) from the study observations (figure 3). In short, the Bayesian framework posits that the inferred probability distribution for the parameters of interest (called the posterior probability distribution and abbreviated to ‘posterior’) depends on both the study observations and some prior probabilities that have been assigned by the researchers. Prior probability distributions (‘priors’) are described below. Monte Carlo Markov chain (MCMC) methods were used to calculate a posterior probability distribution of the parameter set (θ = {α,β,γ}) and posterior probability distributions for functions of those parameters (the latter are termed marginal posterior probability distributions and abbreviated to ‘marginal distribution’) [25]. Marginal distributions were also calculated for the proportion of participants with persistent infections (that is, in the chronic infection state) after 1,2,3, …, and 10 years. A detailed description of the approach taken, including derivation of transition probability matrices and details of the MCMC methods, is given in the electronic supplementary material, appendix. Point estimates from the Bayesian analysis are median posteriors; 95% credible intervals (CrIs) were also calculated. Bayesian terminology is summarized in the electronic supplementary material, table S1.

Figure 3.

Schematic showing how Bayesian post-estimation is used on the real Networks data to estimate unknown parameters, and on simulated data with known parameters to assess model adequacy. The true values of the three parameters of interest (reinfection rate, reinfection duration and reinfection spontaneous clearance probability) are unknown in the Networks study sample and in the population from which study participants were recruited (grey shaded region signifies unknown). However, for the simulated data, the model inputs and resulting characteristics of the simulated samples under perfect observation are known and can be compared with the Bayesian post-estimates and the simple epidemiological estimates in order to assess their accuracy and evaluate how that is related to different factors.

2.5.1. Assumptions and priors

Uniform uninformative priors were assigned to the reinfection rate (α) and probability of spontaneous clearance (β). The reinfection rate was assumed to be greater than zero and clearance probability was assumed to be between 0 and 1. A uniform prior was assigned to the duration of acute reinfection(γ), where the average duration of acute reinfection was assumed to be greater than or equal to 7 days and less than six months (within this interval, all possible values for the duration of acute reinfection were considered equally likely). A six-month maximum was imposed because it is known that the majority of primary infections that spontaneously clear do so within six months and observational studies have shown that reinfection is shorter than primary infection [3,7,26]. A 7 day minimum was imposed because this is the shortest reinfection duration that has been observed in chimpanzees; it was observed in three of nine chimpanzees who were reinfected with the same viral genotype as their primary infection [27].

2.5.2. Likelihood calculations

The likelihood of the observed data was calculated by taking the product of the probabilities of the observed state transitions (defined in §2.4) and the observed state transitions. Because it was not possible to determine whether an infected participant was in the acute state or the chronic state on the basis of the observed data, a hidden Markov model was used. The probability of observing a participant in an infected state was taken as the probability of the participant being in the acute infection state or the chronic infection state. Thus, if a participant tested anti-HCV antibody positive and HCV RNA positive at a given timepoint, and three months later they tested anti-HCV antibody positive and HCV RNA positive again, the transition probability would be taken as the sum of all possible infected state to infected state transition probabilities—for example, the three-month probability of transitioning from the first acute infection state to the first acute infection state, or transitioning from the first acute infection state to the second acute infection state, or transitioning from the acute infection states to the susceptible state and back to one of the acute infection states, etc. Formulae for calculating these probabilities are included in the electronic supplementary material, table S2.

Note that, according to the study definitions (described in detail below), a person is considered to move from the infected to susceptible state only on the basis of observing two consecutive negative tests or one negative test followed by a change in HCV genotype, subtype or viral sequence. If a participant tested HCV RNA positive, then HCV RNA negative and then HCV RNA positive and there was no change in genotype, subtype or viral sequence, we conservatively classified them as being infected at all stages because it is possible that the HCV RNA negative result represented low levels of viraemia rather than viral clearance. However, if the final two tests for a given participant were HCV RNA positive followed by HCV RNA negative, the participant could not be classified as having either spontaneous clearance or low levels of viraemia. For this special case, the probability of moving from infected to susceptible or moving from infected to infected were both allowed, with the relative probabilities of each being defined by calculating the proportion of HCV RNA positive, HCV RNA negative sequences with at least one subsequent follow-up observation that went on to be classified as spontaneous clearances.

Given that the HCV RNA test used (COBAS AMPLICOR 2.0) is highly sensitive (greater than 96%), specific (greater than 99%) and has a very low limit of detection (less than 50 IU ml^–1) [28], no measurement error was assumed for classification as infected (HCV RNA positive) or uninfected (two consecutive negative HCV RNA tests or one negative HCV RNA test followed by detection of a genetically distinct HCV in the subsequent test).

2.6. Model adequacy and data requirements

2.6.1. Evaluating model adequacy

In order to investigate (i) the precision and accuracy of the model predictions given the sparseness of the observed data (i.e. three- to four-month test interval and an average of five follow-up tests per participant) and (ii) how short the testing interval would need to be in order to estimate the primary quantities precisely, the model was tested on simulated data (figure 3). Data similar to those collected in the Networks 2 study, but with variations in test interval and parameter values, were simulated using a continuous individual stochastic model with the same structure as the model depicted in figure 2. The model simulations are described in detail in the electronic supplementary material, appendix, but, briefly, simulated samples were produced using a two-stage process: first, values for the unobserved times of reinfections and clearances for each participant were produced for two different scenarios regarding the assumed duration of acute reinfection, reinfection rate and probability of clearance, and three different scenarios regarding the number of participants (one scenario resembling the confirmed reinfections only dataset with 16 participants, one resembling the confirmed and possible reinfections dataset with 46 participants, and a further scenario with a larger group of 100 participants). Second, observed event occurrence indicators were generated, following an observation scheme that mimicked that used in actual studies. Four different test intervals (half, one, two and four months) were used. The target analysis was applied to each of the resulting simulated samples. Simulations consisted of 100 repetitions of each sample, with each simulation representing a specified scenario with respect to the parameters of the model generating the actual event times, the chosen sample size and the observation scheme (i.e. the test interval). In total, there were 2 (two reinfection duration, reinfection rate and probability of clearance scenarios) × 3 (low, medium or high numbers of participants) × 4 (four test interval scenarios) = 24 scenarios simulated (figure 3 and table 1).

Table 1.

Simulation details.

	no. scenarios	details
reinfection duration, reinfection rate and clearance probabilitya	2	scenario 1:
		—mean duration = 1 month  —mean rate = 109 per 100 PY  —clearance probability = 0.93
		scenario 2:
		—mean duration = 2 months  —mean rate = 72 per 100 PY  —clearance probability = 0.89
no. participants	3	16, 46, 100
test interval	4	0.5, 1, 2, 4 months
repetitions	100
total no. simulations	2400	2 × 3 × 4 × 100

^aReinfection duration is modelled using a gamma distribution with variance equal to 0.5 and 2 for scenarios 1 and 2, respectively. Time to reinfection is modelled using an exponential distribution with mean time to reinfection equal to the inverse of the mean rate of reinfection, and variance equal to the inverse of the mean rate of reinfection squared.

Each simulated sample was analysed using the same methods used to analyse the Networks 2 observational study data to obtain estimates for the reinfection rate, clearance probability and duration of acute reinfection. The quality of the Bayesian model estimates derived using different test intervals was assessed against the characteristics of the simulated samples under perfect observation (figure 3), and the median (95% CrI) error was calculated across the 100 datasets.

2.7. Software

Study data were stored in MS Access and manipulated (including data cleaning and traditional statistical analysis) in Stata 11 (College Station, TX, 2011). All models were implemented in the R programming environment (v. 2.13.1) [29].

3. Results

3.1. Analysis of observational data

3.1.1. Simple epidemiological approach

Forty-six participants were classified as susceptible to reinfection at some point during the study period, did not report having received antiviral therapy and had at least one subsequent follow-up test. Eligible participants had a median of five follow-up tests after becoming susceptible to reinfection (interquartile range: 3–10), and participants were susceptible to reinfection for a total of 106 PY. Overall, nine confirmed reinfection events and 17 possible reinfection events were observed [5]. Estimates for reinfection rate, duration of acute reinfection and reinfection clearance probability calculated using the simple epidemiological approach are presented in table 2.

Table 2.

Estimates calculated using the simple epidemiological approach and model-based approach for reinfection rate, duration of acute reinfection and reinfection clearance probability for the Networks 2 study. Simple epidemiological parameter estimates for reinfection rate and reinfection clearance probability are reported as mean (95% confidence interval); these are calculated based on the assumption that all reinfection events are independent and for consistency with model estimates do not account for within-person correlations. Estimates of reinfection clearance probability are calculated excluding events where there was no subsequent follow-up. Simple epidemiological estimates for duration of acute reinfection are reported as median (interquartile range). All model estimates are reported as median (95% CrI). PY, person-years.

	confirmed reinfections only	confirmed and possible reinfections
data characteristics
reinfection cases (n)	9	26
PY at risk of reinfection	31	106
clearance episodes (n)	4	13
simple epidemiological parameter estimates
reinfection rate (cases per 100 PY)	28.8 (15.0–55.4)	24.6 (16.8–36.1)
reinfection clearance probability	0.50 (0.16–0.84)	0.59 (0.36–0.79)
duration of acute reinfection (months)	3.5 (2.5–11.2)	4.1 (3.0–7.7)
Bayesian model parameter estimates
reinfection rate (cases per 100 PY)	104.1 (21.1–344.1)	61.7 (25.0–231.3)
reinfection clearance probability	0.84 (0.59–0.98)	0.90 (0.80–0.98)
duration of acute reinfection (months)	1.3 (0.3–4.1)	2.5 (0.3–5.2)

3.1.2. Model-based approach

Model estimates for each of the parameters are presented in table 2. Compared with estimates derived from epidemiological analyses, the model estimated reinfection rates were on average 2.5 (for confirmed and possible reinfections)–3.5 (for confirmed reinfections only) times greater, but they lacked certainty with very wide 95% CrIs (ranging from approx. 20 to over 200 per 100 PY). The model-estimated reinfection durations were shorter than the estimates derived using the simple epidemiological approach (one to two months compared with approx. four months for both reinfection classifications) but also had wide 95% CrIs. The model-estimates for spontaneous clearance probabilities were approximately 0.85–0.90 for both reinfection classifications (with CrIs ranging from 0.59 to 0.98 for confirmed reinfections only, and from 0.80 to 0.98 for confirmed or possible reinfections)—that is, on average, 50–70% greater than the epidemiological estimates. The model estimates for cumulative risk of persistent reinfection were 0.12 at 1 year, 0.52 at 5 years and 0.78 at 10 years for confirmed reinfections only (figure 4). Results were similar for analyses of confirmed and possible reinfections.

Figure 4.

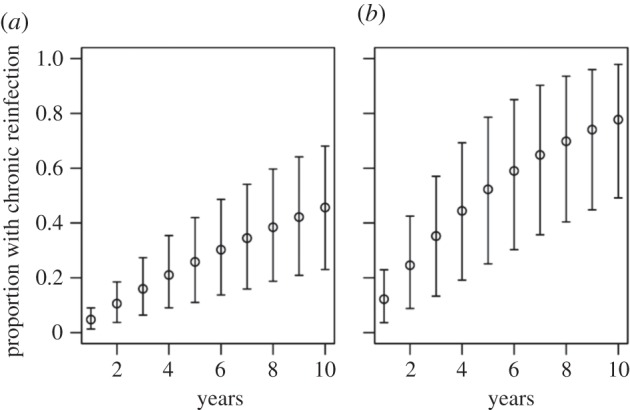
Model estimated risk of persistent reinfection in the Networks study after 1–10 years for (a) confirmed and possible reinfections; and (b) confirmed reinfections only. All results are reported as median (95% CrI).

3.1.3. Relationships between parameters

There was a strong inverse association between the model estimated reinfection rate and reinfection duration (electronic supplementary material, figure S1). This is because based on the available data it was equally likely that there were a relatively large number of short reinfections or smaller numbers of long reinfections. For the same reason, there was also a weaker association between reinfection rate and clearance probability (electronic supplementary material, figure S1).

3.2. Analysis of simulated data

3.2.1. Simple epidemiological approach

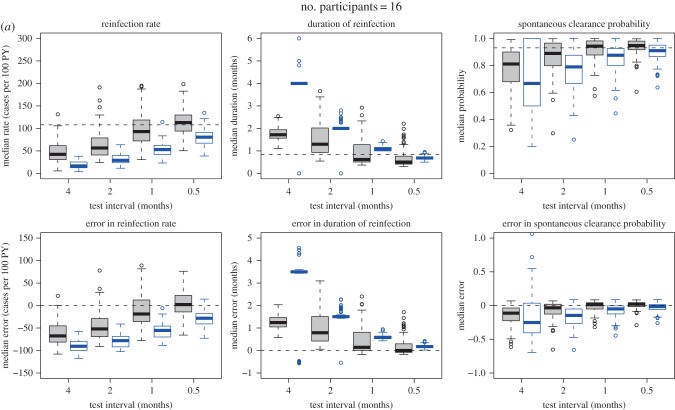
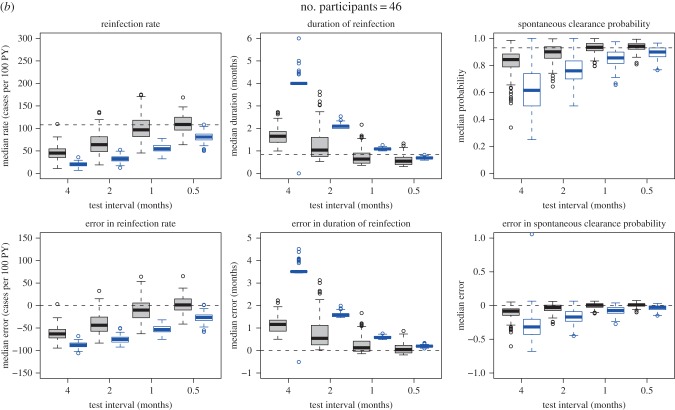
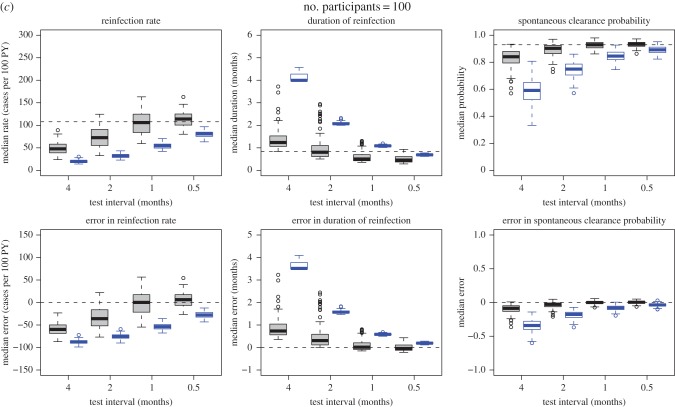
Simulated samples were analysed using the naive and Bayesian approaches defined above. Estimates derived from the simulated samples by applying the simple epidemiological approach were compared with the characteristics of the simulated samples under perfect observation (figure 3). The estimates were biased towards underestimating the reinfection rates and spontaneous clearance probabilities, while overestimating the reinfection durations. As expected, the magnitude of the bias decreased as the testing interval decreased (figure 5 and electronic supplementary material, figure S2).

Figure 5.

(a–c) Estimates and errors for reinfection rate, duration of reinfection and spontaneous clearance, by test interval for the simulated observational data: traditional epidemiological methods compared with model-based approach. Grey, estimates calculated using model-based approach. Blue, estimates calculated using traditional epidemiological methods. Horizontal dotted lines indicate ‘true’ inputs. Model inputs: mean reinfection duration = 1 month (median duration = 0.8 months), reinfection duration modelled using a gamma distribution with the variance equal to 0.5 months. Mean reinfection rate = 109 per 100 PY. Time to reinfection modelled using an exponential distribution with mean time to reinfection equal to the inverse of the mean rate of reinfection, and variance equal to the inverse of the mean rate of reinfection squared. Reinfection clearance probability = 0.93. Errors are relative to the characteristics of the simulated samples under perfect observation. Horizontal dotted lines in the estimate plots indicate ‘true’ inputs; horizontal dotted lines in the error plots indicate no error (error = 0).

3.2.2. Model-based approach

When compared with the characteristics of the simulated samples under perfect observation (figure 3), the Bayesian model estimates were much more accurate than the estimates calculated using the simple epidemiological approach; however, the quality of these estimates varied by the model inputs used to produce the simulated samples, and the test interval (table 1). Three primary parameters were estimated: reinfection rate, reinfection duration and spontaneous clearance probability. Of these, reinfection rate was the most challenging to estimate accurately. Estimates for the reinfection duration were closer to those of the simulated samples under perfect observation (the median error was within 1.2 months for all model scenarios) than were estimates for the reinfection rate (the median error ranged from approx. 0 to over 60 cases per 100 PY). Median model estimates for the spontaneous clearance probability were the most reliable of all the three parameters (the median error was less than 0.11 for all model scenarios).

Estimates for all parameters improved as the ratio of test interval to duration of acute reinfection decreased. When the test interval was half the duration of acute reinfection, the model estimates were unbiased and precise. By contrast, the estimates calculated using the simple epidemiological approach remained inaccurate regardless of the test interval (figure 5 and electronic supplementary material, figure S2). Estimates for all parameters also improved as the number of participants increased from 16 to 46. Although they continued to improve as the number of participants increased from 46 to 100, the improvement was relatively small, with the most important factor influencing precision of estimates being the test interval once the number of participants was at least 46. For example, in the simulations with a model input mean duration of reinfection of one month, when the test interval is 0.5 months, the credible interval for the error in reinfection rate was close to ±30 cases per 100 PY with both 46 participants and 100 participants. Similarly, the credible interval for reinfection duration error was within approximately ±0.5 months, and the credible interval for the error in probability of spontaneous clearance was approximately ±0.05 regardless of whether there were 46 or 100 participants. By contrast, estimates were less precise when only 16 participants were modelled and were biased when the test interval was greater than the average duration of reinfection.

4. Discussion

The aim of this study was to investigate the HCV reinfection rate, probability of spontaneous clearance in reinfection and duration of reinfection from a sparse dataset with a three-month testing interval. A hidden Markov infection transition model was fitted using Bayesian post-estimation. Simulation studies were used to test the method and investigate data requirements for future studies. Findings indicated that HCV reinfections have a high spontaneous clearance probability. The duration of HCV reinfection is likely to be short relative to primary infection and HCV reinfections are likely to occur very frequently, but additional data are required to confirm these findings. Simulation study findings highlighted the importance of frequency of testing in observational studies of HCV reinfection for producing unbiased and precise estimates of reinfection-related parameters. This methodology is not just useful for investigating HCV reinfection, but can also be applied to other infectious diseases for which reinfection or asymptomatic recurrences are difficult to discern clinically but important epidemiologically; including chlamydia, herpes simplex virus 2 (HSV-2) and tuberculosis [30–33].

The approach used in this paper provides important insights into the process of reinfection and clearance for the Melbourne Network study. The spontaneous clearance probability was estimated to be about 0.85–0.90 using the hidden Markov infection transition model; this compares to a simple epidemiological estimate of approximately 0.50–0.60. The main difference between the two estimates is that the simple epidemiological estimate assumes that the reinfections that have been observed are representative of all reinfections in the study population, whereas the model-based estimate accounts for the fact that spontaneously clearing reinfections are less likely to be observed because they may fall between study visits. The hidden Markov infection transition model estimate in particular is very high (much higher than the spontaneous clearance probability in primary infection—approx. 0.25 [3,26]), suggesting either that HCV infection confers partial acquired immunity against future persistent infection even if there is no immunity against future self-limiting infection or that individuals who clear primary HCV infection have characteristics that protect them from HCV infections. This is consistent with a previous observational study that found that, within eight individuals, the duration of primary infection tended to be longer than the duration of reinfection and the spontaneous clearance probability was high [7]. This finding has implications for vaccine development, suggesting that it may be possible to develop a vaccine that protects against persistent HCV infection.

The ‘simple epidemiological’ approach that has been used in this paper as a comparison for the model-based approach has been used in many epidemiological studies of HCV reinfection (e.g. [7,9,10,12,15]). However, more complex approaches are available and have been used in some studies. Kaplan–Meier survival times have been used to estimate the proportion of reinfections that are self-limiting in the context of censored data, where participants may clear after having been lost to follow-up or after the study is completed [20]. A number of Cox-like regression methods are available for investigating factors associated with the hazard of recurrent events [34], and some have been used in the context of HCV reinfection [5]. However, these methods do not account for the possibility that some (or many) of the reinfections are likely to have been missed in between study visits. Methods that incorporate interval censoring can be used to account for intermittent sampling when participants drop out of the study and re-enter [20]. However, even these methods are not appropriate for the situation where events can be missed in between any two study visits, even when participants attend regularly. The problem of estimating recurrent event data from length-biased samples has been recognized previously. Cook and Lawless [35] provide a bibliography of research in this area and distinguish two types of situations in which participants in recurrent event studies are sampled only intermittently during follow-up [35]. In the first, the number of events and the times at which they occurred can be ascertained retrospectively—for example, if participants keep diaries of the events as they occur but only present to study personnel intermittently. In the second case, the number of events can be ascertained retrospectively but the timing cannot—for example, tumours that are detected using medical imaging technologies. In the context of HCV reinfection, the situation is even more complex in that neither the number of events that have been missed nor the event times can be ascertained retrospectively. In this study, a hidden Markov infection transition model was used to estimate HCV reinfection rates, durations and spontaneous clearance probabilities given that reinfections were probably missed between study visits.

All analyses were undertaken for both confirmed reinfections only and a combination of confirmed and possible reinfections. Confirmed reinfections represent the gold standard, whereas analyses that include possible reinfections may be subject to misclassification errors, where some transient fluctuations in viral load may have been classified as possible reinfections. This has been shown to occur after more than six months of sustained viraemia [8,36], but is rare after 10 weeks of undetectability (as occurred for all spontaneous clearances in the Networks 2 study), making misclassification unlikely but still possible in the data used here. With respect to the reinfection duration estimates, the slightly longer durations estimated when including possible reinfections as well as confirmed reinfections may be due to such misclassification errors. Indeed, longer reinfection durations and reduced precision were observed when possible reinfections were included in addition to confirmed reinfections. However, limiting the analyses to confirmed reinfections resulted in fewer participants and reinfection events. Including multiple scenarios for the number of the participants in the simulated samples demonstrated that model estimates were more accurate and precise when applied to larger datasets. Ideally, when sufficient data exist, the modelling approach outlined here would be applied to a larger dataset of confirmed reinfections only. Such a dataset would include at least 40–50 participants who have spontaneously cleared a previous HCV infection. Given that approximately 25% of primary HCV infections clear spontaneously and assuming an attrition rate of 25%, approximately 215–265 participants with primary HCV infection would need to be followed in order to identify a sufficient number of participants to study for reinfection (a large but realistically achievable cohort).

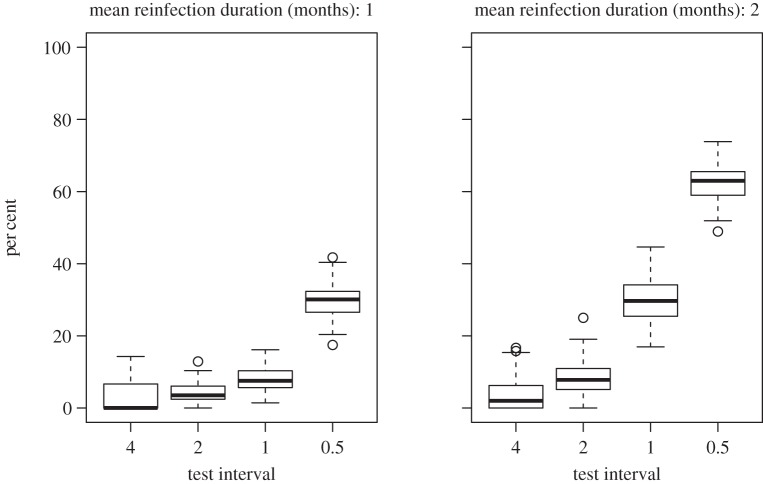
As expected, the simulation studies indicate that greater precision can be achieved by increasing the number of participants, or increasing the frequency of testing, demonstrating that the model developed is likely to produce more reliable estimates if applied to a greater quantity of data. However, once the number of participants was greater than or equal to 46, increases in the number of participants resulted in only relatively small increases in precision compared with increases in the frequency of testing. Simulation results indicate that ideally the test interval should be around half the average duration of reinfection; however, in practice, the average duration of reinfection is unknown. This raises the question of how short the test interval needs to be. In an observational study, if the test interval is greater than the duration of spontaneously clearing reinfections, then at best there will only be one HCV RNA positive test for each reinfection. As the test interval decreases, approaching or becoming less than the reinfection duration, the likelihood of having two positive tests for each reinfection increases. This can be illustrated using the simulated data (figure 6). While it is not a guarantee that the test interval is sufficiently short, aiming for two positive tests in at least one-third of spontaneously clearing reinfections could be used as a rule of thumb for assessing whether the frequency of testing is sufficient. This has been achieved in one study with a one-month testing interval, where four out of 10 spontaneously clearing reinfections had two viraemic time points (table 3). Although the number of events is small, this may indicate that a one-month test interval is sufficiently short.

Figure 6.

The per cent of self-limiting reinfections with at least two HCV RNA positive tests in simulated data. Simulated datasets with 100 participants.

Table 3.

The percentage of spontaneous clearing reinfections that have multiple viraemic time points reported in the published literature and in this study, by test interval.

test interval (months)	study	spontaneously clearing infections (confirmed) n	confirmed infections with multiple viraemic time points n (%)	spontaneously clearing infections (confirmed or possible) n	confirmed or possible infections with multiple viraemic time points n (%)
1	Osburn et al. [7]	10	4 (40)	10	4 (40)
	Page et al. [8]	2	0 (0)	2	0 (0)
	total	12	4 (33)	12	4 (33)
3	Grebely et al. [6]	1	0 (0)	2	0 (0)
	Networks study	4	1 (25)	13	3 (23)
	total	5	1 (20)	15	3 (20)
6	Micallef et al. [14]	2	1 (50)	3	1 (33)
	van de Laar et al. [10]	0	0 (n.a.)	3	0 (0)
	total	2	1 (50)	6	1 (17)

Future work could apply and validate this model with larger datasets. Indeed, one of the advantages of the Bayesian methods used in this study is that they allow incremental refinement of results as more information is accrued. Specifically, the posterior estimates of this study could be used as prior probabilities for future studies with similar design. In this way, study information can be pooled to improve the utility of the data and increase the precision of estimates. In addition, reinfection rates in a variety of contexts and populations can be inferred and compared without needing to spend valuable resources following each population equally frequently. In some cases, where the population of interest is difficult to follow frequently, this is not only a matter of efficient use of resources but allows reinfection rates to be measured where otherwise this would not be possible.

Estimating the timing and frequency of events that can occur between study visits is relevant not only to HCV but also to a range of other infectious diseases. Asymptomatic reinfection with chlamydia, gonorrhoea, malaria, tuberculosis and pertussis among other infections is common and potentially relevant to disease transmission and pathogenesis [30–33]. In the context of chlamydia infection, modelling studies have shown that asymptomatic reinfections occurring between chlamydia tests can affect epidemiological estimates of chlamydia duration, incidence and prevalence [37], and can also make retesting policies ineffectual if most reinfections occur earlier than people commonly present for retesting [38]. Herpes simplex virus (HSV) (particularly type 2) has periods of asymptomatic viral recurrence. HSV-2 asymptomatic viral shedding occurs frequently and is thought to be crucial for onward transmission of the virus [39,40]. HIV viral load is also an important predictor of HIV transmission, which has become very topical recently in the context of HIV antiretroviral treatment being used to prevent HIV transmission [41]. Estimating the frequency and duration of viral breakthrough (that is, a detectable HIV viral load) when on antiretroviral treatment is important for understanding transmissibility in the era of antiretrovirals. The methods presented in this paper can be adapted to studying these (and other) examples of asymptomatic reinfection and/or viral recurrence.

4.1. Limitations

The model includes a number of simplifying assumptions. We did not test the validity of the infection transition model (figure 2) and the superiority of our methods compared with the simple epidemiological approach can only be taken in the context of this assumption. The model constructed, however, is based on the current understanding of the biology of HCV and can account for the observations of changing infection status. Whether reinfection rates or clearance probabilities change after multiple reinfections is unknown (only very few cases of multiple consecutive infection have been reported [7,8]); therefore, we assumed that the rate of reinfection and clearance probability were constant over time. Further, it is not known whether heterologous exposure to different HCV genotypes affects spontaneous clearance of HCV reinfection, so the issue of cross-genotype protection was not addressed. Finally, we have previously shown that reinfection rates differ by injecting risk [15], and a number of studies have shown that gender, IL28B genotype, and other host factors affect spontaneous clearance in primary HCV infection [42–44]. However, because our analysis already involved inferring three parameters (reinfection rate, reinfection duration and clearance probability), on the basis of 26 observed confirmed or possible reinfection events, we did not include additional complexity but assumed similar reinfection rates and reinfection duration for all participants. While we did allow for random variation in the times to reinfection and clearance events, which will have accounted for some of the variation in rates of infection and clearance, when sufficient data exist ideally future studies will investigate the effect of these confounding factors.

In addition to limitations associated with model assumptions, observational data were drawn from a convenience sample of PWIDs, so results cannot necessarily be generalized. The sample was recruited from street-based illicit drug markets and participants reported relatively risky injecting behaviour, so they are likely to represent a high-risk population for HCV acquisition [23]. Finally, analyses presented here were repeated for confirmed reinfections only and for confirmed and possible reinfections. As discussed in more detail above, the analyses that included possible reinfections are subject to misclassification errors and the analyses that included confirmed reinfections only are limited by the small quantity of data.

Finally, whereas under observational study conditions test intervals vary between and within participants, the simulated samples were produced using fixed test intervals. However, additional simulations (not shown) including random variability in test interval length showed it did not affect results.

5. Conclusion

In this paper, we presented an analytical method for estimating HCV reinfection rates and related measures that provides useful information about possible sources and magnitude of bias in estimates of reinfection rates, probability of reinfection clearance and duration or reinfection. Model estimates suggested that spontaneous clearance probability is high. Our findings suggest that the duration of spontaneously clearing reinfection is about one month; however, this result needs to be confirmed with additional data. In order to produce precise estimates, observational study data with test intervals equal to or shorter than the duration of reinfection are required. This method can also be applied to other diseases with asymptomatic reinfection and/or viral recurrence.

Ethics statement

Ethical approval for the study was obtained from the Victorian Department of Human Health Research Ethics Committee (project 02/05).

Data accessibility

Networks study data and stored blood samples can be accessed for collaborative research projects subject to approval by the study investigators and the relevant human research ethics committee.

Funding statement

This work was supported by Australia's National Health and Medical Research Council (project grant 331312, postgraduate scholarship to R.S.D., Career Development Fellowship to J.G., Senior Research Fellowship to M.H.); the Victorian Department of Human Services (public health research grant, 2008–09); the Australian Centre for HIV and Hepatitis Virology Research (ACH2); the Victorian Operational Infrastructure Support Program; the Burnet Institute; the NHMRC Centre for Research Excellence into Injecting Drug Use; and the UK's Medical Research Council (New Investigators Award to P.V. (G0701627)).