Creating the brain and interacting with the brain: an integrated approach to understanding the brain

Abstract

In the past two decades, brain science and robotics have made gigantic advances in their own fields, and their interactions have generated several interdisciplinary research fields. First, in the ‘understanding the brain by creating the brain’ approach, computational neuroscience models have been applied to many robotics problems. Second, such brain-motivated fields as cognitive robotics and developmental robotics have emerged as interdisciplinary areas among robotics, neuroscience and cognitive science with special emphasis on humanoid robots. Third, in brain–machine interface research, a brain and a robot are mutually connected within a closed loop. In this paper, we review the theoretical backgrounds of these three interdisciplinary fields and their recent progress. Then, we introduce recent efforts to reintegrate these research fields into a coherent perspective and propose a new direction that integrates brain science and robotics where the decoding of information from the brain, robot control based on the decoded information and multimodal feedback to the brain from the robot are carried out in real time and in a closed loop.

1. Introduction

Not only scientists but also robotics engineers have been attracted to the elucidation of information processing in the brain. The human brain, which is a complex dynamical system with deep hierarchy and huge degrees of freedom, possesses 10¹¹ neurons [1]. Big projects that have recently started in the USA [2] and the EU [3] ultimately aim to record from all the neurons in the brain, experimentally controlling them and simulating their working by computer. Even if we could record the neural activities of all the neurons, experimentally control their activities and simulate neural circuit behaviours, we would still be far from understanding the brain's information processing unless we understand the computational principles that underlie the problems solved by it [4]. Robotics is a research field in engineering that could be integrated with brain science to elucidate the computational principles relevant to brain information processing [5].

The interdisciplinary fields between brain science and robotics can be classified into the following three types: (1) computational neuroscience in a narrow sense that models the various levels of events and information processing in the brain. This includes representative neural network models [6–11]; (2) brain-motivated robotics, where researchers build an artificial system that reproduces the brain's information processing and generally explore brain-like computations [12]. Different subfields have different emphasis on machine-learning, nonlinear dynamics, neuroscience, cognitive science [13], developmental psychology [14] and so on. But all of them possess some relevance to brain science. Imitation learning, which is partially inspired by a neuroscience study [15], has become one of the most popular approaches in brain-motivated robotics and is now widely studied [12,13,16–18]. In recent years, developmental robotics have also been intensively studied [14,19]; (3) a brain–machine interface (BMI), which is sometimes called a brain–computer interface (BCI), connects the brain with such external devices as spellers [20] or prosthetics [21]. A BMI can be defined as an interface that connects the brain and a computer/robot based on some computational neuroscience theories [22–26]. Typically, a computational model is used to extract necessary information from the brain based on signals, including neural firing, local field potentials, electroencephalography, near infrared spectroscopy and functional magnetic resonance imaging (fMRI) signals. The ‘decoded’ information [27] from the brain is fed to a robotic arm, for example, and visual and/or tactile feedback to the brain closes the loop between the brain and the robot. BMIs are used not only to compensate and substitute for lost or damaged sensory-motor functions including communications but also to recover and repair such functions [22–26,28–33]. Furthermore, there are multiple ongoing projects that are aiming to recover the biped walking functions of spinal-cord injury and stroke patients [29,31,34,35].

The application of computational neuroscience models to robots opened up an approach called ‘understanding the brain by creating the brain’[5,36], which was emphasized in the Japanese promotion of neuroscience about two decades ago [37]. To fully validate the computational feasibility and the efficacy of some theories, we need to apply them to real-world problems; we need an artificial brain and body. The former might be realized as computer software, but the latter necessitates robots as physical substitutions for the body. Actual sensory-motor control and decision-making problems are obliged to deal with a huge amount of d.f., the low signal-to-noise ratios of sensory signals and motor outputs, real-time constraints on computation and feedback, and complicated nonlinear events that are difficult to model mathematically, such as contact dynamics and friction. Using robots forces us to deal with all these difficulties, while computer simulations tend to overlook such difficult boundary conditions and underestimate the complications of the computational problems solved by the brain. Computational neuroscience studies and brain-motivated robotics studies are investigating how the brain can acquire action policies to control its own body, which has a gigantic number of degrees of freedom, while receiving environmental information from a huge number of sensory inputs. Note that the term ‘policy’, which was originally borrowed from reinforcement-learning literature [11], corresponds to ‘control law’ or ‘control rule’ in control engineering studies. These computational neuroscience and brain-motivated robotics can be considered ‘creating the brain’ approaches. On the other hand, BMI studies focused on decoding brain activities to control external devices or extracting brain activities to feed the information back to subjects so that they can modulate their brain activities. BMI research paradigms can be considered ‘interacting with the brain’ approaches.

Recent advances suggest that these previously divergent fields between robotics and brain science can be reintegrated into novel methodologies with higher impacts on science and technology. For example, an electroencephalogram (EEG) BMI-based neurorehabilitation system for stroke patients has been developed [33], where the BMI rehabilitation approach is regarded as an integrated system of the above brain-motivated robotics and BMI elements. The decoded neurofeedback (DecNef) method is another concrete example of the integration of the previously divergent way of understanding brains, because it integrates computational neuroscience and BMI disciplines to experimentally induce spatial voxel patterns in a limited brain region, facial preference and colour. DecNef has already realized the perceptual learning of specific orientation gratings [38], the associative learning for the manipulation of facial preference [39] and the creation of the phenomenal consciousness of colour [40].

The main purpose of this review is to motivate future research directions to reintegrate the above three research fields that straddle robotics and brain science. These three interdisciplinary research fields have made gigantic advances over the past two decades, mainly in parallel. However, more recently, we see more and more interesting research examples that reunite these previously divergent directions, as exemplified above. We argue here that the future of computational neuroscience in a broader sense is the integration of all three disciplines: computational neuroscience, brain-motivated robotics and BMI. In this review, we introduce efforts to bridge and combine them by postulating a new research direction that fully integrates them. Within this paradigm, a brain and a robot are bi-directionally coupled by decoding [27] and physical interaction. A human volunteer wears a whole-body exoskeleton robot. Her/his brain activity is measured and decoding is carried out in real time. The decoded brain information is used to influence the robot control algorithms to realize brain-to-robot information transmission. Because the robot is attached to a human body, robot motion generates multi-modal sensory feedback to the brain by implementing robot-to-brain information transmission. This system could compensate for lost functions, perform therapeutic treatments of disorders or induce significant spatio-temporal neural activity and brain plasticity. A schematic diagram of this unified direction is depicted in figure 1. We provide several theoretical arguments why this experimental paradigm is a powerful approach to reunite the three interdisciplinary research fields between brain science and robotics. Such reunification provides better understanding of the brain using the combined brain-related methodologies and technologies. Simultaneously, future systems developed within this reunification will be very useful in BMI-based neurorehabilitation or revolutionary therapeutics for psychiatric disorders. We then discuss the current research trends in which computational theory is used for brain decoding in BMI and an exoskeleton robot is used for neurofeedback to the brain.

Figure 1.

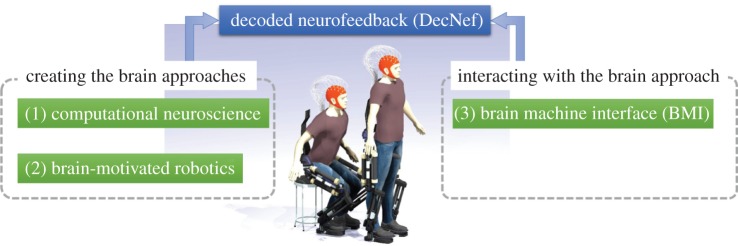
We categorize brain-related theories, models and methodologies into three disciplines: (1) computational neuroscience, (2) brain-motivated robotics and (3) BMI. Computational neuroscience and brain-motivated robotics are ‘creating the brain’ approaches. On the other hand, BMI methods are ‘interacting with the brain’ approaches. The future of computational neuroscience in a broader sense is the integration of all three disciplines. Integration could take the concrete form of a human volunteer wearing a humanoid exoskeleton controlled by brain activity measured, and rich information fedback to the volunteer's body and brain while covering a wide range of sensory modalities based on DecNef [38] methodology. This system might compensate for lost functions, perform therapeutic treatments of disorders or induce significant spatio-temporal neural activity and brain plasticity. (Online version in colour.)

We first review our proposed approach by introducing our computational neuroscience models and brain-motivated humanoid-motor-learning studies and then introduce our BMI exoskeleton robot studies. We discuss our novel unified view of creating the brain and interacting with it approaches by introducing our new humanoid exoskeleton studies and our recently developed DecNef method. For the brain-motivated humanoid-motor-learning studies, we explored the creating the brain approach by developing a series of humanoid robots [36,41], including CB-i, a human-sized humanoid robot (figure 2a) [42]. As a new generation of humanoids, we are developing exoskeleton robots that can physically interact with the human body to assist user movements (figure 2b) [43,44]. An important technical element of DecNef is the real-time neurofeedback of decoded information to the brain. Therefore, as we explained above, a humanoid exoskeleton can be used as an output device to provide a rich set of feedback signals to the body and ultimately to the brain.

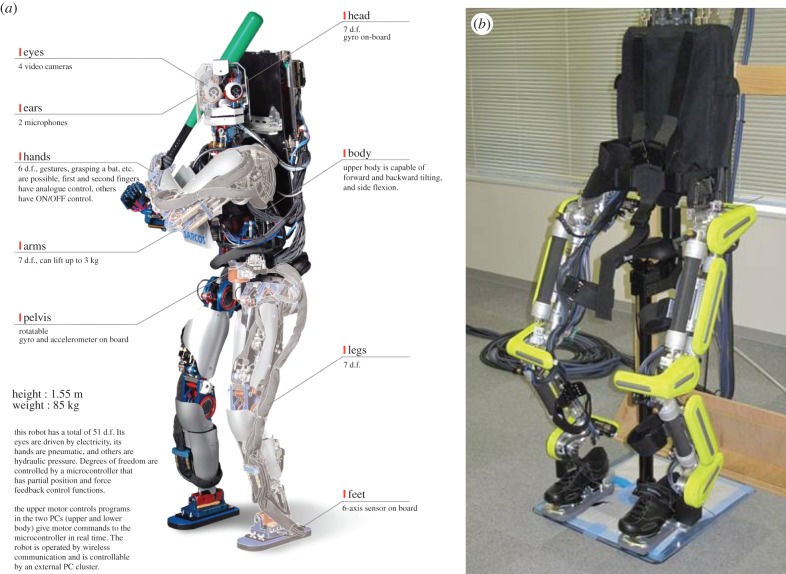
Figure 2.

(a) Human-sized humanoid robot, CB-i [42]: height: 1.55 m, total weight: 85 kg. The robot is equipped with 51 d.f.: 2 × 7 d.f. legs, 2 × 7 d.f. arms, 2 × 2 d.f. eyes, 3 d.f. neck/head, 1-d.f. mouth, 3 d.f. torso and 2 × 6 d.f. hands. It has similar configurations, range of motion, power and strength as a human body to reproduce better natural human-like movements, particularly for locomotion and object manipulation. (b) Exoskeleton robot (XoR) [43]. Height: 1.5 m, weight: 30 kg. XoR has 10 d.f. and six active joints, each of which uses a hybrid actuator composed of an air muscle and an electric motor. It is designed to assist lower limb movements of human users. (Online version in colour.)

The rest of this paper is organized as follows. In §2, we introduce our computational neuroscience models to understand the functional brain mechanisms. We explore modular and hierarchical architectures as possible approaches to deal with high-dimensional systems. In §3, we review our previous research activities using humanoid robots to understand the brain's motor learning mechanisms. In particular, in §3.2, we discuss possible approaches to understand how the brain can acquire behavioural policies using extremely high-dimensional brain activities while simultaneously receiving a huge amount of sensory inputs. In §4, we introduce our newly developed BMI exoskeleton robot and investigate how its movements can affect the subject's brain activities. Finally, in §5, we discuss the possible applications of an exoskeleton robot in the DecNef framework.

2. Creating a brain by computational neuroscience models

Here, we introduce computational neuroscience models to cope with high-dimensional state-space problems. Policy learning in high-dimensional state space is extremely difficult from a computational modelling point of view. To derive an optimal control policy for nonlinear dynamics, dynamic programming [45] and reinforcement learning [11] are used as the standard policy-learning algorithms. In them, a tremendous number of learning iterations are required to find a policy in high-dimensional state space; this difficulty is called the ‘curse of dimensionality’.

In §§2.1 and 2.2, we discuss possible approaches to understand how the brain copes with this policy-learning problem in high-dimensional state space.

2.1. Modular learning approaches

One possible solution for handling large-scale problems is to divide and conquer. As a concrete approach, we introduce the modular selection and identification control (MOSAIC) model, which was originally proposed for supervised learning [46,47] and then extended to reinforcement learning [48]. The most advanced form of the reinforcement MOSAIC [49] has three different sets of expert networks, each of which is specialized for each subproblem. One of these network sets is composed of the predictors of state transitions, which are formally called internal forward models. An internal forward model receives the information of the current state and the current motor command and then predicts the next time-step state. The two other sets approximate actual rewards and reinforcement learning controllers that compute motor commands for optimal control. The responsibility signal for the internal forward model network is determined by the prediction error in the dynamics, and the responsibility signal for the other two networks is determined by the approximation error in the reward and in the reward-prediction error; these signals are used to weight the outputs from the experts. The signals also gate the learning of each expert network by regulating the learning rate.

Switching and weighting by approximation and prediction errors are key features of MOSAIC. The medial prefrontal cortical areas might play an important role in detecting environmental changes by accumulating prediction error. The lesions of monkey medial prefrontal cortex affect the length of the accumulated reward-prediction error in contextual switching behaviour [50]. The responsibility signal could be interpreted as the posterior probability of the Bayesian inference, assuming multiple linear systems have Gaussian noise. In a human imaging study [51], ventromedial prefrontal activities in a stochastic reversal task were correlated with the Bayesian update errors of probability, which are the differences between the posterior and prior probabilities. Circumstantial support of hierarchy and modularity in the context of reinforcement learning was mainly obtained from neuroimaging and lesion studies. The activities of many brain areas, including those of the prefrontal cortex, the orbitofrontal cortex, the premotor cortex, the supplementary motor area, the cerebellum, and the basal ganglia, are correlated with such important variables in reinforcement learning as accumulated reward, learned behaviour, short-term reward and behavioural learning, even in a simple Markov decision process with monetary reward [52]. Furthermore, although activity in the human putamen is correlated with reward prediction that depends on selected actions, which is consistent with a study in monkeys [53], activity in the caudate is correlated more closely with reward-prediction error [54–56]. Topographic representations with different parameters of the discount factor for reward prediction were found in the medial prefrontal and insular cortexes, and topographic representations for reward-prediction error were found in the basal ganglia [57].

As described above, exploring how our proposed model can be implemented as a neural system is crucial for computational neuroscience to understand how the brain deals with real-world control problems.

2.2. Hierarchical learning approaches

The other common strategy to cope with the high-dimensional policy-learning problem is to add hierarchy to the algorithms [58,59]. In the upper part of such a hierarchy, an approximate optimal solution could be found in a reasonable time because the state space that describes a body and an external world is coarsely represented by a reasonable number of discrete regions, cells or neurons (e.g. up to 1 million neurons, a reasonable number for one function). In the lower layer of this hierarchy, the state space is finely represented and the approximate solution that is obtained in the upper layer can constrain the possible range of the exploration space. Thus, the problem could be solved within a reasonable amount of time and with the required accuracy. In most studies, coarse representations have been specified in the upper hierarchy or used to predetermine the motor primitives and/or the subgoals. This recourse is similar to assuming the existence of a homunculus [1], which refers to the somatosensory and motor body maps in the brain, as those factors are all predetermined. However, using predetermined primitive representations is unacceptable from the viewpoint of neuroscience [60]. Most studies have dealt with discrete-state and discrete-time examples, such as a maze, which is artificial from the neuroscience viewpoint. One rare exception that adopted continuous time and continuous state-space examples was a standing-up task carried out by a multi-joint robot [61], which is categorized as an under-actuated system and considered a difficult system to control as the number of actuators is fewer than the number of degrees of freedom of the robot.

For real-world problems, it is unrealistic to design a hard hierarchy of modules (subgoals) that strictly controls how to switch reward predictions and subgoals between higher and lower hierarchical layers. This limitation suggests that in actual animal reinforcement learning, heterogeneous reward predictions are softly combined, depending on their time-varying significance instead of such a hard hierarchy [62]. The most important aspect of this soft hierarchical architecture is that reward prediction made by limbic and cognitive loops is propagated to motor loops by spiral projections between the striatum and substantia nigra. This mechanism allows reward prediction error, coarsely represented by the cognitive loop, to guide the learning of more detailed reward predictions in motor loops, which incorporate more detailed information, such as motor commands. This soft hierarchical structure shows a useful approach to propagate reward information from the upper to the lower layer of a hierarchical policy-learning mechanism.

In §3, we explore how these modular and hierarchical architectures can be applied to actual humanoid robot control.

3. Creating a brain by brain-motivated humanoid-motor-learning methods

An optimal control algorithm for a particular body dynamics may not be optimal for other body dynamics. If a humanoid robot is used for exploring and examining neuroscience theories rather than for engineering, it should be as close as possible to a human body. Therefore, we first developed a humanoid robot Dynamic Brain (DB) (figure 3), which has 30 d.f. and human-like size and weight. It is equipped with an artificial vestibular organ (gyro sensor), which measures head velocity, and four cameras with vertical and horizontal degrees of freedom. Two of the cameras have telescopic lenses corresponding to foveal vision, and the other two have wide-angle lenses corresponding to peripheral vision. The photographs in figure 3 illustrate 14 of the more than 30 different tasks that can be performed by the DB [5]. Most of the algorithms used for these task demonstrations are approximately based on the principles of information processing in the brain, and many contain some or all of the three learning elements: imitation learning [12,17,72–74], reinforcement learning and supervised learning.

Figure 3.

Demonstrations of 14 different tasks by humanoid robot DB: imitation learning was involved in ‘Katya-shi’ (Okinawan folk dance) [63]: (a), three-ball juggling [5] (b), devil-sticking (c), the air-hockey demonstration [64,65] (d) uses not only imitation learning but also a reinforcement-learning algorithm with reward (a puck enters the opponent's goal) and penalty (a puck enters the robot's goal) and skill learning. Demonstrations of pole-balancing (e) and a visually guided arm reaching towards a target (f) used a supervised learning scheme [66], motivated by our approach to cerebellar internal model learning. Demonstrations of adaptation of vestibulo-ocular reflex [67] (g), adaptation of smooth pursuit eye movement (h) and simultaneous realization of these two kinds of eye movements with saccadic eye movements (i) were based on computational models of eye movements and their learning [68]. Demonstrations of drumming (j), paddling a ball (k), sticky-hand interaction with a human [69] (l), manipulating a box [70] (m) and a tennis swing [71] (n). (Online version in colour.)

Subsequently, we developed a full-body humanoid robot called CB-i (figure 2a) with the ‘Humanoid Robots as a Tool for Neuroscience’ approach [75]. CB-i was designed for full-body autonomous interaction with balance control and biped walking. Both posture control and biped locomotion are challenging research topics for a human-like and autonomous humanoid robot. Our exploration focused on biologically inspired control algorithms for locomotion using three different humanoid robots (DB-chan [72,76,77], Fujitsu Automation HOAP-2 [48] and CB-i [78]) as well as a small humanoid robot provided by the SONY Corp. [79].

After the above brief introduction of our previous brain-motivated robotics studies, in §3.1, we present our attempts to apply the modular and hierarchical architectures introduced in §§2.1 and 2.2 to humanoid robot platforms.

3.1. Modular learning approach for humanoid motor learning

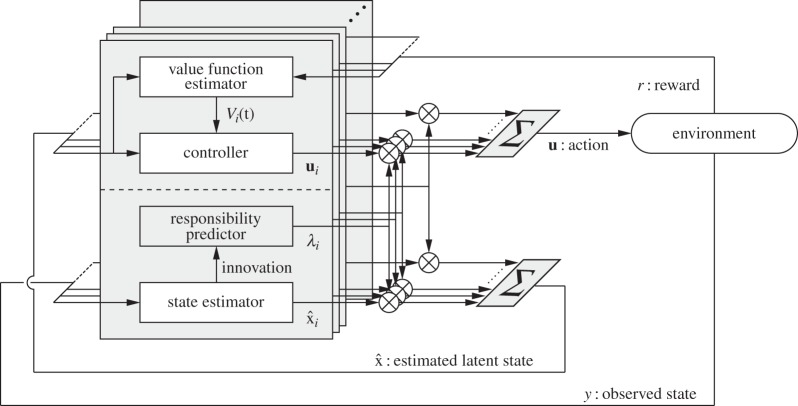
As introduced in §2.1, the MOSAIC architecture is biologically plausible as a human motor-control model. However, two difficulties must be overcome to apply the MOSAIC model to the control of a real humanoid robot: (1) the MOSAIC model does not explicitly consider the existence of noise input to sensory systems and (2) as it assumes full observation, it cannot deal with partially observable systems. To deal with these problems, we proposed an extension of the MOSAIC architecture (figure 4) [80]. Each module of MOSAIC has a forward model, and we can adopt them to construct a state estimator. State estimators can also provide a reasonable model of the sensorimotor function of the central nervous system, as previously suggested [81]. A state estimation strategy using switching linear models is also considered a useful approach for estimating the hidden variables of complicated nonlinear dynamics [82,83]. The modified method, called an extended MOSAIC with state estimators (eMOSAIC), can deal with observation noise and partially observable systems [80]. Based on these advantages, our proposed control framework can be applied to real humanoid robots.

Figure 4.

Extended MOSAIC with state estimators (eMOSAIC) [80]. Each module is composed of a state estimator, a responsibility predictor, a value function estimator and a controller. Nonlinear and non-stationary dynamics are approximated by switching the linear models, and a nonlinear cost function is approximated by switching the quadratic models.

Feedback linearization [84] and gain scheduling control [85] are popular approaches to controlling nonlinear dynamics. However, these methods require either a precise model or prior knowledge of the task and plant structures. On the other hand, for non-stationary systems, adaptive control [86] can be used. However, this method can only handle gradual environmental changes.

We applied eMOSAIC to control our humanoid robot, CB-i (figure 2a), which has highly nonlinear dynamics, to demonstrate that our proposed model can be used in a real environment. Figure 5 shows that a humanoid robot can maintain its balance while performing a squatting task using the eMOSAIC model. Figure 6 shows that a humanoid robot can maintain its balance even when sudden environmental changes are caused by an additional payload.

Figure 5.

Generated humanoid squatting movement using eMOSAIC model [80]. Our humanoid robot maintained its own balance when making a fast squat movement with a frequency up to 1.5 Hz. (Online version in colour.)

Figure 6.

(a) With the eMOSAIC model, humanoid robot maintained its balance by coping with the sudden environmental change caused by additional payload. (b) With only a single module controller, humanoid robot fell over [80]. (Online version in colour.)

3.2. Hierarchical architecture for humanoid motor learning

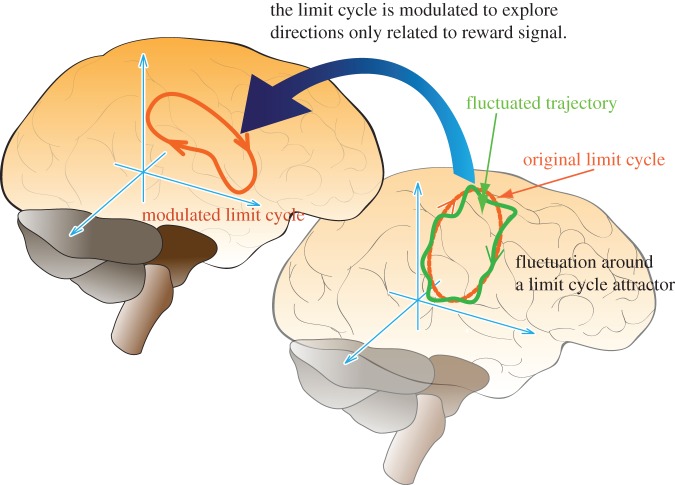
In §2.2, we introduced computational models that use hierarchical architectures to cope with the policy-learning problem in high-dimensional systems. From here, we introduce our idea that the brain modulates the low-dimensional attractor dynamics embedded in high-dimensional state space, where the state space is represented by neural activities (figure 7). The low-dimensional internal dynamics can be task specific and modulated through the policy-learning process. In this review, as a target task, we generate biped walking movement by humanoid robots with a central pattern generator (CPG) model [87] that is used as the bottom-layer controller to generate the low-dimensional internal dynamics. Figure 8 shows our idea of a hierarchical learning framework. In this section, we introduce a two-layered hierarchical model, where the bottom layer represents the CPG and the upper layer learns to modulate the CPG's periodic pattern to improve the control performance. In §3.2.1, we introduce our CPG model and present feature extraction mechanisms for connecting the upper learning and bottom CPG modules in §3.2.2.

Figure 7.

Proposed approach to understanding how brain deals with high-dimensional policy-learning problem. We assume low-dimensional limit cycles are represented by super high-dimensional neural activities. Low-dimensional fluctuated trajectories are generated around the limit cycle by noisy inputs. Limit cycle is modulated to explore directions only related to reward signals. (Online version in colour.)

Figure 8.

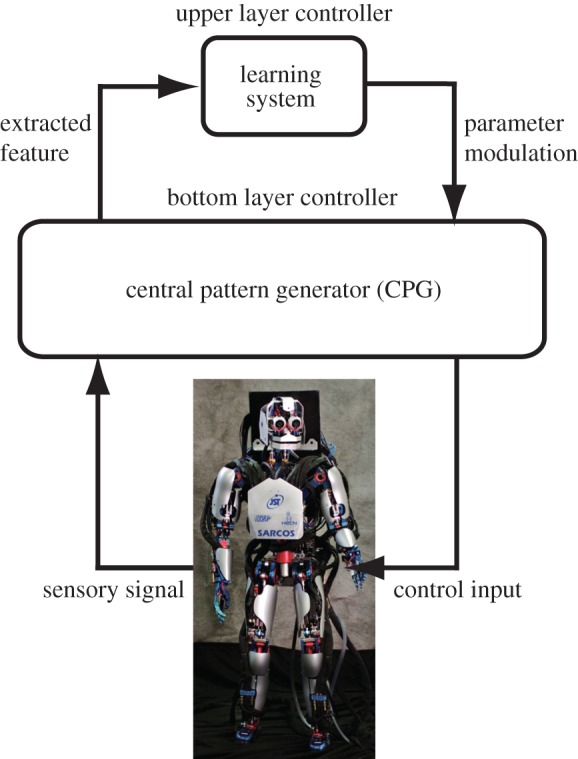
Schematic diagram of our biped learning scheme. The CPG generates periodic patterns for biped locomotion. Detected sensory signals are sent to the CPG and the learning system, which only updates the policy and outputs the modulation command to the CPG when the periodic trajectory passes through the defined Poincare sections. (Online version in colour.)

3.2.1. Central pattern generator as internal dynamics

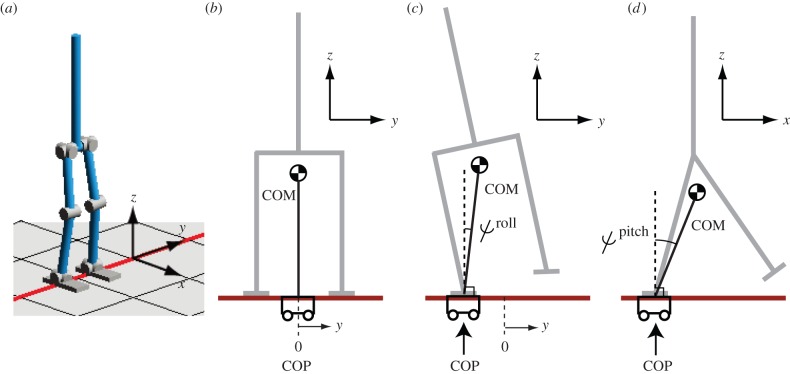
As presented in figure 8, we used a CPG model as the bottom-level controller of our proposed hierarchical framework. Here, we introduce our CPG model composed of coupled phase oscillators, where the CPG is believed to exist in vertebrates [88,89]. As it has been emphasized that humanoid robots have inverted pendulum dynamics, where the top is at the centre of mass (COM) and the base is at the centre of pressure (COP) (figure 9), we proposed using the COP to detect the phase of the inverted pendulum dynamics. Using the inverted pendulum approximation to a humanoid model is a popular approach in biped controller design [91,92]. In the proposed biped controller [87], we used simple periodic functions (sinusoids) as desired joint trajectories and showed that the synchronization of the desired trajectories at each joint with inverted pendulum dynamics can generate stepping and walking. In addition, as our nominal gait patterns are sinusoids, our approach does not require careful design of the desired gait trajectories.

Figure 9.

(a) Simplified biped model of CB-i [90]. (b–d) Inverted pendulum model represented by COP and COM. ψ^roll denotes roll angle of the pendulum. ψ^pitch denotes its pitch angle. (Online version in colour.)

To evaluate the proposed approach in real environments, we applied our proposed biped control method to CB-i. Figure 10 shows its successful walking patterns. The robot walked by using only a simple sinusoidal trajectory, which was composed of at most two sinusoidal basis functions at each joint, modulated by the detected phase from the COP [87].

Figure 10.

(a) Successful walking pattern of CB-i. (b) Turning movement. (Online version in colour.)

3.2.2. Feature extraction for policy improvement

For constructing a hierarchical system, feature extraction mechanisms for connecting the upper learning and bottom CPG modules are necessary. In this section, we introduce our approach to extract low-dimensional feature space for policy updates using kernel dimension reduction (KDR) [93]. As the bottom-level CPG controller can generate the periodic movements, we only consider the robot state at a Poincaré section [94] for policy updates [90].

Low-dimensional feature space needs to contain the information to predict state variable y, which represents reward function r(y), where the policy parameters are updated to increase the accumulated reward in the reinforcement learning framework [11]. We then formulate the problem to find latent state 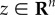as

3.1

where denotes the state vector in the original state space [90]. u is the output of a policy. We consider a projection of the state to low-dimensional feature vector z = Bx such that n < m, where B is a projection matrix. Then in our feature extraction framework, we consider three sets of state variables: (1) those used to represent the reward function in the original state space: y; (2) the original state variables: x and (3) those in the feature space after projection: z. The relationship in equation (3.1) implies that low-dimensional feature space z_k maintains the Markov property for state y. We used the dimension reduction method, KDR, to derive projection matrix B.

We applied our proposed method to improve the walking performance of a simplified model of CB-i, which has 13 d.f., excluding the three translational degrees of freedom of the base link (figure 9a). Therefore, we need to consider a 26-dimensional state space as the original state space that includes the time derivative of each degree of freedom. We applied KDR for the original 26-dimensional state space to find the proper projection to a one-dimensional feature space. The number of dimensions of the feature space is predetermined.

We modulated the amplitude of the hip-pitch sinusoidal joint angles movement to generate forward movement for the biped walking task [90]. The walking task's target is to increase the angular velocity of pendulum (figure 9d) at section (figure 9c). We used the stochastic Gaussian policy model [95] in which exploratory outputs are generated to sample data for policy improvement. The mean and variance parameters of the Gaussian policy were updated using a policy gradient method [96]. Figure 11 shows the acquired walking performance.

Figure 11.

Acquired walking pattern [90]. Thick (red) line represents starting position. We showed one snap in three walking steps. (Online version in colour.)

4. Interacting with brain through brain–machine interface exoskeleton robots

In the previous section, our discussion focused on a possible learning algorithm that modulates a low-dimensional limit cycle embedded in high-dimensional state space. In this section, we turned our focus to introducing our hardware development that modulates user brain activities through physical interaction with our wearable exoskeleton robot.

As many countries are facing the problem of aging populations, the development of an exoskeleton robot to assist user movements is becoming an important research topic [21,97–99]. These exoskeleton robots can be used as assistive or prosthetic devices for stroke and spinal-cord injury patients in rehabilitation programmes [100,101]. In recent years, it has been found that using brain activity to control a robotic assistive system is also useful to help stroke patients recover their motor functions [33]. This rehabilitation approach is called BMI rehabilitation [102].

For BMI rehabilitation, we have developed an EEG-exoskeleton robot system, where an exoskeleton robot is connected to an EEG measurement device that users can control with their brain activities [44]. To activate an exoskeleton robot based on the user's brain activity, we simultaneously need to consider the influence of the exoskeleton robot movement to the brain activity related to somatosensory inputs as there is physical interaction between the robot and the user. Here, we first introduce our study that investigates whether movement intention can be extracted from EEG signals even when the user movement is assisted by the exoskeleton robot. We then introduce our attempt that used an EEG-exoskeleton robot to assist stand-up movements while it was controlled by the user's brain activity.

4.1. Influence of afferent input induced by an exoskeleton robot

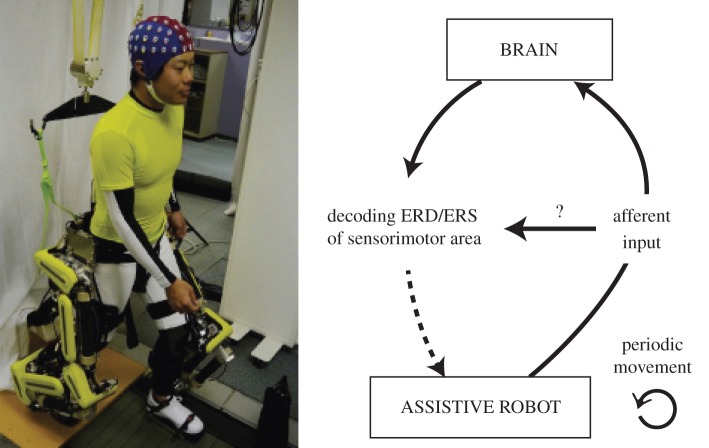
Previous BMI-based robot control studies have dealt with EEG-based neuroprosthesis control [103]. On the other hand, we are focusing on the possibility of interference between the brain activities associated with passive and active movements (figure 12).

Figure 12.

Investigating how afferent input, induced by an assistive robot, influences the decoding of the ERD/ERS of the sensorimotor area [104]. (Online version in colour.)

In particular, we monitored event-related (de)synchronization (ERD/ERS) to control an EEG-exoskeleton system. The ERD/ERS phenomenon is not only related to active movements or motor imagery but also to passive movements (up arrow in figure 12) that highlight that the feet's passive movements produce a significant ERD/ERS over the entire sensorimotor cortex [105,106]. This raises the question whether the somatosensory afferent input, induced by the periodic leg perturbation, interferes with the decoding ability of a BMI system based on the ERD/ERS of the sensorimotor area (horizontal arrow in figure 12). Specifically, we investigated whether the periodic perturbation of lower limbs produces a significant decrease in the classification performance of the actual left- and right-hand finger movements.

We decoded the left and right sensorimotor hand area due to the reliability of the contralateral ERD/ERS spatial distribution [107] and the fact that this approach is exhaustively discussed in the literature [108,109]. Furthermore, the motivation for using real movements instead of motor imagery is that the latter cannot be mechanically measured or visually assessed by experiment operators. Actually, the patterns of µ and β de/synchronization associated with actual movements resemble those of motor imagery, but they just differ in magnitude [110].

In this experiment, our custom-made 1 d.f. exoskeleton robot (figure 13) [104] was used as an assistive robot (figure 13a). The simple exoskeleton robot is actuated using a pneumatic-electric hybrid strategy [43]. The advantage of using a pneumatic actuator is that it can exert a very large torque (maximum of 70 Nm) while generating insignificant electromagnetic noise from the point of view of the EEG system. An electric motor also generates parallel small torque (maximum of 5 Nm) to make fast and precise corrections to the torque generated by the pneumatic actuator. For this specific experiment, the robot was mounted on a custom-made support to allow subjects to sit near to it (figure 13b). A leg-shaped thermoplastic polymer was anchored to the robot to secure the legs of subjects (figure 13c).

Figure 13.

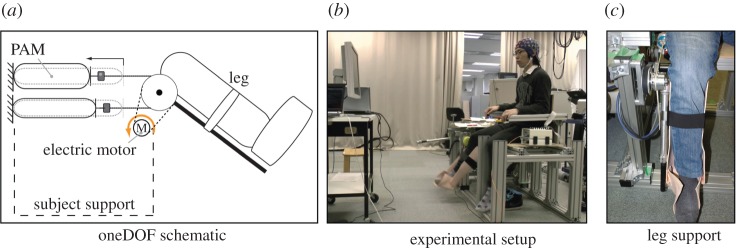
Robot used during our experiment [104]: (a) PAM and electric actuators exert parallel torques to move the leg (1 d.f. design); (b) Experimental set-up; (c) Thermoplastic polymer leg support anchored to robot and holding up subject's leg. (Online version in colour.)

Our study investigates the main effect of the leg afferent input, induced by a lower limb assistive robot, on the decoding performance of the ERD/ERS of the sensorimotor hand area. We experimentally compared a finger-tapping decoding performance under conditions of with and without leg perturbation caused by the exoskeleton robot movements. Our experimental results suggest that the classification performance is always above chance, and we observed no intra-subject significant differences between the with and without-perturbation conditions if we used our proposed decoding procedure [104].

4.2. Electroencephalogram-exoskeleton system

Now we introduce our EEG-exoskeleton system. To decode brain activities from EEG signals, we used a logistic regression method with spectral l₁-norm regularization, which can lead to good generalization performance [111]. We considered assistance for the stand-up movement, which is one of the most frequently made movements in daily life and a standard task movement in rehabilitation training.

We decoded brain activities using the above classification method based on the logistic regression after pre-processing the measured EEG data. The covariance matrix of the processed data was used as the input variable for the classifier. We updated the covariance matrix of the processed EEG signal with a fixed period. According to the classifier's output, the stand-up or sit-down movements of the exoskeleton robot were generated by the torque control method for the exoskeleton robot [44].

Figure 14 shows the results of the EEG-exoskeleton control. A subject tried to control the EEG-exoskeleton system using motor imagery to follow the movement directions that appeared on a display, where the directions indicated stand-up/sit-down movements. This neurofeedback training procedure resembles a bio-feedback training method [112] or a BCI training approach [113]. The user successfully controlled the exoskeleton robot using his brain activities.

Figure 14.

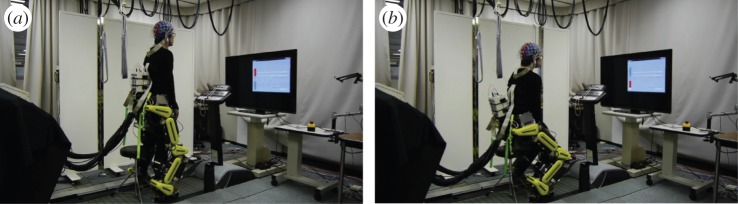
EEG-exoskeleton experiment [44]. Subject controlled EEG-exoskeleton system to follow the stand-up/sit-down directions indicated on the display using motor imagery. Gravity compensation of the lower limb model composed of exoskeleton and human lower limbs was activated when the EEG decoding was ‘stand-up.’ (a) Stand-up state. (b) Sit-down state. (Online version in colour.)

5. Discussion: integrating the three fields by decoded neurofeedback

Finally, in this section, we discuss how the future of computational neuroscience in a broader sense could lead to the integration of all three disciplines, including computational neuroscience, brain-motivated robotics and BMI, based on DecNef methodology.

One of the most critical assumptions in neuroscience and brain science is that the human mind (including consciousness) is caused by the brain's neural activity [114]. Most studies of human learning/memory/cognition have concentrated on examining the correlations between behavioural and neural activity changes rather than establishing cause-and-effect relationships. Even in animal studies, the most frequently used technique is examining the temporal correlation between neural activities and certain hypothetical computational variables proposed by the experimenters. The lack of experimental tools for examining cause-and-effect relationships between brain activity and the mind in systems neuroscience has severely constrained its progress and applicability to such practical problems as robotics or clinical issues [36]. To bridge this gap between major concepts and current technology, we developed a new technique that manipulates neural codes [38] by applying a novel online-feedback method that uses decoded fMRI signals. We call this new technique DecNef. We developed DecNef by spatial activity patterns in a specific brain area that can be non-invasively controlled by real-time fMRI neurofeedback [38]. We induced visual perceptual learning without visual stimulus presentation or conscious awareness of tasks. The experiment consisted of the following four stages. The first and the fourth are psychological performance tests for the visual discrimination of three orientation gratings. In the second stage, a decoder, actually a machine-learning algorithm called multinomial sparse logistic regression (MSLR) [115], was trained to compute the likelihood of the multi-voxel fMRI patterns that are classified into one of the three orientations used in the above visual discrimination task. Ten years ago, Kamitani & Tong [27] showed that the orientation of seen visual gratings could be ‘decoded’ from primary visual cortex fMRI multi-voxel patterns. Our DecNef study, which was based on this pioneering study, used MSLR instead of a support vector machine and fMRI signals from the first and secondary visual cortices. The third stage was real-time neurofeedback training that used the above MSLR decoder for orientation to compute visual neurofeedback signals. Participants manipulated their brain activities to obtain maximum monetary rewards. One out of three orientations was allocated to each subject as the target orientation. Six seconds of brain activity were decoded to compute the target orientation's likelihood, which was visually displayed as the size of a green disc 6 s after the brain manipulation. The total amount of monetary reward was proportional to the likelihood, and thus the summation of the disc size across all trials was given to the subject at the conclusion of each day of training. DecNef is essentially a reinforcement-learning paradigm [11] that is guided by monetary reward. It is also related to ‘neural operant conditioning.’ After 5 or 10 days of DecNef training, when the performances of the first and fourth stages of the experiment were compared, subjects only significantly improved their discrimination performance of the target orientation gratings, but not for the other orientations. Consequently, brain activity as multi-voxel fMRI patterns was experimentally induced without visual stimulus presentation or awareness of the working of the experiment and caused visual perceptual learning. Brain activity was a cause; a behavioural change was the result in this DecNef example.

In a more general framework, DecNef can be described as follows. First, a decoder is constructed that classifies fMRI multi-voxel patterns according to such specific brain information as visual attributes, emotional states or normal and pathological states in psychiatric disorders. In the induction stage, volunteers unconsciously control their brain activity to produce a desirable pattern while being guided by a real-time reward signal computed as decoder output. Thus, the three important elements of fMRI DecNef are the decoding of information from fMRI brain activity, real-time neurofeedback of the decoded information and unconscious reinforcement learning by the participants. DecNef was recently further advanced to manipulate facial preferences [39] or to induce artificial synaesthesia [40]. The basal ganglia was the only brain region that was activated in all three of the above DecNef studies in the induction phase of neurofeedback training; this result is consistent with the reinforcement learning interpretation of DecNef.

Neurofeedback training based on a real-time fMRI has attracted considerable attention for its potential advantages in therapeutic treatment. Most fMRI neurofeedback methods focus on up- or downregulation of a single region-of-interest activation [116–118]. But these have recently been extended by DecNef to control spatial activity patterns within a specific ROI, as explained above [39]. fMRI–DecNef can be used as a non-invasive BMI system for treating abnormal central decision-making functions in psychiatric disorders [119]. Fukuda et al. [120] also demonstrated that fMRI neurofeedback can further modulate spatio-temporal activation patterns across multiple ROIs as well as intrinsic networks. This effect was preserved over a surprisingly long period (more than two months after 3 days' training). Disturbances in intrinsic networks have been reported for a number of neurological and psychiatric diseases. Consequently, the connectivity neurofeedback method could be applied not only as a causal tool for basic neuroscience to alter functional networks but also as a revolutionary therapeutic method by directly curing the pathological connectivity patterns of neurological and psychiatric diseases. DecNef or connectivity neurofeedback [120] might provide revolutionary cures for such psychiatric diseases as autism spectrum disorders for which neither pharmacological nor cognitive/behavioural therapies have proved statistically effective.

DecNef can also be regarded as an extended and specific type of BMI. The neurofeedback itself is one component in a methodology frequently used in BMI. However, DecNef is an extended version of neurofeedback and uses sophisticated decoding and reward feedback, which are not necessarily always involved in BMI. Previous examples of DecNef did not use robots as effectors. BMI directly connects brain activity and an artefact outside the brain for such purposes as sensory substitution, motor compensation and enhancement, neurorehabilitation, suppression of neural circuit maladaptation, and cures of brain lesions and neurological and psychiatric disorders. A BMI usually consists of some of the following electrical, mechanical, and computing elements: a brain activity measurement system (electrodes, amplifier, AD converter, etc.), a computer for decoding brain information and/or controlling stimuli to the brain, an effector system (prosthetic limbs, rehabilitation robots, computer cursors, etc.) and a neural stimulation system. DecNef's current form does not depend on the effector or neural stimulation systems, but as outlined below, the future DecNef might also use them to enhance the reward/penalty effects of the DecNef and make training more efficient. In most BMIs, except the sensory substitution BMI, the brain information is first extracted by a decoder from the measured brain signals. This information is transformed and fed back to users in some sensory modality with/without reward signals, and finally BMI users learn to change their brain networks based on synaptic plasticity. Currently, most neurofeedback signals in BMI and DecNef are given in sensory modalities, such as the visual, auditory and somatosensory information of a restricted body part. Reward signals are very important in these neurofeedbacks, especially for DecNef, because DecNef and many BMIs use reinforcement learning as basic working principles. The most compelling neurofeedback device would be an exoskeleton humanoid robot, as it can provide a rich set of sensory as well as kinaesthetic information of all body parts (figure 15). While decoding from a user brain, we can manipulate an XoR to control the spatio-temporal activity patterns of the user's brain to a larger extent than with the currently available narrow neurofeedback channel. One future direction of our work is studying various uses of XoR in neuroscience in addition to BMI rehabilitation. The main target of a combined exoskeleton/DecNef is to experimentally control brain activity patterns either for scientific purposes or therapeutic interventions. However, inducing plasticity in the brain by DecNef and exoskeleton robots can also improve the control performance of exoskeleton robots by brain activity. We especially need to investigate how the interaction between the human body and the mind with XoR and its control algorithms can produce emotional information that fuel reinforcement learning.

Figure 15.

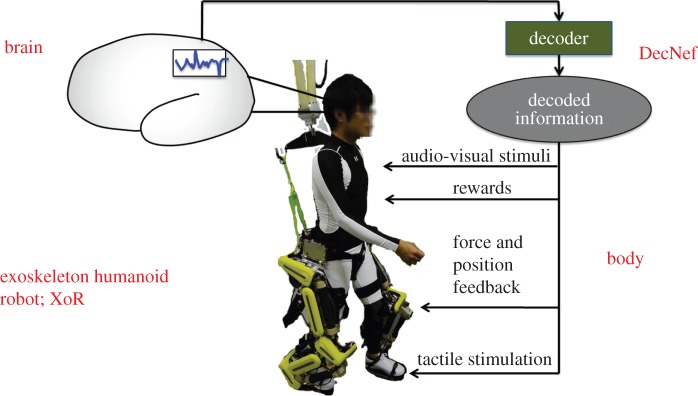
DecNef and humanoid exoskeleton. Reward signal is crucial in these neurofeedbacks, especially for DecNef. The most compelling neurofeedback device would be an exoskeleton humanoid robot, as it can provide a rich set of sensory as well as kinaesthetic information of all body parts. (Online version in colour.)

6. Conclusion

We introduced our novel ‘creating the brain’ and ‘interacting with the brain’ approaches to understand functional brain mechanisms. In our brain-motivated humanoid motor learning method, we introduced our attempts to understand how the brain deals with high-dimensional reinforcement-learning problems. In our proposed hierarchical learning system, we assumed that low-dimensional limit cycles are represented by super high-dimensional neural activities. The low-dimensional fluctuated trajectories are generated around the limit cycle by noisy inputs. The limit cycle is modulated to explore the directions that are only related to reward signals. We also introduced a newly developed exoskeleton robot that can be considered a novel robotics tool for neuroscience. As a future direction, we will develop an integrated system of the brain, body and an exoskeleton robot where the robot is controlled by the brain activities to understand how the brain works in natural situations.

Funding statement

It was partially supported by ERATO, J.S.T.; by ICORP, J.S.T.; by MIC-SCOPE; by SICP, J.S.T.; by KAKENHI 2312004; and by contract with the Ministry of Internal Affairs and Communications entitled ‘Novel and innovative R&D making use of brain structures’.