Warning signals for eruptive events in spreading fires

Significance

As flames spread through forests, buildings, or other complex environments, they can erupt, unexpectedly, into fast-moving conflagrations. This study presents evidence that characteristic patterns in the behavior of spreading flames may indicate when such eruptions are likely to occur. Our results rely on the detection of a phenomenon termed “critical slowing down”—the slowed recovery of multistable systems from perturbations as those systems approach tipping points. Using a bistable combustion system in which flames propagate either as small, slowly moving flames, or as large, rapidly moving flames stabilized by feedback between wind and fire, we provide evidence that slowing responses of spreading flames to sudden changes in environment (e.g., wind, terrain) may anticipate the onset of intense, feedback-stabilized modes of propagation.

Abstract

Spreading fires are noisy (and potentially chaotic) systems in which transitions in dynamics are notoriously difficult to predict. As flames move through spatially heterogeneous environments, sudden shifts in temperature, wind, or topography can generate combustion instabilities, or trigger self-stabilizing feedback loops, that dramatically amplify the intensities and rates with which fires propagate. Such transitions are rarely captured by predictive models of fire behavior and, thus, complicate efforts in fire suppression. This paper describes a simple, remarkably instructive physical model for examining the eruption of small flames into intense, rapidly moving flames stabilized by feedback between wind and fire (i.e., “wind–fire coupling”—a mechanism of feedback particularly relevant to forest fires), and it presents evidence that characteristic patterns in the dynamics of spreading flames indicate when such transitions are likely to occur. In this model system, flames propagate along strips of nitrocellulose with one of two possible modes of propagation: a slow, structured mode, and a fast, unstructured mode sustained by wind–fire coupling. Experimental examination of patterns in dynamics that emerge near bifurcation points suggests that symptoms of critical slowing down (i.e., the slowed recovery of the system from perturbations as it approaches tipping points) warn of impending transitions to the unstructured mode. Findings suggest that slowing responses of spreading flames to sudden changes in environment (e.g., wind, terrain, temperature) may anticipate the onset of intense, feedback-stabilized modes of propagation (e.g., “blowup fires” in forests).

Multistable systems can, when sufficiently perturbed, undergo “critical transitions” in which they shift abruptly between dynamically distinct states. Such transitions represent important steps in the progression of many natural processes [e.g., the sudden demise of ecosystems or populations (1, 2), the onset of climatic shifts (3, 4), the crash of financial markets (5, 6), the collapse of power grids or of Internet communication networks (7, 8), transitions from life to death (9, 10)], and the identification of phenomena that trigger or presage their onset remains an intellectually challenging and practically important goal of research on the dynamics of complex systems.

Recent evidence suggests that a set of generic statistical indicators may warn of impending transitions in a wide range of systems (11, 12). Briefly, as systems approach catastrophic bifurcations, they exhibit slower rates of recovery from perturbations (13), a phenomenon referred to as “critical slowing down;” as the duration of influence associated with those perturbations increases, the fluctuations to which they give rise can become larger (increased variance) (14), more correlated (increased autocorrelation) (15), and/or more asymmetric (increased skewness) (16). Many studies of critical transitions in natural systems have identified corresponding trends in individual variables of state [e.g., increased variance in electrical signals before an epileptic seizure (17)] (2–4, 18), but similar patterns have proven difficult to detect in systems for which variables of state are noisy, interdependent, or poorly defined (as in interconnected, cyclic, or chaotic systems) (11, 12). Warning signals—or, more generally, transitions between alternative stable states—in such systems have, as a result, eluded experimental examination.

Spreading fires are noisy [and potentially chaotic (19)] systems for which warning signals of transitions in dynamics could aid in the development of improved practices for control and suppression. In large-scale natural fires (i.e., wildfires), for example, slowly moving flames can spontaneously erupt into blowup fires—large, rapidly moving fires stabilized by feedback between wind and spreading flames (i.e., wind–fire coupling) (20, 21). Such events, which are not captured by operative models of fire behavior, pose enormous risks to fire response teams, and complicate efforts in fire suppression (22–24).

To examine patterns in dynamics associated with the onset of intense, feedback-stabilized modes of propagation, we built a simple physical model for blowup-like fires based on a bistable combustion system. In this system, flames propagate along strips of nitrocellulose either as slow, structured flames (characterized by well-defined heights and shapes) or as fast, unstructured flames (marked by aperiodic oscillations in size and shape) in which a form of wind–fire coupling sustains 5- to 10-fold faster rates of propagation. Transitions between these modes can be induced by topographical features of the strip: structured flames can, upon encountering folds in the strip become unstructured; similarly, unstructured flames can, upon encountering the same folds (hereafter referred to as “bumps”), become structured and slow. By using this model system to examine (i) conditions that influence the likelihood of perturbation-initiated transitions between modes of propagation and (ii) patterns in dynamics that emerge as these transitions become more likely, we addressed this question: “Do slowly spreading fires exhibit detectable symptoms of critical slowing down prior to transitioning to intense, feedback-stabilized fires?”

Intent of the Model System

Mechanisms of feedback in large-scale fires are far more complex than those exhibited in our model system. In forest fires, wind blows against propagating flames, altering their structure, rate of propagation, and direction of travel, and flames, in turn, release latent heat, sensible heat, and smoke, thereby altering local wind conditions (25, 26). In building fires, flames alter the structure, temperature, and airflow of their local environment, and, subsequently, grow or extinguish in response to those alterations (27). In this study, we did not attempt to develop an experimental system that captures the extremely complex—and varied—mechanisms of feedback between large-scale fires and their environments; instead, we developed a model system that could be controlled, reproduced, and characterized in detail. Despite its simplicity, this model shares important characteristics of large-scale fires—a susceptibility to feedback, and a sensitivity to environmental conditions. This model abstracts a complex system into a simpler one that can be studied, thereby enabling the collection of empirical data—and the development of theoretical hypotheses based on those data—that would be difficult or impossible to obtain with more complicated (and usually intrinsically irreproducible) large-scale systems.

Contour-Initiated Transitions

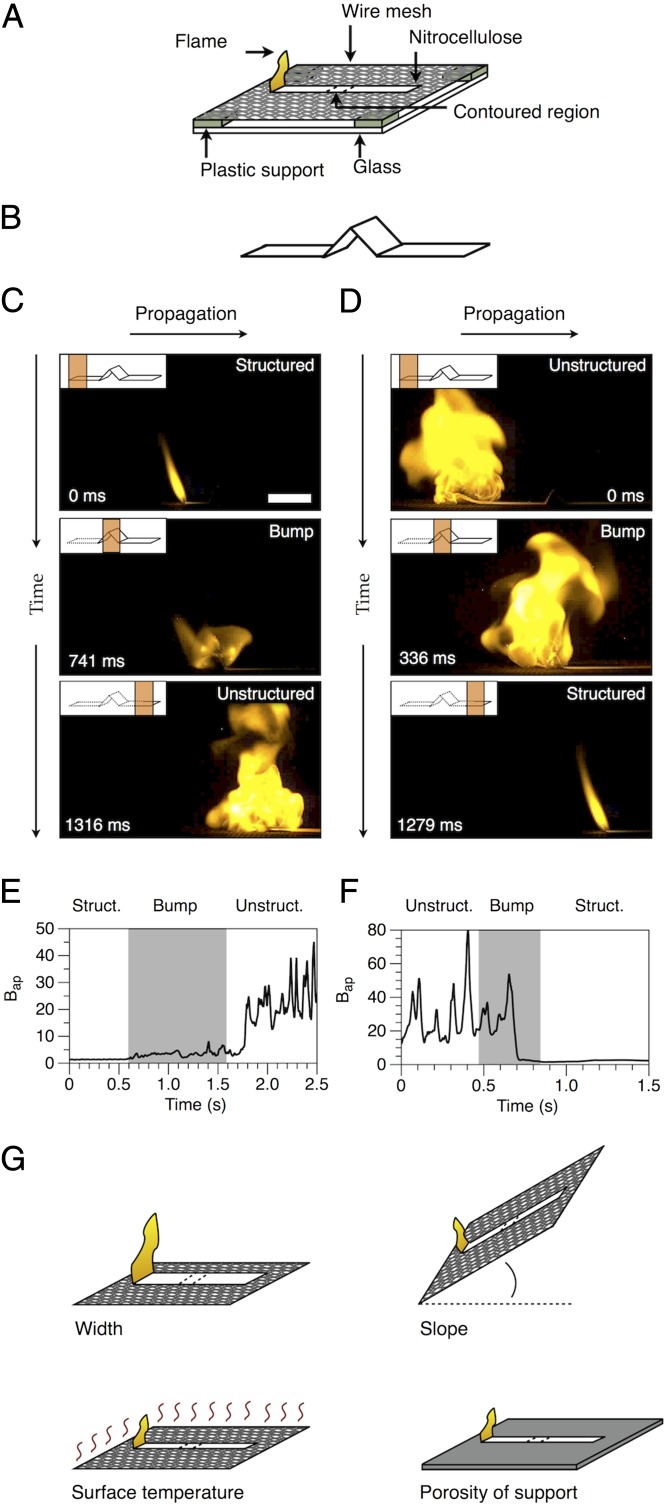
Our model system was based on nitrocellulose strips (30 cm long, 140 μm thick, with widths of 0.5–5 cm), placed on a suspended wire mesh (which allowed air to flow to the bottom of the flames; Fig. 1A and SI Appendix, Fig. S1 A and B). Igniting these strips from one end resulted in highly reproducible burning (SI Appendix, SI Methods). To induce transitions between dynamical states of the flame, we folded bumps into the center of the strips (Fig. 1B). These bumps could, under some circumstances, transform structured flames to unstructured flames and vice versa (Fig. 1 C and D; Movies S1–S5). In building this system, we did not intend the bumps to represent any specific element of weather, topography, or fuel; rather, they supplied a means of introducing perturbations of sufficient magnitude to push the system between alternative basins of attraction. Bumps of different sizes and shapes had different propensities for triggering transitions (SI Appendix, Fig. S1 C and D).

Fig. 1.

Model system. (A) Schematic of the experimental setup. Strips of nitrocellulose (30 cm long, 140 μm thick, with widths of 0.5–5 cm), resting on a suspended wire mesh, were ignited from one end. (B) The bump used in this study: a 1-cm inverted “V” composed of three folds and two sides (each 1 cm in length). (C) Sequential high-speed images showing a structured-to-unstructured transition triggered by the bump from B (scale bar, 2 cm). The frame at t = 0 ms shows a prototypical structured flame. (D) Sequential high-speed images showing an unstructured-to-structured transition triggered by the bump from B (scale bar as in C). The frame at t = 0 ms shows a prototypical unstructured flame. (E) A plot showing the evolution of B_ap for a structured-to-unstructured transition initiated by the bump from B. (F) A plot showing the evolution of B_ap for an unstructured-to-structured transition initiated by the bump from B. (G) Conditions that influence the probability of contour-initiated transitions: width of the strip (w_strip), slope of the strip (θ_strip), surface temperature (T_surface), and the porosity of the mesh (the size and areal density of holes).

To examine patterns in dynamics of structured and unstructured flames, we defined a variable of state that we could monitor over time: the mean apparent brightness (B_ap) of a high-speed image of a flame (i.e., the mean of the pixel values; SI Appendix, SI Methods), a linear function of the area of a flame (SI Appendix, Fig. S3). Plots showing the evolution of B_ap for contour-initiated transitions (Fig. 1 E and F) show distinct differences between structured and unstructured flames: values B_ap for unstructured flames exhibit aperiodic oscillations and are, on average, about an order of magnitude larger than values of B_ap for structured flames.

To facilitate a detailed examination of the conditions that influence the sensitivity of this system to contour-initiated perturbations, we used one type of bump for all experiments in this study—a 1-cm inverted “V” (Fig. 1B)—and we altered the conditions under which this bump was encountered: the width of strips and the slope, surface temperature, and porosity of the mesh (size and areal density of holes) supporting them (Fig. 1G).

Results and Discussion

Feedback in the Unstructured Regime.

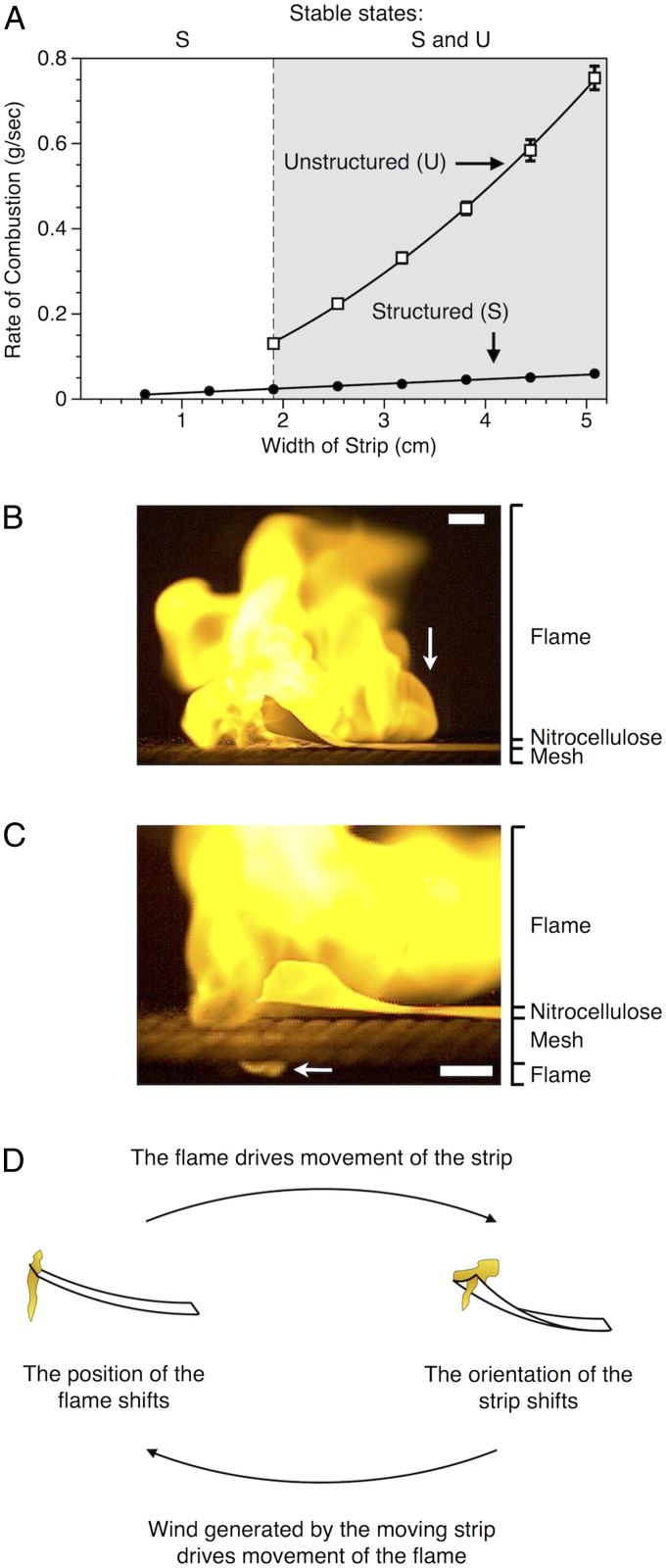
Rates of combustion were 5–10 times higher for unstructured flames than for structured flames (Fig. 2A). To determine the mechanism by which the unstructured regime permitted higher rates of combustion—and, thus, propagation—we used high-speed video and infrared photography. Movies of unstructured flames documented forward-moving bursts of hot gases (white arrow in Fig. 2B; SI Appendix, Movie S2) caused by upward movements of the burning ends of nitrocellulose strips (angled strip in Fig. 2B; SI Appendix, Note 2); analysis of high-speed and infrared images shows that ignition of the underside of strips (Fig. 2C) drives their upward movements through a combination of thrust and buoyancy (SI Appendix, Note 3). Convective bursts, by sustaining ignition of regions of nitrocellulose that are larger than the regions ignited in structured flames (SI Appendix, Fig. S5), permit the unstructured regime to maintain higher rates of combustion and, thus, faster rates of spread than the structured regime.

Fig. 2.

Feedback in the unstructured regime. (A) Rates of combustion associated with structured (closed circle, ●) and unstructured (open square, □) burning regimes for strips of different widths; rates of combustion were 5–10 times higher for unstructured flames than for structured flames. Lines represent fits consistent with trends exhibited by points: structured (linear, r² = 0.99), unstructured (quadratic, r² = 1.00). Regions of stability for structured flames (S), and both structured and unstructured flames (S and U, gray) are labeled at the top of the plot. Error bars represent SE (n ≥ 5). (B) A high-speed image of an unstructured flame showing a forward burst of hot gases (white arrow) caused by a movement of the nitrocellulose strip (scale bar, 1 cm). (C) A high-speed image of an unstructured flame showing how ignition of the underside of the strip (white arrow) drives movements of the strip (scale bar, 1 cm). (D) A simplified representation of the feedback loop (wind–fire coupling) that stabilizes the unstructured regime. Flames drive movements of the strips and simultaneously shift their positions in response to wind generated by those movements; this feedback loop allows for the continuous generation of forward bursts of hot gases that, through convective heat transfer to the surface of the strips, sustain ignition of an area larger than that in the structured regime. In Movie S2, this feedback loop is captured in detail.

Without continuously generating convective bursts of hot gases, unstructured flames would quickly slow and become structured flames. A positive feedback loop stabilizes the unstructured regime against such transitions (Fig. 2D; SI Appendix, Notes 4 and 5). When unstructured flames move a nitrocellulose strip, they encounter convective airflows caused by that movement. These airflows (hereafter referred to as “wind” for simplicity of discussion), in addition to buoyancy (which pushes flames in the vertical direction), cause flames to shift their positions on the moving strip and, in doing so, to push the strip in a new direction. This feedback loop (flame-driven movements of the strip, strip-driven movements of the flame) continuously allows (i) the burning end of the nitrocellulose strip to move back to the surface of the mesh and (ii) flames on the underside of the strip to propel that burning end away from the mesh, and, thus, to generate forward-moving bursts of hot gases.

Our analysis suggests that, in the unstructured regime, propagating flames move the nitrocellulose strips and simultaneously shift positions in response to wind generated by those movements. This interaction constitutes a feedback loop—a form of wind–fire coupling—that leads to regular forward bursts of hot gases that, via convective heat transfer to the surface of the strips, sustain ignition of an area larger than that in the structured regime, and thereby permit rates of propagation that are 5- to 10-fold higher than those of structured flames.

Conditions That Influence the Likelihood of Transitions.

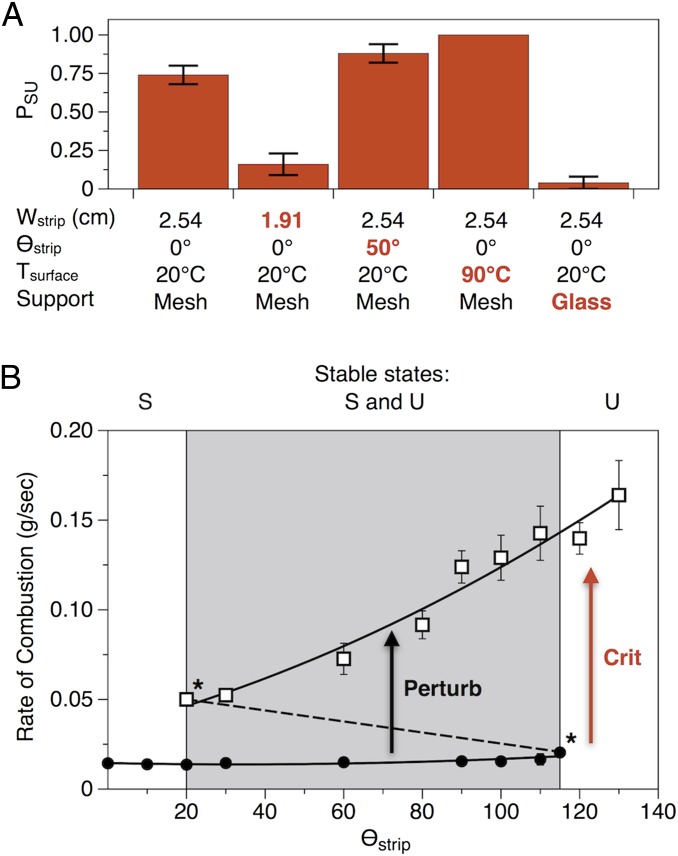
As bistable systems approach bifurcation points, they become less able to absorb perturbations without switching between alternative basins of attraction (28). When perturbations occur with a distribution of possible magnitudes (as in our system), the probability of a perturbation-initiated transition will, accordingly, increase. We used the probability of structured-to-unstructured transitions (P_SU = n_trans/n, where n_trans is the number of successful transitions and n is the total number of experiments) as a metric for proximity of our system to a bifurcation point, and we examined the sensitivity of this parameter to several different conditions of combustion. Values of P_SU increased with the width and slope of the strips, the temperature of the support surface, and the size of the mesh (Fig. 3A; SI Appendix, Fig. S9 and Table S1)—these changes, thus, bring the system closer to structured-to-unstructured bifurcation points.

Fig. 3.

Conditions that alter the probability of transitions. (A) A chart revealing the influence of various environmental conditions on the probability of structured-to-unstructured transitions (P_SU). Values of P_SU increased with the width of the strip and the angle, temperature, and porosity of the support surface. Error bars represent SE (n ≥ 25). (B) An experimentally mapped bifurcation diagram: rates of combustion associated with structured (closed circle, ●) and unstructured (open square, □) flames propagating along 1.27-cm strips positioned at different angles (θ_strip). Lines represent fits consistent with trends exhibited by points: structured (quadratic, r² = 0.73), unstructured (quadratic, r² = 0.97). Bifurcation points associated with structured-to-unstructured (θ_strip = 115°) and unstructured-to-structured (θ_strip = 20°) critical transitions are marked with an asterisk. The dashed line marks a linear approximation of the region of the curve corresponding to unstable fixed points. Arrows are as follows: (white) a contour-initiated transition from the structured regime to the unstructured regime (similar to that shown in Fig. 1C); (red) a critical transition caused by increasing θ_strip beyond the bifurcation point at 115°. Regions of stability for structured flames (S), unstructured flames (U), and both structured and unstructured flames (S and U, gray) are labeled at the top of the plot. Error bars represent SE (n ≥ 7).

Informed by trends in P_SU, we mapped a bifurcation diagram associated with changes in slope. Fig. 3B shows rates of combustion associated with structured and unstructured flames propagating along 1.27-cm strips positioned at various angles (θ_strip): below θ_strip = 20° (the unstructured-to-structured bifurcation point), unstructured flames are not stable; above θ_strip = 115° (the structured-to-unstructured bifurcation point), structured flames are not stable. These points represent fold bifurcations (i.e., points where the curve of fixed points folds back onto itself). Crossing these points (by reducing θ_strip in the unstructured regime, or by increasing θ_strip in the structured regime) leads to catastrophic shifts, or critical transitions, between the two regimes of propagation.

Dynamics Associated with Conditions Where Transitions Are Likely.

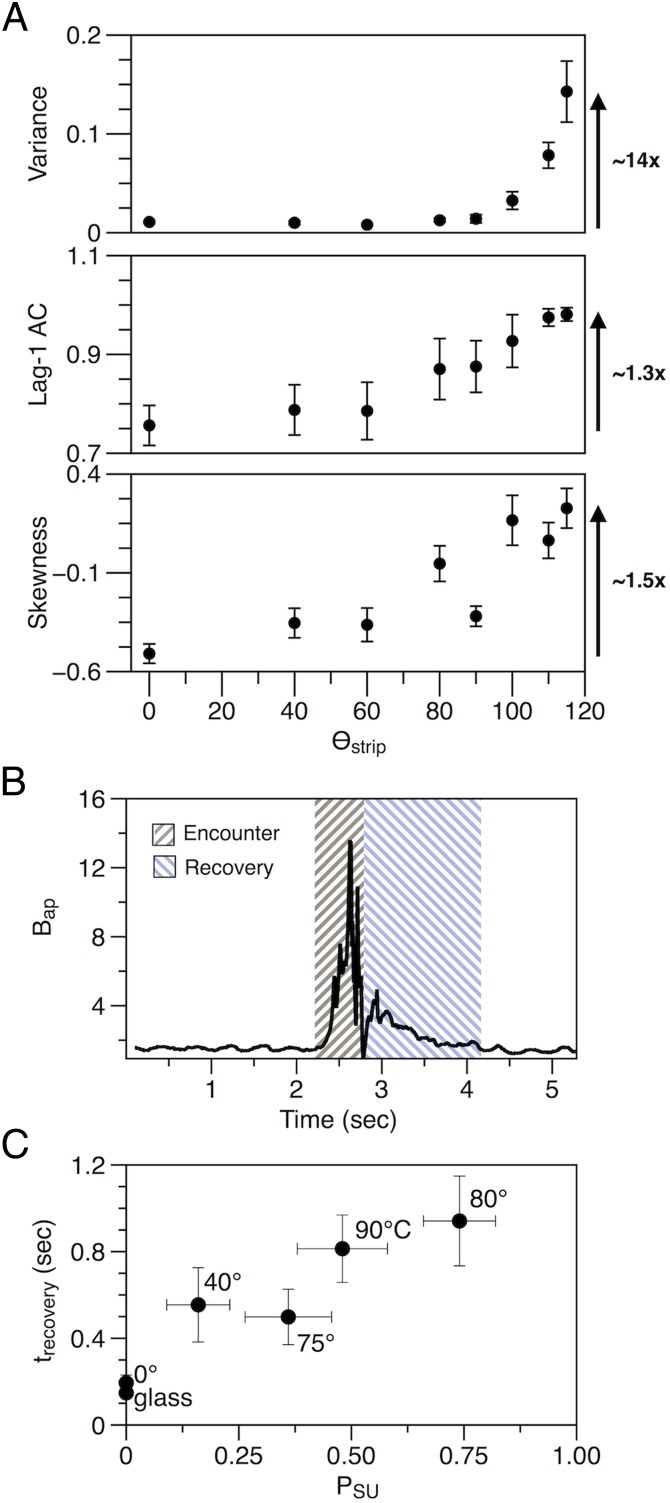
Theoretical studies of patterns in dynamics associated with critical slowing down suggest that fluctuations in B_ap for structured flames should exhibit a set of generic trends near the structured-to-unstructured bifurcation point: (i) the variance (a measure of the spread of B_ap) and the autocorrelation (a measure of the self-similarity of B_ap over time) should increase as a result of the slowed recovery of structured flames from stochastic perturbations (i.e., those caused by irregularities in the mesh, small movements of air, or other random events) (14, 28), and (ii) the skewness (a measure of the asymmetry in the distribution of B_ap) should increase as a result of growing asymmetry in the stability landscape (16). We evaluated these expected trends by calculating the variance, lag-1 autocorrelation, and skewness of B_ap for structured flames propagating along strips positioned at different angles (θ_strip, SI Appendix, SI Methods). Our results show that all three parameters increased upon approach to the bifurcation point at θ_strip = 115° (Fig. 4A); this upward trend, however, was much more pronounced for variance, which increased by an order of magnitude, than for autocorrelation or skewness, which increased only slightly (∼1.5-fold) and showed nonmonotonic irregularities (i.e., values of adjacent data that did not increase with θ_strip, despite an overall trend suggesting they should). As the statistical indicators in Fig. 4A were calculated from the same dataset (i.e., points for a given value of θ_strip in each plot correspond to measurements from the same 10 experiments), differences between the plots correspond to differences in the sensitivities of the statistical indicators to nonstandard (i.e., nonstochastic) attributes of fluctuations in our system, not to differences between experiments.

Fig. 4.

Symptoms of critical slowing down. (A) Variance, lag-1 autocorrelation, and skewness in B_ap for structured flames propagating along strips (1.27-cm) positioned at various angles to a level surface (θ_strip). To the right of each plot, labeled arrows indicate the extent to which each parameter increased from 0° to 115° (i.e., upon approach to the structured-to-unstructured bifurcation point at θ_strip = 115°). Variance increased by an order of magnitude, whereas autocorrelation or skewness increased only slightly (∼1.5-fold). For each value of θ_strip, corresponding values of statistical parameters in each plot were calculated from the same dataset. Error bars represent SE (n ≥ 10). (B) Mean values of brightness for sequential high-speed images of a contour-initiated perturbation (1.27-cm strip, θ_strip = 80°) show a distinct period of recovery after encounter of a bump. (C) The mean duration of the recovery (t_recovery) for different contour-initiated perturbations for a 1.27-cm strip. Values of t_recovery increase with P_SU (i.e., upon approach to structured-to-unstructured bifurcation points), providing direct evidence of critical slowing down. Error bars represent SE (n ≥ 25 for P_SU, n ≥ 10 for t_recovery).

One value of physical models is their ability to provide empirical evidence of inadequacies associated with physical assumptions of theoretical models. Such is the case in the present study. Mathematical models of multistable systems (e.g., those upon which statistical indicators are based) assume that stochastic perturbations drive fluctuations in variables of state about stable fixed points (11, 14–16); in our experimental system, however, fluctuations in B_ap result from both (i) stochastic perturbations and (ii) the natural, but irregular oscillatory behavior of the flame (e.g., the occasional formation of convection cells that cause undulations in the height of the flame, or oscillating asymmetry of the flame front; SI Appendix, Note 6). Our results indicate that theoretically predicted trends in variance are less susceptible to distortion by these oscillatory fluctuations than trends in autocorrelation or skewness, and suggest that, of the three, variance is the most reliable indicator of critical slowing down in systems for which such fluctuations are present.

Direct Observation of Critical Slowing Down.

In general, statistical indicators are useful for examining systems for which information from high-resolution time series is available or easy to collect. For spreading fires and other complex systems where shifts in dynamical patterns emerge over short time scales (i.e., seconds to minutes), however, the collection of such data is not straightforward, nor compatible with real-time monitoring.

To identify behavioral indicators of critical slowing down that might be compatible with direct observation (rather than detection through statistical analysis), we examined the recovery of structured flames that experienced contour-initiated perturbations without transitioning to the unstructured regime. Plots showing the evolution of B_ap for such flames indicate that they, after encountering bumps, took time to recover patterns in B_ap resembling those of their preencounter state (Fig. 4B). We estimated the duration of these periods of recovery (t_recovery) by determining the time required for a local mean of B_ap to reach a value of within 5% of the mean for the structured regime (SI Appendix, SI Methods). A plot showing the average recovery time for conditions with differing values of P_SU suggests that t_recovery increased in scenarios where structured-to-unstructured transitions were more likely—that is, upon approach to a bifurcation point (Fig. 4C). This behavior constitutes the very definition of critical slowing down.

An Example: Forest Fires.

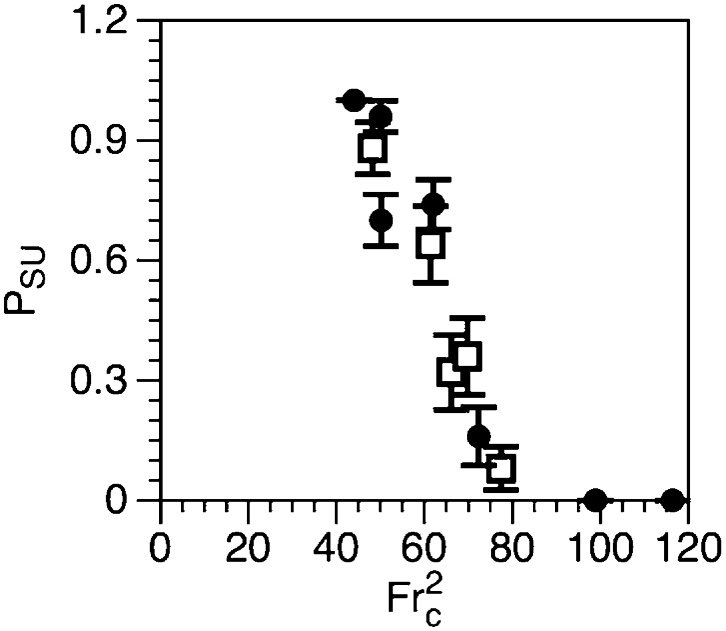
Although the mechanism of wind–fire coupling in our model system is markedly different from the mechanisms of wind–fire coupling in forest fires, the influences of inertial and buoyant forces are similar in both systems. Computational models of forest fires suggest that feedback between wind and spreading fires grows stronger when the flow of hot gases within and around flames is influenced more by buoyant convection than by wind (20, 26, 29). For our system, such scenarios correspond to flames with low convective Froude numbers [Fr_c² is a metric for the relative influence of inertial forces to buoyant forces on the structure of the flame: Fr_c² = U²/(gHΔT/T), where U is the velocity of gases within the flame, g is the acceleration due to gravity, H is the height of the flame, ΔT is the difference between the mean temperature of the flame and the temperature of the room, and T is the temperature of the room (29); SI Appendix, SI Methods]. When we estimated values of Fr_c² for flames propagating along strips of different widths and/or temperatures and plotted those values against P_SU, we observed that transitions became more likely as Fr_c² decreased (i.e., as the relative influence of buoyant forces increased; Fig. 5). This trend implies that low-Fr_c² conditions bring the system closer to a structured-to-unstructured bifurcation point, decrease the resilience of the structured regime to perturbations, and increase the resilience of—and, thus, stabilize—the unstructured regime. A physical interpretation follows: as flames move the nitrocellulose strips, flames that are smaller and/or cooler (high Fr_c²) shift their positions (relative to the surface of the strip) less (smaller overall shifts) than do flames that are larger and/or hotter (low Fr_c²), which are more sensitive to buoyancy and, thus, to the direction of gravity (which changes, relative to the moving strip). Larger, hotter flames, by shifting more in response to movements of the strip, cause greater shifts in the direction and velocity of subsequent strip movements (than do smaller, cooler flames) and, thus, strengthen the feedback loop that stabilizes the unstructured regime.

Fig. 5.

Forces that influence the stability of the unstructured regime. The convective Froude number (Fr_c²) is a metric for the relative influence of inertial forces (velocity of gases within the flame) to buoyant forces (buoyancy of the gases within the flame) on the structure of a flame. The plot shows values of P_SU (the probability of structured-to-unstructured transitions) and Fr_c² for flames propagating along strips of different widths (closed circle, ●) and temperatures (open square, □). The trend in P_SU suggests that the probability of transitions increases as the relative influence of buoyant forces increases (relative to the influence of inertial forces); that is, low-Fr_c² conditions stabilize the unstructured regime (relative to the structured regime). Error bars represent SE (n ≥ 25 for P_SU, n ≥ 5 for Fr_c²).

Forest fires are rarely examined in the context of multistability [although several studies have alluded to the possibility (20, 24)]. Through wind–fire coupling, however, they possess an important ingredient of multistable systems: a mechanism of positive feedback. By presenting a model system in which a form of wind–fire coupling—one susceptible to forces similar to those that influence wind–fire coupling in forest fires—stabilizes the formation of a second stable state, this study provides evidence that feedback between wind and fire may lead to multiple stable states in forest fires. Future examinations of multistability and critical slowing down in forest fires will require the use of coupled atmosphere–fire models that capture the correct mechanisms of feedback between spreading flames and surrounding environmental conditions (20, 25, 30).

Concluding Remarks.

The physical model developed in this work is not a replacement for detailed computational treatments of feedback between flames and their environments [e.g., models of diffusion flames in gravitationally stratified media (31, 32), coupled atmosphere–fire models of forest fires (25, 33)] or for detailed mathematical models of propagating flames [e.g., models of pulsating reaction fronts (34, 35), models of pattern formation in premixed flames (36, 37)]. Rather, it is an experimental tool that enables a focused examination of the patterns in dynamics that arise as transitions to feedback-stabilized modes of propagation become likely.

Results from this study suggest that characteristic patterns in flame dynamics may indicate when blowup fires are likely to occur. Analysis of structured flames shows that, as transitions to the unstructured regime become more likely, (i) fluctuations resulting from a combination of stochastic and oscillatory perturbations exhibit up to a 10-fold increase in variance, and (ii) periods of recovery from contour-initiated perturbations increase. These symptoms of critical slowing down suggest that slowing responses of spreading flames to sudden changes in environment (e.g., wind, terrain, temperature) may presage the onset of intense, feedback-stabilized modes of propagation. Future fire intervention strategies capable of accommodating such warning signals may be effective at slowing the spread of “erratic” fires and minimizing risk to fire response teams.

Beyond fires, the results of this study suggest that three commonly proposed statistical indicators of critical slowing down can exhibit dramatically different sensitivities to oscillatory fluctuations. Several theoretical studies have suggested that statistical indicators should respond differently to shifting regimes of perturbation [or, more generally, to any fluctuations that do not arise entirely from stochastic perturbations about stable fixed points (38, 39)]; the results of this work lend experimental support to those studies by suggesting that variance, but not skewness and autocorrelation, serves as an effective statistical indicator of critical slowing down for flames and, perhaps, other systems marked by irregular oscillatory fluctuations [e.g., power grids (40, 41)]. This result highlights the usefulness of physical models for examining systems for which all sources of perturbation are not known, and motivates future efforts to examine symptoms of critical slowing down in noisy, oscillatory, and/or chaotic systems.

Materials and Methods

SI Appendix, SI Methods details procedures for imaging flames, for estimating combustion rates, and for calculating the probabilities of transitions, the mean apparent brightness of flames, statistical indicators of slowing down, recovery times, and Froude numbers of structured flames.