SEGMENTATION-FREE MEASURING OF CORTICAL THICKNESS FROM MRI

Abstract

Estimating the thickness of cerebral cortex is one of the most essential measurements performed in MR brain imaging. In this work we present a new approach to measure the cortical thickness which is based on minimizing line integrals over the probability map of the gray matter in the MRI volume. Previous methods often perform a pre-segmentation of the gray matter before measuring the thickness. Considering the noise and the partial volume effects, there are underlying class probabilities allocated to each voxel that this hard classification ignores, a result of which is a loss of important available information. Following the introduction of the proposed framework, the performance of our method is demonstrated on both artificial volumes and real MRI data for normal and Alzheimer affected subjects.

1. INTRODUCTION

Measuring the cortical thickness has long been a topic of interest for neuroscientists. Cortical thickness has been shown to change along with the development of certain diseases such as Alzheimer’s [1]–[2]. Examining the changes in the cortical thickness through time can not only lead to an earlier diagnosis but also be an indicator of how well the treatment process is operating.

Various approaches have recently been proposed to automate this cortical thickness measurement on Magnetic Resonance Imaging (MRI) data, e.g., [3]–[10]. The low resolution of the MRI volumes makes it difficult to accurately measure the cortical thickness, given that the latter varies 2 to 5 mm in different regions of the brain and shows up as only a few voxels thick in the volumes. The neuroscience community has not yet agreed on a unique definition of cortical thickness and so far various proposed methods measure slightly different quantities. What is common among them is that they virtually all perform a pre-segmentation of the white matter (WM), gray matter (GM), and the cerebrospinal fluids (CSF), and generally extract the surfaces between them (inner surface between WM and GM and outer surface between GM and CSF). They then use this hard segmentation as the input data to the different tissue thickness measurement algorithms (see Sec. 2 for a brief review of the previous work). The disadvantage of this approach is that in the hard segmentation process, a considerable amount of information is discarded and never used in measurement, not to mention the significant error in measured thickness that could be introduced by a few misclassified voxels (an example is provided in Sec. 4.1).

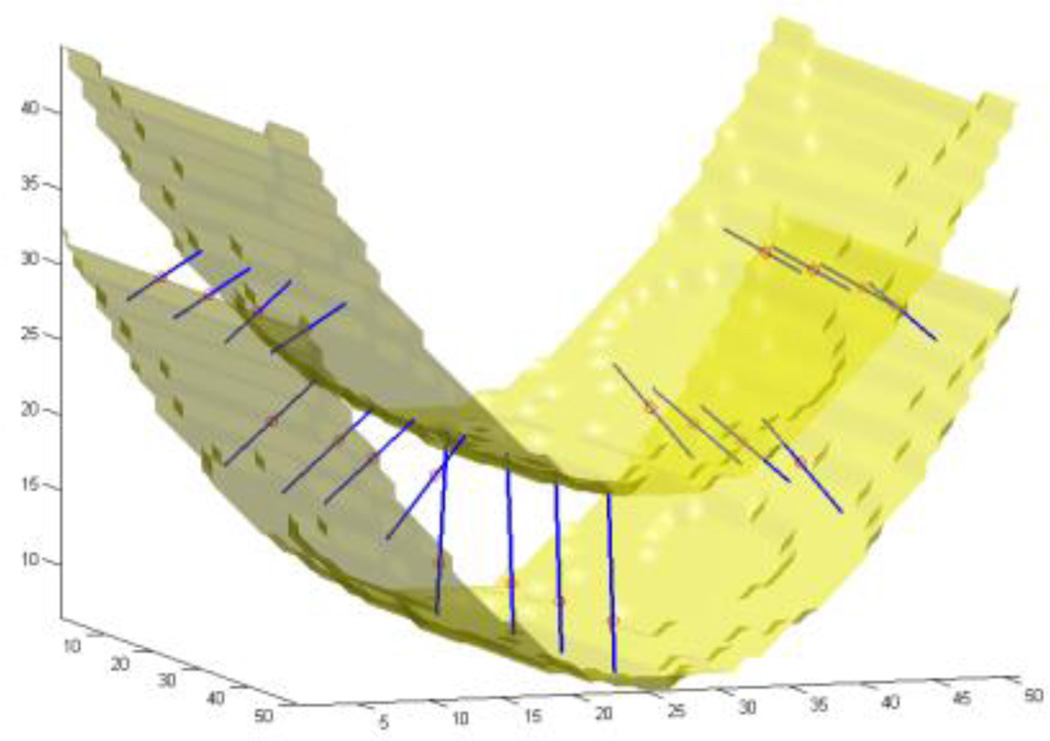
The approach we adopt here uses a soft pre-labeled volume as the input data. Due to the limited resolution of an MRI volume, there are voxels which contain partial amounts of two or more tissue types (see [11] and the references therein). The values on them give us information about the probability of those voxels belonging to any of the categories of WM, GM, or CSF. Rather than a pre-classified volume, we use one containing the probability of each voxel belonging to the GM. These probability values have the same precision as the values in the original MRI volume, and therefore we do not discard any useful information. We compute line integrals of the soft classified data, centered at each voxel and in all possible spatial directions, and then consider their minimum as the local cortical thickness on that voxel (Fig. 1).

Fig. 1.

Experimental results on an artificial probability map. Inner and outer surfaces of a paraboloid-shaped layer of GM are depicted. Line segments are chosen by the algorithm such that they give the smallest integrals (of the probability map) among all line segments passing through every selected test point, shown as small circles.

In Sec. 2 we review previous work on cortical thickness measurement. Sec. 3 describes the proposed framework introduced in this work, and the experimental results are presented in Sec. 4. Sec. 5 concludes with a review of the contributions.

2. PREVIOUS WORK

We now discuss some of the previously reported work for measuring the cortical thickness. We will see that they mostly require a pre-segmentation of the inner and outer surfaces which results in a loss of available information and often inaccuracy of the input to the main measuring algorithm.

The coupled surface methods [3], [12] define the cortical thickness as Euclidean distance between corresponding point pairs on the inner and outer surfaces. A displaced surface may result in an overestimation of the thickness, Fig. 2(a). The closest point methods such as [13] compute for each point on one of the two surfaces the closest point on the other surface and define the thickness as the distance between them. The main drawback to these methods is the absence of symmetry, as seen in Fig. 2(b). In another method introduced in [14], the regional histogram of thickness is estimated by measuring the length of the line segments connecting the inner and outer surfaces of the GM layer which are normal to one of the surfaces. The median of the histogram is then chosen as the local cortical thickness. An edge detection of the WM-GM and GM-CSF boundaries is however necessary.

Fig. 2.

Common ways of measuring cortical thickness. (a) Coupled surface methods. (b) Closest point methods. (c) Laplace methods. (d) Largest enclosed sphere methods.

Laplace Methods [4], [7], [15] solve the Laplace’s equation in the GM region with the boundary condition of constant (but different) potentials on each of the two surfaces. The cortical thickness is then defined on each point as the length of the curve of the gradient field passing through that point, as illustrated in Fig. 2(c). With this approach, the thickness is uniquely defined at every point. Nevertheless, a pre-segmentation of the two surfaces is required, reducing the accuracy of this technique.

Another category of methods define thickness by making use of a central axis or skeleton [9], [16]. Thickness is typically estimated as the diameter of the largest enclosed sphere in the GM layer, which is (in some cases only initially) centered on a point on the central axis. As Fig. 2(d) demonstrates, a relatively sharp change in the thickness can result in a new branch and affect the topology of the skeleton.

The vast majority of the methods reported in the literature carry on possible errors in the segmentation, which is still by itself a challenging problem in brain imaging. Considering that the GM layer is observed merely with a few voxels wide in common 1 to 2 mm resolutions, these errors can be very significant, and measuring tissue thickness avoiding this hard segmentation step can be very beneficial. This is the approach introduced here and described next.

3. METHODS

3.1. Definition

In its simplest form, we define the thickness of the GM at a given voxel as the minimum line integral of the probability map of the GM on lines passing through that voxel. Formally:

$$T(\stackrel{\rightharpoonup }{x})=\underset{l\in L_{\stackrel{\rightharpoonup }{x}}}{\text{min}}\underset{l}{\int }P(\stackrel{\rightharpoonup }{r})dl,$$

where T(x⃑) is the thickness of the GM at a point x⃑ ∈ ℝ³, P(x⃑) is the probability of the point x⃑ belonging to the GM (estimation of this probability is described in Sec. 4.2), and L_x⃑ is the set of all lines in three-dimensional space passing through the point x⃑. In practice, however, L_x⃑ is comprised of all equal-length line segments centered at x⃑which are sufficiently longer than the expected maximum thickness in the volume. Choosing longer line segments do not greatly affect the integral values since P(r⃑) decreases significantly on the non-GM regions. Fig. 3(a) shows an example of this construction for a 2D binary probability map, where the probability of belonging to the GM is 1 inside the shape and 0 outside. While computing thickness on the specified point, the line segment marked with oval arrows is selected as the one giving the smallest line integral. The corresponding integral value, which in this case is the length of its overlap with the GM (in bold), is the thickness of the GM on that point. A more realistic situation is shown in Fig. 3(b), where the probability map varies between zero and one. A blurred border, which is a result of the limited resolution of the MRI, contains voxels which are partially GM. Due to the pre-segmentation, this type of partial volume consideration is absent in the majority of the prior work in this area.

Fig. 3.

Computing line integrals passing through a point, and choosing the minimum integral value. (a) Binary probability map. (b) Continuous probability map.

Our method is based on an intuitive way of measuring the thickness of an object. A simple way to measure the local thickness of an object would be to put two fingers on both edges of the object, and move the finger tips locally (equivalent to varying the angle of the segment connecting them to each other), until the distance between them is minimized. This distance could then be considered as the local thickness of the object. Thus, we are dealing with a constrained optimization problem: minimizing a distance in a specific region. In our approach, however, this region is identified precisely by a point where we want to define the thickness. Therefore the constraint is that the point must be on the line segment connecting the two finger tips, in other words we consider only the line segments passing through the point where we intend to find the thickness. The minimized distance – or the length of the line segment – is in this case the integral of the probability map on the line containing the line segment.

3.2. Algorithm

The algorithm basically computes every line integral centered at each point of the volume starting from that point and proceeding on each of the two opposite directions separately. Once all the line integrals on a point are calculated (meaning in all possible directions), the minimum of them is considered to be the thickness on that point. However, to reduce the effect of noise, an alternative would be for instance to consider the average of some of the smallest integrals.

In practice, a problem may arise typically in narrow sulci where the outer surface of the folded GM layer has two nearby sides (Fig. 4(a)). While computing the thickness on one part of the layer, the GM of the other part may be partially included in some of the line integrals which may result in an overestimation of the thickness (Fig. 4(b)). In order to avoid this error, we propose two stopping criteria which prevent a line integral from further advancing when it is believed that no more summation is necessary or that we are mistakenly considering a different region of the GM layer. The line integral stops proceeding if the probability map:

1. Has been below a specific threshold for a certain number of consecutive voxels, or

2. Has been decreasing at least for a certain number of successive voxels and then increasing for an additional number of voxels.

Fig. 4.

(a) A sulcus that makes two sides of the gray matter layer close to each other. (b) How the algorithm might overestimate the thickness if no stopping criteria were to be used.

We use the first criterion, since if the probability has been low for a while, we are most likely not in the GM region anymore, and by further summing we would just increase the error. An additional advantage of using this stopping criterion is that summation will be stopped quickly after starting measuring the thickness on the voxels which are not in the GM region, as if the algorithm is ignoring those points and so it returns almost zero values as the GM thickness on them.

The second condition happens when two parts of the GM layer are so close to each other that the probability on the gap between them is not small enough for the first stopping condition to become true, therefore the algorithm stops summing after identifying a valley on the probability map. The algorithm can be implemented such that gaps as narrow as one voxel are detected by the above stopping criteria.

4. RESULTS AND DISCUSSION

4.1. Artificial Data

In order to illustrate and validate our approach, we start the results section with artificial input data. Fig. 1 shows the isosurfaces of an artificially created probability map of a paraboloid-shaped layer of GM with varying thickness in a volume of 50×50×50 voxels. The two isosurfaces represent the inner and outer surfaces. Depicted as small circles, a number of sample points have been chosen on which the computed thicknesses are illustrated as line segments. The direction of each line segment is the optimal direction that gives the minimum line integral of the probability map. The thickness is demonstrated on the figure by the length of the line segments.

Next, to show the negative consequences of hard segmentation in the presence of noise and partial volume effects, we lowered the resolution of the volume five times by taking the mean value of every 5×5×5 sub-volume and we also added zero-mean Gaussian noise with standard deviation of 0.2 (Fig. 5(b)), and ran the measurement algorithm on it. In addition, we performed hard segmentation on the low-resolution and noisy volume by substituting the probability values less than 0.5 with 0 and other values with 1 (Fig. 5(c)), and reran the measurement algorithm. Using the results of the high-resolution case as the ground truth, the experiments on the low resolution and noisy volumes showed an average error in the estimated thickness of 1.9 voxels in the segmentation-free case and 2.2 voxels when hard segmentation was performed prior to measurement.

Fig. 5.

(a) A 2D slice of the volume presented in Fig. 1. (b) The same slice in the five-time-lower-resolution volume with additive Gaussian noise. (c) Binary classification of the low-resolution volume.

4.2. Real MRI Data

We tested the proposed technique on 44 MRI scans. We consider the probability of each voxel belonging to the GM as a Gaussian distribution on the intensity value of the voxel in the MRI volume. The mean of the Gaussian is the mean value of manually-selected sample voxels in the GM, while the standard deviation is the difference between the manually estimated mean values of GM and WM. We could use more sophisticated soft classification algorithms, such as Partial-Volume Bayesian algorithm (PVB) [17], Probabilistic Partial Volume Classifier (PPVC) [18], and Mixel classifier [19], to further improve the results.

Our dataset includes pairs of scans over a one-year interval from 22 subjects, 9 of which had been diagnosed with Alzheimer’s disease. The mean thickness in the temporal lobe showed an average of 1% decline over a year in the AD patients, and virtually no decline in the normal brains.¹

A 2D slice of a MRI volume is shown in Fig. 6(a) along with its computed thickness map in Fig. 6(b). Since we do not extract the GM, the results also contain thickness values on other parts of the head such as skull, which should be ignored. Fig. 7 illustrates a 3D mapping of the cortical thickness which was visualized using the mrGray software which follows [20].

Fig. 6.

Experimental results on MRI data. All computations have been done in 3D. (a) A slice of the original volume. (b) The thickness map of the same slice. (blue thinner, red thicker)

Fig. 7.

3D mapping of the cortical thickness. (blue thinner, red thicker) such that gaps as narrow as one voxel are detected by the above stopping criteria.

5. CONCLUSIONS

We have presented a new definition of cortical thickness along with an algorithm for computing it. We were motivated by the importance of measuring the thickness of cerebral cortex in the diagnosis of various brain diseases. Our method calculates the thickness on each voxel, by computing all line integrals of the probability map of the gray matter passing through that voxel, and choosing the minimum integral value. Two stopping criteria are taken into consideration to address issues created by narrow sulci. Unlike most of the previous work, we take into account the probability of each voxel belonging to the gray matter layer and do not carry out a hard segmentation prior to measuring the thickness. We have validated the technique with artificial data and presented supporting results for MRI from normal and Alzheimer subjects.