Interjoint coupling effects on muscle contributions to endpoint force and acceleration in a musculoskeletal model of the cat hindlimb

Abstract

The biomechanical principles underlying the organization of muscle activation patterns during standing balance are poorly understood. The goal of this study was to understand the influence of biomechanical inter-joint coupling on endpoint forces and accelerations induced by the activation of individual muscles during postural tasks. We calculated induced endpoint forces and accelerations of 31 muscles in a 7 degree-of-freedom, 3-dimensional model of the cat hindlimb. To test the effects of inter-joint coupling, we systematically immobilized the joints (excluded kinematic degrees-of-freedom) and evaluated how the endpoint force and acceleration directions changed for each muscle in seven different conditions. We hypothesized that altered inter-joint coupling due to joint immobilization of remote joints would substantially change the induced directions of endpoint force and acceleration of individual muscles. Our results show that for most muscles crossing the knee or the hip, joint immobilization altered the endpoint force or acceleration direction by more than 90° in the dorsal and sagittal planes. Induced endpoint forces were typically consistent with behaviorally-observed forces only when the ankle was immobilized. We then activated a proximal muscle simultaneous with an ankle torque of varying magnitude, which demonstrated that the resulting endpoint force or acceleration direction is modulated by the magnitude of the ankle torque. We argue that this simple manipulation can lend insight into the functional effects of co-activating muscles. We conclude that inter-joint coupling may be an essential biomechanical principle underlying the coordination of proximal and distal muscles to produce functional endpoint actions during motor tasks.

Introduction

Standing balance is an important motor task that requires the control of multiple muscles and joints across the body. Because of this mechanical redundancy, no unique muscle activation pattern exists to perform a balance task (Bernstein 1967). However, during standing balance in humans and animals, stereotyped muscle activation patterns representing the coordination of multiple muscles in a multi-jointed limb are observed (Henry et al. 1998; Macpherson 1988b). These results suggest that a highly specific selection system is used by the nervous system to organize muscle activations in the limb, yet the biomechanical principles underlying this organization remain elusive. Our goal is to understand the influence of mechanical inter-joint coupling in a multi-segmented cat hindlimb to gain insights into inter-muscular coordination mechanisms necessary for neural control of posture.

Musculoskeletal modeling and analysis techniques have revealed the strong influence of biomechanical inter-joint coupling on the specific contribution of a muscle force or joint torque to the performance of motor tasks (Zajac and Gordon 1989). Inter-joint coupling can be identified through the analysis of the equations of motion that describe a musculoskeletal system. Non-diagonal terms in the inverse mass matrix define how the force produced by a single muscle generates an acceleration at remote joints that the muscle may not cross (Zajac and Gordon 1989). Such analyses have helped to reconcile the actions of experimental muscle activation patterns that seem to contradict the anatomical descriptions of the muscles, such as hamstrings activity during knee extension in locomotion (Lombard 1903), or extensor activity during pinch (Valero-Cuevas et al. 1998). In special cases, the net torque generated by a muscle at a joint may oppose its anatomical description--gastrocnemius contributes a net knee extension torque in walking despite its flexor moment-arm about the knee (Zajac 1993; Zajac and Gordon 1989). This type of analysis can be extended to examine the contributions of a muscle to the generation of an endpoint force or acceleration using the Jacobian matrix (Kaya et al. 2005; Valero-Cuevas et al. 1998).

The specific purpose of this study was to investigate the extent to which biomechanical inter-joint coupling mechanisms affect the endpoint force and acceleration induced by a single muscle in an anatomically-based musculoskeletal model of the cat hindlimb (Burkholder and Nichols 2004; McKay et al. 2006). Our ultimate goal is to understand the multiple muscle activation patterns purported to generate endpoint forces during postural control (Torres-Oviedo et al. 2006). The present study was further motivated by experimental evidence in the cat hindlimb demonstrating that the endpoint force and torque directions elicited by direct stimulation of individual muscles change depending upon the experimental fixation conditions of the limb (Abelew et al. 1996; Lawrence et al. 1993; Murinas 2003). Similarly, prior modeling work has demonstrated that the number of degrees of freedom in a musculoskeletal model can dramatically alter the effects attributed to individual muscles (Riley et al. 2001; Siegel et al. 1996). Chen (2006) demonstrated that altering the kinematic context of the model, by including immobile joints that are mechanically redundant, alters the inter-joint coupling expressed in the equations of motion. However, in the behaving animal, joint torques that provide postural support to functionally immobilize a joint arise from muscle activation that must be specified by the nervous system. Therefore, to gain insight into neural control mechanisms for muscle coordination, biomechanical inter-joint coupling effects between a muscle and remote, functionally immobilized joints must be considered.

We hypothesized that, because of inter-joint coupling, altering the kinematic status of any joint would change the endpoint forces and accelerations induced by activation of individual muscles. By systematically immobilizing (excluding) joints in our model, we evaluated the effect of altered inter-joint coupling on the induced endpoint force and acceleration directions of 31 muscles. We defined the inter-joint coupling mechanisms to have a dramatic influence if the induced endpoint force and acceleration directions of a single muscle changed by more than 90° as joints were included or eliminated from the model. We defined the inter-joint coupling to have a substantial influence if the induced endpoint force and acceleration direction of a single muscle changed by more than 45°. We demonstrate that inter-joint coupling effects can dramatically alter the resulting endpoint function, and also interpret these findings in terms of neural coordination of muscles.

Methods

Using a three-dimensional model of the cat hindlimb (Burkholder and Nichols 2000; Burkholder and Nichols 2004; McKay et al. 2006), we examined the contributions of 31 muscles (Table 1) to the mechanical actions at the metatarsophalangeal (MTP) joint, which can be considered to be the endpoint of the limb (Kaya et al. 2005; Macpherson 1988a). The distal phalangeal segments contact the ground during stance without slipping, so the MTP-ground interaction was modeled as a gimbal joint. For each muscle, we examined the force generated at the MTP on the ground when a single muscle was activated. We also examined the acceleration of the MTP when it was elevated and did not contact the ground. Both ground contact and elevation conditions occur in postural and locomotor tasks.

Table 1.

Muscle abbreviations

adf	adductor femoris
adl	adductor longus
bfa	biceps femoris anterior
bfp	biceps femoris posterior
edl	extensor digitorum longus
fdl	flexor digitorum longus
fhl	flexor hallucis longus
gmax	gluteus maximus
gmed	gluteus medius
gmin	gluteus minimus
grac	gracilis
lg	lateral gastrocnemius
mg	medial gastrocnemius
pb	peroneus brevis
pec	pectineus
pl	peroneus longus
plan	plantaris
psoas	iliopsoas
pt	peroneus tertius
pyr	pyriformis
qf	quadratus femoris
rf	rectus femoris
sart	sartorius
sm	semimembranosus
sol	soleus
st	semiteninosus
ta	tibialis anterior
tp	tibialis posterior
vi	vastus intermedius
vl	vastus lateralis
vm	vastus medialis

We performed simulations with the hindlimb placed in a postural configuration based on experimentally measured kinematics during an unrestrained postural task (as in McKay et al. 2006; data taken from Torres-Oviedo et al. 2006). The model had 7 kinematic degrees-of-freedom. The pelvis was stationary, the hip joint was modeled as a gimbal, and the knee and ankle were modeled as a pair of revolute joints with non-intersecting, non-orthogonal axes (Burkholder and Nichols 2000; Burkholder and Nichols 2004). In order to isolate the inter-joint coupling effects on muscle forces, we eliminated the contributions of gravity to the system. However, the addition of gravity to the system did not significantly alter our results (data not shown). Under a quasi-static assumption, we assumed joint velocities to be negligible, thus removing the influence of motion-dependent effects. This reduced the equations of motion to a linear system and allowed calculation of the instantaneous acceleration and force (Kaya et al. 2005). We maximally activated each muscle and determined the directions of endpoint force and acceleration. Because our system was linear with respect to muscle activation, these directions are equally valid for all levels of muscle activation.

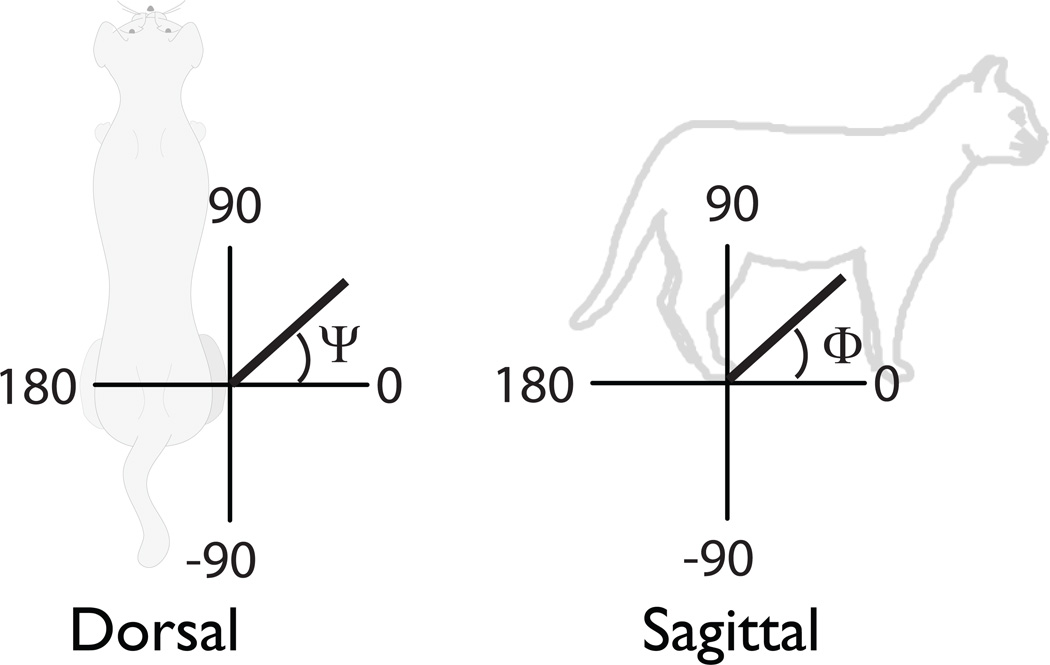
To test the effects of inter-joint coupling on the muscle-induced endpoint accelerations and forces, we systematically immobilized all possible combinations of the hip, knee, and ankle joints (Table 2). For each of the seven conditions, we determined the orientation of the endpoint force and acceleration vectors. We defined ψ and Φ to be the angle in the dorsal and sagittal projections, respectively. Inter-joint coupling was defined to have a “substantial” or “dramatic” influence when the change in ψ or Φ exceeded 45° or 90° across conditions, respectively (Figure 1). A value of NA was reported if all the joints that a muscle crossed were immobilized.

Table 2.

Kinematic conditions

	HIP (H)	KNEE (K)	ANKLE (A)
HKA	free	free	free
HK~	free	free	~
H~A	free	~	free
H~~	free	~	~
~KA	~	free	free
~K~	~	free	~
~~A	~	~	free

~ indicates joint is immobilized

Figure 1. Coordinate system for computing endpoint force and acceleration direction.

(A) dorsal plane angles (Ψ). (B) sagittal plane angles (Φ). These coordinates were used in the reporting of single muscle-induced endpoint accelerations and forces in Tables 3 and 4.

Calculation of muscle-induced endpoint acceleration

The complete equations of motion for the 7 degree-of-freedom model were derived using Autolev software (Online Dynamics, Inc.) in the form:

$$M(\theta )·\ddot{\theta }=R(\theta )F_{\mathit{\text{mus}}}+V(\theta ,\dot{\theta })+G(\theta )$$ (1)

The angular accelerations for each degree of freedom are represented in the 7×1 vector θ̈. M(θ) represents the mass distribution of the system, V (θ,θ̇) is a vector of Coriolis and centripetal terms, and G(θ) represents gravitational contributions. R(θ)F_mus represents the torques produced by muscles at each degree of freedom, where R(θ) is a 7×31 matrix of muscle moment-arms, and F_mus is a 31×1 vector representing individual muscle forces. The state-dependence of M, R, V, and G is omitted in the following sections for clarity.

Under our assumptions of zero-gravity and the no motion-dependent effects, G and V could be eliminated, and the equations of motion reduced to:

$$\ddot{\theta }=M^{-1}[R{F}_{\mathit{\text{mus}}}]$$ (2)

The acceleration vector of the MTP joint was computed from θ̈ through the Jacobian matrix J, as ẍ = Jθ̈ + J̇θ̇ (Sciavicco and Siciliano 2000). In the quasi-static case, this reduced to:

$$ẍ=J\ddot{\theta }$$ (3)

Substitution of (2) in (3) resulted in endpoint acceleration in terms of muscle force:

$$ẍ=J{M}^{-1}[R{F}_{\mathit{\text{mus}}}]$$ (4)

Immobilization of the hip, knee, or ankle joint was accomplished by recalculating M and J of the reduced degree-of-freedom system.

Calculation of muscle-induced endpoint force

Two different computations were used to find endpoint force, depending on the number of degrees of freedom remaining in the system after immobilizing the joints. When one or zero joints were immobilized, there was at least one remaining degree of freedom in the system. In this case, the endpoint force was found by multiplying the instantaneous acceleration in (4) by the “apparent mass”, N, of the endpoint. This is given by N = (JM⁻¹J^T)⁻¹ (Zatsiorsky 2002):

$$F_{ep}={(J{M}^{-1}{J}^T)}^{-1}J{M}^{-1}[R{F}_{\mathit{\text{mus}}}]$$ (5)

When the hip and either the knee or ankle were immobilized, the system was overconstrained. The endpoint force was determined using the static relationship between muscle-induced joint torques and endpoint force with the right-pseudoinverse of the Jacobian transpose:

$$F_{ep}={(J^T)}^{+}R{F}_{\mathit{\text{mus}}}$$ (6)

This method minimized the magnitude of F_ep and the non-contributing reactions due to the indeterminacy (non-trivial null space components).

No force solution existed when the knee and ankle were immobilized. In this case, only the gimbal joints at the hip and MTP were free to move, so only rotation about the axis from the hip to the MTP joint was possible. This motion was independent of the endpoint forces produced and appeared as a singularity in the Jacobian. These cases were not considered and a value of not applicable (NA) was reported.

Co-activation of proximal and distal muscles

To determine the possible effects of multiple, simultaneous, activation of muscles on endpoint forces and accelerations, we investigated the effect of ankle muscle torque generation combined with the activation of individual proximal muscles. First, we maximally activated biceps femoris (BFP) or vastus medialis (VM) with the ankle free and computed the induced acceleration at the ankle. We then activated the BFP or VM simultaneously with ankle torque that canceled 0 to 100% of the induced acceleration at the ankle, and computed the resulting direction of endpoint force and acceleration.

Results

Our results revealed specific effects of inter-joint coupling on endpoint force and acceleration directions induced by the activation of individual muscles throughout the cat hindlimb. Induced directions of endpoint acceleration and force are presented in Tables 3 and 4 for all 31 muscles included in the model. We will discuss the results from a few exemplar muscles in detail.

Table 3.

Sagittal plane directions (Φ) of muscle-induced endpoint actions under various kinematic conditions

	Instantaneous Acceleration							Instantaneous Force
	HKA	HK~	H~A	H~~	~KA	~K~	~~A	HKA	HK~	H~A	H~~	~KA	~K~	~~A
adf	−99	−142	44	169	NA	NA	NA	−91	−125	86	NA	NA	NA	NA
adl	−98	−137	63	169	NA	NA	NA	−91	−125	86	NA	NA	NA	NA
bfa	−93	−140	41	169	NA	NA	NA	−90	−125	86	NA	NA	NA	NA
bfp	45	145	35	169	53	147	NA	79	129	86	NA	83	155	NA
edl	14	159	−2	NA	16	−25	−4	50	−164	80	NA	55	−15	−4
fdl	−174	NA	179	NA	−177	NA	177	−141	NA	−101	NA	−152	NA	177
fhl	−166	NA	178	NA	−164	NA	176	−130	NA	−101	NA	−124	NA	176
gmax	−40	−59	170	166	NA	NA	NA	−76	−107	88	NA	NA	NA	NA
gmed	−29	−42	−179	6	NA	NA	NA	−70	−85	−97	NA	NA	NA	NA
gmin	−26	−35	−176	−6	NA	NA	NA	−68	−60	−96	NA	NA	NA	NA
grac	70	144	53	169	67	144	NA	86	126	86	NA	86	142	NA
lg	−173	131	178	NA	−170	142	176	−152	83	−101	NA	−138	75	176
mg	−171	127	178	NA	−168	145	176	−144	78	−100	NA	−133	150	176
pb	−150	NA	171	NA	−127	NA	171	−116	NA	−97	NA	−98	NA	169
pec	−94	−137	55	169	NA	NA	NA	−90	−125	86	NA	NA	NA	NA
pl	−10	NA	0	NA	−13	NA	−2	9	NA	78	NA	−30	NA	−2
plan	−172	131	178	NA	−169	142	176	−147	83	−101	NA	−135	58	176
psoas	73	24	−160	−10	NA	NA	NA	87	52	−94	NA	NA	NA	NA
pt	−7	NA	0	NA	−11	NA	−2	16	NA	78	NA	−22	NA	−2
pyr	61	80	−10	−11	NA	NA	NA	84	61	−92	NA	NA	NA	NA
qf	167	169	9	171	NA	NA	NA	130	−144	85	NA	NA	NA	NA
rf	−130	−48	−114	−11	−125	−34	NA	−99	−95	−94	NA	−97	−26	NA
sart	112	45	−157	−11	NA	NA	NA	95	56	−94	NA	NA	NA	NA
sm	149	−179	55	169	106	139	NA	111	−135	86	NA	94	9	NA
sol	−166	NA	178	NA	−164	NA	176	−130	NA	−101	NA	−124	NA	176
st	72	144	47	169	70	144	NA	87	126	86	NA	87	137	NA
ta	14	NA	−2	NA	16	NA	−4	50	NA	80	NA	57	NA	−4
tp	175	NA	180	NA	171	NA	178	−160	NA	−102	NA	164	NA	178
vi	−122	−54	NA	NA	−121	−34	NA	−96	−102	NA	NA	−96	−29	NA
vl	−114	−53	NA	NA	−116	−35	NA	−95	−101	NA	NA	−94	−33	NA
vm	−140	−61	NA	NA	−132	−32	NA	−103	−107	NA	NA	−99	−22	NA

Table 4.

Dorsal plane directions (Ψ) of muscle-induced endpoint actions under various kinematic conditions

	Instantaneous Acceleration							Instantaneous Force
	HKA	HK~	H~A	H~~	~KA	~K~	~~A	HKA	HK~	H~A	H~~	~KA	~K~	~~A
adf	−46	−90	105	−85	NA	NA	NA	−100	−90	98	NA	NA	NA	NA
adl	−59	−61	150	−77	NA	NA	NA	−136	−84	101	NA	NA	NA	NA
bfa	−14	−81	103	−82	NA	NA	NA	−5	−88	98	NA	NA	NA	NA
bfp	75	−40	81	−91	78	−98	NA	63	−36	96	NA	62	−151	NA
edl	105	−173	101	NA	105	29	101	104	−170	100	NA	104	16	101
fdl	−154	NA	−154	NA	−151	NA	−154	−157	NA	−145	NA	−154	NA	−156
fhl	−81	NA	−82	NA	−80	NA	−82	−83	NA	−82	NA	−82	NA	−82
gmax	69	7	−158	−8	NA	NA	NA	75	−13	161	NA	NA	NA	NA
gmed	69	10	−158	2	NA	NA	NA	71	2	−140	NA	NA	NA	NA
gmin	71	11	−155	5	NA	NA	NA	73	8	−124	NA	NA	NA	NA
grac	128	−95	129	−80	122	−70	NA	115	−96	99	NA	109	−46	NA
lg	−87	−141	−84	NA	−86	−48	−83	−88	160	−83	NA	−87	2	−84
mg	−76	−65	−76	NA	−75	−81	−76	−76	64	−78	NA	−75	−126	−75
pb	−10	NA	−4	NA	−6	NA	−6	−9	NA	−6	NA	−4	NA	−4
pec	−31	−61	138	−76	NA	NA	NA	−140	−84	100	NA	NA	NA	NA
pl	9	NA	12	NA	13	NA	11	8	NA	17	NA	12	NA	11
plan	−85	−143	−81	NA	−83	−45	−81	−86	163	−81	NA	−85	3	−81
psoas	145	35	−125	67	NA	NA	NA	140	70	−89	NA	NA	NA	NA
pt	10	NA	13	NA	14	NA	12	9	NA	19	NA	13	NA	12
pyr	38	178	37	149	NA	NA	NA	27	142	−27	NA	NA	NA	NA
qf	−91	−165	37	−158	NA	NA	NA	−89	−150	78	NA	NA	NA	NA
rf	−99	146	−19	114	−98	87	NA	−113	−169	−78	NA	−114	32	NA
sart	−143	108	−105	104	NA	NA	NA	−135	94	−85	NA	NA	NA	NA
sm	−150	−110	146	−67	−166	−30	NA	−152	−97	101	NA	−162	8	NA
sol	−82	NA	−82	NA	−81	NA	−82	−83	NA	−82	NA	−83	NA	−83
st	137	−96	131	−68	132	−65	NA	128	−97	100	NA	124	−24	NA
ta	103	NA	104	NA	105	NA	104	103	NA	102	NA	104	NA	104
tp	−169	NA	−166	NA	−165	NA	−167	−170	NA	−160	NA	−166	NA	−167
vi	−87	126	NA	NA	−87	95	NA	−105	−125	NA	NA	−104	44	NA
vl	−69	97	NA	NA	−72	104	NA	−89	−97	NA	NA	−88	84	NA
vm	−111	167	NA	NA	−112	70	NA	−121	−155	NA	NA	−125	24	NA

Proximal muscles

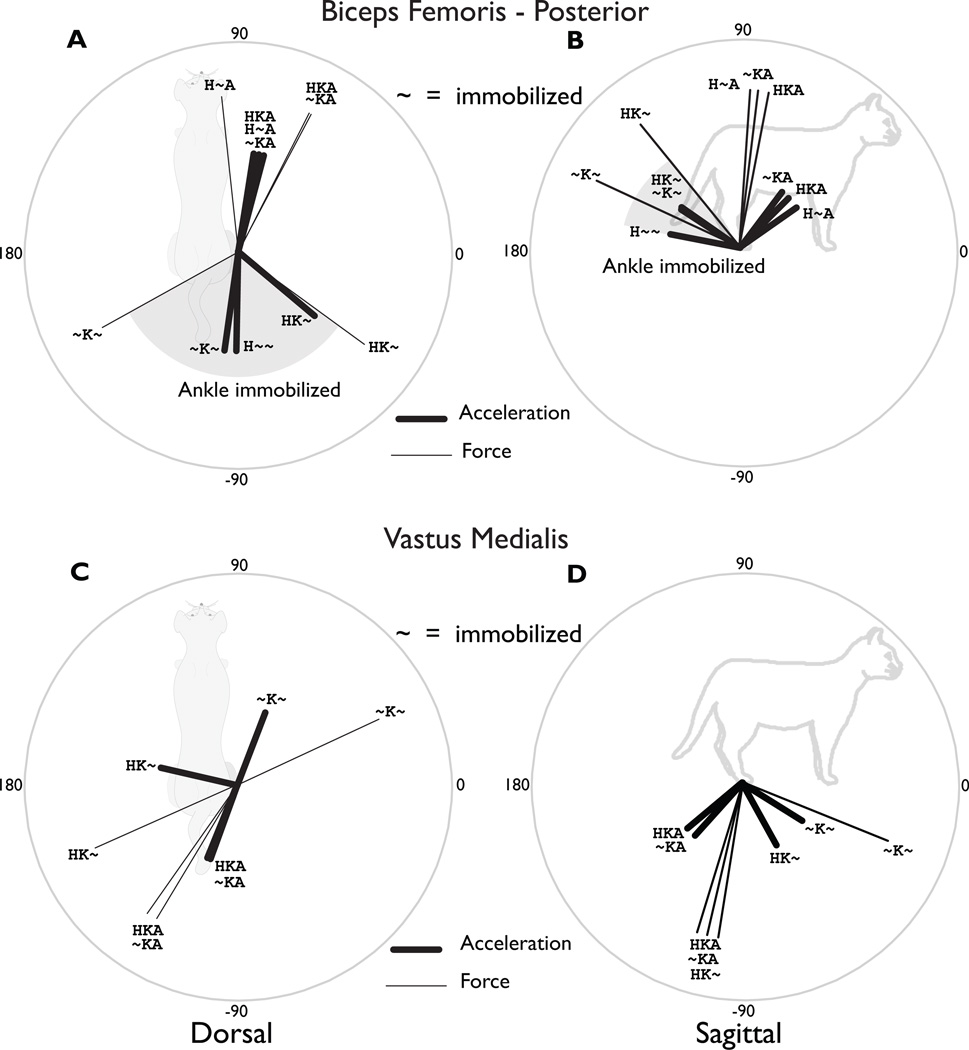
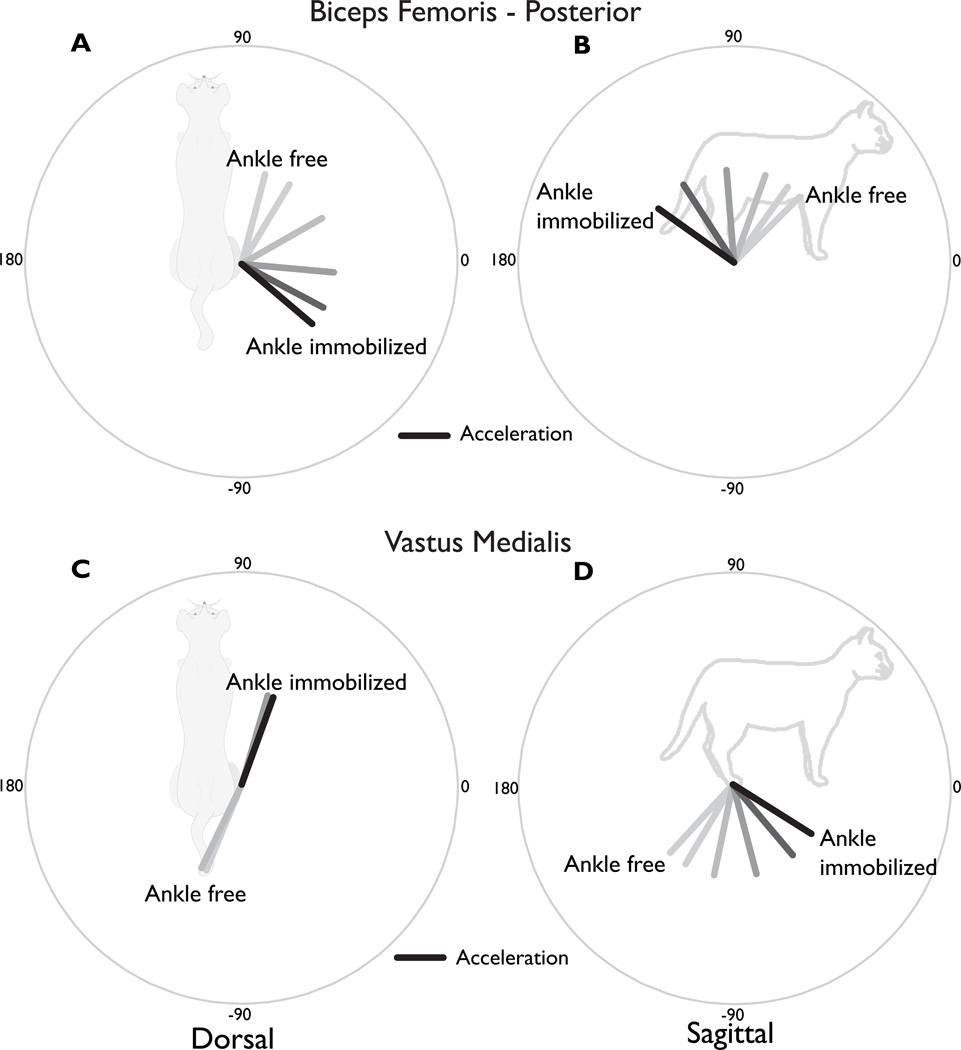
In general, endpoint outputs induced by muscles crossing the hip or knee joints, whether mono- or bi-articular, were dramatically influenced by inter-joint coupling with the ankle. The anterior-posterior direction of the endpoint forces and accelerations for BFP, a hamstring muscle that flexes the knee and extends the hip, and VM, a monoarticular knee extensor, rotated by > 90° in both the dorsal and sagittal planes when the ankle was mobile vs. immobile (Figure 2, compare **A vs. **~ conditions). This demonstrated that BFP significantly accelerated the ankle, which had to be immobilized to generate the dorso-posterior endpoint force direction that was expected based on its anatomical description. Similarly, VM only produced an anterior endpoint force when the ankle was immobilized.

Figure 2. Induced endpoint force and acceleration directions for a representative hamstring and quadriceps muscle.

(A) Dorsal plane endpoint force and acceleration directions induced by BFP. (B) Sagittal plane endpoint force and acceleration directions induced by BFP. The anatomical description of BFP (“hip extensor”/ “knee flexor”) suggests that a posterior and upward force would be generated. Forces and accelerations in these directions were found in all conditions where the ankle was immobilized (gray shaded area). However, when the ankle was free, the forces and accelerations were in the anterior direction. Even when the ankle was immobilized, the medial-lateral direction could vary by more than 90°, depending upon the immobilization of the hip joint (gray shaded area). (C) Dorsal plane directions induced by VM. Only when the hip and ankle were both immobilized did the VM produce a forward-directed endpoint force. It also produced substantial medial/lateral forces and accelerations due to the knee ad/abduction moment arms depending on the mechanical status of the hip joint. (D) Sagittal plane directions induced by VM. The VM force and accelerations were always directed downward, supporting its known role as an anti-gravity muscle. VM and BFP acted as near antagonists in the sagittal plane under all conditions. VI also exhibited this behavior, but not VL. Closer examinations of the moment arms revealed that VI, VM and BFP have similar ratios between the moment arms about the two joints (knee flexion/extension and knee aB/Adduction), whereas VL deviates drastically.

The medial-lateral directions of the endpoint force produced by both the VM and BFP were dramatically influenced by inter-joint coupling with the hip (Figure 2AC, thick lines, compare HK~ vs, ~K~). The inter-joint coupling effects on endpoint acceleration were smaller but still substantial (Figure 2, thin black lines).

Distal muscles

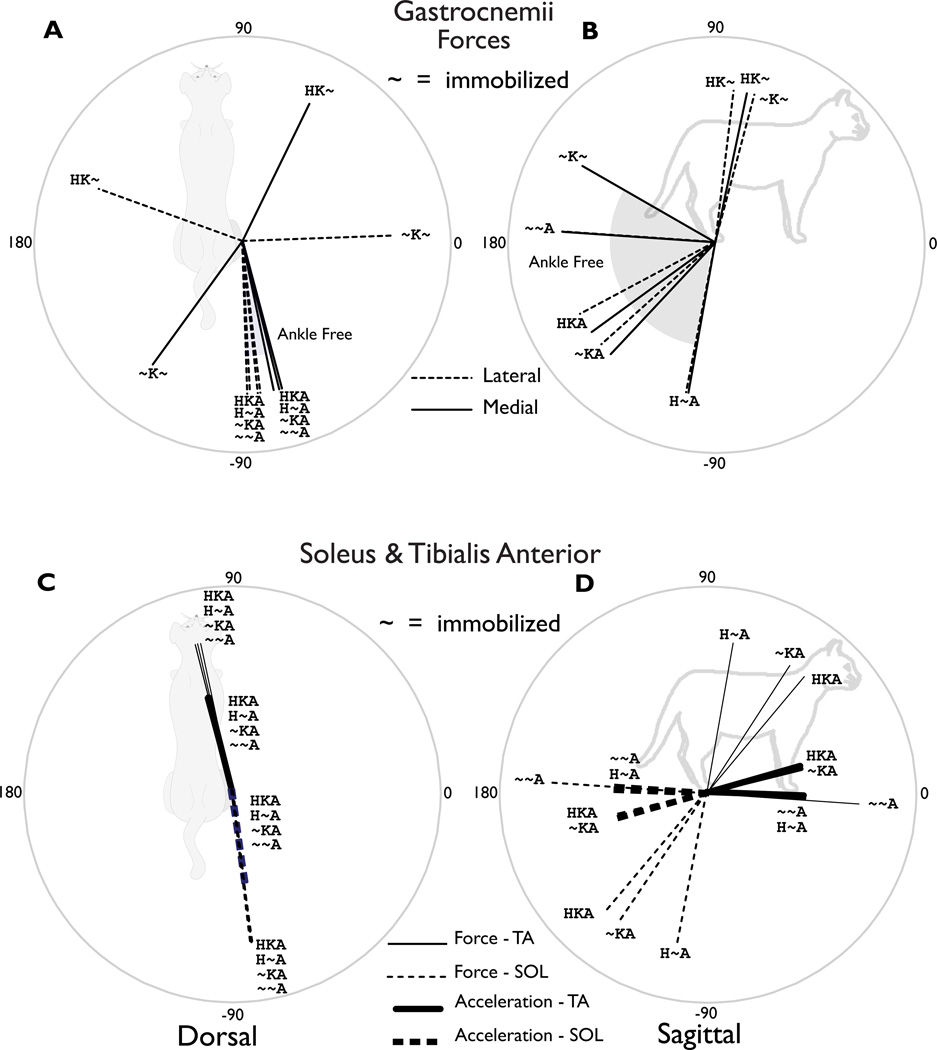
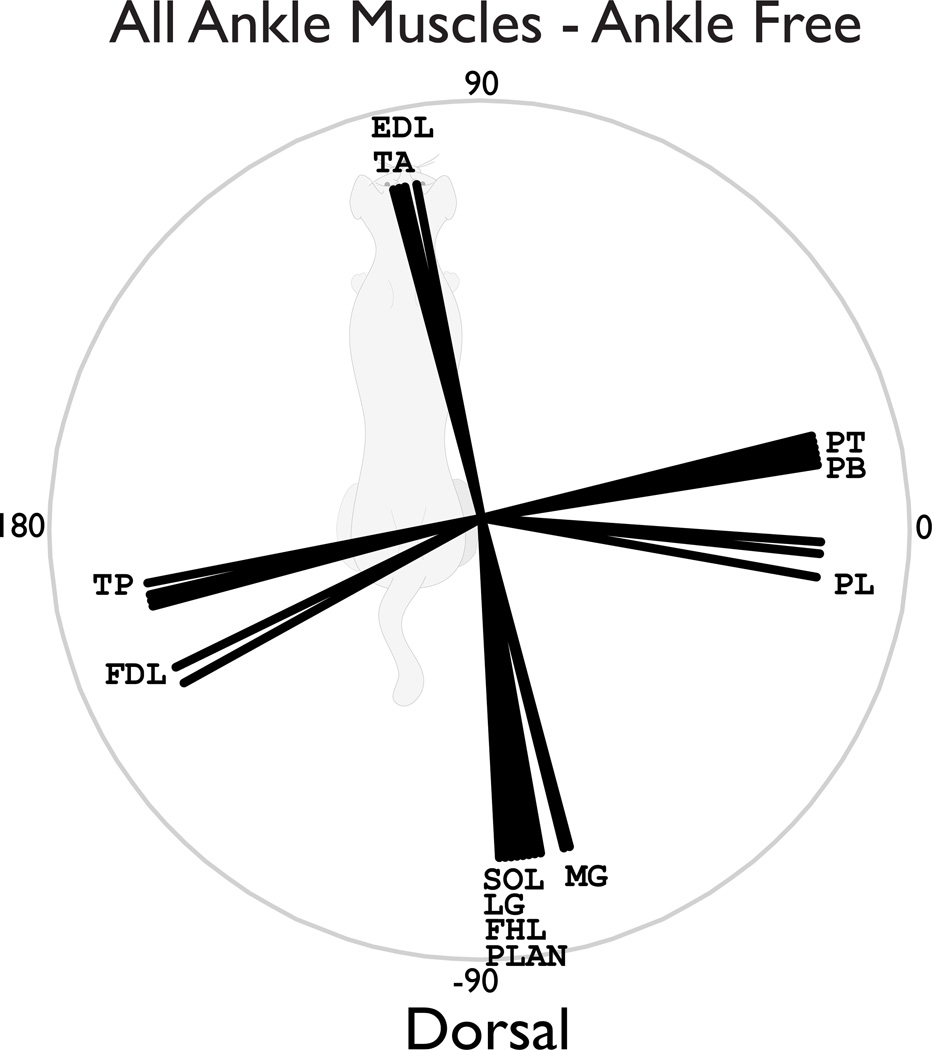
The dorsal plane endpoint force and acceleration directions induced by ankle muscles were relatively unaffected by inter-joint coupling with the hip and knee joints. Dorsal plane forces and accelerations induced by monoarticular ankle muscles, soleus (SOL) and tibialis anterior (TA) were similar regardless of the inclusion of the hip and knee joints (Figure 3C). For both lateral and medial gastrocnemius (LG/MG), dorsal plane forces were similar in all conditions in which the ankle was free (Figure 3A). But, when the ankle was immobilized, the endpoint actions were dramatically influenced by inter-joint coupling with the hip (Figure 3AB, compare HK~ and ~K~). All muscles crossing only the ankle acted consistently in the dorsal plane (Figure 4), consistent with experimental findings (Lawrence et al., 1993).

Figure 3. Induced endpoint force and acceleration directions for bi- and mono-articular muscles crossing the ankle.

(A) Dorsal plane directions induced by MG and LG. When the ankle was free, both the MG and LG generated a posterior and slightly lateral force. These directions were similar whether the hip and knee joints were free or immobilized. However, the aBduction/aDduction action when the ankle was immobilized depended on whether the hip was immobilized. (B) Sagittal plane directions induced by MG and LG. The conditions where the ankle was free exhibited substantial variations in the sagittal plane, but always provided antigravity support and propulsive directed forces. When the ankle was immobilized, the MG actions switched from posterior to anterior. (C) Dorsal plane directions induced by the TA and SOL. The SOL generated posterior and slightly lateral force and accelerations, while the TA generated anterior and slightly medial forces and accelerations. Force and acceleration directions were consistent across all conditions. (D) Sagittal plane directions induced by TA and SOL were relatively consistent across all conditions, with the primary components in the posterior and anterior directions, respectively (thick lines). However, the sagittal plane forces rotated by almost 90° depending on the immobilization of the hip and knee joints (thin lines).

Figure 4. Induced endpoint force directions in the dorsal plane for all ankle muscles under all of the ankle-free conditions.

The EDL and TA consistently induced anterior force directions, while the SOL, MG, LG, FHL, and PLAN consistently induced posterior force directions. The ankle evertors: PL, PT, and PB induced laterally directed endpoint forces, while TP and FDL induced medial force directions. These force direction were similar regardless of whether the knee and/or hip were immobilized.

Distal joint torques modulate proximal muscle actions

The endpoint acceleration directions induced by VM and BFP were modulated by varying the ankle torque between the zero and the torque required to immobilize the ankle joint (Figure 5). As ankle torque increased the endpoint acceleration rotated monotonically between the ankle free and ankle immobilized conditions.

Figure 5. Endpoint acceleration direction induced by hamstrings and quadriceps muscles simultaneous with varying ankle torque.

BFP and VM were maximally activated simultaneously with ankle flexion/extension and ad/abduction torques that canceled 0 to 100% of their induced acceleration at the ankle, respectively. (A) Dorsal plane directions induced by activation of BFP simultaneous with varying ankle torque magnitudes. (B) Sagittal plane directions induced by activation of BFP simultaneous with varying ankle torque magnitudes. All other joints were free. (C) Dorsal plane directions induced by VM and varying ankle torque. (D) Sagittal plane directions induced by VM and varying ankle torque. The hip was immobilized. In both muscles, increasing the ankle torque rotated the endpoint acceleration within the plane subtended by the ankle immobilized and ankle free conditions shown in Figure 2. Total ankle torque levels required to functionally immobilize the joint were relatively low, never greater than 20% of the muscle torques produced by VM or BFP. These results demonstrate how multi-muscle coordination or even the contributions of passive joint torques can dramatically alter the endpoint action of the limb when muscles are activated.

Discussion

The purpose of this study was to investigate the effects of biomechanical inter-joint coupling on the endpoint forces and accelerations induced by single muscles. We demonstrated that the directions of the force and acceleration induced by the activation of a single muscle could vary by up to 180° when joints throughout the limb, both proximal and distal to the muscle activated, were immobilized. These findings suggest how variations in experimental restraints, passive muscle and tissue forces, or muscle activity at remote joints could contribute to inconsistent force directions when single muscles are stimulated in vivo (Abelew et al. 1996; Lawrence et al. 1993; Murinas 2003). In the context of the neural control of muscles, our findings illustrate specific interactions between individual muscles and functionally immobilized joints that support the need for neural mechanisms that couple the control of multiple muscles. Inter-joint coupling may therefore be an important biomechanical principle underlying the coordination of muscles to produce functional endpoint actions during motor tasks. We conclude that our results can provide insight for understanding specific neural mechanisms that coordinate multiple muscles, such as spinal reflexes and muscle synergies.

The substantial dependence of muscle-induced endpoint actions on joint mechanical status was a robust finding that would not be significantly altered by adding more complexity to the model. We studied instantaneous, quasi-static, inter-joint interactions during single muscle force production. We found that the model geometry, embodied in the mass matrix, M(θ) and the Jacobian transformation, J(θ) was sufficient to introduce substantial inter-joint interactions. Our results therefore represent a lower bound of the effects of inter-joint coupling, as the simulation of a dynamic task or the inclusion of gravity would only introduce more sources of inter-joint coupling. However, we predict these differences would be small, as muscle activations patterns from quasi-static and dynamic simulations are similar in simulations of locomotion (Anderson et al. 2004; Kaya et al. 2005). Moreover, our results were largely independent on the inertial distribution of the limb; interchanging the mass of the foot and the thigh did not substantially alter our results.

This work supports inter-joint coupling as an essential biomechanical principle underlying the coordination of proximal and distal muscles in the cat hindlimb to produce functional endpoint actions during motor tasks. The endpoint force or acceleration induced by BFP activation rotated by nearly 180° in a plane from an anterior to a posterior direction as increasing levels of ankle torque were simultaneously activated. The magnitude of ankle torque modulated the direction of endpoint force between the endpoint force induced by BFP in the ankle free (HKA) and immobilized conditions (HK~). Behaviorally, our results may explain how BFP could contribute to the changing endpoint actions during the transition from stance to swing in locomotion (Engberg and Lundberg 1969). Ankle muscle fascicles undergo little or no length change during the stance phase of locomotion (Biewener et al. 1998; Daley and Biewener 2003; Fukunaga et al. 2001; Lichtwark et al. 2007), serving to functionally immobilize the ankle. The combination of ankle muscle and BFP activity would produce a posterior-directed propulsive force at the ground. Towards the end of stance phase, however, ankle muscle activity declines into toe-off; BFP activation in the early swing phase would produce an anterior acceleration of the toe. Similarly, modeling studies have demonstrated that a synergistic activation between hip and ankle muscles is necessary for propulsion in human pedaling (Fregly and Zajac 1996; Raasch and Zajac 1999; Raasch et al. 1997) and walking (Zajac 2002; Zajac et al. 2003).

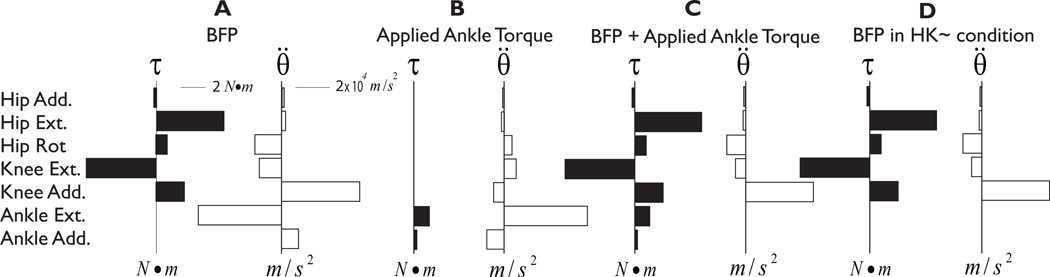
In the context of neural control strategies for muscle coordination, the effect of joint torques that functionally immobilize a joint must be considered whether they are explicity or implicitly included in the model. A torque that provides postural support at a joint cancel the accelerations that would be induced at that joint by other muscles (Chen 2006). However, this torque itself also induces accelerations at non-immobilized joints, altering the endpoint action of the limb. For example, BFP activation produced torque around the axes of rotation at the hip and the knee (Figure 6A, black). Through inter-joint coupling via the mass matrix, these torques induced accelerations at all joints—hip, knee, and ankle (Figure 6A, white). Direct application of torque at the ankle generated ankle accelerations that were equal and opposite to those induced by BFP activation as well as accelerations at the knee and hip (Figure 6B). Functional immobilization of the ankle joint occurred through simultaneous BFP activation and ankle torque application (Figure 6C). The resulting joint accelerations (Figure 6C, white) were identical to the case where the ankle was excluded from the equations of motion (Figure 6D, white). Although in the latter case, the necessary muscular (or passive) torque at the ankle required were not explicitly expressed in the equations of motion, their contribution cannot be ignored in the context of neural control of muscles.

Figure 6. Joint torques and their corresponding induced accelerations in all 7 degrees of freedom for four conditions.

(A) BFP in the all joints free (HKA) condition. BFP induces only relatively small accelerations at the proximal joints, and large accelerations at the ankle. (B) Torque applied at the ankle. The magnitude of the ankle torques exactly cancel the induced ankle accelerations of BFP. The ankle torques also induce small accelerations at the proximal joints. (C) Combined activation of BFP and ankle torque. (D) BFP in the ankle immobilized (HK~) condition. The net accelerations in C and D are identical, but only the former reveals the necessary applied ankle torque and the accelerations that it induces.

Our study revealed specific inter-joint coupling effects that may provide further insight into neural mechanisms necessary to coordinate multiple muscles that produce seemingly simple limb functions (Full and Koditschek 1999; Ting 2007). By immobilizing joints, we demonstrated the degree to which limb function could change when muscles spanning the multi-jointed limb are not coordinated. Our approach may help resolve how and why the nervous system collapses the dimension of the musculoskeletal system such that it can be described by low-dimensional models, like an inverted pendulum (Chen 2006). Immobilization of the joint can thus be used as a proxy for understanding how activation of muscles at that joint could affect the function of the limb. Our results provide a “mapping between the interpretations drawn from simple and complex models” (Chen 2006) and delimit the range of possible endpoint actions through modulation of torque at the immobilized joint. These results can guide studies using the full 3-dimensional musculoskeletal model of the cat hindlimb to determine which muscles should be co-activated to produce a desired limb function, although this step is nontrivial. Using this approach, the biomechanical principles underlying the specific organization of spinal reflexes (Bonasera and Nichols 1996; Wilmink and Nichols 2003), neural circuits for locomotion (Drew et al. 2002; Jankowska et al. 2005; McCrea 2001), or muscle synergy organization for movement (d'Avella et al. 2003; Ivanenko et al. 2004; Ting and Macpherson 2005; Tresch et al. 1999) may be revealed.