Applicability of Estimating GFR Equations in Pediatric Patients: Comparison to a Measured GFR by Iohexol Clearance

Abstract

Estimates of glomerular filtration rate (eGFR) have become popular in clinical medicine as an alternative to measuring GFR (mGFR) but there are few studies comparing them in clinical practice. We determined mGFR by iohexol clearance in 81 consecutive children in routine practice and calculated eGFR from 14 standard equations using serum creatinine, cystatin C, and urea nitrogen that were collected at the time of the mGFR procedure. Non-parametric Wilcoxon test, Spearman Correlation, Bland–Altman analysis, bias (median difference) and accuracy (P₁₅, P₃₀) were used to compare mGFR to eGFR. For the entire study group, the mGFR was 77.9±38.8mL/min/1.73 m². Eight of the 14 estimating equations demonstrated values without a significant difference from the mGFR value and demonstrated a lower bias in Bland–Altman analysis. Three of these eight equations based on a combination of creatinine and cystatin C, (Schwartz et al. 2009, 2012; Chehade et al.), had the highest accuracy with approximately 60% of P₁₅ and 80% of P₃₀. In 10 patients with a single kidney, seven with kidney transplant, and 11 additional children with short stature, values of the three equations had low bias and no significant difference when compared with mGFR. In conclusion, the three equations that employed cystatin C, creatinine, and growth parameters performed in a superior manner over univariate equations based on either creatinine or cystatin C, and also had good applicability in specific pediatric patients with single kidneys, those with a kidney transplant, and/or short stature. Thus, we suggest that eGFR calculations in pediatric clinical practice employ only a multivariate equation.

INTRODUCTION

The glomerular filtration rate (GFR) is considered the best overall index of kidney function in health and disease. Thus, accurate measurement of GFR (mGFR) plays an important role in the clinical management of various diseases; both intrinsic to the kidney and with other diseases in which altered kidney function may influence the use of therapeutic agents, for example. More than 80% of clinical laboratories now report an estimated GFR (eGFR) when serum creatinine (Scr) is measured.¹ However, in recent years there are many studies that have shown that eGFR equations employing additional markers of filtration, such as cystatin C, are superior to conventional equations based on Scr alone.^2,3 Those equations were tested mainly in adult chronic kidney disease (CKD) patients, while only a few studies have evaluated performance of eGFR equations in pediatric CKD outside of a research setting.

The most popular equation currently used in children is the 2009 Schwartz formula, which is based on Scr.⁴ Despite standardization of Scr assays, eGFR remains relatively imprecise owing to variation in non-GFR determinants of Scr.⁵ This equation does not differentiate between gender, despite the known gender difference in linear height and Scr concentrations, beginning in early adolescence. Thus, such anthropometric disparities result in considerable variation in muscle mass and may be a dominant factor in eGFR differences.⁶ Some studies in children have demonstrated that the inclusion of serum cystatin C (Scys) in the estimating equation increases the correlation with the mGFR than Scr, alone.^7,8

We compared 14 published eGFR equations against a gold standard mathematical model for mGFR from iohexol blood clearance,⁹ in order to guide clinicians in optimal eGFR determinations in a diverse group of children with possible kidney dysfunction. We hypothesized that the complex equation using gender, height, Scr, and Scys, may be highly predictive of mGFR.

METHODS

Study design and data

This study was conducted at the Ann & Robert H. Lurie Children's Hospital of Chicago, USA (Lurie Children’s), from November 2012 to January 2014. We used a single cross-sectional data set from 81 consecutive outpatients in which iohexol-based mGFR was calculated, based on the model used by Schwartz, et al. from the CKiD study,⁹ and for which we are a participating center. At the time of the patient’s mGFR study, additional data collected included: Scr, Scys, blood Urea Nitrogen (BUN), visit date, anthropometrics, and demographics. We calculated height-for-age Z score according to the US CDC standards of recumbent length z-scores, birth to 24 months, and stature z-scores, 2 to 20 years in centimeters, by gender and age.¹⁰ Fourteen eGFR equations were included and their respective values for 81 patients were compared against the mGFRs. This retrospective study was approved by the Lurie Children’s Hospital of Chicago Institutional Review Board.

Laboratory Analyses

We measured iohexol in serum by a validated liquid chromatography tandem mass spectroscopy (LC-MS/MS) method from four serial blood samples collected at 10, 30, 120, and 300 minutes post-iohexol injection with the clearance calculated using the concentration of iohexol as a function of time in two curves (fast and slow plasma disappearance).⁹ Serum creatinine was measured using an IDMS-traceable enzymatic method on the Roche Cobas 6000, following the FDA cleared procedure for Roche/Hitachi Cobas C systems. Blood urea nitrogen (BUN) and cystatin C were analyzed in serum on the Roche Cobas 6000, following the FDA cleared procedures for Roche/Hitachi Cobas C systems. The cystatin C method on the Roche Cobas 6000 employs an automated particle-enhanced immunoturbidimetric assay (PETIA).

eGFR calculation formulae

A total of 14 eGFR equations were selected to calculate eGFR (Table 1). These include five equations based on Scr alone, five based on Scys alone, and four based on combinations of both. The method of testing Scys was particle-enhanced nephelometric immunoassay (PENIA) in Filler et al., Bouvet et al., Chehade et al. and Schwartz et al. (2012) equations. The others used the PETIA method. The method of testing Scr was Jaffe method in Gao et al., Bouvet et al., and Chehade et al. equations. The others used the enzymatic assay.

Table 1.

Published estimated GFR equations in children

Equation name	Equation
Serum creatinine based
Schwartz et al.4 (ScrEq2009)	41.3Ht/Scr
Schwartz et al.11 (ScrEq2012)	42.3(Ht/Scr)0.79
Gao et al.12	68(Ht/Scr)-8(Ht/Scr)2+0.48age–21.53 in males or 25.68 in females
Pottel et al.13	107.3/(Scr/Q), Q=0.0270×Age+0.2329
Hoster et al.6	107.3/(Scr/Q), Q = 3.94 −13.4L +17.6L2 − 9.84L3+ 2.04L4
Serum cystatin C based
Bökenkamp et al.14	162/Scys)-30
Grubb et al.15	84.69Scys−1.68×1.384 for age<14 years
Filler et al.16	91.62(1/Scys)1.123
Schwartz et al.4 (ScysEq2009)	41.9(1.8/Scys)0.777
Schwartz et al.11 (ScysEq2012)	70.69Scys−0.931
Serum creatinine and cystatin C based
Bouvet et al.17	63.2(1.2/Scys)0.56 (1.09/Scr)0.35 (weight/45)0.3 (age/14)0.4
Schwartz et al.4 (ScrcysEq2009)	39.1 (Ht/Scr)0.516(1.8/Scys)0.294(30/BUN)0.1691.099male(ht/1.4)0.188
Schwartz et al.11 (ScrcysEq2012)	39.8 (Ht/Scr)0.456(1.8/Scys)0.418(30/BUN)0.0791.076male(ht/1.4)0.179
Chehade et al.18	42(Ht/Scr)-4(Ht/Scr)2−14.5Scys+0.69age+18.25 for female or 21.88 for male

Ht or L, height in m; Scr, serum creatinine in mg/dL; Scys, serum cystatin C in mg/L; BUN, blood urea nitrogen in mg/dl; age in years; weight in kg.

Statistical analyses

Continuous data were described as mean ± SD, median and interquartile range (IQR), and categorical variables were expressed as cases or percentages. Differences between eGFR and mGFR were analyzed by the non-parametric Wilcoxon test, since the data were not normally distributed. Correlations between eGFR and mGFR were established based on the Spearman correlation. Bland–Altman analysis was employed to compare eGFR with mGFR using the average of the overall mean ± SD and the precision was represented as the width between the 95% limits of agreement (LOA), wherein, the smaller the LOA, the greater the precision. Regression analysis and Scatterplot analysis were employed to compare the agreement between eGFR and mGFR. Three parameters used to assess the performance of eGFR equations relative to mGFR were:

• Bias (median difference between mGFR and eGFR) and Absolute Bias (median difference in |mGFR–eGFR|;

• Precision (IQR: P75-P25); and

• Accuracy [percentage of estimates that differed within 15% of mGFR (P₁₅) and 30% of mGFR (P₃₀)]. We selected p <0.05 a priori to be statistically significant. Statistical analyses were completed using SPSS (SPSS, Inc., Chicago, IL, USA) and Medcalc (Medcalc Software, Mariekerke, Belgium).

RESULTS

Demographic and clinical characteristics

Characteristics of interest for our study population of 81 children and adolescents are shown in Table 2. The minimum and maximum ages of the participants were 0.70 and 20 years old, respectively. There were 10 patients with single kidney, and seven with a kidney transplant. The primary diseases that resulted in a kidney transplant were nephropathic cystinosis (4 cases), kidney dysplasia (2 cases), and autosomal recessive polycystic kidney disease (1 case). Five patients with Wilms tumor, one with mesoblastic nephroma, and one with Langer Giedon Syndrome, had single native kidneys after a unilateral nephrectomy performed for clinical care.

Table 2.

Characteristics of study participants

Variable	Value
mGFR test, n	81
Age, years
Mean±SD	12.60±5.14
Median (P25, P75)	14.29 (8.96, 16.88)
Gender, n (%)
Female	37 (45.7)
Male	44 (54.3)
Ethnicity/Race, n (%)
White	47 (58.0)
Hispanic	22 (27.2)
Black	10 (12.3)
Asian	2 (2.5)
Weight (kg), median (P25, P75)	46.30 (29.05, 60.40)
Height (cm)
Median (P25, P75)	152.30 (124.70, 167.60)
Z score	−0.77±1.97
Single kidney, n (%)
Native kidney	3 (3.7)
After nephrectomy	7 (8.6)
Two kidneys, n (%)	64 (79.0)
Kidney transplantation, n (%)	7 (8.6)
Primary kidney disease, n(%)
Congenital anomalies of the kidney and urinary tract (CAKUT)	16 (19.7)
Glomerular disease	6 (7.4)
Tubulointerstitial disease	5 (6.2)
Solid organ transplantation other than kidney	17 (21.0)
Metabolic disease	23 (28.4)
Other	14 (17.3)

Glomerulopathies includes six patients with microscopic polyangiitis, congenital nephrotic syndrome, thin basement membrane, FSGS, Kawasaki Disease, and p-anca positive microscopic polyangiitis, respectively. Tubulointerstitial disease includes five patients with renal tubular acidosis, type I, Fanconi syndrome, interstitial nephritis, Bartter Syndrome, and acute tubular necrosis, respectively. Solid organ transplantation other than kidney includes patients with a transplant of the liver (13), heart (1), lung (2), and bone marrow (1). Metabolic disease includes Cystinosis (5), nephrolithiasis or hypercalciuria (12), and six patients with Hashimoto's thyroiditis, Lennox-Gastaut syndrome, Tuberous Sclerosis, Mainzer-Saldino syndrome, Langer Giedon Syndrome, methylmalonic academia, respectively. ‘Other’ are five patients with Wilms tumor, three with renovascular disease, four with mesoblastic nephroma, STEC-HUS and Diabetes Mellitus, autosomal recessive polycystic kidney disease, and neurofibromatosis, respectively, and two with unknown etiology of CKD.

Analysis of the differences between the eGFR and mGFR values

The values of mGFR and the 14 corresponding eGFR values are shown in Table 3. The mean mGFR for the 81 subjects was 77.9±38.8 mL/min/1.73m². The median and IQR (P₂₅, P₇₅) were 77.8, 52.0, and 96.0 mL/min/1.73m², respectively. The numbers of patients with mGFR ≥90, 60–89, 30–59, and <30 mL/min/1.73 m² were 25, 31, 17, and 8, respectively. The calculated eGFR values were highly correlated (P <0.001) with the mGFR value. However, three equations based on Scr alone, one based on Scys, and all four based on combinations of both demonstrated no significant difference from the mGFR values (p >0.05). These same eight equations also had lower bias compared to the others in the Bland–Altman analysis.

Table 3.

Overall limits of agreement between eGFR and mGFR

	Mean±SD	Wilcoxon test		Correlation analysis		Bland-Altman analysis
		Z	P	r	P	Bias	95%LOA
mGFR	77.9±38.8	-	-	-	-	-	-
Schwartz et al. (ScrEq09)	83.4±48.5	−1.476	0.14	0.77	<0.001	−5.5±26.0	−56.5; 45.5
Schwartz et al. (ScrEq12)	71.2±30.7	−2.229	0.03	0.77	<0.001	5.7±20.0	−33.5; 44.9
Gao et al.	76.4±36.8	−1.490	0.14	0.73	<0.001	1.5±50.0	−96.5; 99.5
Pottel et al.	85.1±44.5	−1.923	0.054	0.72	<0.001	−7.2±26.4	−58.9; 44.5
Hoster et al.	84.9±46.2	−2.281	0.02	0.78	<0.001	−7.0±24.1	−54.2; 40.2
Bokenkamp et al.	126.5±64.0	−7.573	0.00	0.81	<0.001	−48.7±40.4	−127.9; 30.5
Grubb et al.	111.8±81.3	−5.412	0.00	0.80	<0.001	−33.9±54.6	−140.9; 73.1
Filler et al.	94.1±42.6	−5.605	0.00	0.84	<0.001	−16.3±24.3	−63.9; 31.3
Schwartz et al. (ScysEq09)	65.9±21.1	−3.962	0.00	0.84	<0.001	12.0±24. 6	−36.2; 60.2
Schwartz et al. (ScysEq12)	71.2±27.0	−1.937	0.053	0.84	<0.001	6.6±22.5	−37.5; 50.7
Bouvet et al.	73.9±31.1	−0.506	0.61	0.73	<0.001	3.9±28.3	−51.6; 59.4
Schwartz et al. (ScrcysEq09)	77.9±32.3	−0.445	0.66	0.87	<0.001	−0.0±16.5	−32.3; 32.3
Schwartz et al. (ScrcysEq12)	76.2±30.8	−0.186	0.85	0.88	<0.001	1.7±16.6	−30.8; 34.2
Chehade et al.	74.4±28.1	−0.308	0.76	0.79	<0.001	3.4±31.2	−57.8; 64.6

Note: GFR unit is mL/min/1.73 m²; 95% LOA is the 95% limits of agreement; Z is the value of the Wilcoxon test between eGFR and mGFR; r is the Spearman’s Correlation Coefficient between eGFR and mGFR. The shaded rows are equations for which there is no significant difference between eGFR and mGFR in Wilcoxon test.

Consistency analysis of the eGFR and mGFR values

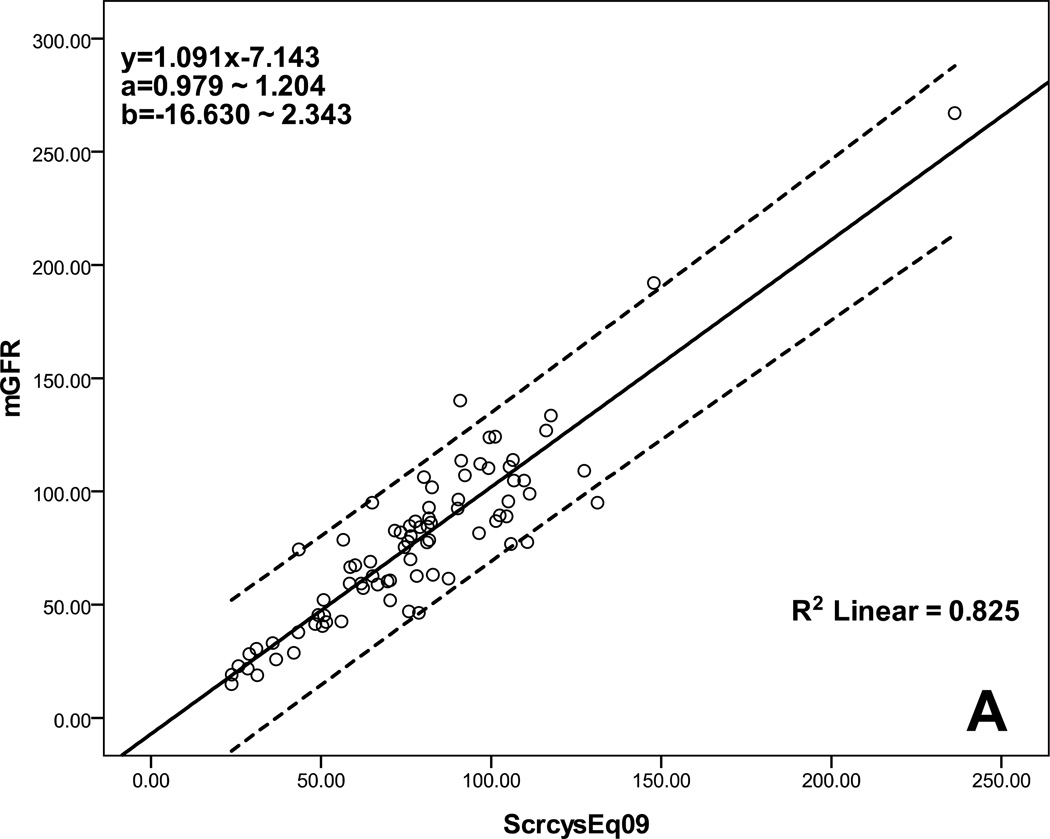
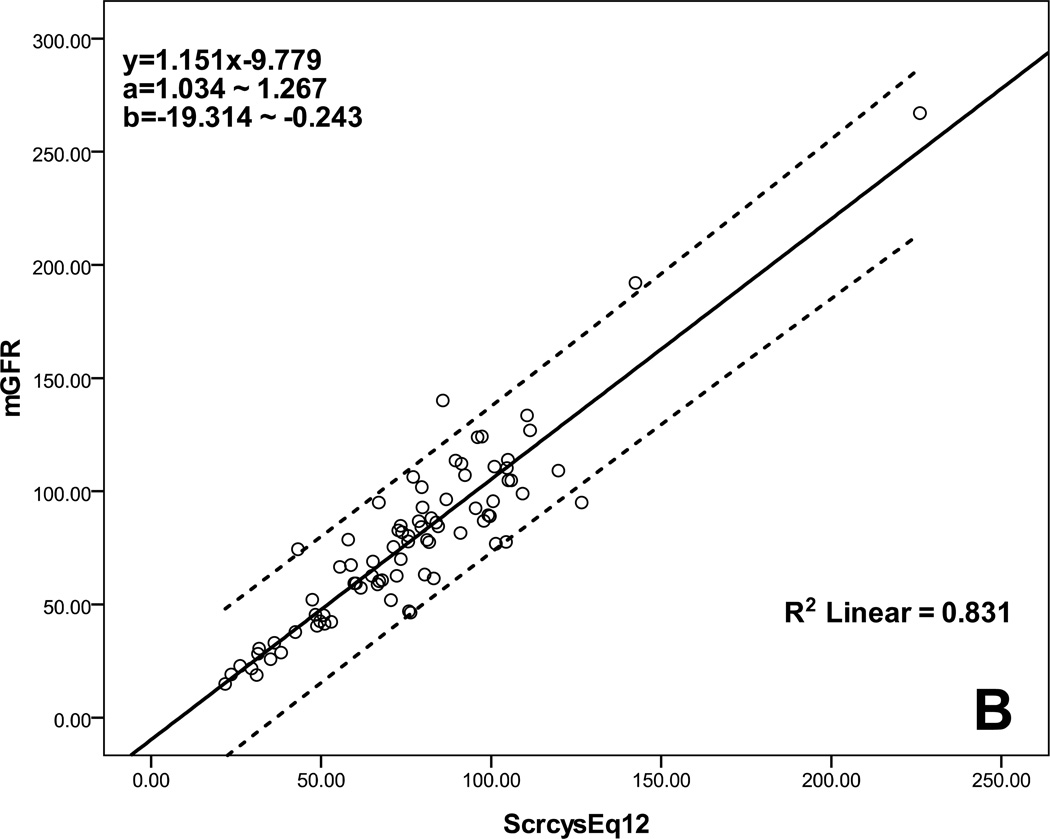
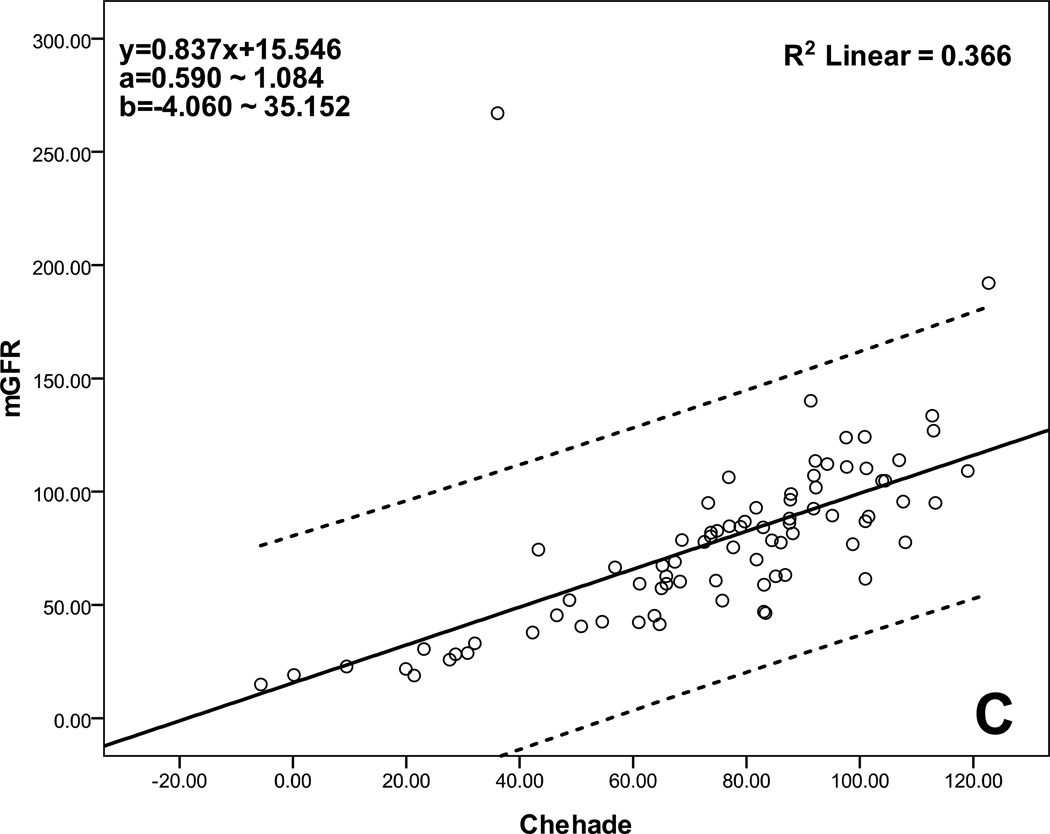
Table 4 lists the performance of the selected eight equations determined by calculating accuracy, bias, and precision. All had low bias, but three multivariate equations based on a combination of Scr and Scys, Schwartz et al. (2009, 2012) and Chehade et al., had the highest accuracy with approximately 60% of P₁₅ and 80% of P₃₀. Figure 1 shows the agreement between eGFR and mGFR for these three multivariate equations. There was good agreement across the GFR range from low to high, especially for equations of Schwartz et al. (2009, 2012).

Table 4.

Performance of the eight equations in the overall sample

	Bias Median	Precision IQR (P25, P75)	Absolute bias	Accuracy (%)
				P15	P30
Schwartz et al. (ScrEq09)	−3.1	27.1 (−16.6, 10.5)	14.0	39.5	65.4
Gao et al.	−2.9	25.4(−16.7, 8.7)	11.5	51.9	71.6
Pottel et al.	−3.1	27.2(−18.5, 8.7)	13.9	44.4	64.2
Schwartz et al. (ScysEq12)	1.9	19.6 (−5.0, 14.6)	8.6	53.1	79.0
Bouvet et al.	−0.2	30.1 (−14.0, 16.1)	15.2	34.6	64.2
Schwartz et al. (ScrcysEq09)	−2.5	18.4(−9.8, 8.6)	9.3	58.0	79.0
Schwartz et al. (ScrcysEq12)	−2.3	18.6 (−8.8, 9.8)	9.2	61.7	82.7
Chehade et al.	0.7	19.9 (−10.1, 9.8)	9.9	59.3	77.8

Note: bias was the median difference between eGFR and mGFR (mGFR–eGFR); absolute bias was |(mGFR–eGFR)|; accuracy was calculated as the percentage of estimates of eGFR that differed from the mGFR within 15% (P₁₅) and within 30% (P₃₀). The shaded rows are the equations with the highest accuracy.

Figure 1.

Scatterplot regression to analyze and compare eGFR with mGFR. A: Schwartz et al. (ScrcysEq2009) eGFR equation explains 82.5% of the variability of mGFR, B: Schwartz et al. (ScrcysEq2012) eGFR equation explains 83.1% of the variability of mGFR, C: Chehade et al. eGFR equation explains 36.6% of the variability of mGFR; a: 95% CI for the slope, b: 95% CI for the intercept; CI: confidence interval; all P<0.001.

Analysis of the differences between the multivariate equation and mGFR in patients with single kidney, kidney transplant, or short stature

Based on the results above, the three multivariate equations had the best performance among all eGFR equations. We analyzed their applicability in 10 patients with a single kidney, seven with kidney transplant, and 11 short stature patients with height Z-score ≤−2.5. From the Wilcoxon test, there was no significant difference between eGFR and mGFR in patients with single kidney, kidney transplant, and/or short stature (p≥0.05). The values of the three equations also showed acceptable bias and precision in the Bland-Altman analysis.

DISCUSSION

Accurate assessment of GFR is essential for interpreting the symptoms, signs, and laboratory abnormalities that may indicate kidney disease, for monitoring side effects of therapeutic drug use, and for detecting and managing CKD and assessing its prognosis, among others. The gold standard for measuring GFR was inulin clearance for many years, and was performed by loading and continuously infusing inulin and collecting timed urine samples from an indwelling bladder catheter; a procedure very cumbersome and difficult to perform in children.¹⁹ Iohexol has been used as a satisfactory marker of GFR in adults and children, based on its ready availability, exclusive elimination by the kidneys without further metabolism, and good agreement with inulin and 51Cr-EDTA clearances. Indeed, iohexol has been heralded as the new gold standard measure of GFR, and especially in children.^20,21

In the current study, eight of the 14 eGFR equations evaluated demonstrated better performance compared to mGFR than the others. These eight were a mix of equations based on Scr only (3/5), Scys only (1/5) and a combination of both Scr and Scys (4/4). Further analysis demonstrated that only three specific multivariate equations had better performance than the univariate ones. Those three equations all included Scr, Scys, gender, and a statural growth parameter. When used in unique patient populations (i.e., those with single kidney, kidney transplant, and/or short stature), the three equations demonstrated high agreement with mGFR.

There are only a few studies that have compared the applicability of eGFR equations based on different included variables in children. The performance of Scr-based equations were studied in several papers.^6,12,13 The bedside CKiD formula, Schwartz et al. (2009), is the most widely used formula for eGFR in children.⁴ However it was derived from data obtained in children with CKD mGFR between 15–75 ml/min×1.73m². Several recent studies validated new Scr-based formulae in children, which all outperformed the bedside CKiD formula compared to mGFR.^6,12,13 Sharma et al.²² studied several Scys-based equations and found the accuracy of various Scys equations varied with the actual mGFR. In a study focused on children with a solitary functioning kidney, the authors employed six eGFR equations based on Scr, Scys, and a combination of both variables, and found the combined formula, Schwartz et al. (2012), had superior precision.²³ For clinical practice, we need to identify the most accurate eGFR equation that can be applied to a diverse pediatric patient population. In adults, there are several, large studies capable of validating the accuracy of eGFR equations. One recent example, the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI), developed an equation based on Scr in 2009 and two others in 2012 (based on Scys alone and combined creatinine–cystatin C). They tested the three equations in very diverse populations with CKD and normal kidney function, and found the combined creatinine–cystatin C equation performed better than equations based on either of both markers alone when compared with mGFR.² The combined equation is commonly employed in adult hospitals as the method for eGFR in adults, replacing the popular MDRD eGFR.^24,25 Similarly to others in adults and children, we found that all three combined (Scr with Scys) equations outperformed equations that used the Scr or Scys, alone.

Cystatin C is freely filtered and catabolized in the proximal tubules, without being secreted. Unlike Scr, it does not depend on gender or muscle mass, and does not change with age between 1–50 years old.²⁶ Scys increases earlier than Scr as GFR decreases, so it may be a valuable marker in detecting early renal dysfunction.^27,28 In an early meta-analysis, Scys has also been reported to be superior to Scr for GFR estimation, particularly in patients with near-normal kidney function.²⁹ In addition to its use in estimating GFR, cystatin C has also been associated with subsequent adverse clinical events. In prior studies in the general population and in the elderly, cystatin C has been shown to be a better predictor of mortality and adverse cardiovascular events than Scr alone.^30–32 Peralta et al.³³ studied cystatin C level in 11,909 participants, and found its level may have a role in identifying individuals with CKD who have the highest risk for complications. The addition of cystatin C may improve mortality risk prediction by stages of kidney function relative to Scr.³⁴ In our study, all three combined equations with Scys exhibited superior agreement and performance, but each of those equations also included patient height and gender. However, including the height and gender does not explain totally the better performance of eGFR equations, because several other Scr-based equations used those variables as well. It is well known that a gender difference in the correlation of growth (height) and blood Scr concentration exists beginning in adolescence. This large variation in body shape and linear height determines extreme variations in muscle mass and may be a dominant factor when developing eGFR formulas for children, teens, and young adults.⁶

Higher cystatin C concentrations have been found in the 1st year of life previously. Bökenkamp et al.³⁵ studied Scys level in 258 children without kidney disease, aged 1 day to 18 years, and found the cystatin C concentration was highest on the first days of life (range 1.64±2.59 mg/l) with a rapid decrease during the first 4 months. Beyond the 1st year, the cystatin C concentration was constant. In a more recent study, SCys level was found to be a superior biomarker to serum Cr in the assessment of GFR in premature infants.³⁶ It is likely that the higher levels of cystatin C in the 1st year of life probably reflect the low GFR of neonates and infants. In our study, we only had one child under 1yr (0.7yr). There was a good agreement between mGFR and eGFR based on multivariate Schwartz equations.

It should be noted that creatinine and cystatin C methodologies differ among the various equations and systematic differences in measurement could contribute to the accuracy of the equations, given the methods used in the current report. Since the relationship of both creatinine and cystatin C to GFR is exponential, the effect of analytical error (bias and precision) will be greater at lower or ‘normal’ creatinine values (corresponding to high GFR) and the same difference will have minimal impact at highly abnormal creatinine values, which correspond to low GFR. Creatinine assays relying on both the Jaffe and enzymatic methods are now standardized to a material characterized by a gold standard method, isotope-dilution mass spectrometry (i.e., IDMS-traceable). Many of the equations evaluated herein utilized an enzymatic IDMS-traceable creatinine method, which is what we use at our institution. The Gao, et al. Scr-only equation is based on a Jaffe IDMS-traceable method and we found this equation, utilizing our creatinine values, to have high agreement with mGFR.

The methodological differences noted between cystatin C assays lead to similar limitations to that were historically experienced with creatinine and various eGFR equations. Efforts are now underway to calibrate different cystatin C methods to a single, traceable reference material. The first report of a virtually assay-independent simple cystatin C-based eGFR equation, based on calibration of different methods to an international reference material was recently published.³⁷ In the current study, our laboratory utilized a PETIA method on the Roche Cobas 6000 e501. Most of the equations evaluated reportedly employed a PENIA method, most commonly that on the Siemens BNII platform. Hansson et al.³⁸ showed in a comparison of 180 patient samples that Passing-Bablok regression analyses yielded a slope of 0.904 and intercept of 0.21 with regression coefficient of 0.9343 for cystatin C measured by Roche cobas e501 cystatin C PETIA and Siemens BNII PENIA. Despite the limitations due to analytical differences among methods, we have shown that the combination of creatinine and cystatin C, improves accuracy to mGFR.

The primary strength of this study is that it compares performance of 14 published eGFR equations in pediatric patients evaluated against an accurate and precise mGFR method in the routine clinical setting. The effects of different variables in the eGFR formulas were compared using a rigorous analytic plan to test the formulae against mGFR. Different analytic methods demonstrated similar results for performance of each equation. No previous study has specifically assessed the comparison of these comprehensive equations in this age group. The limitations of this study include a relatively small sample of subjects and that the analysis was not based on CKD stage, owing to a relatively small number expected in some groups. However, in data shown from the Scatterplot regression analyses, a stronger correlation can be seen with worsening CKD stage than in CKD stage 1, especially for the two Schwartz multivariate equations. Alternatively, the high overall correlation suggests that it would not have been different by differing stage of CKD with greater patient numbers within the lower bounds of mGFR.

In conclusion, the multivariate eGFR equations performed in a superior fashion over the univariate equations. The three eGFR formulae based on a combination of Scr, Scys, gender, and a growth parameter, (Schwartz et al. 2009, 2012) and (Chehade et al.), demonstrated exceptional accuracy among all formulae and had good applicability in special patients, including those with either a single kidney, kidney transplant, and/or short stature. Adding height and Scys to eGFR formula seems to be important in improving accuracy of the estimating equation. Our data suggest that for best accuracy to mGFR, all eGFR calculations in pediatric clinical practice employ only multivariate equations, particularly one of the three above. As this is a small study, our recommendations need to be confirmed in a larger sample size.

Table 5.

Agreements between multivariate equations and mGFR in special patients

	Mean±SD	Wilcoxon test		Bland-Altman analysis
		Z	P	Bias	95%LOA
Single kidney (n=10)
mGFR	66.5±19.2
Schwartz et al. (ScrcysEq09)	77.3±22.0	−1.988	0.05	−10.8±14.5	−39.2; 17.6
Schwartz et al. (ScrcysEq12)	75.0±20.5	−1.682	0.09	−8.5±13.6	−35.2 ; 52.2
Chehade et al.	77.5±21.2	−1.988	0.05	−11.0±15.3	−41.0; 19.0
Kidney transplant (n=7)
mGFR	63.0±18.6
Schwartz et al. (ScrcysEq09)	58.2±18.1	−0.676	0.50	4.8±12.5	−19.7; 29.3
Schwartz et al. (ScrcysEq12)	57.5±17.5	−1.014	0.31	5.4±12.1	−18.3 ; 29.1
Chehade et al.	57.9±24.3	−0.845	0.40	5.0±14.0	−22.4; 32.4
Z-score≤−2.5 (n=11)
mGFR	59.7±28.5
Schwartz et al. (ScrcysEq09)	61.4±20.8	−0.445	0.66	−1.7±14.9	−30.9; 27.5
Schwartz et al. (ScrcysEq12)	59.8±19.6	−0.445	0.66	−0.1±14.7	−28.9; 28.7
Chehade et al.	64.7±29.8	−0.978	0.33	−4.9±19.0	−42.1; 32.3

Note: GFR unit is mL/min/1.73 m²; Z is the value of the Wilcoxon test between eGFR and mGFR; 95% LOA is the 95% limits of agreement.

Abbreviations

eGFR

estimated glomerular filtration rate

mGFR

measured glomerular filtration rate

Scr

serum creatinine

Scys

serum cystatin C

BUN

blood Urea Nitrogen

CKD-EPI

the Chronic Kidney Disease Epidemiology