Propensity Score Matching: A Conceptual Review for Radiology Researchers

Abstract

The propensity score is defined as the probability of each individual study subject being assigned to a group of interest for comparison purposes. Propensity score adjustment is a method of ensuring an even distribution of confounders between groups, thereby increasing between group comparability. Propensity score analysis is therefore an increasingly applied statistical method in observational studies. The purpose of this article was to provide a step-by-step nonmathematical conceptual guide to propensity score analysis with particular emphasis on propensity score matching. A software program code used for propensity score matching was also presented.

INTRODUCTION

In order to compare outcomes between different subject groups, it is important to first assure that the groups are comparable. In other words "comparing apples and oranges" should be avoided. For example, assume a study comparing the effect of oral hypoglycemic agents to insulin in type 2 diabetes patients. Due to differences between the prescription requirements (such as the severity or duration of disease), insulin would be reported for poor outcome (1). Likewise, in a study comparing the effect of 2 different treatments on 2 groups of patients, the patients in each group should have the same baseline characteristics. If one group consists of many easy-to-treat patients, while the other group includes difficult-to-treat patients (i.e., the 2 groups are not comparable in terms of therapeutic difficulty), a better treatment outcome in the former group could merely be a result of differences in population characteristics rather than due to any true difference in treatment efficacy.

The issue of intergroup comparability is generally not a concern in typical prospective studies of diagnostic test accuracy (commonly conducted in radiology), since different imaging examinations are usually performed in the same patient for an intra-subject comparison. However, in therapeutic research studies each patient only receives one treatment. Nevertheless, intergroup comparability remains an important consideration in radiology research, particularly in interventional radiology that is a discipline of therapeutic medicine, research commonly involves different subject groups. Additionally, diagnostic imaging studies can also be designed to evaluate patient outcomes associated with different diagnostic imaging methods/strategies in order to provide higher order evidence beyond mere diagnostic accuracy (2, 3, 4, 5, 6). Multiple diagnostic tests in such studies cannot be performed on the same patient, similar to treatment protocols in therapeutic research studies. Moreover, retrospective diagnostic studies often involve multiple patient groups. Because patients rarely undergo similar multiple imaging studies in clinical practice, including only those patients who have undergone all imaging examinations of interest is often difficult.

Several different methods can be used to address intergroup comparability in research studies. First or all, randomization (i.e., random allocation of the study subjects into different groups) is the most effective method to achieve balance of covariates between groups. Randomization assures that not only observed/measured confounders but also unobserved/unmeasured confounders are equally distributed between groups (7). For this reason, in clinical research, randomized clinical trials result in the most robust evidence. However, randomized research studies are not always feasible or practical due to various issues such as ethical considerations, generalizability, safety, and cost. Furthermore, they cannot be performed on data in a retrospective setting. The comparability of study groups in a retrospective observational study can be crudely assessed by determining whether the distributions of various baseline characteristics are similar between the compared groups (8, 9, 10). Multiple regression analysis is another more sophisticated statistical approach to account for confounding variables (11, 12). However, comparability cannot always be determined using these methods of evaluation.

Propensity score analysis is a statistical method that was introduced in 1983, and applied to various clinical researches (13). Propensity score analysis can effectively adjust for confounders in a retrospective observational study, thus facilitating comparability between patient groups. Although still infrequently used in radiology research studies (14, 15, 16, 17, 18, 19, 20, 21, 22, 23), propensity score analysis is increasingly applied in clinical research. The purpose of this article was to provide a step-by-step nonmathematical conceptual guide to propensity score analysis from a radiology research point of view with particular emphasis on propensity score matching. A software program code used for propensity score matching was also presented (Supplement in the online-only Data Supplement).

When and Why Does Comparability Become an Issue?

Throughout this review, a hypothetical observational study was used as an example i.e., a retrospective comparison of the accuracy of dynamic contrast-enhanced liver MRI and dynamic contrast-enhanced CT for diagnosis of benign vs. malignant hepatic nodules detected on ultrasonography during annual physical examination or surveillance. A total of 940 patients had liver CT (the control group) and 470 patients had liver MRI (the group of interest, referred to as the "intervention" or "treatment" group in methodological terms) were consecutively identified from past clinical practice during a specified period. Table 1 showed the characteristics of the 2 patient groups. Some of the characteristics were deemed similar, whereas others were seemingly different between the 2 groups. The diagnostic accuracy of liver CT and MRI were 73.6% (692/940) and 83.8% (394/470), respectively.

Table 1. Patient Characteristics before and after Propensity Score Matching.

	Before Propensity Score Matching			After Propensity Score Matching
	Liver CT (Control) (n = 940)	Liver MRI (Intervention) (n = 470)	Standardized Mean Difference‡	Liver CT (Control) (n = 293)	Liver MRI (Intervention) (n = 293)	Standardized Mean Difference‡
Propensity score*	0.23 ± 0.21	0.53 ± 0.23	-1.331	0.46 ± 0.25	0.47 ± 0.27	-0.033
Age, years (mean ± SD)	53.8 ± 11.7	60.3 ± 11.6	-0.559	58.1 ± 13.3	59.5 ± 11.9	-0.117
Gender, % male	26.0	45.3	-1.324	42.7	44.0	-0.027
Body mass index, kg/m2 (mean ± SD)	27.1 ± 5.8	25.9 ± 6.1	0.389	26.3 ± 5.9	26.2 ± 6.1	0.015
Lesion diameter, cm (mean ± SD)	2.3 ± 1.6	2.4 ± 1.8	-0.085	2.4 ± 1.7	2.4 ± 1.6	0.031
History of cancer (%)†	21.3	77.0	1.324	63.8	63.8	0.000

Note.- ^*Propensity score represent probability of undergoing liver MRI (as opposed to liver CT). Matching was achieved using nearest neighbor matching including all five variables listed in table, ^†Personal or first-degree relative, ^‡Standardized mean difference (d) for continuous variable is defined as

where X_intervention and X_control are sample means of variable in intervention and control groups, respectively, and s²_intervention and s²_control are sample variances of variable in respective groups. Standardized mean difference (d) for binary variable is defined as

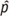where _intervention and 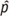_control are sample proportions for variable in intervention and control groups, respectively.

Before we could conclude that liver MRI was more accurate than liver CT, we first needed to identify potential confounders. For example, some clinicians may have preferentially referred patients for MRI when a malignant hepatic nodule was highly suspected (which could have resulted in MRI of many easy-to-diagnose malignant nodules) because they believed that highly suspicious lesions should be evaluated further with a more sophisticated expensive examination. Other physicians may have referred patients for MRI when ultrasonographic findings were particularly indeterminate/obscure (including difficult-to-diagnose lesions at CT or MRI) because they believed that MRI is generally more accurate and reliable for soft-tissue characterization, as compared to CT. Additionally, patients in the MRI group were older than those in the CT group, which may have caused an underestimation of MRI accuracy as older patients are generally less cooperative during imaging examinations (e.g., have more difficulty with respiratory control) and because good patient cooperation is more important during MRI than during CT. Patients are typically not allocated to procedures (diagnostic or therapeutic) randomly in clinical practice but are instead assigned based on the subjective judgment of the providing clinician. Consequently, retrospective analyses of clinical data lead to some degree of unequal distribution of various clinical factors that may substantially affect the therapeutic or diagnostic efficacy across patient groups. Therefore, the mere comparison of "face values" without accounting for all potential confounders may lead to a false conclusion, such as the superior diagnostic accuracy of MRI to CT in our example. This ultimately translates to incorrect medical practice, once described as a "scandal of poor medical research" (24).

Selection bias is the most significant factor among many that results from uneven distribution of patient characteristics among compared groups in a retrospective observational study (23). Indication bias also referred to as confounding by indication, is a specific type of selection bias that is primarily responsible for the incomparability between groups on retrospective analyses of clinical data (1, 25). This bias occurs when a patient's condition that determines the selection of any particular treatment or diagnostic procedure, is associated with the outcome of the treatment/diagnostic procedure. For example, as stated earlier, if patients with obviously benign or malignant nodules (i.e., easy-to-diagnose cases) were selected to undergo MRI or CT, the accuracy of that particular examination would be overestimated. Indication bias is occasionally loosely defined and used synonymously with "referral bias" in radiology literature (26, 27). However, referral bias is actually a synonym for Berkson's bias (i.e., a difference in admission rate between subjects exposed to a factor and control subjects) or verification/work-up bias (i.e., preference for patients with positive index test results who undergo reference standard procedures/work-up). Selection biases are very difficult to control or adjust in retrospective studies because data on certain variables that may influence patient selection and the extent of selection are often not available for study (28).

What Is Propensity Score?

Propensity score is the estimated probability for each individual in the study to be assigned to the group of interest for comparison (i.e., intervention group), conditional on all observed confounders. In our example, the propensity score was the probability of the study patient to receive liver MRI. Propensity score is also an index that describes how all the observed confounders are collectively distributed in each study subject. Therefore, subjects with the same or similar propensity scores can be considered to have the same or similar distribution of all confounding variables used in constructing the propensity score (13). Subjects with the same/similar propensity scores are comparable or "exchangeable", as the confounding variables are balanced. As a result, one can make an unbiased clearer comparison between subjects of the groups compared (e.g., CT vs. MRI) with same or similar propensity scores. Statistically stated, we can draw a causal inference and estimate the unconfounded effect of the variable of interest.

Estimation of the Propensity Score

Multivariable/multiple logistic regression modeling is a method commonly used for constructing a propensity score model, in which potential confounders to be adjusted are included as independent variables ("x" variable), and the group assignment (CT vs. MRI in our example) is included as the dependent variable ("y" variable). It is important to remember that, unlike randomization in clinical trials, the propensity score can be used to balance out only those confounders included in estimating the propensity score. The propensity score method cannot overcome any bias caused by confounders that were not observed/measured and, therefore, not included in the model. Thus, it is generally better to include as many potential confounders in the propensity score model as independent variables.

Proper selection of independent variables during the propensity score estimation is extremely crucial for the validity of the propensity score method. There is controversy about which variables should be included while constructing the propensity score model. The following sets of variables should be carefully considered for possible inclusion in the propensity score model: 1) all observed baseline covariates, 2) all baseline covariates associated with group assignment, 3) all covariates affecting the study outcome (e.g., correct vs. incorrect imaging diagnosis in our example), and 4) all covariates affecting both group assignment and outcome. These variables must also be present prior to the assignment to comparative procedures.

Including every confounder, i.e., those variables that are related to both group assignment and outcome, in estimating the propensity score, can satisfy ignorable group assignment and minimize study bias (29). This can generate a randomized study-like dataset by removing all sources of incomparability between groups. Unfortunately, this approach may not be feasible in real-world clinical research. Fewer variables may be observed/measured in certain cases. However, even including variables related only to outcomes but not to group assignment in the propensity score model can more precisely assess the intervention effect (i.e., intergroup differences) without increasing bias. On the other hand, including variables related only to group assignment but not to study outcomes may actually reduce the precision in evaluating intergroup difference without a substantial reduction in bias (30). Accordingly, in a diagnostic study such as in the example discussed, all confounding variables that might affect the diagnostic accuracy (outcome) should be considered for inclusion rather than only variables that are associated with assignment of the subjects to either diagnostic test group (liver CT or liver MRI). Whether the covariate should be classified as confounder is frequently confusing in practice. Thus, researchers should carefully examine the relationship between baseline covariates and the outcome to identify true confounders and construct an efficient model.

Data on 5 different potential confounding variables, including age (year), gender, body mass index (kg/m²), lesion diameter as measured at ultrasonography (cm), and previous personal or first-degree relative history of malignancy were retrospectively available in the illustrating example. We obtained the estimated probability of each patient undergoing liver MRI instead of liver CT by fitting the multivariable logistic regression model. All 5 potential confounding variables measured were included as independent variables in the model (as also known as "covariates"). The ultimate goal of a propensity score model is to efficiently control for confounding effects instead of merely predicting the probability of group assignment. Although we only considered 5 confounding variables in the regression model for illustration purposes, in actual research analyses would require identification of all variables that are potential confounders.

The c-index (the area under the receiver operating characteristic curve of the logistic regression model) is often used to assess the adequacy of the propensity score model, a process also known as discrimination (which indicates the ability to correctly differentiate between 2 outcome classes). A c-index of 0.8 is often considered an adequate model fit. The logistic model including the 5 variables yielded a c-statistic of 0.803 in our example. The Hosmer-Lemeshow test (p value were 0.083) showed that the propensity score model had an adequate level of calibration (how closely the predicted probabilities agree with the actual outcomes).

Evaluation of Propensity Score Distribution

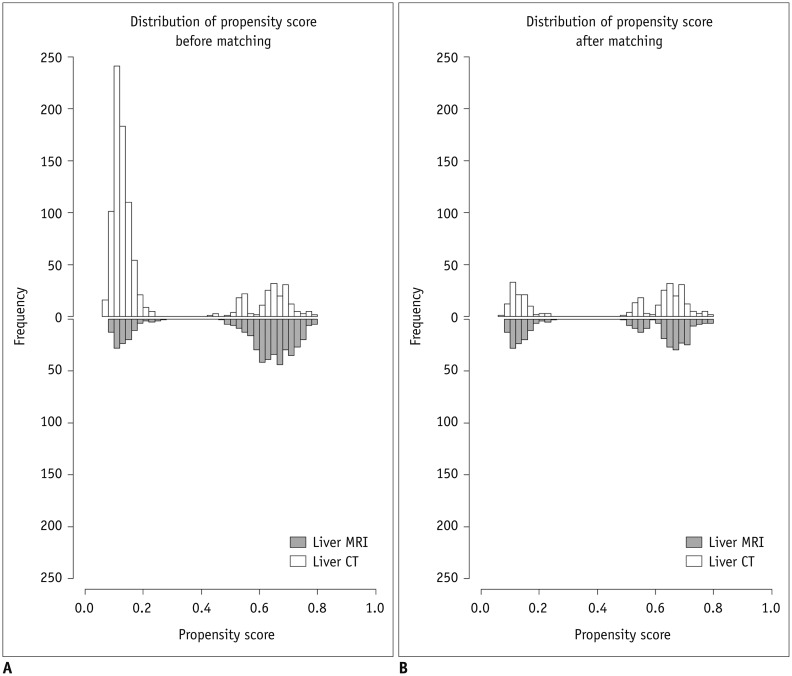
It is important to examine the distribution of propensity scores of the 2 groups, as well as to assess the extent of overlap before using the estimated propensity scores for further analysis. The distributions of propensity scores were shown in Figure 1. If the distributions of propensity scores are very different and share little overlap, the 2 groups may not be comparable in clinical settings. Thus, if it is already clear who will receive one procedure instead of another (liver CT rather than liver MRI, for example), comparison of the different procedures is not required as they would not be used interchangeably/alternatively in practice, and the clinical indications for either procedures are apparently different. If there is extensive overlap in the distributions of the propensity scores, several different analytic approaches using the propensity score such as stratification, matching, modeling, and weighting can be applied and would all produce similar results. However, each analysis should be implemented beyond the specific study hypothesis: while matching is adopted to ensure the comparability between groups (15, 16, 17, 18, 19, 22), weighting dilutes the effect from rare situations among the total patients including both groups (31, 32). However, weighting the entire study sample by inverse probability of treatment weighting derived from the propensity score, which is called inverse probability of treatment weighting, should be performed with caution. Weighted methods have poor performance when the weights for a few subjects are very large. The estimated standard-error-of-treatment effect may underestimate the true difference between the weighted estimator and the population parameter it estimates (33). When there is partial overlap in the distribution of propensity scores between groups, analytic methods should be chosen according to the population of interest. If a small portion of the entire study sample is chosen for the final analysis, generalization of the results to the whole study population may be limited. Figure 1 showed a partial overlap in the propensity score distributions suggestive of the presence of 2 clusters of patients (bimodal distribution) in the histogram of propensity scores.

Fig. 1. Distribution of propensity scores.

A. Distribution of propensity scores among total study subjects (940 and 470 patients who had liver CT and liver MRI, respectively).

B. Distribution of propensity scores after matching for age, gender, body mass index, lesion diameter, and history of cancer (293 pairs of liver CT and liver MRI).

Propensity Score Matching

Propensity score can be used in several different ways, including restriction, stratification, matching, modeling, or weighting to account for confounding effects. Among such methods, we discussed the propensity score matching method that is commonly used in medical research studies. Propensity score matching pairs each subject in the intervention group (e.g., patients who underwent liver MRI), with a subject in the comparison group (e.g., patients who underwent liver CT) based on the similarity of their propensity scores. Therefore, all covariates used for developing the propensity scores were collectively matched.

There are several points to consider regarding propensity score matching. First, a 1:1 ratio between matched subjects is most commonly used. However when the control group includes many more subjects that the intervention group, other ratios may be used. McAfee et al. (34), used a matching ratio of 1:4 for a larger number of control subjects than test subjects in order to improve study power. Second, propensity score matching is generally performed "without replacement", i.e., a subject cannot be included in more than one matched set. Third, 2 matching algorithms, including greedy (also known as nearest neighbor matching) and optimal, are mainly used. In greedy matching, a subject is first selected at random from the intervention group and subsequently paired with a subject in the control group with the closest propensity score, even if that subject in the intervention group would have been a better match for a subsequent subject in the control group (35). This process is repeated until all subjects in the intervention group are matched to subjects in the control group. Nearest neighbor matching within a caliper involves a slight modification. Here, the caliper refers to the allowable difference in propensity scores eligible for use in matching. Using this approach, the propensity scores of the matched sample lie within a specified width of calipers. As an analogy, we can permit a maximum 2-year difference when simply matching for patient age. The choice of caliper involves a tradeoff: a narrower caliper will form more similarly matched pairs but may result in a reduced number of matched subjects. Thus, one may need to experiment with different calipers to optimize the number of balanced pairs. One recommended method is to use a caliper width equal to 0.2 of the standard deviation of the logit of the propensity scores (36). Optimal matching is another method aimed at creating matches that will minimize the sum of within-pair differences in the propensity scores (37). Optimal matching may not necessarily create more balanced matched pairs than greedy matching, and greedy and optimal matching methods mostly find the same sets of control subjects (38). Overall, the most commonly used approach in medical literature is probably the nearest neighbor matching without replacement (37). We chose 1:1 matching using nearest neighbor matching with a caliper width of 0.05 standard deviation of the logit of the propensity scores. The choice resulted in a reduction of the standardized mean difference between groups of < 20% (0.2) for all covariates after propensity score matching (Table 1). A smaller standardized mean difference between groups indicated a greater mean comparability, but can result in less matched pairs.

Assessment of the Balance in Covariates between Groups after Propensity Score Matching

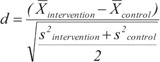
Effectiveness of propensity score matching can be judged by the degree of balance in all the measured baseline covariates between the 2 groups after matching. The standardized mean difference that is not affected by the samples size and represents properties of the sample, is proposed as an adequate method to assess this balance (39). In the current example, the standardized differences decreased to < 0.2 after matching, as shown in Table 1.

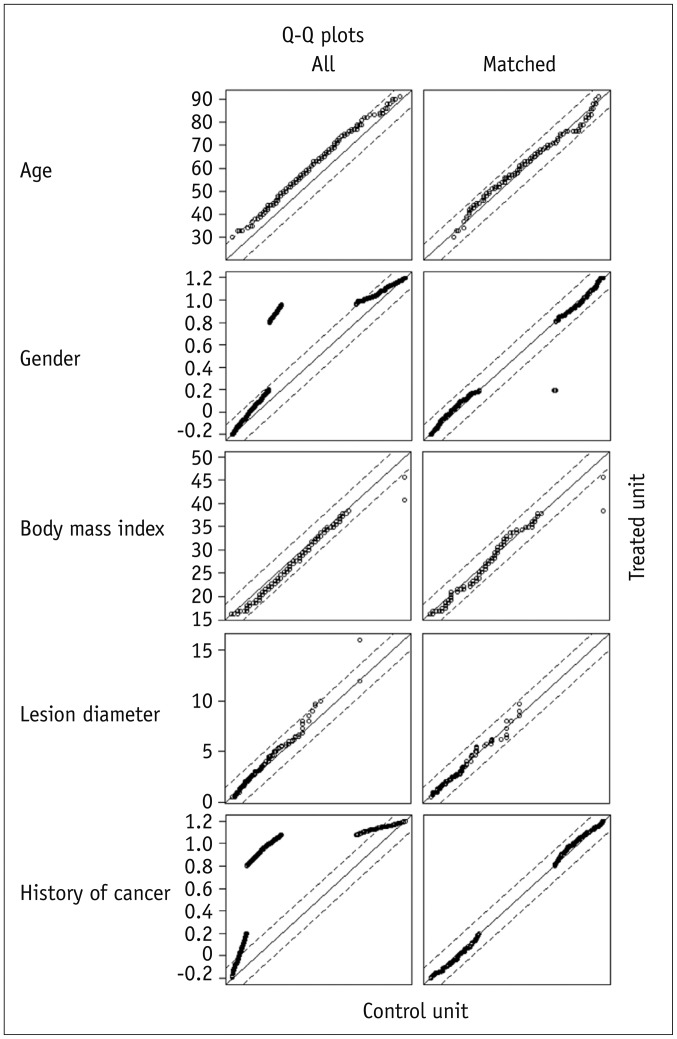
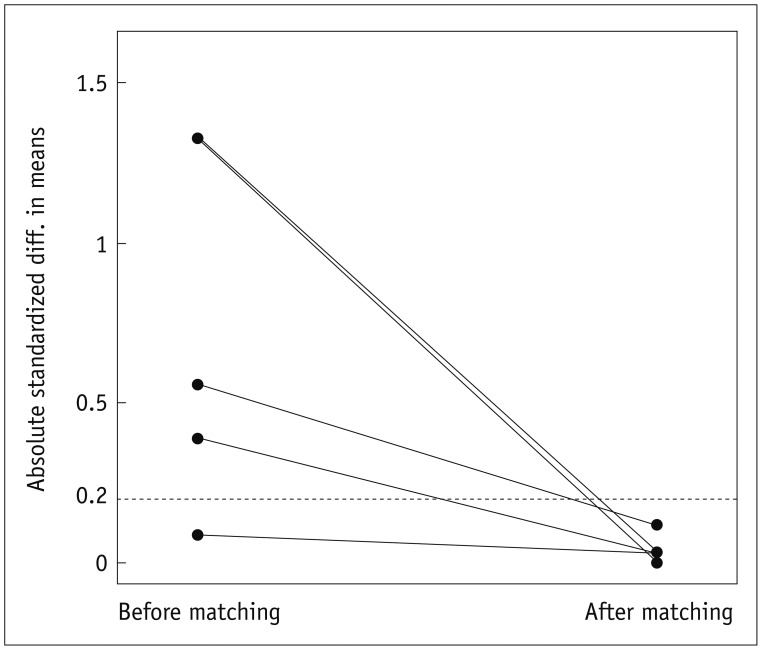
Hypothesis testing and p values are not recommended to check the balance between groups after propensity score matching, since a failure to reject the null hypothesis (i.e., p > 0.05) does not guarantee successful balance of covariates between 2 groups. Instead as described in the previous paragraph, using standardized mean differences is recommended to determine whether the groups are sufficiently balanced. Graphical diagnostics can also be used to assess group balance after propensity score matching, such as Q-Q plots of each covariate, as shown in Figure 2. The points in the Q-Q plots would lie on the 45-degree diagonal line if the empirical distributions are identical in 2 compared groups. Deviations from the diagonal line indicate differences in the distribution of the covariates between the 2 groups. A plot of the standardized differences of means before and after propensity score matching, as shown in Figure 3, also gives a good overview of the degree to which covariate balance improves on propensity score matching. The means of propensity scores after matching were 0.46 for the liver CT group and 0.47 for the liver MRI group.

Fig. 2. Q-Q plots of each covariate from 2 groups before and after propensity score matching.

Fig. 3. Plot of standardized differences in means before and after propensity score matching.

Main Analysis of Between-Group Differences after Propensity Score Matching

Once an appropriate level of between-group balance of the confounders/covariates is achieved, the matched data set is ready for the main analysis of between-group difference in the study outcome. When all the observed confounders have been controlled, an inference of the effect of intervention can readily draw (e.g., liver MRI [intervention] vs. liver CT [control]). Following the matching process, it is generally recommended to conduct the analysis as if the data are paired or repeated measures. Therefore, the inter-group differences in continuous outcomes should be tested by the paired t test or the Wilcoxon signed-rank test. For binary outcomes as in our example, conditional logistic regression or generalized estimating equations (GEE) for logistic regression can be used when the treatment effect (e.g., the effect on diagnostic accuracy when liver MR is used instead of liver CT in the example) is measured with an odds ratio (OR). McNemar's test can identify a significant association between the grouping variables (e.g., CT vs. MRI) and the binary outcome. A stratified log-rank test or a stratified Cox proportional hazard model can be employed for time-to-event data. However, dissimilarity in covariates between the matched pair (i.e., at the individual level) is still a concern despite the collective similarity in distribution of each covariate between groups; hence statistical analysis of matched pairs may not be "the best practice" as suggested by Hill (40).

The OR (MRI-to-CT, where > 1 represents a higher accuracy of MRI compared with CT) obtained from the example study was shown in Table 2. When the data were analyzed without accounting for confounders (i.e., before propensity score matching), MRI appeared to be significantly more accurate than CT even after controlling for confounders {adjusted OR of 1.76 (95% confidence interval [CI], 1.25-2.47) obtained with standard logistic regression analysis}. However, statistically significant differences disappeared after propensity score matching (adjusted OR of 1.38 [95% CI, 0.93-2.05] obtained from GEE), indicating that the accuracies of liver MRI and liver CT were actually not significantly different in this example.

Table 2. Comparison between Liver MRI and Liver CT Using Several Analytic Methods.

	Odds Ratio†	95% Confidence Interval	P
Crude without adjustment for confounders (n = 1410)	1.70	(1.29-2.25)	< 0.01
Multivariable logistic regression* (n = 1410)	1.76	(1.25-2.47)	< 0.01
Propensity score matching* (nearest neighbor) (n = 586)	1.38	(0.93-2.05)	0.11

Note.- ^*Both propensity score matching and multivariable regression analysis included all five covariates listed in Table 1 (age, gender, body mass index, lesion diameter, and history of cancer), ^†Odds ratio is MRI (numerator) to CT (denominator), where > 1 represents higher accuracy of MRI compared to CT.

Precautions and Further Considerations

Propensity score analysis cannot repair the lack of comparability between groups but is rather a statistical process that creates a balanced distribution of all the confounders included in the estimation of the propensity scores (described as "observed/measured confounders" in methodological terms). Therefore, it is of paramount importance to collect information on all relevant confounders and include them in the estimation of propensity scores in order to obtain credible results from any analyses using the propensity scores. For instance, in the example study, the statistical comparison between liver CT and liver MRI groups after propensity score matching with the exclusion of 2 variables, i.e., gender and history of malignancy, led to a false conclusion that MRI has a significantly higher accuracy than CT (Table 3). It is often very difficult or near impossible to acquire sufficient information on all relevant confounders in retrospective observational studies, hence propensity score analysis should be applied and interpreted with caution (21). After all, the quality and credibility of the data ultimately determines the quality and credibility of study results/conclusion.

Table 3. Effect of Variable Selection on Results of Propensity Score Analysis.

	Number of Subjects		Odd Ratio‡	95% Confidence Interval	P
	Liver CT (Control)	Liver MRI (Intervention)
Unmatched but adjusting for all five variables*	940	470	1.76	(1.25-2.47)	< 0.01
Propensity score matching (nearest neighbor) using all five variables*	293	293	1.38	(0.93-2.05)	0.11
Propensity score matching (nearest neighbor) using selected variables†	439	439	1.52	(1.09-2.11)	0.01

Note.- ^*All five variables including age, gender, body mass index, lesion diameter, and history of cancer were considered as confounders, ^†Age, body mass index, and lesion diameter were only considered for estimating propensity score, ^‡Odds ratio is MRI (numerator) to CT (denominator), where > 1 represents higher accuracy of MRI compared to CT.

As briefly mentioned earlier, the effects of confounders can also be adjusted by multivariable regression analysis. Multivariable regression and propensity score matching may result in concordant (Table 2) or discordant results depending on the data. Multivariable regression analysis may not be effective when there are numerous covariates because there may not be sufficient power to demonstrate a statistically significant effect of the main intervention after all adjustments have been made, resulting in misleading data due to over-fitting.

Likewise, propensity scores itself can be used as a covariate in the regression model. There are potential advantages to applying the propensity score for covariate adjustment while modeling for outcome: the propensity score model can allow complexity in modeling with higher order forms and interactions, hence applying the propensity score as a covariate allows a less complex model of outcome that enables a more reliable fit than if many covariates for each were considered. However, Rubin (41) showed that covariance adjustment may in fact increase bias if the covariance matrices are different among groups.

Alternatively, stratification on the propensity score can be considered. Typically, the entire study population in an overall study sample is stratified into 5 approximately equal-size groups using the quintiles of the estimated propensity score. This approximates matching but prevents loss of unmatched patients, since balance in the proportions of experimental and control patients within each stratum are not required (33). Rosenbaum and Rubin (13) demonstrated that stratifying on the quintiles of the propensity score eliminates approximately 90% of the bias. Propensity score matching was shown to eliminate a greater proportion of the systematic differences between groups, as compared to stratification on the propensity score (42).

It is also important to assure that all the variables in the multiple regression model satisfy the assumptions for the statistical analysis, including linearity. Propensity score matching is most effective in dealing with numerous covariates as it combines them into one collective variable, i.e., the propensity score. However, as the statistical comparison after propensity score matching only includes a portion of the original study population, the target population for generalization may be restricted.

Summary

• Retrospective observational studies are limited by various sources of biases and confounders, due to absence of the "balancing principle" inherent in randomized controlled trials. Such limitations affect robust comparison of outcomes between treatment and control groups.

• Propensity score adjustment allows the researcher to account for comparability between groups by balancing the distribution of biases and confounders between groups and, when applied properly, can simulate the random assignment of subjects seen in a randomized trial.

• The propensity score demonstrates each patient's probability of receiving a specific treatment given a set of measured covariates. These covariates usually include various clinical characteristics and must be present prior to the decision of whether to assign compared procedures.

• The selection of covariates to calculate the propensity score is critical, as the omission of important variables will reduce the credibility of the propensity score model.

• Propensity scores between patient groups must overlap to allow for appropriate balancing of patients. A lack of overlap indicates that the patient groups are too different at baseline for suitable comparison.

• Matching is a widely used method for propensity score adjustment of which nearest neighbor matching without replacement is most commonly employed.

• The dataset after propensity score matching should be analyzed using statistical tests for paired data.

• The target population for generalization could be restricted, as the statistical analysis after propensity score matching only includes a portion of the original study population.

Supplementary Materials

The online-only Data Supplement is available with this article at http://dx.doi.org/10.3348/kjr.2015.16.2.286.