The Hitchhiker's Guide to Hi-C Analysis: Practical guidelines

Abstract

Over the last decade, development and application of a set of molecular genomic approaches based on the chromosome conformation capture method (3C), combined with increasingly powerful imaging approaches, have enabled high resolution and genome-wide analysis of the spatial organization of chromosomes. The aim of this paper is to provide guidelines for analyzing and interpreting data obtained with genome-wide 3C methods such as Hi-C and 3C-seq that rely on deep sequencing to detect and quantify pairwise chromatin interactions genome-wide.

Introduction

The human genome consists of over 3 billion nucleotides and is contained within 23 pairs of chromosomes. If the chromosomes were aligned end to end and the DNA stretched, the genome would measure roughly 2 meters long. Yet the genome functions within a sphere smaller than a tenth of the thickness of a human hair (10 micron). This suggests that the genome does not exist as a simple one-dimensional polymer; instead the genome folds into a complex compact three-dimensional structure.

It is increasingly appreciated that a full understanding of how chromosomes perform their many functions (e.g. express genes), replicate and faithfully segregate during mitosis, requires a detailed knowledge of their spatial organization. For instance, genes can be controlled by regulatory elements such as enhancers that can be located hundreds of Kb from their promoter. It is now understood that such regulation often involves physical chromatin looping between the enhancer and the promoter(Jin et al. 2013; Sanyal et al. 2012; Deng et al. 2012; Krivega and Dean 2012; Razin et al. 2013; Vernimmen et al. 2007; Tolhuis et al. 2002). Further, recent evidence suggests chromosomes appear to be folded as a hierarchy of nested chromosomal domains(Lieberman-Aiden et al. 2009; Dixon et al. 2012; Nora et al. 2012; Sexton et al. 2012; Hou et al. 2012; Bickmore and van Steensel 2013), and these are also thought to be involved in regulating genes, e.g. by limiting enhancer-promoter interactions to only those that can occur within a single chromosomal domain(Gibcus and Dekker 2013; de Laat and Duboule 2013; Schwarzer and Spitz 2014; Gorkin et al. 2014; Van Bortle et al. 2014).

The chromosome conformation capture methodology (3C) is now widely used to map chromatin interaction within regions of interest and across the genome. Chromatin interaction data can then be leveraged to gain insights into the spatial organization of chromatin, e.g. the presence of chromatin loops and chromosomal domains. The various 3C-based methods have been described extensively before and are not discussed here in detail (Belton et al. 2012; Naumova et al. 2012). We first discuss methods and considerations that are important for using deep sequencing data to build bias-free genome-wide chromatin interaction maps. We then describe several approaches to analyze such maps, including identification of patterns in the data that reflect different types of chromosome structural features and their biological interpretations.

Comprehensive genome-wide measurement of chromatin interactions

Indiscriminate methods such as microscopy or FISH can study the 3D genome, but have limited resolution and are limited in their capacity tomeasure multiple discrete contacts simultaneously. The Chromosome Conformation Capture (3C) method was the first molecular method to interrogate physical chromatin interactions in an unbiased manner(Dekker et al. 2002). 3C has since been further developed into various other derivatives including 4C(Simonis et al. 2006; Zhao et al. 2006),5C(Dostie et al. 2006) and Hi-C(Lieberman-Aiden et al. 2009). These methods use 3C as the principal methodology by which they capture genomic interactions. They differ in the actual method by which the captured interactions are measured, e.g. by PCR in 3C and by unbiased deep sequencing in Hi-C and 3C-seq. Though the 3C method does capture genome-wide data, it was not until the era of deep sequencing came about that one was able to survey all genome wide interactions in a single experiment, as in Hi-C and 3C-seq.

In 3C, cells are cross-linked using formaldehyde, lysed and the chromatin is then digested with a restriction enzyme of choice (typicallyHindIII or EcoRI). The chromatin is then extracted and the restriction fragments are ligated under very dilute conditions to favor intra-molecular ligation over inter-molecular ligation. The crosslinks are then reversed, proteins are degraded and DNA is purified. The newly generated chimeric DNA ligation products represent pairwise interactions (physical 3D contacts) and can then be analyzed by a variety of down-stream methods. This results in a collection of chimeric DNA fragments consisting of a ligation of DNA sequences from two interacting loci.

Currently, there are two 3C-based methods to obtain genome-wide chromatin interaction data: Hi-C and 3C-seq. In the Hi-C protocol one includes a step to introduce biotinylated nucleotides at ligation junctions which enables specific purification of these junctions(Lieberman-Aiden et al. 2009). This has the important advantage that it prevents sequencing DNA molecules that do not contain such junctions and are thus mostly uninformative. In 3C-seq one employs the classical 3C protocol and often a more frequently cutting enzyme (e.g. DpnII) followed by intra-molecular ligation without biotin incorporation(Sexton et al. 2012). The ligated DNA is then directly sequenced to identify pairwise chromatin interactions genome-wide. The 3C-seq methodology sequences all molecules including unligated molecules which can complicate the processing / filtering steps and can reduce the percentage of usable reads. However, experimental techniques exist to help minimize uninformative (un-ligated, self-ligated etc.) Hi-C products (e.g. exonuclease treatment to remove unligatedbiotinylated ends).

Wepropose guidelines for analyzing genome-wide chromatin interaction maps generated by Hi-C, but many of these considerations also apply to 3C-seq or other equivalent data.

Hi-C data resolution

The space of all possible interactions, which is surveyed by Hi-C experiments, is very large. For example, consider the human genome. Using a 6-bp cutting restriction enzyme, there are almost 10⁶ restriction fragments, leading to an interaction space on the order of 10¹² possible pairwise interactions. Thus, achieving sufficient coverage to support maximal resolution is a significant challenge. However, once can reduce the interaction space, and thus the resolution, by aggregating restriction fragments into fixed-size bins which in turn increases the effective coverage (see Binning section).

In light of this, it is critical to establish the goals of the experiment, meaning whether one is most interested in either large-scale genomic conformations (e.g. genomic compartments) or specific small-scale interaction patterns (e.g. promoter-enhancer looping).

If the goal is to measure large scale structures, such as genomic compartments, then a lower resolution will often suffice (1MB-10MB). Here, Hi-C using a traditional 6bp-cutting enzyme could be used. However if the goal is to measure specific interactions of a small region, e.g. promoter-enhancer looping, then one should choose to use a restriction enzyme that cuts more frequently (e.g. 4bp) and a method that does not measure the entire genome, but instead focuses on exploring only a subset of the genome (i.e. 3C/4C/5C).

In Hi-C the maximal effective resolution of a dataset is determined by several factors, first and foremost is coverage. Given increasing amounts of reads, one will cover more of the interaction space and thus improve the maximal resolution.Library complexity is another factor. Library complexity is defined as the total number of unique chimeric molecules that exist in a Hi-C library, which is a factor of both the number of cells and the quality of the library. A librarywith a low complexity level will saturate quickly with increasing sequencing depth, e.g. less information will be gained from additional sequencing. The saturation curve can be estimated from a dataset by plotting the cumulative number of unique interactions observed versus increasing read depth.

In our experience,an adequately complex Hi-C dataset for the human genome with roughly 100 million mapped / valid junction reads, is sufficient to support a 40kb data resolution. Data below 40kb may be usable, though it will suffer from a higher level of noise. It is important to note that effective resolution scales with genomic distance, such that short-range interactions will typically have higher coverage and thus higher effective resolution.

Computational considerations

Hi-C data produced by deep sequencing is no different than other genome-wide deep sequencing datasets. The data starts out as genomic reads in the traditional FASTQ file format (containing a DNA read string and a phred quality (QV) score string). Hi-C libraries are traditionally sequenced using paired-end technology, where a single read is produced from each 5’ end of the molecule. However, Hi-C ligation products can also be sequenced using single end reads, assuming reads are sufficiently long to cover both parts of the chimeric molecule (ligation product) and are handled appropriately during the mapping steps (see Read Mapping section).

The data storage requirements for Hi-C datasets are almost solely driven by the sequencing depth needed to achieve the desired resolution and the size of the FASTQ files. The processed Hi-C data will normally be order(s) of magnitude smaller than the size of the FASTQ files. It is easy to parallelize the steps needed to map the reads to the genome, and thus achieve a significant speedup in the Hi-C processing steps. The majority of Hi-C-specific filtering and processing steps are independent and can therefore also be parallelized.

Hi-C workflow

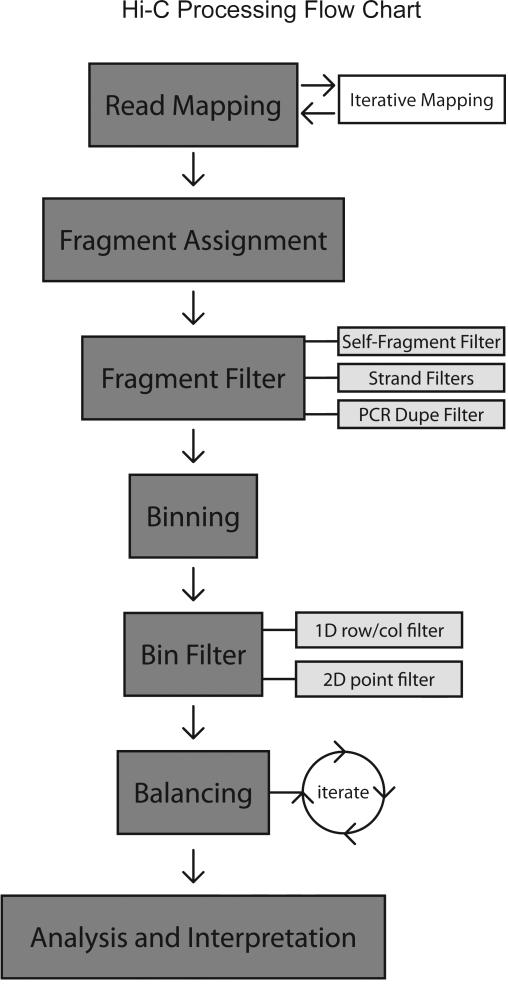
We describe the major steps needed to process a Hi-C dataset (Figure 1):

1. Read Mapping

2. Fragment Assignment

3. Fragment Filtering

4. Binning

5. Bin Level Filtering

6. Balancing

Figure1.

Flow chart for processing Hi-C Data. Reads are first mapped using the iterative mapping approach for paired end reads. Only paired end reads where both ends map uniquely are kept, all others are discarded. Mapped reads are then assigned to a restriction fragment, and fragment-fragment interactions are assembled. Fragment level filtering is applied. Un-ligated fragments and self-ligated fragments are removed. Optional strand-specific filters are applied. PCR duplicates are removed. Data is then binned. Bin-level filtering is then applied. Outlier bin-bin point interactions (2D) are removed. Outlier bins (1D row/cols) are removed.

Read Mapping

Reads can be aligned using any standard read alignment software (i.e. Bowtie(Langmead and Salzberg 2012)) to the genome of interest. Any aligner can be used for mapping Hi-C reads - the goal is to simply find a unique alignment for each read. Even though Hi-C data is sequenced using paired-end reads, the reads are not mapped using the paired-end mode of most aligners. The paired-end mode for most aligners assumes that the ends of a single continuous genomic fragment are being sequenced, and the distance between these two ends fits a known distribution. Since the insert size of the Hi-C ligation product can vary between 1bp to hundreds of megabases (in terms of linear genome distance), it is difficult to use most paired-end alignment modes as is. One straightforward solution is to map each side of the paired end read separately/independently using a standard alignment procedure.

Read Mapping – Iterative Mapping Strategy

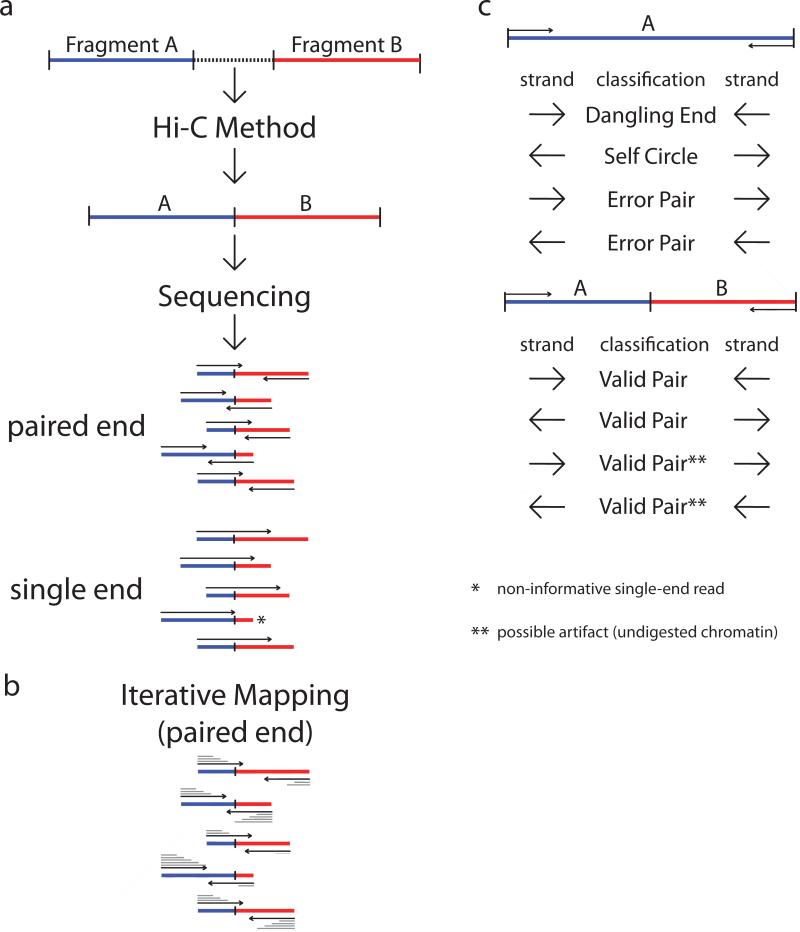
The Hi-C method creates ligation junctions of varying sizes are created (Figure 2a). The molecules are then sheared to the desired size range (normally 100bp – 300bp). Hi-C interactions are simply chimeric ligation products, formed of two distinct genomic fragments joined at the middle. One can thus sequence the ends of the molecule to identify the two pairs in the ligation product most efficiently. However, one could also read the molecule in its entirety and then computationally separate/identify the two distinct genomic fragments, though the exact position of the ligation site is unknown.

Figure2.

Mapping and filtering.(a) Following the Hi-C method, fragments are ligated. Hi-C junctions are then sheared and sequenced. Hi-C junctions can be sequenced by using either paired-end sequencing or single-end sequencing. * - Here a Hi-C junction is incapable of being sequenced by a 100bp single end run, as the read does not extend past the junction into the second fragment. Should the read length increase, then the sequenced read would cross the junction. ** - Here we highlight the fact that same stranded paired reads could be the result of undigested chromatin, and thus would not represent an actual Hi-C interaction. (b) Iterative mapping approach for aligningpaired-end Hi-C reads. In gray, from top to bottom above/below each read, the mapping iterations are shown as the read is extended and re-mapped. Iterative mapping concludes when either the read is uniquely aligned, or the maximal read length is reached. The number of iterations is a factor of mappability and the location of the junction. (c) After mapping, the paired reads can either map to a single fragment, or to different fragments. Reads mapping to a single fragment are considered uninformative. Self-ligations and un-ligated fragments are classified by the read strand. Inward pointing reads are considered un-ligated fragments (“dangling ends”). Outward pointing reads are classified as self-ligated fragments (“self-circles”) as they form circular products. Same-strand reads are classified as “error pairs” as these products are a result of either a mis-mapping, random break, or an incorrect genome assembly. Reads mapping to different fragments are used to assemble the Hi-C dataset. All strand combinations are possible and are expected to be observed in equal proportions (25% per combination). However, inward and outward pairs could be the result of un-digested restriction sites, and then processed as either self-ligated or un-ligated products. Imbalance in the relative proportions of the strand combinations, could suggest the need for additional filtering.

Searching for the ligation junction is possible, but the junction site is not guaranteed to be covered with short reads. For example, given a 300bp Hi-C ligation product where the junction site is located at position 150 (in the center) of the molecule, if one were to perform a traditional 50 base-pair paired end sequencing, only the 50 bases on each end would be sequenced. The 200 internal bases of this molecule would not be sequenced, even though one could still correctly identify each of the interaction pairs. It would be uninformative to first search for the junction site and then split the reads into two, since the junction site is not measured. Instead we favor an iterative mapping approach to solve this problem(Imakaev et al. 2012) (Figure 2b). The idea is to attempt to map as short a sequence as possible before the sequence reaches the junction site. Reads are first truncated to 25bp starting at the 5’ end and mapped to the genome. Reads that do not uniquely map the genome are extended by an additional 5bp and then re-mapped. This process is repeated until either all reads uniquely map or until the read is extended to its entirety. Only paired end reads in which each side can be uniquely aligned are kept. All other paired end reads are discarded.

Fragment assignment

For each mapped read, the genomic alignment location is assigned to one of the restriction fragments, since they can be calculated in advance from the genome sequence. The mapped read is assigned to a single restriction fragment according to its 5’ mapped position. Mapped read positions should fall close to a restriction site, and no further than the maximal molecule length away. Close being a relative term that is defined by the molecule size distribution. Given a normal Hi-C experiment, which is sheared to 100bp-300bp, the location of the ligation junction within each molecule should be normally distributed around the center of the molecule. The mapped reads locationsrelative to the ligation site should then follow this normal distribution. Reads that align more than the maximal molecule length away from the closest restriction enzyme are the result of either non-canonical enzyme activity or non-enzymatic physical breakage of the chromatin. It has been shown that these reads produce informative Hi-C interactions, and thus are not discriminated against (Imakaev et al. 2012). Once each read has been assigned to a restriction fragment, filtering must be applied to discard any technical noise in the dataset.

Fragment-level filtering

After assigning each of the paired-end reads to single fragments, it is necessary to perform some basic filtering. The following two scenarios are possible:

1. The read pair falls within the same restriction fragment.

2. The read pair falls within distinctrestriction fragments.

If the read pair maps to the same restriction fragment, it can represent either an un-ligated fragment (“dangling end”) or a ligated, circularized fragment (“self-circle”). Each of these two cases is considered non-informative, and should therefore be removed. However it is possible that this data could be used for other analyses.

After removing same-fragment pairs, the remaining pairs are filtered to remove any redundant (identical) PCR artifacts. PCR duplicates can be detected by either sharing the exact same paired-end sequence, or by sharing the exact same 5’ alignment positions of the pair. One can also filter for possible undigested restriction sites, which can be identified by both reads mapping to the same strand and the distance between the two mapped positions being small (fits the molecule size distribution).

Binning

The resolution of a Hi-C dataset is determined by the restriction enzyme used. Normally, a Hi-C dataset is not sequenced deep enough to support this maximal data resolution, as it is not yet cost-effective to obtain a sufficient number of reads. Instead, the data can be binned into various fixed genomic interval sizes, to aggregate data and smooth out noise. Hi-C restriction fragments are assigned to bins by their midpoint coordinate. Binning the Hi-C data reduces the complexity and number of possible genome wide interactions which in turn increases the signal to noise ratio. Data is typically binned into sizes ranging from 40kb to 1MB. All bin-bin interactions are simply aggregated by taking the sum, though one could use other more robust methods to aggregate the signal. A single Hi-C dataset can be binned into multiple bin sizes, as each bin size can be used for different analysis goals. Following the binning, the data can be stored in a fixed-size symmetrical matrix format, though this file format may not be optimal for storing large Hi-C datasets since the number of the matrix entries can be much larger than the number of reads.

Bin-level filtering

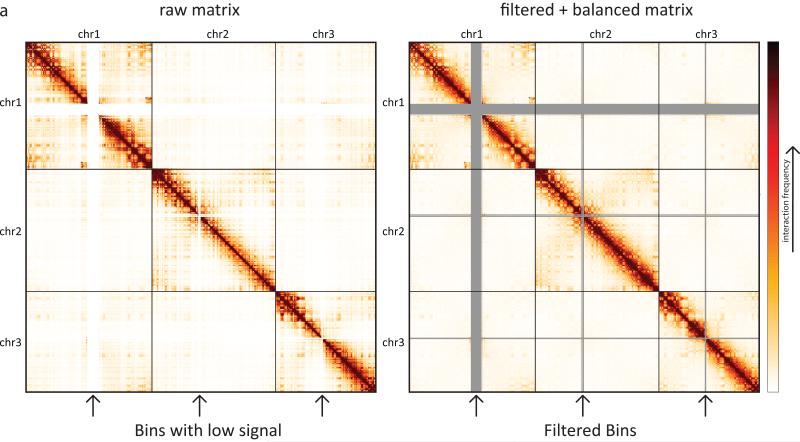
Prior to matrix balancing, it is advised to remove any bins (rows/columns) from the dataset that have either very noisy or too low of a signal. These bins are normally found in genomic regions with low mappability or high repeat content, such as around telomeres and centromeres. Since these bins suffer from such a high noise level, it is useful to remove them rather than attempting to correct them for technical biases (see below). Various methods can be used to detect these bin outliers. Current methods detectbins with low signal by comparing the individual bin sumsto the bin sums of all bins. Outliers can be detected by a percentile cutoff (e.g. removing the bottom 1% of rows/columns), or by using the variance as a measure of noise. Similarly, outlierpointinteractions (bin-bin) can be detected by a percentile-based filter (such as removing the top 0.5% of data points). In some instances, a single binbin point interaction can have a level of reads orders of magnitude higher than one would expect.

Balancing

Hi-C data can contain many different biases, some of known origin and others from an unknown origin. There are two general approaches to Hi-C bias correction: explicit and implicit. Explicit bias models take into account factors such as mappability, GC content and fragment length(Yaffe and Tanay 2011; Hu et al. 2012; Cournac et al. 2012). Alternatively, since it can be quite difficult to know each and every bias, one can use an implicit approachwhich we refer to as balancing (elsewhere known as iterative correction(Imakaev et al. 2012). The balancing procedure is based on the Sinkhorn-Knoppbalancing algorithm(Sinkhorn and Knopp 1967). This procedure attempts to balance the matrix by equalizing the sum of every row/column in the matrix. The procedure is based on the assumption that since we are interrogating the entire interaction space in an unbiased manner, each fragment/bin should be observed approximately the same number of timesin the experiment (interpreted as the sum of the genome-wide row/column in the interaction matrix). The algorithm iteratively alternates between two steps until convergence. First, each row is divided by its mean. Then, each column is divided by its mean.This process is guaranteed to converge. Both explicit bias correction and Sinkhorn-Knopp balancing yield comparable results(Imakaev et al. 2012). Regardless of the method used, it is important to visually assess the data before and after bias correction, in order to determine if the procedure was successful. A successful filtering and bias correction would smooth the interaction matrix such that no obviously high rows/columns would remain.

Analysis and interpretation of Hi-C data

Following the mapping, filtering and bias-correction of the Hi-C data, we are left with a binned, genome-wide interaction matrix, where each entry reflects an interaction frequency between two genomic loci. The measured interaction frequencies are unscaled, in the sense that they cannot be directly translated into an actual fraction of cells. Extraction of relevant biological knowledge from this interaction matrix is one of the major challenges of Hi-C data analysis. This includes differentiating biological signal from noise, identification of interaction patterns and interpretation of these patterns.

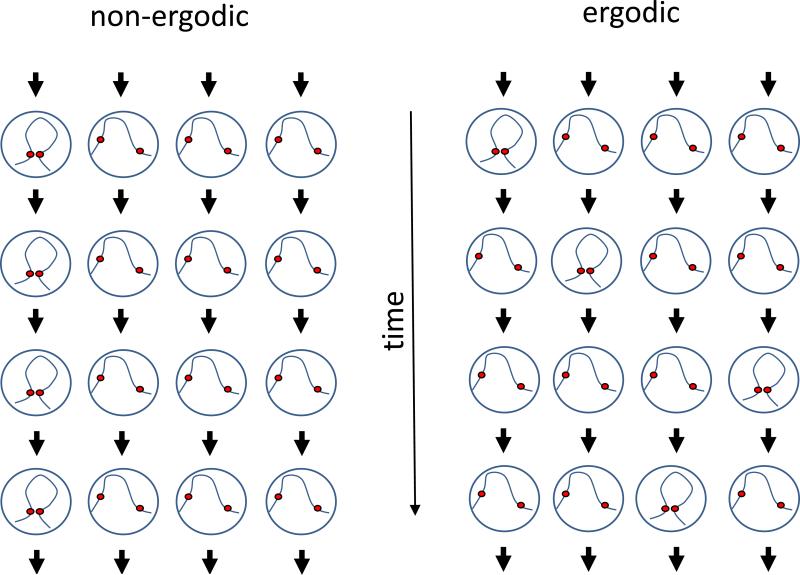
There are a number of factors that complicate this analysis. First, we have to consider the fact that we are measuring interaction frequencies over a population of cells (Figure 4). This is critical in terms of data interpretation since, when we consider an interaction pattern consisting of multiple pairs of loci, we cannot distinguish between scenarios in which interactions will co-occur simultaneously in a single cell, are mutually exclusive, or somewhere in between. Accordingly, observing a “smooth” interaction matrix that shows little position-specific structure does not rule out the existence of structure in the underlying genomes - it simply means that if such structures exist, they are not consistent between cells. Second, a limitation of current analysis methods is that often the patterns are defined implicitly rather than explicitly. In other words, rather than formally define what a specific interaction pattern looks like and search for it in the interaction matrix, interaction patterns are defined as the output of some method. For example, genomic compartments appear as a checkerboard-like interaction pattern (see relevant section), but they are identified using a method that does not explicitly search for this pattern (i.e. Principal Component Analysis). As a result, it is difficult to evaluate the validity of a method or compare methods aimed at identifying the same type of interaction pattern. Third, different types of interaction patterns co-exist and overlap each other. Given that in many cases we lack an explicit definition of these patterns, as mentioned above, it can be difficult to disentangle different types of interaction patterns. In practice, many of the current approaches analyze each interaction pattern separately under a simplifying assumption of independence, i.e. by assuming that either the effect of other patterns is negligible or that the other patterns can be normalized out of the data. Fourth, it is important to remember that Hi-C measures interaction frequency between loci, not distance. Formaldehyde crosslinking will occur only between loci which physically interact. Thus, a weak Hi-C signal between two loci indicates that the interaction occurred in a small fraction of the population, but we cannot determine the distance between the two loci without making some simplifying assumptions about how interaction frequencies relate to physical distances. Finally, we cannot assume ergodicity of interaction frequencies. In other words, frequencies in the cell population cannot necessarily be interpreted as frequencies in time (see Figure 5). For example, an interaction which occurs in a small fraction of cells and thus produces weak signal in Hi-C cannot be concluded to necessarily be an unstable interaction. Alternatively, any assumption of ergodicity should be made consciously.

Figure 4.

Averaging effects in Hi-C data. In this toy example, a square interaction pattern is apparent in the top interaction matrices representing subpopulations, yet its location varies. The final Hi-C interaction matrix, which consists of the average of all subpopulations, does not show the square interaction pattern, and shows a pattern that is not present in individual subpopulations.

Figure 5.

Ergodicity in Hi-C. This toy example follows, over time, the interaction of two loci in a population of 4 cells. Each row represents a time point and each column represents a cell. In the non-ergodic population (left), the interaction is maintained in the same cell over all time points. In the ergodic population (right), the interaction appears in different cells, such that its frequency in time is equal to its frequency in the population (both are 0.25). In Hi-C, which measures a single time point (i.e. a row) in a population of cells, the ergodic and non-ergodic cases are indistinguishable.

Several different types of interaction patterns have been observed in interaction maps. These patterns vary in scale, from genome-wide patterns to point interactions between loci, and in their ubiquity, from constant between different species to condition-specific. Due to the speculative nature of biological interpretation of interaction patterns and the aforementioned complications, it is often useful to separate the process of pattern identification from the process of pattern interpretation. Here we focus mostly on pattern identification, but also briefly discuss common interpretations of each pattern.

We focus on 5 types of patterns typically observed in mammalian genomes. For each pattern, we discuss how it is defined, how it looks visually in the interaction matrix, how it can be identified computationally and how it can be interpreted biologically.

• 1)Cis/trans interaction ratio
• 2)Distance-dependent interaction frequency
• 3)Genomic compartments
• 4)Topological domains
• 5)Point interactions

While we outline possible approaches for independent analysis of each type of pattern, there exist alternative approaches for explicitly considering multiple patterns simultaneously (Sexton et al. 2012). Finally, as with any approach, we advise not to apply the proposed techniques blindly, but rather critically and always visually evaluate the data Indeed, other interaction patterns, which we do not discuss here, have also been observed including patterns resulting from circular chromosomes and centromere clustering (Duan et al. 2010). Such patterns may require careful consideration and the application of specially-tailored methods. Alternatively, methods can be derived given a specific biological question, for example, whether a given set of genes interact more frequently than expected by random.

Following our discussion of individual patterns, we discuss reconstruction of 3D structures from Hi-C data, application of Hi-C data to problems in genome assembly and future directions.

Cis/trans interaction ratio

The strongest interaction patterns which are observed in Hi-C maps are genome-level patterns (Lieberman-Aiden et al. 2009). By genome-level we mean that the patterns are not locus-specific, but instead reflect average genome-wide trends. Two genome-level patterns have consistently been observed in Hi-C data in various species and cell-types.

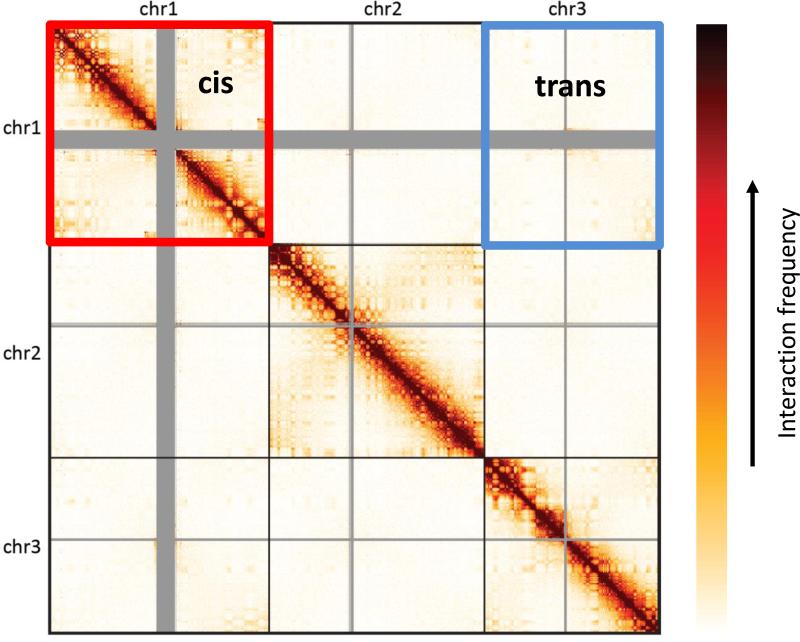
The first pattern is a higher interaction frequency, on average, of pairs of loci which reside on the same chromosome (i.e. in cis) than loci which reside on different chromosomes (i.e. in trans). In a genome-wide interaction matrix, this pattern appears as square blocks, of high interaction centered along the diagonal and matching individual chromosomes (Figure 6). The pattern is likely due, at least in part, to a phenomenon known as chromosome territories, where chromosomes are physically separated and occupy a distinct volume in the nucleus. Since this pattern is largely constant across cell types and species, it is typically less useful for studying aspects that are specific to the given biological system. However, this fact makes this pattern a useful proxy for evaluating the quality of the data. If noise in the matrix, due to factors such as random background ligation, is expected to affect both cis and trans interactions similarly, a noisier experiment will result in a lower ratio between cis and trans interactions. Thus, it is common to use this simple statistic (i.e. the ratio between the sum of the cis interaction frequency and the sum oftrans interaction frequency) to quantify this pattern. Typical values for the cis/trans ratio in high quality experiments are in the range 40-60 for the human genome.

Figure 6.

Cis/trans ratio. A Hi-C interaction matrix (shown on 3 chromosomes for simplicity). Sample cis and trans regions are highlighted.

Distance-dependent interaction frequency

The second genome-level interaction pattern is a distance-dependent decay of interaction frequency. In other words, interaction frequency between loci in cis decreases, on average, as their genomic distance increases. In the interaction matrix this pattern appears as a gradual decrease of interaction frequency the further one moves away from the diagonal. This pattern may be due to random movement of the chromosome, following the intuition that loci which are nearby in the genome will interact frequently if they move randomly in 3D space. The theory underlying this type of intuition is well established in the field of polymer physics (De Gennes 1979; Fudenberg and Mirny 2012). Many basic models of general polymers in polymer physics predict a distance-dependent decay of interaction frequency, where the simplest model, known as the ideal chain, is equivalent to a random walk in 3D space. A central aspect of all these models is that they characterize polymers as distributions, rather than single structures, inherently accounting for randomness and structural variability. Specific models are thus characterized by statistical properties such as the mean interaction probability for a pair of loci separated by a given distance. Thus, by estimating the distance-dependent interaction frequency from our data, which is derived from a population of cells, we can ask which polymer models are consistent with the observed pattern. For example, the distance-dependent interaction frequency of an ideal chain is expected to have the form of the power-law decay p_interaction(x,y)=Z*dist(x,y)^−1.5. In fact, this specific decay matches the distance-dependent interaction frequency observed in yeast.

Analysis of distance-dependent interaction frequency is typically performed using one of two methods. The first method is discrete binning. With this method, we bin all interaction frequencies according to their genomic distance, and calculate the average of each bin. The second method is interpolation. With this method, we fit some continuous function to the data and use this function to represent it. In some cases, binning may be used as a preliminary step for fitting a continuous function. Due to the fact that many polymer models predict a power-law decay, it is helpful to plot the resulting decay function on a log-log plot so that power-law decays will appear linear. However, it is important to perform the calculation of the decay function on the initial data, not on the log-transformed data due to theoretical considerations (Clauset et al. 2009). For related reasons, it is advisable to use logarithmic-sized bins if using the binning scheme, e.g. such that each bin will be double the size of the previous bin.

While it is convenient if the observed distance-dependent interaction frequency matches what is expected by a simple polymer model, this is often not the case. However, it can still be useful to examine a more complicated decay function, since it could provide some insight, such as different regimes of decay at different genomic length scales (Figure 6). This can, in turn, promote the development of more complex polymer models that reproduce the observed pattern. It is important, though, to realize the limitations of this type of analysis. Hi-C data incorporates several different types of patterns, some of which are locus-specific and will thus not be reproduced by these types of models which do not include locus-specific constraints. Additionally, some of these local patterns could affect the shape of the decay function. Finally, even if a Hi-C map contains no locus-specific interaction patterns and is consistent with some polymer model, it is not sufficient by itself to conclude that the model is correct, since other polymer models could potentially produce the same decay function. Ultimately, what matters is how useful such a model is for gaining biological insight and whether it can produce testable hypotheses.

Genomic compartments

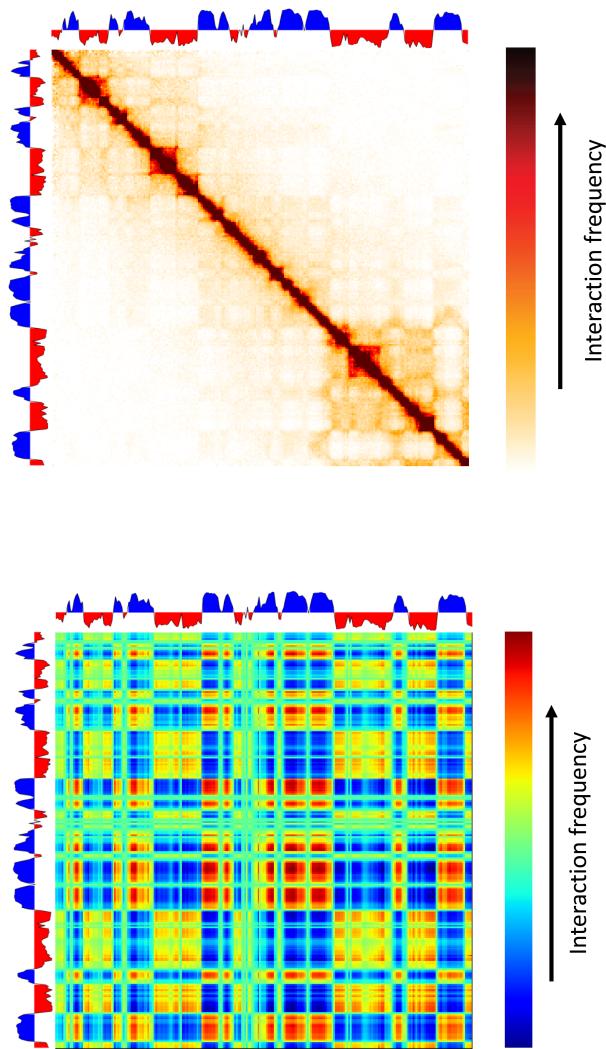
Next, we consider interaction patterns which are position-specific. The largest-scale position-specific interaction pattern is known as genomic compartments(Lieberman-Aiden et al. 2009). This interaction pattern appears on the interaction matrix as a “checker-board”-like pattern consisting of alternating blocks, ~1-10 mb in size (in the human genome), of high and low interaction frequency (Figure 8). This interaction pattern can be explained by a simple underlying principle where chromosomes are composed of two types of genomic regions that alternate along the length of chromosomes and where the interaction frequencies between two regions of the same type tend to be higher than interaction frequencies between regions of different types. We refer to these two types as A and B compartments (Lieberman-Aiden et al. 2009).

Figure 8.

Genomic compartments. Top: Hi-C interaction matrix (shown on 3 chromosomes for simplicity) along with the calculated compartment value (first principal component). Below: outer product of the first principal component with itself yields a rank-1 reconstruction of the interaction matrix.

While this interaction pattern is intuitive, its current definition is implicit - the genomic compartments are usually considered to be given by the first principal component of the interaction matrix. The reasoning for this definition is as follows. Imagine each bin in the 1d genome is assigned a number c(x) quantifying whether it belongs to A (positive value) or B (negative value). Now, we decide that the interaction score between two loci x,y is c(x)c(y). Note that this formulation is sufficient to reproduce a checkerboard pattern: when the types of x,y are the same, their signs will be the same and will yield a positive interaction score, and when their types are different their signs will be different, resulting in a negative interaction score. Thus, given an interaction matrix, we are given all interaction frequencies and want to find the compartment c(x) of each position. It turns out that the first principal component found by a Principal Component Analysis can be viewed as finding the optimal values of c(x) such that difference between the observed interaction frequencies and c(x)c(y) is minimal (mean squared error is minimized). Thus, if the compartment pattern is sufficiently strong, this procedure should find it. Alternatively, one could use any standard clustering approach, such as k-means, to cluster the rows of the interaction matrix into two clusters.

Genomic compartments have been found to be correlated with chromatin state, including DNA accessibility, gene density, replication timing, GC content and histone marks (Lieberman-Aiden et al. 2009). Thus, A-type compartments are defined as the euchromatic gene-dense regions while B compartments are defined as gene-poor heterochromatic regions. Genomic compartments have been found to have high-plasticity, such that they change in different cell-types and biological condition, matching large scale changes in gene activity. Individual compartment blocks tend to be on the order of 1-10 Mb in length, and are thus easy to extract even in experiments with very low sampling. Finally, it is important that while compartment signal is strong and easy to observe in large bins, the interaction frequencies at individual positions that have the same compartment type are quite low. Thus, given that Hi-C measures a population average, it is likely that this pattern reflects a general, highly stochastic, tendency of compartments to interact, rather than a set of deterministic interactions specified by individual loci.

Topological domains

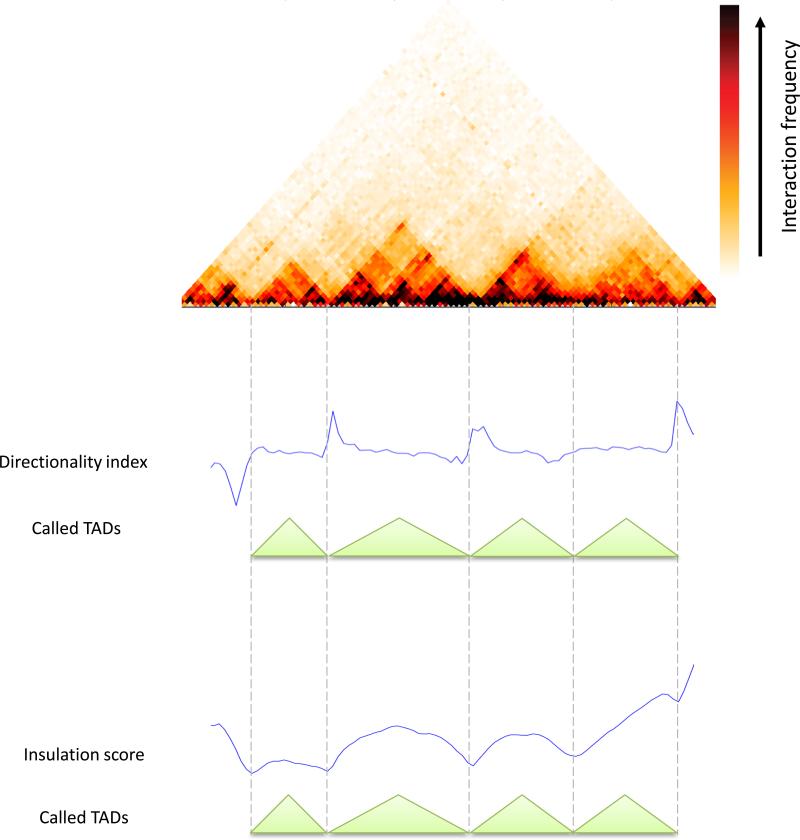
While genomic compartments are useful for understanding general organization principles of the genome, many biological processes occur at a smaller scale. Specifically, enhancer-promoter interactions that underlie gene regulation in metazoans often take place at sub-Mb distances. Recently, 3C-based techniques have revealed the existence of sub-Mb structures that are referred to as topologically associating domains or TADs(Nora et al. 2012; Dixon et al. 2012; Sexton et al. 2012; Hou et al. 2012). TADs are contiguous regions in which loci tend to interact much more with each other than with loci outside the region. In the interaction matrix TADs appear as square blocks of elevated interaction frequency centered along the diagonal (Figure 9). However, the definition of TADs is complicated by the fact that actual interaction patterns are complex and contain multiple hierarchies of overlapping block-like structures, as assessed by visual inspection of chromatin interaction maps. Nonetheless, given some definition of TADs, these domains have been shown to be associated with gene-regulatory features and it is hypothesized that TADs specify elementary regulatory micro-environments in which promoters interact with local enhancers(Gibcus and Dekker 2013; Shen et al. 2012; Symmons et al. 2014). In addition, TAD-like structures of various sizes have been observed in species ranging from mammals to bacteria (Nora et al. 2012; Sexton et al. 2012; Le et al. 2013; Hou et al. 2012; Dixon et al. 2012).

Figure 9.

Topologically associating domains (TADs). A 45-degree rotated interaction matrix shows TAD patterns. Below, the directionality index and insulation score are shown together with the called non-overlapping set of TADs. Data was taken from Dixon et al. (Dixon et al. 2012).

As hinted above, TADs are also often defined implicitly. We outline two such methods for identifying TADs. Both methods take the following approach: First, they summarize the TAD signal using some statistic, such that TAD signal is converted into a 1d profile along the genome. Then, they use the 1d profile to identify potential boundaries between TADs and produce a set of discrete non-overlapping TADs. It is important to note that while these methods provide a useful heuristic for quantifying some of the TAD-level patterns, they do not provide an actual predictive model, or point to physical processes that drive domain formation. Without an explicit definition of TADs, these methods are difficult to compare and evaluate critically. However, it is clear that a discrete set of non-overlapping regions is only a first approximation and likely a significant oversimplification of the interaction patterns which are observed in the data. Alternative approaches are able to accommodate for TADs at different scales (Filippova et al. 2014; Sexton et al. 2012).

An approach by Dixon et al. (Dixon et al. 2012) uses the following statistic: for each bin, we calculate the difference between its average upstream interactions and its average downstream interactions (within some genomic range). This difference is then transformed into a chi-squared statistic and the resulting value is referred to as the directionality index. At the boundaries of TADs, we expect to see a sharp change in the directionality index. Boundaries are then associated with each other using a Hidden Markov Model. Alternatively, others have simply used the ratio between average upstream and average downstream interactions (Naumova et al. 2013).

An alternative approach is to calculate for each bin the average of interaction frequencies crossing over it (within some genomic range). This is referred to as the insulation score and can be thought of as the average of a square sliding along the matrix diagonal(Mizuguchi et al. 2014). We expect that this value will be lower at TAD boundaries. Then one can use standard techniques to find local minima and use those as boundaries, and define regions between consecutive boundaries to be TADs.

The block-like structure of TADs clearly indicates elevated interaction frequency within a TAD. However, given that we measure a population average and the observed intricate hierarchies of such structures, interpretation of TADs is not straight-forward. It has been proposed that TAD-like structure may be driven at least in part by looping interactions between loci located within them (Giorgetti et al. 2014) or by supercoiled plectonemes(Le et al. 2013; Benedetti et al. 2013). Additionally, some genomic features such as CTCF and cohesin binding have been shown to be enriched at TAD boundaries (Dixon et al. 2012; Van Bortle et al. 2014). It remains unclear what physical structures TADs exactly represent and how they are specified in the genome.

Point interactions

The final type of interaction pattern we discuss is point interactions. While TADs may be relevant for constraining promoter-enhancer interactions, the actual regulatory interactions are probably of much smaller scale. Ultimately, protein-mediated interactions of two localized genomic elements, e.g. enhancers and promoters, which are typically up to a kb in length, can activate the expression of a gene. Given sufficient resolution, we expect such point interactions to appear as a local enrichment in contact probability.

As with some of the other interaction patterns, current approaches for finding point interactions do not provide an explicit model of what a point interaction should look like. Instead, these approaches try to find outliers which show higher interaction frequency than expected, where the background model may consist of other previously mentioned interaction patterns (Jin et al. 2013; Sanyal et al. 2012; Ay et al. 2014a). Typically, the background model consists only of the strongest signal, namely the distance-decay function, but other patterns such as TADs can be incorporated as well. Given a background model, we can then test the significance of individual pairwise interactions. The resulting set of significant high outliers would then need to be corrected for multiple testing. It is important to note that without an explicit model of point interactions, it may be difficult to distinguish between real point interactions and experimental noise. Thus, it may be helpful to provide additional evidence including analysis of biological replicates, and from alternative methods as to the validity of such interactions (e.g. by showing enrichment for enhancers and promoters).

While the biological interpretation of point interactions seems to be straightforward, it is important to consider what such methods find. If we look for interactions that have a higher interaction frequency then what is expected given their distance, we are not evaluating their absolute interaction frequency. For example, consider two loci which are nearby in the genomic sequence, and are thus expected to interact very frequently. Such interactions may be functional and biologically important, but they may not have a much higher interaction frequency than expected by distance, and thus may not be found to be point interactions. Similarly, the expected interaction frequency for loci that are separated by large genomic distances is very low. As a result even a small increase in their interaction frequency can make their interaction statistically significant even though their absolute interaction frequency is still low, implying it occurs in only few cells. Thus, careful biological evaluation is always in order for interpreting any statistical approach to identifying point interactions.

Structure reconstruction and polymer modeling

Given that Hi-C measures an aspect of the 3D structure of the genome, it is natural to ask whether we can use Hi-C data to infer the underlying 3D structures. In fact, Hi-C maps are reminiscent of 2D NMR spectrum maps used to infer 3D protein structure with great accuracy. However it is important to realize that there are important differences between protein structure and genome structure that dramatically complicate inference of the genome structure. First, inference of protein structures incorporates knowledge of protein physics and the underlying sequence. There are strong constraints on what conformations are physically possible and there is a relatively good understanding of the physics of various intramolecular interactions. On the other hand, knowledge of chromatin physics is limited and chromatin structure is much less constrained than protein structure. Second, chromatin fibers are much longer than proteins, in the sense that the length of a chromosome may be as much as 10⁵-10⁶ times larger than the smallest structures of interest in the chromosome. Third and most importantly, chromatin structure is much more variable than protein structure, yet we observe only the population average. In fact, it is debatable whether it is even useful to infer a single average “consensus structure”, given the highly-stochastic nature of the genome structure.

With these limitations in mind, we consider 2 general approaches to structure inference from Hi-C data:

• 1)Consensus structure. These methods essentially ignore the fact that structure is variable across the population and try to find a 3D structure that is as consistent as possible with the 3D interaction matrix (Duan et al. 2010; Rousseau et al. 2011; Hu et al. 2013; Zhang et al. 2013; Ay et al. 2014b; Varoquaux et al. 2014; Baù et al. 2011). Most methods follow some form of multidimensional scaling, formalized as seeking 3D coordinates for all loci such that their pairwise distances are as consistent as possible with the observed interaction frequencies. These approaches require making assumptions on how interaction frequency of loci is related to their spatial distance.
• 2)Ensemble of structures. These methods typically try to create a set of structures such that either the average distances or the contact probability between every two loci are consistent with the observed interaction frequencies (Giorgetti et al. 2014; Marti-Renom and Mirny 2011; Hu et al. 2013). While this approach resembles the actual biology more closely, allowing for multiple structures makes the problem even less constrained. In other words, there are likely many different ensembles of structures that could explain a given interaction Hi-C matrix. Additionally, such an ensemble of structures may be difficult to interpret.

Once again, the utility of such models will be measured by whether they can give biological insight and make useful predictions.

Genome rearrangements and genome assembly

Typically, Hi-C data is mapped to a known high-quality genome sequence and is used to answer questions regarding the 3D organization of genomes. However, it has recently been shown in a number of studies that Hi-C data can be useful to learn about the 1D arrangement of the genome sequence and thus solve a number of outstanding problems in the field of genome assembly (Kaplan and Dekker 2013; Burton et al. 2013, 2014; Beitel et al. 2014; Selvaraj et al. 2013). Ironically, the recent major advancement of DNA-sequencing technologies has caused a decrease in the quality of genome assemblies due to the use of short reads. Thus, genomes assembled from short-read data consist of huge sets of contigs (~100000 contigs for Gb-scale genomes), which cannot be grouped and ordered with this type of data. However, by mapping Hi-C data to a set of contigs, we gain interaction frequency data over very large genomic distances. We can then exploit a number of universal principles relating 1d structure to 3D structure in order to associate and order contigs in linear genome. We refer to this set of approaches as DNA triangulation, due to their use of multiple lines of long-range evidence (i.e. Hi-C interactions) to resolve genomic positions.

We list these principles and how they can be used:

1. Interactions of loci located in different nuclei are less frequent than those in the same nucleus. This principle seems obvious, but has important implications. In microbiome studies, which analyze large mixed populations of different species, high-throughput sequencing typically yields a large set of contigs, yet it is difficult to establish which contigs belong to the same genome. Using Hi-C data, we can determine that if two contigs interact frequently in 3D they are likely to belong to the same genome with high probability (Burton et al. 2014; Beitel et al. 2014).

2. Interactions of loci located on different chromosomes are less frequent than those in the same chromosome. As discussed above, this pattern is both strong and ubiquitous. When performing de novo genome scaffolding, we can thus use Hi-C data to determine that contigs that interact frequently are likely to belong to the same chromosome (Kaplan and Dekker 2013; Burton et al. 2013). Additionally, since homologous chromosomes are also separated into distinct territories, this principle can be used to perform haplotype phasing. A Hi-C paired-end read that maps to one SNP on each side is much more likely to come from the same chromosome than from the homologous chromosome (Selvaraj et al. 2013).

3. Interactions of loci located far from each other along a chromosome are less frequent than loci that are near each other. Using Hi-C data, we can arrange contigs which belong to the same chromosome such that strongly interaction contigs are positioned next to each other (Burton et al. 2013; Kaplan and Dekker 2013).

While the goal of these techniques is not necessarily to learn about the 3D structure of the genome, it is clear that they are widely useful. When indeed such techniques will be adopted, they may offer large amounts of Hi-C data as an important side benefit. However, if one's goal is to use Hi-C for DNA triangulation, it could be useful to carefully consider some of the experimental design and analysis choices. For example, locus-specific interaction patterns are important for studying the biology of genome structure but could pose problems for DNA triangulation. Pooling different cell types, computationally or experimentally, could average out some cell-specific interaction patterns.

Future challenges

Since Hi-C is a relatively new method and due to its growing popularity, many of the current analysis methods are based on heuristic approaches that are often tailored to answer a research question specific to one study. As the field matures, it will be important to develop rigorous theoretical foundations for Hi-C analysis. In the specific case of pattern detection, it would be useful to develop methods based on an explicit definition of each pattern. While it is good to have a variety of ways to analyze Hi-C data, it would be helpful to converge on some subset of techniques, rather than reinvent new analysis methods in each published paper. This would help make future results easier to compare and interpret. In this respect, there is a growing need for comparative studies that quantitatively contrast different Hi-C analysis methods (e.g. a comparison of 3D structure reconstruction methods). Such comparisons may not be trivial, since no alternative “gold standard” exists, and would probably need to rely on simulations. Nevertheless, comparative studies can be instrumental in advancing and consolidating some of the existing methodology.

Figure 3.

Hi-C interaction matrix for 3 chromosomes. On the left, raw Hi-C data. On the right, filtered and balanced Hi-C data. The arrows below the heatmaps mark bins (rows/cols) that are filtered. Following the balancing procedure, the sum of each row/col is equal. This results in an overall smootherheatmap.

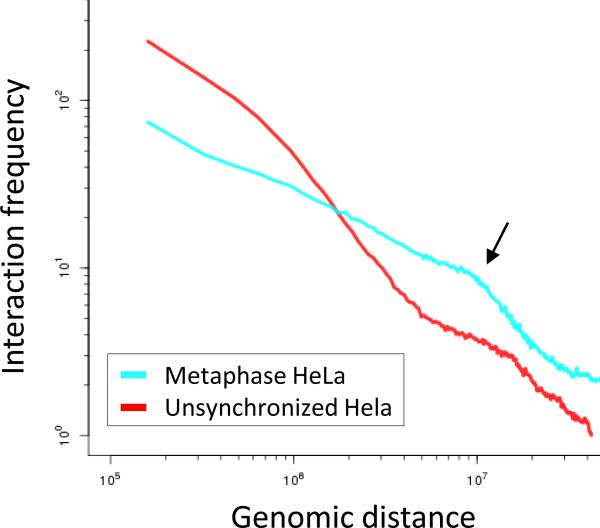
Figure 7.

Distance-dependent interaction frequency.Shown are distance-dependent interaction frequency curves for metaphase and unsynchronized HeLa Hi-C from (Naumova et al. 2013). Note the slope change in the metaphase data which occurs at 10Mb (indicated by the black arrow). Thus, loci separated by fewer than 10 Mb interact frequently, whereas loci separated by more than 10 Mb rarely interact. This information has been incorporated into polymer models of mitotic chromosomes.