Abstract
Increasing interest in understanding dynamic interactions of brain neural networks leads to formulation of sophisticated connectivity analysis methods. Recent studies have applied Granger causality based on standard multivariate autoregressive (MAR) modeling to assess the brain connectivity. Nevertheless, one important flaw of this commonly proposed method is that it requires the analyzed time series to be stationary, whereas such assumption is mostly violated due to the weakly nonstationary nature of functional magnetic resonance imaging (fMRI) time series. Therefore, we propose an approach to dynamic Granger causality in the frequency domain for evaluating functional network connectivity in fMRI data. The effectiveness and robustness of the dynamic approach was significantly improved by combining a forward and backward Kalman filter that improved estimates compared to the standard time-invariant MAR modeling. In our method, the functional networks were first detected by independent component analysis (ICA), a computational method for separating a multivariate signal into maximally independent components. Then the measure of Granger causality was evaluated using generalized partial directed coherence that is suitable for bivariate as well as multivariate data. Moreover, this metric provides identification of causal relation in frequency domain, which allows one to distinguish the frequency components related to the experimental paradigm. The procedure of evaluating Granger causality via dynamic MAR was demonstrated on simulated time series as well as on two sets of group fMRI data collected during an auditory sensorimotor (SM) or auditory oddball discrimination (AOD) tasks. Finally, a comparison with the results obtained from a standard time-invariant MAR model was provided.
Introduction
Functional magnetic resonance imaging (fMRI) utilizing the blood oxygen level dependent (BOLD) effect as an indicator of local activity is a very useful technique to identify brain regions of interest that are especially active during perception, cognition, action, but also during rest. There is considerable interest in identifying relationships between the active regions in order to better understand neural organization. It is already generally believed that human higher cognitive functions emerge from dynamic interactions of brain networks (McIntosh, 2000). This leads to formulation of connectivity analysis methods which attempt to identify associated brain connectivity networks and their interactions.
The concept of functional connectivity in the analysis of fMRI data, which is defined as the correlations between spatially remote neurophysiological events (Friston, 1994), was recently extended to the concept of functional network connectivity (FNC) (Jafri et al., 2008; Londei et al., 2006). The goal of FNC is to characterize distributed changes in the brain by examining the functional interaction among different correlated brain networks, usually identified by independent component analysis (ICA) (Calhoun et al., 2001b; McKeown et al., 1998).
ICA is a method for recovering underlying signals from linear mixtures of these signals and draws upon higher-order signal statistics to determine a set of components that are maximally independent of each other (Calhoun and Adali, 2006). ICA is known to effectively find and characterize functional networks in fMRI data collected during the performance of a task as well as in resting state (Van de Ven et al., 2004). Within a given spatial component, the regions are by definition strongly temporally coherent due to the linear mixing assumed by ICA. In the FNC context we consider weaker dependencies among components. In spatial ICA the spatial maps are maximally independent, but the time courses of the components are not independent and can exhibit considerable mutual temporal dependencies. These temporal dependencies among components time courses are significant, but are not as large as those between regions within a component (where such large dependences are the case, they would likely have been included within a single component) (Calhoun et al., 2003).
In order to quantify the strength of interactions between brain regions and to reveal directed interactions of activated brain areas, Goebel et al. (2003) proposed using a Granger causality test (GC) (Granger, 1969) on fMRI time series of selected regions of interest. They employed the measure of linear influence between two time series suggested by Geweke et al. (1982). Londei et al. (2006; 2007) carried out an analysis similar to (Goebel et al., 2003) except that Granger causality was applied to the time courses associated with ICA components. Subsequently, Demirci et al. (2009) followed the same concept by utilizing GC in the frequency domain. Similarly, Liao et al. (2010) applied conditional Granger causality (Chen et al., 2006) to the ICA time courses extracted from resting state data.
The principle of GC is based on the concept of temporal predictability and its calculation rests upon multivariate autoregressive (MAR) modeling. Accordingly, if considering past values of time series A improves the future prediction of time series B, then A is said to have a causal influence on B.
GC is frequently compared with another common brain connectivity method, dynamic causal modeling (DCM) (David et al., 2008; Friston et al., 2003; Roebroeck et al., 2009). Both of them have their own advantages. Unlike DCM, GC only requires the pre-specification of regions of interest (ROIs) and does not make any assumption about the connections between them. In this sense, the role of GC in fMRI connectivity analysis is rather exploratory (without need of a prior hypothesis). Second, it has the potential to incorporate a large number of ROIs (Deshpande et al., 2008), where the constraint that the number of time points must be greater than number of ROIs is easily satisfied in typical fMRI experiments. On the other hand, GC is based only on predictive power between fMRI signals, i.e. it points out the directional linkage between signals, but it does not have to be consistent with the underlying neurophysiologic mechanism (David et al., 2008).
Recently, a measure of GC more suitable for application to neurophysiologic data, called the generalized partial directed coherence (GPDC) was introduced by Baccala et al. (2007). This measure enables an appropriate extension to multivariate (not only bivariate) analysis and is represented in the frequency domain.
Concerning the frequency domain representation of fMRI data in a connectivity framework, Cordes et al. (2001) performed spectral analysis using cross-correlation maps obtained from time courses of voxels. They found that low frequency fluctuations (< 0.1 Hz) constituted more than 90% of the correlation coefficient spectrum. Physiological (respiratory, 0.1 Hz to 0.5 Hz and cardiac, 0.6 Hz to 1.2 Hz) noise contributed only by 10 % to the functional connectivity maps. Similarly, Sun et al. (2004) found that low frequency coherence maps (< 0.15 Hz) identified functionally relevant regions. Therefore, we believe that investigating the spectral behavior of FNC can also be useful in understanding the complex interactions in the brain and their impact on the brain disorders.
The standard MAR modeling is an adequate approach only when time series are stationary. However, fMRI times series are always at least weakly nonstationary (Gaschler-Markefski et al., 1997). Therefore, the application of a dynamic MAR model should be preferable to trying to make time series stationary by using their time-derivatives (i.e. differences in the discrete case) of each time series (Sato et al., 2009), because this procedure could complicate the interpretation of results; what is being assessed then is the causal connectivity among changes in each time series. Sato et al. (2006) introduced dynamic MAR by fitting time-varying coefficients using wavelet basis functions to access Granger causality in time domain. However, in later publications, the same author returned to using time-invariant MAR models in combination with GPDC (Sato et al., 2009).
Our main aim is to deal with nonstationary properties of fMRI time series, assessing also the interaction of FNC in the frequency domain. For this purpose, we propose a dynamic MAR model based on Kalman filtering (Kalman, 1960) in combination with GPDC as a measure of Granger causality. The utilization of the Kalman filter in order to adaptively estimate the MAR models found an already successful application in processing of EEG data (Arnold et al., 1998). In the present paper, we introduced the combination of forward and backward Kalman filters to obtain smoothed and more consistent results.
The paper is organized as follows. First, we derive an extension of the time-invariant MAR model to a dynamic model based on the Kalman filter. Next, we compare the performance of the standard MAR model with that of our dynamic MAR model on simulated nonstationary fMRI time series. Finally, we apply our proposed approach to two different fMRI group data sets obtained during an auditory sensorimotor task and an auditory oddball task analyzed with group ICA (Calhoun et al., 2001a). We make a comparison with the results obtained by a standard MAR model and investigate the effect of different model orders on results from both models and evaluate results when utilizing fMRI time courses from original data in contrast to ICA time courses.
Methods
Dynamic MAR by two Kalman filters
In this section we present a state-space MAR model with time dependent coefficients and provide a recursive algorithm for implementation of a Kalman filter followed by Kalman smoother based on estimates of two optimal filters. MAR modeling represents a discrete-time multivariate linear stochastic process given by
| (1) |
for t = 1, 2, …, N. Thus, the time series can be considered as the output of a linear all-pole filter driven by a white noise signal, where N is the signal length, p the order of MAR model, yt the i-th measurement vector of dimension d × 1, Ak the k-th d × d coefficient matrix weighting the measurement yt−k, and εt an d × 1 sequence of zero-mean white Gaussian measurement noise.
Considering nonstationarity of fMRI time series we assume the coefficient matrices of the above MAR model to be time-varying,
| (2) |
In order to utilize the Kalman filter algorithm, it is necessary to create a state-space representation of the model shown in Equation (2). This can be achieved by arranging the coefficient matrices into a vector and using the following notation
| (3) |
| (4) |
| (5) |
where Id is an d × d identity matrix and ⊗ represents Kronecker product. An appropriate state-space representation of the MAR model with time-varying stochastic coefficients can be formulated as
| (6) |
| (7) |
where at is the pd2 × 1 coefficient state vector, f(․) is the linear function which describes the state evolution over time, and νt is a pd2 × 1 sequence of state process noise modeled as zero-mean white Gaussian noise with covariance matrix Qt. The measurement equation (7) describes the observation model which transforms the state vector into the measurement space. In this case, the time-varying measurement matrix Ct is assumed to be linear with additive measurement noise εt. The additive measurement noise is considered to be white Gaussian with noise covariance matrix Rt and uncorrelated to the state noise process. Suppose that the evaluation law of the state vector at is a random walk process, which results in the following state space representation instead of Eqs. (6) and (7)
| (8) |
| (9) |
The initial coefficient state vector a0, which is generally unknown, is thus modeled as a random variable, with Gaussian distribution of mean value â0 and covariance matrix P0|0. It is considered to be uncorrelated to the noise processes, ∀t > 0.
According to the standard forward Kalman filter, the recursion prediction step consists of:
| (10) |
| (11) |
where Pt|t−1 is the one step ahead prediction of the state covariance matrix, Pt−1|t−1 is the estimate (error) covariance matrix of the state vector, ât|t−1 is one step ahead prediction of state vector, and ât−1 is the filtering estimate of the state vector at−1.
After the prediction step, the update step follows, where the current state of the system is estimated given the measurement at that time step
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
From the incoming measurement yt and the optimal state prediction ât|t−1 obtained in the previous step, the innovation sequence is defined by (12), which leads to the estimate of noise covariance matrix Rt (13) using the t most recent residuals (Schlogl et al., 2000). The update coefficient λ ∈ (0,1], also referred to as the forgetting factor, is a constant that has to be selected a priori. The matrix Gt is the filter gain, which tells us how much the prediction ât|t−1 should be corrected on time step t, and the covariance matrix Qt of state noise can be calculated according to Eq. (16).
Once the forward recursion estimate of the Kalman filter is performed, we suggest running the filter also in the backward direction using the estimates from the last step of forward filter as an initialization. Finally, by combining the two filters (forward and backward estimates), the optimal smoothed solution (Fraser and Potter, 1969) of the dynamic MAR model is obtained as:
| (18) |
where superscripts f and b represent the pertinence to forward and backward estimates, respectively. In our case, this procedure turned out to be more efficient than the typical Kalman smoother known as the Rauch Tung Striebel smoother (Rauch et al., 1965).
Model order selection criteria
A major concern with parametric analysis methods is the order selection of the autoregressive (AR) model. If the order is too small, the frequency content in the data cannot be resolved and the spectral estimates will be biased and smoothed and consequently, some information will be lost. On the other hand, if the model order is overly large, spurious peaks (instabilities) can occur in the spectral estimates, which result in a large variance of error and might be misleading thus causing wrong identification. AR order selection criteria based on information theoretic criteria are available, e.g. the Akaike information criterion (AIC, (Akaike, 1974) or Bayesian information criterion (BIC, (Schwarz, 1978). Their advantages and disadvantages have been addressed extensively, e.g. (Lütkepohl, 2005).
| (19) |
| (20) |
where p is the model order; T is the length of time series; R is the covariance matrix of the measurement noise; and d is the number of the time series under investigation. Both of these criteria using maximum likelihood principle, make a compromise between model complexity and goodness of fit, and track both the decreasing error power and the increasing spectral variance with respect to an increasing model order. The measurement noise covariance matrix might be obtained as a part of the Kalman algorithm or alternatively, as preferred here, through the standard MVAR model (Schneider and Neumaier, 2001), because we can thus notably cut the computation cost related to this estimation. However in the case of nonstationary time series, this is at the expense of possible less accurate estimate of the model order. The optimal solution could provide order-recursive filters, e.g. adaptive lattice filters (Haykin, 2002), which similarly as the standard MVAR enable obtaining covariance matrices of measurement noise for all model orders less or equal to p during a single run.
Generalized partial directed coherence
The conceptually interesting measure of Granger causality originates in econometrics (Granger, 1969) where it passed several statistical testing procedures (Lütkepohl, 2005). In general, Granger causality is not reciprocal since aij(k) = 0 does not imply aji(k) = 0, which allows detection of possibly uni/bidirectional interactions and one can then speak about directional connectivity. The original version of Granger causality defined in time domain was later extended also to frequency domain (Geweke, 1982), both based on estimates of MAR model. These measures are well defined especially for the pairs of time series, whereas multivariate generalization is not that obvious. The first multivariate approach in the frequency domain based on GC was directed transfer function (DTF) suggested by (Kaminski and Blinowska, 1991). However, a disadvantage of this measure is the inability to distinguish direct and indirect relationships between signals, i.e. if the causality from source A to source B is mediated by a third source C, the DTF would identify a connection between A and B, even though there is no direct relation between these two sources. Later, partial directed coherence (PDC) and direct DTF were introduced, both of which can distinguish direct and indirect connections (Baccala and Sameshima, 2001; Korzeniewska et al., 2003). These quantities were shown to be more appropriate in application to multivariate data and keep the advantage of discriminating frequency content of the involved signals. Both of these properties can contribute to better interpretation and understanding of brain connectivity results deduced from fMRI experiments. Conditional Granger causality (Geweke, 1984) is another measure whose application is restricted to three signals. Because of this, for higher dimensional systems, this method has to be applied multiple times (Chen et al., 2006). In order to improve this procedure, Zhou et al. (2008) suggested using the reference signal based on principal component analysis (PCA) reduction as a composite vector of the remaining signals. Possibly better solution offers partial Granger causality (Guo et al., 2008).
Most recently, a normalized PDC metric called generalized partial directed coherence (GPDC), which includes variance stabilization of the frequency domain representation of Granger causality, was derived (Baccala et al., 2007). It was shown in (Baccala et al., 2006) that this variance stabilization property improves the decision error rate of classified causal influence and is thus especially important in bootstrap-based approaches to test for significant connectivity.
Based on previous experiences (Florin et al., 2010; Sato et al., 2009), we believe that out of all the above mentioned measures the GPDC is the most appropriate for application to fMRI data. Therefore, GPDC will be considered as a representative of multivariate frequency domain Granger causality in our paper.
The GPDC involves the transformation of MAR coefficients into frequency domain via Fourier transform:
| (21) |
where A(f) is the spectral representation of the coefficient matrix A(t) that can be - thanks to our dynamic MAR model - calculated for each time point of time series using smoothed estimates of MAR coefficients. The estimation of GPDC for the information flow from yi time series to yj time series for each time step t is then defined as
| (22) |
here σ2 are diagonal elements of noise covariance matrix Rt. The GPDC is normalized such that |GPDCij(f, t)|2 ≤ 1 and for all 1 ≤ j ≤ N; this can be interpreted as the strength of connectivity between neural structures, when the square modulus of GPDC value from i-th time series to j-th one is understood as the proportion of the power spectra of the j-th time series, which is sent to the i-th series including the effects of other time series. Furthermore, calculating GPDC over time propagation of the dynamic MAR estimates enables us to visualize this measure also in the form of spectrograms.
Hypothesis Testing of Connectivity
The measure of Granger causality is known to have highly nonlinear relationship with original time series from which it is derived, resulting in nonestablished distribution of applied estimator (Kaminski et al., 2001). Additionally, noise in fMRI signals is non-Gaussian (Wink and Roerdink, 2006), which also contributes to difficulty in obtaining null hypothesis of no causality (GPDC = 0) across multiple subjects, especially when number of subject is usually small. Therefore, the performance of statistical significance testing is fastidious task.
Here we have adopted the procedure suggested in (Sato et al., 2009), based on resampling of residuals of estimated MAR model in order to obtain empirical null distribution of no connectivity for group of subjects. The following steps are considered: (1) fit dynamic MAR models for the BOLD time series of each subject separately and obtain residuals and median of coefficient estimates over time for each subject; (2) for each frequency, calculate the GPDC measure according to Eq. (22); (3) obtain the median GPDC across subjects at each frequency (observed GPDC); (4) for each subject, resample the residuals (random sampling with replacement) stored in step 2; (5) to test the influence from time series j to i, assume a model where the MAR coefficients , l = 1, …, p, are set zero. The other coefficients remain as originally estimated by dynamic MAR; (6) by using the resampled residuals obtained in step 4, and the model coefficients specified in step 5, simulate a bootstrap multivariate time series to generate time series under the null hypothesis of “no causality” from time series j to i; (7) calculate the median GPDC for this bootstrap sample; (8) repeat steps 4–7 until desired number of bootstrap samples is achieved; (9) estimate the critical value for each frequency using the median GPDC bootstrap samples. The critical value is defined as the (1 − α) quantile of bootstrap samples, where α is the expected Type I Error; (10) compare the observed median GPDC with the estimated critical value.
Alternative way for statistical significance testing of no causality suggested by (Deshpande et al., 2009) would be to perform bootstrap procedure by reshuffling the phase of time series without replacement in the frequency domain and then transform back into the time.
Simulations
The main purpose of this section is to demonstrate superiority of GPDC obtained by dynamic MAR method based on Kalman filtering compared to standard MAR estimation. In the ideal case when no nonstationarities, only additive Gaussian noise, and no region specific hemodynamic response function are present in the simulated time series, both approaches can perform very well obtaining almost identical results. However, this situation is far away from what is present in real fMRI data. Time series of fMRI data are always at least weakly nonstationary (Gaschler-Markefski et al., 1997), additive noise does not have Gaussian distribution (Wink and Roerdink, 2006), and it is well known that different regions in the brain can have their specific shape of hemodynamic response function (HRF) (Aguirre et al., 1998). Therefore, in order to compare performance of our proposed dynamic method and standard MAR method one needs to consider more realistic simulations, when their properties are closer to real fMRI time series.
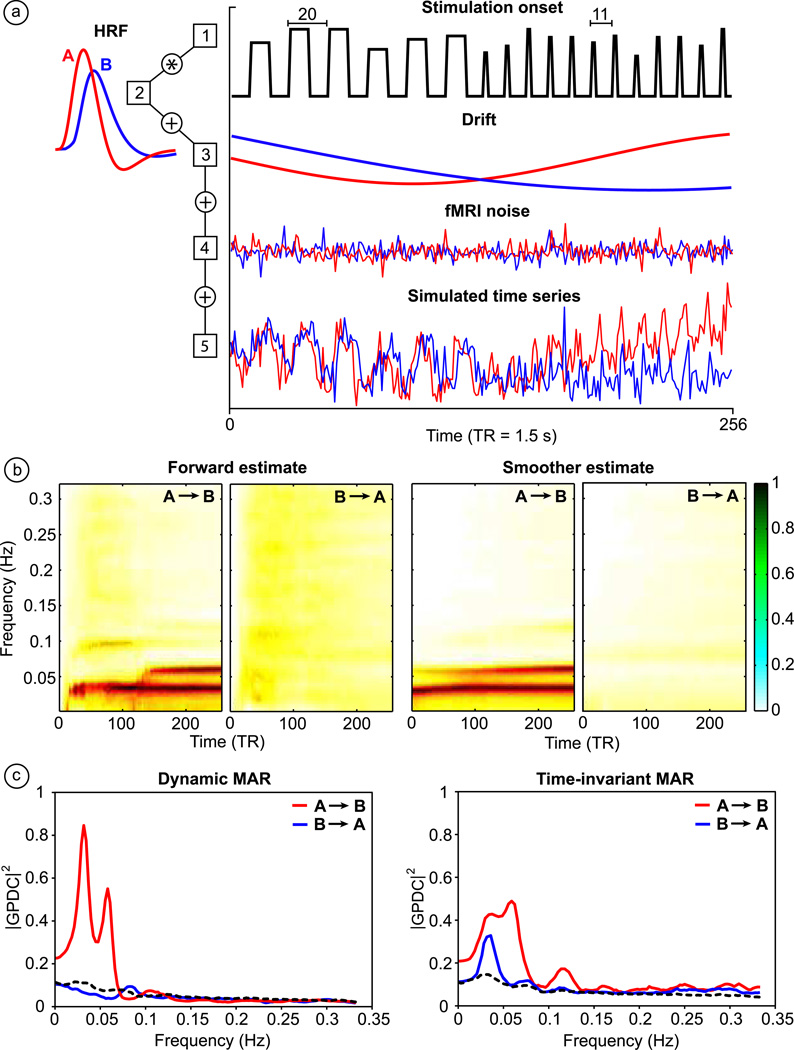
Here we consider two times series A and B of the length of 256 samples with repeat time (TR) 1.5 s, when the time series A causes B modeled as follows. Stimulation onset function consists of two different stimuli (Fig. 1a). Duration of the first onset set is 10 samples, repeating with 20 samples period. Onset of the second stimulus takes 2 samples, repeating with a period 11 samples. Also the variability of amplitude of stimuli is present. The stimulation function is convolved with HRF modeled as difference of two gamma functions using Matlab (MathWorks, Inc.) function from SPM5 toolbox (www.fil.ion.ucl.ac.uk/spm). The HRF is specified by seven model parameters: delay of response relative to onset (in seconds); delay of undershoot relative to onset (in seconds); dispersion of response; dispersion of undershoot; ratio of response to undershoot; onset (in seconds); length of kernel. In order to simulate region specific shape of HRF, for time courses A and B we used HRF parameters (6; 10; 1; 2; 6; 0; 20), and (8; 16; 1; 1; 6; 0; 20), respectively. From the first parameter it is obvious that these two time series are mutually delayed by 2 samples. Next, low frequency drift modeled by cosine functions was added. Finally, to simulate realistic fMRI noise we utilized residual estimates obtained during the typical general linear model approach applied to fMRI data of the auditory sensorimotor task. Twenty percent of the normalized functional maximum of resampled residuals (with replacement) was added to the simulated time series.
Figure 1. Simulated data and comparison of dynamic and standard MAR approach.
Illustration of non-stationary fMRI time series simulation process, where time series A causes time series B (a); spectrograms of GPDC (both directions) obtained by performing dynamic MAR model based on Kalman filtering before and after smoothing procedure (b); median frequency profiles of GPDC for dynamic MAR and time-invariant MAR estimates (c). The dashed line shows upper bound of 95 % confidence interval under the hypothesis of no connectivity between the components.
In this way we have generated 100 pairs of time series. All with the same causal predetermination and character of hemodynamic response, but with slightly different variability of amplitude of stimulation function, with different low frequency drift, and different additive noise.
Before accessing the MAR modeling all pairs of time series were adjusted to have zero mean and unit variance. After this preprocessing step, simulated time courses were further analyzed by the standard MAR model based on the ARfit algorithm (Schneider and Neumaier, 2001) as well as by our dynamic MAR procedure. The selection of model order in this bivariate case was based on AIC, estimated for each of 100 pairs of time series. The common model order 13 was identified as a minimum of the average AIC function. In the case of dynamic model we also had to choose the update coefficients (λ = 10−4) a priori, when this selection was based on minimization of relative error variance (Schlogl et al., 2000) in combination with previously selected model order. In general, slow signal changes require a smaller update coefficient. Also, with a smaller update coefficient (forgetting factor), the previous (older) state estimates are remembered longer by the Kalman filter, resulting in the presence of earlier estimated frequency components in the later time evolution of spectra. Generally, one can expect that a larger model order requires a smaller update coefficient and vice versa.
The GPDC was calculated for each pair of the time series (of 100) based on estimates of the dynamic and standard MAR models, respectively. The dynamic approach allowed us to calculate the GPDC measure for each time point of the time series, i.e. we obtained spectrograms of Granger causality for both tested causal directions. Additionally, we provide also a comparison between results obtained by using only forward Kalman filter estimates and by using Kalman smoother estimates. In this case, it is apparent that using the Kalman smoother step leads to cleaner results. The final results are obtained as a median over all spectrograms (or spectra for standard MAR) related to 100 generated pairs of time series and single frequency profile (in the case of dynamic approach) is received as a median over spectrogram time axis of the smoothed estimate. In principle, it is not necessary to always calculate GPDC for each point of the time series and thus to create spectrograms. Usually, it is sufficient to calculate the median of the estimated MAR coefficients matrices A and the covariance matrices of measurement noise R (over time points), and to obtain GPDC estimate only of single spectra. However, spectrograms can be helpful in order to inspect if the spectral results are more or less stable as time evolves. Since the time resolution is rather low in fMRI and measured sessions are not very long, the spectrograms provide (in case of real data) useful information about the progress of MAR coefficient estimation.
In order to distinguish between relevant causal relations indentified by models and causal relations estimated by chance, a 2000 repetition bootstrapping procedure was performed. We considered the upper bound of 95 % confidence interval from the generated empirical null distribution as a threshold above which the estimated GPDC values are assumed to be consistent and significant (Fig.1c dashed line). This threshold is estimated for each causal direction between time series. Only one threshold for both directions is shown in the Fig. 1c because they were very similar.
From Fig. 1c, it can be seen that the causal influence from time series A to B was identified by both approaches with driving frequencies 0.034 Hz, 0.06 Hz. The first frequency corresponds almost exactly to the repetition period of the first stimulation function, and second frequency matches the period of the second stimuli. However, only results based on the dynamic MAR modeling are consistent within the 95 % confidence interval.
Our simulations show that when nonstationarities are present in the time series, the dynamic MAR model based on Kalman filter and smoother performs better than the standard MAR model, leading to more consistent results of Granger causality (GPDC).
Beside this, we also observed that the lower performance of the standard MAR model is caused mainly by the variation of the HRF shape. For simulations, we defined the shape of HRF by using 6 model parameters. Each of the two time courses (A and B) had different sets of parameters. However, in case of using the same sets of parameters for both time courses and considering a small delay between them, the performance of the standard MAR model turned out to be higher than if the HRF variation was present. Our dynamic approach proved to be more robust with respect to this kind of variation and also more stable in case of increased measurement noise. In real fMRI data, the variability of the HRF including latency can be also severe, resulting in estimation of a directional flow which is opposite the ground truth (David et al., 2008).
fMRI Data
To demonstrate our method applied to real fMRI data we used data collected during both block and event-related experimental designs. The block design was an auditory sensorimotor task (SM) and the event-related design was an auditory oddball discrimination task (AOD). The data set for the SM task was acquired at four different sites: the University of Iowa Hospital (IA); Harvard’s Massachusetts General Hospital (MA); the University of Minnesota (MN) and the Mind Research Network (NM), collected from 70 healthy subjects, as a part of the Mind Clinical Imaging Consortium. The data from the AOD task was acquired at the Olin Neuropsychiatry Research Center at the Institute of Living/Hartford Hospital, collected from 28 healthy subjects.
Auditory sensorimotor task
The SM task consists of an on/off block design each with duration of 16 s. During the on-block, 200 ms tones were presented with a 500 ms stimulus onset asynchrony (SOA). There were eight tones at different pitches along a scale. These tones were presented in ascending and descending cycles and this pattern continued for the ‘on’ block duration. This was followed by an ‘off’ block of 8 s. After each tone, participants are required to quickly press the right thumb using the input device. There were two runs and each lasted about 4 min.
Auditory oddball discrimination task
The AOD task consists of detecting an infrequent sound within a series of regular and different sounds. The task consisted of two runs of auditory stimuli. The standard (nontarget) stimulus was a 500 Hz tone, the target stimulus was a 1,000 Hz tone, and the novel stimuli consisted of nonrepeating random digital noises (e.g., tone sweeps, whistles). The target and novel stimuli each occurred with a probability of 0.10; the standard stimuli occurred with a probability of 0.80. The stimulus duration was 200 ms with a 1,000, 1,500, or 2,000 ms interstimulus interval (ISI). All stimuli were presented at ~80 dB above the standard threshold of hearing. The participants were instructed to respond as quickly and accurately as possible with their right index finger every time they heard the target stimulus and not to respond to the nontarget stimuli or the novel stimuli. The AOD task consisted of two 8 min runs.
Data acquisition
SM functional data were acquired with gradient-echo echo-planar imaging (EPI) sequences on Siemens 3 T scanners, except at the NM site where a 1.5 T Siemens scanner was used. The parameters for functional scans are as follows: repeat time (TR) = 2.0 s; echo time (TE) = 30 ms (TE = 39 ms for NM); flip angle (FA) = 90 °; field of view (FOV) = 22 cm; acquisition matrix = 64 × 64; voxel size 3.4 × 3.4× 4 mm3; slice thickness = 4 mm; gap between slices = 1 mm; number of slices 27; ascending sequential acquisition; total number of scans = 120 in each run.
AOD functional data were acquired with gradient-echo EPI sequences on Siemens 3 T Allegra scanner with the following parameters: TR = 1.50 s; TE = 27 ms; FA = 70 °; FOV = 24 cm; acquisition matrix = 64 × 64; voxel size 3.75 × 3.75 × 4 mm3; slice thickness = 4 mm; gap between slices = 1 mm; number of slices 29; ascending acquisition; total number of scans = 249 in each run.
Data preprocessing
Data were preprocessed using the SPM5 software package. Data were motion corrected and slice-timing corrected, spatially normalized into the standard Montreal Neurological Institute (MNI) space, and spatially smoothed with a 10 × 10 × 10 mm3 full width at half-maximum Gaussian kernel (9 × 9 × 9 mm3 in the case of SM). Following spatial normalization, the data (originally collected at 3.4 × 3.4 × 4 mm3) were slightly subsampled to 3 × 3 × 3 mm3, resulting in 53 × 63 × 46 voxels.
Group spatial ICA (Calhoun et al., 2001a) was used to decompose all the data into components using the GIFT software (http://icatb.sourceforge.net/) as follows. Dimension estimation, to determine the number of components, was performed using the minimum description length (MDL) criteria, modified to account for spatial correlation (Li et al., 2007). Using this approach, the SM and AOD data were estimated to have 20 and 19 components, respectively. It is worth to mention that the selection of decomposition order (equal to number of components) can have an impact on the number of identified brain activation networks. In this article, we chose the number of components to match the number estimated using an information theoretic approach (Li et al., 2007). Once the estimate of the number of components was determined we applied ICA to the data using group ICA as follows. Data from all subjects were concatenated and this aggregate data set reduced to 20 temporal dimensions using PCA (19 temporal dimensions in the case of AOD), followed by a independent component estimation using the infomax algorithm (Bell and Sejnowski, 1995).
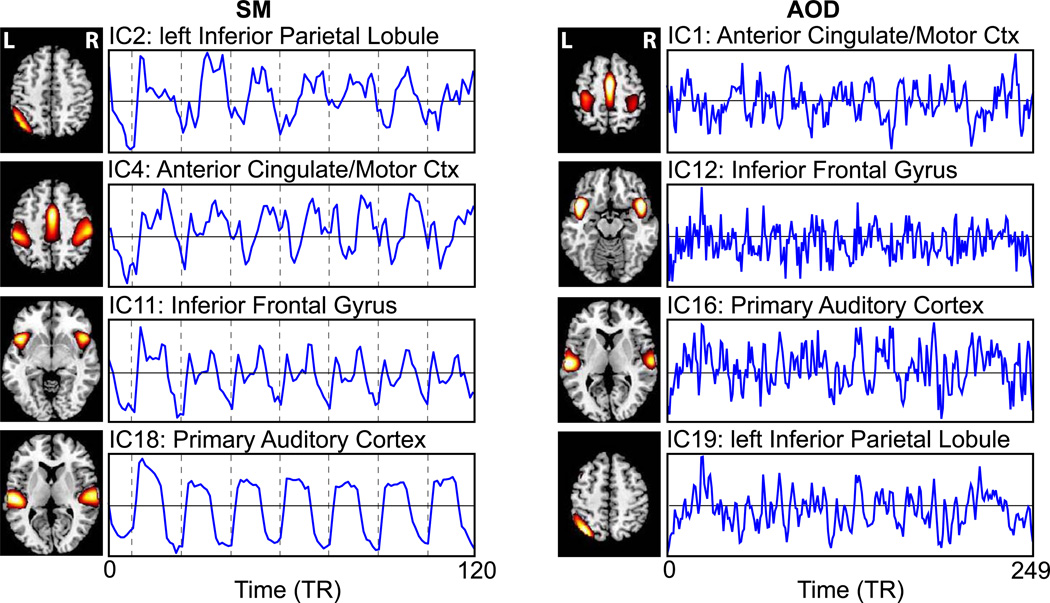
From each set of group ICA special maps we selected four independent components (ICs) corresponding to (SM task/AOD task): (IC2/IC19) = left inferior parietal lobule (sIPL) with slight contribution of left middle frontal gyrus; (IC4/IC1) = anterior cingulate/motor cortex (AC/MC); (IC11/IC12) = bilateral inferior frontal gyrus (IFG); and (IC18/IC16) = bilateral primary auditory cortex (A1). For each of the four ICs, we extracted the subject specific component time courses, obtained during subject level back reconstruction step of the group ICA. Inclusive description of the group ICA and back reconstruction procedure can be found in (Calhoun et al., 2001a).
Consequently, zero mean corrected time series with unit variance were processed by our dynamic MAR model based on Kalman filter followed by the smoother. In order to make a comparison, all data were also processed by the standard MAR model. The model order and the update coefficient were selected based on AIC and the relative error variance (p = 8, λ = 10−5 for SM and p = 8, λ = 10−3 for AOD), respectively. We applied the same model order for the dynamic and the standard MAR. Finally, the GPDC measure was calculated for each time point of the time series forming spectrograms (dynamic MAR), and processed over group of subjects in the same way as the simulations.
Results
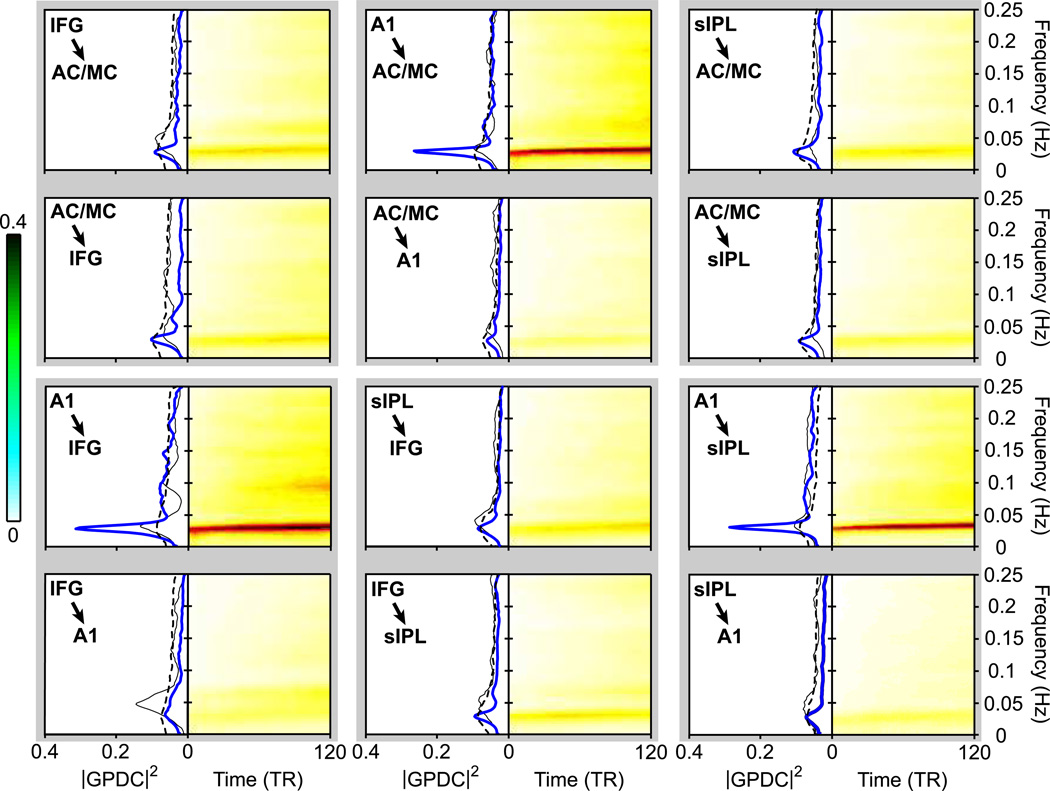
In order to distinguish between significant causal relations identified by dynamic MAR model and relations given by chance, a bootstrap procedure was performed. An empirical null distribution of no causality was created using a 2000 point bootstrapping. The connections whose GPDC values lay above upper bound of 95 % confidence interval are considered as significant (Fig. 4,5 dashed line).
Figure 4. Group results of SM task.
Set of group results of the dynamic GPDC estimates for SM task. The spectrograms of GPDC, associated with particular causal direction between components, represent the median over all subjects and the single frequency profile is the median over time axis of the associate spectrogram. The dashed line shows upper bound of 95 % confidence interval under the hypothesis of no connectivity between the components. The thin line represents GPDC spectra estimates based on standard MAR model.
Figure 5. Group results of AOD task.
Set of group results of the dynamic GPDC estimates for AOD task. The spectrograms of GPDC, associated with particular causal direction between components, represent the median over all subjects and the single frequency profile is the median over time axis of the associate spectrogram. The dashed line shows upper bound of 95 % confidence interval under the hypothesis of no connectivity between the components. The thin line represents GPDC spectra estimates based on standard MAR model.
The results from the SM task indicate that the component consisting of primary auditory cortex (A1) serves as a source, from which the information propagates to all other participating components (sIPL, AC/MC, and IFG) in our considered network. Due to spectral representation of Granger causality, there is clear evidence that indentified causal relation among components at frequency 0.031 Hz is related to the stimulation paradigm of the task (that also repeats with the frequency 0.031 Hz).
Results from the AOD task confirmed the A1 component also as main common source affecting other components. Additionally, unidirectional connections from sIPL to AC/PMC and also from sIPL to IFG were identified. Moreover, linkage between A1 and sIPL was detected in both causal directions. In the case of AOD data, the functional network connectivity was found at frequency around 0.033 Hz. As a consequence of random (not fixed) appearance of events in the experimental paradigm of AOD, it is not possible to find exact match of identified driving frequency with the frequency of stimulation function (e.g. of targets), because there is no main frequency. However, the histogram of gap occurrence between single target stimuli indicates that targets appeared during the task most frequently approximately at frequencies 0.035 Hz and 0.065 Hz, when the first frequency is very close to our driving frequency.
Based on connectivity results provided by the standard MAR we can conclude the following. In the case of SM data we could only identify a causal connection between regions A1 and IFG, where in both directions the upper bound of 95 % confidence interval generated by bootstrap procedure significantly crossed. The prevalent direction from IFG to A1 was detected at a frequency of 0.049 Hz, which is not related to the frequency of the SM experimental task. In contrast, the opposite less prominent direction from A1 to IFG is at the task related frequency of 0.031 Hz. This results indicate a failure of the standard MAR model when applied with the model order estimated by AIC (p = 8). However, there is a chance to slightly improve the results obtained by the standard MAR and get closer to the identified connection structure based on dynamic MAR if a slightly higher model order is used. Even a smaller model order can mean an improvement (based e.g. on BIC) but without a possibility to detect task related frequency component in the estimated spectra.
In the case of AOD data we were able to obtain three same connections as determined by dynamic approach, i.e. from A1 to IFG and to sIPL; and from sIPL to AC/MC, and connection from AC/MC to A1 (see Fig. 5), i.e. in the opposite direction than was determined by dynamic MAR. All these connections passed the significance threshold and were identified around the frequency 0.033 Hz. However, the magnitude of GPDC spectral profiles is much lower than in dynamic estimates. Also reliability of causal identification of information flow from AC/MC to A1 could be questioned if we consider the fact that we work with auditory oddball data and A1 represents the primary auditory cortex.
Discussion
fMRI results
From the neurophysiological point of view the two fMRI data sets derived from SM and AOD tasks definitely share several common functional features; however, at the same time they significantly differ in the involvement of functional networks employing in directed attention, stimulus recognition, executive functions and many others. Nevertheless, in the framework of demonstrating our dynamic approach to evaluate Granger causality, these data provide interesting background for discussion, including the fact that both tasks result in similar brain activation patterns detected by ICA (those we have selected).
First of all, the block design SM task was purposely chosen in order to demonstrate the ability of the dynamic MAR method based on Kalman filter to accurately detect connectivity at frequencies that exactly correspond to fixed repetition of stimulation paradigm. Second, there are obvious theoretical expectations regarding these two different experimental tasks (Kiehl et al., 2005; Liu et al., 2009): the block-design SM task represents a relatively simple task in which we do not expect strong integration of cognitive networks, but rather more automated integration of executive functions based on auditory perception and focused attention. In contrast, the eventrelated AOD task includes more cognitive elements including reorienting of attention to new, unexpected stimuli, updating of working memory, response preparation, and complex executive functions are employed (Clark et al., 2000). One can thus argue that the SM task has a lower cognitive load than the AOD task. In this context, cognitive load refers to the total amount of mental activity imposed on working memory at a particular instance in time (McKiernan et al., 2003; Pyka et al., 2009).
Considering the results from our functional network connectivity structures (Fig. 6), we can clearly see that in the case of SM task, the resulting networks integration is simpler, while in the AOD case, the considered brain networks are unequivocally more integrated. More specifically, in the SM task data significant single causal directions were identified only from the primary auditory cortex (A1) to all other considered brain networks, i.e. to sIPL, AC/PMC, and IFG, whereas in AOD task data additional connections from sIPL to IFG, from sIPL to AC/PMC, and from sIPL to A1 are present. Results found by our dynamic GC approach thus look to be in accordance with theoretical expectations on these types of experimental tasks.
Figure 6. Connectivity results of functional networks integrations.
Directional integrations of functional networks for SM (left) and AOD (right) task, which were revealed as a significant after dynamic MAR estimation, at task-related frequencies 0.031 Hz and 0.033 Hz, respectively. The values above arrows represent magnitudes of GPDC measure at particular driving frequencies. The thin dashed line represents connectivity structure identified by the standard MAR model (without pertinence constrain to single frequency).
Effect of model order selection
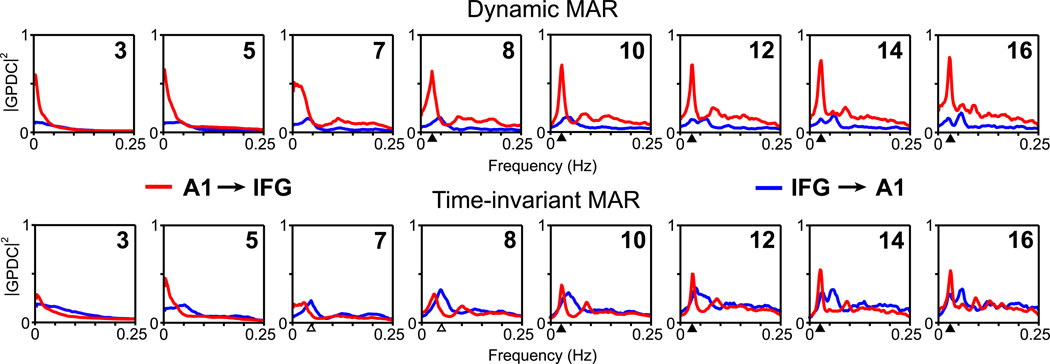
The successful estimation of Granger causality (GPDC in our case) depends primarily on the reliability of the fitted MAR model, since all the necessary information is derived from the estimated model parameters. In practice, this boils down to the choice of an optimal model order. If the model order is too low, the model will not capture the essential dynamics of the data set, whereas if it is too high, it will also capture unwanted components (i.e. noise), leading to overfitting and instability. There are useful criteria for optimal model order selection (e.g. AIC and BIC) which we applied in our analysis of fMRI data. However, it is also interesting to investigate the impact of a range of model orders on the estimated GPDC spectra and identified causal direction, to compare the standard MAR and our dynamic MAR model applied to real fMRI data. We have evaluated the GPDC through bivariate standard and dynamic MAR by using the range from small to high model orders (3; 5; 7; 8; 10; 12; 14; 16). The ICA component time courses from SM data related to A1 and IFG brain regions were used. The obtained results are depicted on Fig 7. It is evident that the dynamic MAR provides stable estimates over all chosen model orders. The spectral peak corresponding to the task related frequency can be captured from the model of order 8, preserving its position with higher orders (no shifting with higher orders is present). In contrast, the estimates provided by standard MAR are rather unstable, not providing significant estimates of causality across all the model orders, and furthermore, a wrong identification of causal direction is obtained by model orders 7 and 8. This demonstrates that application of a standard MAR to fMRI time-series, which are known to be nonstationary, can complicate the correct identification and interpretation of causal dependencies among brain regions.
Figure 7. Comparison of GPDC based on dynamic and standard MAR as an effect of different model order.
The example of GPDC spectra estimates for different model orders (3; 5; 7; 8; 10; 12; 14; 16) obtained by using dynamic MAR (top) and standard time-invariant MAR (bottom), applied to ICA time course of A1 and IFG activations from SM data. Displayed spectra were calculated as a median over all subjects and runs. Black triangle marks correctly estimated spectral peaks that are related to task frequency of fMRI data. White triangle marks wrong identification of causal direction at particular frequency.
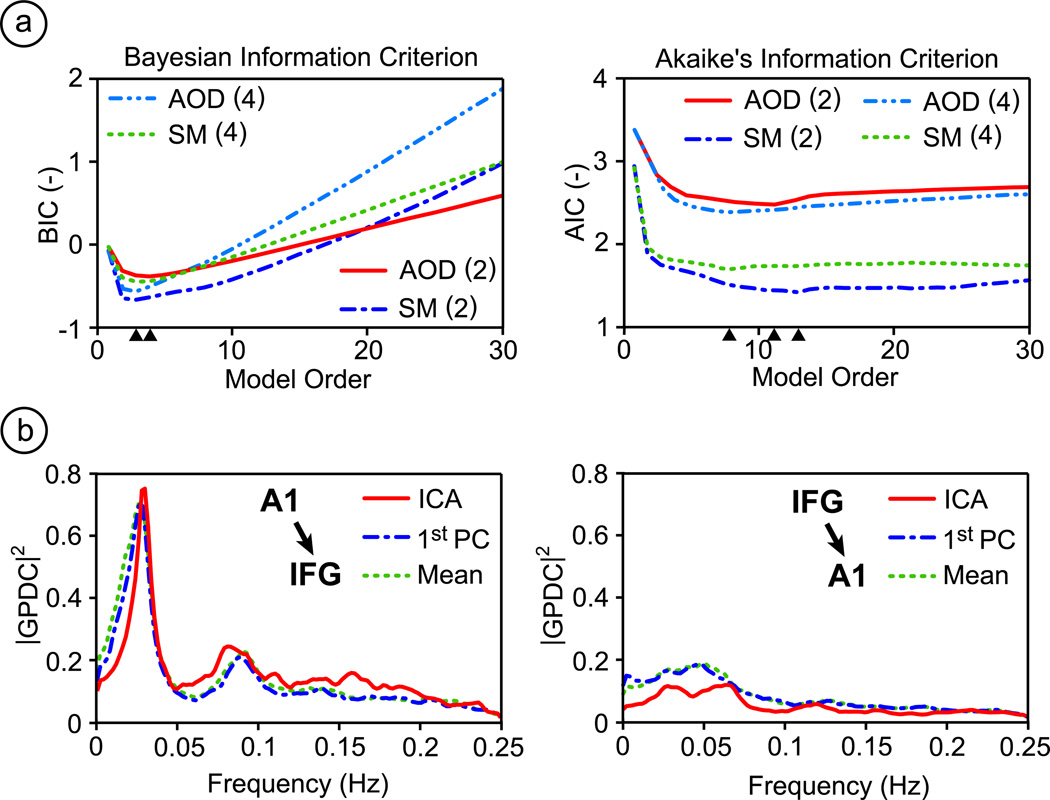
In our application of the frequency domain dynamic GC to fMRI data, we found AIC to be more suitable because it suggested a higher model order than BIC (see Fig. 8a); such a model allowed us to better resolve the spectral information. However, it does not mean that following BIC criterion would lead to different estimates of the final connectivity structure. In this sense, both AIC and BIC criteria, particularly when followed by our dynamic MAR approach, provide reasonable estimates of the optimal model order.
Figure 8. Model order selection based on AIC and BIC, and the effect of using ICA time courses compared to original fMRI time courses on estimated GPDC spectra.
Estimated BIC and AIC criteria functions of model order for bivariate (2 time courses) and multivariate (4 time courses) standard MAR model applied to SM and AOD data (a). Displayed criteria functions represent the median over all subjects and runs, and their minima, which were used as a suggested model order, are marked. The comparison of resulting GPDC spectra, when the ICA time courses and the time courses from original data (the mean and the 1st principle component) were used (b).
We have shown as a demonstration that our dynamic model is less sensitive to different model order and thus provides more consistent results. This is an obvious advantage compared to the standard model, because one does not have to be so strictly tied to model order suggested by the information criterion.
Original data vs. component time courses
Because the ICA decomposition was applied in order to identify functional brain networks represented by spatially independent components, and their corresponding component time courses were then used to infer causal directions among selected networks, one might be concerned if ICA can have any (positive or negative) influence on the final estimated results. On this account, we performed an additional analysis based on fMRI time series from the original data (before the processing by ICA). Spatial clusters of brain activation obtained by ICA were used to define ROI’s. The mean and the 1st principal component of ROI time courses were computed from each subject’s preprocessed fMRI time series and employed to evaluate connectivity by utilizing dynamic MAR and GPDC. The outcome is satisfactory - we did not find any significant differences in results by including extensive testing on SM and AOD data, for both bivariate and multivariate model estimation. An example of comparison of spectral estimation of GPDC between A1 and IFG regions, when the ICA, the mean, and the 1st principal component time courses were used, can be seen on Fig. 8b. Results were essentially unchanged when using either the mean or the 1st principal component time course. A small but insignificant difference was observed when ICA component time courses were included.
Even though this differentiation can slightly change with the model order, it cannot affect the estimated direction of information flow in the connectivity network.
On Granger causality in fMRI
Application of GC to fMRI data is especially attractive due to the high spatial resolution of fMRI signal. However, several limitations then arise from the temporal characteristics of fMRI signal. First, the lower temporal resolution on the order of seconds may not provide enough information for inferring connectivity (Roebroeck et al., 2005). The sensitivity of GC decreases with slower sampling rate and lower signal to noise ratio (SNR) (Deshpande et al., 2010). Second, the BOLD signal is an indirect measure of neural dynamics, and therefore the connectivity relationship does not have to be always correctly identified due to hemodynamic blurring, including also variability in region specific latency and shape of BOLD response (Aguirre et al., 1998; Handwerker et al., 2004).
In order to partially avoid the effect of region specific HRF, the Granger causality can focus on the modulation of causal connectivity under different experimental conditions, as opposed to attempting identification of the causal structure independently (Roebroeck et al., 2005; Seth, 2009). This is possible, since HRFs are not expected to vary between experimental conditions. This strategy also brings GC closer to the concept of effective connectivity (Friston, 1994). A more direct solution to avoid the effect of HRF variability is via HRF deconvolution. Although some promising approaches were recently suggested (Chang et al., 2008; Vakarin et al., 2007), there is still work needed to make such approaches more reliable and accurate. In this sense, the nonlinear Kalman filter could be also very useful, since it enables signal specific nonlinear hemodynamic modeling (Riera et al., 2004), including the ability to estimate the neural signal.
Additionally, because there is evidence that the relationship between fMRI time series is rather nonlinear (Berns et al., 1999), further extension of GC model that would allow nonlinear interactions either at BOLD level or (even better) at the already estimated neural level should be taken into consideration. There are several approaches for nonlinear GC that were already proposed and applied to neurophysiologic data. These include e.g. locally nonlinear autoregressive models (Freiwald et al., 1999); nonlinear kernels such as radial basis functions (Ancona et al., 2004); or nonlinear kernels based on theory of reproducing Hilbert spaces (Marinazzo et al., 2008).
Recently, the issue of filtering time series as a part of preprocessing steps before application to MAR model has been well addressed (Florin et al., 2010; Seth, 2009). Especially low-pass filtering can introduce spurious correlation structure into data which can result in artifactual causal connectivity (on the other hand, high-pass filtering used to remove very low frequencies associated with signal drift is usually safe).
In this context, our proposed method for evaluating GC based on dynamic MAR modeling, besides the fact that it is able to handle nonstationarities present in fMRI time series better, also proved to be more robust against small region specific diversity of HRF. Additionally, in contrast to the standard AR modeling, the Kalman filter is also known to be more powerful in increasing SNR (Oikonomou et al., 2007). This feature very positively contributes to more stable estimate of MAR parameters and to more accurate estimation of power spectra of the GPDC. Especially nuisance frequency components that are mostly present at higher frequencies in fMRI data are effectively suppressed.
We introduced an approach for dynamic evaluation of Granger causality in order to avoid the stationarity assumption in standard MAR modeling. Our method is based on time varying estimation of MAR coefficients by combining forward and backward estimates of a Kalman filter. Even though we demonstrate dynamic GC assessed in the frequency domain, one can expect the same improvement of estimation performance when applied in the time domain GC as well. However, here presented dynamic GC method is not the only one that was designed for application to nonstationary data with the neurophysiologic origin. In an fMRI application, Sato et al. (2006) used the interesting concept of wavelet basis functions aimed at fitting time-varying coefficients of MAR model, which is theoretically able to provide different connectivity structure for each time point of time series (time domain GC). In an EEG application, Hesse et al. (2003) proposed a method based on adaptive recursive least squares (RLS) modeling (time domain GC), which can be seen as a special case of Kalman filtering, and is thus the closest to our approach; Dhamala et al. (2008) introduced a nonparametric approach based on spectral factorization of wavelet transformations (frequency domain GC).
Finally, the fact that MAR models and especially our proposed dynamic model are based on stochastic signal modeling should be considered as an advantage in the concept of causality analysis. It is a very strong and limiting assumption that all state variables of the model will follow deterministic trajectories from the initial condition for a whole epoch, with only the local neural activity influencing their course, as it is assumed e.g. in DCM. It can be easily imagined that disturbances of various kinds are able to perturb the state variables from this deterministic course (Roebroeck et al., 2009). Further, if the true neural activity is not exactly as assumed, namely equal to the known stimulus (or a deterministic function), then the state variables cannot be accurately estimated in this manner.
Conclusion
In this paper we proposed a dynamic approach for MAR modeling based on Kalman filter in order to evaluate Granger causality. The method is introduced in the context of functional network connectivity when the functional networks are first detected by ICA. The effectiveness and robustness of the dynamic method compared to the time-invariant MAR modeling when applied to nonstationary fMRI data is achieved by combining forward and backward filter that provide the optimal smoother estimate. The Granger causality is then evaluated through a well recognized measure of generalized partial directed coherence that is suitable for bivariate as well as multivariate data. The GPDC provides identification of causal relation in frequency domain, which allows one to distinguish the frequency components related to experimental paradigm. Subsequently, the procedure of evaluating Granger causality via dynamic MAR was demonstrated on simulated time series as well as on two sets of group fMRI data of SM and AOD task. Additionally, a comparison with the results obtained from a standard time-invariant MAR model was provided. In accordance with our theoretical expectations based on current neurophysiological knowledge the proposed method obviously revealed higher degree of networks integration in the experimental task with significantly higher cognitive load.
Figure 2. Experimental paradigms.
Experimental paradigms for SM task (left) and AOD task (right).
Figure 3. ICA spatial maps and associated time courses.
Axial slices of selected group spatial maps of independent components, including brain activation of interest, and their associated averaged time courses (over all subjects) for SM (left) and AOD task (right).
Acknowledgment
This work has been sponsored by the research center DAR no. 1M0572, and also supported by the research frame no. MSM0021630513 and no. MSM0021622404, all funded by the Ministry of Education of the Czech Republic. Additional funding was provided by NIH grant no. R01EB000840 from the USA. Further, the authors would like to thank the anonymous reviewers for many constructive suggestions that helped to clarify the presentation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aguirre GK, Zarahn E, D'esposito M. The variability of human, BOLD hemodynamic responses. Neuroimage. 1998;8:360–369. doi: 10.1006/nimg.1998.0369. [DOI] [PubMed] [Google Scholar]
- Akaike H. A new look at the statistical model identification. IEEE transactions on automatic control. 1974;19:716–723. [Google Scholar]
- Ancona N, Marinazzo D, Stramaglia S. Radial basis function approach to nonlinear Granger causality of time series. Physical Review E. 2004;70:056221. doi: 10.1103/PhysRevE.70.056221. [DOI] [PubMed] [Google Scholar]
- Arnold M, Milner XHR, Witte H, Bauer R, Braun C. Adaptive AR modeling of nonstationary time series by means of Kalman filtering. IEEE Transactions on Biomedical Engineering. 1998;45:553–562. doi: 10.1109/10.668741. [DOI] [PubMed] [Google Scholar]
- Baccala LA, Sameshima K. Partial directed coherence: a new concept in neural structure determination. Biological Cybernetics. 2001;84:463–474. doi: 10.1007/PL00007990. [DOI] [PubMed] [Google Scholar]
- Baccala LA, Sameshima K, Takahashi DY, Arnaldo AD. Generalized partial directed coherence. In: IEEE, editor. Proceedings of the 15th International Conference on Digital Signal Processing; 2007. pp. 162–166. [Google Scholar]
- Baccala LA, Takahashi DY, Sameshima K. Computer intensive testing for the influence between time series. In: Schelter B, Winterhalder M, Timmer J, editors. Handbook of time series analysis. Weinheim: Wiley-Vch Verlag GmbH & Co. KGaA; 2006. [Google Scholar]
- Bell AJ, Sejnowski TJ. An information-maximization approach to blind separation and blind deconvolution. Neural Computation. 1995;7:1129–1159. doi: 10.1162/neco.1995.7.6.1129. [DOI] [PubMed] [Google Scholar]
- Berns GS, Song AW, Mao H. Continuous functional magnetic resonance imaging reveals dynamic nonlinearities of "dose-response" curves for finger opposition. Journal of Neuroscience. 1999;19:17. doi: 10.1523/JNEUROSCI.19-14-j0003.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Adali T. Unmixing fMRI with independent component analysis. IEEE Engineering in Medicine and Biology Magazine. 2006;25:79–90. doi: 10.1109/memb.2006.1607672. [DOI] [PubMed] [Google Scholar]
- Calhoun VD, Adali T, Pearlson GD, Pekar JJ. A method for making group inferences from functional MRI data using independent component analysis. Human Brain Mapping. 2001a;14:140–151. doi: 10.1002/hbm.1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Adali T, Pearlson GD, Pekar JJ. Spatial and temporal independent component analysis of functional MRI data containing a pair of task-related waveforms. Human Brain Mapping. 2001b;13:43–53. doi: 10.1002/hbm.1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Adali T, Pekar JJ, Pearlson GD. Latency (in)sensitive ICA Group independent component analysis of fMRI data in the temporal frequency domain. NeuroImage. 2003;20:1661–1669. doi: 10.1016/s1053-8119(03)00411-7. [DOI] [PubMed] [Google Scholar]
- Chang C, Thomason ME, Glover GH. Mapping and correction of vascular hemodynamic latency in the BOLD signal. Neuroimage. 2008;43:90–102. doi: 10.1016/j.neuroimage.2008.06.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Bressler SL, Ding M. Frequency decomposition of conditional Granger causality and application to multivariate neural field potential data. Journal of neuroscience methods. 2006;150:228–237. doi: 10.1016/j.jneumeth.2005.06.011. [DOI] [PubMed] [Google Scholar]
- Clark VP, Fannon S, Lai S, Benson R, Bauer L. Responses to rare visual target and distractor stimuli using event-related fMRI. Journal of Neurophysiology. 2000;83:3133–3139. doi: 10.1152/jn.2000.83.5.3133. [DOI] [PubMed] [Google Scholar]
- Cordes D, Haughton VM, Arfanakis K, Carew JD, Turski P, Moritz CH, Quigley MA, Meyerand ME. Frequencies contributing to functional connectivity in the cerebral cortex in "resting-state" data. American Journal of Neuroradiology. 2001;22:1326–1333. [PMC free article] [PubMed] [Google Scholar]
- David O, Guillemain I, Saillet S, Reyt S, Deransart C, Segebarth C, Depaulis A. Identifying neural drivers with functional MRI: an electrophysiological validation. PLoS Biology. 2008;6:2683–2697. doi: 10.1371/journal.pbio.0060315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demirci O, Stevens MC, Andreasen NC, Michael A, Liu J, White T, Pearlson GD, Clark VP, Calhoun VD. Investigation of relationships between fMRI brain networks in the spectral domain using ICA and Granger causality reveals distinct differences between schizophrenia patients and healthy controls. Neuroimage. 2009;46:419–431. doi: 10.1016/j.neuroimage.2009.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande G, Hu X, Stilla R, Sathian K. Effective connectivity during haptic perception: A study using Granger causality analysis of functional magnetic resonance imaging data. Neuroimage. 2008;40:1807–1814. doi: 10.1016/j.neuroimage.2008.01.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande G, LaConte S, James GA, Peltier S, Hu X. Multivariate Granger causality analysis of fMRI data. Human Brain Mapping. 2009;30:1361–1373. doi: 10.1002/hbm.20606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande G, Sathian K, Hu X. Effect of hemodynamic variability on Granger causality analysis of fMRI. NeuroImage. 2010 doi: 10.1016/j.neuroimage.2009.11.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhamala M, Rangarajan G, Ding M. Analyzing information flow in brain networks with nonparametric Granger causality. NeuroImage. 2008;41:354–362. doi: 10.1016/j.neuroimage.2008.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Florin E, Gross J, Pfeifer J, Fink GR, Timmermann L. The effect of filtering on Granger causality based multivariate causality measures. NeuroImage. 2010;50:577–588. doi: 10.1016/j.neuroimage.2009.12.050. [DOI] [PubMed] [Google Scholar]
- Fraser D, Potter J. The optimum linear smoother as a combination of two optimum linear filters. IEEE Transactions on Automatic Control. 1969;14:387–390. [Google Scholar]
- Freiwald WA, Valdes P, Bosch J, Biscay R, Jimenez JC, Rodriguez LM, Rodriguez V, Kreiter AK, Singer W. Testing non-linearity and directedness of interactions between neural groups in the macaque inferotemporal cortex. Journal of Neuroscience Methods. 1999;94:105–119. doi: 10.1016/s0165-0270(99)00129-6. [DOI] [PubMed] [Google Scholar]
- Friston KJ. Functional and effective connectivity in neuroimaging: a synthesis. Human Brain Mapping. 1994;2:56–78. [Google Scholar]
- Friston KJ, Harrison L, Penny W. Dynamic causal modelling. Neuroimage. 2003;19:1273–1302. doi: 10.1016/s1053-8119(03)00202-7. [DOI] [PubMed] [Google Scholar]
- Gaschler-Markefski B, Baumgart F, Tempelmann C, Schindler F, Stiller D, Heinze HJ, Scheich H. Statistical methods in functional magnetic resonance imaging with respect to nonstationary time-series: auditory cortex activity. Magnetic Resonance in Medicine. 1997;38:811–820. doi: 10.1002/mrm.1910380518. [DOI] [PubMed] [Google Scholar]
- Geweke J. Measurement of linear dependence and feedback between multiple time series. Journal of the American Statistical Association. 1982;77:304–313. [Google Scholar]
- Geweke J. Measures of conditional linear dependence and feedback between time series. Journal of the American Statistical Association. 1984;79:907–915. [Google Scholar]
- Goebel R, Roebroeck A, Kim DS, Formisano E. Investigating directed cortical interactions in time-resolved fMRI data using vector autoregressive modeling and Granger causality mapping. Magnetic resonance imaging. 2003;21:1251–1261. doi: 10.1016/j.mri.2003.08.026. [DOI] [PubMed] [Google Scholar]
- Granger C. Investigating causal relations by econometric models and cross-spectral methods. Econometrica: Journal of the Econometric Society. 1969;37:424–438. [Google Scholar]
- Guo S, Seth AK, Kendrick KM, Zhou C, Feng J. Partial Granger causality--Eliminating exogenous inputs and latent variables. Journal of Neuroscience Methods. 2008;172:79–93. doi: 10.1016/j.jneumeth.2008.04.011. [DOI] [PubMed] [Google Scholar]
- Handwerker D, Ollinger J, D'Esposito M. Variation of BOLD hemodynamic responses across subjects and brain regions and their effects on statistical analyses. Neuroimage. 2004;21:1639–1651. doi: 10.1016/j.neuroimage.2003.11.029. [DOI] [PubMed] [Google Scholar]
- Haykin S. Adaptive filter theory. Prentice hall; 2002. [Google Scholar]
- Hesse W, Möller E, Arnold M, Schack B. The use of time-variant EEG Granger causality for inspecting directed interdependencies of neural assemblies. Journal of Neuroscience Methods. 2003;124:27–44. doi: 10.1016/s0165-0270(02)00366-7. [DOI] [PubMed] [Google Scholar]
- Jafri MJ, Pearlson GD, Stevens M, Calhoun VD. A method for functional network connectivity among spatially independent resting-state components in schizophrenia. Neuroimage. 2008;39:1666–1681. doi: 10.1016/j.neuroimage.2007.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalman RE. A new approach to linear filtering and prediction problems. Journal of basic Engineering. 1960;82:35–45. [Google Scholar]
- Kaminski M, Ding M, Truccolo WA, Bressler SL. Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biological Cybernetics. 2001;85:145–157. doi: 10.1007/s004220000235. [DOI] [PubMed] [Google Scholar]
- Kaminski MJ, Blinowska KJ. A new method of the description of the information flow in the brain structures. Biological Cybernetics. 1991;65:203–210. doi: 10.1007/BF00198091. [DOI] [PubMed] [Google Scholar]
- Kiehl KA, Stevens MC, Laurens KR, Pearlson G, Calhoun VD, Liddle PF. An adaptive reflexive processing model of neurocognitive function: supporting evidence from a large scale (n= 100) fMRI study of an auditory oddball task. Neuroimage. 2005;25:899–915. doi: 10.1016/j.neuroimage.2004.12.035. [DOI] [PubMed] [Google Scholar]
- Korzeniewska A, Manczak M, Kaminski M, Blinowska KJ, Kasicki S. Determination of information flow direction among brain structures by a modified directed transfer function (dDTF) method. Journal of neuroscience methods. 2003;125:195–207. doi: 10.1016/s0165-0270(03)00052-9. [DOI] [PubMed] [Google Scholar]
- Li YO, Adali T, Calhoun VD. Estimating the number of independent components for functional magnetic resonance imaging data. Human Brain Mapping. 2007;28:1251–1266. doi: 10.1002/hbm.20359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao W, Mantini D, Zhang Z, Pan Z, Ding J, Gong Q, Yang Y, Chen H. Evaluating the effective connectivity of resting state networks using conditional Granger causality. Biological Cybernetics. 2010;102:57–69. doi: 10.1007/s00422-009-0350-5. [DOI] [PubMed] [Google Scholar]
- Liu J, Kiehl KA, Pearlson G, Perrone-Bizzozero NI, Eichele T, Calhoun VD. Genetic determinants of target and novelty-related event-related potentials in the auditory oddball response. Neuroimage. 2009;46:809–816. doi: 10.1016/j.neuroimage.2009.02.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Londei A, D'Ausilio A, Basso D, Belardinelli MO. A new method for detecting causality in fMRI data of cognitive processing. Cognitive Processing. 2006;7:42–52. doi: 10.1007/s10339-005-0019-5. [DOI] [PubMed] [Google Scholar]
- Londei A, D'Ausilio A, Basso D, Sestieri C, Del Gratta C, Romani GL, Olivetti Belardinelli M. Brain network for passive word listening as evaluated with ICA and Granger causality. Brain Research Bulletin. 2007;72:284–292. doi: 10.1016/j.brainresbull.2007.01.008. [DOI] [PubMed] [Google Scholar]
- Lütkepohl H. New introduction to multiple time series analysis. Springer; 2005. [Google Scholar]
- Marinazzo D, Pellicoro M, Stramaglia S. Kernel method for nonlinear Granger causality. Physical Review Letters. 2008;100:144103. doi: 10.1103/PhysRevLett.100.144103. [DOI] [PubMed] [Google Scholar]
- McIntosh AR. Towards a network theory of cognition. Neural Networks. 2000;13:861–870. doi: 10.1016/s0893-6080(00)00059-9. [DOI] [PubMed] [Google Scholar]
- McKeown MJ, Makeig S, Brown GG, Jung TP, Kindermann SS, Bell AJ, Sejnowski TJ. Analysis of fMRI data by blind separation into independent spatial components. Human Brain Mapping. 1998;6:160–188. doi: 10.1002/(SICI)1097-0193(1998)6:3<160::AID-HBM5>3.0.CO;2-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKiernan KA, Kaufman JN, Kucera-Thompson J, Binder JR. A parametric manipulation of factors affecting task-induced deactivation in functional neuroimaging. Journal of Cognitive Neuroscience. 2003;15:394–408. doi: 10.1162/089892903321593117. [DOI] [PubMed] [Google Scholar]
- Oikonomou VP, Tzallas AT, Fotiadis DI. A Kalman filter based methodology for EEG spike enhancement. Computer Methods and Programs in Biomedicine. 2007;85:101–108. doi: 10.1016/j.cmpb.2006.10.003. [DOI] [PubMed] [Google Scholar]
- Pyka M, Beckmann C, Schöning S, Hauke S, Heider D, Kugel H, Arolt V, Konrad C. Impact of Working Memory Load on fMRI Resting State Pattern in Subsequent Resting Phases. PLoS ONE. 2009;4:e7198. doi: 10.1371/journal.pone.0007198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rauch HE, Tung F, Striebel CT. Maximum likelihood estimates of linear dynamic systems. AIAA Journal. 1965;3:1445–1450. [Google Scholar]
- Riera J, Watanabe J, Kazuki I, Naoki M, Aubert E, Ozaki T, Kawashima R. A state-space model of the hemodynamic approach: nonlinear filtering of BOLD signals. NeuroImage. 2004;21:547–567. doi: 10.1016/j.neuroimage.2003.09.052. [DOI] [PubMed] [Google Scholar]
- Roebroeck A, Formisano E, Goebel R. Mapping directed influence over the brain using Granger causality and fMRI. Neuroimage. 2005;25:230–242. doi: 10.1016/j.neuroimage.2004.11.017. [DOI] [PubMed] [Google Scholar]
- Roebroeck A, Formisano E, Goebel R. The identification of interacting networks in the brain using fMRI: Model selection, causality and deconvolution. Neuroimage. 2009 doi: 10.1016/j.neuroimage.2009.09.036. In Press. [DOI] [PubMed] [Google Scholar]
- Sato JR, Junior EA, Takahashi DY, de Maria Felix M, Brammer MJ, Morettin PA. A method to produce evolving functional connectivity maps during the course of an fMRI experiment using wavelet-based time-varying Granger causality. Neuroimage. 2006;31:187–196. doi: 10.1016/j.neuroimage.2005.11.039. [DOI] [PubMed] [Google Scholar]
- Sato JR, Takahashi DY, Arcuri SM, Sameshima K, Morettin PA, Baccala LA. Frequency domain connectivity identification: An application of partial directed coherence in fMRI. Human Brain Mapping. 2009;30:452–461. doi: 10.1002/hbm.20513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlogl A, Roberts SJ, Pfurtscheller G. A criterion for adaptive autoregressive models. In: IEEE, editor. Proceedings of the 22nd IEEE International Conference on Engineering in Medicine and Biology; 2000. pp. 1581–1582. [Google Scholar]
- Schneider T, Neumaier A. Algorithm 808: ARfit— - a Matlab package for the estimation of parameters and eigenmodes of multivariate autoregressive models. ACM Transactions on Mathematical Software. 2001;27:58–65. [Google Scholar]
- Schwarz G. Estimating the dimension of a model. The annals of statistics. 1978;6:461–464. [Google Scholar]
- Seth A. A MATLAB toolbox for Granger causal connectivity analysis. Journal of Neuroscience Methods. 2009;186:262–273. doi: 10.1016/j.jneumeth.2009.11.020. [DOI] [PubMed] [Google Scholar]
- Sun FT, Miller LM, D'Esposito M. Measuring interregional functional connectivity using coherence and partial coherence analyses of fMRI data. Neuroimage. 2004;21:647–658. doi: 10.1016/j.neuroimage.2003.09.056. [DOI] [PubMed] [Google Scholar]
- Vakarin VA, Krakovska OO, Borowsky R, Sarty GE. Inferring neural activity from BOLD signals through nonlinear optimization. Neuroimage. 2007;38:248–260. doi: 10.1016/j.neuroimage.2007.06.033. [DOI] [PubMed] [Google Scholar]
- Van de Ven VG, Formisano E, Prvulovic D, Roeder CH, Linden DEJ. Functional connectivity as revealed by spatial independent component analysis of fMRI measurements during rest. Human Brain Mapping. 2004;22:165–178. doi: 10.1002/hbm.20022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wink AM, Roerdink J. BOLD noise assumptions in fMRI. International Journal of Biomedical Imaging. 2006;2006:1–11. doi: 10.1155/IJBI/2006/12014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Z, Chen Y, Ding M, Wright P, Lu Z, Liu Y. Analyzing brain networks with PCA and conditional Granger causality. Human Brain Mapping. 2008;30:2197–2206. doi: 10.1002/hbm.20661. [DOI] [PMC free article] [PubMed] [Google Scholar]