Scaling Up Graph-Based Semisupervised Learning via Prototype Vector Machines

Abstract

When the amount of labeled data are limited, semi-supervised learning can improve the learner's performance by also using the often easily available unlabeled data. In particular, a popular approach requires the learned function to be smooth on the underlying data manifold. By approximating this manifold as a weighted graph, such graph-based techniques can often achieve state-of-the-art performance. However, their high time and space complexities make them less attractive on large data sets. In this paper, we propose to scale up graph-based semisupervised learning using a set of sparse prototypes derived from the data. These prototypes serve as a small set of data representatives, which can be used to approximate the graph-based regularizer and to control model complexity. Consequently, both training and testing become much more efficient. Moreover, when the Gaussian kernel is used to define the graph affinity, a simple and principled method to select the prototypes can be obtained. Experiments on a number of real-world data sets demonstrate encouraging performance and scaling properties of the proposed approach. It also compares favorably with models learned via ℓ₁-regularization at the same level of model sparsity. These results demonstrate the efficacy of the proposed approach in producing highly parsimonious and accurate models for semisupervised learning.

I. Introduction

In Many data analysis and mining applications, the amount of unlabeled data available can be huge. However, the amount of labeled data remains scarce, due to the expensive and tedious human labeling process involved. Semisupervised learning [10], which can use unlabeled data together with the labeled data during training, is thus an effective approach to improve the learner's generalization performance.

In semisupervised learning, the label dependencies among the samples are captured by exploiting the intrinsic geometric structure of the data. This can be implemented using the cluster assumption, which encourages the separating hypersurface to pass through low-density regions [11], [19]. Another popular smoothness assumption is the manifold assumption, which assumes that the underlying function is smooth on a low-dimensional manifold formed by the data. Often, this manifold is approximated by a weighted graph defined on all the labeled and unlabeled data, and with the graph's affinity matrix encoding the similarities between the samples. This leads to the development of various graph-based semisupervised learning algorithms [4], [22], [26], [33], [45], [46], [48]. Besides these, techniques based on generative models [2], [27], self-training [39], co-training [7], and conditional random fields [20], [21] have also been used for semisupervised learning. An excellent survey can be found in [47].

In this paper, we will focus on the graph-based approach [4], [6], [48], which has a clear mathematical framework, good empirical performance and has also been widely applied in a variety of real-world problems. In particular, we will consider the manifold regularization framework [4]. It incorporates an additional regularizer to ensure that the learned function is smooth on the manifold; while at the same time the predictions on the labeled data are required to be consistent with the known class labels. In contrast to some other graph-based learning methods, this regularization framework is semisupervised (not transductive) and allows generalization to out-of-sample (unseen) patterns. Besides semisupervised learning, the use of manifolds has also been successfully applied in other learning problems such as manifold learning, dimension reduction, and clustering [3], [25], [29], [31], [34].

However, as graph-based semisupervised learning needs to manipulate the affinity (kernel) matrix of the graph (which is defined on all the available data), its space complexity has to grow (at least) quadratically with the data set size n [4], [45], [48]. On the other hand, its time complexity typically scales as n³. These pose a big challenge in large-scale applications.

In recent years, many efforts have been devoted to scaling up graph-based semisupervised learning. For example, Zhu and Lafferty [49] proposed an elegant framework that combines the generative mixture model with graph-based regularization. Recently, this is further extended for semisupervised feature selection [38]. However, when the data are high-dimensional, the curse of dimensionality sets in and could prevent the mixture model from fitting the data well [49]. In [13], a nonparametric function induction framework is proposed, which performs prediction based on a subset of preselected samples. However, it cannot enforce smoothness of the target function over those unlabeled data not in the preselected sample subset. In [8], the Nyström method [37] is used to numerically approximate the large matrix inverse associated with the graph-based semisupervised learning method of [45]. This leads to an efficient, transductive algorithm. The Nyström low-rank approximation is also used to scale up support vector training recently in [43], and transfer learning in the Hilbert space [44]. Other very recent attempts, such as the primal Laplacian supported vector machine (LapSVM) [24] and the anchor graph [23] will be presented in Section II-B.

Our key observation is that the computational intensiveness of graph-based semisupervised learning arises from the regularization term. On the one hand, this requires manipulation (multiplication, or inverse) of the n × n kernel matrix, which is impractical for large problems. On the other hand, the representer theorem [4] shows that the learned model spans over both labeled and unlabeled samples, making it inefficient in both training and testing.

The main contribution of this paper is in improving the scalability of semisupervised learning algorithms with the use of prototypes. These refer to a small set of points in the input space that can be used as a replacement of the original data in obtaining an efficient yet accurate predictive solution. Specifically, there are two types of prototypes used in the paper. First, low-rank approximation prototypes, which are used to obtain a low-rank approximation of the kernel matrix. This in turn allows graph-based regularization to be performed efficiently without having to manipulate the n × n kernel matrix. Second, label-reconstruction prototypes, which form a set of basis functions to span the predictive model. Since the number of prototypes is much smaller than the sample size, a highly compact model can be obtained, leading to fast training and testing. Moreover, without this functional representation, the learned model can only be transductive, and is unable to handle out-of-sample patterns. It will also be shown that when the graph affinity is defined by the Gaussian kernel, both kinds of prototypes can be selected in a principled and simple manner. Experiments on a number of real-world data sets demonstrate encouraging performance and scaling properties of the proposed approach.

The rest of this paper is organized as follows. In Section II, we first give a brief review on graph-based semisupervised learning algorithms and low-rank approximation algorithms. In Section III, we discuss the two important roles of prototypes in scaling up graph-based semisupervised learning, namely approximating the graph-based regularizer and simplifying the model parametrization. We also show that when the Gaussian kernel is used to define the graph affinity, these two criteria lead to a simple and unified prototype selection scheme via k-means clustering. In Section IV, we demonstrate how to use the prototypes to reduce the size of the optimization problem associated with semisupervised learning.

In Section V, we perform experiments on a number of real-world data sets to demonstrate the performance of the proposed method. Finally, Section VI gives some concluding remarks. A preliminary version of this paper is published in [42].

In the sequel, the transpose of vector/matrix is denoted by the superscript^⊤, the identity matrix by I, and the n-dimensional vector of all ones by 1_n. Moreover, for matrix A = [a_ij], we use ${\Vert \mathbf{A}\Vert }_F=\sqrt{{\sum }_{\mathit{\text{ij}}}{a}_{\mathit{\text{ij}}}^2}$ for its Frobenius norm; and ‖A‖₂ for its spectral norm (which is equal to the maximum singular value of A). Besides, diag(a) converts a n-dimensional vector a to a n × n diagonal matrix.

II. Related Work

Section II-A first reviews some standard graph-based semi-supervised learning algorithms. Section II-B then introduces a number of representative recent developments that can handle larger data sets. Finally, the approach of low-rank approximation, which will be a core component of the proposed method, is introduced in Section II-C.

A. Graph-Based Semisupervised Learning

In semisupervised learning, we are given a set of l labeled samples ${\{({\mathbf{x}}_i,y_i)\}}_{i=1}^l$ and u unlabeled samples ${\{{\mathbf{x}}_i\}}_{i=l+1}^{l+u}$, where x_i ∈ ℝ^d, and y_i ∈ {−1, 1} is the class label. For simplicity of exposition, we only consider binary classification problems here. The y_i's from all the labeled samples can be concatenated to form the vector y_l ∈ {−1, 1}^l. For a given learning algorithm, let f be the learned function f, f ∈ ℝⁿ be the vector of f's evaluations on the n = l + u samples. This f can be divided into two sub vectors: f_l ∈ ℝ^l for the labeled samples, and f_u ∈ ℝ^u for the unlabeled ones.

A number of graph-based semisupervised learning algorithms can be formulated as the following optimization problem:

$$\underset{f}{min}{\mathbf{f}}^{\top }\mathbf{\text{Sf}}+C_{1}L({\mathbf{f}}_l,{\mathbf{y}}_l)+C_2\mathrm{\Omega }(f)$$ (1)

where C₁ and C₂ are the regularization parameters. The first term in (1) enforces smoothness of the predicted labels with respect to the data's manifold structure, which is captured via the matrix S ∈ ℝ^n×n. Usually, S is chosen as the graph Laplacian matrix

$$\mathbf{S}=\mathbf{D}-\mathbf{K}$$ (2)

where K ∈ ℝ^n×n is the kernel (adjacency) matrix of the graph [with associated kernel function K(·, ·)], and D = diag(K1_n) is the corresponding degree matrix. Alternatively, the normalized graph Laplacian matrix

$$\mathbf{S}=\mathbf{I}-{\mathbf{D}}^{-\frac{1}{2}}{\mathbf{\text{KD}}}^{-\frac{1}{2}}$$ (3)

can also be used. The second term in (1) requires the predictions on the labeled samples be consistent with the known class labels, and the discrepancy is penalized by the empirical loss function L(·, ·). Finally, the third term enforces regularization on the learned function f. Popular choices for Ω(f) include the norm of f in some reproducing kernel Hilbert space (RKHS) [4]. Alternatively, Zhou et al. [45] simply uses Ω(f) = ‖f_u‖, which regularizes predictions on the unlabeled samples only.

Well-known examples that follow the formulation in (1) include:

1. the method of learning with local and global consistency (LGC) [45], where S is the normalized graph Laplacian, and the two regularization parameters C₁ and C₂ are set to be equal;

2. learning using Gaussian fields and harmonic functions [48], where S is the unnormalized graph Laplacian, C₁ approaches infinity, and C₂ = 0;

3. the Laplacian regularized least-squares (LapRLS) and the LapSVM algorithms [4], which will be described in more detail in the following section.

The standard representer theorem in kernel learning can be extended to graph-based semisupervised learning. Specifically, Belkin et al. [4] showed that the learned function in (1) admits a representation as an expansion over all the labeled and unlabeled samples

$$f(\mathbf{x})=\sum _{i=1}^{l+u}{\alpha }_{i}K(\mathbf{x},{\mathbf{x}}_i)$$ (4)

where α_i ∈ ℝ.

1) Laplacian Regularized Least-Squares

In this paper, we will focus on two loss functions commonly used in (1), the square and the hinge loss. The square loss function leads to the LapRLS algorithm [4], which solves the optimization problem

$$\underset{f}{min}\frac{1}{l}\sum _{i=1}^l{(y_i-f({\mathbf{x}}_i))}^2+{\gamma }_A{\Vert f\Vert }_K^2+\frac{{\gamma }_I}{{(l+u)}^2}{\mathbf{f}}^{\top }\mathbf{\text{Sf}}$$ (5)

where ‖f‖_k is the norm of f in the RKHS induced by the kernel function K, and γ_A, γ_I are regularization parameters related to the C₁, C₂ in (1) as C₁ = (l + u)²/γ_Il and C₂ = γ_A(l + u)²/γ_I. By plugging in the form of f in (4), we obtain

$${min}_{\mathbf{\alpha }}\frac{1}{l}{(\mathbf{y}-\mathbf{\text{JK}}\mathbf{\alpha })}^{\top }(\mathbf{y}-\mathbf{\text{JK}}\mathbf{\alpha })+{\gamma }_{\mathbf{A}}{\mathbf{\alpha }}^{\top }\mathbf{K}\mathbf{\alpha }+\frac{{\gamma }_{\mathbf{I}}}{{(l+u)}^2}{\mathbf{\alpha }}^{\top }\mathbf{\text{KSK}}\mathbf{\alpha }$$

where α = [α₁, …, α_l+u]^⊤ ∈ ℝ^l+u, y = [y₁, …, y_l, 0, …, 0]^⊤ ∈ ℝ^l+u, and $\mathbf{J}=\text{diag}({[\underset{l}{\underbrace{1,\dots ,1}},\underset{u}{\underbrace{0,\dots ,0}}]}^{\top })\in {ℝ}^{(l+u)\times (l+u)}$. It can be shown that the solution of α is given by

$${\mathbf{\alpha }}^{\ast }={(\mathbf{\text{JK}}+{\gamma }_{A}l\mathbf{I}+\frac{{\gamma }_{\mathbf{I}}l}{{(l+u)}^2}\mathbf{\text{SK}})}^{-1}\mathbf{y}.$$ (6)

2) Laplacian SVM

Instead of using the square loss in (5), the LapSVM [4] uses the hinge loss, which then leads to

$$\underset{f}{min}\frac{1}{l}\sum _{i=1}^l{(1-y_{i}f({\mathbf{x}}_i))}_{+}+{\gamma }_A{\Vert f\Vert }_K^2+\frac{{\gamma }_{\mathbf{I}}}{{(l+u)}^2}{\mathbf{f}}^{\top }\mathbf{\text{Sf}}$$

where (1 − yf(x))₊ = max(0, 1 − yf(x)). Again, by plugging in (4), we obtain the primal problem

$$\begin{array}{l}{min}_{\mathbf{\alpha },\mathbf{\xi }}\frac{1}{l}\sum _{i=1}^l{\xi }_i+{\gamma }_A{\mathbf{\alpha }}^{\top }\mathbf{K}\mathbf{\alpha }+\frac{{\gamma }_I}{{(l+u)}^2}{\mathbf{\alpha }}^{\top }\mathbf{\text{KSK}}\mathbf{\alpha }\\ \mathrm{s}.\mathrm{t}.y_i\left(\sum _{j=1}^{l+u}{\alpha }_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j)+b\right)\ge 1-{\xi }_i,i=1,\dots ,l,{\xi }_i\ge 0,i=1,\dots ,l\end{array}$$

where ξ = [ξ₁, …, ξ_l]^⊤ ∈ ℝ^l. This leads to the solution

$${\mathbf{\alpha }}^{\ast }={\left(2{\gamma }_A\mathbf{I}+2\frac{{\gamma }_{\mathbf{I}}}{{(l+u)}^2}\mathbf{\text{SK}}\right)}^{-1}{\mathbf{J}}^{\top }\mathbf{Y}{\beta }^{\ast }$$ (7)

where J = [I_l0] ∈ ℝ^l×(l+u) with I_l as the l × l identity matrix, Y = diag([y₁, …, y_l]^⊤), and β* ∈ ℝ^l is obtained by solving the following optimization problem:

$$\begin{array}{llll}{\beta }^{\ast }\hfill & =\hfill & {max}_{\beta }\hfill & \sum _{i=1}^l{\beta }_i-\frac{1}{2}{\beta }^{\top }\mathbf{Q}\beta \hfill \\ \hfill & \hfill & \mathrm{s}.\mathrm{t}.\hfill & \sum _{i=1}^l{\beta }_i{y}_i=0\hfill \\ \hfill & \hfill & \hfill & 0\le {\beta }_i\le \frac{1}{l},i=1,\dots ,l\hfill \end{array}$$

and

$$\mathbf{Q}=\mathbf{\text{YJK}}{(2{\gamma }_A\mathbf{I}+2\frac{{\gamma }_I}{{(l+u)}^2}\mathbf{\text{SK}})}^{-1}{\mathbf{J}}^{\top }\mathbf{Y}\in {ℝ}^{l\times l}.$$

As can be observed from (6) and (7), both LapRLS and LapSVM require the storing of a number of (l + u) × (l + u) matrices (such as K, J and S), and expensive matrix inversion of an (l + u) × (l + u) matrix. Consequently, this costs O(n³) time and O(n²) space (recall that n = l + u). Besides, testing is also expensive as the representation of f in (4) can involve n terms. In many real-world applications, u can be huge as there are often an abundance of unlabeled samples. Hence, both the algorithms can become impractical on large data sets.

B. Scaling Up Graph-based Semisupervised Learning

In this section, we briefly review some of the recent advances in scaling up graph-based semisupervised learning algorithms.

1) Nyström Method for Learning With LGC

A popular method for graph-based semisupervised learning is based on LGC [45]. Its predictions on the set of n (labeled and unlabeled) samples are given by

$${(\mathbf{I}-\eta \mathbf{Q})}^{-1}\mathbf{y}$$ (8)

where y = [y₁, …, y_l, 0, …, 0]^⊤ ∈ ℝⁿ, Q ∈ ℝ^n×n is the normalized similarity matrix on the samples, and η is a regularization parameter. As (8) involves the inverse of the n × n matrix I − ηQ, it is expensive when n is large. To alleviate this problem, Camps-Valls et al. [8] used the Nyström method (which will be reviewed in Section II-C) to speed up the computation of (I − ηQ)⁻¹. Specifically, they use the Nyström method to efficiently obtain an approximate eigenvalue decomposition VΛV^⊤ [where V ∈ ℝ^n×m and Λ ∈ ℝ^m×m] of Q in O(m²n) time. Using the Woodbury formula, (8) can then be written as y − V(ΛV^⊤V − η⁻¹I)⁻¹ΛV^⊤y, which can be computed in O(m²n) time. By choosing m ≪ n, this approach is thus very suitable for large-scale applications. However, as will be demonstrated in Section V-B, empirically this approximation can hamper the prediction accuracy.

2) Primal LapSVM

As discussed in Section II-A1, traditionally the LapSVM is solved in the dual formulation. Very recently, new strategies are proposed to solve the LapSVM in the primal [24], which can be efficiently performed with preconditioned conjugate gradient [30]. Convergence can be further speed up using an early stopping criterion based on the predictions on the unlabeled data or validation examples. The resultant time complexity is reduced to O(cn²), where c is an empirical constant much smaller than n. Though better than the original O(n³) complexity, this quadratic complexity is still more expensive than other competitive methods.

3) Fast Nonparametric Function Induction

Delalleau et al. [13] proposed a nonparametric approach for estimating the continuous labels of unlabeled examples. For an out-of-sample example x, its prediction

$$f(\mathbf{x})=\frac{\sum _{j=1}^{n}W(\mathbf{x},{\mathbf{x}}_j)f({\mathbf{x}}_j)}{\sum _{j=1}^{n}W(\mathbf{x},{\mathbf{x}}_j)}$$ (9)

has the same form as Parzen window regressors. Here, f(x_j) is the estimated label for training sample x_j (which may be unlabeled) obtained in the training phase. A straightforward implementation, however, involves O(n³) time and O(n²) space on training. To reduce these complexities, Delalleau et al. [13] force the summations in (9) to only involve a preselected sample subset S, |S| ≪ n, and do not enforce smoothness among the large number of unlabeled samples not in S. As will be empirically demonstrated in Section V-B, these restrictions can hamper the prediction accuracy.

4) Anchor Graph

Liu et al. [23] borrowed the idea of [13] and [42] and proposed to use the so-called anchor points (which are the same as prototypes in [42]) to build sparse graphs for semisupervised learning. The adjacency matrix is computed by a k-nearest-neighbor graph, or by solving a quadratic program (QP) similar to that in locally linear embedding [29] with additional sparsity constraints. In both cases, the computational cost is very expensive for large-scale applications.

C. Low-Rank Approximation

Given a symmetric, positive semidefinite matrix (such as the kernel matrix) K ∈ ℝ^n×n, a low-rank approximation algorithm [14], [17] produces an approximation of the form GG^⊤, where G ∈ ℝ^n×m and m ≪ n. If the columns of G are linearly independent, GG^⊤ is of rank m. It is well known that the optimal rank-m approximation K^(m) of K (with respect to the spectral or the Frobenius norm) can be easily constructed from its k leading eigenvectors and eigenvalues. Specifically, let the eigenvalue decomposition of K be UΣU^⊤, where the columns of U contain its eigenvectors, and Σ = diag[(σ₁, σ₂, …, σ_n)] contains the corresponding eigenvalues in descending order. Then, K^(m) = U^(m)Σ^(m)U^(m)⊤, where U^(m) contains the m leading eigenvectors and U^(m) contains the m leading eigenvalues. The corresponding low-rank approximation errors with respect to the spectral norm and Frobenius norm are ‖K − K^(m)‖₂ = σ_m+1 and ${\Vert \mathbf{K}-{\mathbf{K}}^{(m)}\Vert }_F^2={\sum }_{i=m+1}^n{\sigma }_i^2$, respectively. However, while K^(m) can be obtained easily from the leading eigenvectors and eigenvalues of K, directly finding this eigenvalue decomposition takes O(n³) time. For large K, this can be expensive and hence more efficient alternatives have to be sought.

In this paper, we will use an efficient low-rank approximation approach called the Nyström method [15], [16], [37]. It first chooses a subset of m rows/columns from K. Let K_nm ∈ ℝ^n×m be the submatrix of K containing these selected columns, and K_mm ∈ ℝ^m×m the submatrix containing the intersection of the selected columns and rows. Using the eigenvalue decomposition ${\mathbf{K}}_{\mathit{\text{mm}}}={\mathbf{U}}_m{\mathbf{\Lambda }}_m{\mathbf{U}}_m^{\top }$, the matrix containing the m leading eigenvectors of K is approximated by the Nyström extension as ${\mathbf{U}}^{(m)}\simeq \mathbf{U}=K_{\mathit{\text{nm}}}{\mathbf{U}}_m{\mathbf{\Lambda }}_m^{-1}$ [37]. A useful consequence is that the whole matrix can then be approximated as

$$\mathbf{K}\simeq \mathbf{U}{\mathbf{\Lambda }}_m{\mathbf{U}}^{\top }={\mathbf{K}}_{\mathit{\text{nm}}}{\mathbf{K}}_{\mathit{\text{mm}}}^{-1}{\mathbf{K}}_{\mathit{\text{nm}}}^{\top }.$$ (10)

Note that, K_nm can be computed in O(mn) time, and ${\mathbf{K}}_{\mathit{\text{mm}}}^{-1}$ in O(m³) time. Thus, using (10), K can be written as GG^⊤, where $\mathbf{G}={\mathbf{K}}_{\mathit{\text{nm}}}{\mathbf{K}}_{\mathit{\text{mm}}}^{-1/2}$, in O(m²n + m³) time, which is linear in the sample size n.

Traditionally, the m columns are sampled randomly from K [37] or by a probabilistic sampling scheme [15]. More generally, they can be chosen as landmark points ${\{{\mathbf{u}}_i\}}_{i=1}^m$ obtained from summarizing the data. The approximation in (10) is then applied as

$$\widehat{\mathbf{K}}={\mathbf{\text{EW}}}^{-1}{\mathbf{E}}^{\top }$$ (11)

where W ∈ ℝ^m×m [with W_ij = K(u_i, u_j)] is the kernel matrix evaluated on the landmark points, and

$$\mathbf{E}=[K({\mathbf{x}}_i,{\mathbf{u}}_j)]\in {ℝ}^{n\times m}$$ (12)

is the cross-similarity matrix between the whole data X = [x₁, …, x_n] and the landmark points. For a number of commonly used kernels (such as the Gaussian, linear, and polynomial kernels), it has been shown that the approximation error ‖K−K̂‖_F is bounded by the encoding errors of these landmark points [40], [41]. Based on this error analysis, we can choose the k-means cluster centers of the data as the landmark points. In the implementation, we further fix the number of k-means iteration to a small number (such as five). The complexity of k-means is then linear in the sample size and dimension (assuming that each kernel evaluation takes time linear in the dimension), and is thus suitable for large-scale problems.

III. Approximations via Prototypes

This section discusses the basic idea of using two types of prototypes to enable the optimization of graph-based semisupervised learning more efficient. By prototypes, we mean a small set of points in the input space that can be used as a replacement of the original data in obtaining an efficient yet accurate predictive solution. In this paper, there are two types of prototypes serving different purposes: 1) low-rank approximation prototypes that are used for low-rank approximation of the graph Laplacian matrix (Section III-A) and 2) label-reconstruction prototypes that are used in label-reconstruction for accurate model representation (Section III-B).

A. Low-Rank Approximation Prototypes

Recall that the graph Laplacian matrix S in (2) or (3) is constructed from the kernel matrix K of the graph. In practice, K usually has a rank much smaller than its size [37]. This offers the opportunity of reducing the computational burden of graph-based regularization by performing low-rank approximation (Section II-C).

Using the low-rank approximation EW⁻¹E^⊤ of K in (11), the unnormalized graph Laplacian S in (2) can be approximated as

$$\mathbf{S}\simeq \stackrel{\sim }{\mathbf{D}}-{\mathbf{\text{EW}}}^{-1}{\mathbf{E}}^{\top }$$ (13)

where D̃ = diag(EW⁻¹E^⊤l_n). The corresponding (approximated) graph-based regularizer is then f^⊤Sf ≃ f^⊤(D̃ − EW⁻¹E^⊤)f. Similarly, when S is the normalized graph Laplacian, it is approximated as

$$\mathbf{S}\simeq \mathbf{I}-\mathbf{E}{\stackrel{\sim }{\mathbf{D}}}^{-\frac{1}{2}}{\mathbf{W}}^{-1}{\mathbf{E}}^{\top }{\stackrel{\sim }{\mathbf{D}}}^{-\frac{1}{2}}$$ (14)

and the corresponding regularizer becomes f^⊤Sf ≃ f^⊤(I − ED̃^−1/2W⁻¹E^⊤D̃^−1/2)f.

B. Label-Reconstruction Prototypes

1) Motivating Example

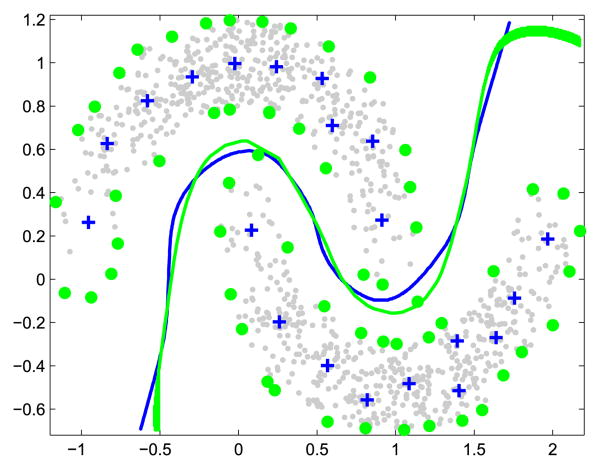
As discussed in Section II-A, the inclusion of a graph-based regularizer results in the model (4) that expands over all the labeled and unlabeled samples. This leads to slow training and testing when n is large. In practice, a classifier seldom needs all the samples as basis functions. Fig. 1 shows a motivating example on a binary classification problem. We first train a standard SVM using the whole data set. The obtained decision boundary (in green) and support vectors (circles) are shown. To construct an alternative classifier, we choose a set of label-reconstruction prototypes (crosses) from each class. To predict the label of a test sample x, we compute its similarities with all the label-reconstruction prototypes, and then linearly combine their labels using the similarities as weights. The resultant decision boundary is shown in blue. As can be observed, the two decision boundaries are very similar. This illustrates that instead of using the whole data set, a small set of properly chosen label-reconstruction prototypes can successfully reconstruct the decision boundary.

Fig. 1.

Decision boundaries of the SVM (green) and a prototype-based model (blue) on a toy data set. Circles are the support vectors and crosses are the prototypes.

2) Formulation

The above idea can be formalized as follows. We assume that the label of any sample x can be reconstructed as a weighted combination of the labels of r label-reconstruction prototypes ${\left\{{\mathbf{v}}_i\right\}}_{i=1}^r$

$$\sum _{i=1}^r{f}_{{\mathbf{v}}_i}K(\mathbf{x},{\mathbf{v}}_i)$$ (15)

where f_vi is the label of prototype v_i. This resembles the nearest-neighbor classifier in that the predicted label of x is mostly dependent on prototypes v_j having large similarities (i.e., K(x, v_j) values) with x. Intuitively, as long as there are enough label-reconstruction prototypes filling the input space, the label of any sample can be reconstructed reliably from these nearby prototypes.

To make the model more flexible, we allow each f_vi in (15) to be real-valued even for classification problems. Note that, (15) can be written more compactly as

$${\mathbf{\text{Hf}}}_{\upsilon }$$ (16)

where f_υ = [f_v1, f_v2, …, f_vr]^⊤ ∈ ℝ^r and

$$\mathbf{H}=[K({\mathbf{x}}_i,{\mathbf{v}}_j)]\in {ℝ}^{n\times r}$$ (17)

is the kernel submatrix defined between the whole data set X and prototypes v_i's. On large data sets, one can additionally enforce sparsity on H by only computing the similarities between the label-reconstruction prototypes and their k-nearest samples. This has been found useful in the construction of large graphs in semisupervised learning [23].

3) Choosing the Label-Reconstruction Prototypes

We now consider how to choose the label-reconstruction prototypes. Note that, (15) can be deemed as an approximation of the complete model in (4). Hence, we want to minimize

$$D(\sum _{i=1}^{l+u}{\alpha }_{i}K(\mathbf{x},{\mathbf{x}}_i),\sum _{i=1}^r{f}_{{\mathbf{v}}_i}K(\mathbf{x},{\mathbf{v}}_i))$$ (18)

where D(·, ·) measures the difference between the complete model ${\sum }_{i=1}^{l+u}{\alpha }_{i}K(\mathbf{x},{\mathbf{x}}_i)$ in (4) and the approximate model ${\sum }_{i=1}^r{f}_{{\mathbf{v}}_i}K(\mathbf{x},{\mathbf{v}}_i)$ in (15).

In practice, as α_i's, f_vi's, and v_i's are unknown during training, it is infeasible to directly minimize (18) with respect to all these variables. Recall that ${\{K(\cdot ,{\mathbf{x}}_i)\}}_{i=1}^{l+u}$ forms a basis for the complete model and ${\{K(\cdot ,{\mathbf{v}}_i)\}}_{i=1}^r$ forms a basis for the approximate model. In order for these two models to have similar representation power, we expect that the two basis can be reliably coded by each other. More specifically, we choose the label-reconstruction prototypes v_i's so as to minimize the error of coding each component in ${\{K(\cdot ,{\mathbf{x}}_i)\}}_{i=1}^{l+u}$ with the best element in ${\{K(\cdot ,{\mathbf{v}}_i)\}}_{i=1}^r$

$$\underset{{\mathbf{v}}_1,\dots ,{\mathbf{v}}_r}{min}\mathcal{Q}\equiv \sum _{i=1}^{l+u}\left(\underset{j=1,2,\dots ,r}{min}D(K(\cdot ,{\mathbf{x}}_i),K(\cdot ,{\mathbf{v}}_j))\right).$$ (19)

Obviously, the choice of v_i's depends on the specific kernel K(·, ·) and discrepancy measure D(·, ·). In the following, we consider the use of the Gaussian kernel K(x, y) = exp (−‖x − y‖²/2h²). Since it has the same form as the normal distribution, we use the cross entropy for probability distribution functions (pdfs) as D(·, ·) in (19). Recall that the cross entropy between the two pdfs p and q is

$$H(p,q)=H(p)+D_{\text{KL}}(p\Vert q)$$ (20)

where H(p) = − ∫ p(x)log(p(x))dx is the entropy of p, and D_KL(p‖q) = ∫ p(x)log(p(x)/q(x))dx is the Kullback–Leibler (KL) divergence between p and q [18]. Since {x₁, …, x_l+u} is fixed, minimizing D(K(·, x_i), K(·, v_j)) = H(K(·, x_i), K(·, v_j)) in (19) is the same as minimizing their KL-divergence, which can be written as [18]¹

$$D_{\text{KL}}(K(\cdot ,{\mathbf{x}}_i)\Vert K(\cdot ,{\mathbf{v}}_j))=\frac{1}{4h^2}{\Vert {\mathbf{x}}_i-{\mathbf{v}}_j\Vert }^2.$$ (21)

The objective in (19) then simplifies as

$$\mathcal{Q}=\frac{1}{4h^2}\sum _{j=1}^r\sum _{i\in S_j}{\Vert {\mathbf{x}}_i-{\mathbf{v}}_j\Vert }^2$$

where S_j is the subset of kernels in ${\{K(\cdot ,{\mathbf{x}}_i)\}}_{i=1}^{l+u}$ whose closest label-reconstruction prototype is K(·, v_j). Interestingly, this is exactly the objective of the k-means clustering (apart from the scaling factor 1/4h²). As in Section III-A, the prototypes v_i's in (15) can again be chosen as the k-means cluster centers. In other words, the low-rank approximation prototypes in Section III-A and the label-reconstruction prototypes introduced here are indeed the same. Consequently, E in (12) is also the same to H in (17).

For other types of kernels, the cross entropy in (20) may no longer be suitable and other distance measures will be investigated in the future.

IV. Prototype Vector Machine

In Section III, we introduced two types of prototypes: 1) low-rank-approximation prototypes ${\left\{{\mathbf{u}}_i\right\}}_{i=1}^m$, which avoid the computation of an n × n graph Laplacian matrix and 2) label-reconstruction prototypes ${\left\{{\mathbf{v}}_i\right\}}_{i=1}^r$, which avoid the use of all the labels in the whole data set. In this section, using the associated simplified equations (13) [or (14)] and (16), we will consider how to realize the proposed prototype vector machine (PVM) with the square and hinge loss functions. As will be seen, since m, r ≪ n (the sample size), the optimization of problem (1) can be made much more efficient.

Algorithm 1 PVM Using the Square Loss
1:	Perform k-means clustering on the given labeled and unlabeled samples, and use the cluster centers as prototypes.
2:	Use (17) to compute H (and thus obtain its submatrices Hl and Hu).
3:	Substitute the approximate graph Laplacian [(13) or (14)] into (23) and obtain ${\mathbf{f}}_{\upsilon }^{\ast }$.
4:	Prediction
	1) on the given unlabeled samples: ${\mathbf{f}}_u={\mathbf{H}}_u{\mathbf{f}}_{\upsilon }^{\ast }$.
	2) on an unseen $\mathbf{x}:[K(\mathbf{x},{\mathbf{v}}_1),\dots ,K(\mathbf{x},{\mathbf{v}}_r)]{\mathbf{f}}_{\upsilon }^{\ast }$.

A. Training

1) Square Loss

Using the square loss, the objective in (1) can be written as

$$\underset{{\mathbf{f}}_{\upsilon }}{min}{({\mathbf{\text{Hf}}}_{\upsilon })}^{\top }\mathbf{S}({\mathbf{\text{Hf}}}_{\upsilon })+C_1{\Vert {\mathbf{H}}_l{\mathbf{f}}_{\upsilon }-{\mathbf{y}}_l\Vert }^2+C_2{\Vert {\mathbf{H}}_u{\mathbf{f}}_{\upsilon }\Vert }^2$$ (22)

where H_l ∈ ℝ^l×r and H_u ∈ ℝ^u×r are submatrices of H containing the rows corresponding to the labeled and unlabeled samples, respectively, and S is as defined in (13). Replacing S with the normalized graph Laplacian (14) is straightforward. Moreover, as in [45], we have used ‖H_uf_v‖² to regularize f. Alternatively, one can use the RKHS norm of f (as in [4]). On using (15), this leads to a slightly different regularizer ${\mathbf{f}}_{\upsilon }^{\top }{\mathbf{K}}_{\upsilon }{\mathbf{f}}_{\upsilon }$, where K_υ is the kernel matrix defined on the r label-reconstruction prototypes, and the results in the sequel can be easily extended.

By setting the derivative of the objective in (22) with respect to f_υ to zero, we obtain the optimal solution of f_υ as

$${\mathbf{f}}_{\upsilon }^{\ast }=C_1{({\mathbf{H}}^{\top }\mathbf{\text{SH}}+C_1{\mathbf{H}}_l^{\top }{\mathbf{H}}_l+C_2{\mathbf{H}}_u^{\top }{\mathbf{H}}_u)}^{-1}{\mathbf{E}}_l^{\top }{\mathbf{Y}}_l.$$ (23)

The complete algorithm is shown in Algorithm 1. Note that, if k-means clustering is used as the selection scheme for both the low-rank-approximation prototypes and label-reconstruction prototypes, then we simply have E_l = H_l in (23).

On using k-means as the unified prototype selection scheme, we have m = r. Step 1 of Algorithm 1 then takes O(ndm) time and O(nm) space. Step 2 takes O(ndr) = O(ndm) time (assuming that each kernel evaluation takes O(d) time) and O(nr) = O(nm) space. In step 3, with the use of the m low-rank approximation prototypes, we have H^⊤SH = H^⊤DH − (H^⊤E)W⁻¹(E^⊤H) from (13). Since D̃ is diagonal, H ∈ ℝ^n×r and E ∈ ℝ^n×m, H^⊤SH can be computed in O(r²n + r²m + m²r + mnr) = O(nr(m + r)) = O(nm²) time and O(n max(r, m)) = O(nm) space. Moreover, the inverse operation in (23) involves a r × r matrix, and takes O(r³) time. Thus, the total time for computing ${\mathbf{f}}_{\upsilon }^{\ast }$ is O(nr(m +r) + r³) = O(nr(m + r)) = O(nm²). Since m ≪ n, the total space and time complexities are both linear in the sample size, which is much faster than the O(n³) time for LapRLS (Section II-A).

2) Hinge Loss

For classification problems (with labels in {±1}), we can use the hinge loss as popularized by the SVM. The other two terms in (22) remain the same, and can be combined together as ${\mathbf{f}}_{\upsilon }^{\top }{\mathbf{\text{Af}}}_{\upsilon }$, where²

$$\mathbf{A}={\mathbf{H}}^{\top }\mathbf{\text{SH}}+C_2{\mathbf{H}}_u^{\top }{\mathbf{H}}_u.$$ (24)

Let e_k be the transpose of the kth row in H_l

$${\mathbf{H}}_l={[{\mathbf{e}}_1,{\mathbf{e}}_2,\dots ,{\mathbf{e}}_l]}^{\top }.$$ (25)

The optimization problem in (1) can then be written as

$$\begin{array}{ll}\underset{{\mathbf{f}}_{\upsilon }}{min}\hfill & \frac{1}{2}{\mathbf{f}}_{\upsilon }^{\top }{\mathbf{\text{Af}}}_{\upsilon }+C_1\sum _{i=1}^l{\xi }_i\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & y_i{\mathbf{e}}_i^{\top }{\mathbf{f}}_{\upsilon }\ge 1-{\xi }_i,i=1,\dots ,l{\xi }_i\ge 0,i=1,\dots ,l\hfill \end{array}$$

where the first term performs regularization, and the second term is the hinge loss incurred by approximating the labels of X_l with the reconstructed ones (H_lf_υ). The Lagrangian can be written as

$$\mathcal{L}=\frac{1}{2}{\mathbf{f}}_{\upsilon }^{\top }{\mathbf{\text{Af}}}_{\upsilon }+C_1\sum _{i=1}^l{\xi }_i-\sum _{i=1}^l{\beta }_i(y_i{\mathbf{e}}_i^{\top }{\mathbf{f}}_{\upsilon }-1+{\xi }_i)-\sum _{i=1}^l{\gamma }_i{\xi }_i.$$

By setting its derivative with respect to f_υ and ξ_i's to zero, we obtain C₁ = β_i + γ_i, and

$${\mathbf{\text{Af}}}_{\upsilon }=\sum _{i=1}^l{\beta }_i{y}_i{\mathbf{e}}_i={\mathbf{H}}_l^{\top }\beta \odot {\mathbf{y}}_l$$ (26)

on using (25). Here, β = [β₁, …, β_l]^⊤, and ⊙ denotes the element wise product. Plugging these back into the Lagrangian, we obtain the dual problem

$$\begin{array}{cc}\hfill {max}_{\beta }& -\frac{1}{2}{({\mathbf{H}}_l^{\top }\beta \odot {\mathbf{y}}_l)}^{\top }{\mathbf{A}}^{-1}({\mathbf{H}}_l^{\top }\beta \odot {\mathbf{y}}_l)+\sum _{i=1}^l{\beta }_i\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& 0\le {\beta }_i\le C_1,i=1,2,\dots ,l\hfill \\ \hfill =& {max}_{\beta }-\frac{1}{2}{\beta }^{\top }\mathbf{Q}\beta +{\mathbf{1}}_l^{\top }\beta \hfill \\ \hfill \mathrm{s}.\mathrm{t}.& 0\le {\beta }_i\le C_1,i=1,2,\dots ,l\hfill \end{array}$$ (27)

where

$$\mathbf{Q}={\mathbf{H}}_l{\mathbf{A}}^{-1}{\mathbf{H}}_l^{\top }\odot {\mathbf{y}}_l{\mathbf{y}}_l^{\top }\in {ℝ}^{l\times l}.$$ (28)

After solving this QP, labels of the prototypes v_i's can be recovered using the Karush–Kuhn–Tucker condition in (26), as

$${\mathbf{f}}_{\upsilon }^{\ast }={\mathbf{A}}^{-1}{\mathbf{H}}_l^{\top }\beta \odot {\mathbf{y}}_l.$$ (29)

The complete algorithm is shown in Algorithm 2.

As in Section IV-A1, H^⊤SH can be computed in O(nm²) time. Hence, matrix A in step 3 can also be computed in O(nr(m + r) + r²u) = O(nr(m + r)) = O(nm²) time, and its inverse in O(r³) time. Moreover, note that the QP in (27) is of the same form as a standard SVM, and so can be solved readily with state-of-the-art SVM solvers. There are only l optimization variables in this QP, and modern SVM implementations typically have a time complexity that scales linearly with l [36]. So, the total time complexity is O(nr(m+r)+r³) = O(nr(m+r)) = O(nm²). Since m ≪ n, this is again much more efficient than the O(n³) time required of the standard LapSVM (Section II-A) and the O(n²) time required of the primal LapSVM (Section II-B2). Moreover, it can be easily seen that its space complexity is O(mn), the same as that when the square loss is used. As a short summary, Table I compares the time and space complexities of a number of semisupervised learning algorithms that will be further studied empirically in Section V-B.

Table I.

Time and Space Complexities for the Training Process of Various Semisupervised Learning Algorithms (Descriptions of the Algorithms Can Be Found in Section V-B). Here, n Is the Total Number of Labeled and Unlabeled Samples, and m Is the Number of Prototypes in the PVM (Which Is Equal to the Sample Subset Size Used in the Other Algorithms)

	LGC [45]	LapRLS [4]	LapSVMp [24]	NYS-LGC [8]	NF1 [13]	Anchor [23]	PVM (sqr)	PVM (hinge)
time	O(n3)	O(n3)	O(m2n)	O(n2)	O(m2n)	O(m2n)	O(m2n)	O(n2)
space	O(n2)	O(n2)	O(n2)†	O(mn)	O(mn)	O(n2)†	O(mn)	O(mn)

^†In the implementation of LapSVMp and Anchor method, the kernel matrix is partitioned into sub-blocks that are loaded into memory sequentially, which can further reduce the O(n²) memory consumption to O(np), where p is a user defined number.

Algorithm 2 PVM Using the Hinge Loss
1:	Perform k-means clustering on the given labeled and unlabeled samples, and use the cluster centers as prototypes.
2:	Use (17) to compute H (and thus obtain its submatrices Hl and Hu).
3:	Use the approximate graph Laplacian [(13) or (14)] to compute A in (24), and subsequently Q in (28).
4:	Solve the QP in (27) to obtain β.
5:	Obtain ${\mathbf{f}}_{\upsilon }^{\ast }$ from (29).
6:	Prediction
	1) on the given unlabeled samples: $sgn({\mathbf{f}}_u)=sgn({\mathbf{H}}_u{\mathbf{f}}_{\upsilon }^{\ast })$
	2) on an unseen $\mathbf{x}:sgn([K(\mathbf{x},{\mathbf{v}}_1),\dots ,K(\mathbf{x},{\mathbf{v}}_r)]{\mathbf{f}}_{\upsilon }^{\ast })$.

B. Prediction

After obtaining ${\mathbf{f}}_{\upsilon }^{\ast }$, the predicted labels on the given unlabeled samples can be computed as ${\mathbf{f}}_u={\mathbf{H}}_u{\mathbf{f}}_{\upsilon }^{\ast }$, and that on an unseen test sample x as $[K(\mathbf{x},{\mathbf{v}}_1),\dots ,K(\mathbf{x},{\mathbf{v}}_r)]{\mathbf{f}}_{\upsilon }^{\ast }$. Since it only depends on the r label-reconstruction prototypes, testing takes O(r) time. This is much faster than LapRLS and LapSVM, which take O(n) time.

C. Number of Prototypes

The number of prototypes is an important factor that affects the performance of the proposed method. More prototypes lead to more accurate approximation on both the kernel matrix as well as the class labels. Therefore, this tends to give a better performance. However, the time consumption also grows. Hence, this involves a tradeoff between the accuracy and the efficiency. Empirically, we choose m as 5% of the sample size (or fewer), which gives satisfactory results. In our empirical evaluations (Section V-A.3), we also observe that when m is beyond a certain threshold the performance would reach a plateau.

We are also interested in performance of PVM with respect to choice of the number of prototype vectors as well as the number of labeled and unlabeled samples. First, the larger the number of prototypes, the more complicated concept (e.g., classification boundary) can be potentially delineated. Therefore, more prototypes will lead to a better performance, as has been shown in our empirical evaluations.

In considering the number of labeled samples, note that given a fixed level of intrinsic difficulty of the learning problem (in terms of the complexity of the classification boundaries), more labeled samples will lead to a better prediction performance. In this case, together with more prototypes, we will also expect a better performance.

If the unlabeled data can improve the performance of learning, more prototypes will be able to summarize the distribution of unlabeled data better, therefore the performance will improve with more prototypes and unlabeled data. However, sometimes, the unlabeled data may not help in semisupervised learning. For example, if the low-density separation assumption is violated [11], [19], [28] then it would be hard to predict whether more prototypes will improve performance, since more prototypes will make the effect of unlabeled samples more significant.

In practice, the decision boundary can be determined in a complicated manner by labeled and unlabeled samples together in semisupervised learning. For example, in [32], it is stated that if the complexity of the distribution under consideration is too high to be learned using labeled data points, but is small enough to be learned using unlabeled data points, then semisupervised learning can improve the performance of the supervised learning task. In this case, we may expect a better performance with more prototypes as well as labeled and unlabeled samples. However, in some cases, the needed relation between labeled and unlabeled samples might not be satisfied. For example, Ben-David et al. [5] concluded that using unlabeled data cannot provide sample size guarantees that are better than those using labeled data only, unless one assumes a very strong relationship between the labeled and unlabeled data distribution. Therefore, in case the desired condition is not satisfied, it would be hard to guarantee that more prototypes will lead to improved performance with more labeled and unlabeled samples.

V. Experiments

In Section V-A, we investigate how the performance of the proposed PVM varies with sample size, the number of labeled samples and prototypes. In Section V-B, the PVM is compared with other state-of-the-art semisupervised learning algorithms on a number of real-world data sets. Experiments will be performed on both binary and multiclass classification problems. Note that for PVM using the square loss, the formulation in (22) can be extended for multiclass classification in a straightforward manner. For PVM using the hinge loss, we first decompose a C-class classification problem into C one-versus-rest binary classification problems. Prediction is then made by assigning the sample to the class with the highest decision function value.

PVM is a sparse model, as only a small number of prototypes are involved in (15). Another popular approach for the construction of sparse models is using the ℓ₁-regularizer, which encourages model coefficients to approach zero. Recently, this ℓ₁ -penalized approach has drawn considerable interest in learning sparse predictive models. For example, lasso [35], the most well-known ℓ₁-penalized sparse model, adds the ℓ₁-regularizer to the square loss function. Hence, a natural question is how the parsimonious model produced by the PVM compares with that obtained by ℓ₁-regularization. This will be addressed in Section V-D.

A. Performance of the PVM

In this section, we study the performance of the PVM by performing experiments on a subset of the MNIST digits data set.³ We use the five digits (represented as 784-D feature vectors) 3, 5, 6, 8, and 9, leading to a total of 29 270 samples. The Gaussian kernel

$$K({\mathbf{x}}_i,{\mathbf{x}}_j)=exp(-\beta {\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2)$$ (30)

is used. As discussed in Section III, this leads to a unified prototype selection scheme, namely that the k-means cluster centers can be used as both the low-rank approximation prototypes and the label-reconstruction prototypes.

1) Variation With Sample Size

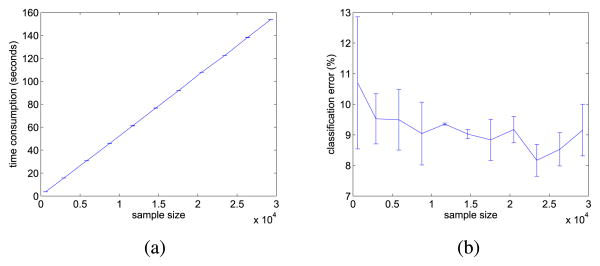
In this experiment, we first study how the performance of PVM (using the square loss) varies when the total number (n) of labeled and unlabeled samples is gradually increased from 1000 to 29270. For each class, 50 samples are labeled. The number of prototypes m is fixed at 200. To reduce statistical variability, results are based on averages over 30 random repetitions.

Fig. 2(a) shows the variation of training time (which includes the time for k-means clustering in step 1 of Algorithms 1 and 2) with n. As can be seen, the time scales linearly with n, which agrees with our analysis in Section IV-A. Fig. 2(b) shows the classification error on the unlabeled samples. Note that although the number of prototypes is fixed, the accuracy remains fairly stable with increasing sample size. This agrees with our intuition that the number of prototypes required for building an accurate model depends largely on the data distribution and class boundary, but not directly on the sample size.

Fig. 2.

Performance of the PVM with different sample sizes. (a) Training time versus sample size (note that the error bars here are very small). (b) Error versus sample size.

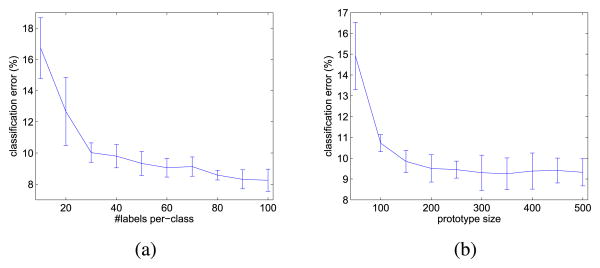
2) Variation With the Number of Labeled Samples

Next, we vary the number of labeled samples used for training, as l = {100, 200, 300, …, 1000}. The number of unlabeled samples is then u = n − l with n = 29270. Fig. 3(a) shows the resultant variation of the classification error (on the unlabeled samples). As can be seen, similar to the other semisupervised learning models, the accuracy increases when more labeled information is available. The improvement in accuracy is particularly prominent when the number of labeled samples is small. This agrees with the observation in [9] that the labeled samples reduce the error exponentially fast.

Fig. 3.

Performance of the PVM at different settings. (a) Different numbers of labeled samples per class. (b) Different numbers of prototypes.

3) Variation With the Number of Prototypes

Finally, Fig. 3(b) examines the variation of the classification error with the number of prototypes m, while fixing the number of labeled samples per class at 50, and the sample size at n = 29720. As can be seen, using more prototypes leads to better performance, though the improvement diminishes when m is beyond a certain value. In this experiment, using m = 200, which is less than 1% of the whole data set size, already suffices to give a good performance.

B. Comparison With the State-of-the-Art

In this section, we compare both versions of PVM: PVM(sqr), using the square loss (Section IV-A1), and PVM(hinge), using the hinge loss (Section IV-A2), with the supervised learner SVM (using only the labeled samples) and a number of state-of-the-art semisupervised learning algorithms, including:

1. LGC: learning with LGC [45];

2. LapRLS: Laplacian regularized least squares [4] (Section II-A1);

3. NYS-LGC: acceleration of LGC using Nyström low-rank approximation [8] (Section II-B1);

4. LapSVMp: primal LapSVM ⁴ trained with preconditioned conjugate gradient [24] (Section II-B2);

5. Nonparametric function induction (NFI): fast nonparametric function induction [13] (Section II-B3);

6. Anchor⁵: the method based on anchor graph [23] (Section II-B4).

All codes are in MATLAB and run on an Intel T2400 1.83-GHz laptop with 1-GB memory.

1) Setup

We use a variety of binary and multiclass benchmark data sets from [10]⁶ and the libsvm data archive.⁷ The number of labeled samples per class is 50 (except for the two-moon data, which has only one labeled sample per class). A summary of the data sets is shown in Table II.

Table II.

Data Sets Used in the Experiment. l Is the Number of Labeled Samples, u Is the Number of Unlabeled Samples, and m Is the Number of Prototypes

DATA	DIM	#CLASSES	l	u	m
G241C	241	2	100	1,400	150
G241D	241	2	100	1,400	150
DIGIT1	241	2	100	1,400	150
USPS	241	2	100	1,400	150
COIL2	241	2	100	1,400	150
COIL	241	6	300	1,200	150
BCI	117	2	100	300	40
TEXT	11,960	2	100	1,400	150
SPLICE	60	2	100	900	100
SEGMENT	29	7	350	1,960	231
DNA	180	3	150	3,036	200
SVMGD1A	4	2	100	6,989	200
USPS-FULL	256	10	500	6,791	200
SATIMAGE	36	6	300	6,135	200

For PVM, the number of prototypes is chosen as m = 0.1n when n ≤ 3000; and m = 200 otherwise. The same number of samples is used in forming the subset for NFI and NYS-LGC. Other parameters of the various algorithms are chosen by fivefold cross-validation.⁸ For example, the β parameter of the Gaussian kernel is chosen from {2⁻⁵β₀, 2⁻⁴β₀, …, 2⁴β₀, 2⁵β₀}, where β₀ is the reciprocal of average distance between the samples. The regularization parameters in LapRLS are chosen from {10⁻⁶, 10⁻⁵, …, 1, 10}; while those for the other algorithms are from {10⁻³, 10⁻², …, 10⁴, 10⁵}. For PVM, we simply set the regularization parameter C₂ = 0 and only tune C₁. To reduce statistical variability, results are based on averages over 30 random selections of the labeled samples.

2) Results

Table III shows the classification errors on the unlabeled samples, and Table IV shows the total training and testing time. The following observations can be made.

Table III.

Classification Errors (%) on the Unlabeled Data Obtained by the Different Algorithms. The Best Results and Those That Are Not Statistically Worse (According to the Two-Sample One-Tailed t-Test, With a p-Value of 0.05) Are in Bold. Note That, LGC and LapRLS Cannot Be Run on the Large Data Sets of Svmgd1a, Usps-Full, and Satimage

	(SUPERVISED)	(SEMI-SUPERVISED)
DATA	SVM	LGC	LapRLS	LapSVMp	NYS-LGC	NFI	ANCHOR	PVM(sqr)	PVM(hinge)
G241C	22.34±1.41	21.92±1.90	22.02±1.73	25.82±1.75	24.19±3.06	28.07±2.71	35.15±1.45	24.50±2.49	23.21±1.95
Q241D	25.14±2.03	28.10±3.27	22.36±1.78	25.89±1.12	30.98±4.22	30.82±5.36	36.61±2.07	25.15±2.58	24.85±2.70
DIGIT1	4.70±1.09	5.74±1.09	5.74±1.50	1.84±0.37	6.68±1.63	9.83±1.43	3.56±0.45	4.18±1.17	3.72±1.07
USPS	9.30±2.81	4.57±1.27	6.11±0.63	5.23±2.34	9.72±1.82	5.49±0.78	15.90±3.41	5.29±0.73	6.35±1.33
COIL2	11.17±0.91	14.37±3.63	10.83±1.94	12.74±2.16	16.90±3.00	13.98±2.48	8.11±1.64	11.69±2.47	14.85±2.36
COIL	12.21±1.81	12.38±1.99	21.17±1.71	7.79±0.74	18.75±1.48	30.93±6.22	12.41±0.67	13.41±1.29	12.26±1.01
BCI	35.17±3.29	44.43±2.28	29.16±3.56	46.23±3.16	45.45±2.62	45.67±2.61	48.37±2.61	33.59±3.01	31.65±2.86
TEXT	24.35±2.14	23.09±1.43	23.99±1.58	22.75±1.30	34.40±3.63	32.54±2.66	27.28±1.01	30.4±4.46	26.29±2.58
SPLICE	24.33±1.13	22.85±1.47	19.78±2.41	33.76±2.53	30.56±3.16	34.56±1.97	29.11±0.97	23.47±1.59	25.32±2.48
SEGMENT	9.91±1.06	8.97±1.20	9.58±1.73	12.15±2.13	13.58±1.95	15.71±2.15	13.75±1.58	10.15±1.21	9.06±1.15
DNA	15.88±1.17	27.31±2.58	17.72±1.29	15.27±0.41	29.53±2.12	43.38±3.94	28.60±1.81	15.87±1.44	14.19±1.28
SVMGD1A	5.85±1.65	–	–	4.23±0.40	6.32±1.88	14.21±2.92	4.S4±0.62	5.24±1.09	6.08±1.55
USPS-FULL	6.39±0.50	–	–	4.16±0.13	17.68±1.57	14.43±0.89	7.43±0.29	7.35±0.62	5.88±0.91
SATIMAGE	14.59±0.71	–	–	13.81±0.22	16.36±0.64	19.27±3.74	14.80±0.56	14.64±0.50	13.27±0.53

Table IV. Total Training and Testing Time (s) of the Different Algorithms.

DATA	SVM	LGC	LapRLS	LapSVMp	NYS-LGC	NFI	ANCHOR	PVM(SQR)	PVM(HINGE)
G241C	0.54	140.84	129.86	33.47	0.86	0.48	11.75	3.30	3.19
G241D	0.55	129.78	142.65	11.95	0.84	0.49	12.33	3.31	3.16
DIGIT1	0.57	140.51	131.08	7.72	0.84	0.48	12.79	3.31	3.15
USPS	0.48	139.23	131.59	21.35	0.74	0.47	12.89	3.28	3.14
COIL2	0.57	151.36	120.48	14.57	0.87	0.48	11.51	3.26	3.47
COIL	1.58	146.92	115.22	31.54	0.79	0.49	13.01	3.35	3.51
BCI	0.08	3.08	1.94	1.12	0.53	0.22	5.89	0.71	1.09
TEXT	25.6	139.67	216.37	59.27	9.14	13.26	47.54	30.24	34.24
SPLICE	1.69	1622.51	1439.51	33.12	2.49	0.83	23.71	4.87	4.24
SEGMENT	4.51	1319.67	1389.80	69.71	1.96	31.67	7.15	6.13	8.81
DNA	2.85	1566.91	1463.75	368.91	3.07	1.22	52.91	8.92	7.57
SVMGD1A	2.71	–	–	1129.44	3.22	1.66	69.21	8.06	5.38
USPS-FULL	19.46	–	–	8920.13	3.96	2.87	125.70	22.48	28.21
SATIMAGE	8.90	–	–	2671.56	3.34	2.57	189.56	11.56	14.32

1. In general, the semisupervised learning algorithms are more accurate than the baseline SVM. In particular, based on the paired student-t test, the proposed PVM(hinge) outperforms SVM on the DIGIT1, USPS, BCI, SEGMENT, DNA, USPS-FULL, and SATIMAGE data sets at the 95% confidence level. It has a comparable performance as the SVM on the G241C, G241D, SPLICE, SVMGD1A data sets, and is only outperformed by the SVM on the two data sets of COIL2 and TEXT.

2. LGC, LapRLS, and LapSVMp do not employ any approximation to scale up training. Hence, they are usually the most accurate, but also computationally most expensive. Indeed, recall that LGC and LapRLS require O(n²) space. Hence, they cannot be run on the three largest data sets (svmgd1a, usps-full, and satimage). Moreover, though LapSVMp is faster than LapRLS and LGC, it is still computationally expensive on the large data sets as its time complexity is quadratic in n.

3. LGC-NYS and NFI are computationally very efficient but not as accurate, especially on the more difficult data sets of TEXT and DNA. As discussed in Section II-B.3, we speculate that it is because NFI cannot enforce smoothness of the function on the unlabeled samples not belonging to the basis set [13].

4. The anchor method is more efficient than LGC, LapRLS, and LapSVMp. However, since it needs to compute the combination coefficients for each sample using QP, its complexity can be huge for large data sets. As can be observed from Table VI, its time consumption is at least several times larger than that of PVM. The larger the data set, the larger the difference.

5. The accuracies of both PVMs are comparable with LGC, LapRLS, and LapSVMp; while their speeds can be several hundred times faster. On larger data sets, this speedup ratio is expected to be more significant. Overall, PVM achieves a good balance between speed and accuracy.

Table VI. Total Training and Testing Time (s) of CB-LapRLS, CB-LapSVMp, and PVM.

DATA	CB-LapRLS	CB-LapSVMp	PVM (sqr)	PVM (hinge)
G241C	10.15	0.47	3.30	3.19
G241D	12.11	0.65	3.31	3.16
DIGIT1	12.54	0.72	3.31	3.15
USPS	13.76	0.35	3.28	3.14
COIL2	11.48	0.57	3.26	3.47
COIL	115.22	0.54	3.35	3.51
BCI	1.15	0.22	0.71	1.09
TEXT	62.15	28.35	30.24	34.24
SPLICE	6.51	3.42	4.87	4.24
SEGMENT	12.17	5.31	6.13	8.81
DNA	15.16	7.41	8.92	7.57
SVMGD1A	23.94	5.58	8.06	5.38
USPS-FULL	57.14	19.85	22.48	28.21
SATIMAGE	39.58	11.29	11.56	14.32

We are also interested in training the full semisupervised learning algorithms (LapRLS and LapSVMp) using only a small subset of representative points (such as cluster centers) as unlabeled data. Results and discussions are in Table VII. As can be observed, using representative points in such a way can improve the computational efficiency of the algorithm but lead to less accurate results.

Table VII. Comparison of the Total Training and Testing Time (s) Between PVM and L₁-Penalized Sparse Model.

	BCI	COIL	COIL2	DIGIT1	USPS-2V7	USPS-5V6	USPS-3V8	USPS-FULL
L1-LRK	178.5	169.1	135.7	165.4	135.0	144.1	108.5	-
PVM (SQUARED)	0.71	3.35	3.26	3.31	4.12	3.98	2.73	8.06

C. Learning With Only the Cluster Centroids

In the PVM, the prototypes are selected from the centroids of k-means clustering. Recall that both the LapRLS and LapSVM (trained in either the primal or dual) have large computational complexities. Hence, one may consider using a computationally less expensive version that replaces the whole unlabeled set with the set of k-means cluster centroids. On the other hand, all the labeled samples are still used, as they are usually much fewer in number. In this section, we compare the performance of these cluster-based (CB) versions (denoted CB-LapRLS and CB-LapSVMp) with PVM.

Tables V and VI show the comparison in terms of the classification error and time consumption, respectively. For easy reference, results for the PVM are also copied from Tables III and IV. As can be seen, though CB-LapRLS and CB-LapSVMp are much faster than the original LapRLS and LapSVMp, their accuracies are often much inferior because of the loss of unlabeled data information. In contrast, the PVM adopts the representative points (cluster centers) in a systematic way for approximations of the whole kernel matrix and the decision function, thus yielding a much better performance in general.

Table V. Classification Errors (%) on the Unlabeled Data Obtained by CB-LapRLS, CB-LapSVMp, and PVM.

DATA	CB-LapRLS	CB-LapSVMp	PVM (sqr)	PVM (hinge)
G241C	27.14±2.15	28.32±2.91	24.50±2.49	23.21±1.95
G241D	28.11±1.78	27.57±1.43	25.15±2.58	24.85±2.70
DIGIT1	6.78±1.91	6.84±1.72	4.18±1.17	3.72±1.07
USPS	19.67±3.46	19.45±2.25	5.29±0.73	6.35±1.33
COIL2	14.98±2.15	17.16±2.81	11.69±2.47	14.85±2.36
COIL	21.17±1.71	12.39±1.45	13.41±1.29	12.26±1.01
BCI	29.16±3.56	46.23±3.16	33.59±3.01	31.65±2.86
TEXT	27.18±2.77	25.31±1.91	30.4±4.46	26.29±2.58
SPLICE	22.35±3.48	28.82±3.97	23.47±1.59	25.32±2.48
SEGMENT	9.19±1.56	11.21±1.81	10.15±1.21	9.06±1.15
DNA	16.57±1.41	15.87±0.44	15.87±1.44	14.19±1.28
SVMGD1A	7.71±0.56	6.92±0.55	5.24±1.09	6.08±1.55
USPS-FULL	14.15±3.41	11.15±2.17	7.35±0.62	5.88±0.91
SATIMAGE	17.85±2.15	15.34±1.66	14.64±0.50	13.27±0.53

D. Comparison With ℓ₁-Penalized Sparse Models

In this section, we compare the sparse models produced by PVM and ℓ₁-regularization. For ℓ₁-regularization, we use the kernel regressor, which involves the optimization problem

$$\underset{\mathbf{\alpha }}{min}{\Vert {\mathbf{y}}_l-{\mathbf{K}}_l\mathbf{\alpha }\Vert }^2+{\lambda }_1{(\mathbf{K}\mathbf{\alpha })}^{\top }\mathbf{S}(\mathbf{K}\mathbf{\alpha })+{\lambda }_2{\Vert \mathbf{\alpha }\Vert }_1$$ (31)

where Kα (for some α ∈ ℝⁿ) is the vector of predictions on all n labeled and unlabeled samples, and K_l ∈ ℝ^l×n is the kernel submatrix. The (Kα)^⊤S(Kα) regularization term encourages smoothness over the data manifold, and the ℓ₁-regularizer ‖α‖₁ encourages sparseness of the coefficient vector α.

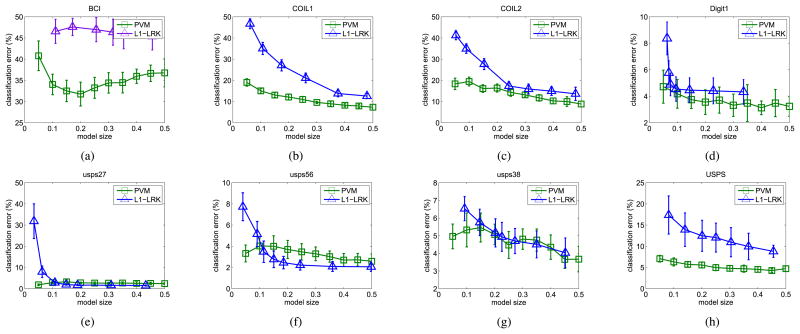
In the following, we compare the performance of PVM and the ℓ₁-penalized formulation in (31) at different sparsity levels. Note that how the sparsity is achieved by the PVM is quite different from that of (31). The former is obtained by extracting a highly compact and representative set of prototypes, from which the structure of the kernel matrix can be faithfully preserved. Hence, for the PVM, sparsity can be explicitly controlled by specifying the number of prototypes. On the other hand, (31) enforces sparsity by penalizing via the ℓ₁-norm. There is no known algorithm that can produce a model with exactly the desired number of nonzero coefficients. Instead, we can only try different regularization parameter settings to obtain a model with approximately the desired size.⁹ This parallel the comparison between VQ-based code-book selection and sparse-coding-based codebook selection in dictionary learning [12]. Moreover, to allow (31) to be used on large data sets, low-rank approximation is first applied on the kernel matrix K. In the sequel, the method will be denoted L1-LRK.

The classification errors on the unlabeled data versus sparsity for the two algorithms are reported in Fig. 4. As can be seen, at the same sparsity level, PVM often has better accuracy than L1-LRK. This demonstrates the efficacy of PVM in building highly efficient, parsimonious, and accurate models in the semisupervised learning setting. In particular, PVM tends to perform better than L1-LRK when the data are high dimensional or have a lot of classes.

Fig. 4.

Performance of PVM and the ℓ₁-penalized formulation at different levels of model sparsity. The x-axis is the ratio of nonzero coefficients in the predictive model to the sample size. (a) BCI. (b) COIL. (c) COIL₂. (d) Digit1. (e) USPS-2v7. (f) USPS-5v6. (g) USPS-3v8. and (h) USPS-FULL.

Table VII compares the time consumption of PVM with L1-LRK. Here, we have chosen the regularization parameters such that the number of nonzero coefficients in the obtained model is around 10% of the sample size. As can be seen, PVM is much more efficient. This is because for the L1-LRK, to transform the problem (31) to a standard LASSO-type problem, O(n²) space and O(n³) time are needed.

VI. Conclusion

In this paper, we proposed the PVM to scale up graph-based semisupervised learning. Using the prototypes to approximate the graph-based regularizer as well as the predictive model, we can drastically reduce the problem size while at the same time guarantee smoothness of the prediction over the data manifold. Experiments on a number of real-world data sets demonstrate that the PVM has appealing scaling behavior (linear in sample size) and competitive performance.

In the future, we will study various extensions of the PVM. For example, we will consider other kernels (besides the Gaussian kernel) and other label reconstruction schemes that can take the local geometrical structure of the samples into account. Moreover, the current prototype selection scheme (k-means clustering) treats the labeled and unlabeled data as equally important. One possibility is to incorporate the label information, and extend the selection scheme to a weighted version so that different importance-based weightings are assigned based on prior knowledge. A similar idea has been successfully used in the context of low-rank approximation [1]. Moreover, we will further study the relationships between the labeled samples, unlabeled samples, and the prototypes.

Biography

Kai Zhang received the Ph.D. degree in computer science from the Hong Kong University of Science and Technology, Hong Kong, in 2008.

He joined the Life Science Division, Lawrence Berkeley National Laboratory, Berkeley, CA, USA. He is currently a Research Staff Member with NEC Laboratories America, Inc., Princeton, NJ, USA. His current research interests include large scale machine learning, matrix approximation, and applications in bioinformatics, time series, and complex networks.

Liang Lan received the B.S. degree in bioinformatics from the Huazhong University of Science and Technology, Wuhan, China, and the Ph.D. degree in computer and information sciences from Temple University, Philadelphia, PA, USA, in 2007 and 2012, respectively.

He is currently a Researcher with the Huawei Noah's Ark Laboratory, Hong Kong. His current research interests include data mining and machine learning.

James T. Kwok received the Ph.D. degree in computer science from the Hong Kong University of Science and Technology, Hong Kong, in 1996.

He is a Professor with the Department of Computer Science and Engineering, Hong Kong University of Science and Technology. His current research interests include kernel methods, machine learning, and pattern recognition.

Prof. Kwok has been a Program Co-Chair for a number of international conferences, and served as an Associate Editor of the IEEE Transactions on Neural Networks and Learning Systems from 2006 to 2012. He is currently an Associate Editor of the Neurocomputing journal. He was a recipient of the 2004 IEEE Outstanding Paper Award, and the Second Class Award in Natural Sciences from the Ministry of Education, China, in 2008.

Slobodan Vucetic received the B.S. and M.S. degrees in electrical engineering from the University of Novi Sad, Novi Sad, Serbia, and the Ph.D. degree in electrical engineering from Washington State University, Pullman, WA, USA, in 1994, 1997, and 2001, respectively.

He is currently an Associate Professor with the Department of Computer and Information Sciences, Temple University, Philadelphia, PA, USA. His current research interests include data mining and machine learning.

Bahram Parvin is a Principal Scientist with the Lawrence Berkeley National Laboratory, Berkeley, CA, USA, and has an adjunct appointment with the Electrical Engineering Department, University of California, Berkeley. His laboratory focuses on the development of machine learning techniques for realization of pathway pathology, and elucidating molecular signatures of aberrant morphogenesis in normal and engineered matrices.

Prof. Parvin was the General Chair of the IEEE International Symposium on Biomedical Imaging: From Nano to Macro, in 2013. He is also a Steering Committee Member for the IEEE Bioimaging and Signal Processing and the IEEE Bioengineering and Health Care.