Abstract
The 2013 decision by the U.S. Supreme Court in the Fisher v. University of Texas at Austin case clarified when and how it is legally permissible for universities to use an applicant’s race or ethnicity in its admissions decisions. The court concluded that such use is permissible when “no workable race-neutral alternatives would produce the educational benefits of diversity.” This paper shows that replacing traditional affirmative action with a system that uses an applicant’s predicted likelihood of being an underrepresented racial minority as a proxy for the applicant’s actual minority status can yield an admitted class that has a lower predicted grade point average and likelihood of graduating than the class that would have been admitted using traditional affirmative action. This result suggests that race-neutral alternatives may not be “workable” from the university’s perspective.
INTRODUCTION
Legal Context
Affirmative action in college admissions has always been controversial and its legality has been under constant challenge for over 40 years. The 1978 decision by the U.S. Supreme Court in the Regents of the University of California v. Bakke case was a split decision. Four justices voted for reversal of the lower court’s ruling that the admissions system used by the Medical School at UC-Davis (which reserved a set number of admissions slots for minority applicants) violated the 14th Amendment of the U.S. Constitution and the Federal Civil Rights Act; four voted for affirmance of the lower court ruling, and Justice Powell voted to affirm the part of the decision that stated that UC-Davis’s two-track admission system was unconstitutional, but rejected the part that enjoined UC-Davis from taking race into account. Rather, Powell concluded that “the goal of achieving a diverse student body is sufficiently compelling to justify consideration of race in admissions decisions under some circumstances” (p. 267). This ruling prompted “diversity” to be the only compelling argument that most universities could use to justify their use of affirmative action, disallowed the use of separate admissions systems for minority applicants, and limited universities to use race as only one factor among many in comparing applicants.
The 4-4-1 split decision in Bakke left the legality of college affirmative action on shaky ground. In 1992, Cheryl Hopwood and three other plaintiffs sued after being denied admittance to the University of Texas Law School. In the Hopwood v. Texas (1996) case, the Fifth Circuit Court of Appeals effectively rejected the Bakke opinion of Justice Powell. They concluded that:
… any consideration of race or ethnicity by the law school for the purpose of achieving a diverse student body is not a compelling interest under the Fourteenth Amendment. Justice Powell’s argument in Bakke garnered only his own vote and has never represented the view of a majority of the Court in Bakke or any other case (p. 25).
The U.S. Supreme Court decided not to hear the case. Subsequently, the Attorney General of Texas interpreted the Hopwood decision as a ban on race-based admissions, financial aid, and recruiting policies at both public and private institutions in the state. The first freshman class to be affected by the ban enrolled in the fall of 1997.
The ambiguities left by the divergence of decisions in the Bakke and Hopwood cases were resolved by the Supreme Court’s 2003 decisions regarding the University of Michigan’s undergraduate and law school admissions in Gratz v. Bollinger and Grutter v. Bollinger. The Court’s decisions found that:
…diversity is a compelling interest in higher education, and that race is one of a number of factors that can be taken into account to achieve the educational benefits of a diverse student body. The Court found that the individualized, whole-file review used in the University of Michigan Law School’s admissions process is narrowly tailored to achieve the educational benefits of diversity … [W]hile race is one of a number of factors that can be considered in undergraduate admissions, the automatic distribution of [a fixed number of points] to students from underrepresented minority groups is not narrowly tailored (Alger, 2003, p. 1).
These decisions essentially allowed for race and ethnicity to be taken into account for admissions, so long as that consideration was not mechanical and was part of a full review of the applicant’s file.
Furthermore, the Grutter decision outlined steps that universities must take prior to using race or ethnicity in their admission decisions. Justice O’Connor’s Opinion of the Court noted that:
Narrow tailoring does not require exhaustion of every conceivable race-neutral alternative. Nor does it require a university to choose between maintaining a reputation for excellence or fulfilling a commitment to provide educational opportunities to members of all racial groups. … Narrow tailoring does, however, require serious, good faith consideration of workable race-neutral alternatives that will achieve the diversity the university seeks (p. 27).
Finally, the Grutter decision concluded that “race conscious admissions policies must be limited in time” (p. 30) and included O’Connor’s note that:
It has been 25 years since Justice Powell first approved the use of race to further an interest in student body diversity in the context of public higher education.… We expect that 25 years from now, the use of racial preferences will no longer be necessary to further the interest approved today (p. 31).1
To some critics of affirmative action, this stated expectation appeared to establish an expiration date for affirmative action, and created an invitation to continue to legally challenge university policies.
Following the Grutter decision, the University of Texas at Austin (UT) announced their return to using affirmative action in 2005 (Faulkner, 2005). UT’s decision prompted a court challenge, Fisher v. the University of Texas at Austin, which was decided by the U.S. Supreme Court in June of 2013. The Supreme Court invalidated the decision by the Fifth Circuit Court of Appeals regarding the Fisher case. The Court determined that “the Fifth Circuit did not hold the University to the demanding burden of strict scrutiny articulated” in the Grutter and Bakke cases (Fisher v. University of Texas, 2013a, p. 1). In remanding the case, they ruled that “the Fifth Circuit must assess whether the University has offered sufficient evidence to prove that its admissions program is narrowly tailored to obtain the educational benefits of diversity” (Fisher v. University of Texas, 2013a, p. 3). The “University must prove [to the reviewing court] that the means it chose to attain that diversity are narrowly tailored to its goal. On this point, the University receives no deference …. The reviewing court must ultimately be satisfied that no workable race-neutral alternatives would produce the educational benefits of diversity” [emphasis added] (Fisher v. University of Texas, 2013b, p. 10).2
The Fisher decision, which surprised many who expected a more conservative set of justices to overturn the Grutter decision and strike down affirmative action in admissions, has yielded a greater degree of legal stability. However, the term “workable” remains vague. Workable seems to mean that the race-neutral alternative would not have too great of an adverse effect on other university objectives (such as in maintaining the “quality” of its admitted students). After the Grutter ruling, the U.S. Department of Education’s Office for Civil Rights (2012) offered the following guidance to universities: “An institution may deem unworkable a raceneutral alternative that would be ineffective or would require it to sacrifice another component of its educational mission.” If challenged, a university would need to convince a court that race-neutral alternatives are not workable because the costs of such policies would be too great.3 The Supreme Court’s decisions are likewise vague regarding what “race-neutral” means. The Grutter decision obliquely makes the following reference:
Universities in California, Florida, and Washington State, where racial preferences in admissions are prohibited by state law, are currently engaged in experimenting with a wide variety of alternative approaches. Universities in other States can and should draw on the most promising aspects of these race-neutral alternatives as they develop (p. 31).
A more cogent discussion of legal “race-neutral” alternatives can be found in Coleman, Palmer, and Winnick (2008), who conclude that “facially race-neutral policies are subject to strict scrutiny (and qualify as legally “race-conscious”) only if they are motivated by a racially discriminatory purpose and result in a racially discriminatory effect” (p. 5). They caution universities that their policies may be deemed “race-conscious” if the policy “would not have been promulgated but for the motivation for achieving segregation or racial impact,” “race is the predominant motivating factor behind the policy,” or “there is a deliberate use of race-neutral criteria as a proxy for race” (p. 5). It would therefore seem that any policy that attempted to give weight in admissions decisions to any other factors aside from race (e.g., socioeconomic status) with the goal of boosting minority admissions would be deemed to be not “race-neutral” and would instead be deemed “race-conscious” and face the strict scrutiny test. Thus, there is an inherent tension in the terms “race-neutral” and “alternative”—if one seeks an “alternative” policy to race-based affirmative action that serves the same goal, then such a policy cannot be deemed “race-neutral.” As an example, after the Hopwood decision, the Texas Legislature passed H.B. 588, which gave state institutions a list of 18 socioeconomic indicators that they could use in making first-time freshman admissions decisions. To the extent that the use of such indicators was intended to serve the purpose of replacing race-based affirmative action, such use would not be “race-neutral.” This tension was recognized in Justice Ginsburg’s dissent in the Fisher case:
I have said before and reiterate here that only an ostrich could regard the supposedly neutral alternatives as race unconscious … As Justice Souter observed, the vaunted alternatives suffer from “the disadvantage of deliberate obfuscation” (Fisher v. University of Texas, 2013c, p. 2).
Research Questions
This paper evaluates the effects of replacing “traditional affirmative action” (which places direct weight on the applicant’s race or ethnicity in the university’s admissions decision) with “proxy-based affirmative action” (which places weight on the applicant’s predicted likelihood of being an underrepresented minority). Nakedly and deliberately engaging in such “proxy-based affirmative action” would not qualify as a “race-neutral alternative.” Yet, such a direct alternate policy approximates the upper-bound impact for other less-transparent alternative policies, such as giving added weight to socioeconomic status or utilizing de facto high school segregation to help boost minority admissions by admitting all students who graduate in the top X percent of their high school classes.4
Using administrative admissions data from the UT, I answer the following research questions. First, if UT used all of the information that they had obtained on an applicant (aside from the student’s race) to predict the student’s race and then used proxy-based affirmative action rather than traditional affirmative action, what effects would that policy change yield in terms of the academic qualities of the admitted student body? Second, what share of minority and nonminority students would be “displaced” (i.e., admitted under one regime but not the other) when using the proxy-based system rather than race-based affirmative action?
This paper builds off the theoretical work of Chan and Eyster (2003), who predicted that universities would respond to affirmative action bans by shifting the weights placed on applicant characteristics in ways to favor minority applicants, and the empirical work of Long and Tienda (2008), who used the same administrative data and found “some evidence that universities changed the weights they placed on applicant characteristics in ways that aided underrepresented minority applicants,” however “these changes were insufficient to restore Black and Hispanic applicants’ share of admitted students” (p. 255). That is, while UT and Texas A&M University did respond to the Hopwood decision by implicitly using correlated indicators for race, their efforts were not sufficient to restore the racial composition of the admitted students. Long and Tienda focused on actual changes enacted by UT, Texas A&M, and Texas Tech University in the years following the Hopwood decision. In contrast, in this paper I estimate hypothetical changes that UT could have taken so as to evaluate the implications of fully restoring minority representation using correlated indicators of the student’s race and ethnicity.
A similar type of simulation was conducted by Fryer, Loury, and Yuret (2008). They used data on students who had enrolled at seven highly selective, “elite” institutions in 1989. Using these data, they simulate the maximum predicted college GPA rank that could be achieved by these universities if they hypothetically “admitted” the subset of these students whose characteristics predict high GPA ranks. They label this policy “laissez-faire.” They then compare this policy to a “color-sighted” affirmative action policy, which gave weight to the student’s race, and a “color-blind” affirmative action policy, which gives additional weight to student characteristics that are correlated with being a minority. They find that color-sighted affirmative action is 98.7 percent as efficient as the laissez-faire policy (i.e., it produces a predicted GPA rank that is 98.7 percent of the maximum possible), while the color-blind policy performed less well, 96.2 percent as efficient as the laissez-faire policy.
Fryer, Loury, and Yuret (2008) lacked data on applicants to these universities, which they noted as a limitation of their analysis. Thus, when they conduct these simulations, they are evaluating how such policy changes would change the composition of hypothetically “admitted” students using data from only students who had, in fact, been admitted to these universities. This paper, in contrast, uses data on applicants to UT, which allows me to answer some richer questions. For example, in the analysis below, I show the extent to which various policies lead to displacement, that is applicants being accepted under one policy but rejected under another. Second, lacking data on applicants means that they cannot ground their simulations in actual admissions criteria used by universities. Their laissez-faire policy assumes, implicitly, that the university is trying to maximize the college performance of their admitted students. But, universities may have other objectives in mind when they make their admissions decisions. For example, as I show below, UT was more likely to admit U.S. citizens and Texas residents despite the fact that both of these characteristics are negative predictors of college GPA. Thus, in the simulations that I conduct below, the default admission policy is estimated based on UT’s actual decisions, rather than an assumed default policy.
Nonetheless, the results that I find for UT (which is somewhat less “elite”) are quite similar to the results in Fryer, Loury, and Yuret (2008), and these results should be seen as reinforcing each other. Simply put, many characteristics that positively predict collegiate success are negatively correlated with the likelihood of being an underrepresented minority, which causes inefficiency in a proxy-based admissions policy.5 I find that UT had limited ability to predict a student’s race or ethnicity just based on the information it collected on applicants during these years. Consequently, if they sought to restore the representation of these minority groups, they would need to place more weight on the applicant’s predicted likelihood of being an underrepresented minority than they previously placed directly on the applicant’s minority status. Doing so, however, comes at the cost of yielding an admitted class that has a lower predicted grade point average (GPA) and likelihood of graduating than the class that would have been admitted using traditional affirmative action. This result suggests that race-neutral alternatives may not be “workable” from the university’s perspective.
METHODS
I begin by estimating the parameters of UT’s “Traditional Race-Based Affirmative Action” admissions system. I estimate the following probit regression using data on UT’s applicants in 1996, which was the last year in which UT could use race-based affirmative action prior to enforcement of the Hopwood ruling:
| (1) |
URMi equals one if the student is an “underrepresentedminority,” which is inclusive of black, Hispanic, and American Indian or Alaskan Native students,6 and X is a vector of other characteristics that the university considers in their admissions decision.
In the remainder of the analysis, I utilize data on UT’s applicants in 1998, 1999, and 2000. Using these data, I evaluate the efficacy of alternative policies in the years immediately following the Hopwood decision.
As salient measures of the educational quality and desirability of each applicant, I estimate the cumulative GPA and likelihood of graduating within six years7 using data on students who enrolled at UT in 1998, using equations (2a) and (2b) (which uses j subscripts to denote enrollees)8:
| (2a) |
| (2b) |
Z includes characteristics that are observable to the university for its applicants.9 Equation (2a) is estimated using a tobit specification with lower and upper bounds of 0.0 and 4.0, respectively. I assume that these parameters, which are estimated based on enrollees, would roughly hold for all applicants, and apply the resulting coefficients to estimate the applicant’s “Quality” from the perspective of the university:
| (3a) |
where .
| (3b) |
Next, using data from 1998 to 2000 applicants, I estimate the probability that the applicant is an underrepresented minority based on observable applicant characteristics using the probit regression shown in equation (4):
| (4) |
I then compute the probability that applicant i is an underrepresented minority, which is subsequently used as the proxy indicator for the student’s race:
| (5) |
Finally, I simulate the racial composition and Quality of admitted students under three admissions systems as follows10:
| (6a) |
| (6b) |
| (6c) |
The beta parameters in equations (6a) to (6c) are derived from the estimation of equation (1). Equation (6a) is used to simulate the class that UT would have admitted had they maintained their pre-Hopwood admissions system. The second admissions system, which I label “Passive Affirmative Action Ban,” holds the weights on X characteristics constant at β̂2, yet sets the weight on URM (β̂1) to zero.11 The idea here is that the university accommodates the affirmative action ban, but makes no other changes to its admissions formula in order to boost minority enrollment. The third admissions system, which I label “Proxy-Based Affirmative Action,” gives positive weight to the likelihood that the student is an underrepresented minority in the university’s admissions decisions. By slowly increasing the value of θ in equation (6c), I demonstrate how (a) using a proxy can increase minority representation among the admitted class, and (b) how doing so has distortionary effects on the set of admitted students and potentially has impacts on the academic quality of the admitted set. For these simulations, I assume that UT would sort applicants based on their AdmissionsIndex scores and admit the top N applicants, where N is the actual number of students who were admitted during these three years.12
DATA
Administrative data for the analysis were compiled by the Texas Higher Education Opportunity Project at Princeton University (http://opr.princeton.edu/archive/theop). Table 1 contains the descriptive statistics. The Appendix contains additional information on the variables and their construction.13 Since some variables are missing in the applicant files (most notably for parents’ education in 1996), I use multiple imputation by chained equations, creating five imputed data sets, and combine the results using Rubin’s (1987) method.14
Table 1.
Descriptive statistics
| (1) Number of non- missing observations |
(2) Mean |
(3) Number of non- missing observations |
(4) Mean |
(5) Number of non- missing observations |
(6) Mean |
|
|---|---|---|---|---|---|---|
| Student is admitted | 16,628 | 66.4% | ||||
| Student’s cumulative GPA in UT classes through Spring 2005 | 6,831 | 2.89 | ||||
| Student graduated from UT within six years | 6,831 | 72.6% | ||||
| Student is an underrepresented minority | 16,628 | 19.2% | 6,831 | 16.8% | 50,705 | 19.0% |
| Student is Asian American | 16,628 | 13.8% | 6,831 | 16.9% | 50,705 | 14.6% |
| Student is from foreign country | 16,628 | 5.0% | 6,831 | 0.7% | 50,705 | 6.5% |
| Student’s SAT/ACT test score (in 100s of SAT points) | 16,187 | 11.97 | 6,831 | 12.07 | 48,907 | 11.92 |
| Student’s high school class rank percentile | 14,580 | 81.3 | 6,083 | 82.8 | 40,186 | 80.9 |
| Student took Advanced Placement (AP) exam | 16,628 | 20.3% | 6,831 | 52.3% | 50,705 | 24.4% |
| Student scored 3+ on AP math exam | 16,628 | 5.8% | 6,831 | 18.4% | 50,705 | 8.8% |
| Student scored 3+ on AP science exam | 16,628 | 2.7% | 6,831 | 9.9% | 50,705 | 4.3% |
| Student scored 3+ on AP foreign language exam | 16,628 | 2.3% | 6,831 | 9.0% | 50,705 | 4.1% |
| Student scored 3+ on AP social science exam | 16,628 | 3.8% | 6,831 | 15.4% | 50,705 | 7.2% |
| Student scored 3+ on other AP exam | 16,628 | 9.9% | 6,831 | 30.9% | 50,705 | 14.4% |
| Student is female | 16,628 | 49.9% | 6,831 | 51.3% | 50,672 | 49.9% |
| Student is a U.S. citizen | 16,628 | 90.0% | 6,831 | 94.7% | 50,705 | 89.1% |
| Parents’ highest education is below high school | 7,553 | 0.2% | 6,579 | 1.0% | 45,198 | 1.2% |
| Parents’ highest education is some high school | 7,553 | 1.7% | 6,579 | 1.2% | 45,198 | 1.4% |
| Parents’ highest education is high school graduate or GED | 7,553 | 5.0% | 6,579 | 5.4% | 45,198 | 5.7% |
| Parents’ highest education is some college | 7,553 | 14.7% | 6,579 | 15.0% | 45,198 | 15.2% |
| Parents’ highest education is bachelor’s degree | 7,553 | 32.0% | 6,579 | 33.6% | 45,198 | 33.0% |
| Parent’s income is <$20,000 | 6,295 | 7.1% | 42,326 | 6.8% | ||
| Parent’s income is ≥$20,000 and <$40,000 | 6,295 | 14.5% | 42,326 | 14.4% | ||
| Parent’s income is ≥$40,000 and <$60,000 | 6,295 | 17.7% | 42,326 | 15.9% | ||
| Parent’s income is ≥$60,000 and <$80,000 | 6,295 | 17.7% | 42,326 | 15.4% | ||
| Student is from a single-parent family | 6,831 | 15.3% | 50,705 | 14.5% | ||
| Student is from Texas | 16,628 | 78.7% | 6,825 | 92.1% | 50,577 | 81.3% |
| Student attended a UT “feeder” high school | 16,628 | 19.5% | 6,831 | 26.3% | 50,701 | 21.7% |
| Student attended a “Longhorn Opportunity Scholarship” HS | 16,628 | 2.3% | 6,831 | 1.7% | 50,705 | 2.6% |
| Student attended a “Century Scholars” high school | 16,628 | 2.1% | 6,831 | 1.9% | 50,705 | 2.2% |
| Student attended a private high school | 11,955 | 8.8% | 6,545 | 8.8% | 45,446 | 11.3% |
| High school’s average SAT/ACT score (in ACT points) | 13,164 | 21.5 | 6,753 | 21.8 | 47,864 | 21.8 |
| HS’s percent who took the SAT + percent who took the ACT exam | 11,354 | 79.4% | 5,854 | 78.9% | 39,626 | 83.9% |
| HS’s percent who receive free or reduced-price lunch | 11,391 | 16.0% | 5,838 | 14.9% | 38,708 | 15.2% |
| HS’s percent who are underrepresented minorities | 11,512 | 35.2% | 5,911 | 33.0% | 39,755 | 32.9% |
| Year of application | 1996 | 1998 | 1998 to 2000 | |||
| Group | Applicants | Enrollees | Applicants | |||
| Used for equation(s) | (1) | (2a), (2b) | (3a), (3b), (4), (5), (6a), (6b), (6c) | |||
Notes: The squares of the following variables are additionally included in both the X the Z vectors: Student’s High school class rank percentile, Student’s SAT/ACT test score, High school’s average SAT/ACT score, and High school’s percentage who took the SAT or ACT exam.
RESULTS
Regression Results
Column 1 of Table 2 contains the parameter estimates reflecting UT’s pre-Hopwood admissions system (i.e., equation (1)). Consistent with prior research, underrepresented minorities are substantially more likely to be admitted than observably similar non-URMs. The average marginal effect of being a URM on the likelihood of admittance is 14.8 percentage points.15 The university also was more likely to admit students with higher SAT/ACT test scores, high class ranks, students who took and scored 3 or higher on Advanced Placement (AP) exams, and students who are from Texas and are U.S. citizens. Notably, there is no evidence that UT attempted to use socioeconomic characteristics in their pre-Hopwood admissions decisions as there was no significant weight placed on parents’ highest education level or the characteristics of the high schools the students attended.
Table 2.
Regression results.
| (1) | (2) | (3) | (4) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Equation (1): Y = admitted | Equation (2a): Y = cumulative GPA |
Equation (2b): Y = graduated within six years |
Equation (4): Y = student is a URM | ||||||||
| Coef. | Std. error |
Ave. marginal effect |
Coef. | Std. error |
Coef. | Std. error |
Ave. marginal effect |
Coef. | Std. error |
Ave. marginal effect |
|
| Student is an underrepresented minority | 0.751 | (0.087)*** | 14.8% | −0.058 | (0.025)*** | 0.019 | (0.057) | 0.6% | |||
| Student is Asian American | −0.074 | (0.043)* | −1.5% | −0.042 | (0.022)* | −0.013 | (0.055) | −0.4% | |||
| Student is from foreign country | −0.062 | (0.156) | −1.2% | 0.082 | (0.113) | 0.011 | (0.233) | 0.3% | |||
| Student’s SAT/ACT test score (in 100s of SAT points) | 0.648 | (0.030)*** | 12.8% | 0.024 | (0.009)*** | −0.042 | (0.018)** | −1.2% | −0.158 | (0.008)*** | −3.1% |
| Student’s high school class rank percentile | 0.039 | (0.005)*** | 0.8% | 0.022 | (0.001)*** | 0.028 | (0.002)*** | 0.8% | −0.001 | (0.001) | 0.0% |
| Student took Advanced Placement (AP) exam | 0.791 | (0.062)*** | 15.6% | 0.036 | (0.023) | 0.081 | (0.052) | 2.4% | −0.104 | (0.030)*** | −2.1% |
| Student scored 3+ on AP math exam | 0.508 | (0.157)*** | 10.0% | 0.096 | (0.023)*** | 0.172 | (0.060)*** | 5.0% | −0.122 | (0.039)*** | −2.4% |
| Student scored 3+ on AP science exam | 0.148 | (0.181) | 2.9% | −0.042 | (0.030) | −0.053 | (0.073) | −1.5% | −0.135 | (0.060)** | −2.7% |
| Student scored 3+ on AP foreign language exam | 0.313 | (0.149)** | 6.2% | 0.120 | (0.025)*** | 0.099 | (0.076) | 2.9% | 0.761 | (0.045)*** | 15.0% |
| Student scored 3+ on AP social science exam | 0.160 | (0.141) | 3.2% | 0.099 | (0.024)*** | 0.129 | (0.067)** | 3.8% | −0.158 | (0.050)*** | −3.1% |
| Student scored 3+ on other AP exam | 0.201 | (0.097)** | 4.0% | 0.052 | (0.022)*** | 0.061 | (0.057) | 1.8% | −0.070 | (0.035)** | −1.4% |
| Student is female | 0.002 | (0.040) | 0.0% | 0.205 | (0.017)*** | 0.164 | (0.035)*** | 4.8% | −0.068 | (0.019)*** | −1.3% |
| Student is a U.S. citizen | 0.251 | (0.063)*** | 5.0% | −0.081 | (0.034)*** | −0.229 | (0.089)** | −6.7% | 0.766 | (0.107)*** | 15.1% |
| Parents’ highest education is below high school | 0.043 | (0.403) | 0.8% | −0.119 | (0.114) | −0.186 | (0.172) | −5.4% | 0.691 | (0.088)*** | 13.6% |
| Parents’ highest education is some high school | 0.000 | (0.106) | 0.0% | −0.146 | (0.076)* | −0.150 | (0.166) | −4.4% | 0.344 | (0.068)*** | 6.8% |
| Parents’ highest education is high school graduate or GED | 0.055 | (0.080) | 1.1% | −0.139 | (0.041)*** | −0.168 | (0.083)** | −4.9% | 0.291 | (0.035)*** | 5.7% |
| Parents’ highest education is some college | −0.001 | (0.048) | 0.0% | −0.105 | (0.027)*** | −0.158 | (0.056)*** | −4.6% | 0.203 | (0.028)*** | 4.0% |
| Parents’ highest education is bachelor’s degree | 0.009 | (0.042) | 0.2% | −0.056 | (0.017)*** | −0.013 | (0.040) | −0.4% | −0.026 | (0.020) | −0.5% |
| Parent’s income is <$20,000 | −0.104 | (0.042)*** | −0.214 | (0.091)** | −6.2% | 0.431 | (0.047)*** | 8.5% | |||
| Parent’s income is ≥$20,000 and <$40,000 | −0.079 | (0.028)*** | −0.234 | (0.067)*** | −6.8% | 0.371 | (0.031)*** | 7.3% | |||
| Parent’s income is ≥$40,000 and <$60,000 | −0.071 | (0.025)*** | −0.251 | (0.058)*** | −7.3% | 0.242 | (0.027)*** | 4.8% | |||
| Parent’s income is ≥$60,000 and <$80,000 | −0.012 | (0.021) | −0.118 | (0.054)** | −3.4% | 0.217 | (0.026)*** | 4.3% | |||
| Student is from a single-parent family | 0.020 | (0.025) | 0.030 | (0.051) | 0.9% | 0.071 | (0.025)*** | 1.4% | |||
| Student is from Texas | 0.659 | (0.124)*** | 13.0% | −0.064 | (0.034)* | 0.133 | (0.076)* | 3.9% | 0.195 | (0.052)*** | 3.8% |
| Student attended a UT “feeder” high school | −0.011 | (0.063) | −0.2% | 0.080 | (0.025)*** | 0.106 | (0.053)** | 3.1% | 0.004 | (0.046) | 0.1% |
| Student attended a “Longhorn Opportunity Scholarship” HS | −0.203 | (0.143) | −4.0% | 0.108 | (0.094) | 0.249 | (0.147)* | 7.3% | 0.468 | (0.099)*** | 9.2% |
| Student attended a “Century Scholars” high school | 0.208 | (0.129) | 4.1% | −0.151 | (0.077)* | −0.311 | (0.149)** | −9.1% | −0.319 | (0.101)*** | −6.3% |
| Student attended a private high school | 0.076 | (0.083) | 1.5% | 0.012 | (0.051) | 0.028 | (0.088) | 0.8% | −0.016 | (0.108) | −0.3% |
| High school’s average SAT/ACT score (in ACT points) | 0.023 | (0.023) | 0.5% | 0.112 | (0.014)*** | 0.166 | (0.025)*** | 4.8% | 0.008 | (0.018) | 0.2% |
| HS’s percent who took the SAT + percent who took the ACT exam | −0.024 | (0.110) | −0.5% | 0.204 | (0.059)*** | 0.321 | (0.114)** | 9.4% | 0.350 | (0.055)*** | 6.9% |
| HS’s percent who receive free or reduced-price lunch | 0.036 | (0.202) | 0.7% | −0.276 | (0.133)*** | −0.538 | (0.274)** | −15.7% | −0.093 | (0.199) | −1.8% |
| HS’s percent who are underrepresented minorities | −0.110 | (0.128) | −2.2% | 0.221 | (0.087)*** | 0.369 | (0.172)** | 10.8% | 2.162 | (0.123)*** | 42.6% |
| Constant | −11.691 | (0.889)*** | −1.801 | (0.306)*** | −5.04 | (0.604)*** | −1.301 | (0.446)*** | |||
| Sigma | 0.623 | ||||||||||
| Number of observations | 16,628 | 6,831 | 6,831 | 50,705 | |||||||
Notes:
Two-sided P-values that are equal to or less than 1%,
two-sided P-values that are equal to or less than 5%, and
two-sided P-values that are equal to or less than 10%. Robust standard errors clustered at the high school level are used.
Columns 2 and 3 of Table 2 contains the parameter estimates for equations (2a) and (2b), which show the relationship of student characteristics to future academic success. Underrepresented minority and Asian American enrollees had lower cumulative GPAs than their white counterparts, but there were no significant racial differences in six-year graduation rates. Test scores and high school class rank were both positively associated with the likelihood of graduation, and class rank (but not test scores) was positively associated with cumulative GPA.16 Taking and “passing” AP exams were positively associated with both collegiate success measures. The following types of students earned higher college GPAs and weremore likely to graduate: Female students; non-U.S. citizens; those who had a parent with a graduate degree and whose parents’ income was over $80,000; and those who graduated from a high school that is a “feeder” to UT, whose students had higher SAT/ACT scores and were more likely to take these tests, and had a higher share of students who are URMs but smaller share of students who receive free or reduced-price lunch.17 Finally, students from Texas earned lower GPAs, but were more likely to graduate from UT. When these coefficients are applied to all applicants in the years 1998 to 2000 using equations (3a) and (3b), the predicted cumulative GPA has a mean (SD) of 2.80 (0.43), while the predicted likelihood of graduation has a mean (SD) of 69.4 percent (17.3 percent).
Column 4 of Table 2 contains the parameter estimates for equation (4), which predicts the applicant’s likelihood of being an underrepresented minority. URM applicants have lower SAT/ACT scores, are less likely to have taken and passed an AP exam (except in AP foreign languages18), are less likely to be female, more likely to be a U.S. citizen, and have parents with lower education and lower income. All of these factors are positively associated with future academic success (as shown in columns 2 and 3). Thus, as the university places more weight on any of these factors in an effort to boost minority admissions, they will obtain an admitted class with lower “quality.”
As robustness checks, I take three alternate approaches to predicting the likelihood that the student is a minority applicant. First, as illustrated in footnote 15, there may be an efficiency gain in using the applicant characteristics to separately predict the likelihood of being a member of each racial or ethnic group. Using the specification shown in column 4 of Table 2, I separately predict the likelihood that the applicant is black, the likelihood that the applicant is Hispanic, and the likelihood that the applicant is an American Indian. I then sum these three likelihoods to yield the likelihood that the applicant is an underrepresented minority. Second, as noted above, many of the factors that are positively associated with being an underrepresented minority are negatively associated with collegiate success. Mechanically then, placing more weight on these factors will lower the “quality” of the admitted class. A more clever university may recognize this problem and respond by only adding weight to factors that are positively related to both being an underrepresented minority and collegiate success. I drop from the specification all variables that fail this test—those variables whose coefficients have opposite signs in columns 3 and 4 of Table 2. I repeat this process until all of the coefficients in the specification predicting the likelihood of being an underrepresented minority have the same sign as the coefficient in column 3.19 Third, the linear specification shown in column 3 of Table 2 might be improved by using a more flexible specification. To test this hypothesis, I add squares and cubes of all continuous variables and then add a full set of interaction terms (i.e., I interact each independent variable with all of the other independent variables, except where the variables are mutually exclusive indicators). Adding these higher order terms and the full set of interactions increases the number of independent variables from 29 to 829.20
The specifications in these three robustness checks imply that the university uses a highly sophisticated admissions rule. While plausible, particularly for a large university such as UT, implementing such a system directly and nakedly could weaken the university’s legal argument that such a process is “race-neutral.” These results should be seen as the limit for what such a process could yield, even if doing so is impractical. Nonetheless, as I show below, there is only a small gain in efficiency to be had in moving from the main specification to these alternatives.
SIMULATION RESULTS
Table 3 shows the extent to which alternative admissions policies displace students from the available slots. Starting with the middle panel, among the URM students who are admitted using the traditional race-based affirmative action admissions policy, only 83 percent are admitted under the passive affirmative action ban system (i.e., 17 percent are “displaced” by the ban). Moving to a proxy-based system would only somewhat offset this displacement. Even when the weight placed on the Proxyi in equation (6c) (i.e., θ) is 2.6 (which is 3.5 times as large as the estimated coefficient on URMi in equation (6a), there are still 8 percent of those who would be admitted under traditional affirmative action admissions policy who are not admitted. Moreover, among URMs who are not admitted under the traditional affirmative action admissions policy, 21 percent would be admitted under the proxy-based system when θ = 2.6. Thus, the proxy system leads to admission of lower “quality” URMs. Finally, as seen in the last two rows of Table 3, the proxy-based affirmative action policy brings in non-URMs who would not be admitted under either the traditional affirmative action or passive ban systems. These rows reveal an inefficiency in the proxy-based system as these newly admitted non-URMs are only admitted in order to improve URMs’ share of admitted students.
Table 3.
Simulation results: displacement of admission slots.
| Percent admitted under | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Proxy-based affirmative action with weight on predicted likelihood of being a URM |
|||||||||
| Traditional affirmative action |
Passive affirmative action ban |
0.1 | 0.6 | 1.1 | 1.6 | 2.1 | 2.6 | ||
| All applicants | Admitted under traditional affirmative action | 100 | 97 | 97 | 98 | 98 | 97 | 96 | 95 |
| Admitted under passive affirmative action ban | 97 | 100 | 100 | 99 | 97 | 96 | 95 | 94 | |
| Not admitted under traditional affirmative action | 0 | 7 | 7 | 5 | 5 | 6 | 8 | 10 | |
| Not admitted under passive affirmative action ban | 7 | 0 | 0 | 3 | 5 | 8 | 10 | 12 | |
| URM applicants | Admitted under traditional affirmative action | 100 | 83 | 84 | 87 | 90 | 91 | 91 | 92 |
| Admitted under passive affirmative action ban | 100 | 100 | 100 | 99 | 99 | 99 | 98 | 98 | |
| Not admitted under traditional affirmative action | 0 | 0 | 0 | 0 | 2 | 7 | 14 | 21 | |
| Not admitted under passive affirmative action ban | 29 | 0 | 1 | 8 | 15 | 21 | 27 | 33 | |
| Non-URM applicants | Admitted under traditional affirmative action | 100 | 100 | 100 | 100 | 100 | 98 | 97 | 96 |
| Admitted under passive affirmative action ban | 96 | 100 | 100 | 98 | 97 | 96 | 95 | 94 | |
| Not admitted under traditional affirmative action | 0 | 9 | 8 | 7 | 6 | 6 | 7 | 8 | |
| Not admitted under passive affirmative action ban | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 6 | |
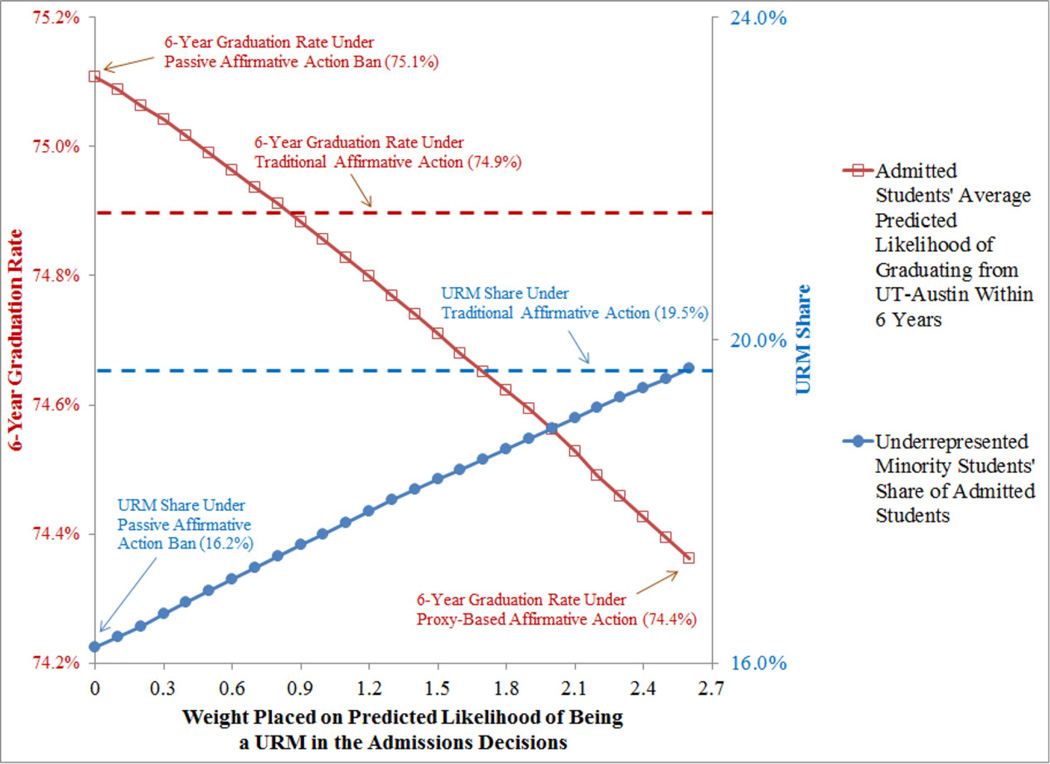
Table 4 shows the effect of the alternate admission systems on the composition and quality of the admitted students. Moving from traditional affirmative action to a passive affirmative action ban system lowers URMs’ share of admitted students from 19.5 percent to 16.2 percent. If the university wanted to restore this URM share using the proxy system, they would need to set θ = 2.6. As the next two rows show, doing so comes at the cost of somewhat lowering student quality. First note that implementing the affirmative action ban only mildly raises quality, increasing average predicted GPAs from 2.944 to 2.951 and predicted likelihood of graduating from UT within six years from 74.9 percent to 75.1 percent. Subsequently, implementing a proxy-based affirmative action system completely undoes this improvement. If such a proxy-based system were implemented such as to fully restore URMs’ share, it would lower average predicted GPAs down to 2.929 and predicted likelihood of graduating from UT within six years down to 74.4 percent. Figure 1 graphically shows the effects of the proxy system on graduation rates. To put these changes in perspective, moving from the passive affirmative action ban system to the fully implemented proxy-based system would lower the average admitted student from the 61st to 59th percentile of the distribution of applicants based on predicted cumulative GPA, and from the 57th to 55th percentile based on predicted likelihood of graduating from UT within six years. Or, for every 10,000 enrollees, UT should expect 75 fewer graduates. And, among all four-year institutions nationally, UT’s six-year graduation rate would fall from the 88.4th to the 87.7th percentile.21
Table 4.
Simulation results: effect of policy changes on quality of admitted students.
| Admitted under | ||||||||
|---|---|---|---|---|---|---|---|---|
| Proxy-based affirmative action with weight on predicted likelihood of being a URM |
||||||||
| Traditional affirmative action |
Passive affirmative action ban |
0.1 | 0.6 | 1.1 | 1.6 | 2.1 | 2.6 | |
| URM’s share of admitted students | 19.5% | 16.2% | 16.3% | 17.0% | 17.7% | 18.4% | 19.0% | 19.6% |
| Predicted cumulative GPA in UT classes | 2.944 | 2.951 | 2.951 | 2.947 | 2.943 | 2.938 | 2.934 | 2.929 |
| Predicted likelihood of graduating from UT within six years | 74.9% | 75.1% | 75.1% | 75.0% | 74.8% | 74.7% | 74.5% | 74.4% |
Figure 1.
Effect of Using a Proxy-Based Affirmative Action System on the Composition of UT-Austin’s Admitted Students.
Table 5 shows that there are very modest gains to be made using more sophisticated specifications to predict the likelihood that the student is a URM. The first row shows that the weight that would need to be placed on the proxy indicator is much higher for alternate 2. Recall that alternate 2 uses only six variables to predict the student’s underrepresented minority status and is thus the least effective in generating admitted URM students. However, alternate 2 uses only factors that are positively related to the likelihood of graduation from UT. The virtue and limitation of alternate 2 effectively offset each other such that alternate 2 has virtually the same efficiency costs as the main specification and the other alternatives. Using each of the alternatives, I find that college performance would be lower using proxy-based affirmative action than using traditional affirmative action. I further compute the “efficiency” of proxy-based affirmative action by dividing the predicted level of college performance under proxy-based affirmative action by the predicted level of college performance under the passive affirmative action ban. I find that proxy-based affirmative action is 99.0 percent to 99.3 percent as efficient as a passive affirmative action ban system. This result can be compared with the findings in Fryer, Loury, and Yuret (2008), who found that a proxy-based system (which they called “color-blind affirmative action”) is 96.2 percent as efficient as the “laissezfaire” policy, which maximizes predicted college GPA rank. I consider these results to be fairly comparable and thus mutually reinforcing.
Table 5.
Simulation results: robustness checks.
| Robustness checks | ||||
|---|---|---|---|---|
| Main specification |
Alternate 1 | Alternate 2 | Alternate 3 | |
| Weight placed on Proxyi (i.e., θ) to fully restore URM share | 2.6 | 2.5 | 3.6 | 2.3 |
| Predicted cumulative GPA in UT classes | 2.929 | 2.930 | 2.932 | 2.932 |
| Change relative to passive affirmative action ban | −0.023 | −0.022 | −0.019 | −0.020 |
| Change relative to traditional affirmative action | −0.015 | −0.014 | −0.011 | −0.012 |
| Efficiency of proxy-based affirmative action | 99.2% | 99.3% | 99.3% | 99.3% |
| Predicted likelihood of graduating from UT within six years | 74.4% | 74.4% | 74.5% | 74.5% |
| Change relative to passive affirmative action ban | −0.75% | −0.72% | −0.65% | −0.65% |
| Change relative to traditional affirmative action | −0.53% | −0.51% | −0.44% | −0.44% |
| Efficiency of proxy-based affirmative action | 99.0% | 99.0% | 99.1% | 99.1% |
| For every 10,000 enrollees, UT should expect this many fewer graduates | −75 | −72 | −65 | −65 |
Notes: Alternate 1: likelihood of being a URM computed as the sum of the likelihoods of being black, Hispanic, and American Indian.
Alternate 2: likelihood of being a URM predicted only using variables that have same sign effect on likelihood of graduation.
Alternate 3: likelihood of being a URM predicted using squared and cubed continuous variables and full set of interactions.
“Efficiency” is defined as college performance under proxy-based AA/college performance under passive AA ban.
Some might view these efficiency costs as minor, or perhaps even trivial. However, from a university point of view, a loss of 65 to 75 graduates out of every 10,000 enrollees may seem substantial. It is important to recognize that the university might have other means at their disposal to improve these results. For example, they could use proxy indicators for race and ethnicity in combination with other alternatives (such as targeted recruiting to increase the rate of applications from minorities), to achieve the goal of increasing minority enrollment. It is possible that the university could use programs to improve students’ transitions into college and strategically use financial aid to helpmitigate students dropping out, and thus offset the inefficiencies caused by the proxy-based system.
Also, it is important to recognize that such alternative admissions practices can have other positive effects that are not evaluated in this paper. Following the Hopwood decision, the Texas Legislature enacted H.B. 588, which guaranteed Texas high school students in the top 10 percent of their graduating high school class admission to any Texas public university. One can think of the top 10 percent policy as a form of proxy-based affirmative action that gives effectively infinite weight to having the characteristic of being in the top 10 percent. As shown in Long, Saenz, and Tienda (2010), this policy had other beneficial effects (aside from its effect on minority admissions) as it opened opportunity to schools with little tradition of sending students to UT yielding “a sizeable decrease in the concentration of flagship enrollees originating from select feeder schools and growing shares of enrollees originating from high schools located in rural areas, small towns, and midsize cities, as well as from schools with concentrations of poor and minority students” (p. 82). Among Hispanic students and students who graduate from predominantly minority high schools, Niu and Tienda (2010a) found a higher likelihood of enrollment at UT and Texas A&M for those who narrowly qualified for automatic admission versus those who barely missed being in the top 10 percent of their high school class. The efficiency costs of implementing the top 10 percent policy are likely modest; Niu and Tienda (2010b) concluded that black and Hispanic beneficiaries of the policy “perform as well or better in grades, 1st-year persistence, and 4-year graduation likelihood” (p. 44) than the white students displaced by those who were automatically admitted.
CONCLUSION
The Grutter and Fisher decisions have created a clear mandate that universities must first show that “workable race-neutral” alternatives are insufficient to produce the benefits of having a diverse class of enrollees before these universities are permitted to use race-based affirmative action. All alternative admissions systems that attempt to boost minority enrollment by giving weight to other nonrace applicant characteristics that are correlated with race (e.g., systems that give advantage to lower socioeconomic status applicants for this purpose) are in essence attempts to create “proxies” for minority status. In this paper, I investigate what would happen if a university directly gave weight to the applicant’s predicted likelihood of being an underrepresented minority applicant (rather than placing arbitrary weights on correlated indicators). I show that while such a system can be used to restore minority’s share of admitted students, doing so can result in a class that has modestly lower predicted likelihood of collegiate academic success. Furthermore, utilizing such a proxy-based admission system is inefficient; in the simulation, I find that it required the university to place 3.5 times as much weight on predicted minority status as the weight it previously placed directly on actual minority status, resulting in nonminority applicants being admitted who would not have been otherwise admitted.
If a university attempted to utilize a proxy-based admissions system, they would encounter a variety of dilemmas. First, to reduce the inefficiencies discussed above, they may be tempted to seek out additional information that is correlated with minority status. In a report I was commissioned to produce for the Educational Testing Service (Long, 2013), I show how the collection of additional information could improve the prediction of minority status. For example, using 195 characteristics of 10th graders in the Education Longitudinal Study of 2002, I was able to correctly predict underrepresented minority status for 82 percent of the students. The top three most predictive characteristics were the minority status of the student’s first, second, and third best friends—such information would be difficult for a university to reliably obtain. I note that “(w)hile the universities may want to go down this path, they may be thwarted by the monetary cost of purchasing such information, the political challenge that would be likely to follow from such privacy invasion, and the distaste it would engender in applicants” (p. 8). Furthermore, a naked and direct use of racial proxies is sure to invite legal challenge as such a policy would not be deemed “race-neutral” as discussed in the introduction. On the other hand, the use of less direct proxy systems (such as arbitrary weighting of correlated indicators) is likely to produce even more inefficiency, distorting the set of admitted students, and further lowering academic quality.
The second challenge universities would face is the extent to which they attempted to restore minority students’ share of admitted students via the proxy-based system. If they sought to exactly offset the decline in minority students’ share of admitted students brought about by the elimination of traditional race-based affirmative action (as was done in the simulation in this paper), they could be deemed guilty of having a quota for minority students, which would violate the Bakke decision. A lower court ruling that went against the University of Michigan Law School in the Grutter case cited the university’s target of 10 to 12 percent minority students as unconstitutional; “by using race to ensure the enrollment of a certain minimum percentage of underrepresentedminority students, the law school hasmade the current admissions policy practically indistinguishable from a quota system” (Grutter v. Bollinger, 137 F. Supp. 2d 851 [E.D. Mich. 2001]).
The third challenge is that implementing the proxy-based system could invite adverse strategic behavioral responses by students if such changes in admissions policies become known. Students may “invest” in characteristics that make them look like they are an underrepresented minority. Cullen, Long, and Reback (2013) demonstrate that students behaved strategically in response to the Texas top 10 percent policy by shifting their enrollment toward high schools where they had a better chance of landing in the top 10 percent. As such high schools have lower achieving peers, such an investment by students is adverse. More generally, Fryer, Loury, and Yuret (2008) caution that a proxy-based system could have an adverse effect on student’s preparation as “flattening of the link between qualifications and success undercuts incentives for [individuals] to exert preparatory effort by reducing the net benefit of investment” (p. 346).
Setting aside these challenges, whether such alternative admissions systems are “workable” is in the eye of the beholder. I find that a proxy-based system (using the information currently available to universities) would modestly lower the predicted collegiate success of admitted students. In the simulation in this paper, the admitted students’ predicted GPAs are found to fall from 2.95 to 2.93, and predicted likelihood of graduating from 74.9 percent to 74.2 percent. Whether this is a large enough cost to the university to be deemed not “workable” is unclear, and would likely vary from university-to-university and court-to-court. At this point, we lack sufficient court precedents to evaluate whether such a policy alternative would be seen as requiring the “university to choose between maintaining a reputation for excellence or fulfilling a commitment to provide educational opportunities to members of all racial groups” (Grutter, p. 27).
ACKNOWLEDGMENTS
I am grateful for the excellent research assistance provided by Mariam Zameer and for helpful comments and discussions with Liliana Garces, BillKidder, Gary Orfield, and Judith Winston. This research uses data from the Texas Higher Education Opportunity Project (THEOP) and acknowledges the following agencies that made THEOP data available through grants and support: Ford Foundation, The Andrew W. Mellon Foundation, The William and Flora Hewlett Foundation, The Spencer Foundation, National Science Foundation (NSF Grant No. SES-0350990), The National Institute of Child Health & Human Development (NICHD Grant No. R24 H0047879), and The Office of Population Research at Princeton University.
Appendix
Data
“Student is from foreign country”: The data contain “International” as its own racial or ethnic group (i.e., no additional racial or ethnic information is obtained on these students).
“Student’s SAT/ACT test score”: ACT test scores were converted into their equivalent SAT test score values using a conversion table provided by the College Board (Dorans, 2002). I then take the higher value, which is consistent in spirit with the findings of Vigdor and Clotfelter (2003), who noted that for students who take the SAT test multiple times, there is a “widespread policy stated by college admissions offices to use only the highest score … for purposes of ranking applicants, ignoring the scores from all other attempts” (p. 2). Consistent with this practice, the University of Michigan’s point system, which was the subject of the Supreme Court’s Gratz decision, used the higher value of the points assigned based on the student’s SAT and ACT scores (see http://www.vpcomm.umich.edu/admissions/legal/gratz/gra-cert.html).
“UT ‘Feeder’ high school”: Feeder high schools are defined as the top 20 high schools based on the absolute number of students admitted to UT in the year 2000 (Tienda & Niu, 2006).
“‘Longhorn Opportunity Scholarship’ high school”: Longhorn high schools are defined as those ever targeted by the University of Texas for the Longhorn Opportunity Scholarships (LOS). According to UT’s Office of Student Financial Services (2005) “these schools were included based on criteria that takes into account their students’ historical underrepresentation, measured in terms of a significantly lower than average percentage of college entrance exams sent to the University by students from this particular school, and an average parental income of less than $35,000.”
“‘Century Scholars’ high school”: Century high schools are the LOS counterparts at Texas A&M University, namely, campuses ever targeted for Century Scholarships.
“High school’s average SAT/ACT score (in ACT points)”: For every high school in the United States, including private schools, data were obtained on average SAT scores for the years 1994 to 2001 and average ACT scores for the years 1991, 1992, 1994, 1996, 1998, 2000, and 2004. Because the ACT data span a greater range of years, SAT scores were converted into ACT equivalents. Average SAT scores were linearly regressed on average ACT scores for the years 1994, 1996, 1998, and 2000. (These regressions were weighted based on the minimum value of the number of test takers on either test.) For these years, a weighted average of the high school’s average SAT and average ACT scores were computed, using the number of test takers on each test as weights. For the years 1995, 1997, 1999, and 2001, the previous year’s regression parameters were used for the conversion of SAT scores into ACT equivalents. For years with missing values for the high school’s average SAT/ACT score, missing values were imputed using the nearest available year and given preference to years in the same period (i.e., before and after the 1996 “recentering” of SAT scores).
“High school’s percentage who took the SAT + percentage who took the ACT exam”: These shares were determined by merging the SAT and ACT data sets discussed in the prior bullet with 11th-grade enrollment data from the U.S. Department of Education, Common Core of Data (CCD). For years with missing information on the shares taking either the SAT or ACT, missing values are imputed using the nearest available year.
“High school’s percentage who receive free or reduced-price lunch” and “High school’s percentage who are underrepresented minorities”: These shares were computed at the school level for all high schools included in the CCD in the years 1996, 1998 to 2000, and then merged with UT’s applicant file by year.
Footnotes
Krueger, Rothstein, and Turner (2006) concluded that this expectation is too optimistic: “Economic progress alone is unlikely to narrow the achievement gap enough in 25 years to produce today’s racial diversity levels with race-blind admissions” (p. 282). For a sample of other recent empirical analyses of affirmative action in college admissions, see Holzer and Neumark (2000, 2006), Long (2004), Arcidiacono (2005), Howell (2010), and Hinrichs (2012).
Following this remand, in a 2to1 decision, the Fifth Circuit upheld UT’s admission system and concluded that they were: “ … persuaded by UT Austin from this record of its necessary use of race in a holistic process and the want of workable alternatives. … To reject the UT Austin plan is to confound developing principles of neutral affirmative action, looking away from Bakke and Grutter, leaving them in uniform but without command—due only a courtesy salute in passing” (Fisher v. University of Texas, Court of Appeals for the Fifth Circuit, 2014, p. 41).
The Fisher decision seems to add some additional uncertainty about the definition of “workable.” The decision includes the following text: “The reviewing court must ultimately be satisfied that no workable race-neutral alternatives would produce the educational benefits of diversity. If ‘a nonracial approach … could promote the substantial interest about as well and at tolerable administrative expense,’ Wygant v. Jackson Bd. of Ed., 476 U.S. 267, 280, n. 6 (1986) … then the university may not consider race” (Fisher v. University of Texas, 2013b, p. 11). It is not clear whether the phrase “tolerable administrative expense” would include a cost to the university’s mission. In Justice Ginsburg’s dissent, she argues that the Fisher opinion did not change the Court’s definition of workable relative to its definition in Grutter: “Grutter also explained, it does not ‘require a university to choose between maintaining a reputation for excellence [and] fulfilling a commitment to provide educational opportunities to members of all racial groups.’ … I do not read the Court to say otherwise. See ante, at 10—acknowledging that, in determining whether a race-conscious admissions policy satisfies Grutter’s narrow tailoring requirement, ‘a court can take account of a university’s experience and expertise in adopting or rejecting certain admissions processes’” (Fisher v. University of Texas, 2013c). Yet, it remains unclear whether Justice Ginsburg’s interpretation of the Fisher opinion is correct and whether subsequent courts will agree. This interpretation is shared by U.S. Department of Education’s Office for Civil Rights (2013), who conclude that Fisher “did not change the requirements articulated in Grutter” (p. 2) and that institutions can “continue to rely on the U.S. Department of Education and U.S. Department of Justice’s [2012] Guidance” (p. 3).
Another race-neutral alternative would be for universities to attempt to boost minority application rates by, for example, doing more recruiting visits to high schools with large minority enrollments. The theoretical potential for such an application-based strategy to be efficacious is established in Brown and Hirschman (2006). Yet, there is scant empirical evidence to document the effectiveness of such recruiting strategies, and there are inferences that such alternative strategies have been ineffective (Long, 2007).
Other older literature has used simulations to evaluate whether class-based affirmative action could effectively substitute for race-based affirmative action, and this literature has reached similar conclusions. Cancian (1998) concludes that “Class-based programs would not achieve the same results as programs targeting racial and ethnic minority youths: many minority youths would not be eligible and many eligible youths would not be members of racial or ethnic minority groups” (p. 104). Using data from the early 1980s, Kane (1998) simulates that selective universities would need to go to extreme lengths in weighting socioeconomic factors in order to produce the same admissions rates for black and Hispanic applicants, and argues that such selective universities would be unlikely to do so.
Affirmative action practices at colleges and universities in the United States have historically not given preference to Asian American students (Bowen & Bok, 1998). Long (2004) and Long and Tienda (2008) found no significant advantage or disadvantage given to Asian applicants relative to white applicants using, respectively, national college admissions data from 1992 and institutional admissions data from the UT in pre-Hopwood years. As the data I use only record race as “Asian,” I cannot determine any greater level of racial or ethnic specificity beyond this category.
There are strong reasons why universities care about these measures as indicators of student quality (e.g., see Bowen, Chingos, & McPherson, 2011; Geiser & Santelices, 2007). There is political pressure being exerted on colleges to raise graduation rates; President Obama launched the College Scorecard in 2013, which rates colleges on a variety of dimensions including their six-year graduation rates.
This analysis is restricted to 1998 enrollees because six years of transcript data are not available for 1999 and 2000 enrollees.
As shown later in Table 1, Z is a vector of applicant characteristics that is inclusive of X.
vi is a random variable, which (consistent with a probit model) is distributed N(0,1). Since a random variable is included in the computation of the student’s AdmissionIndex, I repeat the simulation 10 times and report the mean of the 10 simulations.
I additionally set the coefficient on Asian American to zero.
Note that I am assuming that the university would not adjust N or the parameters in equations (6a)–(6c) to address variation across students in their likelihood of enrolling conditional on being admitted.
All appendices are available at the end of this article as it appears in JPAM online. Go to the publisher’s Web site and use the search engine to locate the article at http://www3.interscience.wiley.com/cgibin/jhome/34787.
I drop from the data set those students with missing data on race or ethnicity. This includes zero students from the first sample of 1996 applicants, four students (0.1 percent) from the second sample of 1998 enrollees, and 209 students (0.4 percent) from the third sample of 1998 to 2000 applicants.
In this specification, Asian Americans are less likely to be admitted than otherwise comparable white applicants. This result, which is weakly significant, is not robust to alternate specifications (e.g., a specification including the squares of continuous variables).
The bivariate relationship of test scores and graduation is positive and significant.
See Black et al. (2014) for a deeper analysis of how high school characteristics predict college performance using administrative data from UT.
In bivariate regressions, scoring three or above on the AP foreign language test has a significant positive association with being Hispanic, but a significant negative association with being black.
This process results in the likelihood of being an underrepresented minority being predicted by just the following six variables: Student is from a single-parent family, Student scored 3+ on AP foreign language exam, High school’s percent of students who took the SAT + percent who took the ACT exam, high school’s percent of students who are underrepresented minorities, student attended a “Longhorn Opportunity Scholarship” high school, and student attended a “Century Scholars” high school.
Given this high number of independent variables, convergence problems were encountered when using a probit specification. I have thus estimated this third specification using a linear probability model. The regression results for these three alternate specifications are available from the author.
Calculated using 2012 data from the Integrated Postsecondary Education Data System.
REFERENCES
- Alger J. Summary of Supreme Court decisions in admissions cases. [Retrieved December 9, 2013];University of Michigan Assistant General Counsel. 2003 from http://www.umich.edu/~urel/admissions/overview/cases-summary.html. [Google Scholar]
- Arcidiacono P. Affirmative action in higher education: How do admission and financial aid rules affect future earnings? Econometrica. 2005;73:1477–1524. [Google Scholar]
- Black SE, Lincove JA, Cullinane J, Veron R. NBER Working Paper No. 19842. Cambridge, MA: National Bureau of Economic Research; 2014. [Retrieved August 5, 2014]. Can you leave high school behind? from http://www.nber.org/papers/w19842. [Google Scholar]
- Bowen W, Bok D. The shape of the river: Long-term consequences of considering race in college and university admissions. Princeton, NJ: Princeton University Press; 1998. [Google Scholar]
- Bowen W, Chingos MM, McPherson MS. Crossing the finish line: Completing college at America’s public universities. Princeton, NJ: Princeton University Press; 2011. [Google Scholar]
- Brown SK, Hirschman C. The end of affirmative action in Washington State and its impact on the transition from high school to college. Sociology of Education. 2006;79:106–130. [Google Scholar]
- Cancian M. Race-based versus class-based affirmative action in college admissions. Journal of Policy Analysis and Management. 1998;17:94–105. [Google Scholar]
- Chan J, Eyster E. Does banning affirmative action lower college student quality? American Economic Review. 2003;93:858–872. [Google Scholar]
- Coleman AL, Palmer SR, Winnick SY. Race-neutral policies in higher education: From theory to action. [Retrieved September 12, 2013];The Access & Diversity Collaborative. 2008 from http://advocacy.collegeboard.org/sites/default/files/Race-Neutral_Policies_in_Higher_Education.pdf. [Google Scholar]
- Cullen JB, Long MC, Reback R. Jockeying for position: Strategic high school choice under Texas’ top-ten percent plan. Journal of Public Economics. 2013;97:32–48. [Google Scholar]
- Dorans NJ. Research Report No. 2002-11. New York, NY: College Board; 2002. The recentering of SAT scales and its effects on score distributions and score interpretations. [Google Scholar]
- Faulkner LR. Address on the state of the University. [Retrieved December 10, 2013];2005 Sep; from http://theop.princeton.edu/publicity/general/UTFaulkerSpeech.pdf. [Google Scholar]
- Fisher v. University of Texas, 570 U.S. [Syllabus] 2013a [Google Scholar]
- Fisher v. University of Texas, 570 U.S. [Opinion of the Court] 2013b [Google Scholar]
- Fisher v. University of Texas, 570 U.S. [GINSBURG, J., dissenting] 2013c [Google Scholar]
- Fisher v. University of Texas, Court of Appeals for the Fifth Circuit. [Retrieved August 4, 2014];2014 No. 09-50822. from http://www.ca5.uscourts.gov/opinions%5Cpub%5C09/09-50822-CV2.pdf.
- Fryer RG, Jr, Loury GC, Yuret T. An economic analysis of color-blind affirmative action. Journal of Law, Economics, & Organization. 2008;24:319–355. [Google Scholar]
- Geiser S, Santelices MV. standardized tests as indicators of four-year college outcomes. Berkeley, CA: Center for Studies in Higher Education, UC Berkeley; 2007. [Retrieved December 20, 2013]. Validity of high-school grades in predicting student success beyond the freshman year: High-school record vs. from http://escholarship.org/uc/item/7306z0zf. [Google Scholar]
- Gratz v. Bollinger, 539 U.S. 244. 2003 [Google Scholar]
- Grutter v. Bollinger, 539 U.S. 306. 2003 [Google Scholar]
- Hinrichs P. The effects of affirmative action bans on college enrollment, educational attainment, and the demographic composition of universities. Review of Economics and Statistics. 2012;94:712–722. [Google Scholar]
- Holzer H, Neumark D. Assessing affirmative action. Journal of Economic Literature. 2000;38:483–568. [Google Scholar]
- Holzer H, Neumark D. Affirmative action: What do we know? Journal of Policy Analysis and Management. 2006;25:463–490. [Google Scholar]
- Hopwood v. Texas, 78 F.3d 932 (5th Cir. 1996), cert. denied, 518 U.S. 1033. 1996 [Google Scholar]
- Howell JS. Assessing the impact of eliminating affirmative action in higher education. Journal of Labor Economics. 2010;28:113–166. [Google Scholar]
- Kane TJ. Misconceptions in the debate over affirmative action in college admissions. In: Orfield G, Miller E, editors. Chilling admissions: The affirmative action crisis and the search for alternatives. Cambridge, MA: Harvard Education Publishing Group; 1998. [Google Scholar]
- Krueger A, Rothstein J, Turner S. Race, income, and college in 25 years: Evaluating Justice O’Connor’s conjecture. American Law and Economics Review. 2006;8:282–311. [Google Scholar]
- Long MC. Race and college admission: An alternative to affirmative action? Review of Economics and Statistics. 2004;86:1020–1033. [Google Scholar]
- Long MC. Affirmative action and its alternatives in public universities: What do we know? Public Administration Review. 2007;67:311–325. [Google Scholar]
- Long MC. The promise and peril for universities using correlates of race in admissions in response to the Grutter and Fisher decisions. Report commissioned by the Educational Testing Service; University of Washington; Working Paper. Seattle, WA. 2013. [Google Scholar]
- Long MC, Tienda M. Winners and losers: Changes in Texas university admissions post-Hopwood. Educational Evaluation and Policy Analysis. 2008;30:255–280. doi: 10.3102/0162373708321384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long MC, Saenz V, Tienda M. Policy transparency and college enrollment: Did the Texas’ top 10 percent law broaden access to the public flagships? Annals of the American Academy of Political and Social Science. 2010;627:82–105. doi: 10.1177/0002716209348741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu SX, Tienda M. The impact of the Texas top 10 percent law on college enrollment: A regression discontinuity approach. Journal of Policy Analysis and Management. 2010a;29:84–110. doi: 10.1002/pam.20480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu SX, Tienda M. Minority student academic performance under the uniform admission law: Evidence from the University of Texas at Austin. Educational Evaluation and Policy Analysis. 2010b;32:44–69. doi: 10.3102/0162373709360063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regents of the University of California v. Bakke, 438 U.S. 265. 1978 [Google Scholar]
- Rubin DB. Multiple imputation for nonresponse in surveys. New York, NY: J. Wiley & Sons; 1987. [Google Scholar]
- Tienda M, Niu S. Flagships, feeders, and the Texas top 10 percent plan. Journal of Higher Education. 2006;77:712–739. [Google Scholar]
- University of Texas at Austin, Office of Student Financial Services. Implementation and results of the Texas Automatic Admission Law (HB588) at the University of Texas at Austin. [Retrieved February 27, 2007];2005 from http://www.utexas.edu/student/admissions/research/HB588-Report7.pdf. [Google Scholar]
- U.S. Department of Education, Office for Civil Rights. Guidance on the voluntary use of race to achieve diversity in postsecondary education. [Last modified on January 3, 2012];2012 Retrieved May 28, 2014, from http://www2.ed.gov/print/about/offices/list/ocr/docs/guidance-pse-201111.html.
- U.S. Department of Education, Office for Civil Rights. Questions and answers about Fisher v. University of Texas at Austin. [Retrieved May 28, 2014];2013 from http://www2.ed.gov/about/offices/list/ocr/docs/dcl-qa-201309.html.
- Vigdor JL, Clotfelter CT. Retaking the SAT. Journal of Human Resources. 2003;38:1–33. [Google Scholar]