A Deep Learning Network Approach to ab initio Protein Secondary Structure Prediction

Abstract

Ab initio protein secondary structure (SS) predictions are utilized to generate tertiary structure predictions, which are increasingly demanded due to the rapid discovery of proteins. Although recent developments have slightly exceeded previous methods of SS prediction, accuracy has stagnated around 80% and many wonder if prediction cannot be advanced beyond this ceiling. Disciplines that have traditionally employed neural networks are experimenting with novel deep learning techniques in attempts to stimulate progress. Since neural networks have historically played an important role in SS prediction, we wanted to determine whether deep learning could contribute to the advancement of this field as well. We developed an SS predictor that makes use of the position-specific scoring matrix generated by PSI-BLAST and deep learning network architectures, which we call DNSS. Graphical processing units and CUDA software optimize the deep network architecture and efficiently train the deep networks. Optimal parameters for the training process were determined, and a workflow comprising three separately trained deep networks was constructed in order to make refined predictions. This deep learning network approach was used to predict SS for a fully independent test data set of 198 proteins, achieving a Q₃ accuracy of 80.7% and a Sov accuracy of 74.2%.

1 Introduction

Experimental methods for determining protein structure are so slow and expensive that they can be applied to only a tiny portion (<0.1%) of the proteins produced by various genome sequencing projects. Therefore, reliable methods for predicting the structure of newly discovered proteins using their amino acid sequences are crucial for accelerating research to determine the role of these proteins in biological systems. Furthermore, computational structure prediction can be used to increase time and resource efficiency when designing artificial proteins[1].

The accuracy of tertiary structure prediction largely depends on the amino acid sequence of the protein under consideration. This is not only because a protein's sequence almost exclusively determines its structure, but also because such prediction of proteins that have close homologs with known structure is exceedingly accurate using comparative modeling[1, 2]. Unfortunately, it is much more challenging to predict the tertiary structure of proteins that do not have a close homolog with known structure, a process called ab initio (or template-free) tertiary structure prediction. However, it is considerably easier to use a sequence to predict one-dimensional protein features such as residue-residue contacts, solvent accessibility and secondary structure, and the use of these intermediate features has been shown to facilitate ab initio tertiary structure prediction[1, 3, 4].

Many early attempts at ab initio secondary structure prediction utilized statistical approaches, employing data collected from proteins with known secondary structure, but these methods could not often achieve accuracy higher than 65%[1, 5, 6]. Machine learning pattern recognition has proved more useful for such prediction, and many methods have utilized support vector machines[7-10] and neural networks[11-17]. Combining such machine learning technology with protein sequence profiles based on homology produced a major breakthrough in secondary structure prediction, raising accuracy to 70-79%[16, 18-21]. Since then, sequence profiles were used in the SPINE neural network method with 79.5% accuracy[22]. A novel approach called SymPred uses concepts based on natural language processing to define synonymous sequences of residues, resulting in a predictor achieving an accuracy of 80.5%[23]. More recently, the SPINE X method, employing neural networks, achieves >80% accuracy as well[24].

However, secondary structure prediction has failed to appreciably improve upon the state-of-the-art 80% accuracy. As noted, recent methods have improved upon this accuracy by a small margin, but we must question how important it is to tweak secondary structure prediction tools to generate such a small improvement in accuracy. It is looking more and more like secondary structure prediction scores may not significantly improve until the discovery of features that can benefit the prediction process over and above the contribution of the sequence profiles alone[25]. One such potential set of features were calculated by Atchley, et al., comprising five numbers derived from a numerical dimensionality reduction of the properties of amino acids, calculated using statistical analyses[26]. Atchley's factors provide a convenient characterization of the similarities between amino acids. They have been used in other areas of protein prediction[27-29], but not secondary structure prediction, so we utilize this novel feature to investigate its potential to contribute to this field.

Secondary structure prediction is most commonly evaluated by the Q₃ scoring function, which gives the percent of amino acids for which secondary structure was correctly predicted. Though it may be futile to attempt to raise the Q₃ accuracy with the same features that have been employed for over a decade, improvement in secondary structure predictions could still be attained if we focus more on improvements in other measures of accuracy, notably the more sophisticated Segment Overlap (Sov) score. The Sov scoring function takes segments of continuous structure types into account in an attempt to reward the appropriate placement of predicted structural elements without harshly penalizing individual residue mismatches, especially at the boundaries of segments[30]. CASP (critical assessment of methods of protein structure prediction) identifies Sov as being a more appropriate measure of prediction accuracy, though we have not found any studies investigating the relative effect of Q₃ versus Sov scores on tertiary structure prediction itself[31, 32].

Although several methods[8, 18, 23] have used Sov scores in their evaluations, it is still not common practice for secondary structure predictors to report their results in terms of this alternative scoring criterion. It is even more unusual for Sov scores to be taken into consideration during the training procedure. During the development of this tool, we utilized a hybrid scoring method that takes the Sov scores as well as the Q₃ accuracy into account in an attempt to improve secondary structure prediction despite the difficulty of surpassing the Q₃ score ceiling.

Neural networks have been effectively used in a variety of prediction algorithms, including speech and face recognition as well as the aforementioned usage in protein secondary structure prediction[11-22, 24, 33-36]. The use of such networks allows predictors to recognize and account for complex relationships even if they are not understood. Weights assigned to nodes of the hidden layer determine whether the node is expressed or not, given the input. The training procedure adjusts these weights to make the output layer more likely to reflect the desired result, derived from documented examples. Once the weights are set, information for an unknown target can be used as input, allowing the network to predict its unknown properties.

Employing multiple hidden layers and training the layers using both supervised and unsupervised learning creates a deep learning (belief) network[37]. Deep learning networks are one of the latest and most powerful machine learning techniques for pattern recognition[37, 38]. They consist of two or more layers of self-learning units, where the weights of fully connected units between two adjacent layers can be automatically learned by an unsupervised Boltzmann machine learning method. This method is called contrastive divergence, and is used to maximize the likelihood of input data (features) without using label information. Thus, sufficiently numerous layers of units can gradually map unorganized low-level features into high-level latent data representations. These are more suitable for a final classification problem, which can be easily learned in a supervised fashion by adding a standard neural network output layer at the top of multi-layer deep learning networks. This semi-supervised architecture substantially increases the learning power while largely avoiding the over-fitting and/or vanishing-gradient problem of traditional neural networks.

Deep learning methods achieve the best performance in several domains (e.g., image processing, face recognition) and have an established place in protein prediction, having been effectively applied to residue-residue contact prediction and disorder prediction[27, 39, 40]. Additionally, a couple of deep learning protein structure predictors have been developed recently, including a multifaceted prediction tool that predicts several protein structural elements in tandem[36] and a predictor that utilizes global protein information[41]. Although we do not directly compare the accuracy of these tools with ours, we provide a methodological comparison in the discussion.

Since these techniques have been successful in other disciplines, we aimed to investigate whether deep learning networks could achieve notable improvements in the field of secondary structure prediction as well. Part of this attempt at improving structure prediction was the incorporation of the Sov score evaluation as part of the development process, and the introduction of the Atchley factors, which are novel to the field. These efforts produced DNSS, a deep network-based method of predicting protein secondary structure that we have refined to achieve 80.7% Q₃ and 74.2% Sov accuracy on a fully independent data set of 198 proteins.

2 Materials and Methods

2.1 Data Sets

Our training data set was a collection of 1425 proteins from the Protein Data Bank (PDB)[42]. This is a non-redundant set representative of the proteins contained in the PDB and originally curated in the construction of a residue-residue contact predictor[27]. This set was randomly divided into a training data set and a testing data set, consisting of 1230 and 195 chains, respectively.

A fully independent evaluation data set was collected from the CASP data sets. 105 proteins from the CASP9 dataset and 93 proteins from the CASP10 dataset were selected according to the availability of crystal structure[43, 44]. All of the proteins in the training data set have less than 25% sequence identity with CASP9 proteins, and only two training proteins have greater than 25% identity with CASP10 sequences (1BTK-A 43% identical to T0657 and 1D0B-A 28% identical to T0650).

2.2 Tools

DSSP, a tool that utilizes the dictionary of protein secondary structure, was used to determine the secondary structure classification from the protein structure files[45]. The eight states assigned during the DSSP secondary structure classification were reduced to a 3-state classification using this mapping: H, G and I to H, representing helices; B and E to E, representing sheets; and all other states to C, representing coils. This 3-state classification for secondary structure is widely used in secondary structure prediction, and was applied to the proteins in the training and testing data sets, as well as the evaluation data sets[8, 22, 24].

PSI-BLAST was used to calculate a position-specific scoring matrix (PSSM) for each of the training and testing proteins[46]. This was done by running PSI-BLAST for three iterations on a reduced version of the nr database filtered at 90% sequence similarity. The resulting PSSMs have twenty columns for each residue in the given chain, where each column represents the estimated likelihood that a residue could be replaced by the residue of the column. This estimation is based on the variability of the residue within a multiple sequence alignment. Furthermore, the information (inf) is given for each residue. With the exception of inf, matrix likelihoods are given in the range [−16, 13], and two methods of scaling these values to the range [0, 1] were evaluated. A simple piecewise function with a linear distribution for the intermediate values (suggested in SVMpsi[8]):

$$f\left(x\right)=\{\begin{array}{cc}0.0\hfill & ifx<-5\hfill \\ 0.5+0.1x\hfill & if-5\le x\le 5\hfill \\ 1.0\hfill & ifx>5\hfill \end{array}\phantom{\}}$$

and a logistic function of the PSSM score (used in PSIPRED[18]):

$$f\left(x\right)=\frac{1}{1+e^{-x}}$$

were compared. The two functions differ in that the logistic function amplifies differences in PSSM scores close to zero and severely diminishes those towards the extremities, whereas the piecewise function ignores scoring differences at the extremities and linearly scales the intermediate scores (Fig. 1).

Fig. 1.

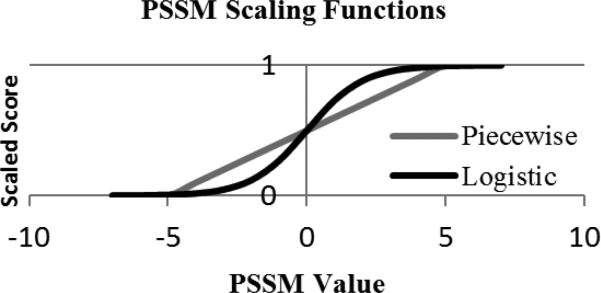
A comparison of the piecewise and logistic functions used to scale PSSM values.

2.3 Deep Learning Network

Deep learning (belief) networks (DNs) are similar to a two-layer artificial neural network but differ in the number of hidden layers and the training procedure. Typically, DNs are trained in a semi-supervised fashion; layer by layer using contrastive divergence and restricted Boltzmann Machines (RBMs)[38]. In its purest form, an RBM is a way to model a distribution over a set of binary vectors, comprising a two layer graph with stochastic nodes[47, 48]. In the graph, one layer corresponds to the input, or visible, data and the other is the hidden, or latent, layer. Each node in the graph has a bias and there are weighted connections between each node in the visible layer and every node in the hidden layer. Given the values of the weights and the states of the nodes, it is possible to calculate an energy score for a particular configuration of the machine using the following function E.

$$E(v,h)=-\sum _{\mathrm{i}}{b}_{\mathrm{i}}{v}_{\mathrm{i}}-\sum _{\mathrm{j}}{c}_{\mathrm{j}}{h}_{\mathrm{j}}-\sum _{\mathrm{i},\mathrm{j}}{h}_{\mathrm{j}}{v}_{\mathrm{i}}{w}_{\mathrm{ij}}$$

In this function, v_i and h_j are the states of the i^th visible and j^th hidden nodes, respectively. The values of the bias terms are denoted by b_i and c_j, and w_ij is the weight of the connection between the i^th visible and j^th hidden nodes.

$$p\left(v\right)=\sum _h\frac{e^{-E(v,h)}}{Z}$$

A probability p(v) can then be defined for a particular input vector v by marginalizing over all possible configurations of the hidden nodes and normalizing (Z). Training an RBM comprises adjusting the weights and biases such that configurations similar to the training data are assigned high probability while random configurations are assigned low probability. This is done using a procedure known as contrastive divergence (CD) which attempts to minimize an approximation to a difference of Kullback-Leibler divergences[47].

RBMs have shown themselves useful for initializing the weights in a DN. This is done by first training an RBM using the training data as the visible layer. Then weights of the learned RBM are used to predict the probability of activating the hidden nodes for each example in the training dataset. In this manner the RBM was applied to the training set to obtain a set of activation probabilities. These activation probabilities were then used as the visible layer in another RBM. This procedure was repeated several times to initialize the weights for several hidden layers.

It is important to note that while an RBM was originally formulated largely with stochastic, binary nodes, it is possible to use other types of nodes or model data other than strictly binary inputs[49]. In particular, real valued data in the range of [0-1] can be modeled in practice using standard logistic nodes and CD training without any modification. This was the approach initially employed by Hinton and Salakhutdinov when working with image data (the inputs to the visible layer were scaled intensities of each pixel)[38]. Indeed, when adding additional layers to their networks, the inputs to higher layers of the network were the real-valued activation probabilities coming from the preceding layer. Generally speaking, an RBM can handle this type of data through logistic nodes, and in this work we rescaled all inputs to be in the range of [0-1], making them compatible with this generalized usage of the RBM with real-valued data.

For the last layer, a standard neural network was trained and the entire network was fine-tuned using the standard back propagation algorithm[37, 38]. To decrease the time needed to train a DN, all of the learning algorithms were implemented with matrix operations. The calculations were performed using CUDAmat on CUDA enabled graphical processing units[50].

2.4 Experimental Design

Our basic formula for training a deep network comprised three principal steps: selecting input profile information; gathering windows of profiles; and training the deep network. By testing configurations and comparing the resulting prediction accuracies, we determined effective parameters for the type and number of features included in the input profile, the window size, and the architecture of the deep network.

We first wanted to show that the ability to deepen the neural network is in itself a benefit. In order to confirm that the deep network architecture improves upon a “shallow” network with only one hidden layer, deep networks were trained while holding all other parameters consistent and varying the number of hidden layers from one to four. Once this proof-of-concept experiment was carried out, we began investigating the components of the three principal steps.

We selected the input profiles from three kinds of features: the amino acid residues themselves (RES), the PSSM information (PSSM), and the Atchley factors (FAC) [26]. Deep networks were trained using windows of adjacent residues including different combinations of these features to determine which assortment would train the deep network most effectively.

Once we selected an input combination, profile information from a window of consecutive amino acids was collected to represent the central residue. Each type of feature was given an extra value which was used to indicate whether the window spanned the terminal residues. Similar machine learning approaches to secondary structure prediction have reported success using a variety of window sizes including 15 [8] and 21 [22], so window sizes from 11 to 25 were tested.

Similarly, using constant input profiles and window size, an effective architecture was determined by varying the depth and breadth of the network. We trained deep networks with 3 to 6 hidden layers and varied the amount of nodes composing each hidden layer. These parameters were tested first using a coarse sampling, where one trial of each depth contained many nodes per layer and another contained few nodes. Variations of the most effective parameter choices were tested to further refine the deep network configuration.

In an attempt to improve the secondary structure predictions, an overall system of three deep networks was developed (Fig. 2). In this system, two independently trained deep networks predict the secondary structure of a protein, and the third deep network uses these predictions as input and generates a refined prediction. In order to train the networks in such a system, the training data was randomly split in half, and each half of the dataset was used to train one of the first two deep networks. We chose to use two first-tier networks to gain the benefit of the refined prediction without overcomplicating the model. Each first tier network was used on the opposite half of the training data to obtain secondary structure predictions, which became the features used to train the second tier deep network. The optimal window size and architecture configuration were determined in a similar fashion to the preliminary deep networks. Once the second tier deep network was trained, all three networks were used to predict the structure of the testing dataset. The structure type probabilities assigned by the first tier DNs were averaged for each residue and used by the second tier deep network to make the final secondary structure prediction.

Fig. 2.

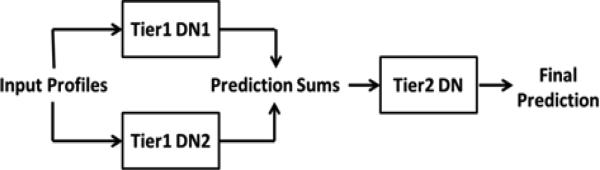
Block diagram showing the DNSS secondary structure prediction workflow.

2.5 Training and Evaluation Procedure

Many processes of training and testing a deep network went into the construction of this tool. For the purpose of this report, we define a trial to include the following steps: the complete training of a deep network using features derived from the training data set of 1230 protein chains; the testing of the deep network by predicting the secondary structure of the testing data set of 195 proteins; and the evaluation of these predictions using the Q₃ and Sov scoring functions to compare the predicted 3-state secondary structure to the true structure. Each trial was repeated over five iterations using identical parameters to account for the stochastic processes involved.

In order to determine which parameters were most successful, the trials were ranked in order of increasing Q₃ and Sov score and assigned one rank for each score. The ranks from both scores for all identical trials were summed, at which point the set of trials with the highest rank sum was deemed to have used the most effective parameter configuration. This rank sum method was chosen instead of comparing average scores because it was found to be more resistant to outliers, so ideally the chosen parameters would not only result in accurate predictions, but also perform consistently while other parameters were being tested.

A rigorous ten-fold cross-validation test was used to determine the accuracy of the predictions using the final DNSS pipeline. After randomly omitting five proteins, the remainder of the combined training data set consisted of 1420 proteins that were divided into ten equal parts, nine of which were used for training and the remaining one for testing. This process was repeated ten times using a different division for testing, and using identical parameters for each trial. This resulted in one secondary structure prediction for each of the 1420 chains, which were evaluated using Q₃ and Sov scores.

In addition to the cross-validation test, an independent test data set composed of 105 proteins from the CASP9 data set and 93 proteins from the CASP10 data set was used to evaluate the performance of the DNSS tool[43, 44]. This data set was also used to assess the accuracy of a variety of secondary structure prediction tools, including three tools employing different kinds of neural network architectures: SSpro v4.0, PSIPRED v3.3, and PSSpred v2[15-17]; and the RaptorX-SS3-SS8 method which utilizes conditional neural fields[51, 52]. Since the final DNSS pipeline was created without consideration for the prediction accuracy over the CASP9 and CASP10 proteins, they can be used as fully independent data sets to provide an unbiased evaluation. The predictions of each tool were evaluated with the Q₃ and Sov scoring functions and compared.

3 Results

3.1 Depth of Network

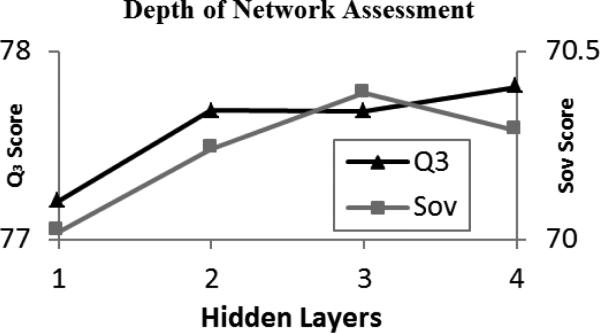
The improvement generated by adding additional layers on top of the basic 1-layer network was modest (~0.5% Q₃ and ~0.25% Sov) (Fig. 3). Still, the mean differences between the 1-layer Q₃ and Sov scores and the scores produced by each of the multi-layered deep networks was statistically significant (p<.05). Our use of deep networks constructed with additional hidden layers was driven not by a desire to increase the model's complexity, but rather to allow for the layer-by-layer, unsupervised initialization procedure, which first learns the patterns in the data. In any case, this preliminary experiment demonstrates that our use of the deeper network does lead to a visible increase of the accuracy of predictions, and the more complex architecture is not detrimental to the performance of the secondary structure prediction tool.

Fig. 3.

Results obtained using varied hidden layers and averaged over 10 trials while keeping all other parameters constant.

3.2 PSI-BLAST Scaling

Training deep networks using both the logistic and piecewise PSSM scaling functions resulted in an average Q₃ score of 77.5% over the test data set. There was a slight difference in the Sov scores, with the piecewise function achieving 70.7% versus the logistic Sov score of 70.4%. Though the difference was small, the piecewise function scored higher, so this scaling function was selected.

3.3 Input Features

Deep networks were trained and tested using all combinations of features including at least one of RES, PSSM and FAC input information (Table 1). As expected, including PSSM profile features greatly improved prediction accuracy, shown by the 13.4% difference in average Q₃ scores and a similar leap for Sov scores between the best-scoring configuration omitting the PSSM features and the worst-scoring configuration including it. Including the RES features proved to be a detriment to the scores, possibly because this resulted in too much noise in the input data since the identity of the residue is contained within the other two inputs. The combination of the PSSM profile and the Atchley factors was found to train the deep network most effectively out of any combination of these three types of features, so this combination was used during future trials.

TABLE 1.

Performance of Input Profile Features

Rank	Features	Q3 (%)	Sov (%)
1	PSSM + FAC	79.1	72.38
2	PSSM	79.07	72.2
3	RES + PSSM	77.15	69.82
4	RES + PSSM + FAC	76.42	64.01
5	RES	63.04	52.36
6	FAC	62.22	54.94
7	RES + FAC	62.21	51.24

Scores show the average accuracy of deep networks trained with indicated input profiles, evaluated using the test data set of 195 proteins and listed from highest to lowest ranked score. RES = Residues, PSSM = Position Specific Scoring Matrix, FAC = Atchley Factors

3.4 DN Architecture for the First Tier

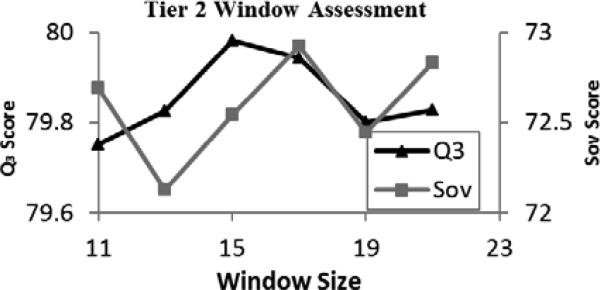
Odd window sizes from 11 to 25 were tested to determine the optimal window size for the deep network (Fig. 4). The average scores generally increased toward a window size of 19, and then sharply dropped off for windows larger than 20. Deep networks constructed using window sizes of 17 and 19 both scored highly, but due to the previously mentioned criteria, a window size of 17 was selected.

Fig. 4.

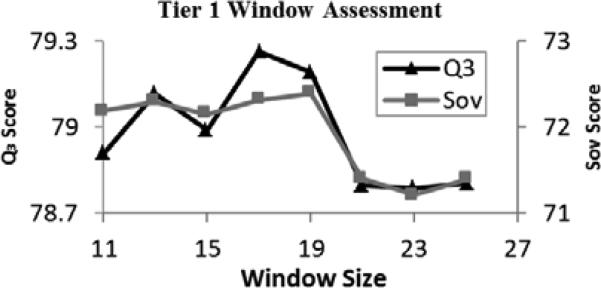
Results obtained using varied window sizes and averaged over 5 trials for the Tier 1 deep learning networks.

Initially, two architectures with each of 3, 4, 5, and 6 hidden layers were tested, using hidden layers with more nodes for one trial and hidden layers with fewer nodes for the second trial of each depth. The scores of these initial tests of variable architecture show that a 4-layered trial with many nodes in each hidden layer was the most accurate, followed closely by a 3-layered trial with few nodes (Table 2). However, using 3 layers with many nodes was found to be much less accurate, whereas both trials with 4 layers yielded favorable results, demonstrating that a 4-layered architecture is most likely to be the optimal choice.

TABLE 2.

Performance of Coarse Architecture Variation

Layers	Nodes	Q3 (%)	Sov (%)
4	Many	79.45	72.36
3	Few	79.4	72.75
4	Few	79.12	72.22
6	Many	79.09	71.78
5	Many	78.73	71.63
6	Few	78.71	71.65
5	Few	78.49	71.68
3	Many	78.18	70.63

Scores show the average accuracy of deep networks trained using a coarse sampling of deep learning network architectures, evaluated using the test data set of 195 proteins and listed from highest to lowest ranked score.

Variations of the more promising architectures of several layer sizes were tested to refine the method, and the trials were ranked in Table 3. 12 configurations were tested overall, consisting of three 3-layer, six 4-layer, and three 6-layer architectures tested using a variety of hidden layer sizes. More architectures containing 4 layers were tested because these networks continually scored highly in comparison to the rest of the tested architectures, so additional variations of 4-layer networks were attempted. The best tested architecture was one with 4 hidden layers and a majority hidden layer size of 500.

TABLE 3.

Performance of Refined Architecture Variation

Rank	Layers	Nodesa	Q3 (%)	Sov (%)
1	4	500	79.17	72.85
2	4	500	79.23	72.71
3	4	600	79.02	72.24
4	4	450	78.93	72.00
5	4	400	78.97	71.90
6	6	500	79.17	71.78
7	6	600	79.09	71.78
8	3	400	79.09	71.72
9	4	300	78.91	72.11
10	3	500	78.97	71.75
11	3	450	78.78	71.54
12	6	300	78.71	71.65

Scores show the average accuracy of deep networks trained using indicted architecture parameters and evaluated using the test data set of 195 proteins and listed from highest to lowest ranked score.

^aNodes refers to the size of the majority of hidden layers, as node amount is not always consistent between layers.

Note that in these tables the configurations are ranked in order from highest to lowest score based on the previously defined ranking scheme. In some cases, such as rows 1 and 2 in Table 2, the trials appear to be inappropriately ranked. This is due to the effect that outliers have on the average scores, but which does not as significantly affect the ranking scheme.

3.5 DN Architecture for the Second Tier

Once the optimal parameters were determined for training a deep network to make a preliminary secondary structure prediction, we used these parameters while training two first tier deep networks in the process described above. These networks were used to predict the structures of the proteins that were not used to train them, and these predictions were used as the input for the second tier deep network. In a similar fashion to determining the optimal parameters for the original deep networks, different parameters were tested for this second tier deep network.

To determine the optimal window size for the second tier, deep networks were trained using odd window sizes from 11 to 21 (Fig. 5). The resulting average Q₃ scores were very similar, with a mere 0.23% difference between the highest and lowest scoring trial. The average Sov scores were slightly more pronounced, with a range of 0.7%, and based on these scores it was determined that a window size of 17 was appropriate for the second tier, as it was for the first tier.

Fig. 5.

Results obtained using varied window sizes and averaged over 5 trials for the Tier 2 deep learning network.

Potential appropriate network architectures were tested in a similar fashion to the process above. After a coarse preliminary sampling of architectures ranging from 3 to 6 hidden layers, variations of the top-scoring networks were further tested and ranked (Table 4). The most successful architecture was found to be a 4-layer network with a majority hidden layer size of 600.

TABLE 4.

Performance of Second Tier Architecture Variation

Rank	Layers	Nodesa	Q3 (%)	Sov (%)
1	4	600	80.24	73.07
2	5	400	79.96	72.67
3	3	500	80.00	72.37
4	4	300	79.84	72.48
5	6	300	79.82	72.50
6	3	400	79.89	72.20
7	6	400	79.87	72.15
8	6	200	79.70	72.24
9	5	500	79.42	71.03
10	4	400	79.35	70.83
11	4	500	79.39	70.31
12	3	600	79.07	70.06

Scores show the average accuracy of deep networks of the second tier, trained using indicted architecture parameters and evaluated using the test data set of 195 proteins, listed from highest to lowest ranked score.

^aNodes refers to the size of the majority of hidden layers, as node amount is not always consistent between layers.

3.6 Evaluation

Our final workflow for using deep networks to predict the secondary structure of proteins was a two-tier process. Two deep networks of 4-layer architecture with hidden layer sizes of 500, 500, 500, and 200 were trained using input profiles constructed by PSI-BLAST profiles and Atchley's residue factors, collected in windows of 17. These networks were used to make secondary structure predictions, which were also collected in windows of 17 and used as the input of a second-tier deep network of 4-layer architecture with hidden layer sizes of 600, 600, 600, and 250 (Fig. 2). This prediction pipeline achieved maximum scores of 80.3% Q₃ and 73.6% Sov on the testing dataset. It was further assessed using a 10-fold validation test, resulting in an average Q₃ score of 78.8% and an average Sov score of 72.2%.

The secondary structures of proteins from two CASP data sets were also predicted. DNSS achieved a Q₃ accuracy of 81.1% and a Sov score of 74.7% over 105 proteins from the CASP9 data set, and 93 proteins from the CASP10 data set were predicted with a Q₃ and Sov accuracy of 80.2% and 73.6%, respectively[43, 44]. The confusion matrices for the DNSS predictions over the combined CASP dataset are given in Table 5 and Table 6. These matrices show that DNSS is most reliable at predicting regions of helices, and predicts coils and sheets with similar accuracy.

TABLE 5.

First Confusion Matrix

	Cpred	Epred	Hpred
C	77.80%	12.54%	9.66%
E	18.78%	79.38%	1.58%
H	13.79%	3.03%	83.19%

Values indicate the relative amounts of predicted structure classes that DNSS assigned to each actual structural element. The combined CASP dataset containing 198 proteins was used. C = Coil; E = Sheet; H = Helix.

TABLE 6.

Second Confusion Matrix

	C	E	H
Cpred	76.91%	11.05%	12.04%
Epred	20.07%	75.65%	4.28%
Hpred	11.47%	1.31%	87.23%

Values indicate the proportion of predicted structure classes that DNSS assigned to each actual structural element. The combined CASP dataset containing 198 proteins was used. C = Coil; E = Sheet; H = Helix.

PSIPRED, SSpro, PSSpred, and RaptorX-SS3 were also used to predict the secondary structure of the same fully independent CASP data sets, and these results are recorded in Table 7, with mean difference significance values listed in Table 8. According to the same system that was used to rank trials during the development of the deep network predictor, DNSS and PSSpred tied for the best scoring tools, as PSSpred ranked highest in Q₃ score and third in Sov score, and DNSS ranked highest in Sov score and third in Q₃ score.

TABLE 7.

Comparison of Secondary Structure Predictions

	CASP9		CASP10		Combined CASP		Min Score
Method	Q3 (%)	Sov (%)	Q3 (%)	Sov (%)	Q3 (%)	Sov (%)	Q3 (%)	Sov (%)
DNSS	81.1	74.7	80.2	73.6	80.7	74.2	50.4	46.1
PSSpred	83.3	72.0	81.0	70.4	82.2	71.3	41.8	33.7
SSpro	79.6	72.6	78.8	71.9	79.2	72.3	49.6	34.0
PSIPRED	80.9	69.3	81.2	68.6	81.0	69.0	33.8	23.2
RaptorX	78.1	70.4	77.9	70.3	78.0	70.3	45.6	33.0

Scores show the average accuracy of secondary structure prediction achieved by three methods over 105 proteins from the CASP9 data set, 93 proteins from the CASP10 data set, and the combined data set of all 198 of these proteins, along with the lowest score achieved for a single protein in this combined data set. Tools are listed from highest to lowest using the same ranking score as used for Tables 1 through 4. Note that DNSS and PSSpred tied for the highest rank.

TABLE 8.

Significance of Differences Between Tools

Q3	DNSS	PSSpred	SSpro	PSIPRED	RaptorX
Sov
DNSS		0.0010	0.0002	0.4383	<0.0001
PSSpred	0.0002		<0.0001	0.0396	<0.0001
SSpro	0.0042	0.2498		<0.0001	0.0081
PSIPRED	<0.0001	0.0172	<0.0001		<0.0001
RaptorX	<0.0001	0.2720	0.0030	0.0800

Values show the significance (p-values) of the mean differences between scores for each pair of tools, calculated using Student's t-test over the combined CASP data set of 198 proteins. The upper triangular portion shows the results of the statistical test for mean difference of Q₃ scores, while the lower triangular portion shows the results for the mean difference of Sov scores.

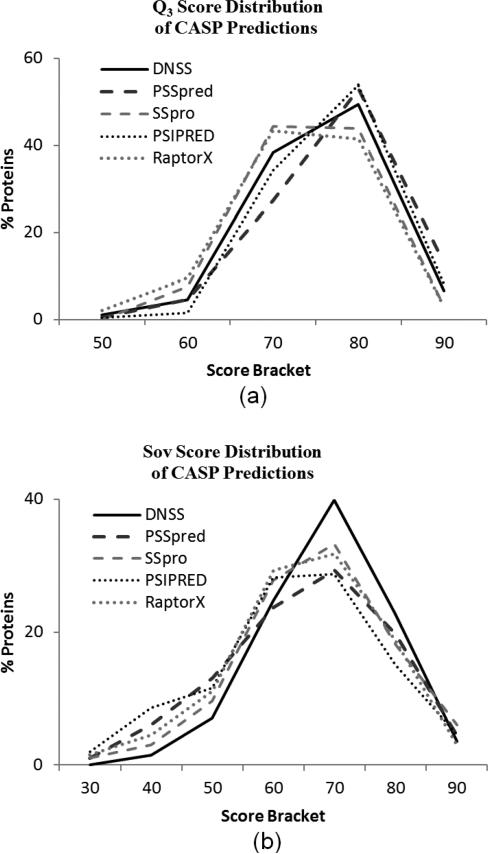
The distributions of the scores obtained by each method are plotted in Fig. 6. Although they are very similar, the slight differences in the score distributions are in some ways more revealing than the simple average scores. In comparison to the Q₃ score distribution of RaptorX, DNSS has fewer predictions in brackets for scores less than 80% and has more predictions in the highest two score brackets, indicating that DNSS outperformed RaptorX over the whole Q₃ distribution (Fig. 6a). In contrast, notice that PSIPRED has fewer 60% predictions, more 70-80% predictions, and fewer 90% predictions than PSSpred. In one sense, PSSpred performed better because it has more predictions that are over 90% accurate. However, PSIPRED's superiority can also be argued, since it had the fewest predictions with scores under 70%, identifying it as a more consistent tool. In a comparison between two tools, the clear superiority of one tool is demonstrated if their distributions cross only once, as is the case between DNSS and RaptorX. If the distributions cross multiple times, as in PSIPRED versus PSSpred, the relationship between tools is considered complex.

Fig. 6.

The distribution of the Q₃ (a) and Sov (b) scores obtained by five predictors over 198 CASP proteins. The score bracket of 90 indicates the amount of protein predictions that scored between 90% and 100%, and so on.

According to this criterion, no tool was consistently best over the Sov score distribution either (Fig. 6b). The DNSS Sov score distribution is close to being ubiquitously superior, with lower prediction counts in the lower brackets and higher prediction counts in the 70-80 and 80-90 brackets than the other tools. However, DNSS has almost the fewest predictions with a Sov score above 90. Though the distribution would be more favorable for the DNSS tool if this were not the case, it is still clear that DNSS performed considerably well in terms of Sov score, especially considering that 67% of the CASP proteins were predicted with a Sov accuracy of 70 or higher, as opposed to the next best 57% achieved by SSpro.

4 Discussion

In this paper, we presented DNSS, an ab initio method of predicting the secondary structure of proteins employing deep learning network architectures trained using the position-specific scoring matrix of the protein sequence and Atchley's factors of residues. A systematic approach was used to determine effective parameters for the training process, which carefully considered a variety of options for the input profile, window size, and architecture in an attempt to make the most effective use of this deep network implementation. We also utilized an advantage of this generalized method by combining the predictions of two fairly accurate predictors into a new set of input that could be used to train a third predictor without modifying the deep learning network implementation. Furthermore, our training method emphasized the improvement of Q₃ and Sov scores in tandem, as opposed to the usual focus on Q₃ score maximization alone. Thus, we produced a workflow capable of producing secondary structure predictions that achieved an average Q₃ score of 80.7% and an average Sov score of 74.2% on a fully independent test data set of 198 proteins, including 105 proteins from the CASP9 data set and 93 proteins from the CASP10 data set.

We compared these results to performance of four competitive secondary structure predictors: PSIPRED, SSpro, PSSpred and RaptorX[15-17, 51]. Overall, the methods performed similarly, with DNSS achieving slightly lower Q₃ accuracy and slightly higher Sov accuracy than the best of the evaluated tools. We conclude that DNSS has approximately the same prediction power as these other methods. Machine learning techniques have traditionally dominated the field of secondary structure prediction, so failing to produce a significant improvement using the most sophisticated implementation of machine learning suggests that there might not be much potential to advance the field of secondary structure prediction.

Perhaps the discovery of better features is necessary to breach the current secondary structure prediction accuracy ceiling of ~80%. As part of this investigation, we tested the impact of including Atchley's factors as features during the training process, and noted that adding them to the typical PSSM information did increase the accuracy of predictions over using PSSM profiles alone (Table 1). However, the benefit of including them was slight, and during the tests for other combinations of features, the addition of FAC appears to have decreased the accuracy of predictions. Because of this, it is unclear whether the Atchley factors were a benefit at all. In any case, they certainly are not the key to boosting secondary structure prediction past the present plateau.

Though DNSS did not appreciably advance the field of secondary structure prediction, it did achieve several favorable results. A comparison of the minimum scores of the evaluated methods shows that every DNSS prediction achieved a Q₃ score greater than 50% and a Sov score greater than 40%, which is an improvement over all of the others (Table 7), showing that this method is an especially consistent predictor. Furthermore, DNSS Sov scores were unrivaled by the tested tools, with a promising mean difference of 2% or more (Table 7), which was highly significant in all comparisons (Table 8). Under the assumption that the Sov score is, indeed, more relevant to tertiary structure prediction, our evaluation method that incorporates both the Q₃ and Sov scoring criteria keeps the overall accuracy of predictions high while ensuring that the results remain particularly useful for tertiary structure methods. Considering the immense effort required of researchers to generate small improvements to the Q₃ score, putting more future focus into enhancing Sov performance is a more realistic goal that may lead to improvements in protein prediction overall.

Our approach has some similarities with a multifaceted tool developed by Qi et al., which simultaneously predicts many aspects of local protein structure (e.g., secondary structure, solvent accessibility, binding, etc.)[36]. Both approaches use deep neural networks but differ in the training methodology, targets and refinement. In the prior work by Qi et al., a feature extraction layer was developed to explicitly map amino acid sequences into a feature space. The map learned was capable of capturing similarities among amino acid types and was used along with other features (e.g., PSSM) as the input into a multi-layer neural network. The network was trained using back-propagation and a Viterbi post-processing was performed to leverage local dependencies among the output classes.

In contrast, our approach learns features in the input data and initializes weights in the deep network via the layer-by-layer training approach and RBMs. After the weights were initialized, the entire network was refined using back-propagation. DNSS did not require any additional mapping for amino acid sequences but made use of the existing Atchley Factors as inputs into the network to characterize similarities between amino acids[26]. For post-processing, we trained an additional deep network to account for dependencies between the predicted secondary structure states and to refine our predictions.

In comparing the two methodologies, our approach is more homogenous with respect to training and prediction. For training, we used direct application of deep networks learned in a semi-supervised, layer-by-layer approach and did not have to train specialized feature extractors. These were learned through layered RBMs. For post processing and prediction, we used an additional deep network, which was unmodified except for the inputs, to consider initial predictions of secondary structure of a residue's neighbors before making a final prediction (i.e., the output of Tier 2).

Zhou et al. also employed a deep architecture for secondary structure predictions, though their approach is much more sophisticated and different in nature than the deep network architectures used in DNSS[41]. This method predicts 8-state secondary structure with competitive results, while our method is tailored to the 3-state prediction task. Furthermore, Zhou et al. utilized more global information through a multi-layer convolutional supervised generative stochastic network while DNSS makes predictions by focusing largely on local sequence information (i.e., a window centered on the residue to be classified).

Although the DNSS method did not produce a staggering improvement to the field of secondary structure prediction, it did perform competitively with other methods in the discipline and displayed some promising characteristics. We believe that further refinements of similarly implemented deep networks could produce more accurate secondary structure predictors. The specified parameters and architectures were the most accurate ones found during these trials, but it is possible that even more optimal parameters can be found by testing more precise variations of the most promising configurations.

In particular, continued experimentation with higher variability of node quantities between hidden layers would almost surely result in a more effective architecture. There are also other parameters common to neural networks that were not addressed as a part of this experiment. Choosing different values for these parameters, such as the batch size and the number of iterations (epochs), could benefit the prediction process as well. Furthermore, we expect that adding more Tier 1 deep networks in the overall prediction workflow would slightly improve predictions, as this would allow the use of more proteins while training each network. Unfortunately, any of this experimentation would involve a considerable investment in resources, and we would expect all such improvements to be slight (cumulatively less than 1%).

Finally, due to the homogeneity of the approach, this DNSS workflow can easily be adapted for use in other applications, whether related to protein prediction or not, as long as there is a sufficiently large and diverse dataset available to train the deep networks.

5 Conclusion

Neural networks have been an integral part of the protein structure prediction process for over a decade. Their introduction considerably improved the accuracy of predictors, and the gradual refinement and extended applications of neural network training methods continues to benefit the field of structure prediction. Deep learning networks are a revolutionary development of neural networks, and it has been suggested that they can be utilized to create even more powerful predictors. This deep learning approach employs a semi-supervised algorithm that allows for an increase in learning power and contains more potential for structural refinements, enhancing the ability to sculpt the network architecture to the nature of the problem being addressed. This comprehensive investigation of an implementation of deep networks in secondary structure prediction yielded a competitive tool, though the method failed to advance the field as much as was suggested by its alluring complexity.

Biography

Matt Spencer

Matt Spencer was awarded a bachelor's degree in Biological Science and Mathematics from the University of Nebraska in 2009. He currently studies as a graduate student in the Informatics Institute at the University of Missouri, Columbia. His research interests include bioinformatics, machine learning, big data and next-generation sequencing.

Jesse Eickholt

Jesse Eickholt received his PhD degree in computer science from the University of Missouri in 2013. Later that year he joined the Department of Computer Science at Central Michigan University where he currently works as an assistant professor. His research interests include bioinformatics, deep learning and data mining.

Jianlin Cheng

Jianlin Cheng received his PhD in information and computer science from the University of California, Irvine in 2006. He is currently an associate professor in the Computer Science Department at the University of Missouri, Columbia. His research is focused on bioinformatics, machine learning, deep learning and data mining.