Automatic Clustering and Thickness Measurement of Anatomical Variants of the Human Perirhinal Cortex

Abstract

The entorhinal cortex (ERC) and the perirhinal cortex (PRC) are subregions of the medial temporal lobe (MTL) that play important roles in episodic memory representations, as well as serving as a conduit between other neocortical areas and the hippocampus. They are also the sites where neuronal damage first occurs in Alzheimer’s disease (AD). The ability to automatically quantify the volume and thickness of the ERC and PRC is desirable because these localized measures can potentially serve as better imaging biomarkers for AD and other neurodegenerative diseases. However, large anatomical variation in the PRC makes it a challenging area for analysis. In order to address this problem, we propose an automatic segmentation, clustering, and thickness measurement approach that explicitly accounts for anatomical variation. The approach is targeted to highly anisotropic (0.4×0.4×2.0mm³) T2-weighted MRI scans that are preferred by many authors for detailed imaging of the MTL, but which pose challenges for segmentation and shape analysis. After automatically labeling MTL substructures using multi-atlas segmentation, our method clusters subjects into groups based on the shape of the PRC, constructs unbiased population templates for each group, and uses the smooth surface representations obtained during template construction to extract regional thickness measurements in the space of each subject. The proposed thickness measures are evaluated in the context of discrimination between patients with Mild Cognitive Impairment (MCI) and normal controls (NC).

1 Introduction

Quantification of the volume and thickness of ERC, PRC and other MTL cortical subregions from in vivo MRI has been increasingly pursued because these structures play important roles in episodic memory models [1] and are the earliest sites affected by AD pathology [2]. However, the PRC exhibits large anatomical variability, which complicates quantitative analysis [3]. By examining a large sample of autopsy brains, Ding et al. [4] conclude that three main variants of the PRC exist, defined by morphology of the collateral sulcus (CS): 1) continuous CS; 2) discontinuous CS with anterior CS shorter than the posterior; 3) discontinuous CS with anterior CS longer than the posterior. Failure to account for this variability can degrade the accuracy of morphometric analysis and reduce the utility of PRC as an imaging biomarker. This paper provides a novel approach for automatically quantifying the thickness of MTL substructures while explicitly accounting for anatomical variability.

Typically, the first step in quantitative MRI analysis is to segment the structures of interest, preferably automatically. However, little work on automatic segmentation of the PRC has been reported in the literature [5]. In this paper, we use the multi-atlas approach [6] in conjunction with a set of expert-labeled atlases that include labels for the ERC, PRC (further partitioned into Brodmann areas BA35 and BA36) as well as the hippocampal subfields (cornu ammonis, dentate gyrus and subiculum) to perform automatic segmentation. The method takes T1-weighted whole-brain scan (1mm³ isotropic resolution) as well as a specialized anisotropic oblique coronal T2-weighted scan of the MTL (0.4×0.4×2mm³ resolution) as inputs, and outputs a multi-label segmentation that has the same resolution as the T2-weighted image. The T2-weighted MRI has high in-plane resolution that allows substructures in the hippocampal region to be distinguished visually in the way that 1mm³ isotropic T1-weighted MRI cannot. Similar T2-weighted MRI scans have been used for manual segmentation of MTL substructures by several authors, e.g. [7,8].

Regional thickness measurements are often preferred to volume in morphometric studies of cortical structures like ERC and PRC because 1) they capture localized changes and 2) they are more robust to the variability of the locations of the boundaries in the automatic segmentation. While there is substantial prior work on measuring cortical thickness in MRI [9,10], most approaches do not provide a specific PRC thickness measurement. The notable exception is [5], who use a probabilistic template derived from postmortem MRI to label and measure the thickness of the PRC in the in vivo MRI. However, this single-template approach does not account for the anatomical variability described by Ding et al. [4]. In this paper, we propose a thickness measurement pipeline that attempts to automatically discover anatomical variants present in the population using a combination of deformable image registration and spectral clustering [11]. Our work is inspired by recent applications of clustering to atlas propagation and group-wise image registration [12], but is distinct in that clustering is applied to the output of multi-atlas segmentation rather than raw MRI data. The main contribution of this paper is introducing this concept in the analysis of PRC, which is the perfect application for this technique.

To demonstrate clinical utility, we evaluate our technique in a dataset from a research study of MCI, often conceptualized as a prodromal stage of AD, and normal aging. The proposed clustering-based approach yields stronger statistical power in discriminating the MCI patients from NC group than volumetric measurements as well as alternative thickness measures.

2 Materials

MRI scans of 83 participants (40 with diagnosis of MCI, 43 controls) from a research study conducted at the Penn Memory Center at the University of Pennsylvania were used to evaluate the proposed technique. Scans were acquired on a 3T Siemens Trio scanner. MRI protocols include a T1-weighted (MPRAGE) 1mm³ isotropic whole-brain scan and a 0.4×0.4×2mm³ T2-weighted (TSE) scan with partial brain coverage and an oblique coronal slice orientation (Fig 1a,b).

Fig. 1.

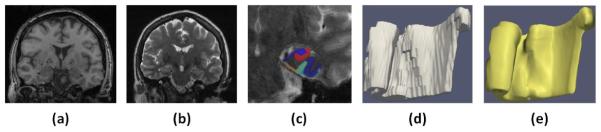
Sagittal slice of T1-weighted image (a) and T2-weighted image (b). (c) Automatic segmentation. (d) Blocky automatic segmentation mesh. (e) Smooth surface mesh representation.

Automatic segmentation for each subject was generated by applying the multi-atlas approach in [6] to the subject`s T1-weighted and T2-weighted scans (Fig 1c). The output segmentations, consist of 7 labels (cornu ammonis, dentate gyrus, subiculum, ERC, BA35, BA36 and CS), were then used for our proposed pipeline.

3 Method

Given the automatic segmentation, which has large step edge discontinuities in the MRI slice direction, our goal is to approximate it with a smooth surface mesh representation that is topologically consistent across all subjects sharing the same PRC anatomical subtype, and from which a regional thickness map can be extracted. Our proposed approach consists of three steps: 1) cluster subjects into groups based on their PRC anatomy; 2) build an unbiased population template for each group and generate a mesh in the template space; 3) warp the mesh back to the space of each subject and measure thickness for each vertex on the mesh. We treat each hemisphere independently throughout the analysis. The computational complexity of clustering and thickness analysis is negligible compared to multi-atlas segmentation. The detail of each step is described below.

3.1 Automatic Clustering of Anatomical Subtypes

Spectral clustering [11] is used to divide subjects into groups with similar PRC anatomy. Spectral clustering is a dimension reduction algorithm that projects the pairwise similarity relationship onto a lower-dimensional space in which anatomical variants can be easily separated using k-means clustering [13].

To compute the pairwise similarity matrix (denoted as S), we first perform pairwise registration between all the multi-label segmentations using ANTs affine and high-dimensional deformable algorithms [14]. The registration minimizes the sum of mean square intensity difference metrics computed separately for each label. Generalized Dice Similarity Coefficient (DSC) [15] is computed for labels BA35 and BA36 between the warped segmentation of subject and the segmentation of subject j, and denoted as D_ij. The underlying assumption is that after registration, overlap between multi-label segmentations will be greater when the pair of subjects have the same anatomical variant of the PRC than when they have different variants. In order to have a symmetric measurement and also exaggerate the similarity value between subjects with similar PRC anatomy, we compute similarity between subject and subject j as:

$$S_{ij}=\exp \left\{\frac{-{\left[\log 0.5(D_{ij}+D_{ji})\right]}^2}{2{\sigma }^2}\right\}$$ (1)

where parameter ρ controls the size of neighborhood in the graph (discussed below).

Based on S, we can construct a fully connected, undirected graph whose vertices are the subjects and weights are the similarity between subjects pairs. Then, the normalized graph Laplacian [11] is computed as L = T^−0.5(T − S)T^−0.5, where T is diagonal matrix with element $t_{ii}={\sum }_{j=1}^{83}{S}_{ij}\mathrm{for}i=1,...,83$. The k (number of clusters) eigenvectors corresponding to the k smallest eigenvalues of L can be regarded as the feature vectors for all the subjects in the lower-dimensional space.

We set the number of clusters k equal to three based on Ding`s observation in his study [4]. By doing this, all the subjects are projected onto a sphere in R<sup>3</sup>. Subsequently, k-means clustering [13] is applied to divide subjects into three groups. Considering both brain hemispheres, six groups in total are generated. Since the k-means algorithm is randomly initialized, and may yield different partitions, we repeat k-means clustering 20 times and choose the partition with the highest average generalized DSC between the warped template segmentation and the subject`s segmentation (will be discussed in Sect. 3.3) to be the final partition.

3.2 Unbiased Population Averaging and Surface Mesh Generation

For each group, an unbiased population template is constructed from the multi-label segmentations by applying the iterative unbiased template building algorithm [14] and implementing the shape averaging approach in [16]. The metric optimized in this step during the subject-template registration is the same as the pairwise registrations above. Within each group, we choose the segmentation that is most similar to the others in its group (based on the pairwise similarity matrix) as the initial template to guide the template building process. The posterior probability maps for all the seven labels in the template space are used to vote to get the template segmentation.

For each group, a surface mesh is then generated for the union of the ERC, BA35 and BA36 labels, which are the structures of interest in this paper. As shown in Fig. 1 (d) and (e), the surface mesh is much smoother than the multi-atlas segmentation.

3.3 Thickness Measurement

Surface meshes are then warped back to the space of each subject using the corresponding diffeomorphic field computed in the template building step. Using this smooth surface approximation of the previous blocky labels (Fig. 1d,e), regional thickness can be computed by extracting the pruned Voronoi skeleton of the smooth mesh [17] and measuring the distance between each surface vertex and the closest point on the pruned Voronoi skeleton.

To measure how faithful the smooth template-based mesh approximation is to the input segmentations, we compute the average DSC between the multi-atlas segmentation of each subject and the segmentation obtained by warping the corresponding template’s segmentation into the space of the subject.

4 Experiments and Results

4.1 Volumetric and Thickness Measurements

We apply our method to the clinical dataset in Sect. 2 and measure the discriminative ability of the thickness measured obtained using the proposed “three-group” (TG) approach to three quantitative measures. As the first alternative, we measure thickness using a “single-group” (SG), which assigns all the subjects in each hemisphere to the same group, and thus does not account for PRC anatomical variation. As additional comparison measures, we (a) compute the normalized volume (volume of structure divided by its length of segmentation in the anterior-posterior direction) for ERC, BA35 and BA36 for both hemispheres directly from the multi-atlas segmentation and (b) extract a cortical thickness map from the T1-weighted MRI using an established method [9], and integrate this map over the ERC, BA35 and BA36 labels, which are first mapped into the space of the T1-weighted MRI using rigid registration.

4.2 Results

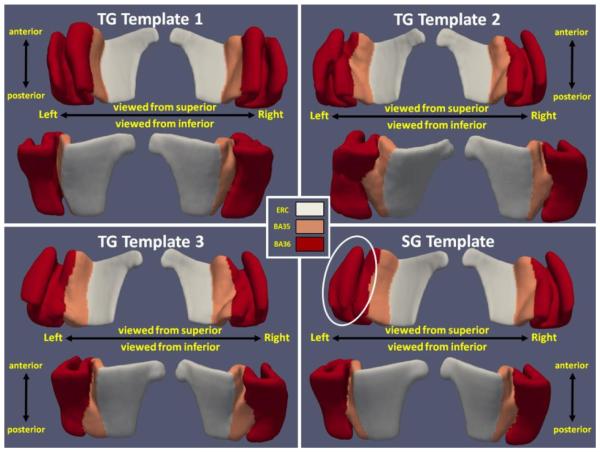
Among the 83 subjects, 30, 20 and 33 of them were clustered into group 1, 2 and 3 separately for the left hemisphere. On the right, the number of subjects in group 1, 2 and 3 are 26, 26 and 31 respectively. Fig. 2 shows the smooth meshes for all the six templates (three per hemisphere) from the TG approach. Group 1 templates resemble the continuous CS variant. Discontinuous CS is observed in group 2 and 3 which differ, as expected, by the relative length of the anterior and posterior CS (i.e. anterior CS is shorter in group 2 while it is longer in group 3). This indicates spectral clustering is able to automatically identify the three anatomical variants [7]. Fig. 2 also shows the meshes for SG, which look like a blend of the three meshes from TG. The odd shape of BA36 of the left SG template (indicated by the white circle in SG templates) is likely the result of ignoring the anatomical variation. The shapes of the templates indicate that a single template is limited in its ability to represent all subject segmentations well.

Fig. 2.

Left and right surface meshes for SG and TG approaches viewing from superior and inferior. White circle shows the odd shape at the left SG template.

To evaluate this in a more quantitative way, we compute the average DSC for ERC, BA35, BA36 and CS between the warped template segmentation and subject`s segmentation in the space of each subject, which are shown in Table 1. As can be observed, the TG approach yields higher overlap for all the labels except ERC. Note the dramatic increase in CS overlap, which indicates the warped meshes are better able to represent the segmentation using the TG approach. Another observation is the overlap remains almost the same for ERC. This demonstrates that TG approach does not degrade the measurement accuracy for a relatively consistent adjacent structure.

Table 1.

Average for ERC, BA35, BA36 and CS between warped template segmentation and subject`s automatic segmentation using “single-group” (SG) and “three-groups” (TG) approaches (computed in subject space)

	Left Hemisphere				Right Hemisphere
	ERC	BA35	BA36	CS	ERC	BA35	BA36	CS
SG	0.983 (± 0.005)	0.954 (± 0.015)	0.934 (± 0.022)	0.591 (± 0.151)	0.982 (± 0.010)	0.948 (± 0.014)	0.962 (± 0.016)	0.666 (± 0.123)
TG	0.983 (± 0.005)	0.965 (± 0.016)	0.959 (± 0.018)	0.803 (± 0.082)	0.983 (± 0.010)	0.958 (± 0.010)	0.970 (± 0.012)	0.749 (± 0.133)

To further evaluate the proposed technique`s performance in clinical applications, we fit a general linear model to the thickness measurements with group membership, age, and intracranial volume as covariates, and report the t-statistic for the NC-MCI contrast. We also perform ROC analysis to the outputs of the four measurement approaches and report area under the curve (AUC) for group discrimination between MCI and NC groups. Intracranial volume is computed the same way as that in [6]. The thickness for each label is computed by integrating thickness value for all the vertices on the surface mesh belong to that label. The results are shown in Table 2.

Table 2.

Statistical analysis results for the four measurements conducted in this paper

Label	Measurement	Left Hemisphere			Right Hemisphere
		T-test	P-value	AUC	T-test	P-value	AUC
ERC	T1 Thickness	2.34	0.022	0.61	2.23	0.029	0.61
	Volume	2.64	0.0099	0.67	1.22	0.23	0.58
	SG Thickness	2.99	0.0037	0.66	2.75	0.0073	0.67
	TG Thickness	3.36	0.0012	0.68	2.73	0.0078	0.66
BA35	T1 Thickness	2.19	0.031	0.63	1.95	0.055	0.66
	Volume	4.46	2.6e-5	0.77	1.91	0.060	0.64
	SG Thickness	5.39	6.8e-7	0.82	2.31	0.023	0.67
	TG Thickness	5.58	3.1e-7	0.83	2.32	0.023	0.65
BA36	T1 Thickness	4.01	1.3e-4	0.73	1.44	0.15	0.60
	Volume	3.18	0.0021	0.68	−0.01	0.99	0.49
	SG Thickness	2.96	0.0040	0.67	0.70	0.49	0.55
	TG Thickness	3.32	0.0014	0.67	1.27	0.21	0.58

From Table 2, it can be observed that SG and TG demonstrate stronger effects in distinguishing the two groups in ERC and BA35 (especially left BA35). However, thickness measurement using T1-weighted MRI turns out to be the best performer for BA36. Importantly, based on the work of Braak and Braak [2], as well as others, greater discrimination in ERC and BA35 is more biologically plausible given the earlier and greater neurofibrillary tangle pathology in these regions than BA36 [1]. Poorer performance in BA36 of SG and TG may result from poorer localization in the T1 approach. Overall, the results of SG and TG are more consistent with the known early pathology of this region in AD [1]. Comparing to SG, which shows relatively good performance, the TG approach, which accounts for anatomic variability, does appear to boost further the statistical power of thickness measurement. Another interesting observation is the left-right asymmetry in PRC, which shows up regardless of how we analyze the data (volumetry vs. thickness, T1 vs. T2) and might be explained by a bias towards verbal memory deficits in the MCI cohort.

5 Conclusion

In this paper, we proposed a novel automatic clustering and thickness measurement pipeline for PRC based on automatic segmentation. For evaluation, we applied our technique to dataset of patients with MCI, often enriched in individuals with prodromal AD, and NC adults. The comparison between the surface meshes for TG and SG approaches demonstrates that group partitioning is a critical step to deal with anatomical variation within PRC, a key for accurately measuring thickness based on automatic segmentation. The statistical analysis supports the notion that the TG approach enhances power of discrimination between MCI and NC adults compared to volumetric measurement, the SG approach, and thickness measurement based on T1-weighted scans. As such, this method may have important utility in the early diagnosis and monitoring of AD, as well as providing accurate measurements to enhance brain-behavior studies of these regions.