Domain generality vs. modality specificity: The paradox of statistical learning

Abstract

Statistical learning is typically considered to be a domain-general mechanism by which cognitive systems discover the underlying distributional properties of the input. Recent studies examining whether there are commonalities in the learning of distributional information across different domains or modalities consistently reveal, however, modality and stimulus specificity. An important question is, therefore, how and why a hypothesized domain-general learning mechanism systematically produces such effects. We offer a theoretical framework according to which statistical learning is not a unitary mechanism, but a set of domain-general computational principles, that operate in different modalities and therefore are subject to the specific constraints characteristic of their respective brain regions. This framework offers testable predictions and we discuss its computational and neurobiological plausibility.

The promise of statistical learning

Humans and other animals are constantly bombarded by streams of sensory information. Statistical learning (SL)—the extraction of distributional properties from sensory input across time and space—provides a mechanism by which cognitive systems discover the underlying structure of such stimulation. SL therefore plays a key role in the detection of regularities and quasi-regularities in the environment, results in discrimination, categorization and segmentation of continuous information, allows prediction of upcoming events, and thereby shapes the basic representations underlying a wide range of sensory, motor, and cognitive abilities.

In cognitive science, theories of SL have emerged as potential domain-general alternatives to the influential domain-specific Chomskyan account of language acquisition ([1], see also [2] for related claims). Rather than assuming an innate, modular, and neurobiologically hardwired human capacity for processing linguistic information, SL, as a theoretical construct, was offered as a general mechanism for learning and processing any type of sensory input that unfolds across time and space. To date, evidence for SL have been found across an array of cognitive functions, such as segmenting continuous auditory input [3], visual search [4], contextual cuing [5], visuomotor learning [6], conditioning (e.g., [7]), and in general, any predictive behavior (e.g., [8,9]).

In this paper, we propose a broad theoretical account of SL, starting with a discussion of how a domain-general ability may be subject to modality- (see glossary) and stimulus-specific constraints. We define ‘learning’ as the process responsible for updating internal representations given specific input and encoding potential relationships between them, thereby improving the processing of that input. Similarly, ‘processing’ is construed as determining how an input to a neural system interacts with the current knowledge stored in that system to generate internal representations. Knowledge in the system is thus continuously updated via learning. Specifically, we take SL to reflect updates based on the discovery of systematic regularities embedded in the input, and provide a mechanistic account of how distributional properties are picked up across domains, eventually shaping behavior. We further outline how this account is constrained by neuroanatomy and systems neuroscience, offering independent insights into the specific constraints on SL. Finally, we highlight individual differences in abilities for SL as a major, largely untapped source of evidence for which our account makes clear predictions.

Domain generality versus domain specificity

Originally, domain generality was invoked to argue against language modularity; its definition therefore implicitly implied “something that is not language specific”. Consequently, within this context, “domain” implies a range of stimuli that share physical and structural properties (e.g., spoken words, musical tones, tactile input), whereas “generality” is taken to be “something that does not operate along principles restricted to language learning”. Note, however, that this approach says what domain generality is not, rather than saying what it is (e.g., [10]). More recent accounts of SL ascribe domain generality to a unitary learning system (e.g., [11]), that executes similar computations across stimuli (e.g., [12]), and that can be observed across domains (e.g., [13]), and across species (e.g., [14,15]).

As a theoretical construct, SL promised to bring together a wide range of cognitive functions within a single mechanism. Extensive research over the last decade has therefore focused on mapping the commonalities involved in the learning of distributional information across different domains. From an operational perspective, these studies investigated whether overall performance in SL tasks is indeed similar across different types of stimuli [16], whether there is transfer of learning across domains (see Box 1), whether there is interference between simultaneously learning of multiple artificial grammars (e.g., [17]) or from multiple input streams within and across domains [18], or whether individual capacities in detecting distributional probabilities in a variety of SL tasks are correlated ([19]).

The pattern of results across these different studies is intriguingly consistent: contrary to the most intuitive predictions of domain-generality, the evidence persistently shows patterns of modality specificity and sometimes even stimulus specificity. For example, studies of artificial grammar learning (AGL, see Glossary) systematically demonstrate very limited transfer of learning across modalities, if at all (e.g., [20,21]). Similarly, the simultaneous learning of two artificial grammars can proceed without interference once they are implemented in separate modalities [17]. Modality specificity is also revealed by qualitative differences in patterns of SL in the auditory, visual, and tactile modalities [16], sometimes with opposite effects of presentation parameters across modalities [22]. To complicate matters even further, SL within modality reveals striking stimulus specificity, so that no transfer (and conversely, no interference) occurs within modality provided the stimuli have separable perceptual features (e.g., [17,23]). Finally, although performance in SL tasks displays substantial test-retest reliability within modality, there is no evidence of any correlation within individuals in their capacities to detect conditional probabilities across modalities and across stimuli (Siegelman & Frost, unpublished). This contrasts with what might be expected if SL was subserved by a unitary learning system: that individual variation in its basic function would manifest itself in at least some degree of correlation across different SL tasks. If not, its unitary aspect remains theoretically empty because it does not have an empirical reality in terms of specific testable predictions. Taken together, these studies suggest that there are independent modality constraints in learning distributional information [16], pointing to modality specificity, and further to stimulus specificity akin to perceptual learning [24].

Whereas this set of findings is not easy to reconcile with the notion of a unitary, domain-general system for SL, it does not necessarily invalidate the promise of SL to provide an overarching framework underlying learning across domains. Instead, what is needed is an account of SL that can explicate the manifestations of domain-generality in distributional learning with the evidence of its modality- and stimulus-specificity, restricted generalization, little transfer, and very low correlations of performance between tasks within individuals. More broadly, any general theory of learning that aims to describe a wide range of phenomena through a specific set of computational principles has to offer a theoretical account of how and why transfer, discrimination, and generalization take place, or not.

Towards a mechanistic model of SL

Our approach construes SL as involving a set of domain-general neurobiological mechanisms for learning, representation, and processing that detect and encode a wide range of distributional properties within different modalities or types of input (see [13], for a related approach). Crucially, though, in our account, these principles are not instantiated by a unitary learning system but, rather, by separate neural networks in different cortical areas (e.g., visual, auditory, and somatosensory cortex). Thus, the process of encoding an internal representation follows constraints that are determined by the specific properties of the input processed in the respective cortices. As a result, the outcomes of computations in these networks are necessarily modality specific, despite multiple cortical and subcortical regions invoking similar sets of computational principles and some shared brain regions (e.g., Hebbian learning, reinforcement learning; for discussion, see [25,26]).

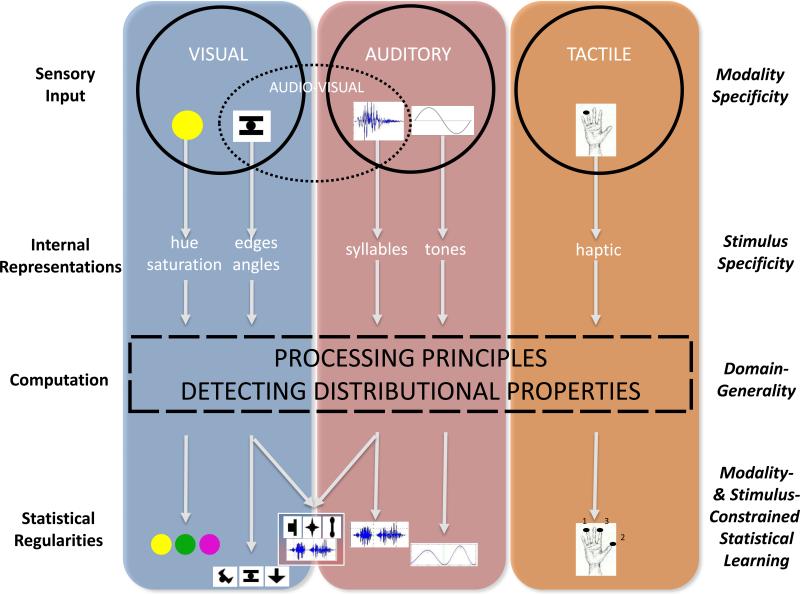
For example, the auditory cortex displays lower sensitivity to spatial information but enhanced sensitivity to temporal information, whereas the visual cortex displays enhanced sensitivity to spatial information, but lower sensitivity to temporal information (e.g., [27,28]). Iconic memory is short-lived (scale of ms), whereas echoic memory lasts significantly longer (scale of seconds; e.g., [29]). Because auditory information unfolds in time, the auditory cortex must be sensitive to the temporal accumulation of information in order to make sense of the input. In contrast, visual information is instantaneous, and although temporal integration is necessary in some cases such as in deciphering motion, the visual cortex is relatively less sensitive to temporal accumulation of information over extended periods of time. These inherent differences are reflected in the way the sensory input eventually is encoded into internal representations for further computation. Moreover, within modality, encoding of events displays graded stimulus specificity given their complexity, similarity, saliency, and other factors related to the quality and nature of the input (see [30,31], for evidence in visual SL). For example, participants are able to learn two separate artificial grammars simultaneously in the visual domain when the stimuli are from separate perceptual dimensions—such as color and shape—but not when they are from within the same perceptual dimension [16]. Figure 1 represents a schematic account of our approach and shows how the same learning and representation principles result in modality and stimulus specificity because they are instantiated in different brain regions, each with their characteristic constraints.

Figure 1. Theoretical Model of Statistical Learning.

Schematic representation of the processing of distributional information in the visual, auditory, and somatosensory cortex, for unimodal and multimodal events. Different encoded representations of continuous input presented in time or space result in task-stimulus specificity, in spite of similar computations and contributions from partially shared neurocomputational networks.

Note that modality-specific constraints do not preclude the neurobiological ability to process multimodal events. Indeed, this has recently been shown within SL using the McGurk effect (see Glossary) in a cross-modal segmentation study [32]. More generally, perception of the world routinely involves multisensory integration (e.g., [33]), occurring at both low levels (i.e., the thalamus, [34]; the dorsal cochlear nucleus, [35]) and higher levels of cortical processing (e.g., anterior temporal poles; [36]). Critically, however, each of these multimodal areas would be subject to its own distinct set of constraints, which would not necessarily be the same as those from the unimodal regions that feed into it or to the constraints in other multimodal areas. For example, coherence in the timing at which an auditory and a visual stimulus unfold is important for specific types of integration [18] in audio-visual brain areas [37], but not as important for detecting regularities in the case of integrating two different visual representations in the visual system. Note that this view is distinct from alternative accounts suggesting that a unitary learning mechanism operates on “abstract” amodal representations (e.g., [38]; see Glossary). Instead, we suggest that multimodal regions are shaped by their own distinct sets of constraints.

This brings us to an operational definition of ‘domain generality’. Within our framework, domain generality primarily emerges because neural networks across modalities instantiate similar computational principles. Moreover, domain generality may also arise either through the possible engagement of partially-shared neural networks that modulate the encoding of the to-be-learned statistical structure [39], or if stimulus input representations encoded in a given modality (e.g., visual or auditory) are fed into a multi-modal region for further computation and learning. As we shall see next, the current neurobiological evidence is consistent with both of these latter possibilities.

The neurobiological bases of SL

Recent neuroimaging studies have shown that statistical regularities of visual shapes results in activation in higher-level visual networks (e.g., lateral occipital cortex, inferior temporal gyrus; [40,41]), whereas statistical regularities in auditory stimuli result in activation in analogous auditory networks (e.g., left temporal and inferior parietal cortices; frontotemporal networks including portions of the inferior frontal gyrus, motor areas involved in speech production, [42]; and the pars opercularis and pars triangularis regions of the left inferior frontal gyrus; [43]). Since these studies contrasted activation for structured vs. random blocks of stimuli, the stronger activation for structured stimuli in the above ROIs is consistent with the notion that some SL occurs already in brain regions that are largely dedicated to processing unimodal stimuli, thus allowing for modality-specific constraints to shape the outcome of computations.

In addition to identifying modality-specific learning mechanisms, imaging and ERP studies point to some brain regions that are active regardless of the modality in which the stimulus is presented. Often, this work has associated SL effects with the hippocampus, and more generally with the medial temporal lobe (MTL) memory system (see, e.g., [44]). This is consistent with considerable systems neuroscience work that has established the hippocampus as a locus for encoding and binding temporal and spatial contingencies presented in multiple different modalities [40,44–48], as well as for consolidation of representations.

Hippocampal involvement in SL could consist of indirect modulation of the representations in sensory areas or direct computations on hippocampal representations that are driven by sensorimotor representations (see [48] for a discussion). Note, however, that even in the case of direct hippocampal computations, the computed representations are not necessarily amodal, as traces of their original specificity nevertheless remain (e.g., [49]). Sub-regions of the hippocampus have been shown to send and receive different types of information from different brain regions, while developing specialization for representing those different types of information [50]. In addition, representations within the hippocampus itself are typically sparse, and are wired to be maximally dissimilar even when stimuli evoke similar activation in a given sensorimotor region [51–54]. Thus, even with a direct hippocampal involvement in SL, such computations would likely result in a high degree of stimulus specificity, as observed across many SL studies.

Additional imaging work has identified regions of the basal ganglia [55] and thalamus [42,56] as important collaborating brain regions that work with the MTL memory system to complete relevant sub-tasks involved in statistical learning. For instance, the thalamus may provide synchronizing oscillatory activity in the alpha-gamma and theta-gamma ranges that enables the rapid and accurate encoding of sequences of events [56]. Thus, as summarized in Figure 2, the current neurobiological evidence indeed suggests that detection of statistical regularities emerges from local computations carried out within a given modality, and through a multi-domain neurocognitive system that either modulates or operates on inputs from modality-specific representations. Whether unimodal computations are necessary or sufficient for SL, remains an open question. Whereas some studies report no learning following hippocampal damage [44], other report significant SL in spite of such damage (e.g., [57]). In this context we should note, that lack of SL cannot be unequivocally attributed to neurobiological impairment. Many normal participants do not show SL even with an intact MTL system (see, for example, performance of a subset of the control participants observed by [44], who do not fare better than the specific reported patient). This leads us to our next section on individual differences.

Figure 2. Key Neural Networks involved in Visual and Auditory Statistical Learning.

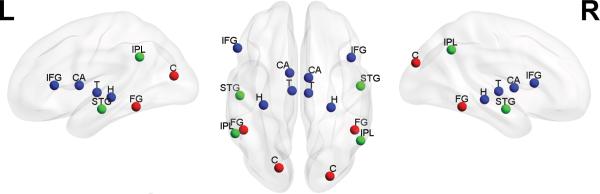
Key brain regions associated with domain-general (blue), and lower- and higher-level auditory (green) and visual (red) modality-specific processing and representation, plotted on a smoothed ICBM152 template brain. The depicted regions are not intended to constitute an exhaustive set of brain regions subserving each domain. C = Cuneus, FG = Fusiform Gyrus, STG = Superior Temporal Gyrus, IPL = Inferior Parietal Lobule, H = Hippocampus, T = Thalamus, CA = Caudate, IFG = Inferior Frontal Gyrus. Generated with the BrainNet Viewer [89].

Individual and group differences in SL

The proposed framework leads us to argue that individual differences provide key evidence for understanding the mechanism of SL. In past work, it has often been assumed that individual variance in implicit learning tasks is significantly smaller than that of explicit learning (e.g., [58]). Consequently, the source of variability in performance in SL has been largely overlooked, and had led researchers to focus on average success rate (but see [19,59–61]).

In the context of SL, however, measures of central tendency can be particularly misleading, as often about one third of the sample or more is not performing the task above chance level (e.g., [12,60,61]). Moreover, tracking individual learning trajectories throughout the phases of a given SL task has recently suggested that there is a commensurate high level of variability in the learning curves of different individuals (e.g., [43,61]). In several areas of cognitive science, it is now well established that understanding the source of individual differences holds the promise of revealing critical insight regarding the cognitive operations underlying performance, leading to more refined theories of behaviour. Furthermore, a theory that addresses individual differences should aim to explain how learning mechanisms operate online to gradually extract statistical structure, as opposed to focusing strictly on the outcome of a learning phase in a subsequent test (e.g., [62]).

As a first approximation, our theoretical model splits the variance across individuals into two main sources. First, as indicated by Figure 1, there is the variance related to efficiency in encoding representations within modality in the visual, auditory, and somatosensory cortex. This variance could derive from individual differences in the efficacy of encoding fast sequential inputs or complex spatial stimuli, and thus potentially could be traced to the neuronal mechanisms that determine the effective resolution of one's sensory system. The second variance relates to the relative computational efficiency of processing multiple temporally and spatially encoded representations and detecting their distributional properties. This variance potentially could be traced to cellular- and systems-level differences in factors that include (but are not limited to) white matter density, which have been shown to affect AGL performance [63], and variation in the speed of changes in synaptic efficacy [64]. In modeling terms, these factors would relate to parameters such as connectivity, learning rates, and the quality and type of information to be encoded and transmitted by a given brain region (see Box 2).

The advantage of this approach is that it offers precise and testable predictions that can be empirically evaluated. Thus, individuals can display relatively increased sensitivity in encoding auditory information, but a relative disadvantage in encoding sequential visual information. Conversely, two individuals that have similar efficiency in terms of representational encoding in a given modality could differ in their relative efficiency in computing the distributional properties of visual or auditory events. In either case, low correlation in performance within individuals in two SL tasks, would be the outcome, as has been reported in recent studies (e.g., [19]). However, as exemplified in Box 3, accurate individual trajectories of SL can in principle be obtained by employing parametric designs that independently target the two sources of variance.

Individual differences are particularly intriguing given recent claims regarding developmental invariance in some types of SL (e.g., [65]). If SL capacities per se do not change, and brain maturation and experience are primarily driving improvements in processes “peripheral” to SL such as attention, then the bulk of variability in individual developmental trajectories in SL abilities should be explained by these peripheral factors only. We believe that the current empirical support for this claim is limited (see [66] for a discussion). Further progress, however, requires a better fundamental understanding of individual differences in SL, as elaborated in Box 3.

Summary and conclusions

The present paper offers a novel theoretical perspective on SL that considers computational and neurobiological constraints. Previous work on SL offered a possible cognitive mechanistic account of how distributional properties are computed, with explicit demonstrations being provided only within the domain of language [65,67]. The perspective we offer has the advantage of providing a unifying neurobiological account of SL across domains, modalities, neural and cognitive investigations, and cross-species studies, thus connecting with and explaining an extensive set of data. The core claim of our framework is that SL reflects contributions from domain-general learning principles that are constrained to operate in specific modalities, with potential contributions from partially shared brain regions common to learning in different modalities. Both of these notions are well grounded in neuroscience. Moreover, they provide our account with the flexibility needed to explain the apparently contradictory SL phenomena observed both within and between individuals, such as stimulus and modality specificity, while still being constrained by the capacities of the brain regions that subserve the processing of different types of stimuli. In addition to descriptive adequacy, our approach also provides targeted guidance for future investigations of SL via explicit neurobiological modeling and studies of the mechanics underlying individual differences. We therefore offer our framework as a novel platform for understanding and advancing the study of SL and related phenomena.

BOX 1: Generalization and transfer in statistical learning.

A key aspect of learning is to be able to apply knowledge gained from past experiences to novel input. In some studies of SL, for example, participants are first presented with a set of items generated by a pre-defined set of rules, and then in a subsequent test phase asked to distinguish unseen items generated by these rules (i.e. “grammatical items”) from another set of novel items that violate these rules (i.e. “ungrammatical items”). If they are able to correctly classify the unseen items as “grammatical” or “ungrammatical” at above chance levels, generalization from seen items to the novel exemplars is assumed.

Many scientists initially interpreted successful generalization as evidence that the participants had acquired the rules used to generate the stimuli and applied them to the novel stimuli. However, several studies have shown that participants’ performance at test can be readily explained by sensitivity to so-called “fragment” information, consisting of distributional properties of subparts of individual items [16]. Consider a hypothetical novel test item, ABCDE, which consists of various bigram (AB, BC, CD, DE) and trigram (ABC, BCD, CDE) fragments. The likelihood of a participant endorsing this test item as grammatical will depend on how frequently these bigram and trigram fragments have occurred in the training items. If a test item contains a fragment that has not been seen during training, then participants will tend to reject that item as ungrammatical (see [68]) . Thus, generalization in SL is often, if not always, driven by local stimulus properties and overall judgements of similarity, rather than the extraction of abstract rules.

Another possible way in which past learning could be extrapolated to new input is through the transfer of regularities learned in one domain to another (e.g., from visual input to auditory input). Although early studies appeared to support cross-modal transfer (e.g., [58,69]), more recent studies have shown that there is little, or no evidence for transfer effects, once learning during test based on repetition or simple fragment information is taken into account (e.g., [20,21,70]).

Generalization and transfer significantly differ in their contribution to theories of learning. Whereas generalization has been demonstrated in SL studies—which is important for the application of SL to language—there is little evidence of cross-modal transfer, likely because of the substantial differences in neurobiological characteristics of the visual, auditory and somatosensory cortices.

BOX 2: Advancing SL Theory via Computational Modeling.

Computational modeling serves an important dual role in both providing a quantitative account of observed empirical effects as well as the means to generate novel predictions that can guide empirical research (see, e.g., [67,71,72]). Within our framework, such modeling should reflect the relevant neural hardware of sensory cortices (e.g., different time-courses for iconic vs. echoic memory), as well as advances related to what and how the neural networks track distributional properties [40,56,73]. It should also make direct contact with neural measures as opposed to focusing strictly on behavioral measures that reflect the end-state of processing (for related discussion, see [72,74,75]).

The development of explicit models allows for the parametric variation of different aspects of the SL system, including the contributions of different learning mechanisms (e.g., Hebbian learning, reinforcement learning), different brain regions (e.g., the MTL system and modality specific areas), as well as of the quality and nature of the representations in different parts of the system (Figure I). This allows the probing of the model's ability to account not only for group-averaged effects, but also for individual differences (see Box 3; [76]), and establish how and why variation in parameters affecting different aspects of the system modulate overall performance.

Recent advances in “deep” neural networks have also enabled interesting insights into the effects of allowing intermediate representations to emerge as a function of learning [77,78], as opposed to being explicitly stipulated. This relates directly to the issues of modality and stimulus specificity that currently challenge SL theories. For instance, representations closer to the sensory cortices are learned earlier and are more strongly shaped by the specific characteristics of individual stimuli. This contrasts with higher-order (but possibly modality specific) areas that operate on these early sensory representations, and which can detect commonalities in higher-order statistics despite little similarity in the surface properties or lower-order statistical relationships amongst the stimuli (for related work using a Bayesian approach, see [79]). This predicts that SL tasks that involve stimuli whose relationships are only detectable in higher-order statistics should be more likely to show at least some generalization relative to early sensory regions, which are predicted to exhibit stronger stimulus-specificity (for a related proposal see [80]). For instance, the purpose of some brain regions is primarily to distinguish between highly-similar complex inputs (e.g., visual expertise areas such as the putative fusiform face area; [81]), or to transmit similar outputs to multiple brain regions regardless of the source of its input (e.g., the semantic memory system; [82]). Such a model is also able to account for stimulus specificity in some higher-order domains and to predict the possibility of generalization in others.

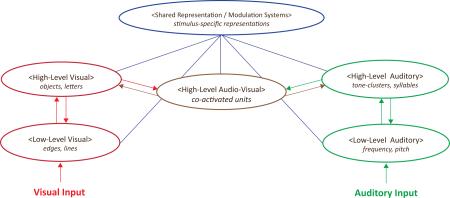
Box 2 - Figure I – Candidate computational architecture for explaining and predicting the neural and behavioural data pertaining to statistical learning

Depiction of candidate SL model architecture. In this model, visual and auditory sensory input are first encoded and processed in pools of units (neurons) that code for low-level sensory features (e.g., sound frequency, edge orientation). These pools then project to higher-level visual and auditory areas which are better suited for detecting higher-order statistics and developing more sophisticated representations (e.g., of objects or syllables). Bimodal representations may also be learned in an area that receives inputs from both modalities. All of these modality-specific and bimodal areas also project to and receive feedback from shared representation and memory modulation systems. Arrows denote connections that send representations from one pool to another; blue lines denote connections that can either send representations, modulate processing, or both. Note that this figure is not intended to be exhaustive: other representations (e.g., low-level audio-visual) are assumed to be part of a more complete model, as is the coding of more detailed sensory information inputs (e.g., color, shape, movement, taste, smell).

BOX 3: Mapping individual trajectories in statistical learning.

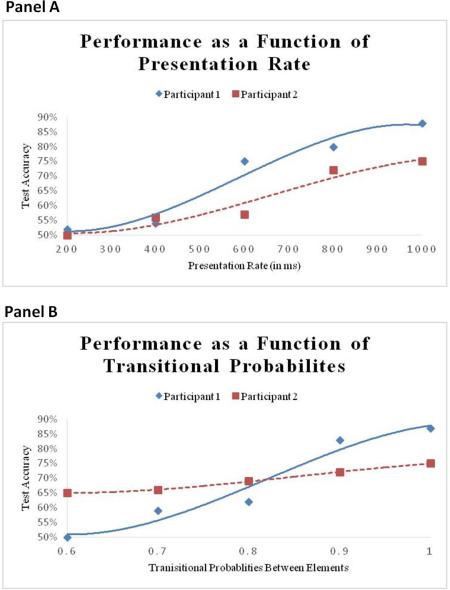
The present theoretical approach outlines a methodology for investigating individual performance in SL tasks by orthogonally manipulating the experimental parameters hypothesized to affect encoding efficacy on the one hand, and parameters related to efficiency in registering distributional properties, on the other. In general, manipulations that center on input encoding parameters (temporal rate of presentation, number of items in a spatial configuration, stimuli complexity, saliency of distinctive features, boundary information, etc.), will probe individual abilities in encoding stimuli in a given modality. In contrast, manipulations that center on transitional probabilities (i.e., the likelihood of Y following X, given the occurrence of X), level of predictability of events, type of statistical contingencies (e.g., adjacent or non-adjacent), or the similarity of foils to targets in the test phase, will probe the relative efficiency of a person's computational ability for registering distributional properties (see [6] for manipulation of transitional probabilities in an SRT (Serial Reaction Time) task). Such parametric experimental designs would reveal, for any given individual, a specific pattern of interactions of two main factors driving SL, outlining how their joint contribution determines his or her performance on a specific task.

Figure I presents hypothetical plots of the performance of two possible individuals in such parametric manipulations. The figure demonstrates differential trajectories of individual sensitivities to either type of manipulation, one that probes stimulus encoding efficacy (manipulating inter-stimulus intervals), and one that probes inter-stimulus statistic encoding efficiency (manipulating transitional probabilities). This experimental approach has the additional promise of revealing systematic commonalities or differences in sensitivity to various types of distributional properties across domains or modalities.

A possible extension of this line of research would incorporate the impact of prior knowledge on SL. The process of encoding representations of any continuous input is dependent on the characteristics of the representational space that exist at a given time point for a given individual. Thus, encoding an input of continuous syllabic elements (e.g., [12]) is different than encoding a sequence of non-linguistic novel sounds (e.g., [83]), affecting SL efficacy. This could generate significant individual differences in SL in domains such as language, where individuals differ significantly in their linguistic representations (e.g., vocabulary size, number of languages spoken).

Note that most current research on individual differences in SL focuses on predicting general cognitive or linguistic abilities from performance in SL tasks [19,59–61,84,85] or showing similar neural correlates within subjects for SL and language [86,87]. Investigating the various facets of performance in SL, as outlined above, is a necessary further step to describe and explain the specific sources of potential correlations between SL test measures and the cognitive functions they are aimed to predict. Identifying these sources would, in turn, allow researchers to refine predictions and generate well-defined a priori hypotheses.

Box 3 - Figure I - Predicted empirical results illustrating how stimulus encoding and transitional probability shape individual differences

The two graphs above present hypothetical data from two participants and illustrates how the ability to detect regularities and to encode inputs may be separated experimentally. Panel A demonstrates the manipulation of rate of presentation and shows that whereas Participant 1 performs well even in relatively fast rates, Participant 2 shows no learning when stimuli are presented at or above a rate of one per 600 ms. Panel B displays the manipulation of transitional probabilities. Here the rate of presentation is the same across all 5 tasks, but transitional probabilities vary from 0.6 to 1. The results show that Participant 2, who performs above chance in the test even when the transitional probabilities between elements are low, is more efficient in detecting probabilities than Participant 1.

BOX 4: Outstanding questions.

• To what degree are high-level cognitive SL effects and low-level sensorimotor SL effects modulated by the partially shared SL systems (e.g., hippocampus, basal ganglia, inferior frontal gyrus) versus modality-specific systems?

• Can a better understanding of low-level cellular and systems neurobiology guide theoretical advance by predicting the specific types of information that a brain region will be most suited to encode and, consequently, the types of statistical learning that may take place?

• To what degree does variability in the quality and nature of an individual's modality-specific representations of individual stimuli, and variability in sensitivity to the dependencies between stimuli, explain individual differences in SL experiments?

• To what degree are the modality-specific and partially-shared neural processing systems that underlie SL modulated by experience versus neuronal maturation throughout development?

Highlights.

• Statistical learning (SL) theory is challenged by modality/stimulus-specific effects.

• We argue SL is shaped by both modality-specific constraints and domain-general principles.

• SL relies on modality-specific neural networks and partially-shared neural networks.

• Studies of individual differences provide targeted insights into the mechanisms of SL.

GLOSSARY

Amodal representations

“Amodal” representations are typically taken to be “abstract” in the sense that they are not bound by specific sensory features (e.g., visual or auditory). Apart from the problem of defining a theoretical construct in terms of what it is not, the neurobiological evidence for such representations is scarce.

Artificial Grammar Learning (AGL)

In a typical AGL experiment, participants are exposed to sequences generated by a miniature grammar. Participants are only informed about the rule-based nature of the sequences after the exposure phase, when they are asked to classify a new set of sequences, some of which follow the grammar while others do not. AGL is also considered to be a kind of implicit learning task.

Generalization

Refers to extension of learned statistical structure to unseen stimuli, typically from within the same modality or stimulus domain.

Internal Representation

In neurobiological terms, an internal representation of a stimulus is the pattern of neural activity evoked by a stimulus in a brain region (or network of brain regions).

McGurk effect

The McGurk effect [88] illustrates the potentially complex interactions between two conflicting streams of information from the auditory and visual modalities. For instance, if a video of an individual pronouncing /ga/ is combined with the sound /ba/, a listener will tend to hear /da/ because the sound /da/ is most consistent with the visually-perceived positions of the lips and with the auditorily-perceived sound.

Modality

The sensorimotor mode in which the stimulus was presented (e.g., vision, audition, touch). One modality may contain several sub-modalities (e.g., visual motion, color), each of which is subserved by distinct neuroanatomy.

Multimodal representations

Representations that form when information from two or more modalities are integrated in a representational space and associated brain region (or network of regions). Importantly, these representations are, therefore, not “amodal”.

Transfer

A broader type of extension of learned knowledge than generalization, and refers to the application of learned regularities to novel domains and/or modalities.