Solar drying of whole mint plant under natural and forced convection

Abstract

Two identical prototype solar dryers (direct and indirect) having the same dimensions were used to dry whole mint. Both prototypes were operated under natural and forced convection modes. In the case of the later one the ambient air was entered the dryer with the velocity of 4.2 m s⁻¹. The effect of flow mode and the type of solar dryers on the drying kinetics of whole mint were investigated. Ten empirical models were used to fit the drying curves; nine of them represented well the solar drying behavior of mint. The results indicated that drying of mint under different operating conditions occurred in the falling rate period, where no constant rate period of drying was observed. Also, the obtained data revealed that the drying rate of mint under forced convection was higher than that of mint under natural convection, especially during first hours of drying (first day). The values of the effective diffusivity coefficient for the mint drying ranged between 1.2 × 10⁻¹¹ and 1.33 × 10⁻¹¹ m² s⁻¹.

Introduction

Open air sun drying is the dominant method that is used to preserve agricultural products, in which agriculture plants are directly exposed to solar radiations in an open environment. However, the contamination with dust, soil, sand particles and insects are some problems associated with this method [1,2]. To overcome previous problems, solar drying method could be used to dry agriculture products instead of traditional sun drying method as the drying process takes place in enclosed structures [3]. Utilization of solar energy as a reliable energy source to dry foods in Egypt has a great potential, as, the annual daily average solar radiation on a horizontal plane in Egypt is 8 kW m⁻² day⁻¹ and the measured annual average daily sunshine duration is approximately 11 h [4].

Mint is a genus of the Labiatae family, which comprises a wide number of species, varieties and hybrids. It helps in colds, flu, fever, poor digestion, motion sickness, food poisoning and for throat and sinus ailments [5–7]. Mint as flavoring agent is coming after vanilla and citrus flavors over the world [8].

Several researches have investigated the drying kinetics of mint leaves and evaluated various mathematical models to describe thin layer drying characteristics [5,6,9,10]. The best drying models to explain thin layer drying behavior of mint leaves under different drying methods were Wang and Singh model [9], logarithmic model [6] and Midilli and Kucuk model [5,10].

However, the literature is scarce on the drying kinetics of mint as a whole plant. Müller et al. [11] found that, the drying of whole mint in greenhouse solar dryer from initial moisture content of 80% (w.b.) to final moisture content of 10% (w.b.) took 3 days. Lebert et al. [12] examined the effect of drying conditions (air temperature, humidity and air velocity) on drying kinetics of mint, and they concluded that, the drying air temperature was the main factor in controlling the rate of drying. The effect of the drying temperature schemes on the drying kinetics of chopped mint in a rotary dryer was investigated by Tarhan et al. [13]. They found that, the drying durations were decreased from 15 to 18 h for constant temperature profile to 12–15 h when rectangular wave-shaped temperature profiles were used.

As mentioned above, the literature is scarce on the drying kinetics of the solar drying of mint as a whole plant. Besides, most previous studies used small amounts in their investigations. So, this study was carried out to study the drying kinetics of mint as a whole plant using pilot scale solar dryers considering the effect of solar dryer type (direct and indirect) and drying air flow mode. In addition, ten mathematical models were used to fit the drying curves of mint. Finally, the effective diffusivity of drying of mint was calculated.

Material and methods

Drying experiments

Fresh mint was purchased at a local market in Giza, Egypt. Before drying, the foreign materials, as weeds, spoiled and discolored plants were removed. Drying experiments were carried out using direct and indirect prototype solar dryers. The two prototypes are constructed from wood frames and have the same dimensions as shown in Figs. 1 and 2. The direct prototype solar dryer was covered by transparent polyethylene film; while black polyethylene film was used to cover the indirect prototype solar dryer. Each dryer has six perforated galvanized steel trays with the dimension of 1.00 × 0.90 × 0.04 m, and the spacing between them was 0.12 m. Each tray was loaded with 1.2 kg of fresh whole mint, which was spread as a single thin layer. The two prototypes were installed on the roof of the Department of Food Science and Technology building, Faculty of Agriculture, Cairo University, Giza (latitude of 30°00N and longitude of 31°10E).

Fig. 1.

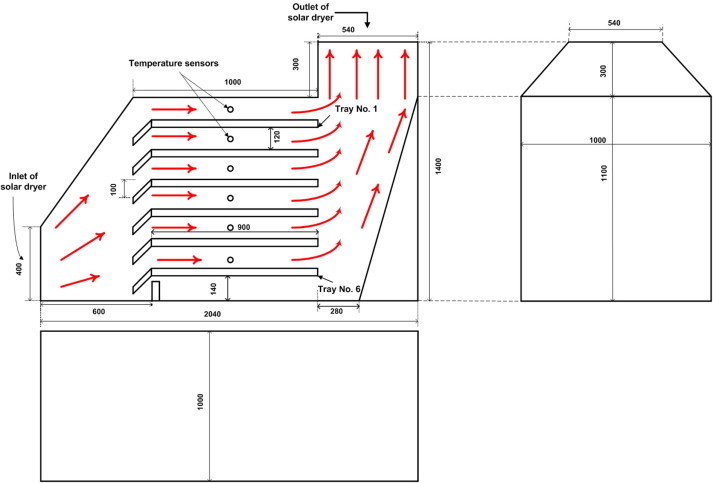
A diagram of the solar dryer (dimensions in mm – the bold arrows refer to air streamlines).

Fig. 2.

Photograph of the direct solar dryer.

The experimental data were manually recorded every 2 h from 10 a.m. to 6 p.m. over two days, except forced convection drying runs which were started at 12 noon in the first drying day. Natural convection runs were conducted during 10–11/07/2012, while forced convection runs were conducted during 5–6/08/2012. Both prototypes (the direct and indirect solar dyers) were operated under natural and forced convection. In the forced convection mode, a fan (0.50 m diameter and 0.75 kW) was mounted in the exit channel of each prototype, where the air velocity at the entrance channel of both solar dryers was 4.2 m s⁻¹ as measured. The dryers were shut down during the night, and experimentation was resumed the next day at 10 a.m.

Measurements and calculations

Drying air temperatures in the middle of the dryer, 6-cm above each tray was measured using a calibrated thermocouple (±0.75 °C) (EXTECH, EA15, Taipei, Taiwan), also ambient air temperature was measured with the same instrument. The drying air velocity at the entrance channel of both solar dryers during forced convection runs only was measured using a calibrated hot wire thermo-anemometer (±3%) m s⁻¹) (EXTECH,). A digital balance of XWZ, Shanghai, China (±0.001 kg) was used to measure the mass loss of the product during the drying process. The weight of the goods on each tray was measured by removing the tray outside the dryer for approximately 2 min. The data for the hourly solar irradiance during the drying experiments were obtained from the Central Laboratory for Agricultural Climate, Dokki Meteorological Station, Giza, Egypt. The initial moisture content M_o of mint was determined using the method described in the AOAC [14]. Moisture ratio (MR) was calculated using the following equation:

$$\mathit{MR}=\frac{M-M_e}{M_o-M_e}$$ (1)

where M, M_o and M_e (kgwater/kgmatter) are the moisture content at any time, initial moisture content and equilibrium moisture content, respectively.

The moisture ratio was simplified to Eq. (2) by some investigators [6,15] due to the continuous fluctuation of the relative humidity of the drying air during solar drying. Moreover, Dissa et al. [16] considered that the M_e was relatively small compared to M_o and M and could be neglected.

$$\mathit{MR}=\frac{M}{M_o}$$ (2)

The drying rate, (kg/h), was determined using the following equation:

$$\text{Drying rate}(\text{kg}/\text{h})=\frac{M_{t+\mathrm{\Delta }t}-M_t}{\mathit{dt}}$$ (3)

where M_t and M_t+Δt (kg water/kg dry matter) are the moisture content at time t (hours) and moisture content at time t + Δt, respectively.

Fitting of drying curves

Ten empirical models were used to fit the drying curves of mint as shown in Table 1. The regression analysis was performed using curve fitting toolbox of MATLAB program version 7.12.0. The goodness of the fit was evaluated according to the values of adjusted coefficient of determination (adjusted R²), as primary criterion, and the values of Root Mean Square Error (RMSE), as secondary criterion. Good fit has values closer to 1 of adjusted R² and lower values of RMSE.

Table 1.

Mathematical models widely used to describe the drying kinetics.

Model No.	Model name	Reference	Model
1	Newton	[17]	MR = exp(−kt)
2	Page	[18]	MR = exp(−ktn)
3	Henderson and Pabis	[8]	MR = a exp(−kt)
4	Logarithmic	[19]	MR = a exp(−kt) + c
5	Two – term	[20]	MR = a exp(−kot) + b exp(−k1t)
6	Two – term exponential	[20]	MR = a exp(−kt) + (1 − a) exp(−kat)
7	Wang and Singh	[19]	MR = 1 + at + bt2
8	Diffusion approach	[15]	MR = a exp(−kt) + (1 − a) exp(−kbt)
9	Verma et al.	[21]	MR = a exp(−kt) + (1 − a) exp(−gt)
10	Modified Henderson and Pabis	[9]	MR = a exp(−kt) + b exp(−gt) + c exp(−ht)

Determination of effective diffusivity coefficient

Fick’s second law (Eq. (4)) is used to describe the drying behavior of any material in the falling rate drying period [6].

$$\frac{\partial M}{\partial t}=D_{\text{eff}}{\mathit{\nabla }}^{2}M$$ (4)

where D_eff is the effective diffusivity, t is time, and ∇ is the one-dimensional nabla squared operator.

The solution of Fick’s second law in slab geometry, with the assumptions of moisture migration being by diffusion, negligible shrinkage, constant diffusion coefficients and constant temperature was as follows [6]:

$$\mathit{MR}=\frac{8}{{\pi }^2}{\displaystyle \sum _{n=1}^{\infty }}\frac{1}{{(2n-1)}^2}\exp \left(\frac{-{(2n-1)}^2{\pi }^2{D}_{\text{eff}}t}{4L^2}\right)$$ (5)

where L is the thickness of the slab in sample and n is the positive integer.

For long drying periods, Eq. (5) can be further simplified to only the first term of the series (n = 1). Using the moisture ratio (MR) from Eqs. (2) and (5) can be written in the following logarithmic form:

$$\ln \frac{M}{M_o}=\ln \frac{8}{{\pi }^2}-\left(\frac{{\pi }^2{D}_{\text{eff}}t}{4L^2}\right)$$ (6)

Thus, the effective diffusion coefficients can be calculated by plotting experimental drying data in terms of ln(MR) versus drying time to give a straight line with a slope (k_o) of the following:

$$k_o=\frac{{\pi }^2{D}_{\text{eff}}}{4L^2}$$ (7)

Results and discussion

Ambient air, drying air temperatures above each tray and solar radiation during solar drying of mints are shown in Fig. 3. During the drying experiments, the solar irradiance ranged from 50 to 944 W m⁻² and from 39 to 900 W m⁻² for natural and forced convection runs, respectively. The temperature of ambient air for natural and forced convection ranged from 32.6 to 40 °C and from 31.2 to 40.3 °C, respectively. The temperature of drying air above each tray during natural convection runs ranged from 32.6 to 55.1 °C and from 32.6 to 46.5 °C for direct and indirect solar dryer, respectively. While, the temperature of drying air above each tray during forced convection runs ranged from 31.2 to 38.4 °C and from 31.2 to 38.7 °C for direct and indirect solar dryer, respectively.

Fig. 3.

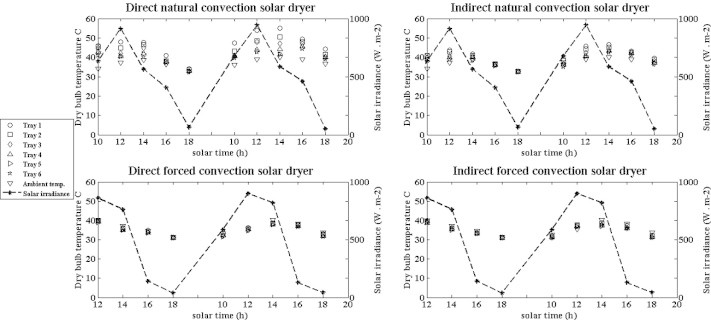
Variation in ambient temperature, drying air temperature above each tray and solar irradiance on a horizontal surface with time.

For natural convection runs, data illustrated in Fig. 3 show that the ambient temperature increased until afternoon and decreased after the afternoon. The highest ambient temperature was 40 °C at 2 p.m., while the maximum drying air temperatures were 55.1 °C and 46.5 °C for direct and indirect solar dryer, respectively. Drying air temperatures inside direct solar dryer were higher than drying temperatures inside indirect solar dryer, which could be attributed to greenhouse effect associated with transparent plastic cover.

For forced convection runs, data illustrated in Fig. 3 show that the ambient temperature increased until afternoon and decreased afterward. The highest ambient temperature was 40.3 °C at 2 p.m., while the maximum drying air temperatures were 38.4 °C and 38.7 °C for direct and indirect solar dryer, respectively. The drying air temperatures were slightly below the ambient temperature since the air residence time inside the dryer was not sufficient to increase its temperature. On the other hand, the evaporation of water from mint plants during drying is responsible for this slight decrease in the temperature.

Moreover, data illustrated in Fig. 3 show that the patterns of ambient and drying air temperature change under all tested conditions are almost similar for all drying runs. The drying air temperatures depend on the ambient temperature, the intensity of solar irradiance and the air residence time inside the dryer.

Drying curves

Since the initial moisture content of mint was not the same for the different runs (77.3% and 81% on wet basis for natural and forced convection runs, respectively), the dimensionless moisture ratio versus time was plotted to normalize the drying curves as shown in Fig. 4. It is apparent that the moisture ratio decreased continuously with drying time.

Fig. 4.

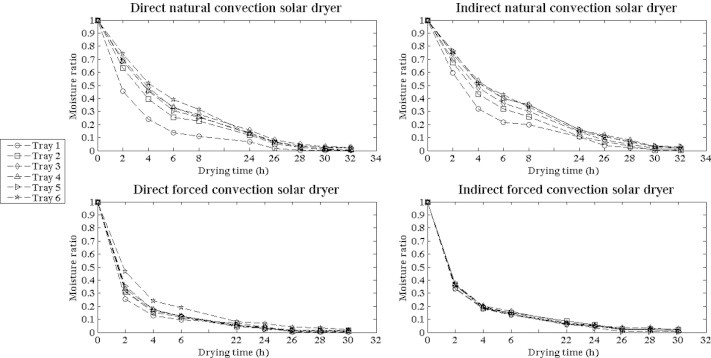
Variation in the mint moisture ratio with drying time.

In natural convection runs, the total drying time in the direct solar dryer was less than in the indirect one. Both solar dryers were operated under the same atmospheric conditions (ambient air temperature, ambient air velocity and ambient relative humidity). However, due to the greenhouse effect associated with transparent plastic films, the drying air temperature inside the direct solar dryer increased than the air temperature of indirect one as shown in Fig. 3. Therefore, this reduction in drying time could be related to the higher drying air temperature above each tray in the direct dryer. Moreover, the drying time of mint in the first tray was the lowest time in all runs which could be also related to the higher temperature above this tray as a consequence of direct exposure to sun radiation. These results are in agreement with that found by Lebert et al. [12]; where they investigated the effect of drying air temperature, relative humidity and drying air velocity on the drying kinetics of mint using full automated oven dryer. They stated that drying air temperature was the main factor affecting the drying rate of mint.

Variations in drying rate with drying time are shown in Fig. 5 for different operating conditions. Under all operating conditions, there were no constant rate for all curves and all the drying operations occur in the falling rate period. Similar trend was observed by Fatouh et al. [22]. They dried several whole herbs using heat pump dryer. They found that the drying of whole jaw’s mallow at lower surface area load (3.5 kg m⁻²) occurred in the falling rate period only, while at higher surface area loads (7–28 kg m⁻²) the drying rate curves showed a constant drying period at the beginning of the drying process followed by a falling rate period. Moreover, they found that the constant rate period was increased with increasing surface area loads. They related shortens of constant rate period associated with low surface area load to area shrinkage, which caused the drying rate to decrease continuously. This explains why the drying process for lowest surface loads (3.5 kg m⁻²) exhibited no constant drying rate period and lies completely in the falling rate period.

Fig. 5.

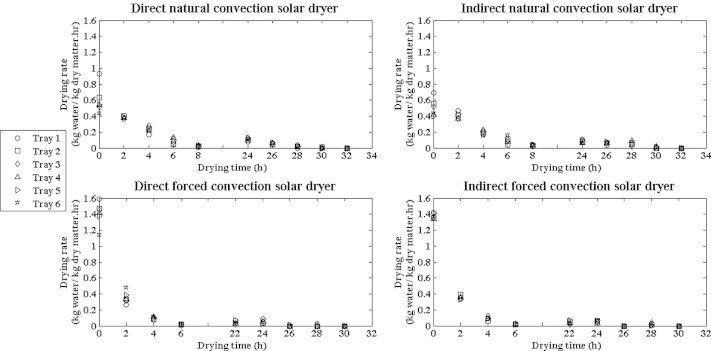
Variation in the mint drying rate with drying time.

For natural convection runs, the data illustrated in Fig. 5 show that the drying rate of mint in first tray was higher than drying rate of mint in other trays especially during the initial hours of the drying experiments. This higher drying rate is related to the effect of higher drying air temperature above this tray, and its direct exposure to the solar irradiance, as explained earlier.

It is also noticed that the drying rate for all the trays is very close after the first couple of hours in all runs. During the first couple of hours, the drying rate is the highest and the drying is gas-phase controlled, thus it depends much on the drying air conditions. However, after the initial high drying rates, the conditions of the drying air are not the main effective variable, since the diffusion inside the plants becomes slower (due to lower moisture content). Thus, by approaching the final dry plants, the drying rate over the trays becomes closer.

The results presented in Fig. 5 show that the drying rate of mint under forced convection was much higher than that of mint under natural convection, especially during the initial hours of drying (first day). The average moisture removal over the six trays during first day was (70.0–75.4%) and (85.5–86.8%) for natural and forced convection runs, respectively. This higher drying rate in the forced convection runs in the first drying day could be due to higher mass transfer coefficient associated with forced convection, since the higher air velocity in the forced convection runs reduced the gas mass transfer resistance. This is in accordance with what Jain and Tiwari [23] reported, where they stated that the convective mass transfer coefficient in greenhouse drying under forced mode is higher than that of natural convection in the initial stages of drying.

It is also to be noticed that the drying rate for forced convection is almost the same for both direct and indirect convection. This phenomenon could be explained by the data presented in Fig. 3, which show that the temperature inside both dryers is similar to the ambient temperature. Therefore, both dryers operated at the same operating condition (drying air temperature, air velocity and relative humidity) and hence, the drying rates for them were similar.

The data in Fig. 5 show that drying rate at the end of the first drying day is virtually zero. This reduction in the drying rate could be related to lower evaporation rate associated with low temperature inside dryers during night. Moreover, data in Fig. 5 show that the drying rate was increased again in the next day, which could be attributed to the increase in the drying air temperature.

Fitting of drying curves

The arithmetic average moisture ratio of the six trays was computed and then ten empirical models were fitted to determine the moisture content as a function of the drying time. The statistical analysis results for natural and forced convection runs of mint are presented in Tables 2 and 3, respectively. These models were evaluated based on adjusted R² and RMSE.

Table 2.

Modeling of moisture ratio according to the drying time for the thin layer natural convection solar drying of mint.

Model	Reference	Dryer type	Constant	Adjusted R2	RMSE
Newton	[17]	Direct dryer	k = 0.1989	0.9797	0.0464
		Indirect dryer	k = 0.1646	0.9738	0.0532
Page	[18]	Direct dryer	k = 0.3026; n = 0.7241	0.9886	0.0348
		Indirect dryer	k = 0.2563; n = 0.7315	0.9882	0.0357
Henderson and Pabis	[8]	Direct dryer	a = 0.9815; k = 0.1941	0.9776	0.0488
		Indirect dryer	a = 0.9718; k = 0.1575	0.9715	0.0555
Logarithmic	[19]	Direct dryer	a = 0.9454; k = 0.2192; c = 0.04707	0.9880	0.0357
		Indirect dryer	a = 0.9343; k = 0.187; c = 0.0579	0.9853	0.0398
Two – term	[20]	Direct dryer	a = 0.6803; b = 0.3243; ko = 0.3293; k1 = 0.06829	0.9913	0.0305
		Indirect dryer	a = 0.5676; b = 0.4399; ko = 0.3281; k1 = 0.06957	0.9897	0.0334
Two – term exponential	[20]	Direct dryer	a = 0.316; k = 0.4413	0.9850	0.0399
		Indirect dryer	a = 0.2895; k = 0.3955	0.9836	0.0422
Midilli and Kucuk	[19]	Direct dryer	a = −0.1083; b = 0.002588	0.7839	0.1514
		Indirect dryer	a = −0.09901; b = 0.002282	0.8335	0.1342
Diffusion approach	[15]	Direct dryer	a = 0.6785; b = 0.2089; k = 0.3257	0.9925	0.0283
		Indirect dryer	a = 0.5711; b = 0.2163; k = 0.3173	0.9911	0.0310
Verma et al.	[21]	Direct dryer	a = 0.3239; g = 0.327; k = 0.06834	0.9925	0.0283
		Indirect dryer	a = 0.4357; g = 0.3215; k = 0.06928	0.9911	0.0310
Modified Henderson and Pabis	[9]	Direct dryer	a = 7.973; b = 0.2351; c = −7.205; g = 0.8349; h = 0.1578; k = 0.1563	0.9671	0.0591
		Indirect dryer	a = 0.7433; b = 67.29; c = −67.04; g = 0.8272; h = 0.8287; k = 0.1095	0.9711	0.0559

Table 3.

Modeling of moisture ratio according to the drying time for the thin layer forced convection solar drying of mint.

Model	Reference	Dryer type	Constant	Adjusted R2	RMSE
Newton	[17]	Direct dryer	k = 0.4729	0.9836	0.0409
		Indirect dryer	k = 0.4431	0.9779	0.0471
Page	[18]	Direct dryer	k = 0.8212; n = 0.4846	0.9959	0.0204
		Indirect dryer	k = 0.803; n = 0.4592	0.9955	0.0211
Henderson and Pabis	[8]	Direct dryer	a = 0.9884; k = 0.4679	0.9814	0.0435
		Indirect dryer	a = 0.9859; k = 0.4372	0.9751	0.0500
Logarithmic	[19]	Direct dryer	a = 0.9563; k = 0.5252; c = 0.03697	0.9901	0.0318
		Indirect dryer	a = 0.9471; k = 0.5024; c = 0.04514	0.9885	0.0340
Two – term	[20]	Direct dryer	a = 0.8171; b = 0.1831; ko = 0.7579; k1 = 0.07181	0.9982	0.0134
		Indirect dryer	a = 0.4683; b = 0.5316; ko = 10.51; k1 = 0.2213	0.9827	0.0416
Two – term exponential	[20]	Direct dryer	a = 0.2922; k = 1.232	0.9878	0.0352
		Indirect dryer	a = 0.2825; k = 1.195	0.9826	0.0417
Midilli and Kucuk	[19]	Direct dryer	a = −0.1406; b = 0.00386	0.3311	0.2610
		Indirect dryer	a = −0.1377; b = 0.003762	0.3547	0.2545
Diffusion approach	[15]	Direct dryer	a = 3.015; b = 0.9973; k = 0.4701	0.9781	0.0473
		Indirect dryer	a = 3.442; b = 0.9982; k = 0.4409	0.9706	0.0543
Verma et al.	[21]	Direct dryer	a = 0.1831; g = 0.7578; k = 0.07181	0.9985	0.0122
		Indirect dryer	a = 0.2026; g = 0.7516; k = 0.06631	0.9985	0.0125
Modified Henderson and Pabis	[9]	Direct dryer	a = 0.1865; b = 0.8865; c = −0.07296; g = 0.8034; h = 11.97; k = 0.07233	0.9971	0.0171
		Indirect dryer	a = −9.383; b = 9.81; c = 0.568; g = 0.2281; h = 1.027; k = 0.2298	0.9741	0.0510

Data in Table 2 show that for natural convection runs the adjusted R² for all models were higher than 0.96 except that for Wang and Singh model. The same data show that, Diffusion approach and Verma et al. models were the best models for thin layer natural convection solar drying of mint for the direct and indirect drying.

The data in Table 3 show that the adjusted R² for forced convection runs for all models were higher than 0.97 except that for Wang and Singh model. Also Verma et al. model was the best model for thin layer solar drying of mint for both plastic covers. Thus, all the tested models except Wang and Singh may be assumed to represent solar drying behavior of mint in thin layer beds to an acceptable degree of accuracy.

Determination of effective diffusivity

The values of effective diffusivity obtained for mint at different operating conditions as presented in Table 4 ranged between 1.2 × 10⁻¹¹ and 1.33 × 10⁻¹¹ m² s⁻¹. It could be noticed that the effective diffusivity values of forced convection runs were higher than that of natural convection ones. The results are in agreement with that found by Park et al. [7], where they reported that the effective diffusivity is expressed as a function in air temperature and air velocity. They found that increasing of drying air velocity from 0.5 m s⁻¹ to 1 m s⁻¹ at 50 °C increased the effective diffusivity of mint from 2.261 × 10⁻¹² to 2.945 × 10⁻¹² m² s⁻¹, respectively. They related this increase in the effective diffusivity to the effect of air velocity on reducing the external resistance of mass transfer.

Table 4.

Effective diffusivity obtained for mint under different operating conditions.

Flow type	Covering material	R2	Effective diffusivity (Deff) (m2 s−1)
Natural convection	Direct dryer	0.9296	1.29 × 10−11
	Indirect dryer	0.918	1.2 × 10−11
Forced convection	Direct dryer	0.9057	1.33 × 10−11
	Indirect dryer	0.9061	1.21 × 10−11

Conclusions

In this study, the drying of mint was investigated under solar drying conditions with natural and forced convection modes. Solar drying of mint with both natural and forced convection modes occurred in the falling rate period; where no constant rate period of drying was observed. The drying rate of mint under forced convection was higher than that of mint under natural convection, especially during first hours of drying (first day). For forced convection, the rate of drying was the same in both direct and indirect drying, since the temperatures and the air velocity above the trays were almost the same.

To explain the drying behavior of mint, ten thin layer drying models were applied. The results showed that for natural convection runs, Diffusion approach and Verma et al. models were the best models able to describe thin layer solar drying of mint for both direct and indirect drying, respectively. For forced convection, Verma et al. model was the best model for thin layer solar drying of mint for both direct and indirect drying.

The values of the effective diffusion coefficients for the drying of mint (as a whole plant) ranged between 1.2 × 10⁻¹¹ and 1.33 × 10⁻¹¹ m² s⁻¹.

Conflict of interest

The authors have declared no conflict of interest.

Compliance with Ethics Requirements

This article does not contain any studies with human or animal subjects.