Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Mar 4;5:8761. doi: 10.1038/srep08761

Pressure-induced zigzag phosphorus chain and superconductivity in boron monophosphide

Xinyu Zhang 1, Jiaqian Qin 2,a, Hanyu Liu 3, Shiliang Zhang 1, Mingzhen Ma 1, Wei Luo 4,6, Riping Liu 1,b, Rajeev Ahuja 4,5,6,c
PMCID: PMC4348669  PMID: 25737341

Abstract

We report on the prediction of the zinc-blende structure BP into a novel C2/m phase from 113 to 208 GPa which possesses zigzag phosphorus chain structure, followed by another P42/mnm structure above 208 GPa above using the particle-swarm search method. Strong electron-phonon coupling λ in compressed BP is found, in particular for C2/m phase with the zigzag phosphorus chain, which has the highest λ (0.56–0.61) value among them, leading to its high superconducting critical temperature Tc (9.4 K–11.5 K), which is comparable with the 4.5 K to 13 K value of black phosphorus phase I (orthorhombic, Cmca). This is the first system in the boron phosphides which shows superconductivity from the present theoretical calculations. Our results show that pressure-induced zigzag phosphorus chain in BP exhibit higher superconducting temperature TC, opening a new route to search and design new superconductor materials with zigzag phosphorus chains.

The crucial thermodynamic parameter-high pressure has been emerging as a powerful tool to investigate physical and chemical behaviours of materials, especially to synthesize or design materials with excellent properties such as superhardness and superconductivity1,2,3,4,5,6. Recently, B and P have been studied extensively in physical, chemical, and material science fields due to their interesting structural properties when pressure is applied4,5,7,8,9. Boron has always been recognized as a complex element, both structurally and electronically: its crystalline phases are numerous and inevitably complicated, which is related to its electron deficiency and thus the tendency to form multicenter bonds5,7. Phosphorus, on the other hand, has six known phases at room temperature under high pressure10,11,12,13,14,15. Black phosphorus phase I (orthorhombic, Cmca) is known to be most stable under ambient temperature and pressure15. The experiment at low temperature and high pressure showed that the superconducting temperature of phase I increased from 4.5 K to 13 K under pressure14. These peculiar physical properties of compressed B and P solids have motivated our attention on high-pressure study of BP. The binary semiconductor boron phosphide (BP) is the zinc-blende crystal structure (space group F-43m) with lattice parameter a = 4.537 Å16, which has extraordinary properties, such as high hardness, high temperature stability, resistance to chemical corrosion, high thermoelectric powers for direct energy conversion, and is regarded as an important candidate for electronic, optical, and other engineering applications17,18,19,20,21. In order to understand in detail the pressure-induced structural behaviour, including mainly the phase transitions of BP, further high-pressure studies are essential.

Here, on the basis of comprehensive density functional theory (DFT) computations, we report the design of two new high pressure structures of BP. We performed variable-cell structure prediction simulations using CALYPSO22,23 approach for BP at 0, 50, 100, 150, 200, 250, and 300 GPa, respectively. For comparison, the structures reported in boron nitride (P-3m1, P63mc, P63/mmc) experimentally and theoretically, are also considered in our calculations. Our calculations demonstrate that, F-43m is the most stable phase at ambient conditions, two new high pressure phases C2/m and P42/mnm can be predicted during compression up to 300 GPa. We further elucidate the energetic, mechanical, electronic and superconducting properties of the obtained novel phases, confirming that F-43m is semiconductor, and discovering two high-pressure superconducting phases C2/m and P42/mnm.

Results

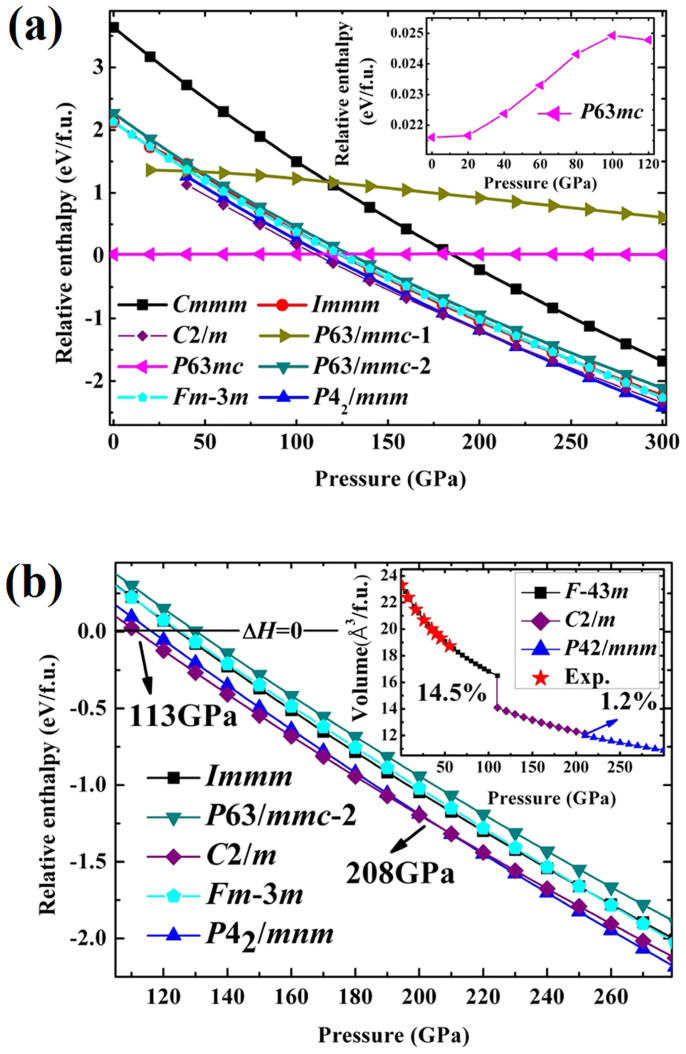
The analysis of the predicted structures gives us a list of candidate structures with space groups F-43m, C2/m, P42/mnm, P63mc, Cmmm, Immm, P63/mmc-I, P63/mmc-II, and the previously reported high pressure rock salt structure Fm-3m20 are depicted in Figure S1 (Supporting Information). The relative enthalpies per chemical formula unit vs. pressure curves of selected structures are plotted in Figure 1(a). Considering that F-43m and P63mc structures hold very close enthalpy, the enthalpy difference vs. pressure curves for the two phases are specially inserted in Figure 1(a), and it indicates that F-43m has lower enthalpy, which is consistent with the experimental results. In order to investigate the phase transition pressures clearly, the enthalpies vs. pressure curves for F-43m, Immm, P42/mnm, C2/m, and P-3m1 are given in Figure 1(b). From Figure 1, one can see that, for compressed BP, the zinc-blende crystal structure F-43m is the most stable structure below 113 GPa, a C2/m phase takes over the pressure range from 113 to 208 GPa, followed by another P42/mnm structure above 208 GPa. The pressure evolution of the unit cell volume of BP in the structures F-43m, C2/m, and P42/mnm is inserted in Figure 1(b). The experimental equation of state data24 for single-crystal BP with F-43m structure up to 55 GPa were listed for comparison. It can be seen that our calculated data are in good agreement with the experimental results. The zinc-blende crystal structure F-43m is stable on compression to 113 GPa, and then complete change to C2/m is observed. Comparisons with the F-43m cell at 113 GPa shows a 14.5% reduction in volume. Upon further compression into the region of P42/mnm above 208 GPa, the volume difference peaks at only 1.2%.

Figure 1.

Figure 1

Open in a new tab

(a) The relative enthalpy per formula unit as a function of pressure for competing structures. The enthalpies are referenced to that of F-43m phase. The insert is the enlarged view of relative enthalpy of P63mc phase as a function of pressure. (b) The relative enthalpy per f.u. as a function of pressure with the region from 105 GPa to 280 GPa around the phase transition pressure. The insert is the pressure dependence of volume for F-43m, C2/m and P42/mnm phases of BP.

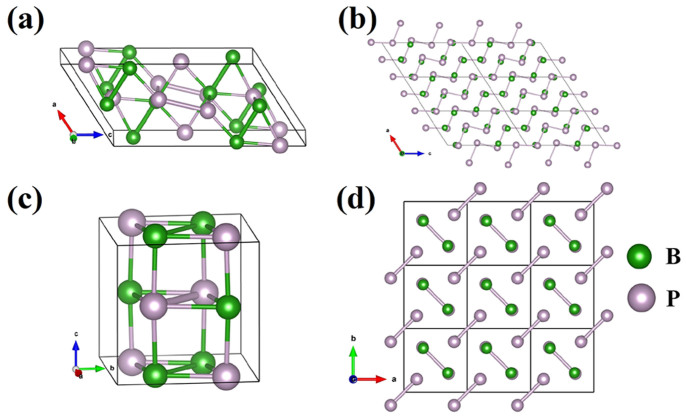
The optimized structural parameters of zinc-blende crystal structure F-43m are listed in Table S1. For this phase, the equilibrium lattice constants are 4.547 Å and 4.492 Å, for PBE and LDA calculation, respectively. The present results are in good agreement with the previous results21,25,26,27. In this structure, four boron atoms lie in the Wyckoff 4a site and four phosphorus atoms occupy the 4c site, in which three-dimensional (3D) boron and phosphorus network in this structure is formed, as shown in Figure S1. The optimized structural parameters of another two phases C2/m and P42/mnm at high pressure are presented in Table 1. For monoclinic C2/m phase, the equilibrium lattice constants at 120 GPa are a = 4.275 Å, b = 3.681 Å, c = 8.357 Å and β = 122.627 degree. The structure of C2/m is shown in Figure 2(a) and Figure 2(b), it can be seen that the 1D-zigzag phosphorus chain is formed, which is connected by boron atoms. For hexagonal P42/mnm phase (Figure 2(c)), the equilibrium lattice constants at 210 GPa are a = 3.631 Å, c = 3.640 Å. The B-P, B-B, and P-P bonds are formed in this structure, but P-P bonds are not continuous (Figure 2(d)).

Table 1. Optimized structural parameters for two high-pressure structures of BP.

Space group Pressure (GPa) Lattice parameters (Å or degree) Atomic coordinates (fractional)
C2/m 120 a = 4.275, b = 3.681, c = 8.357 B1(4i)(1.48905, 0.00000, 0.89375)
      B2(4i)(1.05110, 0.00000, 0.65390)
    α = γ = 90, β = 122.627 P1(4i)(0.99081, 0.00000, 0.13299)
      P2(4i)(0.56959, 0.00000, 0.39201)
P42/mnm 210 a = 3.631, c = 3.640 B (4g)(0.30702, 0.69298, 0.00000)
      P (4f) (0.70572, 0.29428, 0.50000)
Open in a new tab

Figure 2. Predicted structures of BP at ambient and high pressures.

Figure 2

Open in a new tab

The green and pink balls represent B and P atoms, respectively. (a) and (b) The high-pressure phase C2/m. (c) and (d) The high-pressure phase P42/mnm. One-dimensional phosphorus chain is formed in the structure of C2/m.

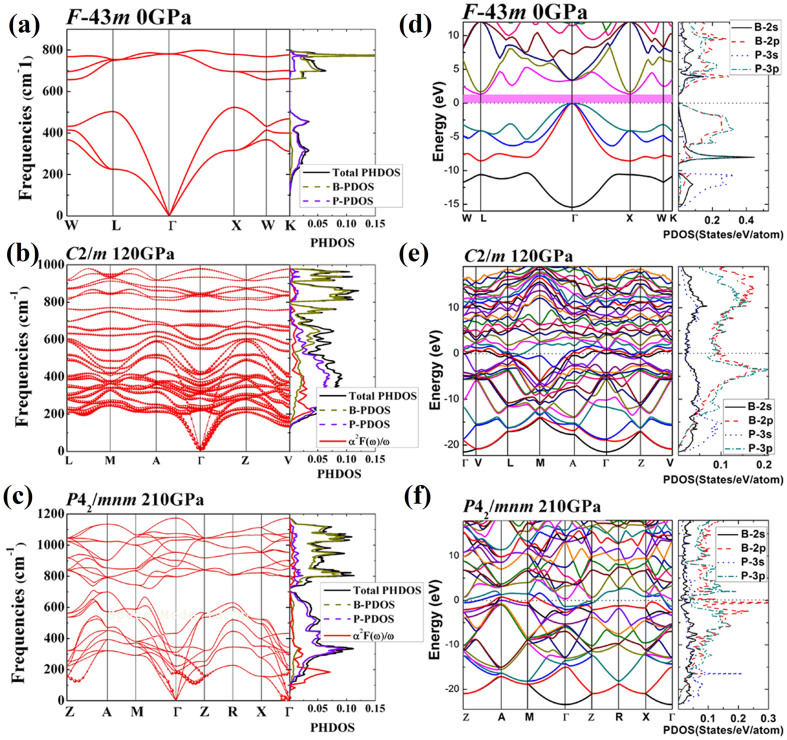
The calculated elastic constants for three BP phases with low enthalpy are presented in Table 2. From Table 2, the elastic constants reveal that all BP phases satisfy the mechanical stable criterion at the corresponding pressures. Furthermore, the hexagonal phase P42/mnm can remain stable at ambient pressure, but monoclinic C2/m does not match the mechanical stable criterion at ambient pressure, which only keeps stable at the high pressure range. Also, the calculated negative formation enthalpies of C2/m and P42/mnm phases at the pressure ranges indicate the stability against decomposition of BP into the elements boron and phosphorus7. Phonon calculations show that BP phases (F-43m, C2/m and P42/mnm) are dynamically stable at their thermodynamically stable pressure regions. Phonon dispersions and partial phonon density of states (PPHDOS) of BP phases at their stable pressure ranges are shown in Figure 3. The maximum optical branch frequencies are 803.5 cm−1 for F-43m phase at atmospheric pressure, 983.7 cm−1 for C2/m phase at 120 GPa, and 1175.2 cm−1 for P42/mnm phase at 210 GPa. One can see that the maximum optical branch frequencies increase with increasing pressure due to an obvious structural difference. From PPHDOS, the lower frequency region is associated with phosphorus atoms, whereas boron atom contributes to the high-frequency region for high-pressure phases (C2/m and P42/mnm) at their corresponding pressure regions. But in the F-43m phase, the boron atom dominates the high-frequency region, whereas phosphorus atom contributes almost equally to the high and low frequency region.

Table 2. Independent elastic constants Cij, bulk, shear, and Young's moduli (B, G and E all in GPa), Poisson's ratio ν and G/B of the stable phases of BP.

Space group P C11 C22 C33 C44 C55 C66 C12 C13 C15 C23 C25 C35 C46 B G E ν G/B
F-43m 0 340     189     73             162 165 369 0.120 1.016
C2/m 120 761 1327 830 390 268 449 313 451 −10 355 6 −35 −15 563 319 805 0.261 0.567
P42/mnm 210 1326   2025 575   78 670 350           821 354 929 0.311 0.431
Open in a new tab

Figure 3. Phonon spectrum and electronic structures.

Figure 3

Open in a new tab

(a) The phonon spectrum and partial atomic phonon density of states for phase F-43m. (b) The phonon spectrum, partial atomic phonon density of states and Eliashberg phonon spectral function α2F(ω)/ω for phase C2/m. (c) The phonon spectrum, partial atomic phonon density of states and Eliashberg phonon spectral function α2F(ω)/ω for phase P42/mnm. Red solid circles in (b) and (c) show the electron-phonon coupling with the radius proportional to their respective strength. Energy band and projected density of states (PDOS) for phase (d) F-43m, (e) C2/m, and (f)P42/mnm.

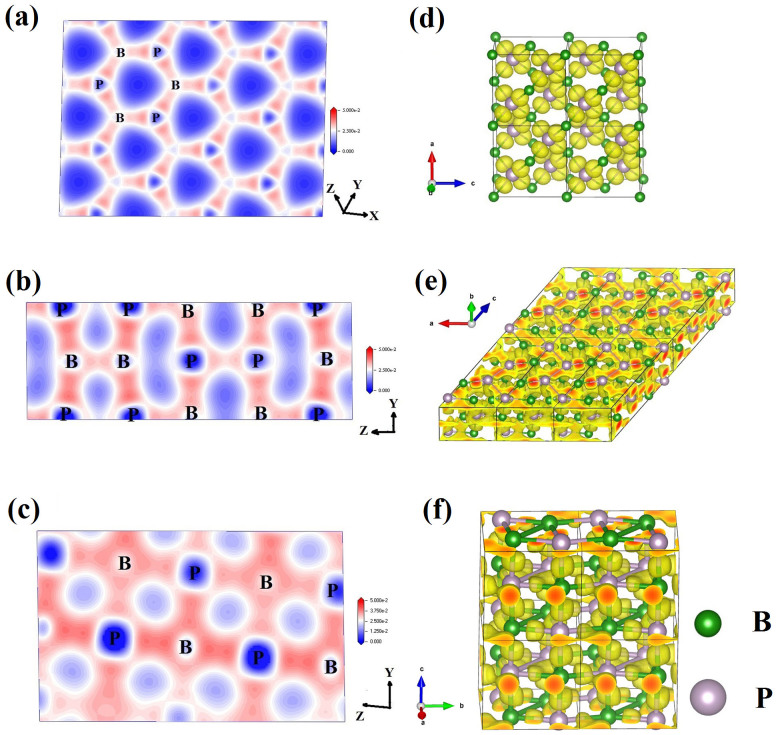
To investigate the possibility of pressure induced metallization and superconducting transition, band structures for F-43m, C2/m and P42/mnm phases have been calculated to examine the electronic properties of these polymorphs of BP at their pressure ranges as shown in Figure 3. Electronic structure calculations indicate that F-43m phase is a semiconductor, whereas C2/m and P42/mnm phases are metallic. From projected density of states (PDOS) plotted in Figure 3, it can be observed that all phases of BP have consistent electronic distributions. B-2p and P-3p electrons dominate in the wide energy range and form the strong covalent bonds as suggested by the matching B-2p and P-3p curve shapes. The contour plots of charge density on the chosen planes are also shown in Figure 4. The strong covalent B-P bonding within in the 3D B-P network is evidenced (Figures 4(a), 4(b) and 4(c)). Moreover, according to Mulliken population analysis, P-P bonding does not exist in F-43m phase, but it exists in C2/m and P42/mnm phases. Interestingly, P-P zigzag chains in phase C2/m transfer to discontinuous bonding in phase P42/mnm. This conclusion is further substantiated by the electron localization function (ELF) shown in Figures 4(d), 4(e) and 4(f), where the calculated ELF patterns have isosurface values of 0.8, 0.65, and 0.7 for F-43m, C2/m, and P42/mnm, respectively.

Figure 4. Electron density and Electron localization function(ELF).

Figure 4

Open in a new tab

(a), (b), and (c) Electron density for phase F-43m, C2/m, and P42/mnm, respectively. (d) Calculated ELF with an isosurface ELF value of 0.8, 0.65, and 0.7 for phase F-43m, C2/m, and P42/mnm, respectively.

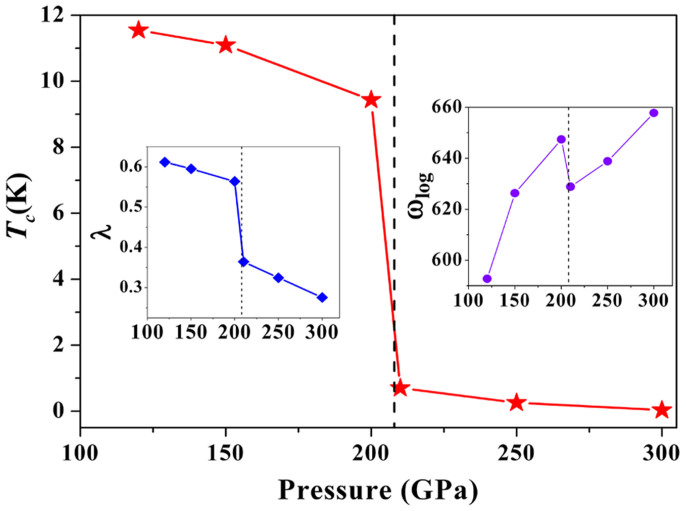
The high-pressure C2/m phase of BP exhibits interesting features in its electronic band structure. As shown in Figure 3(e), the electronic bands of the C2/m phase crossing the Fermi level along the Γ -V-L and A-Γ-Z-V are quite flat, and this section of band within a narrow energy window centered at the Fermi level gives rise to large electronic density of states near the Fermi energy. The corresponding confined conduction electrons near the band gap possess large effective mass with their group velocities approaching zero. In contrast, the bands along the L-M-A direction steeply cross the Fermi level, providing itinerant electrons with high conduction electron velocity. Such flat bands with highly mobile and localized electrons have been shown to enhance superconductivity28,29,30. Similar electronic structures have previously been found in niobium that has the highest transition temperature TC of 9.3 K31 in all element superconductors at ambient pressure, 9.8 K in CaC228 and 220–235 K in CaH6 at high pressure of 150 GPa32. This motivates us to further investigate the superconductivity of BP at high pressures. The calculated spectral function α2F(ω) of BP phases C2/m and P42/mnm at 120 GPa and 210 GPa were plotted in Figures 3(b) and 3(c). At 120 GPa (Figure 3(b)), the coupling parameter λ is 0.61 with the average phonon frequency ωln of 593 K. Using the strong coupling Allen-Dynes equation, an extension of the McMillan theory, with a nominal Coulomb pseudopotential parameter (μ*) of 0.12 the estimated superconducting critical temperature TC is 11.5 K. With increasing pressure, the calculated TC become slightly lower as 11.1 K at 150 GPa and 9.4 K at 200 GPa due to slightly smaller λ of 0.59 at 150 GPa and 0.56 at 200 GPa, respectively. Here the TC of two high-pressure phases for BP and TC's dependence on pressure is shown in Figure 5. Calculated coupling parameter λ values and logarithmic phonon momentum ωlog vs. pressure curves are also presented in Figure 5. It can be seen that logarithmic phonon momentum ωlog increases with pressure, and coupling parameter λ decreases with pressure. Among these two high pressure phases, C2/m phase has the strongest electron-phonon coupling and so has the highest TC. Apparently, the fairly high TC is due to the large electron phonon coupling (λ). The origin can be traced from comparing the calculated Eliashberg spectral function (α2F(ω)/ω) with the projected phonon DOS. As shown in Figure 3(b), nearly 80% of the electron phonon coupling is contributed by the low-frequency vibrations in the frequency region from 100 to 600 cm−1. The low-frequency vibrations in the frequency region from 100 to 600 cm−1, which are mostly attributed to the P atom. At wide range of pressure, C2/m phase has comparative superconducting critical temperatures (from 11.5 K at 120 GPa to 9.3 K at 200 GPa) with 11.5 K value of CaC633,34. However, TC of BP is close to zero above 210 GPa due to the smaller electron-phonon coupling parameter (λ < 0.4). We thus further analyze the coupling parameter in each q-point (Figures 3(b) and 3(c)). It is clearly seen that the coupling parameters in Γ-Z and X-Γ are very strong. This superconducting feature is typical anisotropy, leading a low superconductivity value.

Figure 5. Superconducting temperature (TC) vs. pressure.

Figure 5

Open in a new tab

The coupling parameters, the average phonon frequencies ωln and superconducting temperatures of BP as a function of pressure.

To summarize, using the PSO technique on crystal structure prediction, we designed two new high-pressure phases of BP, C2/m and P42/mnm, which are stable in the pressure ranges of 113–208 GPa and 208–300 GPa, respectively. Elastic constants and phonon calculations have shown their mechanical and dynamical stability at the dominating pressure ranges. Our calculations reveal that the phosphorus atomic arrangement form from single atoms to 1D zigzag chains to discontinuous bonding. The high superconducting transition temperature of the C2/m phase benefits from the simultaneous presence of the steep bands (highly mobile electrons) and extremely flat bands (highly confined electrons), which is known to favor the electron paring and superconducting behavior.

Computational Methods

The search of high-pressure structures was performed with variable-cell PSO35 structure prediction simulations using CALYPSO approach22,23 in combined with Vienna ab initio simulation package (VASP)36. CALYPSO was designed to predict stable or metastable crystal structures requiring only chemical compositions of a given compound at specified external conditions. All structures were locally optimized using the DFT method. The 60% structures of each generation with lower enthalpies were selected to generate the structures for the next generation by PSO operation, and the other structures in new generation were randomly generated to increase the structural diversity. The underlying ab initio calculations were performed using density functional theory within the generalized gradient approximation (GGA)37, as implemented in the Vienna ab initio simulation package (VASP). The total energy calculations were carried out with the VASP code. The all-electron projector augmented wave (PAW) method38 was employed with a plane-wave cutoff energy of 600 eV for all phases. The k-point samplings in the Brillouin zone were performed using the Monkhorst-Pack scheme39. The total energy convergence tests showed that convergence to within 1 meV/atom was achieved with the above calculation parameters. Single crystal elastic constants were calculated via a strain-stress approach. i.e., by applying a small strain to the equilibrium lattice of the unit cell and fitting the dependence of the resulting stress on the strain. The bulk modulus, shear modulus, Young's modulus, and Poisson's ratio were determined by using the Voigt-Reuss-Hill approximation40. The lattice-dynamical and superconducting properties are calculated using the density functional perturbation theory (DFPT)41 as implemented in the Quantum Espresso package42 using with the Troullier-Martins pseudopotentials with cutoff energies of 50 and 500 Ry for the wave functions and the charge density, respectively. Fine k-points mesh of MP was used and the estimated energy error in self-consistency was less than 10−4 a.u. The electron–phonon coupling was convergent with a finer grid and a Gaussian smearing of 0.02 Ry. In order to check the results, the phonon calculations were also carried out by using a supercell approach as implemented in the PHONOPY code43.

Author Contributions

X.Z., J.Q., R.L. and R.A. designed and coordinated the research. X.Z., J.Q., H.L. and S.Z. did the calculations. X.Z., J.Q., H.L., S.Z., M.M., R.L., W.L. and R.A. analyzed all data. X.Z., J.Q., H.L., R.L. and R.A. wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary information

srep08761-s1.doc (1.7MB, doc)

Acknowledgments

The authors acknowledge funding from NBRPC (grant 2013CB733000), NSFC (grants 51171160/51171163), J.Q. thanks the support from Ratchadaphisek sompoch Endowment Fund (2013), Chulalongkorn University (CU-56-805-FC), Ratchadapisek Sompoch Endowment Fund, Chulalongkorn University, granted to the Surface Coatings Technology for Metals and Materials Research Unit (GRU 57-005-62-001). This research was supported by Swedish Foundation for Strategic Research, Sweden and the Leading Foreign Research Institute Recruitment Program through theNational Research Foundation of Korea funded by Ministry of Education, Science and Technology Grant 2014-039452.

References

  1. McMillan P. F. Chemistry at high pressure. Chem. Soc. Rev. 35, 855–857 (2006). [DOI] [PubMed] [Google Scholar]
  2. Haines J., Léger J. & Bocquillon G. Synthesis and design of superhard materials. Ann. Rev. Mater. Res. 31, 1–23 (2001). [Google Scholar]
  3. Qin J. et al. Is Rhenium Diboride a Superhard Material? Adv. Mater. 20, 4780–4783 (2008). [Google Scholar]
  4. Qin J. et al. Polycrystalline γ-boron: As hard as polycrystalline cubic boron nitride. Scripta Mater. 67, 257–260 (2012). [Google Scholar]
  5. Qin J. et al. Phase relations in boron at pressures up to 18 GPa and temperatures up to 2200°C. Phys. Rev. B 85, 014107 (2012). [Google Scholar]
  6. Raza Z., Errea I., Oganov A. R. & Saitta A. M. Novel superconducting skutterudite-type phosphorus nitride at high pressure from first-principles calculations. Sci. Rep. 4, 5889; 10.1038/srep05889 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Oganov A. R. et al. Ionic high-pressure form of elemental boron. Nature 457, 863–867 (2009). [DOI] [PubMed] [Google Scholar]
  8. Ma Y., Prewitt C. T., Zou G., Mao H.-k. & Hemley R. J. High-pressure high-temperature x-ray diffraction of β-boron to 30 GPa. Phys. Rev. B 67, 174116 (2003). [Google Scholar]
  9. Ma Y., Tse J. S., Klug D. D. & Ahuja R. Electron-phonon coupling of α-Ga boron. Phys. Rev. B 70, 214107 (2004). [Google Scholar]
  10. Kikegawa T. & Iwasaki H. An X-ray diffraction study of lattice compression and phase transition of crystalline phosphorus. Acta Crystallogr. B 39, 158–164 (1983). [Google Scholar]
  11. Akahama Y., Kobayashi M. & Kawamura H. Simple-cubic–simple-hexagonal transition in phosphorus under pressure. Phys. Rev. B 59, 8520–8525 (1999). [Google Scholar]
  12. Akahama Y., Kawamura H., Carlson S., Le Bihan T. & Häusermann D. Structural stability and equation of state of simple-hexagonal phosphorus to 280 GPa: Phase transition at 262 GPa. Phys. Rev. B 61, 3139–3142 (2000). [Google Scholar]
  13. Akahama Y., Endo S. & Narita S. Electrical properties of single-crystal black phosphorus under pressure. Physica B + C 139–140, 397–400 (1986). [Google Scholar]
  14. Kawamura H., Shirotani I. & Tachikawa K. Anomalous superconductivity in black phosphorus under high pressures. Solid State Commun. 49, 879–881 (1984). [Google Scholar]
  15. Brown A. & Rundqvist S. Refinement of the crystal structure of black phosphorus. Acta Crystallographica 19, 684–685 (1965). [Google Scholar]
  16. Peret J. L. Preparation and Properties of the Boron Phosphides. J. Am. Ceram. Soc. 47, 44–46 (1964). [Google Scholar]
  17. Archer R. J., Koyama R. Y., Loebner E. E. & Lucas R. C. Optical Absorption, Electroluminescence, and the Band Gap of BP. Phys. Rev. Lett. 12, 538–540 (1964). [Google Scholar]
  18. Motojima S., Ohtsuka Y., Kawajiri S., Takahashi Y. & Sugiyama K. Boron phosphide coatings on molybdenum by chemical vapour deposition, and their composition and microhardness. J. Mater. Sci. 14, 496–498 (1979). [Google Scholar]
  19. Schroten E., Goossens A. & Schoonman J. Photo- and electroreflectance of cubic boron phosphide. J. Appl. Phys. 83, 1660–1663 (1998). [Google Scholar]
  20. Wentzcovitch R. M., Cohen M. L. & Lam P. K. Theoretical study of BN, BP, and BAs at high pressures. Phys. Rev. B 36, 6058–6068 (1987). [DOI] [PubMed] [Google Scholar]
  21. Wentzcovitch R. M., Chang K. J. & Cohen M. L. Electronic and structural properties of BN and BP. Phys. Rev. B 34, 1071–1079 (1986). [DOI] [PubMed] [Google Scholar]
  22. Wang Y., Lv J., Zhu L. & Ma Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116–094123 (2010). [Google Scholar]
  23. Wang Y., Lv J., Zhu L. & Ma Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070 (2012). [Google Scholar]
  24. Godec Y. et al. Equation of state of single-crystal cubic boron phosphide. J. Superhard Mat. 36, 61–64 (2014). [Google Scholar]
  25. Meradji H. et al. First-principles elastic constants and electronic structure of BP, BAs, and BSb. Phys. Status. Solidi. B 241, 2881–2885 (2004). [Google Scholar]
  26. Lambrecht W. R. L. & Segall B. Electronic structure and bonding at SiC/AlN and SiC/BP interfaces. Phys. Rev. B 43, 7070–7085 (1991). [DOI] [PubMed] [Google Scholar]
  27. Zaoui A. & Hassan F. E. H. Full potential linearized augmented plane wave calculations of structural and electronic properties of BN, BP, BAs and BSb. J. Phys.: Condens. Matter 13, 253–262 (2001). [Google Scholar]
  28. Li Y.-L. et al. Pressure-induced superconductivity in CaC2. Proc. Natl. Acad. Sci. USA 110, 9289–9294 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Ranninger J., Robin J. M. & Eschrig M. Superfluid Precursor Effects in a Model of Hybridized Bosons and Fermions. Phys. Rev. Lett. 74, 4027–4030 (1995). [DOI] [PubMed] [Google Scholar]
  30. Simon A. Superconductivity and chemistry. Angew. Chem. Int. Ed. 36, 1788–1806 (1997). [Google Scholar]
  31. Broom R. F., Raider S. I., Oosenbrug A., Drake R. E. & Walter W. Niobium oxide-barrier tunnel junction. Ieee. T. Electron Dev. 27, 1998–2008 (1980). [Google Scholar]
  32. Wang H., Tse J. S., Tanaka K., Iitaka T. & Ma Y. Superconductive sodalite-like clathrate calcium hydride at high pressures. Proc. Natl. Acad. Sci. USA 109, 6463–6466 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Emery N. et al. Superconductivity of Bulk CaC6. Phys. Rev. Lett. 95, 087003 (2005). [DOI] [PubMed] [Google Scholar]
  34. Weller T. E., Ellerby M., Saxena S. S., Smith R. P. & Skipper N. T. Superconductivity in the intercalated graphite compounds C6Yb and C6Ca. Nat. Phy. 1, 39–41 (2005). [Google Scholar]
  35. Call S. T., Zubarev D. Y. & Boldyrev A. I. Global minimum structure searches via particle swarm optimization. J. Comput. Chem. 28, 1177–1186 (2007). [DOI] [PubMed] [Google Scholar]
  36. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
  37. Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
  38. Kresse G. & Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999). [Google Scholar]
  39. Monkhorst H. J. & Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976). [Google Scholar]
  40. Hill R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. A 65, 349–355 (1952). [Google Scholar]
  41. Baroni S., de Gironcoli S. & Dal Corso A., Giannozzi P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515–562 (2001). [Google Scholar]
  42. Giannozzi P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter 21, 395502–395530 (2009). [DOI] [PubMed] [Google Scholar]
  43. Togo A., Oba F. & Tanaka I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106–134114 (2008). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary information

srep08761-s1.doc (1.7MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES