Abstract
In plant and animal breeding studies a distinction is made between the genetic value (additive plus epistatic genetic effects) and the breeding value (additive genetic effects) of an individual since it is expected that some of the epistatic genetic effects will be lost due to recombination. In this article, we argue that the breeder can take advantage of the epistatic marker effects in regions of low recombination. The models introduced here aim to estimate local epistatic line heritability by using genetic map information and combining local additive and epistatic effects. To this end, we have used semiparametric mixed models with multiple local genomic relationship matrices with hierarchical designs. Elastic-net postprocessing was used to introduce sparsity. Our models produce good predictive performance along with useful explanatory information.
Keywords: genomic selection, epistasis, mixed models, GenPred, shared data resource
SELECTION in animal or plant breeding is usually based on estimates of genetic breeding values (GEBVs) obtained with semiparametric mixed models (SPMMs) (Meuwissen et al. 2001; Lee et al. 2008). In a mixed model, genetic information in the form of a pedigree or markers is used to construct an additive kernel matrix that describes the similarity of line-specific additive genetic effects. These models have been successfully used for predicting the breeding values in plants and animals. Studies show that using similarities calculated from sufficient genome-wide marker information almost always leads to better prediction models for the breeding values compared to the pedigree-based models (Meuwissen et al. 2001; Habier et al. 2007; Hayes et al. 2009). In both simulation studies and empirical studies of dairy cattle (Hayes et al. 2009; Vanraden et al. 2009); mice (Lee et al. 2008; Legarra et al. 2008); and biparental populations of maize, barley, and Arabidopsis (Lorenzana and Bernardo 2009; Heffner et al. 2011) marker-based SPMM GEBVs have been quite accurate.
A SPMM for the response vector y is expressed as
| (1) |
where X is the design matrix for the fixed effects, β is a vector of fixed effect coefficients, and Z is the design matrix for the random effects; the vector random effects are assumed to follow a multivariate normal distribution with mean 0 and covariance
where K is a kernel matrix.
The similarity of the kernel-based SPMMs and reproducing kernel Hilbert spaces (RKHS) regression models has been stressed recently (Gianola and Van Kaam 2008). In fact, this connection was previously recognized by Kimeldorf and Wahba (1970), Harville (1977), Robinson (1991), and Speed (1991). RKHS regression models use an implicit or explicit mapping of the input data into a high-dimensional feature space defined by a kernel function. This is often called the “kernel trick” (Schölkopf and Smola 2002).
A kernel function, maps a pair of input points x and into real numbers. It is by definition symmetric and nonnegative. Given the inputs for the n individuals we can compute a kernel matrix K whose entries are . The linear kernel function is given by . The polynomial kernel function is given by for c and d ∈ R. Finally, the Gaussian kernel function is given by , where .
RKHS regression extends SPMMs by allowing a variety of kernel matrices, not necessarily additive in the input variables, calculated using a variety of kernel functions. Some common choices are the linear, polynomial, and Gaussian kernel functions, although many other options are available (Schölkopf and Smola 2002; Endelman 2011).
For the marker-based SPMMs, a genetic kernel matrix calculated using a linear kernel matrix incorporates only additive effects of markers. A genetic kernel matrix based on the polynomial kernel of order k incorporates all of the one to k order monomials of markers in an additive fashion. The Gaussian kernel function allows us to incorporate additive and complex epistatic effects of the markers implicitly.
Simulation studies and results from empirical experiments show that the prediction accuracies of models with Gaussian are often higher than those of the models with linear kernel (De Los Campos 2008; González-Camacho et al. 2012; Heslot et al. 2012). However, it is not possible to know how much of the increase in accuracy can be transferred to subsequent generations because some of the predicted epistatic effects will be lost by recombination. This is related to the distinction made between the commercial value of a line (defined as the overall genetic effect, additive plus nonadditive) and the breeding value (the potential for being a good parent, additive only). It can be argued that the linear kernel model estimates the breeding value whereas the Gaussian kernel model estimates the genetic value. In this article, we argue that the breeder can take advantage of some epistatic marker effects in regions of low recombination. Epistatic interactions that span short map segments (i.e., ∼20 cM) are considered “local.” The models introduced here aim to estimate local epistatic line heritability by using genetic map information and combining the local additive and epistatic effects. Since only local epistatic effects are used, there is a reduced chance that these effects will disappear with recombination.
The final models we propose are SPMMs with semisupervised kernel matrices that are obtained as a weighted sum of functions of many local kernels. The principal aim of this article is to measure and incorporate additive and local epistatic genetic contributions since we believe that the local epistatic effects are relevant to the breeder. Locally epistatic models in this article can be adjusted so that the genetic contribution of the whole genome, the chromosomes, or local regions can be obtained.
In most genome-wide association studies (GWAS) the focus is on estimating the effects of each marker and lower-level interactions (Cantor et al. 2010). However, the number of SNP markers can easily exceed millions. The methods used in GWAS lack statistical power, and they are computationally exhaustive. The local kernel approach developed in this article remedies these problems by reducing the number of hypothesis tests by focusing on regions.
Another argument for focusing on short segments of the genome as distinct structures comes from the “building-blocks” hypothesis in evolutionary theory. The schema theorem of Holland (1975) predicts that a complex system that uses evolutionary mechanisms such as fitness, recombination, and mutation tends to generate short, well-fit, and specialized structures. These basic structures then serve as building blocks. For example, when the alleles associated with an important fitness trait are scattered all around the genome, the favorable effects can be lost by independent segregation. Therefore, inversions that group these alleles physically together would be selected.
The sum of the building-blocks approach we propose in this article is parsimonious since only a few genomic regions are used in the final model. In addition, importance scores for genomic regions are obtained as a by-product.
The rest of this article is organized as follows: In the next section, after briefly reviewing some multiple-kernel approaches from the statistics and machine-learning literature, we introduce our model that is more suitable to use in the context of traditional SPMMs. We discuss the issues of model setup, parameter estimation, and hypothesis testing here. We illustrate our model with four benchmark data sets and simulations. We conclude with a section that includes a summary of main findings and discussions.
Materials and Methods
Multiple-kernel learning
In recent years, several methods have been proposed to combine and use multiple-kernel matrices instead of using a single one. These kernel matrices may correspond to using different notions of similarity or to using information coming from multiple sources.
Some early literature related to use of multiple kernels simultaneously included Hartley and Rao (1967) and Rao (1971) and more recently Bach et al. (2004) and Sonnenburg et al. (2006). Their use in the context of genetic information and mixed models also gained attention (De Los Campos 2008; De Los Campos et al. 2010; Jarquín et al. 2013; Tusell et al. 2014).
Multiple-kernel learning methods use multiple kernels by combining them into a single one via a combination function. The most commonly used combination function is linear. Given kernels , a linear kernel is of the form
The kernel K can also include interaction terms like , , or perhaps , where the ⊙ is the element-wise matrix multiplication operator and the ⊗ is the matrix Kronecker product operator. For example, if is the environment kernel matrix and is the genetic kernel matrix, then a component can be used to capture the gene-by-environment interaction effects.
The kernel weights are usually assumed to be positive, and this corresponds to calculating a kernel in the combined feature spaces of the individual kernels. Therefore, once given the kernels, multiple-kernel learning boils down to estimating the kernel weights.
A locally epistatic genomic model for genomic association and prediction
Our model-building approach has three stages:
Subsets of the genome: Divide the marker set into k subsets.
Local genetic values (GEVs): Use the training data to obtain a model to estimate the local GEVs for each genome region .
Postprocessing: Combine the local GEVs using an additive model fitted in the training data set.
In the rest of this section, we describe each step in more detail.
Locally epistatic kernels from mapped marker data:
To obtain k kernels for marker data, we need k possibly nested or overlapping subsets of the marker set. These subsets can be obtained using any annotation of the markers. However, since our aim is to capture the additive plus locally epistatic genetic effects in the model, we concentrate only on contiguous although possibly nested and overlapping regions of the genome.
Although it is possible to define genomic regions in an informed fashion (for example, see Xu 2013 for a division based on recombination hotspots), in our illustrations we carry out this task hierarchically as illustrated for a hypothetical organism with three chromosomes in Figure 1. In Figure 1, at the root of the hierarchy we have the whole genome; the second level of the hierarchy divides the genome into chromosomes. The third and the following levels of the hierarchy are obtained in an iterative fashion by splitting each of the partitions of the previous level into a specified number (called “nsplit”) of “roughly equal-sized” nonoverlapping sets of consecutive markers. For both the simulated and the real data, we used the map positions to order the markers; then, the splits were done such that the partitions at a certain level of splits on a chromosome had approximately the same number of markers. The splitting is stopped at a prespecified level that is called “depth.” The nsplit and the depth become the hyperparameters of the model. The Hyperparameters of the model section and the illustrations herein give some insight into how these parameters can be adjusted.
Figure 1.
A hypothetical hierarchical setup for an organism with three chromosomes. This division has two main parameters, namely the “depth” and the “nsplit.” Depth controls how many levels of splits should be performed. A depth of zero corresponds to the root of the tree, a depth of one corresponds to chromosomes, a depth of two corresponds to splitting the chromosomes, and so on. The nsplit parameter controls the number of divisions after the chromosome level. Here, a setup with depth two and nsplit three is illustrated.
Multiple-kernel SPMMs:
Some multiple-kernel approaches use fixed weights for combining kernels; however, usually the weight parameters need to be learned from the training data. Some principled techniques used to estimate these parameters include minimum norm quadratic unbiased estimation (Rao 1971), the variance least-squares approach (Amemiya 1977; Demidenko 2004, p. 223), and the Bayesian approaches implemented in the R package BGLR (Rodrıguez and De Los Campos 2012). However, these methods are more suitable for cases where only a few kernels are being used because they fail to give satisfactory solutions in high-dimensional settings, i.e., when the number of kernels is large. In the rest of this section, we develop a model that is more suitable for use in high-dimensional settings.
To obtain the local GEVs, one possible approach is to use a SPMM with multiple kernels in the form of
| (2) |
where for , , and are mutually independent.
Another SPMM incorporates the marginal variance contribution from each kernel matrix,
| (3) |
where for . is the random effect corresponding to the input components other than the ones in group j and stands for the kernel matrix obtained from markers not in group j. and , , are mutually independent.
A simpler approach is to use a separate SPMM for each kernel. Let and be the estimated variance components from the SPMM model in (1) with kernel . The markers corresponding to the random effect that mainly accounts for the sample structure can now be incorporated as fixed effects via the first principal components. Let the matrix of the first few principal components of the markers not in group j be denoted by the matrix . The model is written as
| (4) |
where is considered a fixed effect, for , , and , are independent. In the rest of this article, we combine the fixed-effect terms into one as for notational ease.
Estimating the parameters of the model in (2) is very difficult with a large number of kernels. The models in (3) or (2) are more suitable for such cases. The model in (4) is our preferred model for estimating local GEVs in the rest of this article since there are very efficient algorithms for estimating the parameters of this model.
Once the fixed effects and the variance parameters of the model in (4) are estimated for the jth region, the vector of the expected value of the genetic effects (EBLUP) specific to region j can be estimated by
for .
Postprocessing:
Let x be the p-dimensional vector of fixed effects and m be the vector of markers partitioned into k regions. Using the methods discussed in the previous section it is possible to obtain the EBLUP specific to region j for an individual with marker set m, which we denote by . Also, let denote the standardized EBLUPs of random-effect components that correspond to the k local kernels for regions and individuals with markers m. Consider a final prediction model in the following form:
| (5) |
Estimate the model coefficients using
| (6) |
where is the shrinkage operator, and larger values of λ decrease the number of kernels included in the final prediction model.
When k is large compared to the sample size N, we can estimate the parameters of the model using the elastic-net penalty; i.e.,
| (7) |
to allow for more than N nonzero coefficients in the final estimation model. are the shrinkage operators.
In our examples, we used as the estimated genotypic value for an individual with markers m, where . Since has standardized columns, can be used as importance scores for the regions in the model.
Hyperparameters of the model:
While fitting the model in (5) we need to decide on the values of a number of hyperparameters. Apart from the model setup that involves the definition of genomic regions and inclusion or exclusion of some environmental or structural covariates, these parameters are the kernel parameters and the parameters related to the elastic net used in the postprocessing step.
Low accuracies due to poor selection of the bandwidth parameter, h, for the Gaussian kernel have been documented previously. Several methods such as use of multiple Gaussian kernels simultaneously or model averaging have been recommended to overcome these shortcomings (González-Camacho et al. 2012; Tusell et al. 2014). We have experimented with these approaches, but they did not produce consistent results for the data sets we analyzed. Therefore, we chose to compare a few predetermined values [, where m is the number of markers that contribute to a kernel and n is the number of genotypes] and selected the value that gave the best 10-fold cross-validated accuracy within a given training set.
The other hyperparameters we varied were the depth and nsplit parameters of the hierarchical model setup scheme in Figure 1. These parameters may be selected by comparing the cross-validated accuracies within the training data set for several reasonable choices.
Inclusion of structural components in the models by which the local GEVs are evaluated is mainly to exclude the cosegregation effects due to family structure in the final model. For the examples in this article, we have used the first five principal components as covariates during the calculation of local GEVs. These covariates are later dropped from the model during the postprocessing step.
In our opinion, the hyperparameter choice for the multiple-kernel models should reflect the available resources and the aims of the researcher. For instance, the number of regions that we can define depends on the number of markers, and a more detailed analysis might be suitable only when the number of markers and the number of genotypes in the training data set are large. The hyperparameters of the shrinkage estimators in the postprocessing step allow us to control the sparsity of the model. These parameters can be optimized for accuracy using cross-validation, but their value can also be influenced by the amount of sparsity desired in the model. The multiple-kernel models provide the user with the flexibility of models with a range of detail and sparsity.
Illustrations
In this section, for four data sets that represent a variety of situations, we compare the locally epistatic model with its counterpoints linear and Gaussian kernel SPMMs. The last examples are simulation studies to show that the short-range interactions can be effectively captured by the locally epistatic models and that the cross-validated accuracies within the training set can be used to adjust the hyperparameters.
In the following examples, the measure of accuracy is the correlation between the phenotypic values and the corresponding estimated genotypic values. Comparisons of accuracy among the different models are based on repeated evaluations of the accuracy in a randomly selected subset (test set) based on models trained with the remaining individuals (training set).
If two traits are similar in terms of their importance scores, we can expect to have a genetic correlation between these traits. Genetic trait correlations are caused by pleiotropy, close linkage, or correlated physiological functions (Chen and Lübberstedt 2010), and they are important to the breeders for improving correlated traits simultaneously or for reducing linkage drag. For the data sets that have several traits, we can provide a graphical representation of the importance scores from which the closeness of traits can be inferred. This representation is also useful for identifying QTL hotspots that were observed in other studies (Gardner and Latta 2007; Breitling et al. 2008; Weber et al. 2008; Zhao et al. 2011).
For fitting the mixed models, we developed and used the EMMREML package (Akdemir and Godfrey 2014) and for the postprocessing step we used the glmnet package (Friedman and Hastie 2013), both of which are available in R (R Core Team 2014). The remaining software packages were also programmed in R, and some of these are provided in supporting information, File S1.
Example 1 (wheat data):
This data set was downloaded from triticeaetoolbox.org. A total of 3735 markers on 21 chromosomes (1A–7A, 1B–7B, and 1D–7D) for 337 elite wheat lines (SW-AM panel) were available for the analysis. The traits [flowering date (FD), heading date (HD), physiological maturity date (MD), plant height (PH), yield (YD), and waxiness (WX)] were obtained in two trials during the years 2012 and 2013. We sampled 90% of the lines for training the models, and we used the rest of the lines to evaluate the fit of our models. The whole genome was divided similarly to that in Figure 1 with a depth of two. The accuracies of the multiple-kernel model compared with the linear and Gaussian kernel SPMMs and the mean genome-wide importance scores for regions used in our multiple kernel model over 30 replications of the experiment are summarized for different choices of the number of splits in Figure 2. The mean accuracies of the models for different traits are provided in Table 1. In addition, the importance scores from the multiple-kernel models are used to cluster the traits, and the dendrograms describe the resulting similarities of the traits in Figure 3.
Figure 2.
Wheat data: accuracies of the multiple-kernel (MK) model compared to the Gaussian (Gaus) kernel model for six traits. Circles below the line in red correspond to the cases where the MK model is more accurate than the Gaus model. (A) Two regions per chromosome. (B) Three regions per chromosome.
Table 1. The mean accuracies of models compared for several models of wheat data.
| Model | MK 2 splits | MK 3 splits | MK 4 splits | MK 5 splits | MK 6 splits | Gaus | Lin |
|---|---|---|---|---|---|---|---|
| FD | 0.48 | 0.47 | 0.46 | 0.48 | 0.47 | 0.48 | 0.47 |
| MD | 0.46 | 0.46 | 0.42 | 0.42 | 0.42 | 0.41 | 0.41 |
| PH | 0.66 | 0.64 | 0.63 | 0.65 | 0.62 | 0.63 | 0.61 |
| GP | 0.53 | 0.47 | 0.5 | 0.51 | 0.48 | 0.46 | 0.44 |
| YLD | 0.81 | 0.81 | 0.82 | 0.82 | 0.83 | 0.83 | 0.83 |
| HD | 0.56 | 0.55 | 0.53 | 0.53 | 0.55 | 0.56 | 0.53 |
| WX | 0.51 | 0.57 | 0.53 | 0.55 | 0.51 | 0.55 | 0.51 |
The best two accuracies for each trait are marked by boldface characters.
Figure 3.
Wheat data: associations from the multiple-kernel (MK) model for the six traits. (A) Two regions per chromosome. (B) Three regions per chromosome.
Example 2 (mouse data):
The mouse data set we use for this analysis is available as a part of the R package SynbreedData (Wimmer et al. 2013a). Genotypic data consist of 12,545 biallelic SNP markers and are available for 1940 individuals. The body weight at 6 weeks of age (grams) and growth slope between 6 and 10 weeks of age (grams per day) are measured for most of the individuals. The data are described in Valdar et al. (2006) and the heritabilities of these two traits are reported as 0.74 and 0.30. Here, we present the results from replication of the following experiment for the two traits at two different settings 30 times. A random sample of 1500 lines was selected in the training sample. The whole genome was divided in a similar fashion to that displayed in Figure 1 with a depth of three. Two different multiple-kernel models were obtained by using two vs. three splits at each hierarchical level following the split by chromosomes (i.e., each chromosome was divided into four or nine regions). In addition, a Gaussian kernel model and a linear kernel model are fitted. The boxplots comparing accuracies of the models and the mean importance scores for different regions from the multiple-kernel models over the 30 replications are displayed in Figure 4 and Figure 5. For both traits, the multiple-kernel model is substantially more accurate. In addition, the association derived as an output of this model supports the previously reported association of body weight-related traits to the X chromosome (Dragani et al. 1995).
Figure 4.
Mouse data: accuracies and associations for multiple-kernel (MK) model and accuracies for linear kernel (Lin) and Gaussian kernel (Gaus) models for “weight at age of 6 weeks (grams).” (A) Four regions per chromosome. (B) Nine regions per chromosome.
Figure 5.
Mouse data: accuracies and associations for multiple-kernel (MK) model and accuracies for linear kernel (Lin) and Gaussian kernel (Gaus) models for “growth slope between 6 and 10 weeks of age (grams per day).” (A) Four regions per chromosome. (B) Nine regions per chromosome.
Example 3 (barley data):
α-Tocotrienols are in the class of fat-soluble chemical compounds related to vitamin E activity. Vitamin E deficiency is connected to many health problems; therefore, increased levels of α-tocotrienols are a desirable property for crops. In an experiment carried out by the Barley Coordinated Agriculture Project during the years 2006 and 2007, α-tocotrienol levels for 1723 barley lines were recorded in a total of four environments (2 years and three locations). A total of 2114 markers on seven chromosomes were available for the analysis.
We sampled 1500 lines for training the models, and we used the rest of the lines to evaluate the fit of our models. The whole genome was divided in a similar fashion to that displayed in Figure 1 with a depth of three with two splits at each level and only the regions at the most detailed level are used for multiple-kernel model building. This is repeated 30 times. Accuracies and associations are summarized in Figure 6.
Figure 6.
Barley data: accuracies and associations for multiple-kernel (MK) (four regions per chromosome) model and accuracies for linear kernel (Lin) and Gaussian kernel (Gaus) models for tocotrienol levels.
Example 4 (maize data):
These data are given in Romay et al. (2013) and were also analyzed in Wimmer et al. (2013a,b). A total of 68,120 markers on the 2279 U.S. national inbred maize lines and their phenotypic means for degree days to silking compose the data set. Accuracies for multiple kernel (MK) (five regions per chromosome), linear kernel (Lin), and Gaussian kernel (Gaus) models for degree days to silking and the importance scores from the MK model are displayed in Figure 7 and Figure 8.
Figure 7.
Maize data: accuracies and associations for multiple-kernel (MK) (25 regions per chromosome) model and accuracies for linear kernel (Lin) and Gaussian kernel (Gaus) models for degree days to silking.
Figure 8.
Maize data: accuracies for multiple-kernel (MK) (36 regions per chromosome), linear kernel (Lin), and Gaussian kernel (Gaus) models for degree days to silking.
Example 5 (simulated phenotypes: accuracies):
The purpose of this simulation study is to compare the accuracies of the SPMM with single Gaussian kernel and the multiple-kernel models for traits that are generated by short-range to long-range interactions. For each replication and each setting of the experiment a set of 2000 genotypes was generated using the R Package “hypred” (Technow 2013), starting by randomly mating two founders with three chromosomes each of length 1 M and 1000 markers per chromosome. After random mating for 300 generations and then selection on a complex quantitative trait over 200 generations with selection intensity 50%, followed by another 100 generations of random mating, the final traits for the analysis were generated using short-range to long-range epistatic marker effects.
The final phenotypes in this example were generated randomly for each replication of the experiment by the following scheme: Given the set markers and the corresponding map, we first randomly select six markers and assign these markers effects from a zero-centered normal distribution with variance one. Second, in an iterative fashion, we select one of the markers selected in the first step, say , and two additional markers from previously not selected markers, say and , and make an interaction term using the formula
| (8) |
where r has a zero-centered normal distribution with variance 3 for the low-interaction case and up to 6 for the high-interaction case. , and independently and identically distributed random variables have a zero-centered normal distribution with variance 1 and w is selected at random from the set with equal probability. While generating the local interaction scenarios, the three markers that generate the interaction are restricted to the same chromosome and the maximum distance between these markers is restricted to 1, 4, 10, 20, 30, or 50 cM, depending on the local interaction scenario. For the genome-wide case, no restrictions were imposed while generating the interactions. When a total of 100 interaction effects are generated, the genotypic value of an individual is calculated by adding the main and the interaction effects. An independent error term from a zero-centered normal distribution is added to each genotypic value to obtain the final phenotypic values while the error variance is chosen such that the heritability of the trait is 1/2. Finally, the markers that were used to generate the phenotypic values were excluded from the marker set before further analysis.
After the genotypes and the phenotypes are generated, a training sample of size 500, 1000, or 1500 is selected at random to estimate the phenotypes of the remaining individuals (test set) with the following models: A single Gaussian kernel model (SK) and multiple kernel models with 2, 5, 10, 20, or 30 splits per chromosome (MK_2, MK_5, …, MK_30). The performances of the models measured in terms of mean correlations between the true and the predicted values for the test data over 50 replications are summarized by the plots in Figure 9.
Figure 9.
Simulations: accuracies of models are compared for traits that are generated by short-range to long-range interactions. On the horizontal axis the scenarios are displayed in increasing order from left to right with respect to the range of interactions (, and 50 cM and genome-wide). The vertical axis displays the accuracy.
It is clear from these results that as the range or the intensity of the interactions increases, the accuracies of all the models decrease. As expected, all models get more accurate as the sample size increases. For all of the cases, there is at least one multiple-kernel model that outperforms the single-kernel model, and the optimal number of splits seems to be a function of interaction range and the sample size. As the interaction range decreases, a larger number of splits produce more accurate models. On the other hand, for small sample sizes a relatively low number of splits should be used. The locally epistatic models adequately capture local interactions, leaving out the irrelevant parts of the genome, and obtain high accuracies.
Example 6 (simulated phenotypes: associations):
The purpose of this second simulation is to evaluate the performance of the importance scores obtained from the multiple-kernel models. For each replication of the experiment a set of 500, 750, 1000, or 1500 genotypes was generated using the R Package hypred (Technow 2013), starting by randomly mating two founders with three chromosomes each of length 1 M and 1000 markers per chromosome. After random mating for 300 generations, the genotypic values were simulated for the individuals by randomly selecting two loci per chromosome and assigning the minor allele at each of these loci an effect of one. The phenotypic value for each individual was obtained by adding to the genotypic values an independent error from a zero-centered normal distribution with a certain variance so that the heritability of the trait was 1/2. For each of these data sets, multiple-kernel models with , or 50 splits per chromosome were trained. The whole experiment was replicated 100 times.
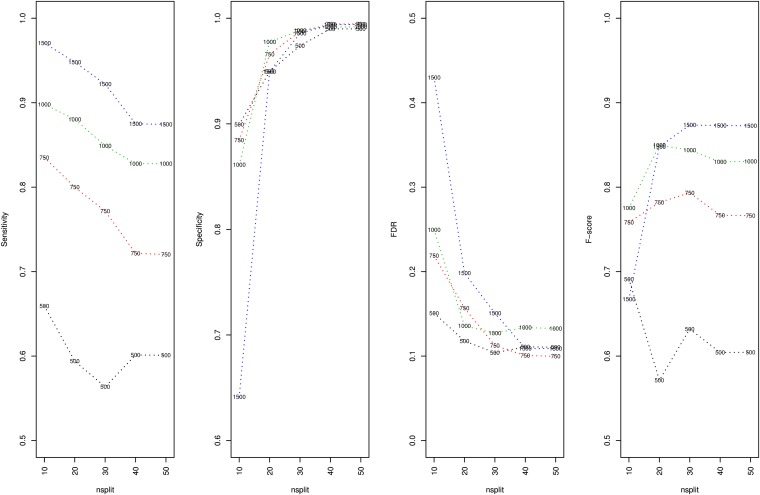
The importance scores of the regions obtained from the multiple-kernel models cannot be directly used in formal hypothesis testing for association. Nevertheless, they provide important information about the contribution of genomic regions. For each of the replications of the experiment and the multiple-kernel models with differing numbers of splits per chromosome, we made a confusion matrix from the true classification of regions based on whether or not they contained an actual QTL and the classification based on whether the regions had zero or nonzero importance scores. In Figure 10, we report the results of our experiments, using four measures of classification model performance averaged over the 100 replications. Sensitivity measures the proportion of the regions that contain QTL, which are correctly identified. Specificity measures the proportion of the regions that contain no QTL that are correctly identified. The false discovery rate (FDR) measures the proportion of falsely identified positives to all positives that are identified. The F score is a single measure of performance that is the harmonic mean of precision and sensitivity where precision is defined as one minus the FDR. Although these results are promising, they should be interpreted with caution: The elastic-net penalties we have used are tuned for accuracy and as the sample size increases more terms are allowed to enter the model as an artifact of linkage disequilibrium (LD). Having a nonzero importance score does not immediately imply a formal rejection of no effect in a region since this would also depend on many other things like the size of the importance score, the sample size, the number of regions being fitted, the LD in the population, etc.
Figure 10.
Simulations: four measures of classification model performance averaged over the 100 replications for sample sizes 500, 750, 1000, and 1500 and multiple-kernel models with 10, 20, 30, 40, or 50 splits per chromosome.
In summary, the importance scores obtained from the multiple-kernel models are indicative of the regions that include QTL. As the sample size increases or the number of splits decreases, the ability to identify regions (sensitivity) improves. However, this is accompanied by a deterioration in the ability to correctly identify regions with no QTL (specificity and FDR). According to the F score, the overall performance improves as the sample size increases. For larger sample sizes, increasing the number of splits increases the F score. However, it seems like this trend might not be the same for smaller sample sizes.
Example 7 (simulated phenotypes: number of splits):
The number of splits is an important hyperparameter affecting the accuracies. In this example, we check the plausibility of a cross-validation-based method for identifying the correct number of splits. For each of the 30 replications of the experiment a set of 1000 genotypes with 1000 markers on each of the three chromosomes was generated as in Example 6 (simulated phenotypes: associations). The marker set was divided into three, five, or seven regions per chromosome and the trait values for the genotypes were generated by summing randomly generated locally epistatic effects from these regions and an independent error term with variance adjusted so that the heritability of the trait was 0.5. Models with 1–10 numbers of splits per chromosome were fitted to the genotypic and phenotypic data of a randomly selected training set of genotypes of size 800. The remaining genotypes were assigned to the test set. During the model-fitting process, a 10-fold cross-validated accuracy measured in terms of correlation was obtained within the training set for each of these models. In addition, the accuracies of the models were calculated in the test data. The results of this experiment are summarized in Figure 11. The estimates of prediction accuracy obtained within the training set followed the same trend as the accuracies of the models calculated in the test data. The highest accuracies in both cases were observed at the true number of splits.
Figure 11.
Simulations: the estimated prediction accuracies (measured by correlation, r) by cross-validation in the training set for number of splits = 1–10 and estimated prediction accuracies in the test set for the same splits. The red vertical dotted line indicates the correct number of splits for each case.
Results and Discussion
The locally epistatic models proposed in this article have good accuracy and explanatory value. Although the final results seem to depend on the complexity of the trait and population structure, similar or better accuracies were obtained for a number of populations compared to single-kernel models. The multiple-kernel models have the additional advantage that only a small fraction of genomic regions are used in the final model and the importance scores for these regions are readily available as a model output.
The locally epistatic models incorporate only the additive and local epistatic genetic contributions and exclude genome-wide interactions. The breeder can have confidence that these effects can be passed on to several generations. In addition, the information about the importance of genome regions produced from these models is also relevant since it points to regions that are relevant for introgression.
The approaches introduced in this article allow us to use the markers in naturally occurring blocks. The multiple-kernel approach overcomes the memory problems that we might incur when the number of markers is very large by loading only subsets of data in the memory at a time. When studying the interactions, an order of magnitude of reduction of complexity can be obtained by studying only the interactions among the blocks instead of interactions among single loci. This block interaction approach will be a subject for future study.
The local kernels use information collected from regions of the genome and, because of linkage, will not be affected by a few missing or erroneous markers. In our examples, we have used the mean imputation to impute missing markers.
The accuracy of the multiple-kernel model compared to its genome-wide counterparts partially depends on the trait architecture as illustrated by the contrast between the examples where a trait is affected only by a few regions (the multiple-kernel model has high accuracies) or effects distributed homogeneously to the entire genome (genome-wide models have higher accuracies).
Another factor that influences the accuracies is the strength and structure of interactions. If the interactions are, in fact, local, the multiple-kernel models outperform the single-kernel ones. In conclusion, the locally epistatic models are most accurate when a few major genes with local interactions generate the trait under study.
We can obtain local kernel matrices by defining regions in the genome and calculating a separate kernel matrix for each group and region. These regions can be overlapping, hierarchical, or discrete. If some markers are associated with each other in terms of linkage or function, it might be useful to combine them together. The whole genome can be divided physically into chromosomes, chromosome arms, or linkage groups. Further divisions could be based on recombination hotspots or just merely based on local proximity. We could calculate a separate kernel for introns and exons and noncoding, promoter, or repressor sequences. We can also use a grouping of markers based on their effects on low-level traits like lipids, metabolites, and gene expressions or based on their allele frequencies. When some markers are missing for some individuals, we can calculate a kernel for the presence and absence states for these markers. When no such guide is present, we can use a hierarchical clustering of the variables. It is even possible to incorporate group membership probabilities for markers, so the markers have varying weights in different groups. We are in the process of preparing another article in which different sources of marker annotations are used with the multiple-kernel models.
The hierarchical setup defines nested regions from coarse to fine, the regions are divided into subregions, and this is repeated to the desired detail level. An advantage to using a hierarchy is the availability of hierarchical testing procedures that have good cost/power properties (Blanchard and Geman 2005). Multiple-testing procedures where coarse to fine hypotheses are tested sequentially have been proposed to control the family-wise error rate or false discovery rate (Reiner et al. 2003; Meinshausen 2008). For example, to deal with the inflation of the error probabilities due to testing k hypotheses in the hierarchical setup, Meinshausen’s hierarchical testing procedure (Meinshausen 2008) controls the family-wise error by adjusting the significance levels of single tests in the hierarchy. The procedure starts testing the root node at level α. When a parent hypothesis is rejected, one continues with testing all the child nodes of that parent while the significance level to be used at each node is adjusted by a factor proportional to the number of variables in that node. Recently, there have also been some advances in significance testing for the lasso (Lockhart et al. 2014) regression. These procedures can be used with the multiple-kernel models to obtain formal significance tests with desirable properties. An article concerning the formal hypothesis testing with the multiple-kernel models will also be ready shortly.
Supplementary Material
Acknowledgments
This research was supported by the U.S. Department of Agriculture-NIFAT (The National Institute of Food and Agriculture)-AFRI (The Agriculture and Food Research Initiative) Triticeae Coordinated Agricultural Project, award 2011-68002-30029.
Footnotes
Available freely online through the author-supported open access option.
Supporting information is available online at http://www.genetics.org/lookup/suppl/doi:10.1534/genetics.114.173658/-/DC1.
Communicating editor: F. Zou
Literature Cited
- Akdemir, D., and O. U. Godfrey, 2014 EMMREML: Fitting Mixed Models with Known Covariance Structures R Package Version 2.0. Available at: http://CRAN.R-project.org/package=EMMREML.
- Amemiya T., 1977. A note on a heteroscedastic model. J. Econom. 6(3): 365–370. [Google Scholar]
- Bach, F. R., G. R. Lanckriet, and M. I. Jordan, 2004 Multiple kernel learning, conic duality, and the SMO algorithm, p. 6 in Proceedings of the Twenty-First International Conference on Machine Learning. ACM., New York, NY DOI: 10.1145/1015330.1015424. [Google Scholar]
- Blanchard G., Geman D., 2005. Hierarchical testing designs for pattern recognition. Ann. Stat. 33: 1155–1202. [Google Scholar]
- Breitling R., Li Y., Tesson B. M., Fu J., Wu C. et al, 2008. Genetical genomics: spotlight on QTL hotspots. PLoS Genet. 4(10): e1000232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantor R. M., Lange K., Sinsheimer J. S., 2010. Prioritizing GWAS results: a review of statistical methods and recommendations for their application. Am. J. Hum. Genet. 86(1): 6–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y., Lübberstedt T., 2010. Molecular basis of trait correlations. Trends Plant Sci. 15(8): 454–461. [DOI] [PubMed] [Google Scholar]
- de Los Campos G., Gianola D., Rosa G. J., Weigel K. A., Crossa J., 2010. Semi-parametric genomic-enabled prediction of genetic values using reproducing kernel Hilbert spaces methods. Genet. Res. 92(04): 295–308. [DOI] [PubMed] [Google Scholar]
- Demidenko, E., 2004 Mixed Models: Theory and Applications (Wiley Series in Probability and Statistics). Wiley-Interscience, New York. [Google Scholar]
- Dragani T., Zeng Z.-B., Canzian F., Gariboldi M., Ghilarducci M. et al, 1995. Mapping of body weight loci on mouse chromosome x. Mamm. Genome 6(11): 778–781. [DOI] [PubMed] [Google Scholar]
- Endelman J. B., 2011. Ridge regression and other kernels for genomic selection with R package rrBLUP. Plant Genome 4(3): 250–255. [Google Scholar]
- Friedman, J., T. Hastie, N. and R. Tibshirani, 2010 Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 33: 1–22. [PMC free article] [PubMed] [Google Scholar]
- Friedman, J., T. Hastie, N. Simon, and R. Tibshirani, 2013 glmnet: Lasso and Elastic Net Regularized Generalized Linear Models; 2008. R Language Available at: http://www.jstatsoft.org/v33/i01.
- Gardner K. M., Latta R. G., 2007. Shared quantitative trait loci underlying the genetic correlation between continuous traits. Mol. Ecol. 16(20): 4195–4209. [DOI] [PubMed] [Google Scholar]
- Gianola, D., and G. de Los Campos, 2008. Inferring genetic values for quantitative traits non-parametrically. Genet. Res. 90(06): 525–540. [DOI] [PubMed] [Google Scholar]
- Gianola D., Van Kaam J., 2008. Reproducing kernel Hilbert spaces regression methods for genomic assisted prediction of quantitative traits. Genetics 178: 2289–2303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- González-Camacho J., de Los Campos G., Pérez P., Gianola D., Cairns J. et al, 2012. Genome-enabled prediction of genetic values using radial basis function neural networks. Theor. Appl. Genet. 125(4): 759–771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habier D., Fernando R., Dekkers J., 2007. The impact of genetic relationship information on genome-assisted breeding values. Genetics 177: 2389–2397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartley H. O., Rao J., 1967. Maximum-likelihood estimation for the mixed analysis of variance model. Biometrika 54(1–2): 93–108. [PubMed] [Google Scholar]
- Harville D., 1977. Maximum likelihood approaches to variance component estimation and to related problems. J. Am. Stat. Assoc. 72(358): 320–338. [Google Scholar]
- Hayes B., Bowman P., Chamberlain A., Goddard M., 2009. Invited review: genomic selection in dairy cattle: progress and challenges. J. Dairy Sci. 92(2): 433–443. [DOI] [PubMed] [Google Scholar]
- Heffner E. L., Jannink J.-L., Iwata H., Souza E., Sorrells M. E., 2011. Genomic selection accuracy for grain quality traits in biparental wheat populations. Crop Sci. 51(6): 2597–2606. [Google Scholar]
- Heslot N., Yang H.-P., Sorrells M. E., Jannink J.-L., 2012. Genomic selection in plant breeding: a comparison of models. Crop Sci. 52(1): 146–160. [Google Scholar]
- Holland J. H., 1975. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. University of Michigan Press. Ann Arbor, MI. [Google Scholar]
- Jarquín D., Crossa J., Lacaze X., Du Cheyron P., Daucourt J. et al, 2013. A reaction norm model for genomic selection using high-dimensional genomic and environmental data. Theor. Appl. Genet. 127: 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimeldorf G., Wahba G., 1970. A correspondence between Bayesian estimation on stochastic processes and smoothing by splines. Ann. Math. Stat. 41: 495–502. [Google Scholar]
- Lee S. H., van der Werf J. H., Hayes B. J., Goddard M. E., Visscher P. M., 2008. Predicting unobserved phenotypes for complex traits from whole-genome snp data. PLoS Genet. 4(10): e1000231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legarra A., Robert-Granié C., Manfredi E., Elsen J.-M., 2008. Performance of genomic selection in mice. Genetics 180: 611–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lockhart R., Taylor J., Tibshirani R. J., Tibshirani R., 2014. A significance test for the lasso. Ann. Stat. 42(2): 413–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenzana R. E., Bernardo R., 2009. Accuracy of genotypic value predictions for marker-based selection in biparental plant populations. Theor. Appl. Genet. 120(1): 151–161. [DOI] [PubMed] [Google Scholar]
- Meinshausen N., 2008. Hierarchical testing of variable importance. Biometrika 95(2): 265–278. [Google Scholar]
- Meuwissen, T. HHayes B. J., Goddard M. E., 2001. Prediction of total genetic value using genome-wide dense marker maps. Genetics 157: 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team, 2014 R: A Language and Environment for Statistical Computing Vienna, Austria. Available at: http://www.R-project.org.
- Rao C. R., 1971. Estimation of variance and covariance components MINQUE theory. J. Multivariate Anal. 1(3): 257–275. [Google Scholar]
- Reiner A., Yekutieli D., Benjamini Y., 2003. Identifying differentially expressed genes using false discovery rate controlling procedures. Bioinformatics 19(3): 368–375. [DOI] [PubMed] [Google Scholar]
- Robinson G., 1991. That BLUP is a good thing: the estimation of random effects. Stat. Sci. 6(1): 15–32. [Google Scholar]
- Rodrıguez, P. P., and G. de Los Campos, 2012 BGLR: A Statistical Package for Whole-Genome Regression Available at: http://CRAN.R-project.org/package=BGLR. [DOI] [PMC free article] [PubMed]
- Romay M. C., Millard M. J., Glaubitz J. C., Peiffer J. A., Swarts K. L. et al, 2013. Comprehensive genotyping of the USA national maize inbred seed bank. Genome Biol. 14(6): R55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schölkopf, B. and A. Smola, 2001 Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond. MIT Press, Cambridge, MA.
- Sonnenburg S., Rätsch G., Schäfer C., Schölkopf B., 2006. Large scale multiple kernel learning. J. Mach. Learn. Res. 7: 1531–1565. [Google Scholar]
- Speed T., 1991. [That BLUP is a good thing: the estimation of random effects]: comment. Stat. Sci. 6(1): 42–44. [Google Scholar]
- Technow, F., 2014 hypred: Simulation of Genomic Data in Applied Genetics. R Package Version 0.5.
- Tusell L., Pérez-Rodríguez P., Forni S., Gianola D., 2014. Model averaging for genome-enabled prediction with reproducing kernel Hilbert spaces: a case study with pig litter size and wheat yield. J. Anim. Breed. Genet. 131: 105–115. [DOI] [PubMed] [Google Scholar]
- Valdar W., Solberg L. C., Gauguier D., Burnett S., Klenerman P. et al, 2006. Genome-wide genetic association of complex traits in heterogeneous stock mice. Nat. Genet. 38(8): 879–887. [DOI] [PubMed] [Google Scholar]
- VanRaden P., Van Tassell C., Wiggans G., Sonstegard T., Schnabel R. et al, 2009. Invited review: reliability of genomic predictions for North American Holstein bulls. J. Dairy Sci. 92(1): 16–24. [DOI] [PubMed] [Google Scholar]
- Weber A. L., Briggs W. H., Rucker J., Baltazar B. M., de Jesus Sánchez-Gonzalez J. et al, 2008. The genetic architecture of complex traits in teosinte (zea mays ssp. parviglumis): new evidence from association mapping. Genetics 180: 1221–1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wimmer, V., T. Albrecht, H.-J. Auinger, and M. V. Wimmer, 2013a R Package “synbreedData”. Available at: http://CRAN.R-project.org/package=synbreedData.
- Wimmer V., Lehermeier C., Albrecht T., Auinger H.-J., Wang Y. et al, 2013b Genome-wide prediction of traits with different genetic architecture through efficient variable selection. Genetics 195: 573–587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu S., 2013. Genetic mapping and genomic selection using recombination breakpoint data. Genetics 195: 1103–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao K., Tung C.-W., Eizenga G. C., Wright M. H., Ali M. L. et al, 2011. Genome-wide association mapping reveals a rich genetic architecture of complex traits in oryza sativa. Nat. Commun. 2: 467. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.