A high-resolution XAS study of aqueous Cu(II) in liquid and frozen solutions: Pyramidal, polymorphic, and non-centrosymmetric

Abstract

High-resolution EXAFS (k = 18 Å⁻¹) and MXAN XAS analyses show that axially elongated square pyramidal [Cu(H₂O)₅]²⁺ dominates the structure of Cu(II) in aqueous solution, rather than 6-coordinate JT-octahedral [Cu(H₂O)₆]²⁺. Freezing produced a shoulder at 8989.6 eV on the rising XAS edge and an altered EXAFS spectrum, while 1s → 3d transitions remained invariant in energy position and intensity. Core square pyramidal [Cu(H₂O)₅]²⁺ also dominates frozen solution. Solvation shells were found at ∼3.6 Å (EXAFS) or ∼3.8 Å (MXAN) in both liquid and frozen phases. However, MXAN analysis revealed that about half the time in liquid solution, [Cu(H₂O)₅]²⁺ associates with an axially non-bonding 2.9 Å water molecule. This distant water apparently organizes the solvation shell. When the 2.9 Å water molecule is absent, the second shell is undetectable to MXAN. The two structural arrangements may represent energetic minima of fluxional dissolved aqueous [Cu(H₂O)₅]²⁺. The 2.9 Å trans-axial water resolves an apparent conflict of the [Cu(H₂O)₅]²⁺ core model with a dissociational exchange mechanism. In frozen solution, [Cu(H₂O)₅]²⁺ is associated with either a 3.0 Å axial non-bonded water molecule or an axial ClO₄⁻ at 3.2 Å. Both structures are again of approximately equal presence. When the axial ClO₄⁻ is present, Cu(II) is ∼0.5 Å above the mean O₄ plane. This study establishes [Cu(H₂O)₅]²⁺ as the dominant core structure for Cu(II) in water solution, and is the first to both empirically resolve multiple extended solution structures for fluxional [Cu(H₂O)₅]²⁺ and to provide direct evidence for second shell dynamics.

I. INTRODUCTION

Ever since the opening provided by the neutron diffraction and molecular dynamics study of Pasquarello et al.,¹ the solution structure of [Cu(aq)]²⁺ has come under renewed and intensive scrutiny.^2–14 All studies agree on the stable presence of four equatorial water ligands, which exhibit a uniform Cu–O_w distance of about 1.96 Å. However, studies of the very rapid solution dynamics^15–17 have typically reported difficulties in detecting the number and even presence of the axial water ligands.¹⁸

X-ray spectroscopy can be used to query the average structural or electronic environment of any element within virtually any milieu.¹⁹ EXAFS is methodologically well established. MXAN applies Extended Continuum Multiple Scattering (ECMS) theory to the first 200 eV of x-ray absorption (XAS) spectra, including the x-ray absorption near-edge structure (XANES) region. The symmetry constraints of XANES intensities allow MXAN analysis to yield both distances and angles to proximate scatterers around the x-ray absorber.^20–23 Ideally, a local structural model of near x-ray diffraction resolution is produced. We have recently combined the EXAFS and MXAN x-ray spectroscopic approaches in an attempt to resolve the structure of dissolved aqueous Cu(II) complex ions.^9,24,25 In this combination, EXAFS modeling is used to provide physically grounded initial-guess structures to be tested and refined by means of MXAN fits to the full XAS spectrum, including the XANES plus continuum energy region to 200 eV.

Previously, combined EXAFS and MXAN studies found the complex ions of Cu(II) in aqueous ammonia or imidazole solutions to be strongly solvated axially elongated square pyramids, each with a single axial water ligand at a distance of about 2.18 Å or 2.13 Å, respectively. These were accompanied in the transverse axial position by a non-bonded ∼3 Å distant N/O scatterer that could only be described as a localized solvating molecule, most likely water. For each complex ion, clear evidence of a solvation shell was also found. In the case of the ammonia complex, the solvation shell contributed strong multiple scattering features to the rising K-edge.

For dissolved [Cu(aq)]²⁺ itself, initial MXAN studies were unambiguous in favoring a homologous axially elongated square pyramid, [Cu(H₂O)₅]²⁺ (Cu–O_ax = 2.35 Å), as the dominant average structure in liquid aqueous solution.^2,8 Square pyramidal five-coordinate Cu(II) has since also been found to be the predominant structure in methanol and DMSO.²⁶ These results are not inconsistent with gas-phase clustering experiments indicating preferred [Cu(H₂O)₄]²⁺ and [Cu(H₂O)₈]²⁺ assemblies,^10,27 when it is considered that the solution-phase ground state of metal ions includes extended solvent shells that must merge into bulk solvent.^28–30

Here, we report a new combined EXAFS and MXAN structural study of dissolved [Cu(ClO₄)₂] in both liquid and frozen aqueous 1M HClO₄. Use of low-Zn CuO to prepare these solutions extended useful EXAFS up to k = 18 Å⁻¹, allowing exceptionally high resolution. The average first shells of water molecules about Cu(II) in liquid and frozen milieus are described, compared, and contrasted. The high-resolution XAS further reveals the organization of a previously undetected second water shell. Elements of the fluxional behavior of solution-phase cupric ion are also evident.

II. MATERIALS AND METHODS

A. Sample preparation

Stock 0.10M Cu(ClO₄)₂ in 1M HClO₄ was prepared using 99.995% CuO (Aldrich Chemicals, lot # 08909TD) containing 0.26 ppm Zn by the supplier certificate of ICP analysis. All glassware was pre-washed using dilute low-zinc 37% HCl (Aldrich Chemicals, Lot # 16391JH, <1 ppm total metals) in 18 MΩ doubly deionized water followed by several rinses using the same deionized water.

CuO, 99.995%, (406.3 mg, 5.1 mmol; Aldrich Chemicals, Lot #08909TD, 0.26 ppm Zn) was sonicated overnight with 5.2 ml of 69.4% HClO₄ (60 mmol; Baker Analyzed; <1 ppm metals) in 39 ml total volume made with 18 MΩ water, within a 50 ml glass mixing cylinder. The resulting light blue solution was finally diluted to 50.0 ml again using 18 MΩ water to yield the stock solution of 0.10M Cu(ClO₄)₂ in 1M HClO₄.

Samples of 0.10 M Cu(ClO₄)₂ in 1M HClO₄ were prepared for measurement as a liquid solution at room temperature or as a frozen solution at 10 K. The liquid solution XAS sample was contained within a Teflon spacer cell of 2 mm thickness, with cell windows consisting of 35 μm thickness Kapton tape. The frozen solution was prepared within a 2 × 2 × 20 mm Delrin pinhole cell faced with a 35 μm thickness Kapton window, and then flash-frozen by immersion in a freezing iso-pentane slush (−159.9 C).

B. XAS measurements

Liquid and frozen copper K_α fluorescence excitation XAS spectra were measured on Stanford Synchrotron Radiation Lightsource (SSRL) beam line 7-3 using a Si(220) monochromator, fully tuned at 9684 eV or 10 248 eV and optimized at 9200 eV or 9500 eV, respectively, and with ring conditions of 3 GeV and 100 or 300 mA current. Baseline I₀ was measured using an in-line nitrogen-filled ionization chamber situated in front of the sample.

The frozen solution sample was held at ∼10 K using an Oxford Instruments CF1208 continuous flow liquid helium cryostat. The sample was positioned 45° to the beam and K_α fluorescence excitation XAS spectra were measured using a Canberra 30-element liquid-nitrogen-cooled germanium array detector. Beam size was set to 1 × 5 mm using in-hutch slits. Four beam-spots were chosen per frozen sample, and two XAS scans were measured per spot. The second scans always showed a trace of photo-reduction, judged by slightly increased intensity in the 8980-8985 eV range. Extent of reduction was estimated by comparing the two-scan XAS difference spectrum to the 0.74 normalized unit intensity of the prominent 8983 eV rising K-edge XAS shoulder of Cu₂O, taken as a model for the XAS of [Cu(I)(H₂O)₂]⁺.^11,31,32 The difference intensity maximum of 0.0082 unit implied average 1.1% photo-reduction. If it is assumed that the 1.1% photo-reduction noted in scan 2 all occurred in scan 1, and occurred at a constant rate, then the average of each two-scan set included 1.7% Cu(I). Apart from the small change in intensity at the base of the rising K-edge, the reduction was otherwise invisible to a comparative XAS overlay and had a negligible effect on the overall XAS. Thus, all eight scans were averaged into the XAS used for analysis.

The liquid samples measured at room temperature were positioned at 0° relative to the x-ray beam. K-edge XAS were collected as transmission spectra using an in-line nitrogen-filled ionization chamber (I₁) behind the sample as the detector. For each data set, a copper foil positioned after the I₁ chamber provided the calibration XAS, which was simultaneously measured using a third in-line nitrogen-filled ionization chamber (I₂). The second and third scans again showed traces of photo-reduction. The total difference intensity increase in the third scan was 0.002 normalized unit in the 8980-8985 eV range. This is equivalent to an average of 0.18% Cu(I), again using the XAS of Cu₂O as a standard. The three scans were again otherwise superimposable, and thus were averaged to produce the XAS spectrum used in subsequent analysis; XAS average Cu(I) ∼0.3%.

Figures S1.1 and S1.2 in the supplementary material compare XAS spectra from successive scans of liquid- and frozen-phase 0.10M Cu(ClO₄)₂ in 1M HClO₄.⁹² Figure S1.3 compares analogous scans of EXAFS spectra.⁹²

XAS spectra were analyzed using the program EXAFSPAK, which was written by Professor Graham George, University of Saskatchewan and is available free of charge on the SSRL website: http://ssrl.slac.stanford.edu/~george/exafspak/exafs.htm. XAS spectra were calibrated against the first inflection of the first derivative of the copper foil rising K-edge XAS, set to 8980.30 eV. Normalization of the XAS spectra and extraction of EXAFS was carried out using the program PySpline, which was written by Dr. Adam Tenderholt and is available as open source software: http://pyspline.sourceforge.net.³³

The XAS background subtraction was performed by fitting a second order polynomial to the pre-rising-edge energy region of the energy-calibrated XAS spectrum, and then subtracting it from the entire spectrum. The fitted pre-edge energy range was chosen empirically to produce the best match between the slopes of the data and of the polynomial. A polynomial spline function was then fitted to the background-subtracted XAS spectrum over the entire post-edge energy range, and extrapolated on through the pre-edge energy region. For the liquid solution XAS, the spline knot-points and polynomial orders were (eV, polynomial order): 9021.94, 2; 9217.16, 3; 9555.08, 3; 9866.69, 3; 10 208.78 eV. For the frozen solution XAS, these were: 9021.61, 2; 9206.18, 3; 9491.86, 3; 9790.46, 3; 10 035.03, 3; 10 544.18, 3; 11 380.94. The choice of spline included the criterion that it pass through the XANES features at unit intensity. Normalized XAS spectra were obtained by dividing the baseline-subtracted XAS by the fitted polynomial spline.

C. XAS fits

Pseudo-Voigt fits to the XANES energy region of the XAS spectra were carried out using the EDG_FIT program within EXAFSPAK. Pseudo-Voigt energy positions, half-widths, and intensities were floated, while the Gaussian-Lorentzian ratio was fixed at 0.50. The pre-edge feature representing the 1s → 3d transition was fitted separately over the energy range 8968-8987 eV (liquid solution) or 8968-8989 eV (frozen solution). The full XANES was fitted over the range 8968-9020 eV. The 1s → 3d pseudo-Voigt from the short-range fit was included in the full-range fit and fixed in energy position and intensity. Small differences between the background intensity of the pre-edge fits and the full fits required small adjustments to the parameters of the fixed pre-edge pseudo-Voigt. The parameters from the final full fit to the XANES spectrum of Cu(II) in frozen 1M HClO₄ provided the first guess for the full fit to the XANES of Cu(II) in liquid 1M HClO₄.

D. EXAFS fits

FEFF8 was used for calculation of EXAFS phase and amplitude functions, employing structural models produced using CS Chem3D Pro (CambridgeSoft Corp., Cambridge, MA). EXAFS spectra were fit over the range, k = 2-18 Å⁻¹ or k = 2-17 Å⁻¹, using the program OPT within the EXAFSPAK suite. The methodology has been fully described previously.^24,25 EXAFS goodness-of-fit is

$${\displaystyle F={[\sum k^6{({\mathrm{\chi }}_{\exp }-{\mathrm{\chi }}_{\mathit{calc}})}^2/\sum k^6{\mathrm{\chi }}_{\exp }^2]}^{1/2}.}$$ (1)

The expected resolution between shells, given by ΔR = π/2δk, where δk is the k-range of the fitted data in Å⁻¹, is 0.1 Å for each of the fitting ranges.

E. MXAN fits

Normalized K-edge XAS spectra were fit over the relative energy range E-E₀ = − 7.5 < ΔeV < 200, where E₀ = 8990.00 eV. The ECMS theory of the MXAN method has been described in detail.^20,23,34 The muffin tin (MT) approximation was used for the atomic potentials. The effects of the non-MT corrections on XANES calculations are still not well understood. Nevertheless, evidence exists that their influence, if present, is confined to the very low energy part of the spectrum with a very weak influence on the structural determination. This is not surprising, because for potentials of any shape it is possible to write a theory having the same formal structure as the usual MS theory but with appropriate modification of the propagators and scattering matrices.^34,35 Thus, one can write

$${\displaystyle \mathrm{\sigma }\left(E\right)\approx \mathrm{Im}\left[{(I-TG)}^{-1}T\right]=\mathrm{Im}{[T-G]}^{-1},}$$ (2)

where σ(E) is the cross section of energy calculated by MXAN, I is the identity $\mathrm{matrix}=1,T$ is the T-matrix of the atomic cluster, G is the photoelectron wave propagator, and Im denotes the imaginary part of the expression. In the correction, the quantities in Eq. (2) are re-expressed as, $T=T_a^{-1}+\mathrm{\Delta }T,\mathit{and}G=G_{MT}+\mathrm{\Delta }G$. $T_a^{-1}\mathit{and}{G}_{MT}$ are the usual quantities calculated within the MT approximation while the corrections Δ T and Δ G are proportional to the interstitial volume. Writing Δ = ΔT + ΔG, the total cross section can be expanded in series using Δ as a parameter,

$${\displaystyle \mathrm{\sigma }\left(E\right)\approx \mathrm{Im}\left\{\sum _{n=0}^{\infty }{\left[{(\underset{a}{\overset{-1}{T}}-G_{MT})}^{-1}\mathrm{\Delta }\right]}^n{(T_a^{-1}-G_{MT})}^{-1}\right\},}$$ (3)

i.e., σ(E) = σ_MT(E) + corr(E; V_int), where V_int is the potential in the interstitial volume. In other words, the total non-MT cross section can be written as the sum of the cross section calculated in the MT approximation and corrections that decrease with the energy and depend on the potential in the interstitial volume. These corrections depend on the system and go to zero as the energy increases. Their influence is strongly reduced in fits over the energy range from the edge up to 200 eV.³⁴ Thus, the geometrical arrangements restrain the numerical results of the fitting procedure. The non-MT corrections also modify the values of the T-matrices and propagators, which likewise depend on the muffin-tin radii and the interstitial potential. This points to the possibility of mimicking the effect of the non-MT correction by judicious optimization of the radii and the potential. This consideration from theory is the basis of the potential optimization procedure normally applied to MXAN analysis.²²

MT potentials were optimized during MXAN fits to all tested models. Trans-equatorial water ligand distances were linked, as were the trans L_eq-Cu-L_ax θ-angles. Axial Cu(II)-oxygen (water) distances were either linked when testing axially symmetric models or independently floated when testing for axial asymmetry. The function minimized during the MXAN fit was R_sq, defined as

$${\displaystyle R_{\mathit{sq}}=n\frac{\sum _{i=1}^m{w}_i{\left[(y_i^{th}-y_i^{\exp }){\epsilon }_i^{-1}\right]}^2}{\sum _{i=1}^m{w}_i},}$$ (4)

where “n” is the number of independent parameters, “m” is the number of data points, “$y_i^{th}$” and “$y_i^{\exp }$” are the theoretical and experimental values of the absorption, respectively. Finally, “ε_i” is the error in each point of the experimental data set, and the parameter “w_i” is a statistical weight. When w_i = 1, the square residual function R_sq becomes the statistical χ² function. Here, w_i = 1 was assumed and the experimental error ε = constant = 1.0% of the main experimental edge jump over the whole data set. Hydrogen atoms were included in the fits. Statistical errors were calculated by the MIGRAD routine. MXAN also introduces a systematic error of 1%-2% into the bond lengths, that must be added to the MIGRAD statistical error. Atomic coordinates for the MXAN input files were derived from structural models constructed within the program CHEM 3D Pro. Final systematic error in the bond lengths for the two-site fits was calculated as the root-sum-square (r.s.s.) of 1.5% systematic error in each of the step-wise iterations (see text). A full discussion of sources of error in MXAN fits has been given elsewhere.^20–22,36

III. RESULTS

The K-edge XAS spectra of 100 mM Cu(ClO₄)₂ in liquid (RT) and frozen (10 K) 1M HClO₄ solution have been measured to exceptionally high energies. Use of ultra-pure CuO (26 ppm Zn), along with other high-purity reagents, avoided the zinc absorption artifact that plagues copper EXAFS. Copper K-edge XAS were measured to 10.2 keV (liquid solution) and 11.4 keV (frozen solution). The liquid solution EXAFS spectra contained useful oscillations to k = 18 Å⁻¹. The frozen solution EXAFS spectra included a high-k artifact that left them usable to k = 17 Å⁻¹.

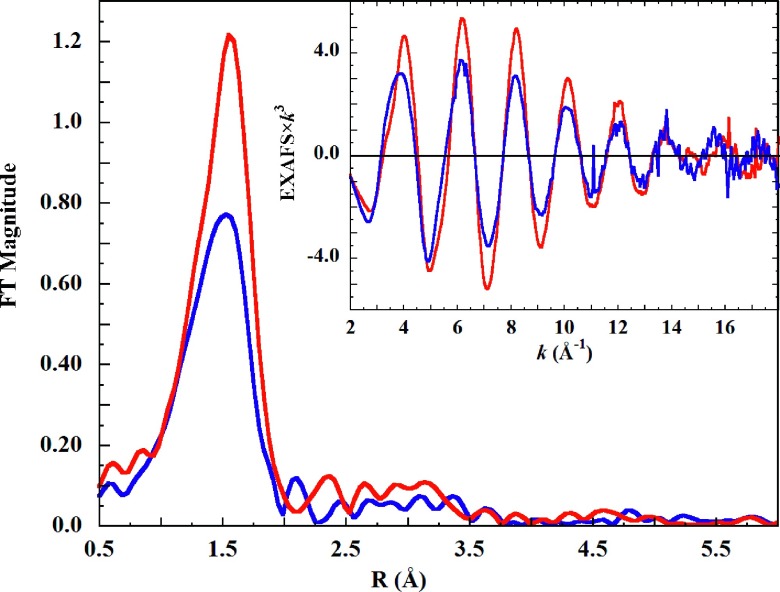
Figure 1 shows the full XAS spectra of 0.1M Cu(II) in aqueous 1M HClO₄, in liquid and frozen solution. The dissimilarity of the spectra over the entire energy range, including emergence of a strong shoulder at 8989.6 eV on the rising K-edge of the frozen solution, provides clear evidence of disparity of Cu(II) in these two phases.

FIG. 1.

K-edge XAS of 0.1M Cu(ClO₄)₂ in 1M HClO₄ aqueous solution in (blue solid line) liquid (ambient temperature) and (red solid line) frozen (10 K) phase. Inset (a): The bound-state energy region of the same Cu(II) K-edges, and the unique 8989.6 eV shoulder (arrow) in the frozen solution XAS. Inset (b): Disparity of the XAS spectra continues throughout the continuum energy region.

Further assessment was made by fitting the pre-edge and XANES spectra using pseudo-Voigts. These fits revealed that the entire 8975-8990 eV XANES energy region changed markedly between phases (Figures S2.1 and S2.2 in the supplementary material).⁹² However, the fitted pre-edge intensities, Table I, showed that the electronic state of the Cu(II) 3d_x²-_y² orbital was unaffected by freezing.

TABLE I.

[Cu(aq)]²⁺ pre-edge energy positions and intensities.^a

Phase	Pre-edge energy (eV)b	Intensityc
Liquid solution	8978.3	0.029
Frozen solution	8978.5	0.032
[Cu(H2O)6](ClO4)2d,e	8978.4	0.039
[Cu(H2O)4SO4]H2Od	8978.4	0.028

^aFrom pseudo-Voigt fits.

^bFitted energy resolution is ∼ ± 0.2 eV.

^cIntegrated area of the pseudo-Voigt in (normal fraction-eV) units; estimated precision is ±0.001 unit.

^dCrystalline solid, JT-O_h symmetry.

^eReference 9.

Therefore, the phase-induced modification of the rising edge XANES features cannot reflect an altered Cu(II) ligand field. It thus appears that the immediate rising K-edge of [Cu(aq)]²⁺ is dominated by more distant structural elements.³⁷ That is, the liquid-to-frozen phase change is accompanied by a modification of the structure surrounding the copper absorber, without any electronically important alteration of the immediate ligand environment. We return to this point below.

The K-edge EXAFS spectra of the liquid and frozen Cu(II) solutions, and their Fourier transforms, are shown in Figure 2. For both solution states, EXAFS intensity continues well past the usual zinc cutoff at k = 13 Å⁻¹. Distinct differences in phase are apparent between 2-5 Å⁻¹, and after 14 Å⁻¹.

FIG. 2.

Fourier transform of the K-edge EXAFS spectrum of 0.1M Cu(ClO₄)₂ in aqueous 1M HClO₄ solution in (blue solid line), liquid, (ambient temperature) and (red solid line), frozen (10 K) states. Inset: The EXAFS spectra of the same solutions.

The amplitude of the liquid phase EXAFS is lower than that of the frozen phase (Figure 2, inset). If this attenuation was due only to larger thermal motions in the liquid phase, the ratio of the liquid-to-frozen EXAFS amplitudes would be proportional to e^−2k2γ, where k is the photoelectron wave vector and γ is Δσ², the difference in ligand mean displacement (Eq. (S1) in the supplementary material⁹²). However, the ratio of EXAFS amplitudes does not follow an exponential profile (Figure S3.1⁹²). Therefore, a phase-induced structural difference is again implied.

In the following structural studies, EXAFS modeling was carried out first. The final EXAFS structural models were then used as initial guesses for the MXAN fits. Unlike EXAFS, MXAN analysis includes the XANES energy region and is sensitive to scattering angle. Therefore, the final structural models are from MXAN analysis. In view of past results,^{1,2,7,8,13,38–41} the structural search was limited to Jahn-Teller (JT) axially elongated square pyramidal, octahedral, or split axial (two axial distances) models.

A. EXAFS analysis of liquid-phase [Cu(aq)]²⁺

The high resolution provided by k = 18 Å⁻¹ EXAFS was first used to appraise the coordination environment about Cu(II). Axial distance tests were carried out, in which an axial oxygen scatterer was added to a 4- or 5-coordinate geometry and the Cu–O_ax distance was step-wise changed. The Cu–O_eq distances, linked ΔE₀, and all σ²-parameters were allowed to float. These fits showed clear F-value minima at 2.25 Å and 3.26 Å (square plane + O), or 2.50 Å and 3.26 Å (square pyramid + O), (Figure S4.1 in the supplementary material⁹²), implying disparate axial Cu–O distances as well as a shell of distant scatterers.

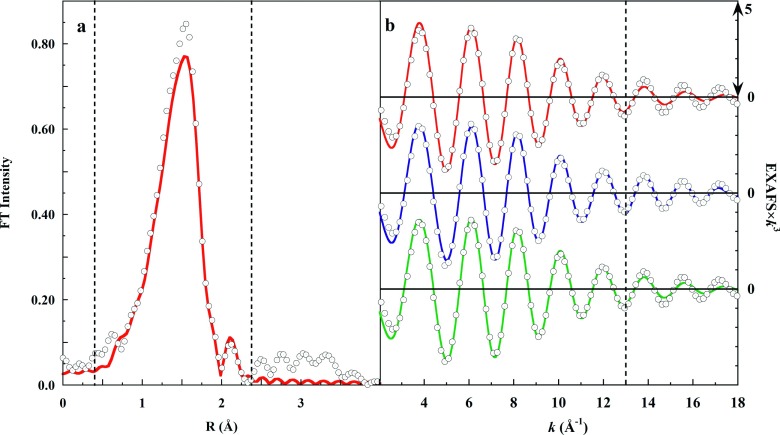
The EXAFS Fourier transform spectrum was then back-transformed using a Gaussian window of range R = 0.4-2.3 Å, yielding the filtered EXAFS spectrum of the ligand shell alone (Figure 3(a)). Fits were then carried out using the filtered EXAFS over the range k = 2-18 Å⁻¹, to test candidate structural models.

FIG. 3.

Panel (a): (∘), Fourier transform (FT) of the K-edge EXAFS spectrum of 0.1M Cu(ClO₄)₂ in 1M HClO₄. The dashed vertical lines show the limits of the Gaussian filter, and the red line (red solid line) shows the filtered FT. Panel (b): Fits to the back-transformed filtered EXAFS over the range k = 2-18 Å⁻¹ used the following models: (red solid line), axially elongated square pyramid, (blue solid line), split axial, or (green solid line), JT-octahedral. The vertical dashed line shows the usual zinc cutoff. Panel (b) includes only 20% of the data points for line visibility.

Figure 3(b) shows that while the three models yielded indistinguishable fits over k = 2-13 Å⁻¹, beyond k = 14 Å⁻¹ the split axial model produced the superior fit. The metrics of these fits, including the goodness-of-fit weighted F-values, are provided in Table II.

TABLE II.

First shell oxygen scatterers from Fourier-filtered EXAFS.^a

Model	[CN] R (Å)	σ2 × 103	[CN] R (Å)	σ2 × 103	[CN] R (Å)	σ2 × 103	ΔE0	F
Sq. Pyr.	[4] 1.96	6.39	[1] 2.29	9.07	…	…	−9.320	0.2572
JT-Oh	[4] 1.96	6.19	[2] 2.29	16.53	…	…	−8.471	0.2488
Split Ax.	[4] 1.97	6.07	[1] 2.20	4.02	[1] 2.36	4.24	−7.735	0.1963

^a[CN] is coordination number. Debye-Waller factor (σ²) is in units of Ų.

Following the first shell analysis, the same three structural models were tested against the unfiltered EXAFS. The eight equatorial hydrogens were added as a single shell, which was allowed to refine to an average Cu–H_eq distance. Equatorial hydrogens were not linked to the equatorial oxygens, under the rationale that a correctly assigned hydrogen shell should independently refine to a reasonable Cu–H distance. Axial hydrogens were excluded because axial water ligands are structurally dynamic,^42,43 leading to a loss of scattering amplitude. The Fourier transform features at R = 2.5-4 Å required inclusion of second shell oxygen scatterers in all the fitting experiments. Previous work had assigned these features as due to equatorial 180° O–Cu–O multiple scattering.⁴⁴ This scattering path proved to be exactly 180° out of phase with that of the 3.91 Å second shell oxygen scatterer (see below), and of similar intensity. Their inter-substitution thus produced equivalently good fits. However, the water path produced an unfit residual of somewhat less intensity over the relevant FT range of 3.0-3.8 Å. Additionally, eliminating the entire second shell of oxygens in favor of the O–C–O multiple scattering path produced a significantly poorer fit (weighted F = 0.1818), with considerable unfit FT intensity in the 2.3-3.8 Å range. Selective inclusion of the 3.91 Å oxygen path was thus favored.

The results of these fitting experiments are shown in Figure 4 and Table III. The split axial model (two axial distances) produced the lowest weighted F-value. The statistical distinction of the fits was evaluated using the F-test of Michalowicz et al., which takes into account any difference in the number of fit degrees of freedom.⁴⁵ The F-test value, revealing the relative merit of two fits, is given by

$${\displaystyle \mathrm{F}=[(\mathrm{\Delta }{\chi }_1^2-\mathrm{\Delta }{\chi }_2^2)/({\nu }_1-{\nu }_2)]/(\mathrm{\Delta }{\chi }_2^2/{\nu }_2),}$$ (5)

where $\mathrm{\Delta }{\chi }_n^2$ is the Chi-squared statistic of fit “n,” ν_n = N_ind − N_par is the degrees of freedom in the fit, N_ind is the number of independent data points, and N_par is the number of adjustable parameters. In an EXAFS fit N_ind = (2 × ΔRΔk/π) + 2, where Δ R(Å) is the Fourier transform data range and Δ k(Å⁻¹) is the fitted EXAFS range.⁴⁶

FIG. 4.

(∘), phase-shift uncorrected K-edge Fourier transform EXAFS spectrum of 0.1M Cu(ClO₄)₂ in liquid 1M HClO₄ solution. Fits including a second shell of oxygen scatterers are (thick blue solid line), JT-octahedral; (red solid line), split axial. Inset: The EXAFS fits, over the range k = 2-18 Å⁻¹. Unfit residual: (light blue solid line), JT-O_h, and; (pink solid line), split axial.

TABLE III.

EXAFS structural models for [Cu(aq)]²⁺ in liquid aqueous solution.^a

	JT-octahedral		Split axial		Sq. pyramidal
Scatterer	[CN] R (Å)	σ2 × 103	[CN] R (Å)	σ2 × 103	[CN] R (Å)	σ2 × 103
Oeq	[4] 1.97	5.82	[4] 1.97	5.92	[4] 1.97	6.11
Oax1	[2] 2.22	9.96	[1] 2.19	2.94	[1] 2.21	3.65
Heq	[8] 2.29	4.71	[8] 2.35	8.49	[8] 2.26	3.06
Oax2	…	…	[1] 2.33	3.23	…	…
Ow1	[1] 3.20	9.01	[1] 3.21	8.76	[1] 3.19	8.61
Ow2	[1] 3.41	14.99	[1] 3.40	14.20	[0.5] 3.39	4.92
Ow3	[1] 3.78	2.36	[1] 3.78	2.79	[1] 3.77	2.49
Ow4	[1] 3.91	3.80	[1] 3.91	4.39	[1] 3.91	4.11
Avg. 2nd	3.6 ± 0.3 Å		3.6 ± 0.3 Å		3.6 ± 0.3 Å
ΔE (eV)	−5.449		−5.485		−6.575
F-value	0.172 8		0.160 5		0.164 4
Δχ2	0.084 17		0.072 66		0.076 25

^a[CN] is coordination number. Average statistical e.s.d. in bond lengths are: first shell, ±0.002 Å; second shell, ±0.01 Å. Debye-Waller factor (σ²) is in units of Ų.

Alternative fits are statistically distinguishable when F > 1. All fits were over EXAFS range k = 2-18 Å⁻¹, Fourier transform Δ R = 3.5 Å, and N_ind = 37. For the JT-octahedral (JT) and split axial (SA) fits, $\mathrm{\Delta }{\chi }_{JT}^2=0.084\hspace{0.17em}17$ and ν_JT = 22, and $\mathrm{\Delta }{\chi }_{SA}^2=0.072\hspace{0.17em}66$ and ν_SA = 20, respectively, and F = [(1.15 × 10⁻²)/2]/(3.63 × 10⁻³) = 1.58.

For the split axial and square pyramidal models, F = 0.49, and these fits are statistically indistinguishable. When ν_n is constant between fits, as in the JT-octahedral and square pyramidal fits, then

$${\displaystyle F=(\mathrm{\Delta }{\chi }_1^2/{\upsilon }_1)/(\mathrm{\Delta }{\chi }_2^2/{\upsilon }_2)}$$ (6)

and F = 3.83 × 10⁻³/3.47 × 10⁻³ = 1.1, indicating the square pyramidal fit represents a statistical improvement.

As found with the filtered EXAFS result, the fits became visually distinguishable only at k > 14 Å⁻¹. The fit using the axially elongated square pyramidal model was indistinguishable from the split axial, and both were better than the JT-octahedral fit. The individual fits are shown separately in supplementary material Figures S5.1–S5.3.⁹²

An alternative test was carried out to determine whether the additional fitted degrees of freedom provided by the split axial model were responsible for the improved F-value. In this, the JT-octahedral fit was modified to include two independent axial oxygen scatters. Each axial scatterer began the fit with the identical prior JT-octahedral best-fit distance and σ²-value, which were then allowed to float independently. However, these conditions proved unstable. The freed axial distances and σ²-values quickly diverged to the best-fit split axial values.

B. EXAFS analysis of frozen-phase [Cu(aq)]²⁺

The EXAFS was truncated at k = 17 Å⁻¹ because intensity spikes at higher energy made those data unusable. Integer coordination numbers were used, and the same axially elongated square pyramidal, JT-octahedral, and split axial models were tested.

The axial distance vs. fit weighted F-value tests for an oxygen scatterer were again carried out. Fixed 4- or 5-coordinate geometry starting models showed clear minima at 2.35 Å and 3.21 Å, or 2.44 Å and 3.32 Å, respectively (Figure S6.1 in the supplementary material), again implying two axial Cu–O distances as well as a shell of distant scatterers.⁹²

Figure 5 compares the visually nearly indistinguishable JT-O_h and split axial fits. The only obvious O_h misfits are the small intensity shortfall in the main Fourier peak, and the excess intensity at R = 2.25 Å reflecting the two 2.32 Å oxygen scatterer paths. The same fit F-value hierarchy of JT-O_h > axially elongated square pyramidal > split axial emerged here as found for the liquid aqueous Cu(II) EXAFS fits. Table IV provides the fit metrics, and the individual fits are shown in Figures S7.1–S7.3 in the supplementary material.⁹²

FIG. 5.

(∘), phase-shift uncorrected K-edge Fourier transform EXAFS spectrum of 0.1M Cu(ClO₄)₂ in frozen 1M HClO₄ solution, and; (thick blue solid line), JT-octahedral, or; (red solid line), split axial model fit. Both models include a second shell of oxygen scatterers. Inset: The EXAFS spectrum fitted over the range k = 2-17 Å⁻¹. Unfit residuals: (light blue solid line), JT-O_h, and (pink solid line), split axial.

TABLE IV.

EXAFS structural models for [Cu(aq)]²⁺ in frozen aqueous solution.^a

	JT-octahedral		Split axial		Sq. pyramidal
Scatterer	[CN] R (Å)	σ2 × 103	[CN] R (Å)	σ2 × 103	[CN] R (Å)	σ2 × 103
Oeq	[4] 1.95	4.55	[4] 1.95	4.51	[4] 1.95	4.49
Oax1	[2] 2.32	4.83	[1] 2.30	1.14	[1] 2.30	0.97
Heq	[8] 2.38	1.20	[8] 2.46	19.29	[8] 2.35	1.26
Oax2	…	…	[1] 2.44	2.11	…	…
Ow1	[2] 3.24	9.86	[2] 3.23	11.40	[2] 3.22	11.19
Ow2	[2] 3.42	9.88	[2] 3.41	9.24	[2] 3.41	9.88
Ow3	[2] 3.76	5.39	[2] 3.77	5.37	[2] 3.77	5.45
Ow4	[2] 3.92	10.98	[1] 3.94	5.69	[2] 3.94	10.64
Avg. 2nd	3.6 ± 0.3 Å		3.6 ± 0.3 Å		3.6 ± 0.3 Å
ΔE (eV)	−7.859		−7.682		−7.313
F-value	0.105 7		0.088 2		0.098 4
Δχ2	0.056 84		0.039 57		0.049 26

^a[CN] is coordination number. Average statistical errors in bond length are: first shell, ±0.003 Å; hydrogen shell ±0.02 Å; second shell, ±0.01 Å. Debye-Waller factor (σ²) is in units of Ų.

The Michalowicz et al., F-test was again carried out to evaluate the relative merit of these fits. Over the EXAFS Δ k = 2-17 Å⁻¹ range and the Fourier transform Δ R = 3.5 Å, N_ind = 35, ν_JT = 20, and ν_SA = 18. The F-test calculated as in Sec. II yielded JT-O_h/SA, F = 3.93; JT-O_h/(Sq Pyr), F = 1.15, and (Sq Pyr)/SA = 2.20, i.e., definitively in favor of the split axial model.

In contrast with the case for the liquid aqueous Cu(II) EXAFS fit, the JT-O_h model proved stable to the extra two degrees of freedom provided by two independent axial oxygen scatterers, yielding 2 × Cu–O = 2.32 Å (σ² = 0.0048), and F = 0.1045. Neither the Cu–O distances nor the σ² values moved away from their initial values. The fitted EXAFS and FT spectra of this test fit were superimposable on the JT-O_h fit shown in Figures 5 and S7.1.⁹²

1. Axial perchlorate

It seemed possible that freezing could induce an associational complex between perchlorate and Cu(II). Indeed, perchlorate oxygen and chlorine scatterers (initial Cl–O = 1.44 Å, O–Cu = 2.90 Å) substituted into the split axial model refined (F = 0.0945) to a perchlorate Cu–O distance of 3.23 Å (σ² = 0.007 88) with Cu–Cl = 4.63 Å (σ² = 0.0225), implying a reasonable O–Cl distance of 1.41 Å.⁴⁷ Although the fit was good, the Cl scattering amplitude was very low and made a negligible contribution to the fit. Thus, the question of an associated axial perchlorate cannot be confidently resolved with the present EXAFS data. See, however, the MXAN analysis in Sec. III D below.

C. Best-fit split axial EXAFS models for [Cu(aq)]²⁺

All three models produced good to excellent fits to the EXAFS spectrum of Cu(II) in liquid or frozen solution. Nevertheless, the split axial model invariably produced the best fit by the F-test criterion. For the liquid phase EXAFS, the JT-O_h model was discernibly poorer at k > 14 Å⁻¹. For frozen-phase [Cu(aq)]²⁺, the decision between the split axial and square pyramidal models is statistically unambiguous, marking a distinct contrast with the liquid phase case. In each phase, either of the alternatives proved superior to the JT-O_h model. Figure 6 shows the EXAFS structural models for [Cu(aq)]²⁺ in liquid and frozen 1M HClO₄ solution.

FIG. 6.

Split axial EXAFS models for [Cu(aq)]²⁺ in left panel, liquid solution; right panel, frozen solution, with Cu–O axial bond lengths of 2.19 Å and 2.33 Å, or 2.30 Å and 2.44 Å, respectively. The second shell water molecules (wire-frame structures) were arranged symmetrically, with more distant waters assigned to the longer axial arm. Equatorial hydrogens were included in the fits as a single shell.

D. MXAN analysis

The three EXAFS models (Tables III and IV) were used to construct initial 3-dimensional structural models analogous to those of Figure 6. The models included all the hydrogen atoms and were used as initial inputs for MXAN analysis. In general, MXAN fits were carried out over the relative energy range −7.5 eV ≤ E − E₀ ≤ 200 eV, where rising K-edge E₀ = 8990.00 eV. The ECMS theory of MXAN has been described.^{8,20,22,24,34} Trans-equatorial bond lengths and bond angles were linked during a fit. Trans-axial bond lengths were linked in the O_h model fits. The goodness-of-fit R_sq sensitivity tests are described below.

1. Liquid-phase [Cu(aq)]²⁺

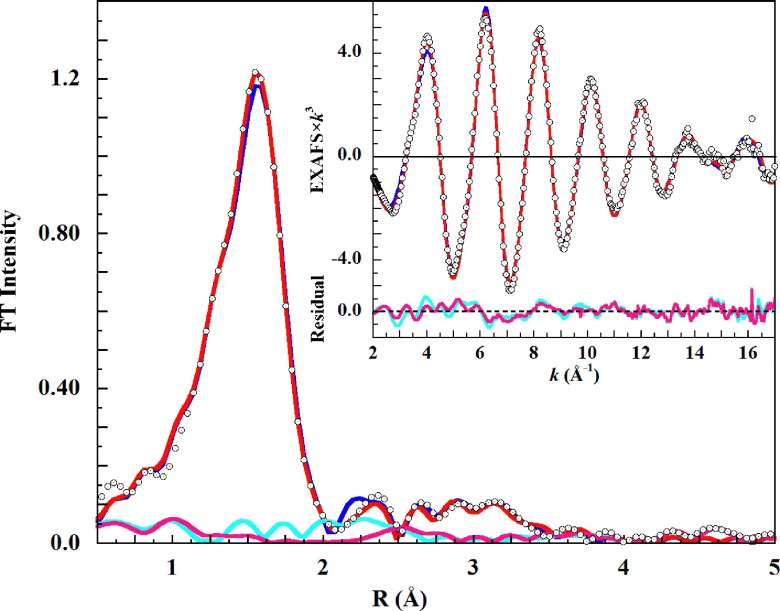
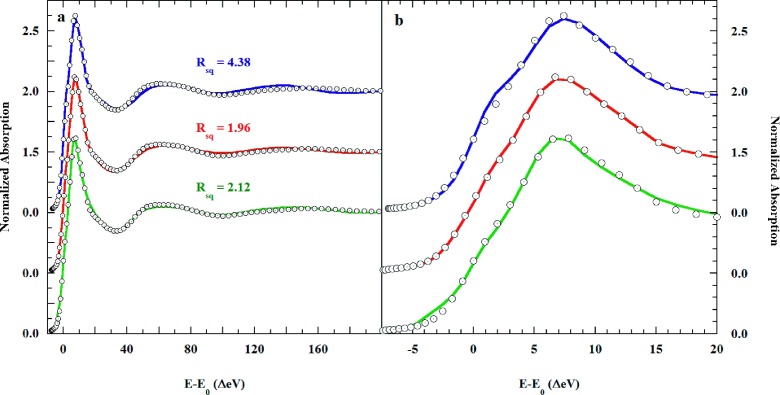
Initially, the JT-O_h, the split-axial, and the axially elongated square pyramidal models were tested at the level of the first coordination shell. The results are shown in Figure S8.1 of the supplementary material.⁹² The respective goodness-of-fit R_sq = 6.86, 2.55, and 2.24, clearly disfavored the JT-O_h model, which produced a poorer fit over the entire energy range. The axially elongated square pyramidal model produced the best fit, while the difference in R_sq with the split axial model is not significant. In Figure S8.1,⁹² the rising K-edge shoulder intensified with the number and proximity of axial water molecules. This behavior reflects a significant multiple scattering contribution to the rising edge,^{24,25,37,48,49} as inferred from the pseudo-Voigt fits described earlier. The fit metrics are shown in Table S8.1.⁹²

Following these experiments, the second shell of eight water molecules inferred from the prior EXAFS fits was added to the MXAN models. The water molecules were placed at the centers of the pyramidal faces of an octahedron and set at the EXAFS distances. In addition to bond-length optimization, the MXAN fits allowed adjustment of the trans-paired O_ax–Cu–O_eq angles. In a final step, and following structural optimization, the MT potentials of the scattering atoms were optimized. Figure 7 shows the fits that resulted.

FIG. 7.

(∘), K-edge XAS of 0.1M Cu(ClO₄)₂ in liquid 1M aqueous HClO₄, and the MXAN fits using the (blue solid line), the JT-O_h; (red solid line), split axial, and; (green solid line), axially elongated square pyramidal structural models. Eight second shell water molecules are included in the JT-O_h and split axial models, but not in the square pyramidal (see text).

This second water shell improved both the JT-O_h (R_sq = 6.96 → 4.38) and split axial (R_sq = 2.55 → 1.96) fits but surprisingly worsened the square pyramidal fit (R_sq = 2.24 → 3.42). Therefore, Figure 7 includes the fit for the bare square pyramidal model. The slightly improved square pyramidal R_sq = 2.24 → 2.12 resulted from opening O_ax–Cu–O_eq angle (90° → 94°) and optimization of the MT potentials.

Two further fits using the split axial model produced slightly different axial water distances and O_ax–Cu–O_eq angles. Table S8.2 in the supplementary material shows these results.⁹² The very slightly poorer R_sq values of 1.99 and 2.05 are statistically indistinguishable from the best fit R_sq. An explanation is that the best-fit phase valley may have three almost identical minima. The consensus structure shows very stable Cu–O_eq distances of 1.94 Å in all three structures. The axial water distances vary only slightly more than the limits of resolution, Cu–O_ax1 = 2.10 ± 0.03 Å and Cu–O_ax2 = 2.84 ± 0.08 Å.

In the split axial fits, the very distant axial water, O_ax2, is in all cases near the elemental copper-H₂O van der Waals distance of 2.92 Å,⁵⁰ and longer than the ionic 3dz² Cu(II)–OH₂ contact radius of 2.61 Å.⁵¹ Thus, the long axial water is not even weakly bonded to Cu(II). A better description of the split axial MXAN model is an axially elongated square pyramid with a trans-axially localized solvent water.

The square pyramidal fit, sans second shell waters, is also comparable in quality to the split axial fits. Not only did this fit become worse when second shell waters were added to the model, but addition of a distant axial water alone also worsened the fit (Figure S8.1⁹²). Therefore, both structural elements, a distant axial water and a second shell of waters, must both be present in order to produce a pattern of photoelectron back-scattering that can improve the bare square pyramidal fit. This combination then converts the axially elongated square pyramidal model into the solvated split axial model.

The nearly equivalent quality of the fits using the axially elongated square pyramidal model and the solvated split axial version of this model suggests that each is approximately equally representative of dissolved [Cu(aq)]²⁺. Therefore, a step-wise iterative two-site MXAN fit that employed both the square pyramidal and split axial plus second shell structures was tested. This approach is illustrated in Scheme 1.

Scheme 1.

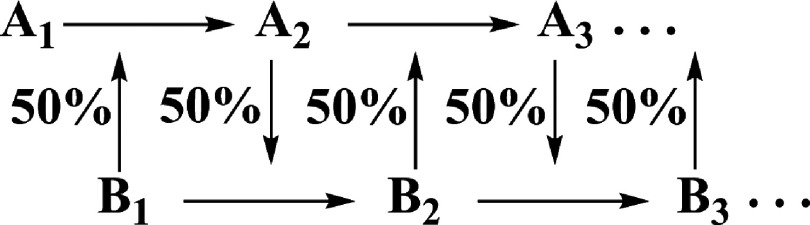
Iterative approach to the two-site MXAN fit to the copper K-edge of 0.1M Cu(ClO₄)₂ in 1M HClO₄ in liquid or frozen (10 K) solution.

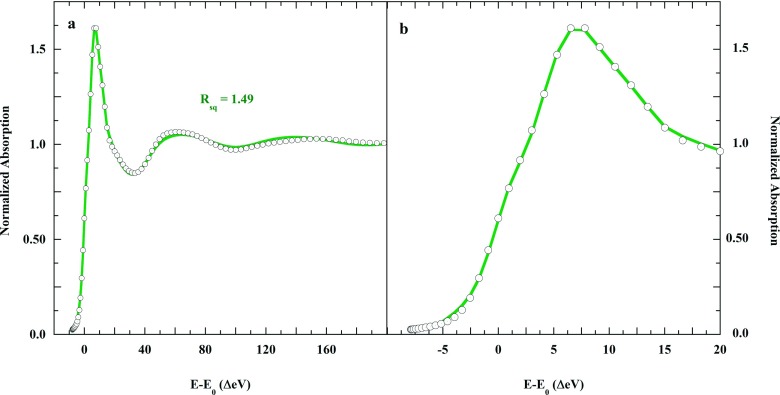
The two models were combined into each single fit in a sequential set of fits. In each step, each model was given a 0.5 weight. In a first step, the final fit of the square pyramidal model (A₁), weight = 0.5, was refined, while the final fit of the split axial model (B₁), weight = 0.5, was held constant. The A₁ distances and angles were fit in the structural context of 0.5 B₁, producing intermediate fit A₂B₁, with goodness-of-fit R_sqA2B1. The distances and angles of A₂ were then held fixed while those of B₁ were fitted, producing fit file A₂B₂ and R_sqA2B2. The sequence was repeated until R_sqA(n−1)Bn and R_sqAnBn converged to within ±0.01 of the same value. The result was that the over all goodness of fit dropped from R_sqA1 = 2.12, R_sqB1 = 1.96 to R_sqA4B4 = 1.43.

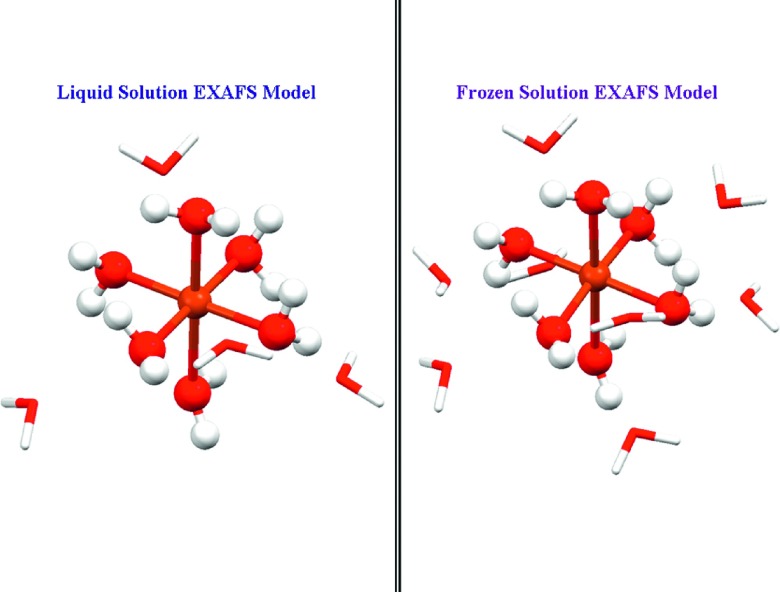
A physical rationale for the equivalence of these models is that there exist two solvation structures for square pyramidal [Cu(aq)]²⁺: one with a localized axial solvent water and an organized second shell, and one lacking both these attributes. The two-site fit for [Cu(aq)]²⁺ in liquid solution is shown in Figure 8, and the derived solution structures are presented in Figure 9. Table V provides the single-site metrics for the two-site fit and for the individual JT-O_h fit.

FIG. 8.

(∘), K-edge XAS of 0.1M Cu(ClO₄)₂ in 1M liquid aqueous HClO₄, and (green solid line), the iterative two-site fit using the square pyramidal and solvated split axial models.

FIG. 9.

Alternative MXAN structures for [Cu(aq)]²⁺ in liquid water solution. The axially elongated square pyramid in a disorganized solvation shell is approximately equally as probable as the homologous structure including a trans-axial solvent water molecule and an organized second shell. Cu(II) is slightly above the equatorial O₄ plane in both models (see Table V).

TABLE V.

MXAN fit metrics for liquid phase [Cu(aq)]²⁺.

	Model
	JT-octahedral		Split axiala		Square pyramidala
Structural water	CN	R (Å)	CN	R (Å)	CN	R (Å)
(H2O)eq	4	1.99 ± 0.01	4	1.94 ± 0.02	4	1.95 ± 0.02
(H2O)ax1	2	2.58 ± 0.03	1	2.06 ± 0.07	1	2.23 ± 0.11
(H2O)ax2	…	…	1	2.99 ± 0.22	…	…
Second shell H2O	8	3.8 ± 0.6	8	3.8 ± 0.1	…	…
∠Oax–Cu–Oeq	90°		99°		94°
Rsq	4.38		1.49		1.51

^aMetrics from the iterative two-site fit. Systematic plus statistical uncertainty for the second shell water molecules is about ±0.1 Å. The uncertainties in second shell water distances include the positional variation of eight water molecules. Bond angle uncertainty is ±2°.

Although both structures must be surrounded by solvating water molecules, the solvation shell may become more organized, and thus more detectable, when a water molecule becomes trans-axially associated with the square pyramidal complex ion. This point is discussed further below.

Finally, at the suggestion of a reviewer, the validity of the derived solution structures were tested by comparative EXAFS and MXAN analyses of the XAS of authentically JT-octahedral crystalline [Cu(H₂O)₆](ClO₄)₂, which includes two axial water molecule ligands uniformly at 2.38 Å.⁵² This study is too extensive to describe fully here, but may be found in the Addendum at the end of the supplementary material.⁹² EXAFS was restricted to the k = 2-13 Å⁻¹ range, because of the usual small zinc impurity in the copper lattice. As in past studies, the EXAFS fits alone could not distinguish square-pyramidal and JT-O_h models over this range. Nevertheless, the dependence of EXAFS of goodness-of-fit on axial distance, and comparison of EXAFS amplitude ratios clearly favored the square pyramidal core model. The corresponding MXAN analysis was definitive, showing first that the JT-octahedral model could not reproduce the XAS of Cu(II) in liquid solution. Likewise, the split axial model could not reproduce the XAS of the crystalline complex. Overall, the comparative analysis was unambiguously in favor of the axially elongated [Cu(H₂O)₅]²⁺ core model for Cu(II) liquid aqueous solution.

2. Frozen-phase [Cu(aq)]²⁺

The same three structural models were again tested. The first-guess models were the best-fit structures taken from the single-site MXAN fits to the liquid-phase K-edge XAS spectrum (Table V). However, none of the fits based on these models converged to a fully acceptable result. Nevertheless, as before, the split axial and square pyramidal models produced better fits than the JT-octahedral model. These results are shown in Figure S9.1 and Table S9.1 of the supplementary material.⁹²

a. Axial perchlorate.

The possibility that freezing could induce a proximate perchlorate was again tested. During this fit, shown in Figure S9.2 and Table S9.2 in the supplementary material, the axial water and perchlorate ion migrated from 2.22 Å to 2.37 Å and 2.90 Å to 3.2 Å, respectively.⁹² The final R_sq = 3.77 for this model was again not fully acceptable. However, comparison of Figures S9.1 and S9.2 shows that the perchlorate model better reproduced the shoulder on the rising K-edge than did any of the other models. The perchlorate model also better reproduced the structured continuum feature in the 40-80 eV XAS region that is more poorly fit using the split axial and square pyramidal models.

Nevertheless, at this point, the individual models could not produce a fully acceptable fit, while exhausting the most likely structural arrangements for frozen solution [Cu(aq)]²⁺. A step-wise iterative two-site fit was thus again tested (Scheme 1), employing the split axial and the axial perchlorate models. This produced a fit better than any of the single-site models, with R_sq = 2.39. Over the iterative course, the split axial equatorial Cu–O_eq distances remained unchanged and the O_ax1–Cu–O_eq angle remained 90° within the limits of error. The Cu–O_ax1 bond length contracted by 0.11 Å, while the Cu–O_ax2 distance lengthened by about 0.14 Å. The average second shell distance also increased by 0.3 Å.

In the perchlorate model, all five inner sphere Cu–O distances were stable during the fit. Only the second shell shifted position, migrating out by an average of 0.5 Å. However, the four O_ax1–Cu–O_eq angles increased from 97° in the single site model to 105° in the two-site model. All these movements are statistically significant. The adjustments in scatterer positions indicate that the iterated two-site fit is not just a linear average of the two single site fits. This comparison is made in Figure S9.3 of the supplementary material.⁹² The 3.2 ± 0.2 Å perchlorate Cu–O distance found using MXAN is identical to the tentative EXAFS perchlorate Cu–O = 3.23 ± 0.01 Å distance noted above. The MXAN and EXAFS Cu–Cl distances were likewise identical, 4.6 ± 0.2 Å and 4.63 ± 0.01 Å (Sec. II A), respectively.

The structural metrics of each two-site model and the fitted XAS are shown in Table VI and Figure 10, respectively, and can be compared with the analogous single-sites in Tables S9.1 and S9.2 in the supplementary material.⁹²

TABLE VI.

MXAN two-site fit for 0.1M [Cu(ClO₄)₂] in frozen 1M HClO₄.^a

	Model
	Axial perchlorate		Split axial
Structural shells	CN	R (Å)	CN	R (Å)
(H2O)eq	4	1.94 ± 0.02	4	1.97 ± 0.02
(H2O)ax1	1	2.38 ± 0.22	1	2.44 ± 0.13
(H2O)ax2	…	…	1	3.0 ± 0.1
(O3Cl–O)ax	1	3.2 ± 0.2	…	…
Cu–Cl	1	4.6 ± 0.2	…	…
2nd Shell waters	8	3.9 ± 0.6	8	3.8 ± 0.7
∠Oax1–Cu–Oeq	105°		90°
Rsq	2.39		2.39

^aSystematic plus statistical uncertainty in equatorial Cu-O bond lengths is about ±0.03 Å, and for the axial water is about ±0.05 Å. The uncertainty in second shell water distance includes the positional variation of eight water molecules.

FIG. 10.

(∘), K-edge XAS of 0.1M Cu(ClO₄)₂ in 1M aqueous HClO₄, and (solid blue line), the two-site fitted axial perchlorate and split axial models. Second shells of eight water molecules each were included.

Systematic plus statistical uncertainty in equatorial Cu–O bond lengths is about ±0.03 Å, and for the axial water is about ±0.05 Å. The uncertainty in second shell water distance includes the positional variation of eight water molecules.

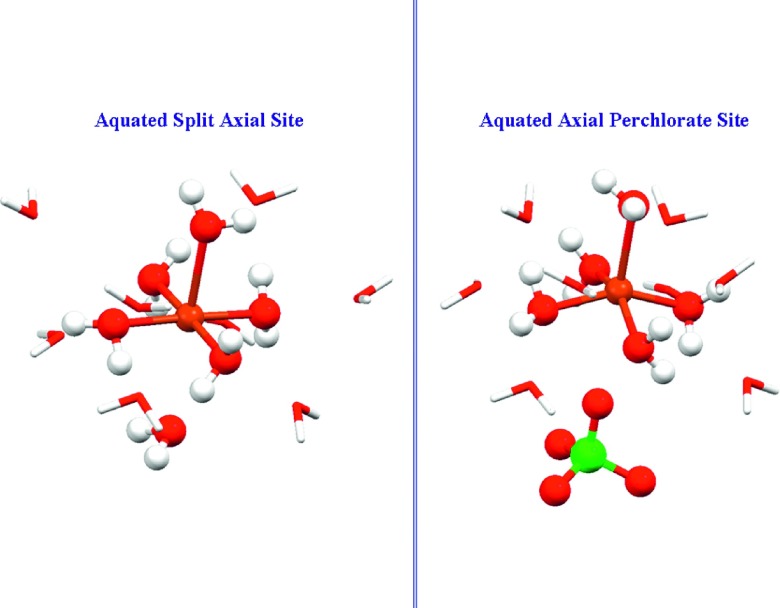
Figure 11 shows the two structures arising from the two-site fit: split axial and axially associated perchlorate. The long-distance axial water and perchlorate ion, at 3.0 Å and 3.2 Å, respectively, are again too distant to permit any bonding interaction with Cu(II).

FIG. 11.

Site structures for Cu(ClO₄)₂ in frozen 1M HClO₄ solution, derived from the MXAN two-site fit. The long axial water (left panel) or long axial perchlorate (right panel) are represented as unbound but associated. The 105° O_ax1–Cu–O_eq angular bend in the perchlorate site is very evident, and the copper is 0.5 Å above the mean O₄ equatorial plane.

While the fit to the XAS is good, it does not achieve the level of the final two-site fit to the XAS of Cu(ClO₄)₂ in liquid 1M HClO₄ solution. Clearly, room for improvement exists. Likely, this is to be found in additional sites for Cu(II) in frozen solution. The bare square pyramidal model is an obvious candidate. If an improved fit resulted, this minimal structure would again imply a locally disorganized second shell of water molecules, absent a distant axial association. Again, the second shell would organize itself during freezing with the entry of either a distant water molecule or a captured perchlorate ion.

IV. DISCUSSION

We begin by noting that implicit in this study is the hypothesized existence of a discrete structural ground state for [Cu(aq)]²⁺ in water solution at ambient temperature. This hypothesis requires that, despite rapid solution dynamics, the structure of [Cu(aq)]²⁺ represents an energetic minimum and is not just the mean of stochastic fluctuations. In the event, two discrete structures were found to strongly dominate the XANES and EXAFS. These likely represent roughly equivalent minima in the potential energy surface governing the structure of Cu(II) in water. The structured EXAFS Fourier features at R = 2-3.5 Å, and the second shell in the MXAN fits also indicate extended order. Nevertheless, the weak axial bond strength and rapid axial exchange around Cu(II) mean that any fitted single structure is a compromise.

While the EXAFS and MXAN equatorial Cu–O distances are nearly identical, the EXAFS axial Cu–O distances are always shorter. These differences can arise because, relative to EXAFS, MXAN analysis assesses more of the information in an XAS spectrum. Further, the EXAFS models did not include the axial hydrogen atoms, while explicit Cu–H scattering was calculated during the MXAN fits. Likewise, in the EXAFS fits, the equatorial hydrogens were represented as a single shell at 2.3-2.4 Å while the MXAN fits took into account all the individual Cu–H_eq scattering paths. The mean MXAN Cu–H_eq distance is 2.44 ± 0.18 Å in the three basic models, compared to 2.43 ± 0.02 Å in crystalline [Cu(H₂O)₆](ClO₄)₂.⁵² Thus, the final structures from the MXAN fits are a better representation of the physical state of Cu(II).

The immediate environment around Cu(II) is phase-dependent. Nevertheless, the energy positions and intensities of the 1s → 3d pre-edge transitions indicate the phase-induced modifications are not accompanied by any important alterations in the Cu(II) 3d electronic state or ligation symmetry.

The inability of k = 2-13 Å⁻¹ EXAFS analysis to distinguish the octahedral and square pyramidal models provides an explanation for previous ambiguities regarding axial ligation in dissolved Cu(II).^3,8,37,53 Until recently,^1,2,9,54 the deduced hexa-coordinate Jahn-Teller axially elongated octahedron (JT-O_h) was generally accepted as the average solution structure of [Cu(aq)]²⁺.^3,42,55–62 With the improved resolution of EXAFS to k = 2-18 Å⁻¹, the non-centrosymmetric square pyramid with a distant axially associated water molecule was unambiguously the best model.

The MXAN fits further showed that two distinct but structurally related non-centrosymmetric axially elongated square pyramidal complex ions were needed to reproduce the experimental XAS spectrum of Cu(II) in both liquid and frozen aqueous solution. The four structures are energetically close to the homologous JT-O_h hexaaqua complex ion.¹³ Of these, three include a non-bonded axial water or counter ion (perchlorate) at Cu–O ≈ 3 Å, while in liquid solution, one model is axially elongated square pyramidal alone, without any trans-axial association.

In liquid solution, both the trans-axial water and an organized solvent second shell are either simultaneously present around [Cu(aq)]²⁺, or simultaneously absent. This is suggestive that the associated 3 Å trans-axial water molecule organizes the solvation shell, possibly by providing a second axial strut in support of a circumlocalized network of hydrogen bonds.^13,14

A minimal description of liquid phase [Cu(aq)]²⁺ then requires two square pyramidal structures. One has the 3 Å trans-axial water and an organized solvent shell. The second lacks both. These features are offered as two exchange structures in the solution dynamics of liquid-phase [Cu(H₂O)₅]²⁺.

The known Jahn-Teller fluxional nature of [Cu(aq)]²⁺ in solution produces state lifetimes of order 5 ps.^{15,17,55,63–67} This lifetime governs exchange of the longer and shorter axial water distances. Axial exchange with bulk proceeds at a slower nano-second rate.^17,64,68 The association of the organized second shell with the distant axial water implies that the pico-second axial flux may be accompanied by a concomitant xz, yz flexure of the solvation shell. Finally, the [Cu(H₂O)₅]²⁺ solvation shell itself may then organize–disorganize with the nano-second association-dissociation dynamics of the 3 Å axial water. Flexure of the equatorial ligands, promoting Cu(II) to ∼0.5 Å above the mean L₄ plane, is now indicated in both [Cu(H₂O)₅]²⁺ and [Cu(NH₃)₄(NH₃, H₂O)]²⁺.²⁴

The 3 Å axial association solves the apparent conflict between a 5-coordinate [Cu(H₂O)₅]²⁺ in liquid water solution and the dissociative mechanism of ligand water exchange.⁶⁹ That is, both axial positions can be occupied, even though only one of the axial occupants constitutes a ligand. The water exchange mechanism then involves departure of the 3 Å axial water molecule.

The axial association of perchlorate in frozen solution also provides a direct explanation for the slightly increased intensity and blue-shift of the 805 nm band in the NIR spectrum of [Cu(aq)]²⁺ with added perchlorate ion, as noted by Libus and Sadowska,⁷⁰ as well as the concentration-dependent K-edge XAS of dissolved [Cu(ClO₄)₂] described by Nomura and Yamaguchi.⁷¹ The latter reported the appearance of an 8990 eV shoulder on the rising K-edge XAS of [Cu(aq)]²⁺ with increasing [ClO₄⁻]. Both groups explained their observations in terms of an emergent outer-sphere ion pair, i.e., perchlorate located next to the ligand sphere of JT-O_h [Cu(H₂O)₆]²⁺. However, these effects can now perhaps be better understood as reflecting the emergence of the ∼3 Å axial association of perchlorate with [Cu(H₂O)₅]²⁺. This solution complex may be described as a meso-sphere ion pair, because while the Cu(II)–OClO₃⁻ association is direct, the interaction is across a nearly second-shell distance.¹³

The intensity of the rising K-edge XANES spectra of Cu(II) are typically described as arising principally from the bound-state 1s → np (n = 4, 5, …) electronic transitions plus two-electron shake-up or shake-down transitions.^72,73 However, multiple scattering resonances can contribute intensity to a K-edge XANES spectrum. The total x-ray absorption cross section can be written in terms of the scattering path operator, $\tau ={(T_a^{-1}+G)}^{-1}$, where G is the free electron propagator and ${\left(T_a^{-1}\right)}_{L,L^{\prime }}^{\mathit{ij}}=\left[{\left(t_l^i\right)}^{-1}\right]{\delta }_{\mathit{ij}}{\delta }_{L{L}^{\prime }}$ and $t_l^i$ are the atomic scattering amplitudes defined in terms of phase shift.⁷⁴ The modulus of G behaves as |G| ≈ 1/kR, where the photoelectron wave vector k = (E − V_mt)^1/2 and where V_mt is the muffin tin interstitial potential and R is the interatomic distance.^74–76 This 1/kR dependence means scattering from distant atoms (high R) can produce features in the rising edge energy region (low k). Further, the photoelectron mean free path is very large (∼7-10 Å) at low energies.⁷⁷ Therefore, a feature appearing on an XAS rising K-edge need not derive from a bound state transition. The possible origin in multiple scattering should be eliminated, e.g., by comparison with a density functional theory (DFT) model, before a bound state assignment is made.^24,25,49

Garcia et al.⁷⁸ predicted that, in the K-edge XAS of [Cu(aq)]²⁺, the energy difference between the 8989.6 eV rising K-edge shoulder and the absorption maximum (their peaks A and C) should correlate positively with axial disorder about the absorber. In this regard, the liquid- and frozen-phase solutions display energy differences of 5 eV and 6 eV, respectively, implying greater distortion in the frozen phase complex ion. Inspection of the structures in Figures 6, 9, and 11 verifies this prediction. In liquid water, Cu(II) is ∼0.2 Å above the mean square pyramidal O₄ plane, and is about half the time associated with a ∼3 Å axial water molecule. In frozen solution, square pyramidal Cu(II) is either in-plane and associated with a distant water molecule at ∼3 Å or about 0.5 Å above the mean equatorial O₄ plane and associated with a ∼3 Å perchlorate ion.

In previous investigations of dissolved [Cu(aq)]²⁺, X-ray scattering from aqueous 3.55M Cu(II)-perchlorate produced a peak at 2.9 Å, which was assigned to O–O scattering between water molecules or between water and ClO₄⁻.⁷⁹ In the present context, the 2.9 Å scattering peak may have reported the non-bonded trans-axial water molecule described here. Gomez-Salces et al. reported an interesting visible spectroscopic study based on comparison with a CuO₅ model in silica glass.⁵⁴ Although they deduced a split axial structure for dissolved [Cu(aq)]²⁺, their study suffered because the siliceous CuO₅ reference model was uncharacterized. Their case for CuO₅ loci in glass rested upon acceptance of the EXAFS analysis of a piece of archaeological Roman glass that exhibited a XANES spectrum clearly indicative of considerable Cu(I).⁸⁰

Gas-phase mass spectrometric examination of Cu(II)–H₂O clusters have confirmed the stability of the [Cu(H₂O)₄]²⁺ equatorial complex ion, and have gone further to show the existence of the [Cu(H₂O)₈]²⁺ cluster as a second stable system.^27,81 Although an equatorially 4 + 4 co-planar {[Cu(H₂O)₄](H₂O)₄}²⁺ structure was assigned, a $5+1+2\hspace{0.17em}{\left\{\left[\mathrm{Cu}{\left({\mathrm{H}}_2\mathrm{O}\right)}_5\right]{\left({\mathrm{H}}_2\mathrm{O}\right)}_{\mathit{ax}}^{3\AA }{\left({\mathrm{H}}_2\mathrm{O}\right)}_2\right\}}^{2+}$ structure need not be excluded. Recent DFT calculations, expanded to include solvating water molecules, have indicated a preferred 5-coordinate square pyramidal inner ligand sphere within an extended solvation shell,^13,14 while the JT-O_h 6-coordinate complex, though energetically proximate, was disfavored.

Finally, the 1976 linear electric field effect (LEFE) EPR studies of Peisach and Mims presciently showed that dissolved aqueous low molecular weight complex ions of Cu(II) are uniformly non-centrosymmetric.^82,83 Their findings, which went unremarked for three decades, have now been corroborated here and elsewhere.^{1,2,8,24–26}

Including [Cu(H₂O)₅]²⁺, the basic first shell axially elongated square pyramidal motif seems to be the preferred structure of solution Cu(II). The combination of EXAFS and MXAN analyses have moved the known fluxional dynamics of dissolved Cu(II) into a structural regime. The fluctuational structures available to Cu(II) are extensive and evidently far from regular. These findings may find application in catalysis,⁸⁴ and show that copper is uniquely able to adapt itself to the diverse structural and symmetry requirements of protein active sites, and of rapid electron transfer in biological systems.^8,9,85 Thus, a 70 kJ/mol protein rack,^62,86,87 apart from being energetically inconsistent with the low conformational stability of proteins themselves (ΔG_UN ∼ 10-90 kJ/mol),^88,89 is now also clearly superfluous to an explanation of the non-centrosymmetric site structure in blue copper proteins.^8,9,90,91

Lastly, combined EXAFS and MXAN analysis has proven extremely powerful in resolving the structure of copper complex ions in dissolved phases. The models presented here are the first to provide empirical resolution of the dominant dynamical structures for [Cu(H₂O)₅]²⁺ in liquid aqueous solution. Further work exploring the dynamical, complexation, and solvation behavior of [Cu(H₂O)₅]²⁺ is in progress, combining XAS, MXAN, and QMMD.