On the Role of Cell Signaling Models in Cancer Research

Abstract

The main objective of this review is to emphasize the role and importance of the careful mathematical/computational modeling of signaling networks for the understanding of aberrant signaling in cancer and for the development of targeted therapies.

Introduction

An important characteristic of every living cell is its ability to communicate with the surrounding environment. This exchange of information is called cellular signaling and is based on the capacity of the cell to give proper responses to environmental signals (1, 2) Cellular signaling is carried out by a complex network of interactions. Within this network, it is possible to identify different pathways or routes of information consisting of multiple sequential events, including protein-protein interaction, allosteric alteration, posttranslational modification, and compartmentalization (3, 4). The input-output relationships characterizing signaling pathways are usually nonlinear: with the proper elements in the circuit, the cell is able to convert continuous stimuli into discrete responses, and can “remember” a stimulus long after it has been withdrawn, two properties that have proven to be of critical importance for several cellular tasks (5). Mathematical/computational modeling based on biological information can be used to improve our understanding of cellular signaling, thereby enhancing predictive accuracy.

Mathematical modeling of cellular communication

Mathematical models of signaling networks describe the temporal and spatial evolution of certain representative components of the signaling system, termed “nodes,” provided that their relationships between and among each other or “connectivity” are known. The nodes could represent distinct protein species and their connections being different biomolecular transformations. Together, the nodes and the connections linking them comprise the network topology. Once the components and connectivity of the signaling network are selected, it is critical to determine the values of the parameters. This can be accomplished by direct measurements whenever possible, or obtained from the literature, or estimated by comparing model predictions and experimental data.

The most compelling question one must ask oneself whenever engaged in mathematical modeling of networks is whether the structure of the model is sufficient to accurately and completely describe the system being studied or to fulfill the preset goals of the modeling effort. Investigation of the answer invariably leads to more in-depth analyses of the literature. Are there published experimental results that fall clearly outside what the model predicts? If so, what causes this discrepancy and how can it be addressed? Only by dealing with this iterative process of verification/validation, will the model become a reliable tool for understanding the available experimental observations and for predicting the outcome of other potential lines of experimentation.

Simplified models

Depending on the goals of the modeling effort, in principle, two approaches can be followed. In one case—at least in theory—all the complexities of the system are included, whereas in the other one, only essential complexities are considered and worked on. We will refer to them as a complete and a reduced model, respectively. Complete models, although in principle more realistic, are also less amenable to developing insights into the process being modeled. It is appealing then to find out under which set of hypotheses the complete model can be approximated by a simpler one. This reduced model so derived is only valid in a particular limiting set of conditions. A different approach, in essence, is to design a simple model from its inception and to construct it phenomenologically. This means that it is not obtained from first principles or derived from a complete description. Instead, certain ingredients are included to ensure that, as simply as possible, the model reproduces what are believed to be fundamental properties of the system studied. Interestingly, and although phenomenological descriptions have proven their utility in many contexts (6–8), if the observer is not aware of some of the critical properties of the system, these could be easily left out of the description and perhaps major and important behaviors of the system would not be predicted. Simplified model approaches could very well succeed in providing both explanatory and predictive tools, provided that they capture the much-sought-after essential underlying mechanisms of the system being considered.

The Era of Utilization of Mathematical Tools in Cancer Research Is Emerging from Infancy

Although mathematical biology is an established branch of applied mathematics, until recently, major efforts at developing predictive models that may guide experiments have lagged behind the advances in theories and in new tools. One of the main purposes of the new section of mathematical oncology within the Systems Biology and Emerging Technologies area is to accelerate progress through the use of sophisticated mathematical frameworks to model and make predictions about biological behavior in cancer. Below, we provide two brief examples of the potential reach and power of mathematical approaches applied to fundamental biological processes that effect cancer research.

Example that illustrates how uncovering the oversimplification in mathematical models of cell signaling has led to fundamental new insights in signal transduction

Cycles involving covalent modification of proteins are key components of the intracellular signaling machinery. A classic signaling pathway is structured by a cascade of basic cycle units in such a way that the activated protein in one cycle promotes the activation of the next protein in the chain, and so on. By analyzing and reducing the basic kinetic equations of this system, we have constructed a new mathematical model of an intracellular signaling cascade (9). The model we derived is distinct from the one that has been in use in the literature for several years, which is a phenomenological extension of a well-studied model for a single cycle (10). A key feature of our new model is that a negative feedback emerges naturally, exerted between each cycle and its predecessor, successively. Due to this backwards transmission of information, the system propagates perturbations bidirectionally. This last attribute profoundly challenges the widespread notion of unidirectionality in signaling cascades. It is widely accepted that information travels both from outside the cell in and from the inside out in signaling pathways. Conversely, cascades, even while being main components of those pathways, have been thus far understood as structures where signal transmission occurs in a manner analogous to a domino effect: the information flows in only one direction, from one cycle unit to the next. The model we have proposed shows that a cascade can naturally exhibit bidirectional propagation without invoking extra rewiring. This property, termed “retroactivity” in a more general framework (11) inspires novel interpretations of experimental data; because signaling pathways are usually reconstructed from such data, this outcome could have far-reaching implications in the understanding of cell signaling.

Importantly, the model we have proposed is a simplified version of a complete mechanistic description of the cascade. The bidirectional propagation property is shared by both the complete and the simplified models (and not the phenomenological one), but in the complete approach was hidden in the complex structure of the model equations, whereas it is automatically revealed in the simplified one, proving once more the utility of simplified modeling approaches.

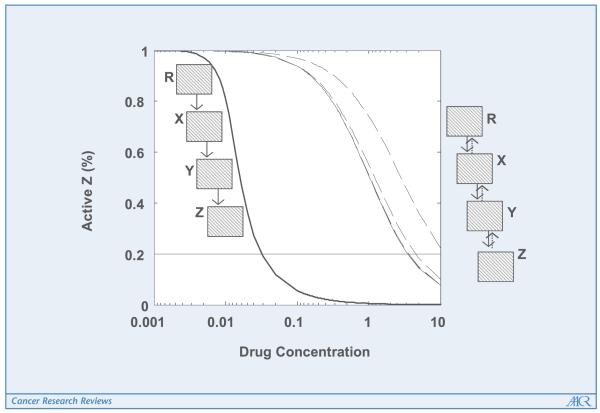
After the very instructive discussion of feedback circuitry and drug efficacy in (12), we have considered the signaling pathway and variables therein to show the extent of the property just described. We are not including feedback; however, let us consider a simple pathway in which signaling is initiated by the activation of a receptor R, which phosphorylates a protein X into Xp, and Xp phosphorylates a second protein Y into Yp, which in turn phosphorylates a third one Z into Zp. The activity of Zp is crucial for the proliferation rate of a particular cancer cell, so one might aim to treat a patient by applying a drug that affects one of the proteins in the pathway so as to inhibit the outcome of the pathway, namely an increase of Zp in this case. In Fig. 1, we show the results of considering both models for the R-X-Y-Z signaling pathway, the phenomenological model (10), and our description. An inhibitor is applied at level X, by affecting the V_max of the corresponding reaction. The steady-states of active Z concentrations were scaled to 100% to compare both models. For the model on the right, we have included several curves representing the drug-response outcome because that model has more variables than the phenomenological model on the left. Figure 1 indicates that the phenomenological model overestimates the effect of the drug in inhibiting the response of the pathway: a much higher drug concentration is needed to inhibit the pathway by 80% in the detailed model than in the phenomenological one. The underlying reason for this striking result is the following: when module X is inhibited in the pathway, there is less activation of module Y but also less sequestration of the variable corresponding to the module upstream to where the inhibitor is applied, R. This means that R has a greater response than it has within the phenomenological modeling framework. This apparently subtle dual mechanism has an overall nonnegligible consequence: the drug concentration needed to inhibit the pathway to a certain extent is much higher than predicted by an oversimplified modeling approach.

Figure 1.

Drug-response curves predicted by mathematical modeling. A simple signaling pathway R-X-Y-Z with an outcome related to cancer progression is inhibited at level X. The steady-states of active Z concentrations are scaled to 100% and plotted as predicted by two different modeling approaches. The model underlying the results on the right considers sequestration effects in the pathway. Not considering these effects (results depicted on the left) leads to an oversimplified model that underestimates the drug concentration needed to inhibit the pathway to a desired extent. Because much more is required to achieve a given extent of inhibition, this therapy is likely to be either ineffective (if given at the predicted doses) or toxic (if given at the more realistic doses predicted by the more sophisticated model).

Mathematical models linking cell signaling to cell phenotype

A critical challenge of experimental therapeutics for cancer is to decide which drugs are the best candidates for clinical trials. Mathematical modeling strategies can be of help in this regard. By accurately quantifying how cells interpret coupled signals from a variety of stimuli and connect these molecular processes to the temporal changes in tumor cell and microvessel density, mathematical oncology can help to determine which anticancer agents have the most potential for therapeutic benefit for a given tumor profile.

Recent experiments show that vascular endothelial growth factor (VEGF) is the crucial mediator of downstream events that ultimately lead to enhanced endothelial cell survival and increased vascular density within many tumors. A key pathway involves up-regulation of the antiapoptotic protein Bcl-2, which in turn leads to increased production of interleukin-8 (CXCL8). The VEGF–Bcl-2–CXCL8 pathway suggests new targets for the development of antiangiogenic strategies. We have recently developed a mathematical model that is the first to connect the molecular events associated with VEGFR2 (the major endothelial cell surface receptor for VEGF) dimerization and intracellular signaling with the temporal changes in endothelial cell proliferation, migration, and survival (13). This model is used to predict the effect of decreasing the bioavailability of VEGF, CXCL8, and Bcl2 on tumor growth and vascular structure and is validated with data from human tumors vascularized with human blood vessels in immunodeficient mice. The coupled, cell signaling–tissue response model was able to predict the efficacy of two novel antiangiogenesis treatment strategies, anti-CXCL8 and anti-BCL2, in a defined experimental assay. The result highlights specific differences in the effects of each therapy on tumor growth and vascular development and predicts a significant threshold effect for anti-BCL2 therapy.

This type of modeling effort underscores the potential of these approaches as predictive tools to guide in vivo experiments aimed at testing novel antiangiogenic therapies. These results led to the development of several hypotheses that are currently being tested by explicitly modeling the intracellular signals and tissue level response to cellular variations in proapoptotic and antiapoptotic proteins in the Bcl family, as well as the administration of specific antiangiogenic therapies targeted against Bcl2 at early, middle, and late stages of tumor development.

Concluding Remarks—Where Do We Go from Here?

As a collection of heterogeneous genetic disorders, cancer presents some of the most challenging problems for basic scientists, clinical investigators, and practitioners. To design treatments that are capable of specifically targeting the invasive cancer cells that drive malignant tumor growth, it is necessary to understand the underlying mechanisms in this process. Due to the inherent complexity involved, conventional experimental approaches alone are often unable to penetrate to the core of these issues. Furthermore, given the multiscaled pathophysiology involved, it is becoming ever so important for cancer research to make use of crossdisciplinary, systems science approaches, in which innovative mathematical/computational cancer models play a central role. Mathematical modeling together with numerical simulation and carefully designed experiments provide a unique combination to cope with these challenges and to improve cancer treatment. Pioneering work of this kind written in a manner accessible to the diverse readership of Cancer Research will usher a new era of applications of mathematical modeling to help diagnose, prevent, and treat cancer.