Biomechanical 3-Dimensional Finite Element Analysis of Obturator Protheses Retained with Zygomatic and Dental Implants in Maxillary Defects

Abstract

Background

The objective of this study was to investigate the stress distribution in the bone around zygomatic and dental implants for 3 different implant-retained obturator prostheses designs in a Aramany class IV maxillary defect using 3-dimensional finite element analysis (FEA).

Material\Methods

A 3-dimensional finite element model of an Aramany class IV defect was created. Three different implant-retained obturator prostheses were modeled: model 1 with 1 zygomatic implant and 1 dental implant, model 2 with 1 zygomatic implant and 2 dental implants, and model 3 with 2 zygomatic implants. Locator attachments were used as a superstructure. A 150-N load was applied 3 different ways. Qualitative analysis was based on the scale of maximum principal stress; values obtained through quantitative analysis are expressed in MPa.

Results

In all loading conditions, model 3 (when compared models 1 and 2) showed the lowest maximum principal stress value. Model 3 is the most appropirate reconstruction in Aramany class IV maxillary defects. Two zygomatic implants can reduce the stresses in model 3. The distribution of stresses on prostheses were more rational with the help of zygoma implants, which can distribute the stresses on each part of the maxilla.

Conclusions

Aramany class IV obturator prosthesis placement of 2 zygomatic implants in each side of the maxilla is more advantageous than placement of dental implants. In the non-defective side, increasing the number of dental implants is not as suitable as zygomatic implants.

Background

Maxillectomy defects are very common clinically because of tumors and trauma. After a maxillectomy operation, part of the maxilla and the buttresses are lost, and the oral cavity communicates with the nasal cavity and a maxillary sinus. This operation greatly impairs articulation, mastication, and speech, as well as causing facial disfigurement and difficulty in swallowing and deglutition [1,2]. In general, there are many alternatives for maxillary reconstruction, such as conventional obturator protheses, regional pedicled flaps and bone grafts with titanium plates or meshes, and zygomatic and dental implant-retained obturator protheses [2,3]. Maxillary obturator prostheses have a long history of effectively resolving the functional, cosmetic, and psychological problems associated with the maxillary defects, but the mobility of maxillary protheses impairs function. In maxillary defects, achieving success in retention and optimum stability of obturator prothesis by traditional techniques is very difficult [1] Conventional dental implants have been used to enhance the stability and retention of maxillofacial prosthetic obturators and to restore oral function [4]. Occasionally in such cases conventional dental implant treatment cannot be applied because an inadequate amount of maxillary bone remains following maxillectomy. When the remaining bone does not offer enough retention and support, the placement of zygoma implants can enhance the stability of the prosthesis [5]. Zygoma implants, first introduced by Brånemark in 1988, to provide retention and stability for conventional removable prosthesis [6].

A recent review of studies including 1143 zygomatic implants showed a survival rate of 98.4% after follow-up from 6 months to 10 years [7]. Schmidt et al. found that the combination of zygomatic and standard endosseous implants can be used for retaining and stabilizing of maxillary obturator prostheses after extensive resection of the maxilla [8].

Obturator prostheses framework models focus on the Aramany class IV obturator model. Aramany class IV defects are well known in the resection of the premaxilla and the posterior maxilla on 1 part [9,10].

This kind of enormous defect has an excessive and egregious impact on the biomechanic supporting tissues [11]. Bone remodelling corresponds to the charge degree stresses between 4 MPa and 8 MPa and behaves as stimuli and increases bone density. However, 9 MPa causes resorption and reduced bone density [12].

FEA has been used widely to estimate the biomechanical performance of different dental implant designs and their effect on clinical factors in implant success. In the last 20 years, FEA has become an increasingly useful method for the evaluation of the effects of stress on the implant and its surrounding bone [13]. FEA separates a complex body into smaller pieces that can be individually modelled on the basis of mathematical equations [14].

These pieces are called elements and they are joined by nodes. When the forces are applied to the whole body of known material specificity, the stresses can be measured at any desired point.

The placement of zygoma implants in maxillary defects is related to many problems, such as deficiency of bone tissue, loss of soft tissue, and overloading of zygoma and implant [11].

To the best of our knowledge, the stress distribution of zygoma and dental implant-retained Aramany class IV edentulous maxillary obturator prostheses have not yet been analyzed.

The purpose of this study was to evaluate, by using FEA, the effect of number of implants and zygomatic implants used on the stress distribution on the maxilla when the Aramany class IV obturator prosthesis was subjected to 3 different loadings.

Material and Methods

Construction of 3D FEMs

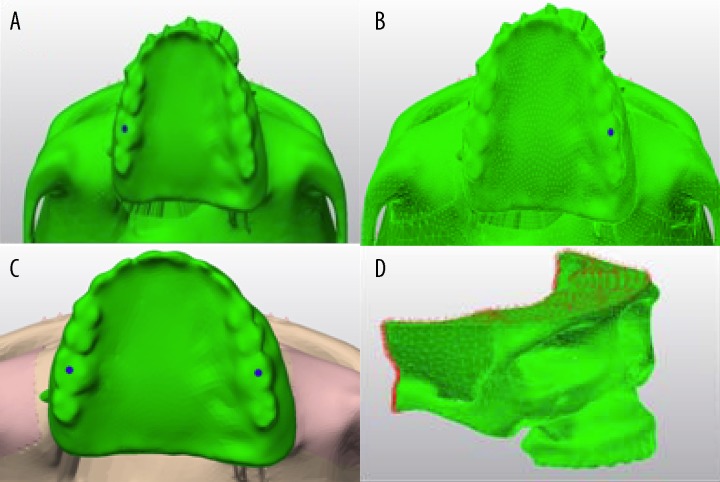
A three-dimensional (3D), finite element, solid model of the human skull was constructed based on CT data. The CT data was obtained from a 65-year-old Turkish man with unilaterally and premaxillary defects of the edentulous maxilla. Three-dimensional data of the maxilla and zygomatic bone were acquired from CT (ILUMA CBCT, ImtecImaging, Ardmore, OK), which were transferred into 3D-Doctor software (Able Software Corporation, Lexington, MA) and Rhinoceros software (McNeel, Seattle, WA) to generate a 3D finite element model of the maxilla and zygomatic bone with 1.0-mm slice thickness.

The 3D finite element model of dental and zygomatic implants, superstructures, and obturator prosthesis was constructed from digitized surface data using a NextEngine (Santa Monica, Calif) device. The data were then transferred into the 2 software packages – 3D-Doctor and Rhinoceros.

The 3D model that was created from 3D-Doctor and Rhinoceros was then transferred to Fembro software (Algor, Pittsburgh, Pa) with a scene export format stl file to allow the necessary refinements and to constitute the final finite element mesh model.

Construction of study configuration maxillary prosthesis models

Cortical bone with 1.5-mm thickness was uniformly defined around the trabecular core body. Mucosa was assumed to be 1.5 mm in thickness.

We used standard dental implants (Institute Straumann, Waldenberg, Switzerland) with a diameter of 4.1 mm and a length of 10 mm, and zygomatic implants (Brånemark System, Nobel Biocare AB, Goteborg, Sweden) with a diameter of 4 mm and length of 35 mm and locator attachments. Models of maxillary obturator prostheses with different numbers of implants were designed for an Aramany class IV right maxillary defect.

The dental and zygomatic implants were projected to the defective maxilla in 3 different configurations. The 3D finite element model of 3 different types of obturator prostheses was established according to these designs. The 3 study configuration models were as follow.

Model 1

This design consisted of placement of 1 zygomatic implant on the defected side of the maxilla in combination with 1 dental implant placed on the non-defective side and completion of the restoration with locator attachments (Figure 1).

Figure 1.

(A, B) Finite element model of the configuration 1 (model 1): 1 zygomatic implant and one dental implant.

Model 2

This design consisted of placement of 1 zygomatic implant on the defected side of the maxilla in combination with 2 dental implants placed on the non-defective side and completion of the restoration with locator attachments (Figure 2).

Figure 2.

Finite element model of the configuration 2 (model 2) 1 zygomatic implant and 2 dental implant

Model 3

This design consisted of placement of 2 zygomatic implants on each side of the maxilla and completion of the restoration with locator attachments (Figure 3).

Figure 3.

Finite element model of the configuration 3 (model 3) 2 zygomatic implant

Mesh creation

A mesh was generated from the solid models using the Fempro software package. After meshing, the first model consisted of 94.530 nodes and 367.609 elements, the second model consisted of 96.489 nodes and 382.142 elements, and the third model consisted of 93.038 nodes and 359.168 elements.

Loading

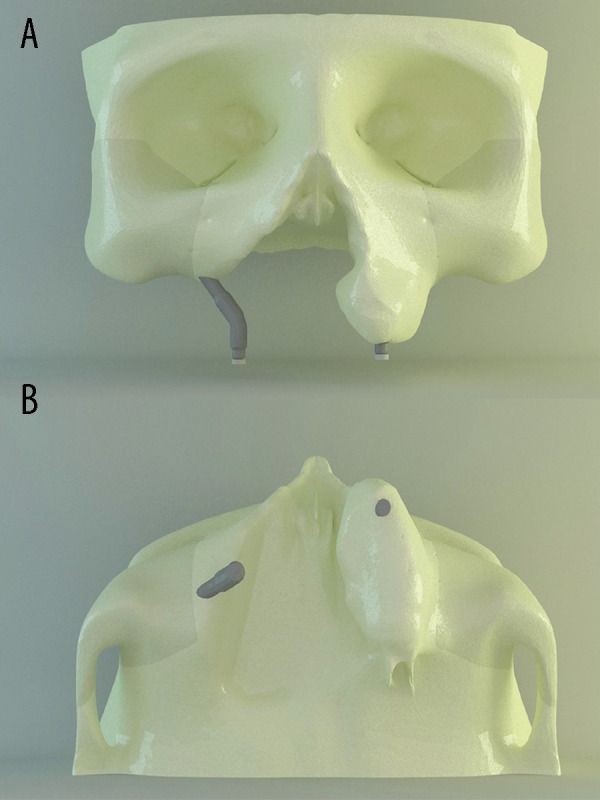
The non-defective side of the maxilla and zygomatic bone on that part and zygomatic bone of the non-defective part of the maxilla were created as fixed in all directions to the skull with zero displacement. It was predicted that the prosthesis and maxilla would have perfect connection. To simulate a clinical circumstance, a bite force of 150 N was loaded. 150-N vertical force was loaded in 3 various processes: first, loading was applied to the defective part; second, to the non-defective part; and third, loading was applied progressively to both parts. Then maximum principal stresses were evaluated. The analysis process was realized using Fempro technologies.

A vertical force of 150 N was loaded at the occlusal surface. Boundary conditions, loading locations, and directions of the finite element models are shown in Figure 4.

Figure 4.

Boundary conditions and loadings configuration in FEA models (A) occlusal view of the first loading; (B) occlusal view of the second loading; (C) occlusal view of the third loading; (D) boundary conditions

The results depended on a qualitative analysis, according to the degree of maximum principal stress (shown by a color scale) and a quantitative analysis in MPa.

The properties of materials used in this study, including Young’s modulus and Poisson’s ratio, were obtained from early studies (Table 1).

Table 1.

Material properties of analysis objects.

Material	Young’s modulus (E) (MPa)	Poissson’s ratio (v)	References
Mucosa	680	0.45	[11,15]
Cortical bone	13700	0.30	[18]
Ti6Al4V	110000	0.30	[18]
Acriylic resin (pmma)	2700	0.30	[2]
Titanium	115000	0.35	[2,18]
Zygoma	11507	0.30	[2]

Results

Solution of model 1

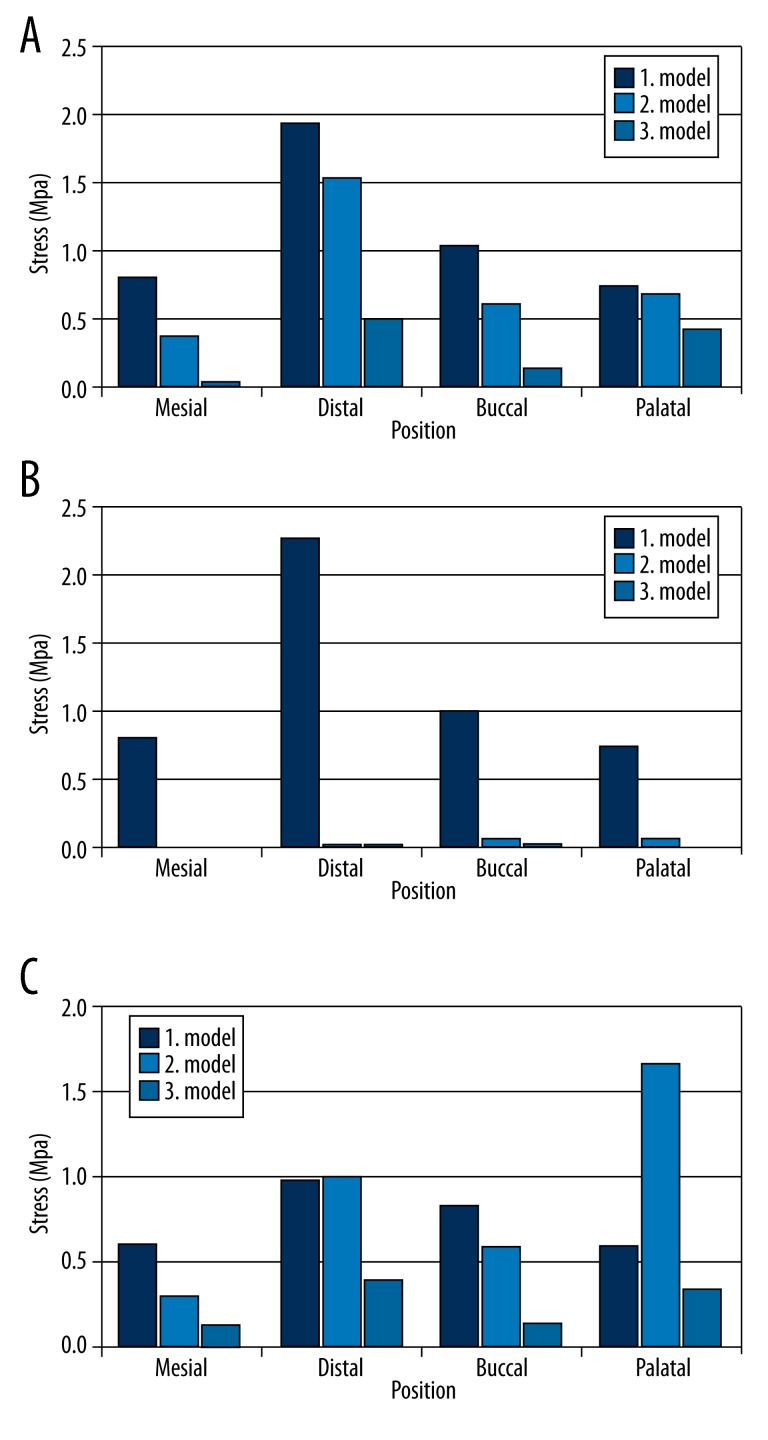
Maximum principal (tensile) stress values model 1 (1 zygomatic implant, 1 dental implant) shown in Figure 5 for the first loading (defective side) (Figure 5A), second loading (non-defective side (Figure 5B), and third loading (both sides) (Figure 5C) condition. In the case of model 1, the highest tensile stress value (2.3 MPa) was established in the second loading on the defective part of the maxilla distal side of the zygomatic implant (Figure 6).

Figure 5.

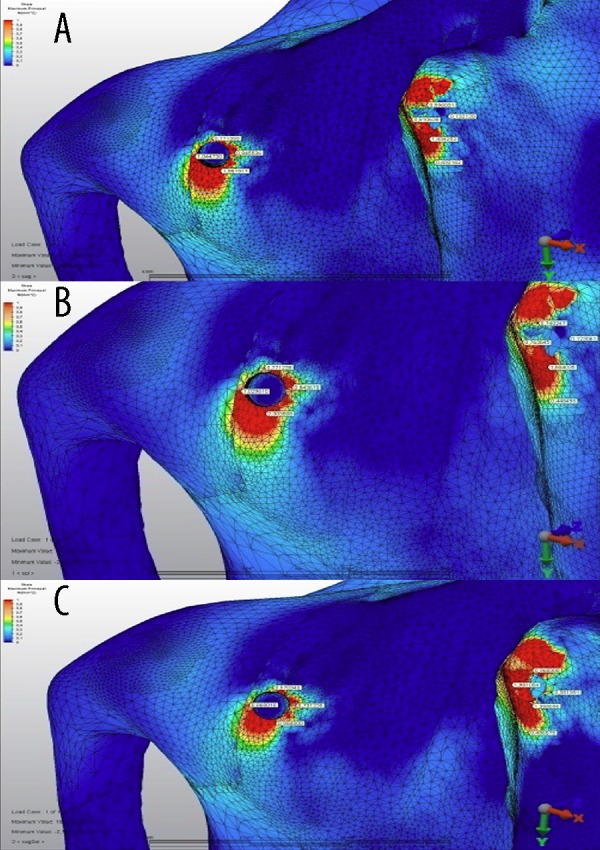
The maximum principle stress distributions in the maxilary bone around implants under (A) first loading, (B) second loading, and (C) third loading conditions for model 1 (unit: MPa). Colors show level of stress from dark blue (lowest) to red (highest).

Figure 6.

Comparison of the stress distribution on defected side a round the zygomatic implant for different loading conditions. (A) First loading, (B) second loading, (C) third loading.

Solution of model 2

Maximum principal (tensile) stress values model 2 (1 zygomatic implant, 2 dental implants) shown in Figure 7 for the first loading (defective side) (Figure 7A), second loading (non-defective side (Figure 7B), and third loading (both sides) (Figure 7C) condition. In the case of model 2, the highest tensile stress value (1.65 MPa) was established in the third loading on the defective part of the maxilla palatal side of the zygomatic implant (Figure 6).

Figure 7.

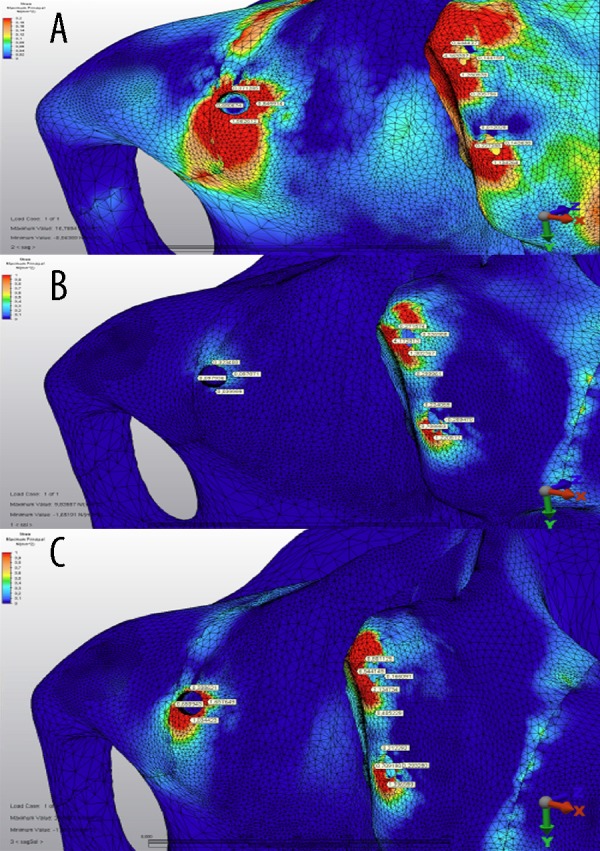
The maximum principle stress distributions in the maxilary bone around implants under (A) first loading, (B) second loading, and (C) third loading conditions for model 2 (unit: MPa). Colors show level of stress from dark blue (lowest) to red (highest).

Solution of model 3

Maximum principal (tensile) stress values model 3 (2 zygomatic implants in each side) shown in Figure 8 for the first loading (defective side) (Figure 8A), second loading (non-defective side (Figure 8B), and third loading (both sides) (Figure 8C) condition. In the case of model 3, the highest tensile stress value (0.51 MPa) was established in the third loading on the defective part of the maxilla distal side of the zygomatic implant (Figure 6).

Figure 8.

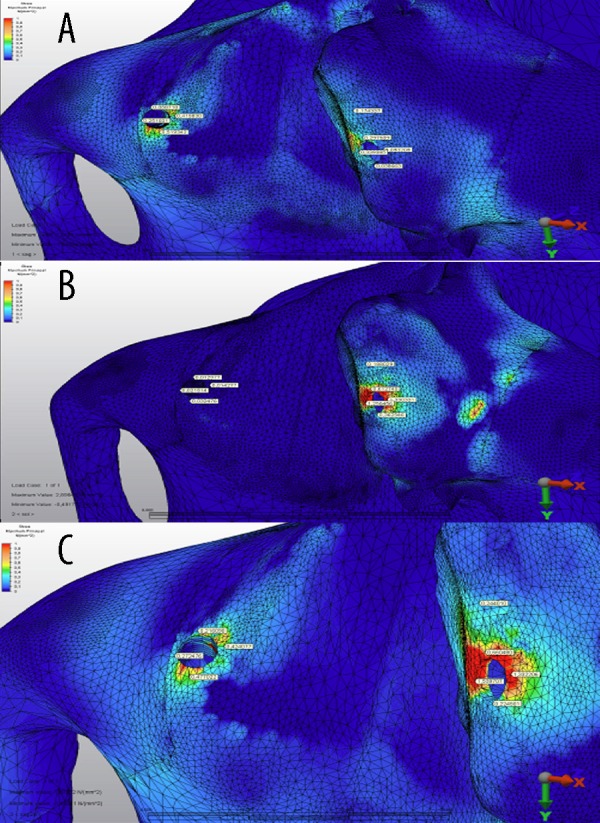
The maximum principle stress distributions in the maxilary bone around implants under (A) first loading, (B) second loading, and (C) third loading conditions for model 3 (unit: MPa). Colors show level of stress from dark blue (lowest) to red (highest).

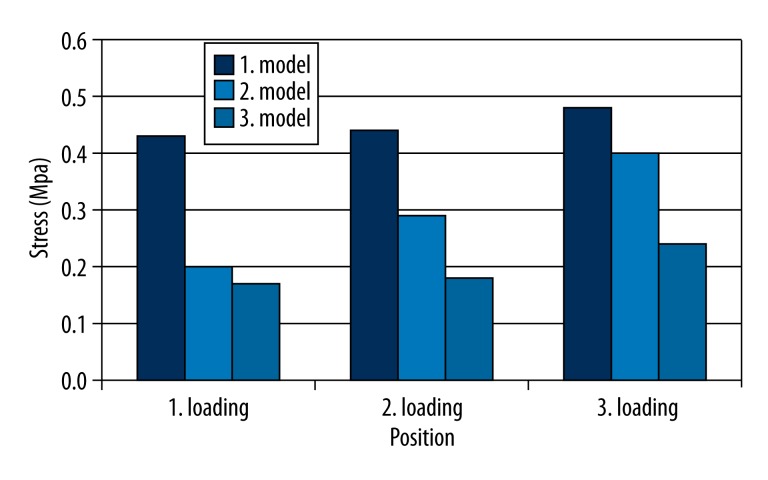
Comparing the stress distrubution on the non-defective side at the place of second premolar teeth level for different loading conditions, the highest tensile stress value (0.48 Mpa) was determined under third loading condition in model 1. Similar highest stress values were established in model 1 under first loading (0.43 MPa), and second loading (0.44 MPa) conditions were determined (Figure 9).

Figure 9.

Comparison of the stress distrubition on undefected side at the place of 2. premolar teeth level for different loading conditions.

In all loading conditions, model 3 when compared to models 1 and 2 presented the lowest maximum principal stress value.

Discussion

Occasionally, maxillary defects have been treated with large bone grafts from the iliac crest. However, the procedure is based on resources, requires much time, and can occur risk morbidity of the emitter site [16]; therefore, some researchers considered the obturator prosthesis was a better option for the patients with maxillary defects although it lacks retention and stability [17]. To enhance the retention and stability, zygomatic implants are an alternative and useful method. However, the estimation of the appropriate level of stress and design of superstructures are importance for the success of rehabilitation.

Various techniques (e.g., photoelastic stress analysis, strain-gage analysis, and FEA) have been widely used for stress analysis [18]. The FEA is a numerical stress-analysis technique widely used in the fields of engineering and biomechanics. This method is approved by many physicians worldwide. It is non-invasive and flexible enough to simulate different types of defects and corresponding reconstruction plans in the same model. Moreover, the process of evaluation is visible and vivid and permits the researcher to evaluate and search any locations contacted [2].

In the present study we designed 3 different implant-supported locator attachment-retained obturator prosthesis models for Aramany class IV maxillary defects by using FEA. We found that use of a zygomatic implant on the non-defective side provided decreased stress values and using zygomatic implants on the non-defective side is more useful then applying 1 or 2 dental implants with locator attachments.

Korkmaz et al. constructed 4 different zygoma- and dental implant-supported bar-retained obturator prosthesis models for Aramany class I maxillary defects by using FEA. Various researchers have reported that on the unaffected side, use of zygomatic implants provided decreased stress values, and when the number of dental implants on the unaffected side was increased, it had less influence on VM stress, which is in agreement with results of Chao et al. and Meijer et al. [19–21]. This correlates with the findings of the current study.

Freedman et al. [22] investigated the importance of alveolar bone support for zygomatic implants. They suggest that the support provided by alveolar bone is valuable for zygomatic implants. This correlates with the findings of the current study that in the non-defective side of the maxilla, use of zygomatic implants provided decreased stress values. In addition, using zygomatic implants on the non-defective side is more useful than using 1 or more dental implants. On the other hand, in the present study, although there is an insufficient alveolar bone on the defective part in our models, maximum principal stress did not exceed the physiological limits of the maxillary bone.

A study reported that the maximal bite force in patients with osseointegrated oral implants was 144,4 N [23]. In the present study, 150 N was applied in our models. The reason for choosing this load was to simulate the actual maximum biting force. Besides the value, the direction of the loading is also an important aspect to consider. However as in each FEA study, we can see particular limitations in our study. One of them is that vertical loads were taken into consideration. When applying FEA to dental implants, we have to underline the importance of applying not only axial loads and horizontal forces but also an integrated load, because an integrated load mimics the masticatory pattern more realistically and produces regional stress in bone [18,24].

In the actual study, complete osseointegration between implants and surrounding osseous tissue was predicted. Implants were in-situ in the zygomatic and maxillary alveolar bones on the defective and non-defective parts, and different designs of maxillary prostheses were computed. Radio and chemotheraphy generally destroy the bone substance and affect the success ratio of implants [25].

From the studies cited above, it is obvious that use of CT data or Ostell machine for each patient is essential in order to analyse bone defects.

We hope our results will be useful for surgeons and prosthodontists to obtain desired designs of prostheses in clinical practice to improve patient quality of life.

Conclusions

Within the limitations of this study, the following conclusions were mentioned: Firstly in Aramany class IV obturator prosthesis, placement of 2 zygomatic implants on each side of the maxilla (defective and non defective part) is more advantageous than placement of dental implants. In the non-defective side, increasing the number of dental implants it is not as suitable as zygomatic implants. Secondly, second loading (non-defective side) presented lower stress levels when compared with first and third loading.