The coordination of movement: optimal feedback control and beyond

Abstract

Optimal control theory and its more recent extension, optimal feedback control theory, provide valuable insights into the flexible and task-dependent control of movements. Here, we focus on the problem of coordination, defined as movements that involve multiple effectors (muscles, joints or limbs). Optimal control theory makes quantitative predictions concerning the distribution of work across multiple effectors. Optimal feedback control theory further predicts variation in feedback control with changes in task demands and the correlation structure between different effectors. We highlight two crucial areas of research, hierarchical control and the problem of movement initiation, that need to be developed for an optimal feedback control theory framework to characterise movement coordination more fully and to serve as a basis for studying the neural mechanisms involved in voluntary motor control.

The problem of coordination

The defining feature of coordination is that multiple effectors work together to achieve a goal. Coordination occurs at many levels of the motor control hierarchy: between individual muscles, between joints and between limbs. Movements are made to achieve goals and effectors are coordinated to control task-relevant states of the body and environment (the physical plant). Consider the example of reaching to press an elevator button. The task-relevant state is the position of the index finger and the goal of the reach is to bring the fingertip to the button. A fundamental problem of coordination is that the number of effectors involved (in this example ten possible degrees of freedom of movement between shoulder and index finger, and >40 muscles to actuate these movements) exceeds the dimensionality of the task requirements (three spatial dimensions). Thus, there are many different ways to achieve the movement goal. Despite this inherent redundancy [1], a large body of experimental data indicates that the motor system consistently uses a narrow set of solutions. A central issue in research on coordination is how and why the brain selects particular movements given the large set of possibilities.

Several theories have suggested that there are inherent constraints in the nervous system that limit the number of choices, therefore making the problem of coordination tractable. The concept of motor synergies (see Glossary) captures the idea that there is a set of fixed combinations of muscles, which are preferably controlled as functional units [2]. Research in this area has attempted to identify muscle combinations that are stable across different task goals and movement types [3–5]. Dynamical system theory posits that coordinative behaviour arises from the entrainment of dynamically coupled oscillators [6], highlighting why the nervous system exhibits biases for certain patterns such as a preference to produce mirror-symmetric movements [7]. More cognitively oriented theories have posited that the motor system achieves coordination by setting common parameters for multiple effectors during the process of motor planning [8–10].

Optimal control theory (OCT) and its recent extension, optimal feedback control theory (OFCT), offer a different perspective. Rather than focusing on internal constraints in the control system, these theories emphasise that coordination can be understood as the solution of an optimisation process for the tasks that the organism faces. The characteristics of coordination are therefore determined by the structure of the task and the body, and less so by internal constraints of the nervous system.

Here, we highlight how, especially in its current form (OFCT), the theory accounts for the distribution of work across different effectors, the task dependency of feedback control and the structure of variability in coordination. We consider two areas of current research (hierarchical control and the problem of movement initiation) that require further development for OFCT to serve as a useful theoretical framework for understanding how coordination is achieved, in terms of the underlying psychological and neural mechanisms.

Optimal (feedback) control theory

OCT assumes that biological systems learn to produce motor commands, which optimise behaviour with respect to biologically relevant task goals. These goals can be formally defined as cost functions. One part of the cost function encodes the external goal of the organism; for example, for eating, grasping a food item and bringing it to the mouth. A second part of the cost function, the regularisation term, penalises some inherent feature of the movement. In earlier formulations of OCT, this term was based on the integrated jerk [11,12] or integrated torque change [13]. In more recent versions, the regularisation term consists of the sum of the squared motor commands. Motor commands are conceptualised here as the neural drive to the muscles that can be measured as rectified EMG and that, after low-pass filtering, translates proportionally to muscle force [14]. A cost function of this form defines an optimal solution that achieves the goal (reasonably well) while exerting as little effort as possible. OCT models can account for the temporal shape of movements [15], the solution to new task environments [16] and the distribution of work across multiple effectors [17].

Initial developments of OCT defined the optimal solution as a sequence of feed-forward motor commands [11,13,15]. Optimal feedback control theory (OFCT) [12,18] provided an important extension by integrating the role of sensory feedback. The optimal solution now could be defined as a control policy (Box 1), a function that translates a current state estimate of the body into the next motor command. The control policy originally minimised a kinematic descriptor, such as squared jerk [12], and later a measure of effort (squared force). In its current form, OFCT also incorporates important factors such as the noisy nature of motor commands and sensory observations [19]. Whereas OFCT predicts the shape of the average movement just as well as earlier non-feedback versions of OCT (indeed, when we make statements about OCT we always mean to include OFCT), only the latter predicts how the organism will react to perturbations [20–22]. As we discuss below, it is this conceptual advance that enables the theory to account for many aspects of the correlation structure between different muscles observed during coordinated movements.

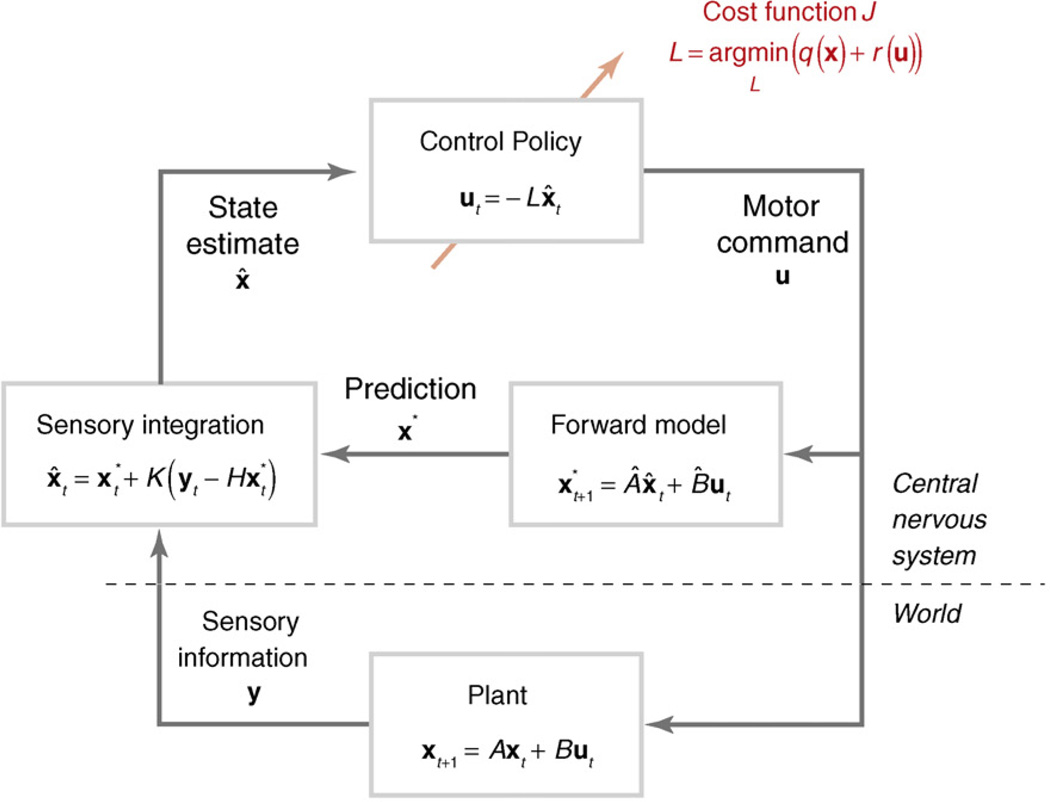
Box 1. Optimal feedback control.

The motor system interacts with the environment via a set of effectors that are controlled by the motor commands u (Figure I). The current state of the plant (the body plus environment) is represented by the state vector x, and its dynamics characterised by the (state-dependent) matrices A and B. To calculate motor commands, the system requires an accurate estimate of the state of the plant. Sensory information from the plant (y_t = Hx_t) is delayed in time and corrupted by noise. To overcome instabilities that arise from these factors, the motor system uses an efference copy of the motor commands and an internal forward model to generate predictions of the next state of the system (x*). This prediction can then be integrated with the incoming sensory information, resulting in a state estimate (x̂). The Kalman gain K for this integration is adjusted such that each source of information is weighted according to the inverse of its variance [74]. Motor commands are then determined using a control policy, a set of rules that dictates what to do given a certain goal and state estimate. Thus, according to OFCT, there is no conceptual difference between feed-forward and feedback control; the control policy governs both. Rather, feed-forward and feedback control constitute a continuum that depends on the degree to which the current state estimate is influenced by an internal prediction (such as early in the movement, or under sensory deprivation) or by sensory feedback.

A central problem for this architecture is to determine the appropriate control policy. Optimal control theory proposes that the selected control policy minimises a task-dependent cost function, J. The first component of this cost function, q(x), encodes the external goal of the organism in terms of task-relevant states; for example, the state that leads to reward. Because of redundancy in the motor system, this term alone does not define a unique solution. Therefore, a regularisation term, r(u), is introduced that penalises the expenditure of unnecessary motor commands, often taking the form of the weighted sum of the squared motor commands (Box 2).

Architecture of optimal feedback control.

Distribution of work across multiple effectors

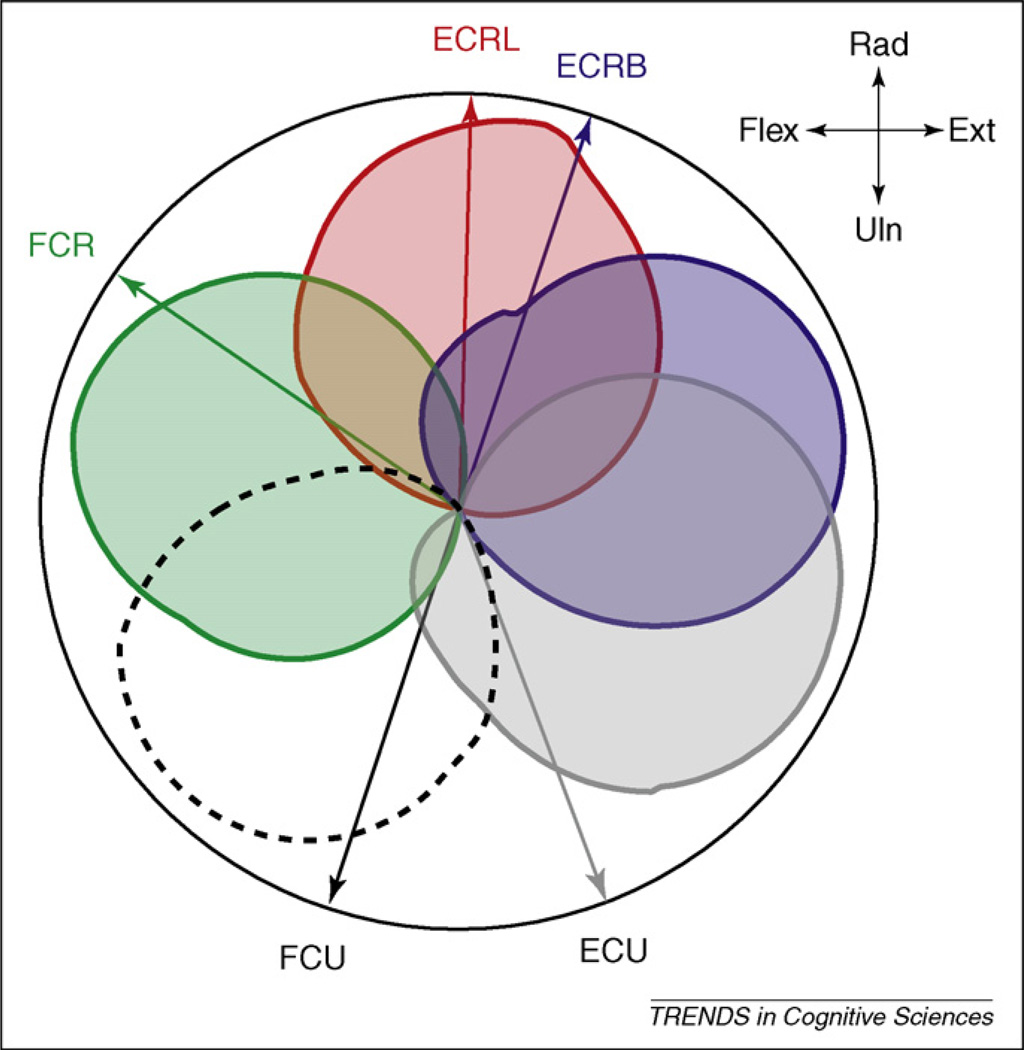
As an example of how the brain solves muscular redundancy, consider movements around the wrist joint. Figure 1 shows the pulling directions (the direction of movement evoked by electrical stimulation of that muscle) of the five main wrist muscles [23]. How would the brain combine these muscles for different movement directions? Because muscles need to work harder to achieve movements that do not lie in their pulling direction, the direction of movement for which each muscle shows the highest activation deviates from the pulling direction. This characteristic arises from the minimisation of the task-dependent term of the cost function, q(x), the squared distance between intended and produced movement direction. The exact distribution of work across effectors, however, depends on the form of the regularisation term, r(u).

Figure 1.

Pulling direction of the right extensor carpi ulnaris (ECU), extensor carpi radialis brevis (ECRB), extensor carpi radialis longus (ECRL), flexor carpi ulnaris (FCU) and flexor carpi radialis (FCR) in a midrange wrist position. The coloured circles indicate the normalised muscle activation for each movement direction based on a minimisation of the cost function [17]. The tuning function for each muscle, as well as the deviation of the preferred direction from the pulling direction, matches well with empirical results.

When using the sum of motor commands as a regularisation term, one would predict that, if the movement parallels the pulling direction of a particular muscle, then only that muscle should be active. For intermediate directions, activation would be restricted to muscles with neighbouring pulling directions. Indeed, this cost function would never predict co-activation in more than two muscles (for a 2D-task). Wrist muscles, however, show relatively wide cosine-like tuning functions spanning a wide range of movement directions. For most movement directions, at least three muscles are simultaneously recruited [23].

This pattern of muscular activity can be explained by using the sum of squared motor commands as the regularisation term [17,24,25]. Here, optimality is achieved when the system distributes work across multiple effectors, even if task goal could be achieved by the activation of a single muscle (Figure 1; see also Ref. [26]). This can be seen in the simple case in which two muscles have nearly the same pulling direction. The sum of the squared motor commands is minimised when the forces are distributed evenly across effectors. Importantly, by minimising the sum of squared motor commands, the motor system reduces both effort and movement variability (Box 2).

Box 2. Why u²? Effort versus variability.

Why should the nervous system minimise the sum of the squared motor commands rather than the sum of the motor commands or some other function? One possibility is that the function calculated by squaring the motor commands closely reflects energy expenditure during movement. However, ATP consumption by muscle fibres is roughly related to the product of force and contractile change or, under isometric conditions, to the product of force and time [75]. As such, ATP consumption is approximately proportional to the sum of motor commands, rather than to the sum of squared motor commands. Nonetheless, it is often assumed that the motor system minimises the squared motor commands to preserve internal resources. We refer to such a cost as ‘effort’ rather than ‘energy’.

An alternative interpretation lies in the reduction of movement variability [15]. Noise in the motor system is signal dependent: the variance of produced force increases proportionally with the squared mean [76]. Consider how such noise characteristics would influence endpoint variability. Suppose there is a dynamical system in which motor command u is affected by noise ε (Equation I):

$${\mathrm{x}}_{t+1}=A{\mathrm{x}}_t+B(u_t+{\epsilon }_t)$$ (I)

By applying this formula iteratively, any state can be expressed as a function of the initial state and the intervening motor commands (Equations II and III).

$${\mathrm{x}}_3=A^2{\mathrm{x}}_1+AB(u_1+{\epsilon }_1)+B(u_2+{\epsilon }_2)\dots$$ (II)

$${\mathrm{x}}_p=A^{p-1}{\mathrm{x}}_1+\sum _{t=1}^{p-1}{A}^{p-t-1}B(u_t+{\epsilon }_t)$$ (III)

The variance of this state will be (Equation IV):

$$\text{var}[{\mathrm{x}}_p]=\sum _{t=1}^{p-1}{A}^{p-t-1}B\text{var}[{\epsilon }_t]{(A^{p-1-t}B)}^T$$ (IV)

If the noise is signal dependent, for example it is composed of elements ε_t = u_tcϕ_t where c is a constant and ϕ is a Gaussian random variable with mean zero and variance 1, then the variance of the noise and the final state can be written in terms of the motor commands (Equations V and VI):

$$\text{var}[{\epsilon }_t]=c^2{u}_t^2$$ (V)

$$\text{var}[{\mathrm{x}}_p]=\sum _{t=1}^{p-1}{A}^{p-1-t}B{c}^2{u}_t^2{(A^{p-1-t}B)}^T$$ (IV)

This expression indicates that the variance of the state grows as a ‘square’ of the motor commands. Thus, to minimise endpoint variance, the sum of the squared motor commands should be minimised.

Whether interpreting the u²-cost as effort or variability, predictions derived from the two approaches are often indistinguishable [19]. However, when the task requires coordination across multiple effectors, effort and variability can be dissociated. Assume that two effectors are combined with a similar pulling direction, but with different signal-dependent noise characteristics, $\text{var}(u_i)=c_i^2{u}_i^2$. If the system only minimises noise, it should weight each effector by the inverse of its noise constant $c_i^2$, similar to the optimal integration rule when combining information from multiple sensory channels [77]. If the system minimised effort, the work should be distributed evenly or according to the strength of each effector. Both factors have a significant role [78], with a higher weight put on effort compared with variability costs. Although minimisation of effort and variability might frequently result in similar behaviours, it is important to distinguish between these two causes when considering how the nervous system evaluates the cost function during the acquisition of new coordinative motor skills.

The idea of distributing motor commands across a set of redundant effectors has also been explored in kinematic networks (e.g. Ref. [27]). The idea here is that one can determine the distribution of work across a set of joints, by simulating how much each joint would move if the endpoint was moved towards the final goal by a small amount. An OCT model arrives at a similar formulation, but explicitly introduces the control cost r(u), additionally to the stiffness of the joint, as a regularisation term.

In sum, OCT can predict how muscles work in a synergistic manner without using the concept of synergies as an explanatory concept [2–5,28,29]. Rather, synergies (in the descriptive sense) arise from the structure of the controlled physical plant, the task requirements and the regularisation term. Indeed, recent implementations of OCT to planar reaching movements closely replicate the patterns of muscular synergies observed in the human arm [30] and account for the structure of force variability in finger movement tasks [31].

Task-dependent feedback control

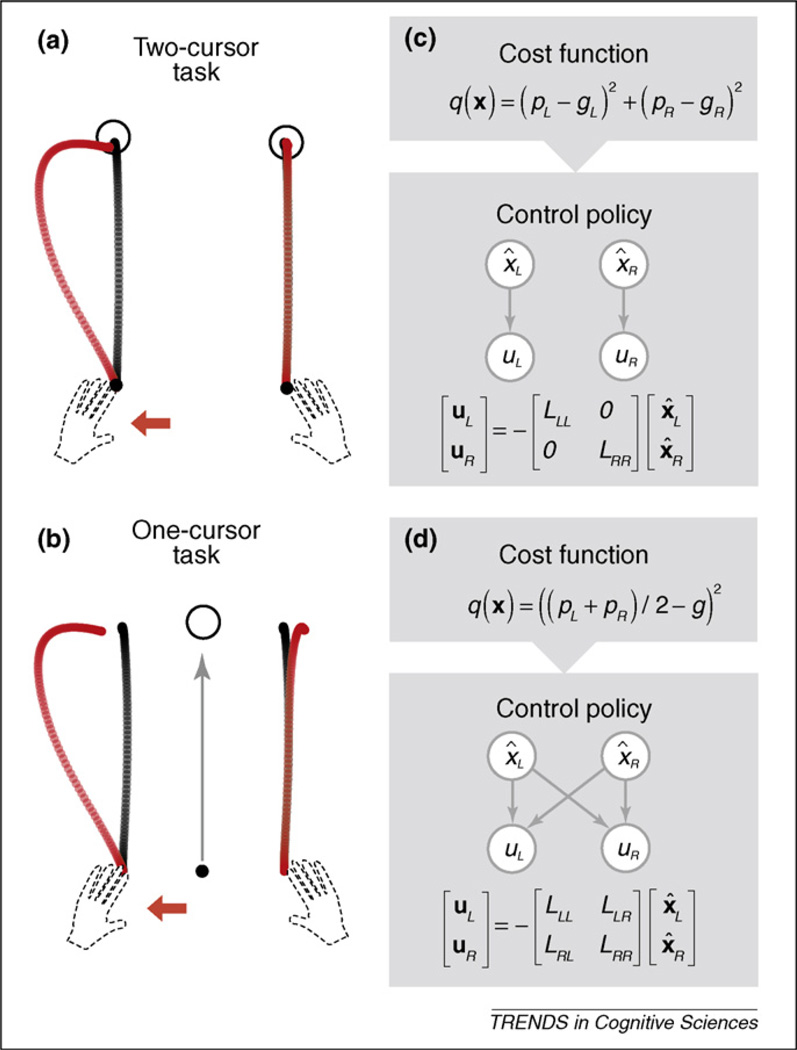
Whereas both feedback and non-feedback versions of OCT can account for the sharing of the work across effectors, the power of the approach becomes especially clear when considering optimal feedback control. An example of this is provided by a study on bimanual reaching movements (Figure 2; [32]). In the two-cursor task, participants were instructed to reach for two separate targets, one with each hand. The task-dependent component of the cost function here contains two separate terms, one that minimises the distance between the left hand and its goal and a second that minimises the distance between the right hand and its goal. In the one-cursor task, a single cursor, presented at the spatial midpoint between the two hands, was moved to a single target through the combined actions of both hands. The task-dependent component of the cost function for this condition minimises the distance between the single cursor and the goal. Despite the difference in cost functions, the average trajectories for these two tasks are identical, yielding straight movements with bell-shaped velocity profiles (black trajectories).

Figure 2.

Task-dependent feedback control during a bimanual task. (a) In the two-cursor task, a force field applied to the left hand is corrected by the action of the left hand alone. (b) In the one-cursor task, part of the correction is performed by the right hand. (c) The task dependent component q(x) of the cost function comprises the distance between the position of the left hand (p_L) and its goal (g_L) and the distance between the right hand (p_R) and its goal (G_R). Minimisation of this cost function results in independent control gains (L) for the two hands. (d) The cost function for the one-cursor task predicts feedback control in which motor commands for the left hand (u_L) depend on the state of both the left hand and right hands (x̂_L and x̂_R, respectively). Reproduced with permission from Ref. [32].

However, OFCT also predicts that feedback corrections for the one- and two-cursor tasks should differ. In the two-cursor task, the optimal control policy specifies that motor commands to each hand will only depend on the state of that hand and not on the state of the other hand (Figure 2c). Therefore, if one hand is perturbed during a reach, solely that hand should correct for that perturbation. Independent control of the two hands could also work in the one-cursor task. However, this policy would not be optimal. Rather, according to OFCT, the motor system should exploit the redundancy of the one-cursor task by distributing the correction across both hands, thus minimising the effort term. Indeed, this latter prediction was confirmed. When a robotic device was used to create lateral perturbations in one hand, online corrections in the one-cursor task were shared across the two hands [32] (see also Refs [33,34]). Interestingly, this behaviour was observed even if visual feedback of the cursor(s) was absent during the movement.

Task-dependent changes in coordinative feedback appear to involve the modification of basic reflex mechanisms. In a series of studies, Marsden et al. [35] examined the task dependency of intermanual reflex responses. Fast (60 ms) postural reflexes in the right arm in response to perturbations of the left arm reversed direction depending on whether the right arm held on to external support or whether it needed to stabilise a cup full of tea (see also Ref. [36]). Similarly, in the one-cursor task described above, perturbations to one arm resulted in EMG responses in the other arm at latencies as short as 60 ms [37]. Thus, even medium loop reflex responses appear to be modified by task requirements.

Although such changes are consistent with OFCT, at least qualitatively, there are components of the feedback response that do not change with task requirements [21,32,38]. Indeed, it would be unrealistic to assume that the whole system is completely re-optimised whenever the motor system faces a new task. This point highlights the need to modify OFCT models such that they incorporate hierarchies of goals and control [39]. This extension would provide one way in which only certain parts of the control structure are modified in a task-dependent fashion.

Structure of movement variability

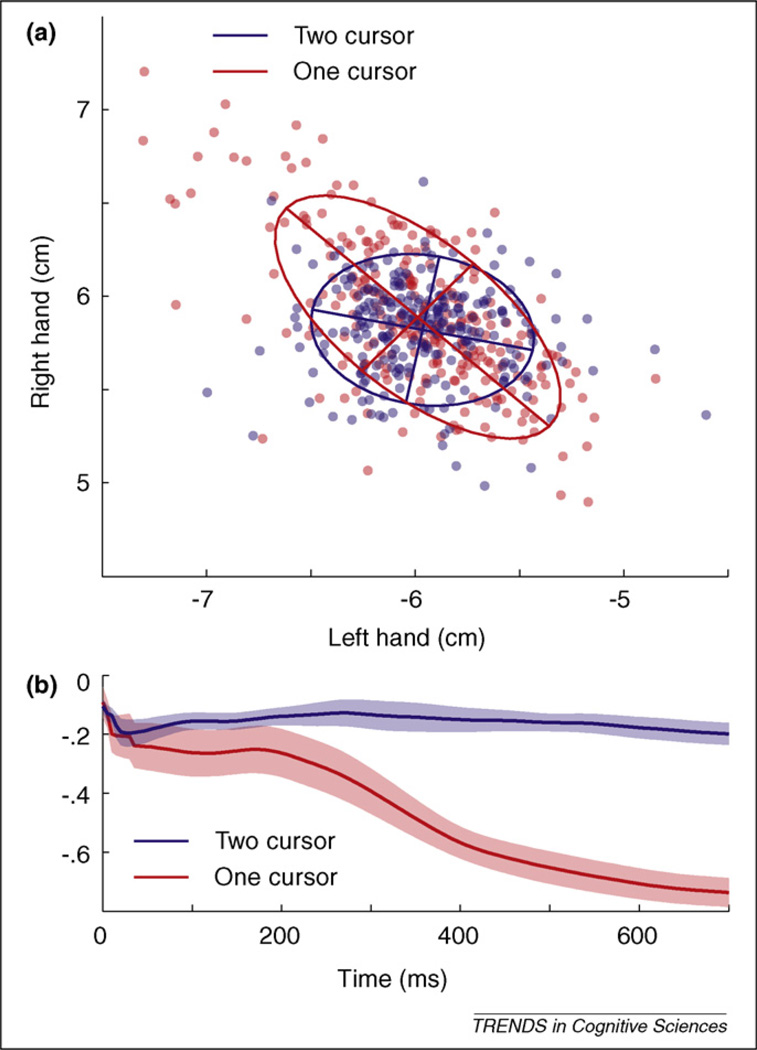
An intriguing characteristic of coordinated movement is that variability is structured; systematic correlations can be found between the actions of different effectors. This structure is often task dependent. In the bimanual one-cursor task described previously, the positions of the two hands are negatively correlated at the end of the movement, deviating in opposite directions from straight ahead (Figure 3a). This correlation minimises variability along the task-relevant dimension (the position of the cursor) even though the variability in a task-redundant dimension (the distance between the hands) increases. In the two-cursor task, this correlation is absent.

Figure 3.

Structured variability induced by task-dependent feedback gains. (a) Correlations of horizontal endpoint position of the left (x) and right (y) hands are found in the one-cursor task (red line and dots) but not in the two-cursor task (blue line and dots). In the one-cursor task, variability along the task-redundant dimension (distance between hands, left up–right down diagonal) is not corrected. (b) The negative correlation develops during the movement, indicating that it arises from a feedback control law rather than from correlations in the initial motor commands [32].

Task-dependent structure of effector (co-) variances is often analysed using the concept of the ‘uncontrolled manifold’ [40–42], the parameter region within which there is equivalence in terms of the task-relevant variables. The observation that variability in this parameter subspace is increased is ubiquitous and can be observed, for example, in the correlation structure of the seven muscles controlling the index finger [43]. In the temporal domain, structured variability can be observed in the synchronisation of bimanual movements. For example, when one hand is used to open a drawer and the other to retrieve an object from the drawer, intermanual time lags are small when the object is picked up, but variable during other phases of the action [44].

Correlations between effectors are often attributed to synergies (in an explanatory sense). In the context of OFCT, however, structured variability emerges naturally from task-dependent feedback control [18]. The regularisation term of the cost function enforces the minimal intervention principle: Deviations relevant to the external task goal should be corrected, whereas deviations along task-irrelevant dimensions need not be compensated and can thus accumulate. The interplay of these two factors induces structured variability. Importantly, OFCT holds that this structure arises through feedback control rather than reflecting inherent correlations between the feed-forward commands to different effectors. Consistent with this prediction, the negative correlation of the lateral hand positions in the one-cursor task arises over the time course of the movement (Figure 2c).

Initial gating mechanism

There are situations in which systematic correlations between effectors cannot be attributed to task-dependent feedback control. For example, when the two hands are used to reach simultaneously for two separate goals, OFCT would predict independent control of the two movements. However, strong correlations are observed in both reaction time and initial acceleration [45,46]. This form of coupling is generally considered a hard constraint in coordination [10]: it is not easily modified by task requirements [47]. Indeed, it remained present even when the primary connections between the two cerebral hemispheres were absent, despite the fact that the human subjects exhibited considerable independence of the two limbs once the movements are initiated [48,49]. Thus, there appears to be a general mechanism, probably subcortical [50], that synchronises the onset of different movements, even if they are unrelated. How can the existence of such a strong inherent constraint be reconciled with OFCT?

We propose that, at least for related movements, a coupling mechanism of this sort is necessary within the control architecture assumed by OFCT. Consider the task of raising one’s arm quickly while standing freely. The forces induced by the sudden movement of the arm are destabilising; if large enough, the actor might fall over backwards. To ensure stability, the motor system briefly activates the ankle flexors to shift the centre of gravity forwards, even before EMG changes are observed in the agonists of the arm movement [51].

In the context of OFCT, coordination between effectors is ensured because the commands of one effector depend on the state estimates of another (Figure 2d). This state-dependent mechanism is not sufficient for the coordination of the initial motor commands, because, before the onset of movement, there are changes in the respective state estimates and, hence, no exchange of information between the control processes. For accurate and fast movements, however, the initial bursts across different effectors need to be finely coordinated in both time of onset and initial strength [52].

How does OFCT solve this problem? In current simulations, each effector starts to produce motor commands simultaneously at time ‘zero’. Thus, the theory assumes implicitly the existence of a common command that synchronises the onset of all effectors recruited for the movement. Other models of movement production include such an initial gating mechanism as an explicit component. In these models, a common go-signal (VITE model [53]) or an internal phase keeper [54], specifies the time of onset and the initial strength of activation across all involved effectors. Although the neuronal substrate for an initial gating signal remains unknown, it is clear that such a mechanism is required for successful coordination over and above the state-dependent mechanisms implemented in current OFCT models.

Movement-to-movement variability of the initial gating mechanism will induce positive correlations between different effects at the onset of the movement. We propose that even unrelated movements, when initiated sufficiently close together, will share the same gating mechanism, resulting in the coupling and correlation of these effectors. Future research is required to distinguish between inter-effector correlations that are due to task-dependent coordinative feedback control and those that are due to the influence of a common gating signal. OFCT in it current form does not have an explicit mechanism to model variability in movement initiation. We expect that it will be necessary to integrate such a concept for the theory to account fully for the co-variance structure of human movements.

Coordination through high-level state estimates

In OFCT, coordination is achieved by making the motor commands for one effector dependent on the state of another effector (Figure 2d). Such direct dependence is appropriate when two effectors are biomechanically coupled. Elbow and shoulder muscles need to compensate mutually for the effects of interaction torques [22,55]. In this case, the two joints always need to be controlled as a single entity.

In other situations, the need for coordination arises because two effectors act on the same task-relevant variable even if the mechanical linkage between them is weak or non-existent. Examples here include coordinated movements of the fingers and arm to control the release of a ball during throwing, the manipulation of a single object with two hands, or the coordination of head and arm movements when eating or drinking. In all of these situations, the coordination of the effectors depends on the state of the controlled object and the nature of the task.

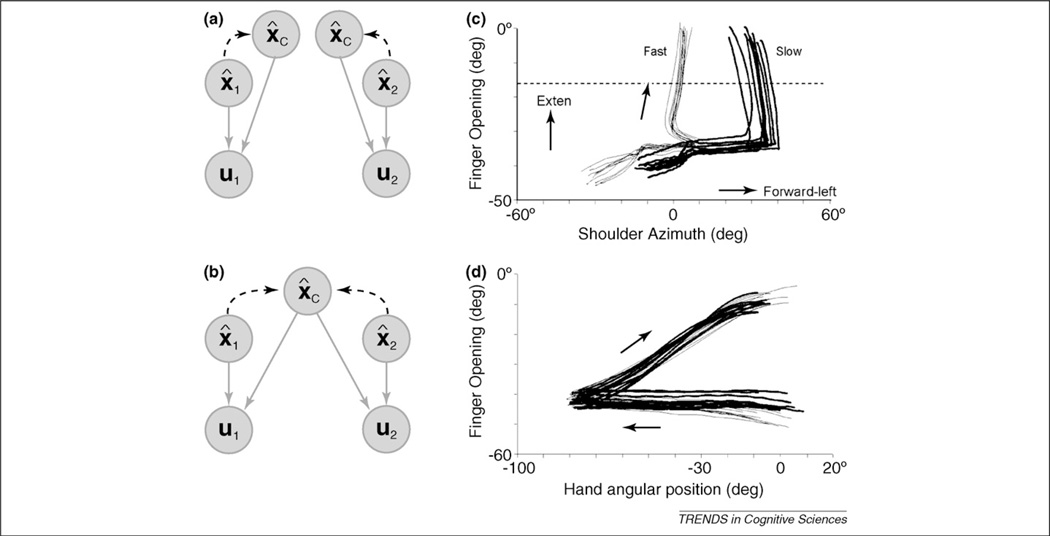
We propose that coordination for such tasks is based on higher-level state estimates of task-relevant variables (see Ref. [56] for related ideas). Returning to our example of the one/two-cursor task, the system would not only estimate the state of each hand, but also the state of the controlled cursor(s). In the two-cursor task, separate estimates for the two cursors keep control independent (Figure 4a). In the one-cursor task, a single state estimate leads to shared bimanual corrections. Coordination would be maintained even when the cursor was invisible because the common state estimate of the inferred cursor position is determined through a forward model that depends on the sensed state of both hands (Figure 4b).

Figure 4.

Coordination between effectors based on higher-level state estimates. (a) Control signals to the left hand (u₁) depend on a state estimate of that hand (x̂₁) and of the controlled object (x̂_C). The higher-level state is estimated through a dynamic forward model based on information from the effector (dashed curve). (b) In the one-cursor task, both hands influence the state estimate for the common cursor and, thus, the motor commands to the two hands become coordinated. (c) During throwing, the opening of the fingers to release the ball (y axis) is not invariant across slow and fast throws, when plotted against the shoulder azimuth. (d) Hand opening is invariant across throwing speeds only when plotted against the angular position of the hand in space. Reproduced with permission from Ref. [59].

Such hierarchical control models (Figure 4a,b) [57] can facilitate flexibility of control. When switching between control regimes in the one- and two-cursor task, the system need only change predictions about how the hands influence the movement(s) of the cursor(s). By contrast, if when coordination is achieved directly through lower-level state-estimates (Figure 2c,d), the motor system would have to reconfigure flexibly how the left hand should react to signals from the right hand with every change in task. A recent study demonstrated the flexibility with which the motor system can switch between different controllers, if each situation is associated with a different manipulated object [58].

For any constant task, the hierarchical and direct ways of expressing a coordinative control law are basically equivalent. However, the models make different predictions in terms of how a learned coordination skill would generalise to a novel task context. The direct model (Figure 2c,d) predicts that coordination should generalise in the reference frame of the state of the involved effectors (e.g. joint coordinates), whereas the hierarchical model (Figure 4a, b) predicts that coordination should generalise in a reference frame defined by higher-level state variables.

Learning to throw a ball at different speeds provides a clear example of this issue [59]. To throw a ball accurately, the release of the ball by the fingers must be timed to the forward movement of the arm [60]. What state estimate is used for this coordination problem? The relationship between the state of the fingers and the azimuth of the shoulder is not stable across different throwing speeds (Figure 4c). A similar problem is evident when finger position is plotted against a reasonable range of elbow and shoulder joint angles. Moreover, the interval between the arm movement and finger release varies systematically with speed; as such, the motor system cannot rely on an internal timing mechanism for this skill (see also Refs [61,62]). The only variable that provides an invariant relationship is the angular position of the hand in external space (Figure 4d). Thus, to learn a control policy that is flexible with respect to the speed of throwing, the motor system should estimate hand position in external space and use this to control the timing of the release. This example also emphasises that accurate state estimates require a predictive forward model given the speed of arm rotation; feedback loops would be insufficient given processing delays. Consistent with this hypothesis, the timing of ball release is properly adjusted following perturbations to the arm as long as the perturbation occurs at least 100 ms prior to the opening of the fingers [63].

Similarly to throwing, finger-arm coordination during grasping is based on an estimate of how far the hand has travelled towards the object, rather than on lower-level estimates of the state of the arm or on internal estimates of time [62,64,65]. Another example comes from bimanual object manipulation, where one hand has to learn to compensate for forces produced by the other. This skill generalises across the workspace in extrinsic or object coordinates [66] rather than in joint coordinates. By contrast, following adaptation to a force field, generalisation within each arm is observed in intrinsic, joint-based coordinates [67].

Considering the role of higher-level state estimates in coordination provides an important link to numerous experimental results demonstrating that the symmetry constraint observed in bimanual coordination [68] depends on perceptual variables and task demands [69–71]. More generally, many demonstrations of constraints in bimanual coordination appear to reflect limitations in the simultaneous estimation of high-level, task-relevant states [9], rather than hard-wired coordination constraints between the two hands. The human coordination system has evolved to achieve single goals flexibly using many effectors rather than to achieve multiple goals simultaneously.

Current limitations and outlook

Here, we have outlined how OTC, especially OFCT, provides a powerful tool for understanding coordination. It is important to emphasise that OCT (and OFCT) as a theoretical framework is underspecified and has limitations in terms of generating testable predictions. It is possible to explain any behaviour as ‘optimal’ if the cost function can be chosen without restriction. To avoid circularity, the cost function needs to be specified a priori and tested across different experimental contexts.

We have also highlighted the importance of specifying the state estimates that subserve coordination (e.g. joint-based or high-level), as well as differentiating between elements within a hierarchical control scheme that can be modified in a task-dependent fashion from those that are hard wired. Furthermore, we have stressed the importance of integrating a plausible model of movement initiation, and the variability arising from this process, into OFCT. We expect that future exploration of these issues will serve to constrain predictions derived from an OFCT framework, and make it possible to relate the control processes to their underlying neural substrate.

Another important area of research is how coordinated movements are learned. OCT (and OFCT) can only tell us what the optimal solution to a problem should be, but not how this solution is learned. Is there as neural representation of the overall cost of the movement [72]? Or can cost-functions be optimised in a distributed fashion? Which neural mechanisms are involved in the optimisation of cost functions?

Finally, OFCT teaches us that flexibility in the nervous system does not involve the recall of rigid motor commands, but rather a flexible reconfiguration of how the brain reacts to environmental stimuli. In that, the problem of motor control is closely related to the problem of flexible cognitive control [73].

Glossary

Control policy

a function that translates a state estimate of the body and task goal into a motor command for the next moment. This function is also referred to as a ‘next-state planner’.

Cost-function

a function that assigns each possible movement a scalar cost. The motor behaviour that minimises this cost function is optimal. Cost functions are unit-less and typically consist of one component that expresses the external task goal and a second component that serves as a regularisation factor, expressing an internal cost (e.g. energy or effort).

Effector

here, a part of the motor system that is controlled as a unit. Depending on the level of analysis, an effector can refer to a muscle, joint or limb.

State estimate

an internal representation of the state of the body and task-relevant variables (e.g. a joystick), derived from sensory input and predictions from a forward model. Optimal state estimates can be derived from a Kalman filter.

Synergy

as a descriptive concept, synergy refers to systematic correlations between different effectors observed over a set of behaviours; as such, it is an empirical fact. As an explanatory concept, it refers to a hypothetical control structure in the motor system that activates different effectors as a single unit.