Analysis of the contribution of experimental bias, experimental noise, and inter-subject biological variability on the assessment of developmental trajectories in diffusion MRI studies of the brain

Abstract

Metrics derived from the diffusion tensor, such as fractional anisotropy (FA) and mean diffusivity (MD) have been used in many studies of postnatal brain development. A common finding of previous studies is that these tensor-derived measures vary widely even in healthy populations. This variability can be due to inherent inter-individual biological differences as well as experimental noise. Moreover, when comparing different studies, additional variability can be introduced by different acquisition protocols. In this study we examined scans of 61 individuals (aged 4–22 years) from the NIH MRI study of normal brain development. Two scans were collected with different protocols (low and high resolution). Our goal was to separate the contributions of biological variability and experimental noise to the overall measured variance, as well as to assess potential systematic effects related to the use of different protocols. We analyzed FA and MD in seventeen regions of interest. We found that biological variability for both FA and MD varies widely across brain regions; biological variability is highest for FA in the lateral part of the splenium and body of the corpus callosum along with the cingulum and the superior longitudinal fasciculus, and for MD in the optic radiations and the lateral part of the splenium. These regions with high inter-individual biological variability are the most likely candidates for assessing genetic and environmental effects in the developing brain. With respect to protocol-related effects, the lower resolution acquisition resulted in higher MD and lower FA values for the majority of regions compared with the higher resolution protocol. However, the majority of the regions did not show any age–protocol interaction, indicating similar trajectories were obtained irrespective of the protocol used.

1. Introduction

Diffusion tensor imaging (DTI) is a magnetic resonance imaging technique that allows in vivo characterization of tissue (Basser et al., 1994; Pierpaoli et al., 1996) and has been used extensively to analyze brain white matter. DTI has been used to study healthy development (Huppi et al., 1998; Lebel et al., 2008) as well as neurological and psychiatric disorders that affect brain white matter (Cassol et al., 2004; Walker et al., 2013). Several pediatric studies have reported normative developmental trajectories for quantities of interest derived from diffusion tensors (Mukherjee et al., 2001; Barnea-Goraly et al., 2005; Snook et al., 2005; Hermoye et al., 2006; Ashtari et al., 2007; Bonekamp et al., 2007; Eluvathingal et al., 2007; Lebel et al., 2008; Faria et al., 2010; Lebel and Beaulieu, 2011; Sadeghi et al., 2013b). A common finding in these studies has been a rapid increase of fractional anisotropy, FA, and a rapid decrease of mean diffusivity, MD (defined as trace of the diffusion tensor/3), during early childhood (Hermoye et al., 2006; Faria et al., 2010; Sadeghi et al., 2013b) with continued development into adulthood (Ashtari et al., 2007; Lebel et al., 2008; Lebel and Beaulieu, 2011). Despite the general trend, it is evident that these derived tensor measures vary widely in healthy populations (Bonekamp et al., 2007; Lebel et al., 2008; Lebel and Beaulieu, 2011), making clinical diagnosis based on diffusion metrics a challenging task. This variability can be due to inherent inter-individual biological differences as well as experimental noise. Moreover, potential bias can be introduced by different acquisition protocols (e.g., different resolution, signal to noise ratio (SNR)) (Pierpaoli and Basser, 1996; Jones et al., 1999; Skare et al., 2000; Jones, 2004; Gao et al., 2009), scanner manufacturer (e.g., differences in gradient calibrations and gradient non-linearities) (Pfefferbaum et al., 2003; Vollmar et al., 2010) and magnetic field strength (e.g. different levels of echo planar imaging (EPI) distortions), to name a few confounding factors. The goal of this study is to separate the contribution of biological inter-individual differences and experimental noise in the observed variance of diffusion metrics.

We measure DTI metrics, specifically FA and MD, in several brain regions to characterize brain development from childhood to adulthood using publicly available data from the NIH MRI Study of Normal Brain Development (PedsMRI) (http://pediatricmri.nih.gov). To achieve our goal of separating the observed variability of diffusion indices into biological variability and experimental noise we included only subjects that had repeated scans. We reason that variability due to true inter-individual biological differences should be highly correlated between scans, while effects due to experimental noise should be uncorrelated. Dividing the variance of these metrics into these components has important implications: if the observed variability is mainly due to experimental noise, then experimental design and quality of data acquisition should be improved. On the other hand, if high variability stems from intrinsic differences in brain structure between individuals, then its association to inter-individual behavioral and cognitive differences should be investigated.

2. Materials and methods

2.1. Subjects

Subjects included in the PedsMRI study were recruited to produce a database representative of the U.S. population for race, ethnicity, and socio-economic status according to the 2000 census. Subjects were to be typically developing children, with strict inclusion/exclusion criteria. Included subjects underwent an MRI scanning session as well as an extensive cognitive and behavioral assessment. All subjects received anatomical (T1-weighted, T2-weighted and proton density weighted) scans. If the subject agreed, DTI and MRS data were also acquired. The PedsMRI design was mixed cross-sectional and longitudinal; subjects were asked to return annually if they continued to pass inclusion/ exclusion criteria. In this work, we used a cross-sectional subset of the data including only individuals that underwent two different diffusion protocols during the same scanning session or within a week. In total, 61 subjects (age range 4.1–22.2 years, mean age = 14.2, female: 29, male: 32) from a single site were included in our study.

2.2. Image acquisition

The MRI scanner used in this study was a 1.5T system from Siemens. The DTI data were acquired with a spin echo EPI sequence. The DTI protocol originally included a low resolution acquisition, which we refer to as conventional DTI (cDTI). The cDTI protocol utilized 6 diffusion gradient directions with 4 repetitions at b = 1000 s/mm² and 4 non-weighted images (b = 0 s/mm²) with isotropic voxel size of 3 mm³. The field of view was either 384 mm with TE = 90 ms, or 192 mm with TE = 75 ms, TR = 9 s with full echo acquisition. Subsequently an improved DTI acquisition protocol was added for subjects who could tolerate a longer scan. We refer to this protocol as expanded DTI (eDTI). The eDTI protocol was multi-shell using a maximum b-value of 1100 s/mm², (b = 0 n = 10, b = 100 n = 10, b = 300 n = 10, b = 500 n = 10, b = 800 n = 30, b = 1100 n = 50), where n represents number of volumes for each b value. However, in this study we only used volumes that were acquired at b = 0 or b = 1100 to have similar b values to the cDTI protocol. The voxel size for the eDTI protocol was 2.5 mm³. The field of view was 240 mm with TE = 87 ms,TR = 7.8 s with full echo acquisition. T2 weighted (T2W) images were also acquired for each subject with TR = 3500 ms, TE₁ = 17 ms, TE₂ = 119 ms, axial slices, 80–90 slices of 2 mm thickness to cover the apex of the head to the bottom of the cerebellum. The head coil was the same single channel coil for all acquisitions. Total acquisition time was about 4–7 min for the cDTI protocol and about 20 min for the eDTI protocol.

2.3. Data processing

The anterior commissure (AC) and posterior commissure (PC) were manually identified on T2W images; subsequently AC–PC was aligned using MIPAV software (Bazin et al., 2007). Individual diffusion weighted images were processed using the TORTOISE pipeline (Pierpaoli et al., 2010a) to reduce the effects of motion and eddy current distortions (Rohde et al., 2004). EPI distortion correction was performed using nonlinear B-splines registration of diffusion and non-diffusion weighted images (b = 0) to the individual's T2W image (Wu et al., 2008). All the corrections were done in the subject's native space, with a single interpolation step, and appropriate rotations were applied to the b-matrix (Rohde et al., 2004).

Tensor estimation was performed after correction for motion, eddy current, and EPI artifacts. Nonlinear tensor estimation was used for eDTI scans, whereas, informed robust estimation of tensors by outlier rejection (iRESTORE) (Chang et al., 2012), was used for tensor fitting of cDTI scans. iRESTORE is specifically designed for datasets acquired with low redundancy (fewer than 30–40 diffusion weighted image volumes), which makes it appropriate for the cDTI data consisting of only 28 image volumes.

2.3.1. Spatial normalization

All the tensors were registered to a common coordinate space in a two step process previously described by Pierpaoli et al.(2010b). Briefly, the template creation included the following steps: first, age-specific average brain tensor templates (minimum of 10 scans) were created using the nonlinear tensor registration software, DTI-TK (Zhang et al., 2007). Subsequently, all the age-specific templates were registered to the template from 18 to 21 year old subjects and the corresponding transformations were saved. All tensors for all subjects included in our study were registered to the template from 18 to 21 year old subjects by combining the deformations of individual subject to its age-specific template and of the agespecific template to the template from 18 to 21 year old subjects. This approach was used to warp the diffusion tensor of each subject into the template from 18 to 21 year old subjects with one interpolation ensuring minimal degradation of the quality of the tensor metrics. Finally, MD and FA maps were recomputed for each subject in this normalized space from the warped tensors.

2.3.2. Regions of interest

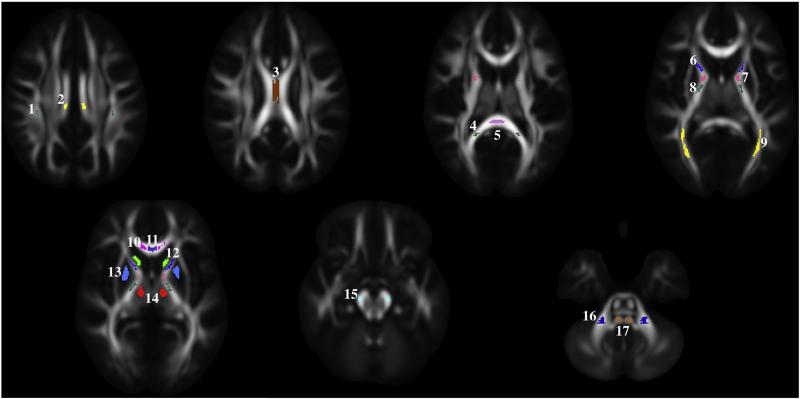
Seventeen regions of interest (ROIs) were drawn by an expert on the template from 18 to 21 year old subjects in both gray and white matter regions as shown in Fig. 1. The white matter ROIs were drawn in commissural, projection, and association fiber tracts. ROIs of commissural tracts include the body of the corpus callosum (BCC), medial and lateral parts of the genu, and the splenium of the corpus callosum (GCC and SCC). ROIs of projection fiber tracts consist of the corticospinal tract (CST) at the level of the cerebellar peduncle; medial lemniscus (ML); middle cerebellar peduncle (MCP); anterior limb, genu, and posterior limb of the internal capsule (ALIC, GIC, and PLIC); and optic radiations. ROIs of association fiber tracts include the cingulum and the superior longitudinal fasciculus (SLF). The gray matter ROIs include the caudate, putamen, and thalamus. All regions were drawn separately in both the right and left hemispheres of the template from 18 to 21 year-old subjects. FA and MD within each ROI for all subjects were extracted from the respective maps spatially normalized to the template space. We decided to extract the individual ROI values in the warped images rather than warping the ROI into the subject's native space, as the former approach has been shown to be preferable (Irfanoglu et al., 2014).

Fig. 1.

Regions of interest are shown overlaid on the FA map computed from the template of 18–21 year-old subjects. Note that the ROIs are 3D structures; however, here axial slices are used as an example. The following ROIs were analyzed: 1 — superior longitudinal fasciculus (SLF), 2 — cingulum, 3 — body of corpus callosum (BCC), 4 — lateral part of splenium of corpus callosum (SCC lateral), 5 — middle part of splenium of corpus callosum (SCC medial), 6 — anterior limb of internal capsule (ALIC), 7 — genu of internal capsule (GIC), 8 — posterior limb of internal capsule (PLIC), 9 — optic radiations, 10 — lateral part of genu of corpus callosum (GCC lateral), 11 — middle part of genu of corpus callosum (GCC medial), 12 — caudate, 13 — putamen, 14 — thalamus, 15 — corticospinal tract (CST), 16 — middle cerebellar peduncle (MCP), and 17-medial lemniscus (ML).

2.3.3. Theoretical basis of the statistical model

We use linear mixed effects (LME) (Laird and Ware, 1982) to model age-related changes of FA and MD, to model protocol differences (cDTI and eDTI), and to account for within-subject correlation (cDTI and eDTI scans of same subject). In the mixed effects model, the observed data are assumed to be a combination of fixed effects (parameters associated with the entire population) and random effects (individual deviations from the average parameters).

For a given ROI, the diffusion metric y = {FA, MD} of scan j, subject i, and protocol k ∈ {cDTI, eDTI} is modeled as:

$$y_{ijk}=A_k+B_k\ast Age+b_i+e_{ijk},$$

where A_k and B_k are parameters to be estimated describing the intercept and slope of the mean value of the diffusion metric of interest for the population as a function of age.

Individual variations are modeled by inclusion of random effects, $b_i\sim \mathcal{N}(0,{\sigma }_b^2)$, in the model. The fact that this term is the same regardless of acquisition protocol and scan replicate (k and j do not appear) satisfies our assumption that biologically determined variability should be highly correlated between scans of the same subject. Inter-subject biological variability is captured by ${\sigma }_b^2$.

Noise is modeled as $e_{ijk}\sim \mathcal{N}(0,{\sigma }_e^2)$ and is independent of b_i. Although cDTI and eDTI protocols may have different noise characteristics, a single σ_e is used to describe the overall estimate of the experimental noise. We used Monte Carlo simulation (see Sections 2.4 and 3.1) to verify that using a single σ_e representing the pooled variance of cDTI and eDTI does not have negative effects on the estimation of the parameters of the model. In addition, inclusion of the two separate σ_e for each protocol can cause the model to be over-parameterized, thus creating problems in the estimation.

2.3.4. Application of the statistical model

The general formulation of the model would estimate the intercept at age 0 and result in high correlation of estimates of the slope and the corresponding intercept. We can remove this correlation by centering the data. In this case, we model the FA and MD as a linear function of Age–mean(Age), where the mean(Age) of our population is 14.2 years. In this model, the estimated intercept for FA and MD is at 14.2 years rather than at 0.

For structures present in both brain hemispheres, left and right ROIs were defined and measurements were first evaluated separately for differences in developmental trajectories. Significant differences of small magnitude were found in the intercept for several regions, but no differences in slope of FA or MD were found between right and left regions. However, because evaluation of right and left differences was not a goal of this study, given that small differences in intercept may be an unavoidable consequence of ROI placement, and because there were no differences in the developmental trajectories from the right and left regions, right and left measurements were combined in our analysis for statistical parsimony.

Intercept and slope (A and B parameters) of the mean value for MD and FA as a function of age for each region of interest were analyzed with the LME model. We tested for statistical differences in the intercept and slope between the two acquisition protocols. P-values were obtained using the conditional t-test provided in the R¹ nlme package (Pinheiro et al., 2012). Subsequently, p-values were adjusted using false discovery rate procedure to correct for multiple comparisons (Benjamini and Hochberg, 1995).

2.4. Validation of the statistical model

We performed Monte Carlo simulations to validate the model and investigate its robustness in the range of experimental conditions typical of our data (SNR, differences between protocols in the test– retest replicates, relatively small number of subjects, etc.). For a large range of biological variability and experimental noise values, we tested the accuracy (potential bias effects) and uncertainty (standard error) of the estimated A, B, and biological variability term for the diffusion metric of interest: MD and FA. In particular, we covered all values found in the ROIs of the population. The Monte Carlo simulations consisted of 1000 replicates of our real experiment with 61 subjects and 2 scans per subject, using different noise realizations from the given noise distribution. For statistical parsimony, in our model we assumed that the experimental noise for all scans was drawn from the same distribution. However, in our experimental setup, the repeated scans were acquired with different protocols and, therefore, were likely to have different noise characteristics. Again, we used Monte Carlo simulations to assess if having different experimental noise distributions for repeated scans would negatively affect our ability to estimate both fixed effects (A and B) and biological variability (σ_b). We first used the method proposed by Chang et al.(2012), to measure the SNR of the DWIs used in the cDTI and eDTI protocol. Given the measured SNR, we then calculated the expected variance of FA and MD due to white noise in each ROI using the approach proposed by Pierpaoli and Basser(1996). The results of this analysis indicate that, taking an average of all ROI values, the experimental noise of cDTI is expected to be 3.2 (range 2.7–3.7) and 2.9 (range 2.3–3.6) times that of eDTI for MD and FA respectively. Finally, we performed simulations in which the added noise was sampled from two distributions so that ${\sigma }_{e_{cDTI}}^2=\alpha {\sigma }_{e_{eDTI}}^2$ to assess the effects on the estimated parameters mentioned above. We report results for α = 4, which is higher than what we found in any ROI. We compared the dual distribution results with those obtained assuming a single noise distribution for both protocols with the same overall variance; in this simulation 1000 replicates were also used.

3. Results

3.1. Monte Carlo simulations

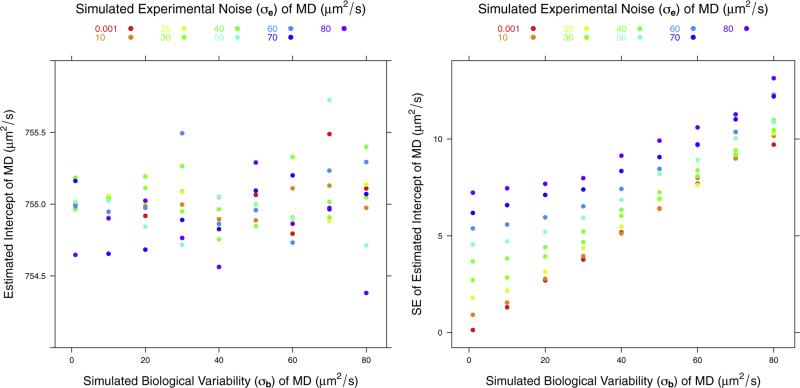
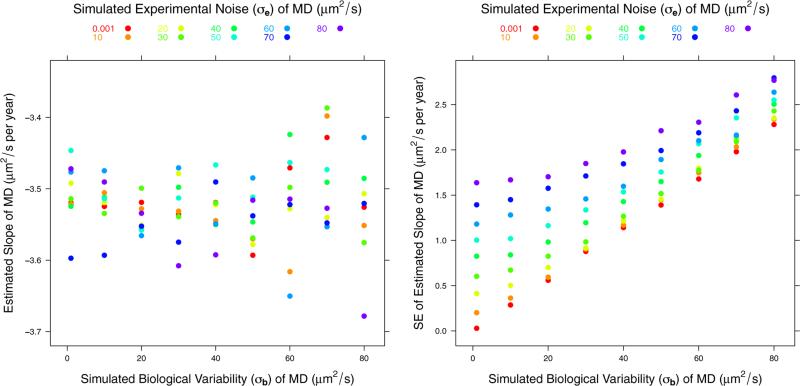
For both MD and FA, the simulation showed no bias in the estimated fixed effects: A and B. Even for the ROIs with the largest experimental noise and biological variability, the simulation showed that the expected uncertainty in the intercept should be less than 2% for both MD and FA. The uncertainty in the slope was much higher, reaching 57% for MD and 54% for FA. For example, Fig. 2 shows the result of the simulation for the intercept for MD assuming a true value of A of 755 μm²/s, which is the average for all ROIs we consider. Fig. 3 shows the result of the simulation for the slope for MD assuming a true value of B of −3.52 μm²/s per year, which is the average for all the ROIs we consider.

Fig. 2.

Plots of the estimated mean and standard error of the intercept term, parameter A in the model, for MD. The simulation results are computed for an assumed true value of A of 755 μm²/s.

Fig. 3.

Plots of the estimated mean and standard error of the slope, parameter B in the model, for MD. The simulation results are computed for an assumed true value of B of −3.52 μm²/s per year.

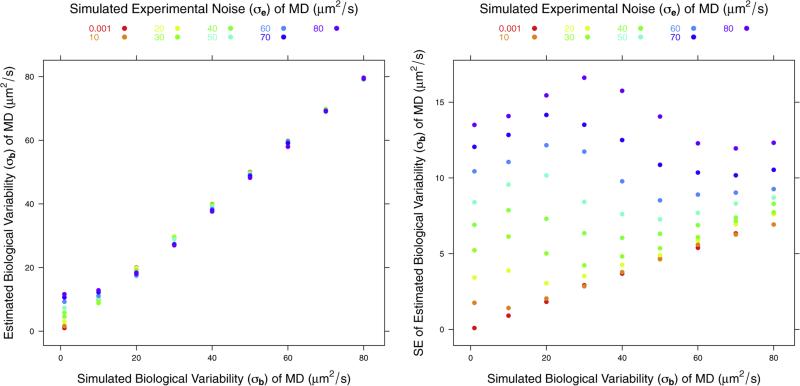
Fig. 4 shows the simulation results for the effects on the estimated biological variability for MD. The panel on the left shows that the estimated biological variability is generally unbiased but it is slightly overestimated when biological variability is close to 0 and experimental noise is larger by a factor of approximately 10. The right panel shows that the standard error (SE) of the estimated biological variability (σ_b) is a linear function of the true σ_b when experimental noise is small. As noise increases, SE of the estimated σ_b also increases but its dependence on the value of the σ_b decreases. The standard error of estimated biological σ_b can be quite high for high noise levels, in particular if the biological variability contribution to total variance is small.

Fig. 4.

Plots of estimated σ_b and standard error of σ_b of MD.

We compared the results of using two protocol dependent distributions for experimental noise in our simulation to those obtained by assuming a single noise distribution for both protocols with the same overall variance. We did not detect any differences in the estimates of mean and the slope of diffusion metrics between the two simulations. Because we used a range of biological variability in our simulation, we used regression to evaluate whether different experimental noise distributions for repeated scans would introduce a bias in the estimate of biological variability. We obtained a coefficient of determination, r², of .99974 for the estimate of biological variability of MD; this result indicates a very good match between the results obtained with dual distribution for experimental noise and those with only one distribution. The intercept and slope for the regression line were 1.0058 and −0.3118, respectively. For FA, r² = .99959, intercept = 1.002, and slope = −0.0044. Again, indicating a very good match between using two separate distributions for experimental noise vs. using only one. Overall, our simulations indicate that assuming a single distribution for experimental noise does not negatively affect our estimates of intercept, slope, and biological variability for either FA or MD.

3.2. Effect of age

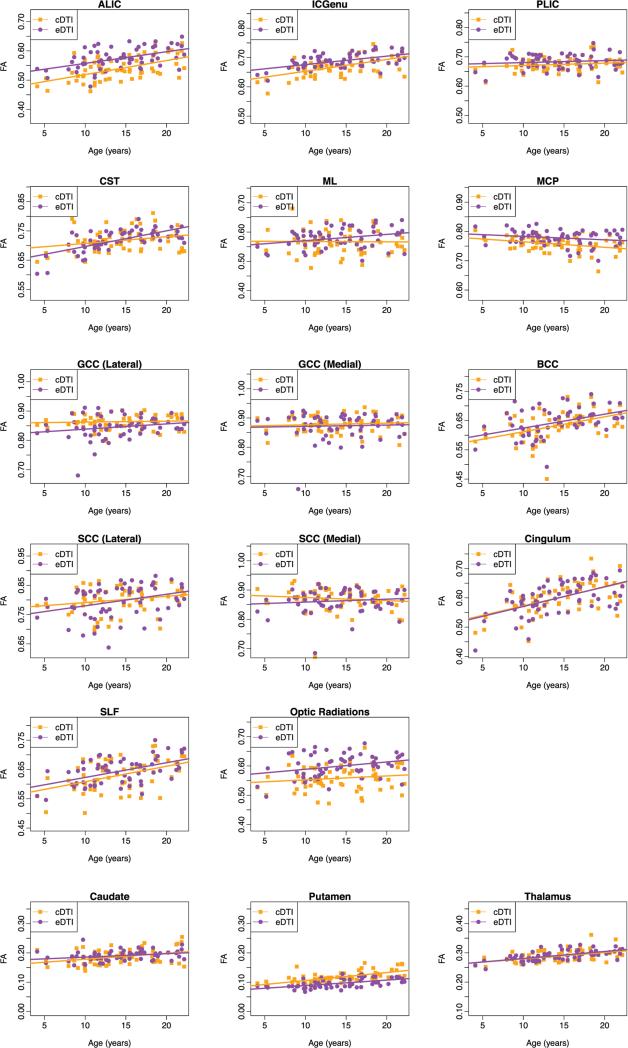
The estimates of the intercept and slope for FA are presented for cDTI and eDTI scans in Table 1. For both protocols, FA showed a significant increase from 5 to 21 years. The FA increase with age was statistically significant in more than half of white matter regions for both cDTI and eDTI scans (slope is significantly different from zero) and all gray matter regions. However, there were large differences in magnitude of the slope across regions. The steepest changes were found in the cingulum and SLF, in the CST (in eDTI), and in the BCC. Most white matter regions showed similar trends between cDTI and eDTI scans; however, the lateral part of the splenium of the CC showed a significant increase in FA with age in eDTI but not in cDTI. Plots for all ROIs are provided in Appendix A.

Table 1.

Fractional Anisotropy (FA).

cDTI				eDTI
ROI	Intercept (SE)	Slopea (SE)	q b	Intercept (SE)	Slopea (SE)	q b
White matter regions	(×10−3)	×10−3 (×10−3)		(×10−3)	×10−3 (×10−3)
GCC (medial)	0.88(4.12)	0.57(0.92)	0.61	0.87(4.12)	–0.34(0.92)	0.76
GCC (lateral)	0.86(3.64)	0.32(0.81)	0.74	0.84(3.64)	1.01(0.81)	0.27
BCC	0.63(5.81)	5.11(1.30)	<.01*	0.64(5.81)	4.69(1.30)	<.01*
SCC (medial)	0.87(5.28)	–1.05(1.18)	0.46	0.86(5.28)	0.53(1.18)	0.74
SCC (lateral)	0.80(6.53)	2.13(1.46)	0.23	0.79(6.53)	3.42(1.46)	0.04*
ALIC	0.54(4.16)	4.79(0.93)	<.01*	0.56(4.16)	3.83(0.93)	<.01*
GIC	0.67(3.20)	4.04(0.72)	<.01*	0.67(3.20)	2.75(0.72)	<.01*
PLIC	0.67(3.31)	0.80(0.74)	0.38	0.67(3.31)	0.21(0.74)	0.78
Optic radiations	0.56(5.03)	1.33(1.13)	0.34	0.59(5.03)	2.34(1.13)	0.06
Cingulum	0.60(5.86)	6.44(1.31)	<.01*	0.59(5.86)	6.38(1.31)	<.01*
SLF	0.63(5.80)	5.28(1.30)	<.01*	0.63(5.80)	4.89(1.30)	<.01*
CST	0.72(4.16)	2.27(0.93)	0.03*	0.70(4.16)	4.89(0.93)	<.01*
MCP	0.76(3.25)	–1.89(0.73)	0.02*	0.77(3.25)	–1.67(0.73)	0.04*
ML	0.57(4.99)	–0.12(1.12)	0.92	0.58(4.99)	2.13(1.12)	0.08
Gray matter regions
Caudate	0.19(2.67)	2.03(0.60)	<.01*	0.19(2.67)	1.52(0.60)	0.03*
Putamen	0.12(1.78)	2.73(0.40)	<.01*	0.09(1.78)	2.09(0.40)	<.01*
Thalamus	0.29(2.09)	2.19(0.47)	<.01*	0.28(2.09)	2.20(0.47)	<.01*

^aSlope changes are per year.

^bq-values of age-effect (slope different than zero) are based on the false discovery rate adjustment of p-values.

^*Indicates differences were significant at q < 0.05.

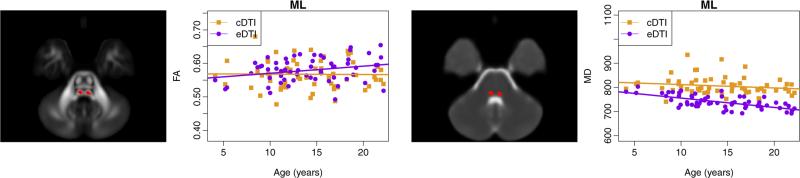
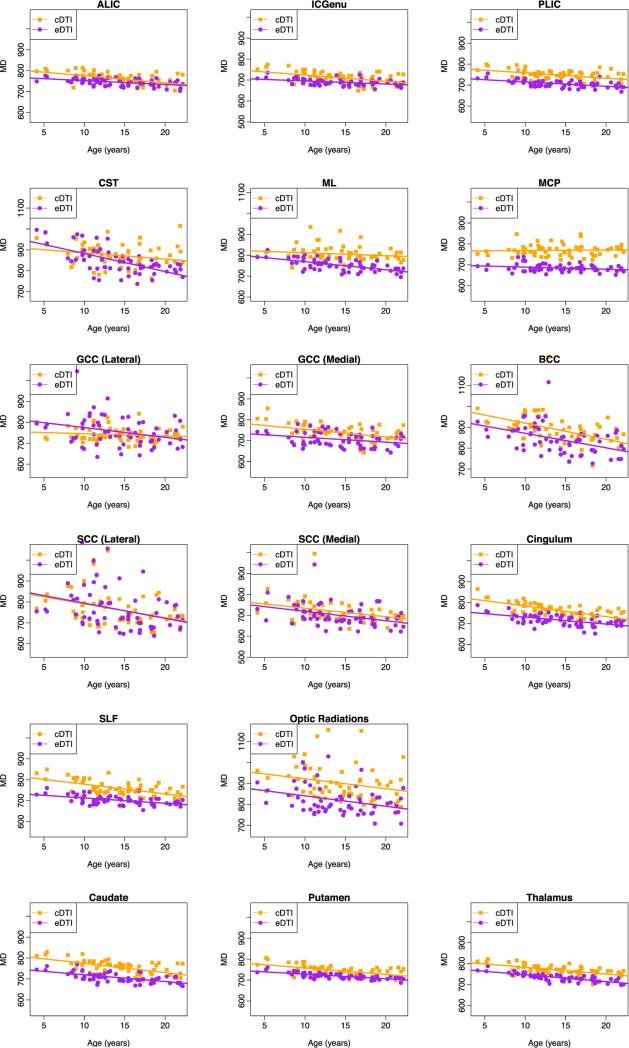
The estimates of the intercept and slope for MD are presented in Table 2, and the corresponding plots for all ROIs are provided in Appendix B. A majority of white matter regions showed a significant decrease in MD in the cDTI scans, and all of the white matter regions except MCP showed a significant decrease in MD in the eDTI scans. Also, all gray matter regions showed a significant decrease in MD in both protocols. As observed for FA, the magnitude of the slope of the effect of age varied across regions. A large decrease of MD with age was observed in the BCC and the lateral part of SCC for both cDTI and eDTI protocols. A large decline in MD was observed for CST in the eDTI scan. In general, both protocols showed similar age-effect for MD with a few exceptions, the following regions did not show a significant decrease in MD with age in the cDTI protocol while the age effect was significant in the eDTI protocol: GCC (lateral), CST, and ML. The GCC (medial) showed no significant age effect in FA, while there was a significant decrease in MD. As an example of these atypical findings we show in Fig. 5 the age dependence plot of FA and MD for ML. A significant decrease in MD with age was found in this region for eDTI but not for cDTI.

Table 2.

Mean Diffusivity (MD).

cDTI				eDTI
ROI	Intercept (SE)	Slopea (SE)		Intercept (SE)	Slopea (SE)
White matter regions	×10–6mm2s–1			×10–6mm2s–1
GCC (medial)	739(4.2)	–3.67(0.95)	<.01 *	691(4.2)	–2.00(0.95)	0.04*
GCC (lateral)	741(6.3)	–1.11(1.40)	0.46	741(6.3)	–3.41(1.40)	0.03 *
BCC	887(8.6)	–7.73(1.93)	<.01 *	832(8.6)	–6.73(1.93)	<.01 *
SCC (medial)	717(6.5)	–4.06(1.46)	0.01 *	683(6.5)	–4.21(1.46)	0.01 *
SCC (lateral)	763(10.4)	–6.62(2.33)	0.01 *	738(10.4)	–5.19(2.33)	0.04*
ALIC	761(2.6)	–3.41(0.59)	<.01 *	746(2.6)	–1.89(0.59)	<.01 *
GIC	711(2.7)	–2.99(0.61)	<.01 *	686(2.7)	–1.31(0.61)	0.04*
PLIC	748(2.4)	–2.54(0.54)	<.01 *	705(2.4)	–1.94(0.54)	<.01 *
Optic radiations	902(8.9)	–4.72(1.98)	0.03 *	809(8.9)	–4.36(1.98)	0.04*
Cingulum	762(2.9)	–5.08(0.66)	<.01 *	713(2.9)	–3.30(0.66)	<.01 *
SLF	759(3.0)	–4.63(0.68)	<.01 *	701(3.0)	–2.64(0.68)	<.01 *
CST	874(6.5)	–2.99(1.45)	0.05	845(6.5)	–8.44(1.45)	<.01 *
MCP	769(3.1)	0.25(0.69)	0.71	670(3.1)	–0.73(0.69)	0.29
ML	806(3.8)	–1.39(0.85)	0.12	740(3.8)	–3.87(0.85)	<.01 *
Gray matter region
Caudate	756(2.9)	–4.41(0.65)	<.01 *	705(2.9)	–3.04(0.65)	<.01 *
Putamen	745(2.0)	–3.10(0.45)	<.01 *	723(2.0)	–2.15(0.45)	<.01 *
Thalamus	769(2.0)	–3.21(0.45)	<.01 *	735(2.0)	–3.20(0.45)	<.01 *

^aSlope changes are per year.

^bq-Values of age-effect (slope different than zero) are based on the false discovery rate adjustment of p-values.

^*Indicates differences were significant at q < 0.05.

Fig. 5.

Plots of FA and MD (μm²/s) versus age for medial lemniscus (ML). Regions are overlaid on the FA and MD maps computed from the template of 18–21 year-old subjects. There is a protocol-dependent bias, and the effect of age is different depending on the protocol used.

3.3. Protocol bias

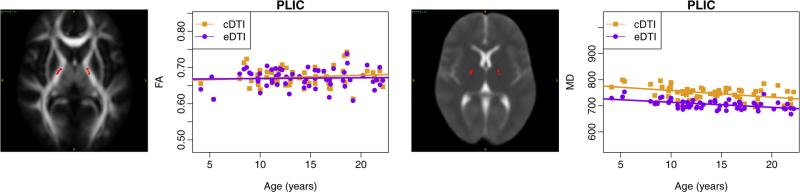
Differences in the intercept and slope between cDTI and eDTI are summarized in Table 3. Approximately half of the ROIs showed a significant difference in the intercept of the FA trajectory between the two protocols, whereas no region showed significant slope differences. For MD, all regions with the exception of lateral parts of the GCC showed a significant difference in the intercept, with the eDTI intercept being consistently lower than the cDTI one. Only cingulum, GIC, SLF, and CST showed significant differences in the slope. The lower intercept for eDTI may be due to differences in CSF partial volume contamination: MD of CSF is much higher than the parenchymal MD and the eDTI scans have higher resolution and, therefore, would suffer less from CSF partial volume contamination.

Table 3.

Differences between cDTI and eDTI (eDTI-cDTI) in FA and MD.

ROI White matter regions	FA		MD
	Intercept differencea	Slope difference	Intercept differencea	Slope difference
	×10−3	×10−3	×10−6mm2 s−1	×10−6mm2 s−1
GCC (medial)	–7.77	–0.91	–48.46*	1.67
GCC (lateral)	–21.19*	0.69	0.09	–2.29
BCC	4.59	–0.42	–55.54*	0.99
SCC (medial)	–9.16*	1.59	–33.76*	–0.15
SCC (lateral)	–9.10	1.29	–24.94*	1.43
ALIC	19.36*	–0.96	–15.19*	1.52
GIC	2.06	–1.28	–25.24*	1.68*
PLIC	–3.39	–0.59	–42.49*	0.60
Optic radiations	31.84*	1.00	–93.09*	0.36
Cingulum	–13.25*	–0.07	–49.22*	1.79*
SLF	–4.32	–0.39	–58.29*	1.99*
CST	–15.87*	2.62	–28.13*	–5.46*
MCP	12.67*	0.22	–99.18*	–0.98
ML	11.92	2.25	–66.35*	–2.48
Gray matter regions
Caudate	0.63	–0.51	–50.74*	1.36
Putamen	–24.51*	–0.64	–21.93*	0.95
Thalamus	–6.16*	0.01	–34.45*	0.01

^aIntercept is calculated at mean age (14.2 years).

^*Indicates differences were significant at q < 0.05 based on the false discovery rate adjustment of p-values.

Fig. 6 shows the estimated trajectories of FA and MD for the PLIC, as an example of a region where we can see clear differences in the intercept between eDTI and cDTI (for MD), but no differences in the slope.

Fig. 6.

Plots of FA and MD (μm²/s) versus age for posterior limb of internal capsule (PLIC). Regions are overlaid on the FA and MD maps computed from the template of 18–21 year-old subjects. Similar trajectories are observed for both cDTI and eDTI, however, there is a protocol dependent bias.

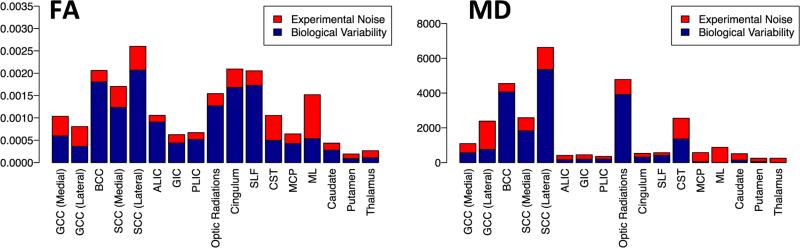
3.4. Overall variability

Once the effects of age and protocol are taken into account, we can examine the remaining variability, which should be due to experimental noise and biological inter-subject differences. The overall variance was highly variable across regions. Gray matter regions showed an overall low variability $({\sigma }_b^2+{\sigma }_e^2)$ for both FA and MD (Fig. 7).

Fig. 7.

Sources of variability. Left: biological variability and experimental noise of FA. Right: biological variability and experimental noise of MD.

In addition to gray matter regions, internal capsule regions, cingulum, MCP, and SLF showed low variability in MD. Whereas, SCC (lateral) and optic radiations showed very high overall variability in MD as shown by the height of the bars in Fig. 7. SCC (lateral) also showed the highest variability in FA and optic radiation was among regions with relatively high variability. Other regions such as cingulum, SLF, SCC (medial), and BCC also showed high overall variability.

3.5. Biological variability and experimental noise

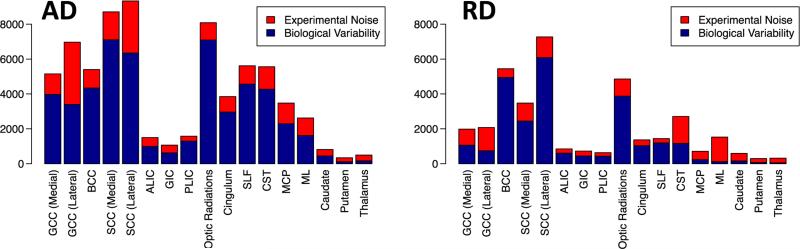
The mixed effects model allows analysis of variability in terms of biological variability, ${\sigma }_b^2$, and experimental noise, ${\sigma }_e^2$. Fig. 7 shows the sources of variability for FA and MD (see Appendix C for sources of variability with respect to axial diffusivity (AD) and radial diffusivity (RD)). Regions that showed large biological variability for FA relative to other regions are BCC, SCC (medial and lateral), optic radiations, cingulum, and SLF. For MD, BCC, SCC (lateral), and optic radiations had large subject variability. Cingulum and SLF showed relatively large biological variability for FA, but not for MD. ML, CST, and GCC (medial and lateral) were among the regions with the highest levels of experimental noise for FA. GCC (lateral), SCC (lateral), CST, and ML were among the regions with the largest levels of noise for MD. These areas have been reported as having a high percentage of artifactual data points (outliers) in the DWIs (Pierpaoli et al., 2003; Walker et al., 2011).

4. Discussion

In this study, we proposed a methodological framework to allow separating the contributions of biological variability and experimental noise from the overall variance of diffusion MRI study in a population using a linear mixed effects model. The key idea was that effects pertaining to the biology of each subject should be highly correlated across repeated scans, while experimental noise should not be correlated. Repeated scans are not common in pediatric studies; however, here we took advantage of the NIH MRI Study of Normal Brain Development, which has repeated scans for a subset of subjects. Additionally, because different diffusion acquisition protocols for repeated scans were used in this study, we had the unique opportunity to analyze the effect of using different DTI protocols when assessing the effects of developmental changes on diffusion metrics. The two protocols differed mainly in the resolution of the images and the number of diffusion weighted volumes. However, the different protocols for the repeated scans may be seen as a complicating factor because the experimental noise is not constant across replicates. Moreover, in our model we assume that the experimental noise for all scans is drawn from the same distribution. We used Monte Carlo simulations to assess if different experimental noise distributions for repeated scans would negatively affect our ability to estimate both fixed effects (A and B) and biological variability (σ_b) with our model. The results of these simulations showed convincingly that there were no adverse effects from using a single pooled variance noise term in the model.

Moreover, additional Monte Carlo simulation tests have demonstrated that given our experimental conditions we can achieve unbiased estimates of the slope and intercept (population value of FA and MD at the age of 14.2 years) of the developmental trajectories for both FA and MD. The error in the estimate of the intercept is expected to be lower than 2%, while the uncertainty in the estimate of the slope is much higher (up to 57%). Finally the model appeared quite robust in separating experimental noise (uncorrelated across repeats) from biological variability (correlated across repeats).

After having tested the reliability of our model using Monte Carlo simulations, we applied the model to the pediatric data. We observed widespread changes in FA and MD resulting from brain maturation in both cDTI and eDTI from childhood into adulthood. Previous early developmental studies have shown a rapid increase in FA and decrease in MD in the early years of life, especially during the first 12 months (Hermoye et al., 2006; Sadeghi et al., 2013a, 2013b). However, maturation of white matter continues at a slower rate into adolescence and even adulthood (Lebel and Beaulieu, 2011). In this study, we found a continued maturation for most white matter regions and deep gray matter structures during adolescence; these findings are similar to those of previous studies (Schmithorst et al., 2002; Ashtari et al., 2007; Bonekamp et al., 2007; Lebel et al., 2008; Lebel and Beaulieu, 2011).

In a study by Bonekamp et al., 2007, FA was shown to increase significantly from 5.5 to 19.1 years in ALIC, SLF, and cingulum in agreement with our findings. In addition, we found a significant age effect in the FA trajectory of SCC (lateral) in eDTI scans. Significant FA increase was also observed in CST, MCP, BCC, GIC, and deep gray matter regions in both cDTI and eDTI. Different factors may give origin to significant differences in tensor-derived metrics in different regions. For example, in deep gray matter regions such as the caudate and putamen where anisotropy is low, we observed a significant increase of FA with age. This phenomenon might represent a true biological effect, but it may also be related to a decrease in SNR due to reduced water content with maturation. We know from the literature, that FA has an upward bias if SNR is low (Pierpaoli and Basser, 1996). Therefore, the increase in FA might be due to lower SNR rather than to actual micro structural changes in this region. Moreover, in addition to assessing if effects reach statistical significance, one should also look at their magnitude. For caudate and putamen the slope was 1.52 × 10⁻³ − 2.09 × 10⁻³ in eDTI scans and 2.03 × 10⁻³ − 2.73 × 10⁻³ in cDTI, which, although significant, is a smaller value than what was found in virtually all white matter regions that reach statistical significance. The age effect of small magnitude was significant in both caudate and putamen because of the low inter-subject variability in these regions.

Brain maturation in the internal capsule and corticospinal tracts has also been reported by others (Schmithorst et al., 2002; Barnea-Goraly et al., 2005). We found a significant increase in FA and decrease in MD in the anterior limb (ALIC) and genu of the internal capsule, but no significant increase was observed in FA of the posterior limb of the internal capsule (PLIC). It is known that brain maturation follows a spatio-temporal pattern from posterior to anterior and central to peripheral regions, i.e., the PLIC matures earlier than ALIC. Most of the maturational changes in PLIC may have occurred before the age of the youngest children included in our sample (4 year old). From the age of four to adulthood we see much greater changes of FA in ALIC (slope = 3.83 × 10⁻³ − 4.79 × 10⁻³) than in PLIC (slope = 0.21 × 10⁻³ − 0.80 × 10⁻³).

Bonekamp et al.(2007), also reported significant reduction in ADC in 13 out of the 15 brain regions they examined. Eight of these regions were similar to areas we analyzed in this study: GCC, BCC, SCC, cingulum, SLF, ALIC, PLIC, and CST. We found significant decrease in MD in these regions as was previously reported. In addition, we found significant decrease of MD with age in BCC and GCC (medial) in both cDTI and eDTI scans, and GCC (lateral) in eDTI scans. The slope of MD for BCC was −6.73 × 10⁻⁶mm²s⁻¹ for eDTI scans and −7.73 × 10⁻⁶mm²s⁻¹ for cDTI scans, which was the highest reduction in MD per year for cDTI scans among all the regions analyzed. Bonekamp et al.(2007), also had reported a reduction in ADC for BCC. However, changes in ADC were not significant in BCC in their study, most likely due to high variability among subjects. The magnitude of changes was not reported in that study, so we cannot compare it here.

As mentioned earlier, we are interested in analyzing the effect of protocol on the assessment of changes in diffusion metrics with age. One would hope that the age effects in MD and FA are minimally influenced by the protocol used, as these quantities should reflect inherent developmental changes within subjects. However, we observed more regions with significant age effects in MD when using the eDTI protocol than when using the cDTI protocol. Specifically, out of 17 regions analyzed, 16 regions showed a significant age effect for MD when eDTI scans were used compared with 13 when cDTI scans were used. Also fewer regions showed a significant age effect with FA compared with MD.

In some regions, the eDTI protocol may be more sensitive to detecting changes with age as this protocol has higher resolution and consequently suffers less from partial volume contamination. For example, age shows a significant effect for MD in ML for eDTI scans, but not for cDTI scans. This difference may arise by the fact that ML is a small structure surrounded by CSF and therefore parenchymal changes may be masked by CSF partial volume contamination when the cDTI protocol is used (Fig. 5). In addition to evaluating protocol dependent differences, our main objective was to analyze the variance of diffusion tensor derived quantities and the role of potential contributors to the observed variability. Previous Monte Carlo simulation studies have shown that, for a given SNR, the variance of FA increases as anisotropy decreases. Moreover, for constant anisotropy, the variance of FA increases as SNR decreases (Pierpaoli and Basser, 1996). It is also worth noting that SNR is lower in white matter regions compared with gray matter and CSF regions because of T2* weighting of the DWIs. The observed larger experimental noise related variance found in this study in white matter regions compared with that of the gray matter regions is consistent with the lower SNR in white matter; this finding confirms previous observations (Walker et al., 2012). The variance of FA in deep gray matter regions (putamen, caudate, and thalamus) was very low compared to that of other regions analyzed. Farrell et al.(2007), reported a larger coefficient of variation (variance divided by mean) of FA in deep gray matter (putamen) compared to that of adjacent white matter (internal capsule), which is in apparent disagreement with our results. However, they reported the coefficient of variation of FA, and here we reported the variance of FA. We argue that the coefficient of variation is not a good metric in isotropic regions as the denominator approaches zero, which can lead to artificially high values. Our analysis showed that experimental noise is a larger fraction of the overall variance of FA in gray matter (red regions in Fig. 7) compared with the majority of the white matter regions. Similar to FA, MD in gray matter regions showed small total variance, with most of the variance attributed to experimental noise.

A majority of white matter regions, with the exception of the body and splenium of the corpus callosum and the optic radiations, also showed small total variance of MD. In these regions, biological variability was the main source of observed variability. Optic radiation is a region close to the periphery that has a higher structural inter-subject variability. Part of the observed biological variability could be due to morphological differences existing in the population that are not fully accounted for by the registration.

Another interesting finding in this study is the large variance of FA and low variance of MD in cingulum and SLF. Cingulum is an area surrounded by CSF where a slight misregistration can have a substantial effect on values of MD. Given that the cingulum is surrounded by CSF, which has a much larger diffusivity than the parenchyma, the relatively small variance of MD we measured in this region indicates a good registration between subjects for this structure and demonstrates that the large levels of variance of FA are not due to misregistration. A closer look at contributors to variance indicates that the main source of variability in FA of cingulum and SLF are due to biological variability and not experimental noise (Fig. 7). The low variance of MD and high variance of FA for cingulum can be a further indicator that MD and FA are complementary measurements and that they reflect different physiological processes. MD is related to the overall water content, while FA is more related to the architecture of the underlying tissue. A longitudinal study by Lebel et al. (Lebel and Beaulieu, 2011) (age range 5–32 years) reported that FA in cingulum and SLF in many, but not all, young adults was increasing, showing the diversity of brain development in these regions. Many psychiatric disorders such as bipolar disorder and schizophrenia emerge in adolescence and young adulthood (Paus et al., 2008), and are related to white matter abnormalities in frontal areas, uncinate, cingulum, and inferior and superior longitudinal fasciculus (Lim et al., 1999; Kubicki et al., 2007; Heng et al., 2010). The large biological variability of FA between subjects in these areas is indicative of underlying microstructural differences between subjects that might be important in studying risk factors related to psychiatric disorders.

5. Conclusions

In this study, we showed continuous brain maturation from childhood to adulthood using two different diffusion protocols. We highlighted the potential differences in observed measurements based on the protocol. For a majority of the regions, using different protocols introduced differences in the measured averages of FA and MD, but the rate of change of diffusion metrics with age was unaffected.

This study has some limitations. We had only two repeated scans per subject. Ideally, we would like to have many repeats per subject for a robust estimation of biological variability and experimental noise. The results of our Monte Carlo simulations, however, showed that we are able to achieve reliable estimates of most parameters in our model with the experimental data set available to us. It is worth noting that we did not add gender as a covariate in our model because of the small sample size. Longitudinal DTI studies have reported no gender differences during adolescence (Bava et al., 2010; Giorgio et al., 2010), or few differences with small magnitude (Lebel and Beaulieu, 2011). We also note that physiological noise can present itself as biological variability; for example, artifacts related to cardiac pulsation can manifest as biological variability. The fundamental assumption of our model is that biological features will be consistently present in repeated scans. Physiological noise can present this characteristic. Even though cardiac pulsation is due to the biology of the individual subject, it is not related to brain structure. The same is true for brain morphological variability that might not be adequately accounted for by the spatial normalization step. In our model if the shape of a region of a subject's brain is highly abnormal and that region is consistently misregistered to the template, the biological variability component, not the experimental noise component, would increase.

Despite these limitations, to our knowledge this is the first population study that attempts to divide the total variability of MRI metrics into components of biological variability and experimental noise in population studies. By doing so, we enable the identification of regions that show biological differences within the population. This study provides valuable information about the variability of FA and MD in population of typically developing children. It should be expected that regions showing high biological variability of the diffusion MRI metrics within the population should be the most likely to show correlation with cognitive and behavioral metrics that assess brain development. The methodology presented here can be extended to the analysis of other conditions such as aging and neuro-degeneration.

Appendix A. Plots of FA versus age

Fig. A.1 displays trajectories of fractional anisotropy for all of the regions analyzed.

Fig. A.1.

Plots of fractional anisotropy (FA) versus age for white matter and gray matter regions.

Appendix B. Plots of MD versus age

Fig. B.1 displays trajectories of mean diffusivity for all of the regions analyzed.

Fig. B.1.

Plots of mean diffusivity (MD (μm²/s)) versus age for white matter and gray matter regions.

Appendix C. Sources of variability for AD and RD

Fig. C.1 displays sources of variability for axial and radial diffusivity.

Fig. C.1.

Sources of variability. Left: biological variability and experimental noise of axial diffusivity (AD). Right: biological variability and experimental noise of radial diffusivity (RD).