Improving Propensity Score Estimators' Robustness to Model Misspecification Using Super Learner

Abstract

The consistency of propensity score (PS) estimators relies on correct specification of the PS model. The PS is frequently estimated using main-effects logistic regression. However, the underlying model assumptions may not hold. Machine learning methods provide an alternative nonparametric approach to PS estimation. In this simulation study, we evaluated the benefit of using Super Learner (SL) for PS estimation. We created 1,000 simulated data sets (n = 500) under 4 different scenarios characterized by various degrees of deviance from the usual main-term logistic regression model for the true PS. We estimated the average treatment effect using PS matching and inverse probability of treatment weighting. The estimators' performance was evaluated in terms of PS prediction accuracy, covariate balance achieved, bias, standard error, coverage, and mean squared error. All methods exhibited adequate overall balancing properties, but in the case of model misspecification, SL performed better for highly unbalanced variables. The SL-based estimators were associated with the smallest bias in cases of severe model misspecification. Our results suggest that use of SL to estimate the PS can improve covariate balance and reduce bias in a meaningful manner in cases of serious model misspecification for treatment assignment.

Methods based on the propensity score (PS) (1) have become a common approach to causal effect estimation, especially in the medical literature (2, 3). These methods rely on estimation of an individual's probability of receiving a treatment conditional on a set of observed covariates (1). The estimated PS may be used to match treated persons with untreated persons (4), as a covariate in a regression of the outcome on the PS and exposure (1, 5), or to reweight the sample in order to estimate the treatment effect (6).

While investigators have extensively studied the best way to use PS to better balance the distributions of covariates between the treated and the untreated (7) and to provide an optimal bias/variance tradeoff for the estimation of treatment effects (8–10), there are few guidelines on how to estimate the PS. A common practice is to use logistic regression (11). Rubin (12) recommended using complex, nonparsimonious PS models, including interactions and/or quadratic terms (6). However, estimating the PS using a parametric model requires accepting strong assumptions concerning the functional form of the relationship between treatment allocation and the covariates. PS model misspecification may in turn both affect the covariate balance and result in bias in the treatment effect estimate (13–15). Hence, some have argued for and applied data-adaptive methods (6, 16–21). Classification trees or neural networks have been proposed as an alternative to parametric models for PS estimation (22, 23). However, the question of the best method remains unanswered. Moreover, if, for a particular cohort, a parametric logistic regression model is correctly specified, it will provide an efficient estimator of the true treatment mechanism and thus may outperform data-adaptive algorithms.

Super Learner (SL) was proposed by van der Laan et al. (24, 25) as a method for choosing the optimal regression algorithm among a set of candidates, which can include both parametric regression models and data-adaptive algorithms. The selection strategy relies on cross-validation and on the choice of a loss function. A weighted linear combination of the candidate learners is then used to build a new estimator, the so-called SL estimator. It has been demonstrated that this convex combination performs asymptotically at least as well as the best choice among the library of candidate algorithms if the library does not contain a correctly specified parametric model, and it achieves the same rate of convergence as the correctly specified parametric model otherwise.

In the present study, we implemented PS-matched and inverse-weighted effect estimators using SL to estimate the PS and evaluated their performance in simulated data.

METHODS

We conducted a series of Monte Carlo simulations in order to compare the performance of PS matching and inverse weighting with the PS estimated using SL and main-term logistic regression.

Data generation

Let Y be the continuous outcome, A be the binary exposure, and W be a vector of 10 covariates (4 confounders associated with both exposure and outcome, 3 exposure predictors, and 3 outcome predictors). For each simulated data set, the 10 covariates W_i (i = 1, …, 10) were generated from a normal distribution with mean 0 and variance 1 using the 2-step procedure proposed by Setoguchi et al. (22). First, 8 covariates (V_i, i = 1 … 6, 8, 9) were generated as independent standard normal random variables. Second, an additional 8 covariates (W_i, i = 1 … 6, 8, 9) were generated as a linear combination of V_i, i = 1 … 6, 8, 9. Additionally, 2 covariates (W₇, W₁₀) were generated as independent standard normal random variables. In the second step, correlations between some of the variables were introduced, with correlation coefficients varying from 0.2 to 0.9. The correlation matrix of the covariates, as well as the coefficients for data generation models, is given in Web Table 1 (available at http://aje.oxfordjournals.org/) and is illustrated using a causal graph in Web Figure 1. These values refer to the magnitude of the correlation coefficient before dichotomizing 6 out of the 10 covariates (W₁, W₃, W₅, W₆, W₈, W₉).

The probability that the exposure A was equal to 1, that is, the true PS, was generated as a function of the covariates W_i:

$$\text{Pr}(A=1|{\mathbf{W}}_i)=f({\mathbf{W}}_i,\beta ).$$ (1)

The shape of the function f as well as the values for β varied across the scenarios, but in all cases the true PS was bounded from 0 and 1 and the average exposure probability was approximately 0.5. The random variable A was drawn from a Bernoulli distribution with probability set by f(W_i, β).

The continuous outcome Y was generated from a linear combination of A and W_i:

$$Y={\alpha }_0+{\alpha }_i\times {\mathbf{W}}_i+\gamma \times A+ϵ,$$ (2)

where the effect of exposure, γ, was fixed at −0.4 and ϵ is an error term generated from a normal distribution with mean 0 and variance 0.09.

Simulation scenarios

In order to evaluate the performance of SL and of each candidate algorithm, we simulated 4 scenarios for the true PS model. These scenarios were characterized by various degrees of deviance from the linear, additive relationship (on the log odds scale) between the exposure and the covariates that is commonly assumed when estimating the PS. The scenarios were designed such that the true PS model had the following properties:

• A: additivity and linearity (main effects only);

• B: nonlinearity (3 quadratic terms);

• C: nonadditivity (10 two-way interaction terms);

• D: nonadditivity and nonlinearity (10 two-way interaction terms and 3 quadratic terms).

Performance was assessed for each of these scenarios (A–D), using 1,000 replicated data sets of size n = 500. Additional results are provided with size n = 5,000 and average exposure probability of 0.10.

Super Learner

SL has been proposed as a method for selecting an optimal regression algorithm from a set of candidates using cross-validation (24, 26, 27). The selection strategy relies on the choice of a loss function (L2 squared error in the present study). Comparison of performance between candidates relies on V-fold cross-validation. For each candidate algorithm, SL averages the estimated risks across the validation sets, resulting in the so-called cross-validated risk, for each candidate algorithm. Cross-validated risk estimates can be used to choose the weighted linear convex combination of the candidate learners with the smallest estimated risk. This convex combination, applied to algorithms run using all of the learning data, is referred to as the SL estimator (25).

We included the following algorithms in the SL library:

• Logistic regression: standard logistic regression, both 1) including only main terms for each covariate and 2) also including interaction terms (glm function) (28).

• Stepwise regression: using a forward variable selection procedure (step function) and based on the Akaike Information Criterion (stepAIC function), again both with and without interactions (29).

• Generalized additive model (gam function) (29).

• Generalized linear model with penalized maximum likelihood (glmnet function) (30).

• Bayesian generalized linear model (bayesglm function) (31).

• Multivariate adaptive regression splines (earth function) (32).

• Classification and regression routines (caret function) (33).

• k-nearest neighbor classification (knn function) (34).

• Random Forest (randomForest function) (35).

• Neural Networks (nnet function) (34).

• Classification and regression trees (CART): recursive partitioning (rpart function) (36).

• Bagged CART: bootstrap aggregated CART (ipredbagg function) (37).

• Pruned CART: (rpart and prune functions) (36).

• Boosted CART (gbm function) (38).

• Support vector machine (svm function) (39).

All functions were used with the default parameters, except for those algorithms used by Setoguchi et al. (22) and Lee et al. (23) in their respective studies. In the latter situation, we used the same parameters as those reported by the authors (specifically Neural Networks with 1 layer and 10 hidden nodes and boosted CART with 20,000 iterations and a shrinkage parameter of 0.0005). However, the version of boosted CART based on the gbm function (package gbm for R (40)) that was included in the SL library is slightly different from the version used by Lee et al. (23) through the ps function (package twang for R (41)), where the authors used an iteration stopping point that minimized a measure of the balance across pretreatment variables (specifically the mean of the Kolmogorov-Smirnov test statistics).

Propensity-based estimation of the treatment effect

We chose as the estimand the statistical parameter corresponding to the average treatment effect (ATE), defined as

$$\sum _w(E(Y|A=1,\mathbf{W}=w)-E(Y|A=0,\mathbf{W}=w))\times P(\mathbf{W}=w).$$

Two classes of PS-based estimators were used to estimate the ATE.

PS matching

While PS matching is usually used to estimate the ATE among the treated, we used a matching method that targets the marginal effect (ATE) instead of the effect among the treated, provided that there is sufficient overlap between the treated and control groups' propensity scores to estimate the ATE. This is allowed in the R package Matching (42). PS matching relies on a k:1 nearest-neighbor procedure. Each treated subject is randomly selected and matched once to the nearest untreated subject based on calipers of width of 0.2 of the standard deviation of the logit of the PS. In order to allow for ATE estimation, some tuning parameters are fixed to reduce the number of subjects discarded from the matched sample: matching is performed with replacement and ties are allowed. The ATE estimate is then defined as the difference in average outcomes between the treated and the untreated in the matched population. The Abadie-Imbens estimator (43) (package Matching for R (42)) was used for variance estimation, as it takes into account the uncertainty related to the matching procedure.

Inverse probability of treatment weighting

To estimate the ATE using inverse probability of treatment weighting (IPTW), we fitted a weighted regression of Y on A using as weights the inverse estimated probabilities of treatment actually administered, A, as follows:

$$\text{IPT}{\text{W}}_i=\frac{A}{g({\mathbf{W}}_i)}+\frac{1-A}{1-g({\mathbf{W}}_i)},$$ (3)

where $g({\mathbf{W}}_i)$ is the PS. Variance estimation was based on large-sample standard errors (package causalGAM for R (44)) as previously described (45).

Performance metrics

For each scenario, we evaluated the performance of the various PS fitting approaches through several measures:

• The prediction performances of each candidate algorithm, including the SL-weighted algorithm, for estimation of the PS. The prediction performance measure was assessed using the cross-validated L2 squared error and the area under the receiver operating characteristic curve (AUROC).

• The balance in the covariates between treated and untreated subjects was assessed in the original, matched, and weighted data sets using 1) the standardized mean difference (the difference in mean values standardized by the common standard deviation of the particular covariate) for each covariate and 2) the average standardized absolute mean difference (ASAM), expressed as a percentage. Standardized differences of 10% or greater were considered to be of concern (46).

• The distribution of the weights for the IPTW estimators and the average sample size and the number of subjects discarded by the matching procedure for the matching estimator.

• The performance of the point estimate of the treatment effect in terms of the bias, empirical standard error, and mean squared error of each estimator. We reported absolute bias as well as relative bias (percentage difference from the true treatment effect, which was fixed to be −0.4).

• The performances of the variance estimators. This was evaluated in terms of the bias of the standard error estimator (the average estimated standard error minus the empirical standard error of the estimator), the variability of the standard error estimator, and the 95% coverage.

All performance measures were averages of the 1,000 replications. These performance measures were used to compare the matching and IPTW estimates obtained using main-term logistic regression, SL, Neural Networks, or boosted CART (ps function, twang package for R (41)) to fit the PS.

All analyses were performed using R statistical software, version 2.15.1 (R Foundation for Statistical Computing, Vienna, Austria), running on a Mac OsX platform (Apple, Inc., Cupertino, California). Basic R codes for SL-based PS modeling are provided in the Web Appendix.

RESULTS

The results obtained from the simulations for the 4 scenarios are presented in Table 1.

Table 1.

Simulation Results Obtained Under 4 Different Scenarios Characterized by Various Degrees of Deviance From the Usual Main-Term Logistic Regression Model for the True Propensity Score^a

Scenario and Estimator	Estimate	Absolute Bias	Empirical SEb	Estimated SEc	SD of Estimated SEd	MSE	95% CI Coverage, %e	ASAM, %	No. of Subjects Discardedf
Scenario A
Naive	−0.223	0.177	0.700	0.700	0.002	0.036	26.9	27.971
Logit matching	−0.398	0.002	0.063	0.088	0.003	0.001	99.5	5.322	6
SL matching	−0.381	0.019	0.061	0.101	0.002	0.002	100.0	6.734	4
Logit IPTW	−0.401	0.001	0.047	0.033	0.003	0.001	84.3	3.354
SL IPTW	−0.391	0.009	0.045	0.031	0.002	0.001	83.7	4.660
Scenario B
Naive	−0.250	0.150	0.072	0.070	0.002	0.027	44.4	23.958
Logit matching	−0.403	0.003	0.057	0.079	0.002	0.001	99.6	4.840	5
SL matching	−0.403	0.003	0.067	0.085	0.003	0.001	98.5	6.067	11
Logit IPTW	−0.404	0.004	0.038	0.030	0.002	0.001	87.6	2.369
SL IPTW	−0.392	0.008	0.045	0.033	0.003	0.001	83.8	4.470
Scenario C
Naive	−0.215	0.185	0.069	0.070	0.002	0.039	24.4	30.319
Logit matching	−0.405	0.005	0.065	0.087	0.003	0.001	98.9	5.618	6
SL matching	−0.381	0.019	0.065	0.097	0.003	0.002	99.4	7.025	4
Logit IPTW	−0.411	0.011	0.051	0.034	0.003	0.001	82.0	3.927
SL IPTW	−0.391	0.009	0.050	0.032	0.003	0.001	79.1	4.996
Scenario D
Naive	−0.261	0.139	0.070	0.071	0.002	0.024	50.4	28.002
Logit matching	−0.471	0.071	0.074	0.091	0.004	0.007	92.9	8.310	7
SL matching	−0.418	0.018	0.113	0.082	0.008	0.003	85.6	10.781	12
Logit IPTW	−0.513	0.113	0.084	0.035	0.004	0.014	28.8	11.100
SL IPTW	−0.389	0.011	0.073	0.044	0.009	0.002	77.8	8.472

Abbreviations: ASAM, average standardized absolute mean difference; CI, confidence interval; IPTW, inverse probability of treatment weighting; MSE, mean squared error; SD, standard deviation; SE, standard error; SL, Super Learner.

^aAll tabulated results represent average values from 1,000 independent replications.

^bEmpirical Monte Carlo SE across the 1,000 simulated data sets.

^cEmpirical mean of the estimated SEs.

^dEmpirical SD of the estimated SE.

^eEmpirical coverage of nominal 95% CIs across the 1,000 simulated data sets.

^fNumber of subjects discarded by the matching procedure.

Matched sample size and distribution of the weights

We first assessed the number of subjects who were discarded by the matching procedure. A large number of subjects discarded could indicate practical violations of the positivity assumption (e.g., the assumption stating that each possible treatment level occurs with some positive probability within each stratum of W (47)). However, this number remained very limited regardless of the scenario and the modeling method (minimum, 0%; maximum, 2.4%).

The distribution of the weights used for the IPTW analysis is shown in Table 2. The distributions were similar for the different modeling methods and well-centered around 1.

Table 2.

Distribution of the Inverse-Probability-of-Treatment Weights for Each Modeling Approach and Simulation Scenario

Scenario and Method	Weight Distribution
	Minimum	Quartile 1	Median	Mean	Quartile 3	Maximum
Scenario A
Logistic regression	1.0	1.3	1.6	2.0	2.2	16.7
Super Learner	1.0	1.3	1.6	2.0	2.2	13.2
Scenario B
Logistic regression	1.1	1.4	1.7	2.0	2.2	11.9
Super Learner	1.0	1.3	1.6	1.9	2.2	13.7
Scenario C
Logistic regression	1.0	1.3	1.5	2.0	2.1	19.9
Super Learner	1.0	1.3	1.6	2.0	2.2	15.6
Scenario D
Logistic regression	1.0	1.2	1.5	2.1	2.1	36.6
Super Learner	1.0	1.1	1.3	1.9	1.9	29.5

Predictive performance of PS models

The predictive performances of the PS models were assessed by computing the average cross-validated L2 squared error as well as the average cross-validated AUROC over the 1,000 replications. In terms of L2 squared error, whatever the scenario, SL performed at least as well as each candidate algorithm, including main-term logistic regression (scenario A—SL: 0.209, best candidate: 0.206; scenario B—SL: 0.188, best candidate: 0.190; scenario C—SL: 0.194, best candidate: 0.193; scenario D—SL: 0.192, best candidate: 0.193). While the AUROC from SL (0.741) was slightly below that of the main-term logistic regression model (0.769) in scenario A, the opposite was observed for scenario D (logistic regression: 0.782, SL: 0.851).

Balance diagnosis

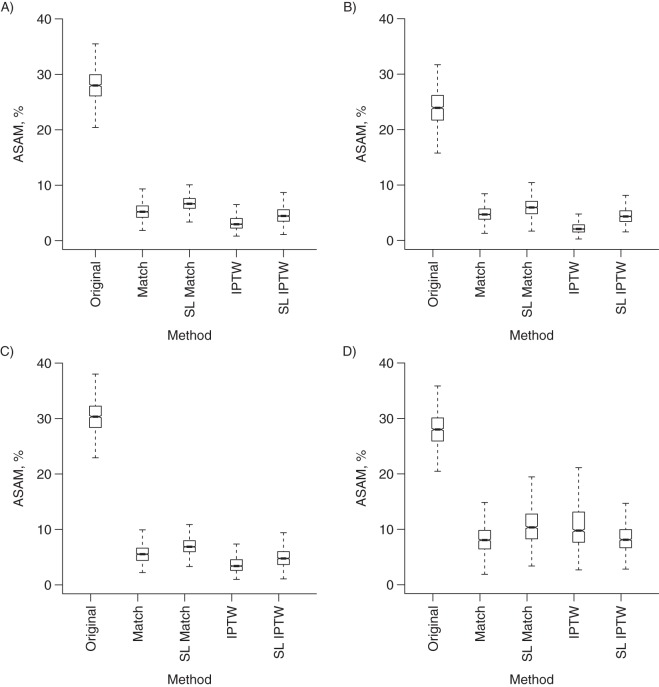
The distribution of the ASAM values is plotted in Figure 1. As expected, all covariates except X8 and X10 were highly imbalanced between treatment groups. An acceptable covariate balance was achieved with both modeling approaches and both PS approaches (Table 1). However, in scenario D, when evaluating each covariate separately (Web Table 2), the balance achieved by the SL-based matching procedure was better than the one achieved when using logistic regression for PS estimation.

Figure 1.

Distribution of the average standardized absolute mean difference (ASAM) for each method and each scenario. The ASAMs are expressed as percentages. A) Scenario A (i.e., additivity and linearity (main effects only)); B) scenario B (i.e., nonlinearity (3 quadratic terms)); C) scenario C (i.e., nonadditivity (10 two-way interaction terms)); D) scenario D (i.e., nonadditivity and nonlinearity (10 two-way interaction terms and 3 quadratic terms)). The midline represents the mean value, and the dashed lines show the 2.5% and 97.5% quantiles.

We compared the balance obtained using SL with the balance obtained using the best candidate learners previously proposed for PS matching (Neural Networks (22)) and for IPTW (boosted CART (23)) (Table 3). Whatever the scenario, the covariate balance achieved with SL was better than that achieved with the 2 candidate learners. This was true for PS matching as well as IPTW (Table 3).

Table 3.

Performance of the Propensity Score Estimator When Using Super Learner, Neural Networks, and Boosted CART for Propensity Score Estimation^a

Method and Scenario	ASAM, %	Estimate	Absolute Bias	MSE	Empirical SEb	Estimated SEc	95% CI Coverage, %d
Matching
Boosted CART
Scenario A	17.003	−0.521	0.138	0.041	0.092	0.117	81.6
Scenario B	15.762	−0.510	0.135	0.041	0.091	0.119	84.5
Scenario C	17.598	−0.520	0.140	0.044	0.094	0.122	84.5
Scenario D	21.470	−0.523	0.157	0.060	0.113	0.149	86.2
Neural Networks
Scenario A	13.862	−0.399	0.001	0.036	0.082	0.132	94.3
Scenario B	14.915	−0.404	0.004	0.040	0.086	0.138	94.1
Scenario C	14.354	−0.404	0.004	0.038	0.082	0.137	94.5
Scenario D	20.287	−0.395	0.006	0.069	0.114	0.176	91.0
Super Learner
Scenario A	6.734	−0.381	0.019	0.002	0.061	0.101	100.0
Scenario B	4.840	−0.403	0.003	0.001	0.067	0.085	98.5
Scenario C	7.025	−0.381	0.019	0.002	0.065	0.097	99.4
Scenario D	10.781	−0.418	0.018	0.003	0.113	0.082	85.6
Inverse Probability of Treatment Weighting
Boosted CART
Scenario A	13.297	−0.338	0.066	0.011	0.043	0.079	95.8
Scenario B	12.505	−0.343	0.062	0.011	0.040	0.074	96.7
Scenario C	14.473	−0.328	0.074	0.013	0.043	0.076	93.5
Scenario D	14.262	−0.354	0.058	0.011	0.040	0.079	97.3
Neural Networks
Scenario A	39.586	−0.561	0.257	0.150	0.180	0.226	83.0
Scenario B	36.317	−0.530	0.241	0.149	0.189	0.231	86.2
Scenario C	39.695	−0.558	0.256	0.153	0.183	0.230	84.3
Scenario D	35.386	−0.475	0.256	0.169	0.193	0.249	83.3
Super Learner
Scenario A	4.660	−0.391	0.009	0.001	0.045	0.031	83.7
Scenario B	4.470	−0.392	0.008	0.001	0.045	0.033	83.8
Scenario C	4.996	−0.391	0.009	0.001	0.050	0.032	79.1
Scenario D	8.472	−0.389	0.011	0.002	0.073	0.043	77.8

Abbreviations: ASAM, average standardized absolute mean difference; CART, classification and regression trees; CI, confidence interval; MSE, mean squared error.

^aAll tabulated results represent average values from 1,000 independent replications.

^bEmpirical Monte Carlo SE across the 1,000 simulated data sets.

^cEmpirical mean of the estimated SEs.

^dEmpirical coverage of nominal 95% CIs across the 1,000 simulated data sets.

Performance of ATE estimator

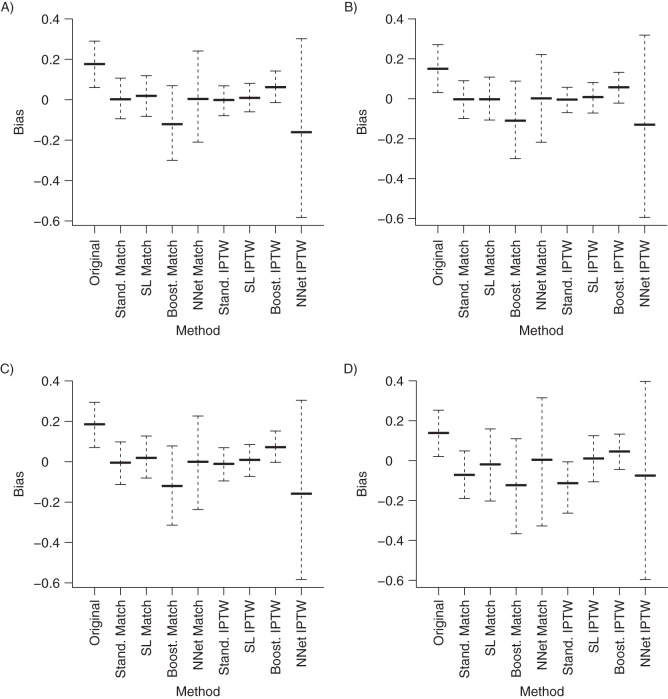
The mean value of the outcome was −3.85 (standard deviation, 0.03) for scenarios A, B, and C and −3.86 (standard deviation, 0.03) for scenario D. The treatment effect was set to be −0.4. For PS matching, the bias associated with logistic regression–based estimators was limited when the model was correctly specified or when the true PS model was either nonlinear or nonadditive (relative bias in scenarios A–C: 0.50%, 0.75%, and 2.50%, respectively) (Figure 2). However, the bias increased substantially when the true PS was nonlinear and nonadditive (relative bias in scenario D: 17.25%). For PS matching, the bias associated with SL-based estimators was slightly larger when the PS model was correctly specified (relative bias in scenario A: 4.75%), but it remained stable even in the case of severe model misspecification (relative bias in scenarios B–D: 0.75%, 2.25%, and 4.50%, respectively). For IPTW estimators, the impact of model misspecification was greater when logistic regression was used to estimate the PS (relative bias in scenarios A and D: 0.25% and 28.25%) as compared with the corresponding SL-based estimator (relative bias in scenarios A and D: 2.25% and 2.75%).

Figure 2.

Distribution of the absolute bias for each method and each scenario. The y-axis represents the bias as defined by the point estimate minus truth. A) Scenario A (i.e., additivity and linearity (main effects only)); B) scenario B (i.e., nonlinearity (3 quadratic terms)); C) scenario C (i.e., nonadditivity (10 two-way interaction terms)); D) scenario D (i.e., nonadditivity and nonlinearity (10 two-way interaction terms and 3 quadratic terms)). The midline represents the mean value, and the dashed lines show the 2.5% and 97.5% quantiles. Boost. IPTW, boosted CART IPTW; Boost. Match, boosted CART matching; CART, classification and regression trees; IPTW, inverse probability of treatment weighting; NNet IPTW, Neural Networks IPTW; NNet Match, Neural Networks matching; SL, Super Learner; SL IPTW, Super Learner IPTW; SL Match, Super Learner matching; Stand. IPTW, standard IPTW estimator; Stand. Match, standard matching estimator.

The performance of the SL- and logistic regression–based estimators was also compared with the best candidate learners previously proposed for PS matching (Neural Networks (22)) and for IPTW (boosted CART (23)) (Table 3). As previously reported, the Neural Networks matching estimator was associated with limited bias regardless of the scenario. However, when it was used to estimate the weights for the IPTW estimator, the Neural Networks estimator produced severely biased estimates. In contrast, the boosted CART matching estimator was severely biased regardless of the scenario, while it offered better performance for IPTW. Concerning IPTW estimators, SL performed better than both candidates in terms of bias. Concerning PS matching, SL performed better than boosted CART but exhibited slightly greater bias than Neural Networks. However, because of smaller variance estimates, the mean squared error observed with SL was similar to or even smaller than the one associated with Neural Networks (according to the scenario, 0.036–0.069 with Neural Networks vs. 0.001–0.003 with SL).

The empirical standard errors were similar with logistic regression and SL and were not affected by scenario. However, IPTW estimators exhibited smaller empirical standard errors than did matching estimators.

We found no correlation between the AUROC and the magnitude of bias in the effect estimates. Pearson's correlation coefficient ranged from 0.024 to 0.241 according to scenario.

Performance of variance estimator

Concerning PS matching, the standard error estimators systematically overestimated the empirical standard errors, resulting in greater-than-nominal coverage of the 95% confidence intervals when the estimator of the ATE was unbiased (Table 1). No clear difference was observed between logistic regression– and SL-based estimators.

For IPTW estimators, the large-sample standard error estimators underestimated the empirical standard errors. Consistently, the 95% coverage rates were below 90% regardless of the scenario and the estimation method. Notably, the coverage observed with the logistic regression–based IPTW estimator in scenario D was extremely low (28.8%). The variability of the standard error estimates was very limited, and variabilities were similar regardless of the scenario and the method used for PS estimation.

Large sample size and low treatment prevalence

Because in medical studies sample sizes are often much larger than 500 and treatment groups are often imbalanced, we performed additional simulations with n = 5,000 and average treatment prevalence = 0.10. Results in terms of bias were similar to those obtained in smaller samples and with an average treatment probability of 0.5: relative bias decreased from 18% to 10% with SL matching as compared with standard matching and from 28% to 8% with SL IPTW as compared with standard IPTW.

DISCUSSION

Propensity-based methods have encountered great success, especially in the medical literature. These methods are very sensitive to misspecification of the PS model (22, 23). Although the impact of PS model misspecification might be less than that of response model misspecification (13), the former may still result in poor balancing properties (23) and biased estimates (14, 15, 22, 23). Machine learning algorithms, which are designed to learn the relationship between an outcome and a set of predictors under a nonparametric model, may thus be of great interest for PS modeling. Several data-adaptive approaches have been proposed for this purpose (17, 22, 23). However, differing results make it difficult to propose definitive guidelines. Moreover, the relative performance of different algorithms is highly dependent on the underlying data distribution. In addition, if the relationship between the PS and the covariates is linear and additive, the main-term logistic regression will outperform any data-adaptive method for modeling the PS.

SL (24, 25) is a weighted linear combination of candidate learner algorithms that has been demonstrated to perform asymptotically at least as well as the best choice among the library of candidate algorithms, whether or not the library contains a correctly specified parametric statistical model. To assess the benefit of using SL for PS modeling, we used a simulation plan close to the one proposed by Setoguchi et al. (22) in order to generate different scenarios with increasing degrees of PS model misspecification when main-term logistic regression was used. When increasing PS model misspecification, the performance of the logistic regression–based PS estimator decreased, while the SL-based PS estimators remained somewhat stable. These results were observed for both PS matching and IPTW estimators.

Predictive performances and balance properties

The SL performed at least as well as or better than the alternative candidate algorithms considered (including logistic regression) for estimating the PS, as reflected by the L2 squared errors, the AUROC, and the covariate balance achieved. However, prediction performances and balance properties are 2 different issues. Indeed, whatever the method, PS adjustment aims to balance the distribution of confounding covariates between groups rather than to accurately predict treatment allocation. As previously reported (48, 49), we found no correlation between the AUROC and the magnitude of bias in the effect estimates. This is also consistent with results reported by Setoguchi et al. (22). Indeed, predictive performance is improved by adding into the PS model any variable that is related to treatment allocation, regardless of whether this variable is associated with the outcome. However, introducing in the PS model a covariate that is strongly associated with A but not with the outcome (i.e., an instrumental variable) can result in an estimator with worse performance, while the predictive performance of the PS model is improved (50).

The fact that model predictive performance is not associated with reduced bias might seem to contradict the main idea of using SL in its present form to estimate the PS. However, the benefit of SL in cases of severe model misspecification may outweigh this limitation. Indeed, we found that SL provided adequate covariate balance, as reflected by ASAMs below 10% for all scenarios, particularly in the case of severe model misspecification, where it seemed to better balance the strong confounders. In order to provide a direct comparison of the balancing properties of the different methods, we reran our analyses using the best algorithms for the PS model proposed by Setoguchi et al. (22) (Neural Networks) and Lee et al. (23) (boosted CART) and compared the results with those obtained with SL. Consistent with previous results (22, 23), Neural Networks outperformed boosted CART for PS matching, while the opposite was observed for the IPTW estimator. However, whatever the PS estimator, SL outperformed both methods in terms of balancing properties. Note that for boosted CART, such results were obtained despite the use of an iteration stopping point that minimized a measure of the balance across pretreatment variables.

Effect estimation

For PS matching, the logistic regression–based estimate had no meaningful bias when the model was correctly specified or when the true PS model was either nonlinear or nonadditive. However, the bias increased substantially when the true PS was nonlinear and nonadditive. When using SL, the bias was slightly greater when the logistic regression model was correctly specified, but the bias was smaller than it was with logistic regression when nonlinearity and nonadditivity were introduced. For IPTW, nonlinearity and nonadditivity were associated with increasingly biased estimates when logistic regression was used to estimate the PS, while the bias remained remarkably stable and low when using SL. Similar results were reported with the best candidate learning proposed by Lee et al. (23) and Setoguchi et al. (22). For IPTW estimators, the bias associated with boosted CART was close to that obtained with SL. Neural Networks–based estimates were more biased. However, for PS matching, Neural Networks clearly outperformed boosted CART and led to the same range of biases as SL.

Adequate covariate balance could be associated with poor estimation performances. Indeed, we found that, despite constant and acceptable ASAM values over the 4 scenarios, logistic regression–based estimators exhibited large biases in cases of model misspecification. Such a result was also reported by Lee et al. (23). This should probably provide some warnings concerning the usual diagnostic methods for assessing PS balancing properties, such as standardized differences or ASAM. Such methods do not evaluate balance in the entire covariate distribution between the groups, and particularly do not evaluate the balance in potential interactions (46). Moreover, model predictive performance, as evaluated by the AUROC, was not found to be associated with estimation bias. This is consistent with results reported by Setoguchi et al. (22) and with other previous work suggesting that goodness-of-fit measures for the PS might not be appropriate for assessing the performance of a PS model (48). Indeed, predictive performance is improved by adding into the PS model any variable that is related to treatment allocation, whether or not this variable is associated with the outcome. However, introducing into the PS model a covariate that is strongly associated with A but is not a confounder (i.e., an instrumental variable) can result in an estimator with worse performance in terms of mean squared error (because of both increased variance and increased bias due to practical positivity violations), while predictive performance of the PS model is improved (11, 51). We illustrated this by rerunning our simulations after removing from our PS model the variables that were only associated with the exposure (W5–W7). This resulted in worse balancing properties but in better estimates (in the worse-case scenario (scenario D), the relative biases with SL decreased to 3.25% and 0.25% for PS matching and IPTW estimators, respectively). Hence, doing a better job in predicting treatment allocation does not ensure doing a better job on the ATE. This argues for 1) using clever variable-selection methods, such as high-dimensional propensity scores (52–54), that would recognize that selecting confounders based on the fit of the PS model can lead to serious problems in the presence of approximate instrumental variables and 2) moving beyond PS-based estimators to targeted approaches, such as targeted maximum likelihood estimators or collaborative targeted maximum likelihood estimators (14, 55). The benefit of using targeted approaches for PS estimators was recently highlighted by van der Laan (56).

The performances of the variance estimators were disappointing with regard to both matching and IPTW estimators. The simulations are quite simple, and one can imagine that, in reality, things may be even worse in some specific situations. Thus, this is an important concern, as these variance estimators are the most commonly used in practice and are supposed to offer the best properties in this context. For PS matching, the Abadie-Imbens variance estimators (43) overestimated the standard errors, leading to coverage rates above the expected 95%. The Abadie-Imbens standard error is known to have correct coverage if the PS is known, because it takes into account the uncertainty of the matching procedure (43). However, if an estimated PS is used, the uncertainty involved in its estimation is not accounted for, resulting in poor coverage rates. Inconsistently with the results reported for the robust sandwich variance estimator (10, 57), the large-sample IPTW variance estimator was found to be very anticonservative whatever the scenario. We might expect some benefit from using the robust Lunceford-Davidian variance estimator, which is associated with limited bias and better coverage rates, especially when the PS is estimated (58). Bootstrapping might be an alternative solution for estimating the confidence intervals, although specific studies are needed to confirm the validity of bootstrap-based inference in this context. Alternatively, targeting approaches for PS modeling might be of interest in this context to obtain valid statistical inferences, as recently demonstrated by van der Laan (56).

Limitations

Our analysis had some limitations. First, for most algorithms, we included in the SL library only the off-the-shelf versions of available algorithms. Expanding the library with more algorithms or more finely tuned versions of the present algorithms should improve the performance of SL, especially if the choice of the candidates reflects any knowledge about the underlying data distribution. Second, we intended to include the candidate algorithms proposed by Lee et al. (23) and Setoguchi et al. (22). However, the version of boosted CART included in our SL library is different from the one used by Lee et al. (23). Third, our conclusions might be restricted to our simulation scenarios and might not apply to situations not represented by our simulated data. More specific situations, such as small or very large sample sizes, low treatment prevalence, and the presence of unmeasured confounders, would require further investigation. Fourth, our results were not strictly comparable with those previously published (22, 23). Indeed, we chose the ATE as an estimand, while Lee et al. (23) and Setoguchi et al. (22) focused on the ATE among the treated. Fifth, most of the relative bias in this study was limited. However, the simulations performed in this study were quite simple; in reality, relative bias may be even worse in some cases. Sixth, we used a matching-with-replacement algorithm that targets the marginal effect instead of the effect among the treated, as allowed in the R package Matching (42). Some authors suggest that matching with replacement produces matches of higher quality than matching without replacement, by increasing the set of possible matches (43). However, recent results (59) suggest that matching-with-replacement estimators might be associated with greater variability and thus larger mean squared errors. Seventh, the IPTW estimators were used without weight stabilization. As others have highlighted (60, 61), weight stabilization is recommended in practice to limit the effects of practical violation in the positivity assumption. Eighth, our simulation scenarios did not really explore the situation of sparse data. Hence, some additional analysis would be needed to address potential problems arising from significant positivity violations. Finally, like most nonparametric modeling methods, SL may be considered a “black box,” which does not allow appraisal of the contribution of each variable included in the model. However, note that when appraising the results of PS modeling with SL, it remains possible to report the results of several kinds of diagnostic procedures, such as the PS distribution. Then, in cases of predictions close to 0 and 1 (i.e., suggesting near-violation of the positivity assumption), one can still further investigate when and why that is happening. Moreover, we emphasize that computational feasibility may sometimes be an issue with SL, as the procedure relies on cross-validation. However, the multicore option made available in the most recent version of the R package (version 2.0-15) speeds up the procedure considerably.

Conclusion

Because the true shape of the relationship between treatment allocation and observed covariates is generally unknown, the use of nonparametric methods to model the PS is of interest. Among those methods, SL seems to be associated with good results in terms of bias reduction and covariate balance, for PS matching as well as IPTW estimators. For the future, one can imagine that modifying the loss function in SL to explicitly pick up an optimal method according to what provided the optimal covariate balance rather than optimal PS prediction could offer a significant boost in its performance. Finally, further work is needed to improve the performance of both PS matching and IPTW variance estimators.