Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Mar 1.
Published in final edited form as: Nurs Res. 2015 Mar-Apr;64(2):140–145. doi: 10.1097/NNR.0000000000000079

The Problem with Cronbach's Alpha: Comment on Sijtsma and Van der Ark (2015)

Claudio Barbaranelli 1, Christopher S Lee 2, Ercole Vellone 3, Barbara Riegel 4
PMCID: PMC4351779  NIHMSID: NIHMS650258  PMID: 25738626

Abstract

Knowledge of a scale's dimensionality is an essential preliminary step to the application of any measure of reliability derived from classical test theory—an approach commonly used is nursing research. The focus of this article is on the applied aspects of reliability and dimensionality testing. Throughout the article, the Self-Care of Heart Failure Index is used to exemplify real-world data challenges of quantifying reliability, and to provide insight into how to overcome such challenges.

Keywords: psychological measurement, psychometrics, questionnaires, reliability, reproducibility of results, Self-Care of Heart Failure Index

Sijtsma and Van der Ark discussed three approaches to reliability: classical test theory (CTT); factor analysis (FA); and generalizability theory (GT) in the special and infrequent case of three-way data structure (i.e., when there is more than one rater). It is much more often the case, however, that scientists in nursing and other health disciplines are concerned with the reliability of a measure that is ascertained from a single respondent such as a study participant. Sijtsma and Van der Ark correctly identified that Sirotnik (1970) demonstrated that the generalizability coefficient derived from GT-based approaches is equivalent to coefficient alpha when there is a single respondent to the items of interest. Thus, GT-based methods provide no additional value over CTT and FA approaches for the most pressing and real-world challenges in reliability that we face. Moreover, the examination of reliability according to CTT principles and examination of scale dimensionality (through FA) are oftentimes undertaken as if they were separate issues. We believe that knowledge of a scale's dimensionality is an essential preliminary step to the application of any measure of reliability developed within the framework of CTT.

Accordingly, this article focuses on the applied aspects of reliability and dimensionality testing. As GT applies only to designs uncommon in nursing research, we focus specifically on CTT and FA, which are commonly used in nursing research. Throughout the article, we use the Self-Care of Heart Failure Index (SCHFI; Riegel, Lee, Dickson, & Carlson, 2009) to exemplify real-world data challenges of quantifying reliability and to provide insight into how to overcome such challenges.

Reliability Assessment and the Study of Scale Dimensionality

A first issue raised by Sijtsma and Van der Ark that we want to address is related to the relationship between CTT and FA models. We believe that it is crucial to first examine scale dimensionality and then conduct FA before quantifying any index of reliability. This advice applies to Cronbach's alpha in particular because this approach assumes a unidimensional scale.

As noted by Sijtsma and Van der Ark, in CTT there is no assumption of covariance among items that have been produced to measure a construct within a scale. As such, there is no reason to expect that a scale's items would be correlated because CTT models simply decompose measurement values into systematic and random measurement parts (Sijtsma and Van der Ark). For the hypothetical nature of a CTT model, however, reliability cannot be computed directly from the basic formulas that define the model. Instead, reliability needs to be estimated by other models (see Sijtsma and Van der Ark, p. xx). A common strategy to get these estimates is based on the use of scores from a single-test, single-administration design, where “estimates based on the covariances of all item pairs provide lower bounds to the reliability” (Sijtsma and Van der Ark, p. 11), and Cronbach's alpha “is the best known representative of this category” (Sijtsma and Van der Ark, p. 11). As is well known, a scale's alpha is a function of correlations among scale items, and other things being equal, the more substantial the average items correlate the higher the alpha. Then, while the “theoretical” CTT model does not require that items are correlated in order to have a reliable measure, the more commonly used method for deriving reliability estimates provides better estimates when items are highly correlated (other things being equal).

The dependence of CTT-based reliability on more common methods for estimating reliability within the same model stems from the fact that CTT is a hypothetical model that is not anchored in reality. As specified by Sijtsma and Van der Ark, the theoretical model in CTT implies the administration of the same items over and over again to the same individual. In contrast, reality implies that a set of items is administered once or maybe twice to a sample of individuals. In the extension of this hypothetical model to reality, it is necessary that items composing a scale at least measure the same construct—if not with the same precision—in order to obtain unbiased measures of reliability by means of alpha coefficient (i.e. the tau-equivalence or true score equivalence; Raykov & Marcoulides, 2011). We are now faced with a paradox. Specifically, the CTT definition of reliability ignores what each item measures, and items are not required to be correlated. But in the real world, the method used for estimating reliability with this model cannot ignore what items measure; alpha is an accurate measure of reliability only if items measure the same construct and are sufficiently correlated.

In the practical application of CTT, one cannot ignore that the items are correlated. In fact, alpha must be high to empirically demonstrate reliability. That is, items must measure the same construct with the same unit of measurement in order to have an unbiased measure of reliability. If one considers the formula for Cronbach's alpha, however, it is clear that alpha depends only on item average correlations (or inter-item covariances)(Sijtsma, 2009), assuming they are all positive and from the number of items forming the scale (Nunnally & Bernstein, 1994). In contrast, alpha is not dependent on a particular structure. In fact, item intercorrelations may be generated by different latent structures. Here is where FA comes into play. Factor analysis does not simply assume that items are correlated, but FA gives a structure to the correlations in order to explain their origin.

Confusing homogeneity with internal consistency, high values of Cronbach's alpha are often improperly interpreted as evidence of a single factor explaining correlations among scale items (Raykov, 2012; Raykov & Marcoulides, 2011). Homogeneity refers to a situation when there is only one latent dimension explaining item correlations, while internal consistency refers to the intercorrelation among scale items (Schmitt, 1996). Since alpha is an index of internal consistency, it provides no information regarding the number of factors explaining item correlations. Such information can be obtained only after a careful examination of the items’ latent structure (e.g., dimensionality)—obtained from FA. Simply put, only the results of FA provide evidence of which items should be summed in order to obtain scores that reflect the intended construct. Relying solely on the results of alpha—to inform structure—poses a risk of ending up with summed scores that reflect mixed sources of variance.

Due to the great interdependency of reliability on dimensionality, we argue that scale dimensionality must be assessed with FA before choosing an appropriate method of estimating reliability. A variety of reliability indices have been developed. Below we describe how the results of FA can be used to identify which reliability index to use.

Some Reliability Indices from Which to Choose After Assessing Dimensionality

When items are congeneric (i.e., a model with one homogenous factor that fits the data) and measurement errors are not correlated, composite scale reliability can be defined as shown in Equation 1 (Fornell & Larcker, 1981):

ρη=(∑i=1pλi)2(∑i=1pλi)2+∑i=1pVar(εi) (1)

where λ is the factor loading of the indicator, and Var(εy) is its residual variance—assuming that φ, the variance of the factor—is fixed at 1 for identification purposes, and that the factor and the measurement error are independent. This coefficient gives consistent estimators of scale reliability (Raykov, 2012), and has a close resemblance to the omega coefficient discussed below (McDonald, 1999; Revelle & Zinbarg, 2009).

While omega can be used as a measure of reliability when one latent variable accounts for item correlations (McDonald, 1999), the composite scale reliability coefficient can be extended to consider the more general case of a multidimensional scale, that is, a scale where more than one latent variable explains correlations among observed variables in a dataset (Camilli, Wang, & Fesq, 1995).

The formula for a global reliability index for multidimensional scales proposed by Raykov and Marcoulides (2011) is shown in Equation 2:

ρU=1′AΦA′1(1′AΦA′1+1′ϴ1) (2)

where A is the matrix of factor loadings onto common factors and A’ its transpose, Φ is the covariance matrix of the common factors, Θ is the covariance matrix of measurement errors, 1 is a unity vector and 1’ its transpose.

Another index that can be used when a scale has more than one factor is the model-based internal consistency index proposed by Bentler (2009) and shown in Equation 3:

ρ^xx=1−1′Ψ^11′Σ^1 (3)

where Σ^ is the fitted covariance matrix obtained from model parameter estimates, and Ψ^ is the error covariance matrix.

All these coefficients can be easily computed using standard output from structural equation modeling programs, as well as standard output from software for exploratory FA. We do not have space here to dwell on a discussion of other indices. The interested reader is referred to Raykov (2012) and Revelle and Zinbarg (2009).

Empirical Examples: The Self-Care of Health Failure (SCHFI)

As noted in the introduction, the empirical examples we provide refer to the analysis of the SCHFI (Riegel et al., 2009)—a measure that has broad use in clinical research and practice, in spite of the fact that we have been grappling for years with its reliability. The situation-specific theory of heart failure (HF) self-care (Riegel & Dickson, 2008) defines self-care as a naturalistic decision-making process composed of two dimensions: self-care maintenance and self-care management. Self-care maintenance reflects behaviors in which patients engage to maintain stability and prevent an exacerbation, including monitoring for signs and symptoms like dyspnea and edema, and adhering to prescribed therapies like medicines and dietary restrictions. Self-care management is a process of recognizing symptoms when they occur, engaging in self-initiated symptom treatment strategies like reducing salt and fluid intake or taking an extra diuretic, and evaluating the effectiveness of the implemented treatments. Self-care confidence (i.e., self-efficacy related to the specific tasks of HF self-care) is thought to be an important factor influencing the effectiveness of HF self-care (Cené et al., 2013; Lee et al., 2011; Lee, Suwanno, & Riegel, 2009; Vellone et al., 2014). The SCHFI version 6.2 directly reflects this naturalistic decision-making process and, thus, is useful to investigators seeking to describe self-care and test the effectiveness of interventions. In an earlier version (SCHFI v.4), when all three scales were added to yield a single self-care score, Cronbach's alpha was 0.76 for the full scale and 0.56, 0.70, and 0.82 for the self-care maintenance, management, and confidence scales, respectively (Riegel et al., 2004). When the SCHFI v.6.2 update was published, scale scores are no longer added together. Considering the separate scales, Cronbach's alpha was reported to be 0.55 for self-care maintenance, 0.60 self-care management, and 0.83 for self-care confidence (Riegel, et al., 2009).Similarly poor alpha coefficients of the SCHFI have been reported by others (Kato et al., 2013; Yu et al., 2011).

The data considered here refer to a sample of 549 subjects described in detail elsewhere (Barbaranelli, Lee, Vellone, & Riegel, 2014). In these examples, confirmatory FAs were conducted using Mplus 7.1 (Muthén & Muthén, 1998-2012). Due to some non-normality in the data, parameter estimation was conducted using a robust maximum likelihood estimator (i.e., Satorra-Bentler correction implemented via the estimator MLM).

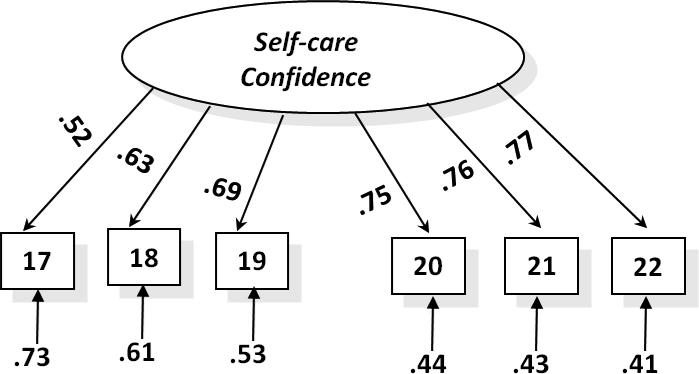
As the first example we consider the analysis of the Self-Care Confidence scale. Riegel et al. (2009) posited a single factor underlying the six items composing this scale. Accordingly, we specified a one-factor model. This model showed an excellent fit: χ 2 (df = 9, N = 554) = 23.35, p < .01, Tucker-Lewis Index (TLI) = .99, Comparative Fit Index (CFI) = .99, Standardized Root-Mean Square Residual (SRMR) = .023, and Root Mean Square Error of Approximation (RMSEA) = .05, p = .37. Figure 1 presents the final fitted model: all factor loadings were high, significant, and positive.

FIGURE 1.

FIGURE 1

Open in a new tab

Confirmatory factor analysis model for the Self-Care Confidence Scale. N = 554. Adapted from Barbaranelli et al. (2014) with permission from John Wiley and Sons.

Reliability estimates for this model converged to the same value of 0.84 using both alpha and the composite reliability (or omega) coefficients. This convergence is mainly due to the substantial homogeneity of factor loadings. Although these loadings are not strictly equal, they are almost uniformly high (see Raykov, 1997, in this regard).

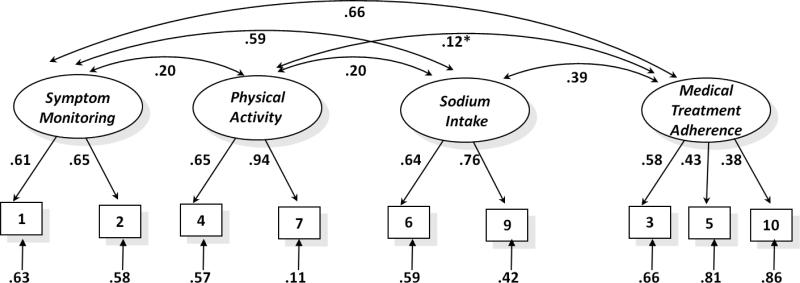
The second analytical example refers to the Self-Care Maintenance Scale. Self-care maintenance was hypothesized as an unidimensional scale by Riegel et al. (2009). However, when testing a one-factor model with our data, the model proved to be largely unsatisfactory, with the following poor-fit indices: χ 2 (df = 35, N = 549) =380, p < .001, TLI = .41, CFI = .54, SRMR = .09, and RMSEA = .13, p < .001. Conversely, a four-factor model adapted from Vellone, Riegel, and colleagues (2013), resulted in an excellent fit: χ 2 (df = 21, N = 549) = 49.19, p < .001, TLI = .93, CFI = .96, SRMR = .035 and RMSEA = .049, p = .49. Figure 2 provides a graphical representation of this four-factor model. Factor loadings were generally medium to high, thus attesting to a substantial proportion of common variance among the items. Factor correlations were all positive and significant (except for one, see Figure 2), attesting to a significant and coherent association among the different facets of self-care maintenance.

FIGURE 2.

FIGURE 2

Open in a new tab

Confirmatory factor analysis model for the Self-Care Maintenance Scale. All factor correlations are significant (p < .05) except the one with the asterisk. N = 549. Adapted from Barbaranelli et al. (2014) with permission from John Wiley and Sons.

The self-care maintenance scale was intended to yield a single score, not four different scores related to the different aspects of the construct. One item in the scale was problematic and eliminated for this analysis, but even when the alpha coefficient was computed on the nine items of the scale, a poor coefficient of .65 was obtained. Knowing that there are four dimensions represented in this scale, more appropriate reliability coefficients that take into account the multidimensionality of the scale are the global reliability index for multidimensional scales (Raykov & Marcoulides, 2011), and the model-based internal consistency coefficient (Bentler, 2009).

These coefficients were respectively .75 and .76 when derived from results in Figure 2. Although the dimensionality of this scale is complex, as noted by Bentler (2006), “every multidimensional coefficient implies a particular composite with maximal unidimensional reliability” (p. 343). Thus, the final reliability estimates derived with appropriate methods “can be interpreted to represent a unidimensional composite” (Bentler, 2006, p. 341).

What if Items Are Ordinal or Dichotomous?

Many of the scales used in nursing research are composed of items having an ordinal or dichotomous response format. As a matter of fact, SCHFI items have a Likert-style graded response format. One may question in this case whether the indices discussed in this article adequately handle ordered categorical data. (Sijtsma and Van der Ark briefly refer to this case on page x of their article.) Since ordinal and dichotomous response formats are not uncommon in nursing research, we believe it is important to devote some extra space to this issue. First, since the late 1970s, there has been concerted effort to develop estimation methods suitable for conducting FA on ordinal and dichotomous data, especially by Muthén (1984). More recently, new estimators have been developed and implemented in the Mplus software. In particular, WLS-MV estimators are designed for use with ordinal or dichotomous observed indicators of underlying continuous latent variables and have performed well in sampling experiments using factor analysis models (Flora & Curran, 2004).

When the models in Figures 1 and 2 were analyzed, using these estimators, results overall confirmed what is presented here, with estimates of factor loadings and of factor correlations generally a little higher than those derived from robust maximum likelihood (ML) (Barbaranelli et al., 2014). Raykov & Marcoulides (2011) advocate using internal coherence coefficients, such as those discussed in this article, when items have less than five ordinal responses options. The problem is that these methods for analyzing categorical ordinal variables in FA consider these variables as discretization of underlying continuous variables. Thus, when internal coherence estimates are computed from parameters derived from WLS-MV, these estimates correspond to the continuous variables that underlie the observed categorical responses—not the categorical responses themselves. The result is that methods like WLS-MV tend to overestimate the value of internal consistency coefficients. Conversely, when maximum likelihood methods are used in the analysis of ordinal or dichotomous data in FA, and parameters from this solution are used to compute reliability estimates, reliability indices are generally underestimated. To our knowledge, the only procedure that gives unbiased estimates of reliability coefficients derived from the analysis of ordinal or dichotomous data is the one developed by Green and Yang (2009). When this procedure was applied to our models using estimates derived from the WLS-MV method (Barbaranelli et al., 2014), nonlinear structural equation model (SEM) reliability coefficients of 0.84 and of 0.74 were obtained, thus substantially confirming the results obtained with ML-robust estimators.

Concluding Remarks

We took advantage of this short article to expand upon issues raised by Sijtsma and Van der Ark, and to provide practical examples of how reliability indices using the results of FA can be applied to real-world data challenges that are common in nursing research. As we stated throughout the article, dimensionality must be tested using FA before choosing an appropriate measure of internal consistency. The two real data examples provided here illustrate this process both in the case of a unidimensional scale (SCHFI Self-Care Confidence), as well as a multidimensional scale (SCHFI Self-Care Maintenance). In both cases, scale dimensionality was established by model fit, and internal consistency coefficients developed from the results of FA generally outperformed values of Cronbach's alpha. In fact, the reliability of the self-care maintenance scale was adequate only when a coefficient was employed that reflects its multidimensional nature.

In closing, we want to draw your attention to Equation 8 of the Sijtsma and Van der Ark article. This equation underlines the important issue that when row item scores are summed, one is summing true-reliable scores with measurement error. Too often, applied researchers and practitioners rely on the illusion that FA removes any sources of extraneous variability. Sijtsma and Van der Ark also noted that factor models account for common variation of indicators, but do not remove other sources of variability unless explicitly modeled. When scale items are simply summed together to obtain a total scale, however, the scale will contain variability that is due to common factor as well as that due to residual components (DeShon, 2004). To limit, at least in part, the impact of such unwanted variance components, factor scores can be used as an alternative to observed scores (Tabachnick & Fidell, 2012). In computing factor scores, observed variables are not all treated the same; instead, they are weighted by a coefficient that is proportional to the factor loading obtained in the factor solution. We must acknowledge, however, that this practice may introduce dependency from the particular sample on which these scaling coefficients were developed. Consistent with this approach to scale construction, factor score determinacy coefficients can be used (as an alternative to alpha) for evaluating the internal consistency of the factor solution. Factor score determinacy represents the correlation between the estimated and true factor scores; thus, it describes how well the factor is measured (Muthén & Muthén, 1998-2012). The larger the coefficient (e.g., ≥ .70 up to 1; Tabachnick & Fidell, 2007), the better the factor is defined by the observed variables.

Acknowledgments

The authors acknowledge this work was funded by the National Heart, Lung & Blood Institute (RO1 HL084394), by the Philadelphia Veterans Affairs Medical Center, VISN 4 Mental Illness Research, Education, and Clinical Center (MIREC), by the American Heart Association (11BGIA7840062), and by the U.S. Office of Research on Women's Health and National Institute of Child Health and Human Development (K12 HD043488-08). The content is solely the responsibility of the authors and does not necessarily represent the official views of the American Heart Association, Office of Research on Women's Health, or the National Institutes of Health.

The authors also gratefully acknowledge Sam Green for having applied his SAS macro for computing nonlinear structural equation model (SEM) reliability coefficients to their data.

Footnotes

The authors have no conflicts of interest to report.

Contributor Information

Claudio Barbaranelli, Department of Psychology Sapienza University of Rome, Italy.

Christopher S. Lee, Schools of Nursing and Medicine, Oregon Health & Science University, Portland, OR.

Ercole Vellone, Department of Biomedicine and Prevention Tor Vergata University, Rome, Italy.

Barbara Riegel, School of Nursing University of Pennsylvania, Philadelphia, PA.

References

  1. Barbaranelli C, Lee C, Vellone E, Riegel B. Dimensionality and reliability of the Self-Care of Heart Failure Index Scales: Further evidence from confirmatory factor analysis. Research in Nursing & Health. 2014;37:524–537. doi: 10.1002/nur.21623. doi:10.1002/nur.21623. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bentler PM. EQS 6 structural equations program manual. Multivariate Software, Inc.; Encino, CA: 2006. http://www.econ.upf.edu/~satorra/CourseSEMVienna2010/EQSManual.pdf. [Google Scholar]
  3. Bentler PM. Alpha, dimension-free, and model-based internal consistency reliability. Psychometrika. 2009;74:137–143. doi: 10.1007/s11336-008-9100-1. doi:10.1007/s11336-008-9100-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Camilli G, Wang M-M, Fesq J. The effects of dimensionality on equating the law school admission test. Journal of Educational Measurement. 1995;32:79–96. doi:10.1111/j.1745-3984.1995.tb00457.x. [Google Scholar]
  5. Cené CW, Haymore LB, Dolan-Soto D, Lin F-C, Pignone M, Dewalt DA, Corbie-Smith G. Self-care confidence mediates the relationship between perceived social support and self-care maintenance in adults with heart failure. Journal of Cardiac Failure. 2013;19:202–210. doi: 10.1016/j.cardfail.2013.01.009. doi:10.1016/j.cardfail.2013.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. DeShon RP. Measures are not invariant across groups with error variance homogeneity. Psychology Science. 2004;46:137–149. http://www.pabst-publishers.de/psychology-science/1-2004/ps_1_2004_137-149.pdf. [Google Scholar]
  7. Flora DB, Curran PJ. An empirical evaluation of alternative methods of estimation for confirmatory factor analysis with ordinal data. Psychological Methods. 2004;9:466–491. doi: 10.1037/1082-989X.9.4.466. doi:10.1037/1082-989X.9.4.466. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Fornell C, Larcker DF. Evaluating structural equation models with unobservable variable and measurement error. Journal of Marketing Research. 1981;18:39–50. [Google Scholar]
  9. Green SB, Yang Y. Reliability of summed item scores using structural equation modeling: An alternative to coefficient alpha. Psychometrika. 2009;74:155–167. doi:10.1007/S11336-008-9099-3. [Google Scholar]
  10. Kato N, Kinugawa K, Nakayama E, Tsuji T, Kumagai Y, Miura C, Komuro I. Psychometric testing of the Japanese version of the Self-Care of Heart Failure Index [Abstract #131]. Journal of Cardiac Failure. 2013;19:S46. doi:10.1016/j.cardfail.2013.06.152. [Google Scholar]
  11. Lee CS, Moser DK, Lennie TA, Tkacs NC, Margulies KB, Riegel B. Biomarkers of myocardial dtress and systemic inflammation in patients who engage in heart failure self-care management. Journal of Cardiovascular Nursing. 2011;26:321–328. doi: 10.1097/JCN.0b013e31820344be. doi:10.1097/JCN.0b013e31820344be. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lee CS, Suwanno J, Riegel B. The relationship between self-care and health status domains in Thai patients with heart failure. European Journal of Cardiovascular Nursing. 2009;8:259–266. doi: 10.1016/j.ejcnurse.2009.04.002. doi:10.1016/j.ejcnurse.2009.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. McDonald RP. Test theory: A unified treatment. Erlbaum; Mahwah, NJ: 1999. [Google Scholar]
  14. Muthén B. A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators. Psychometrika. 1984;49:115–132. doi:10.1007/BF02294210. [Google Scholar]
  15. Muthén LK, Muthén BO. Mplus user's guide. 7th ed. Muthén & Muthén; Los Angeles, CA: 1998-2012. https://www.statmodel.com/download/usersguide/Mplus%20Users%20Guide%20v6.pdf. [Google Scholar]
  16. Nunnally JC, Bernstein IH. Psychometric theory. 3rd ed. McGraw Hill; New York, NY: 1994. [Google Scholar]
  17. Raykov T. Scale reliability, Cronbach's coefficient alpha, and violations of essential tau-equivalence for fixed congeneric components. Multivariate Behavioral Research. 1997;32:329–353. doi: 10.1207/s15327906mbr3204_2. doi:10.1207/s15327906mbr3204_2. [DOI] [PubMed] [Google Scholar]
  18. Raykov T. Scale construction and development using structural equation modeling. In: Hoyle RH, editor. Handbook of structural equation modeling. The Guilford Press; New York, NY: 2012. pp. 472–492. [Google Scholar]
  19. Raykov T, Marcoulides GA. Introduction to psychometric theory. Routledge; New York, NY: 2011. [Google Scholar]
  20. Revelle W, Zinbarg RE. Coefficients alpha, beta, omega, and the GLB: Comments on Sijtsma. Psychometrika. 2009;74:145–154. doi:10.1007/s11336-008-9102-z. [Google Scholar]
  21. Riegel B, Carlson B, Moser DK, Sebern M, Hicks FD, Roland V. Psychometric testing of the Self-Care of Heart Failure Index. Journal of Cardiac Failure. 2004;10:350–360. doi: 10.1016/j.cardfail.2003.12.001. doi:10.1016/j.cardfail.2003.12.001. [DOI] [PubMed] [Google Scholar]
  22. Riegel B, Dickson VV. A situation-specific theory of heart failure self-care. Journal of Cardiovascular Nursing. 2008;23:190–196. doi: 10.1097/01.JCN.0000305091.35259.85. doi:10.1097/01.JCN.0000305091.35259.85. [DOI] [PubMed] [Google Scholar]
  23. Riegel B, Lee CS, Dickson VV, Carlson B. An update on the Self-Care of Heart Failure Index. Journal of Cardiovascular Nursing. 2009;24:485–497. doi: 10.1097/JCN.0b013e3181b4baa0. doi:10.1097/JCN.0b013e3181b4baa0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Schmitt N. Uses and abuses of coefficient alpha. Psychological Assessment. 1996;8:350–353. doi:10.1037/1040-3590.8.4.350. [Google Scholar]
  25. Sijtsma K. On the use, the misuse, and the very limited usefulness of Cronbach's alpha. Psychometrika. 2009;74:107–120. doi: 10.1007/s11336-008-9101-0. doi:10.1007/s11336-008-9101-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Sirotnik K. An analysis of variance framework for matrix sampling. Educational and Psychological Measurement. 1970;30:891–908. doi:10.1177/001316447003000410. [Google Scholar]
  27. Tabachnick BG, Fidell LS. Using multivariate statistics. 5th ed. HarperCollins; New York, NY: 2007. [Google Scholar]
  28. Tabachnick BG, Fidell LS. Using multivariate statistics. 6th ed. Allyn & Bacon; Boston, MA: 2012. [Google Scholar]
  29. Vellone E, D'Agostino F, Buck HG, Fida R, Spatola CF, Petruzzo A, Riegel B. The key role of caregiver confidence in the caregiver's contribution to self-care in adults with heart failure. European Journal of Cardiovascular Nursing. 2014 doi: 10.1177/1474515114547649. doi:10.1177/1474515114547649. [DOI] [PubMed] [Google Scholar]
  30. Vellone E, Riegel B, Cocchieri A, Barbaranelli C, D'Agostino F, Glaser D, Alvaro R. Validity and reliability of the caregiver contribution to Self-Care of Heart Failure Index. Journal of Cardiovascular Nursing. 2013;28:245–255. doi: 10.1097/JCN.0b013e318256385e. doi:10.1097/JCN.0b013e318256385e. [DOI] [PubMed] [Google Scholar]
  31. Yu DSF, Lee DTF, Thompson DR, Jaarsma T, Woo J, Leung EMF. Psychometric properties of the Chinese version of the European Heart Failure Self-Care Behaviour Scale. International Journal of Nursing Studies. 2011;48:458–467. doi: 10.1016/j.ijnurstu.2010.08.011. doi:10.1016/j.ijnurstu.2010.08.011. [DOI] [PubMed] [Google Scholar]

RESOURCES