Functional consequences of age-related morphologic changes to pyramidal neurons of the rhesus monkey prefrontal cortex

Abstract

Layer 3 (L3) pyramidal neurons in the lateral prefrontal cortex (LPFC) of rhesus monkeys exhibit dendritic regression, spine loss and increased action potential (AP) firing rates during normal aging. The relationship between these structural and functional alterations, if any, is unknown. To address this issue, morphological and electrophysiological properties of L3 LPFC pyramidal neurons from young and aged rhesus monkeys were characterized using in vitro whole-cell patch-clamp recordings and high-resolution digital reconstruction of neurons. Consistent with our previous studies, aged neurons exhibited significantly reduced dendritic arbor length and spine density, as well as increased input resistance and firing rates. Computational models using the digital reconstructions with Hodgkin-Huxley and AMPA channels allowed us to assess relationships between demonstrated age-related changes and to predict physiological changes that have not yet been tested empirically. For example, the models predict that in both backpropagating APs and excitatory postsynaptic currents (EPSCs), attenuation is lower in aged versus young neurons. Importantly, when identical densities of passive parameters and voltage- and calcium-gated conductances were used in young and aged model neurons, neither input resistance nor firing rates differed between the two age groups. Tuning passive parameters for each model predicted significantly higher membrane resistance (R_m) in aged versus young neurons. This R_m increase alone did not account for increased firing rates in aged models, but coupling these R_m values with subtle differences in morphology and membrane capacitance did. The predicted differences in passive parameters (or parameters with similar effects) are mathematically plausible, but must be tested empirically.

1 Introduction

Normal aging in primates is often accompanied by significant declines in executive system functions mediated primarily by the prefrontal cortex (PFC) (Fristoe et al. 1997; Gallagher and Rapp 1997; Herndon et al. 1997; Moore et al. 2003). There is no widespread death of PFC neurons in normal aging, but individual neurons undergo electrophysiological and morphological changes that are associated with cognitive decline (Peters 2002; Duan et al. 2003; Chang et al. 2005; Hara et al. 2012); review: (Hof and Morrison 2004; Dickstein et al. 2007; Luebke et al. 2010; Dickstein et al. 2013; Hara et al. 2012; Morrison and Baxter 2012)). Layer 3 (L3) pyramidal cells in in vitro slices prepared from the lateral PFC (LPFC) of aged rhesus monkeys exhibit increased action potential (AP) firing rates in response to depolarizing current steps (Chang et al. 2005). Because sustained firing rates of LPFC neurons represent temporally precise encoding of information during memory tasks (Funahashi et al. 1989; Funahashi et al. 1990; Goldman-Rakic 1995; Constantinidis et al. 2001), age-related changes in firing rate may be associated with reduced cognitive performance. Indeed, a quadratic relationship has been demonstrated to exist between firing rates and cognitive performance of aged monkeys, such that monkeys with the lowest and highest firing rates exhibit reduced performance compared to those with intermediate firing rates (Chang et al. 2005). The mechanisms of age-related increased firing rates remain to be determined. They may plausibly be due to alterations in synaptic inputs, passive membrane properties, and/or active dendritic conductances. Alterations in morphological structure may also contribute to increasing firing rates, as these properties constrain synaptic integration and neural firing patterns (Mainen and Sejnowski 1996; Euler and Denk 2001; Vetter et al. 2001; Krichmar et al. 2002).

Previous work has demonstrated reductions in apical dendritic length and in the number and density of dendritic spines of L3 pyramidal neurons that project from the superior temporal cortex to the LPFC of the aged rhesus monkey (Page et al. 2002; Duan et al. 2003; Kabaso et al. 2009). Age-related reductions in the length and diameter of manually traced dendrites of ‘locally projecting’ L3 neurons within the LPFC was minimal, but spine density was reduced significantly (Kabaso et al. 2009). Electrotonic analyses from passive models of these neurons showed that these morphologic changes accounted for a significant reduction in voltage attenuation from the soma out towards apical dendrites in aged versus young neurons. Kabaso et al. (2009) predicted that these changes could lead to increased excitability of aged neurons, but no empirical electrophysiological data were available to constrain models and test that hypothesis.

In this study we set out to: 1) obtain high-resolution 3D reconstructions, including spines (Rodriguez et al. 2008), of electrophysiologically characterized pyramidal neurons; 2) use these empirical data to directly test the hypothesis that morphological changes are associated with the physiological changes observed in aged LPFC neurons; and 3) apply computational modeling to explore parameters that are difficult to assess empirically. We recently used a similar combined experimental and modeling approach to show that dendritic morphology can account largely for differences in passive but not active properties between neurons from the LPFC and the primary visual cortex (V1) (Amatrudo et al. 2012). Our findings on the extent to which changes to dendritic morphology may account for increased firing rates of aged versus young neurons have broad implications for understanding how dendritic signal integration is altered with aging in neocortical pyramidal cells.

2 Materials and Methods

2.1 Experimental Materials and Methods

2.1.1 Experimental subjects

Coronal slices of the LPFC (area 46) were collected from 4 young (8.0 ± 2.8 years old; 1 female, 3 male) and 2 aged (22.4 ± 3.4 years old; 1 female, 1 male) rhesus monkeys (Macaca mulatta) that were obtained from the Yerkes National Primate Research Center at Emory University and perfused as a part of an ongoing integrated study of normal aging. The monkeys were maintained at the Yerkes National Primate Research Center and subsequently at the Boston University Laboratory Animal Science Center (LASC) in strict accordance with animal care guidelines as outlined in the NIH Guide for the Care and Use of Laboratory Animals and the U.S. Public Health Service Policy on Humane Care and Use of Laboratory Animals. Both the Boston University LASC and the Yerkes Center are fully accredited by the Association for Assessment and Accreditation of Laboratory Animal Care. All procedures were approved by the Institutional Animal Care and Use Committees of both institutions.

2.1.2 Preparation of slices

Slices were prepared from blocks of the LPFC obtained following perfusion with a Krebs-Henseleit buffer. Monkeys were tranquilized with ketamine (10 mg/ml) and then deeply anesthetized with sodium pentobarbital (to effect 15 mg/kg, i.v.). While under deep anesthesia, the monkeys underwent a thoracotomy and were sacrificed by exsanguination while perfused through the ascending aorta with 4 l of ice-cold Krebs-Henseleit buffer (concentrations, in mM: 6.4 Na₂HPO₄, 1.4 Na₂PO₄, 137 NaCl, 2.7 KCl, 5 glucose, 0.3 CaCl₂, 1 MgCl₂; pH 7.4, all chemicals from Sigma, St. Louis, MO). A craniotomy was performed and immediately after perfusion, the dura was opened, the brain was removed from the calvarium and an ~10 mm-thick block of the LPFC was removed. The LPFC block was then cut into 400 µm-thick coronal slices with a vibrating microtome in ice-cold oxygenated Ringer’s solution (concentrations, in mM: 26 NaHCO₃, 124 NaCl, 2 KCl, 3 KH₂PO₄, 10 glucose, 2.5 CaCl₂, 1.3 MgCl₂; pH 7.4, all chemicals from Sigma). The average time from the beginning of the perfusion of the monkey to obtaining a slice of the LPFC (10–15 min) did not differ between the two age groups. Slices were placed into oxygenated Ringers solution where they were equilibrated at room temperature for at least 1 h, after which a single slice was positioned under nylon mesh in a submersion type slice recording chamber (Harvard Apparatus, Holliston, MA) on the stage of a Nikon E600 infrared-differential interference contrast (IR-DIC) microscope (MicroVideo Instruments, Avon, MA). In the recording chamber, slices were superfused at a rate of 2–2.5 ml/min with room temperature, oxygenated Ringer’s solution.

2.1.3 Whole-cell patch-clamp recordings

Whole-cell patch-clamp recordings were performed on visually identified L3 pyramidal neurons located in the lower bank of the principal sulcus and at least 200 µm deep to layer 1. Standard, tight-seal, whole-cell patch clamp recordings (Edwards et al. 1989; Luebke et al. 2004; Chang et al. 2005; Chang and Luebke 2007) were made with patch electrodes pulled from nonheparinized microhematocrit capillary tubes (Fisher, Pittsburgh, PA) on a Flaming and Brown horizontal micropipette puller (Model P-87, Sutter Instruments, Novato, CA). Recording pipettes were filled with an internal solution of the following composition (in mM): 100 potassium aspartate, 15 KCl, 3 MgCl₂, 5 EGTA, 10 Na-HEPES and 1% biocytin (pH 7.4, all chemicals from Sigma-Aldritch, St. Louis, MO). With this internal solution, recording electrodes had resistances of 3–6 MΩ in the external (Ringer’s) solution. Voltage measures were corrected for a liquid junction potential of ~7 mV. Experiments were performed in the current clamp mode with List EPC-9 and EPC-10 patch clamp amplifiers and with Patchmaster and Pulse acquisition software from HEKA Elektronik (Lambrecht, Germany). Recordings were low-pass filtered at 10 kHz and access resistance was monitored throughout each experiment.

2.1.4 Characterization of passive membrane and AP firing properties

Resting membrane potential was determined by recording the membrane voltage in the absence of current input. To assess passive membrane properties, a series of 200-ms hyperpolarizing and depolarizing current steps (10 steps, ranging from −160 to +20 pA) were applied to the cell from a baseline potential of −70 mV. A series of 2000-ms steps (7 steps, ranging from +30 to +330 pA), also from a −70 mV holding potential, were then applied to examine repetitive AP firing properties. Membrane voltage responses to the 200-ms current steps were measured at steady state, approximately 180 ms after test pulse onset where the voltage response was linear, and plotted on a voltage-current (V-I) graph. Input resistance for each neuron was determined by the slope of the best-fit line through the linear portion of the graph (Fig. 1a). Frequency-current (f–I) plots were generated by plotting the frequency of APs elicited by a given depolarizing current step vs. the amplitude of the current step. For single APs evoked by just suprathreshold current steps, the threshold voltage (at maximal dV/dt), the amplitude (peak membrane potential relative to resting potential), duration at half amplitude, rise time (the time from the start of the AP to the peak membrane potential) and decay time (the time from the peak membrane potential to a return to steady state) were recorded. All electrophysiological data were initially analyzed using the Pulse-Fit analysis program from HEKA Elektronik, and further analyzed with Igor Pro 6.2 software (WaveMetrics, Lake Oswego, OR).

Figure 1. Input resistance and AP firing rates are significantly greater in the aged neurons.

a) Top: voltage responses to 200 ms injected subthreshold current steps from representative young and old neurons. Scale bar: 10 mV and 40 ms. Bottom: voltage response vs. current step plots for the data shown above. Input resistance is calculated as the slope of the linear portion of the IV-relation, illustrated by the solid region of the best-fit lines shown. b) Trains of APs evoked by 2-s depolarizing current steps for representative young and aged neurons. Scale bar: 25 mV and 650 ms. Current steps were applied from a holding potential of −70 mV, shown as arrows in (a) and (b). c) Frequency-current plot demonstrating significantly increased mean frequency of AP firing evoked at each depolarizing current step for aged neurons (p < 0.05). d) AP firing rate in response to 2-s +230 pA current step versus input resistance of young and aged neurons. These responses were not assessed in one of the aged neurons, so only five aged neurons are shown in the graph.

2.1.5 Processing and confocal scanning of filled neurons

Following recordings, slices were transferred to a 4% paraformaldehyde/0.1 M phosphate-buffered saline (PBS) solution, pH 7.4, and stored at 4°C overnight. The next day, slices were processed as follows: PBS, 3 rinses of 10 min each; 0.1% Triton X-100 in PBS 2 h at room temperature; and streptavidin-Alexa 488 (1:500, Vector Laboratories, Burlingame, CA) at 4°C for 48 h. Following processing, slices were rinsed in PBS, mounted in Prolong Gold (InVitrogen, Eugene, OR) and cover-slipped. The fluorescence emitted by Alexa 488 under Argon laser excitation was detected with a Zeiss 510 confocal laser scanning microscope equipped with a Plan-Apochromat 40×/1.3 NA, 210 µm working-distance oil objective and a 505 nm long-pass filter. Approximately 10 stacks per neuron were acquired at very high resolution.

2.1.6 Preprocessing of image stacks

Each image stack was deconvolved to reduce optical smear in the z-plane due to the microscope’s point spread function, using AutoDeblur X1.4.1 software (Media Cybernetics, Bethesda, MD). Alignment of the deconvolved stacks and integration into a single 8-bit grayscale volumetric dataset was performed using custom software (Coskren, unpublished code). Alignment was performed manually, informed by orthographic projections of the maximum pixel value along the x, y, or z axes, and partial skeletonizations of individual stacks (see description of skeletonization below). Integrated datasets could be as large as 13 GB each. Image subsampling, a technique which uses weighted averaging to combine adjacent voxels to create a lower-resolution image, reduced these image sizes by a factor of four. Subsampling was performed by TIFF Stack Sub-Sampler software, available at http://research.mssm.edu/cnic/tools-tss.html.

ImageJ software (Schneider et al. 2012) was used to record the distance to the base of the soma from the pial surface for each neuron. Distance from the pial surface was compared using a two-tailed Student’s t test to ensure there was no significant difference between young and aged neurons (young, 463 ± 101 µm; aged, 425 ± 108 µm; p = 0.51).

2.1.7 Digital reconstruction and morphometric analyses

Reconstruction of a morphologically detailed model neuron (skeletonization) from each neuron’s subsampled dataset was performed using NeuronStudio software (Wearne et al. 2005; Rodriguez et al. 2008; Rodriguez et al. 2009); available at: http://www.mssm.edu/cnic). Reconstructed neuron models were stored in standard neuroanatomical format (.SWC format; (Cannon et al. 1998)) as a series of tapering cylindrical compartments with coordinates (x, y, z, and diameter) at each node. Each neuron was inspected and minor corrections made using the NeuronStudio interface. Corrections included the connection of dendritic branches that NeuronStudio left distinct because of gaps in the fluorescent trace of the dendrite due to occlusion, inconsistent binding of fluorophore, and occasional minor jumps at the boundaries of substacks.

NeuronStudio was used to detect spine locations around the reconstructed dendrites using a Rayburst-based algorithm (Rodriguez et al. 2006; Rodriguez et al. 2008). Custom Python scripts were written to count spines and compute spine density (number of spines per µm of dendritic length) from the NeuronStudio output. Spine count and density were computed for the apical and basal dendritic trees and for the neuron as a whole. For each cell, spines were also manually counted along samples of dendritic arbor to verify NeuronStudio's output; the difference between automated and manual counts ranged from 0–10% and did not differ between young and aged cells. Because spine size could not be reliably measured at the resolution of the subsampled dataset, the same representative spine geometries were used for both young and aged neuron models. These geometries were computed as averaged dimensions from a dataset of 233 apical and 190 basal spines from a young neuron, imaged and computed for a previous study (Kabaso et al. 2009). The apical spine dimensions employed were: head length, 0.71 ± 0.01 µm; head diameter, 0.47 ± 0.01 µm; neck length, 0.44 ± 0.02 µm; neck diameter, 0.19 ± 0.01 µm, from which was computed a surface area of 1.31 µm² and a volume of 0.14 µm³. The basal spine dimensions employed were: head length, 0.82 ± 0.02 µm; head diameter, 0.56 ± 0.01 µm; neck length, 0.54 ± 0.02 µm; neck diameter, 0.16 ± 0.01 µm, from which was computed a surface area of 1.71 µm² and a volume of 0.21 µm³.

Soma surface area was estimated with custom manual image tracing software written in Objective-C++. The surface area and volume of the axon initial segment was assessed manually using NeuronStudio, measured from the proximal 30 µm of axon. The following morphological measures were quantified for each neuron using custom-written scripts in Python and Hoc: surface area and volume of the apical and basal dendritic trees; number and mean length of unbranched dendritic sections; and spine count and density. Apical and basal dendritic intersection, total cross-sectional area and mean branch diameter distributions were determined by 3D Sholl analyses using regularly spaced concentric spheres centered on the soma at 20-µm intervals. Distance from the soma was defined for this purpose as running along the dendrite; that is, the Sholl analysis was performed in dendrogram space. The spatial distributions of spines (number and density along apical and basal dendritic trees) were assessed with 3D Sholl analyses using regularly spaced concentric spheres centered on the soma at 20-µm intervals.

Custom Python scripts were written to convert the SWC files to the Hoc language used by the neuron simulator NEURON (Carnevale and Hines 2006). Each neuron was stored as one model each of the apical tree, the basal tree, and the complete neuron. In either case the apical or basal tree was discarded if the dendrites and spines were insufficiently visible over the entire region of interest. These reconstructions are available at NeuroMorpho.org (http://neuromorpho.org/neuroMorpho).

2.2 Mathematical model

All simulations were performed using the NEURON compartment modeling simulator (Carnevale and Hines 2006). Upon publication the models presented here will be available at ModelDB (http://senselab.med.yale.edu/ModelDB; (Hines et al. 2004)). Compartment size was chosen to be less than 1/100 of the electrotonic length constant at 100 Hz, rounded down to produce an odd number of compartments. The time step was reduced incrementally until further reduction had a negligible effect on the simulations, down to 0.05 ms. To evaluate whether age-related morphologic differences in dendritic morphology contribute to differences in physiological function of these neurons, the same soma (length and diameter 8.28 µm) and phenomenological axon were used for all models (Mainen et al. 1995; Mainen and Sejnowski 1996). Initially, the passive cable properties of model neurons were taken from published measurements of typical neocortical pyramidal neurons: axial resistivity R_a = 150 Ω·cm (Stuart and Spruston 1998; Trevelyan and Jack 2002), and C_m = 1 µF/cm² (Stratford et al. 1989). Membrane resistivity R_m = 26.316 kΩ·cm² was determined by matching the simulated input resistance and resting potential of one model neuron to its corresponding empirical values (Amatrudo et al. 2012), then applied to all neurons in this study. These passive parameters were initially held constant for all model neurons. Then, to quantify the effect of passive parameters and morphology together, values of R_m and C_m were estimated manually for each model neuron, so that the simulated input resistance and membrane time constant (estimated as τ_m = R_m·C_m) were both within 10% of the empirically measured values. As in Amatrudo et al. (2012), axonal parameters were C_m = 0.04 µF/cm² in the myelin sheath and R_m = 50 kΩ·cm² in the nodes of Ranvier; ḡ_NaF and ḡ_KDR in the axon hillock, initial segment, and nodes of Ranvier were scaled relative to their soma values by 1000 and 16.67 respectively.

2.2.1 Hodgkin-Huxley active conductance model

Two types of active conductance models were used in this study. The first was identical to our recent L3 pyramidal neuron model (Mainen and Sejnowski 1996; Vetter et al. 2001; Amatrudo et al. 2012) available on ModelDB (Accession Number 144553), including a passive leak conductance with Hodgkin-Huxley fast sodium (Na⁺) and delayed-rectifier potassium (K⁺) currents (with maximal conductances ḡ_NaF and ḡ_KDR respectively), distributed uniformly in the soma and dendrites. Channel kinetics parameters and proportional scaling of axonal parameters were identical to those in (Amatrudo et al. 2012). To characterize firing patterns in each of the twelve young and aged model neurons, parameters ḡ_NaF and ḡ_KDR in each model were sampled systematically at a total of 1,521 parameter combinations (i.e. points in parameter space defined by ḡ_NaF and ḡ_KDR), varying from 10 to 200 mS/cm² in 5 mS/cm² increments (Amatrudo et al. 2012). In the empirical protocols, a bias current was applied to hold the somatic membrane potential of each neuron at −70 mV, on top of which were applied 2-s current steps so that the total injected current varied from +30 to +330 pA. To simulate this procedure, each model cell was first voltage clamped to −70 mV at the soma for 80 ms, a time period that was sufficient for all models to reach a steady state voltage. At the end of the 80 ms voltage clamp the current I_hold (pA) required to maintain the holding potential was recorded. The voltage clamp was then replaced with a current clamp injecting a constant I_hold pA, on top of which 2-s current steps were applied totaling +230 and +330 pA (modified from (Carnevale 2010)). This procedure was followed for each model neuron, for each parameter combination tested. Simulated firing rates in response to the +330 pA injection at each of the 1,521 points in parameter space were then compared to the corresponding firing rates recorded empirically (ranging from 3.5 to 15 Hz for young neurons, and from 11.5 to 29.5 Hz for aged neurons). It was desirable to use the same fitting criterion for all model neurons, but generally it was easier for the Hodgkin-Huxley model to fit the higher firing rates of the aged neurons than the lower rates of the young neurons. Thus for each model aged neuron, each of the 1,521 points in parameter space was classified as fitting the corresponding empirical data if its simulated firing rate at +330 pA was within 50% of the empirically measured rate. Applying a similar criterion requiring no more than 50% deviation from the corresponding empirical firing rates yielded virtually no good fits for the young model neurons. Therefore the criterion for a parameter space point to fit the young data was relaxed, requiring only that its simulated firing rate in response to a +330 pA injection was nonzero but less than 250% of its empirically measured rate.

2.2.2 Expanded active conductance model

The second type of active conductance model used here was chosen for its wide range of voltage- and Ca²⁺-dependent conductances and its ability to display spike frequency adaptation. Ten active conductances and their channel kinetics were taken directly from the neocortical pyramidal neuron model of (Traub et al. 2003) available on ModelDB (Accession Number 20756): fast Na⁺ (NaF), persistent Na⁺ (NaP), delayed rectifier K⁺ (KDR), transient A-type K⁺ (KA), slowly activating and inactivating K⁺ (K2), muscarinic receptor-suppressed K⁺ (KM), fast voltage-and Ca²⁺-dependent K⁺ (KC), slow Ca²⁺-dependent K⁺ (KAHP), high threshold L-type noninactivating Ca²⁺ (CaL), and hyperpolarization-activated cyclic nucleotide-gated channels (H). To match the slow afterhyperpolarization observed empirically in these neurons (Luebke and Amatrudo 2012), a phenomenological very slow Ca²⁺-dependent K⁺ conductance (SKAHP) was added. Its kinetics were identical to the KAHP conductance already included in the model, except its time constant was an order of magnitude slower to fit the empirical data better. Intracellular Ca²⁺ dynamics were modeled by a phenomenological first-order equation dχ/dt = −B · I_Ca − χ/τ_Ca, where χ is the intracellular Ca²⁺ concentration in arbitrary units and I_Ca the Ca²⁺ current in a given compartment (Traub et al. 2003). The parameter B = 5000 was constant throughout the soma and dendrites, while τ_Ca equaled 20 ms in the dendrites and 100 ms in the soma. The firing rates of the Traub et al. (2003) model were closer to the in vitro firing rates reported here for aged neurons rather than young ones. Therefore, the physiology and morphology of one representative aged neuron were chosen for model fitting via manual parameter tuning. Passive parameters were C_m = 0.83 µF/cm², R_a = 150 Ω·cm, R_m = 17.5 kΩ·cm² (R_m = 1 kΩ·cm² in the axon), and E_L = −80 mV. Maximal conductance parameters in the soma were tuned manually to fit the firing patterns of the empirical data, in response to +230 pA and +330 pA somatic current injections, with maximal conductances in the dendrites and axon adjusted proportionally. The maximal conductances ḡ_NaF and ḡ_KDR in the dendrites decreased linearly with distance from the soma (Migliore and Shepherd 2002), to a minimum of 20% of their somatic values. All other conductances were constant in the soma and dendrites. Maximal conductance ḡ_NaF was 2.13 times higher in the axon than in the soma, and ḡ_KDR was 3.2 times higher in the axon, following Traub et al. (2003). The maximal conductances in the soma, measured in mS/cm², were ḡ_NaF= 110, ḡ_NaP = 0.003, ḡ_KDR = 80, ḡ_KA = 2, ḡ_K2 = 0.1, ḡ_KM = 5.1, ḡ_KC = 250, ḡ_KAHP = 0.1, ḡ_SKAHP = 0.4, ḡ_CaL = 0.054, ḡ_H = 0.1. These parameter values are hereafter named the ‘Baseline parameters’.

2.2.3 Including dendritic spines

In the models, the surface area due to spines on each dendritic segment was accounted for by adjusting the segment’s length and diameter in such a way as to increase its surface area but preserve its electrotonic length, following the commonly used algorithm of (Stratford et al. 1989). Spines were individually counted for each dendritic segment based on the 3D spine location data. Spine surface areas were computed using the representative apical and basal spine dimensions measured from the typical imaged cell described above. Explicit spines were then removed from the model. In Kabaso et al. (2009) we previously verified that this approach to modeling spine surface area does not alter the electrotonic measures used in this study, but did not test its effect on input resistance. Simulations excluding the spine surface areas were also performed, in order to determine the effect of the spines’ cumulative surface area on the neuron’s electrotonic properties.

2.2.4 Measures of dendritic signal integration

The log attenuations of voltage for transfer of signals propagating outward from, or inward toward, the soma have been established as a generalization of the classical electrotonic distance measure (Brown et al. 1992; Tsai et al. 1994; Carnevale et al. 1997). These dimensionless measures, abbreviated L_out and L_in, were calculated for each of the neurons in the present study and then averaged over all paths throughout the dendritic arbor to obtain mean outward and inward attenuation lengths L̅_out and L̅_in (Kabaso et al. 2009). As in our previous work (Kabaso et al. 2009; Amatrudo et al. 2012), L̅_out and L̅_in were calculated at input frequencies ranging from 0 to 500 Hz. Electrotonic analyses were performed with the same passive membrane parameters for all neurons, excluding all active voltage-gated channels. Including active membrane channels had a negligible effect on the results (not shown).

As a functional analog of the L̅_out measure, the efficacy of AP backpropagation was assessed by the ‘normalized backpropagation amplitude’ (hereafter ‘NBPamp’, measured in mV), introduced as NBParea in Kabaso et al. (2009). To compute NBPamp, an empirically measured AP was used as a voltage clamp command to the soma of the neuron model and the voltage in all other compartments was recorded. For each constant value of dendritic arclength s, peak voltage was averaged over all dendritic compartments at that arclength distance from the soma. NBPamp is the mean value of that average over all arclengths s. The AP was recorded in vitro at the soma of a L3 LPFC pyramidal neuron obtained as part of this study. Each NBPamp calculation was performed twice, with either the apical or basal arbors deleted. This prevented any morphologic features of the deleted arbors from affecting the NBPamp calculation of the remaining arbors.

To estimate how excitatory postsynaptic currents (EPSCs) are filtered by the dendrites of young and aged neurons, simulations were conducted to investigate spontaneous EPSCs following an empirical protocol introduced elsewhere (sEPSCs; (Luebke et al. 2004; Amatrudo et al. 2012)). Briefly, the model included excitatory synaptic currents due to α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptor-gated channels, modeled as a sum of two exponentials (ḡ_AMPA = 0.54 nS, rise time 0.15 ms, decay time 4.0 ms, reversal potential 0 mV). No other excitatory or inhibitory synapses were included. Postsynaptic currents were modeled as described for the LPFC neuron in Amatrudo et al. (2012), with a representative 10% of the number of detected spines inserted uniformly across the dendritic arbors of each of the young and aged model neurons. The soma voltage was clamped to −80 mV, then the somatic current in response to activation of each individual synapse (every 200 ms) was recorded.

2.3 Statistical analyses

Electrophysiological and morphological data were analyzed with SPSS statistics software (IBM, Armonk, NY). Statistical comparisons between young and aged neurons of morphometric features with distance from the soma, inward and outward dendritic attenuation at varying input frequencies, and firing rate versus varying current injection levels were performed using a mixed-design analysis of variance (ANOVA). Assumptions that must be met to use a mixed ANOVA include (1) samples drawn from a normal distribution; (2) homogeneity of variance; (3) sphericity of the covariance matrix. Validity of these assumptions were evaluated using Shapiro- Wilk’s, Levene’s, and Mauchly’s tests respectively (Girden 1992). When the assumption of sphericity was violated, the Greenhouse-Geisser correction was applied to the ANOVA results (Geisser and Greenhouse 1958). With only two between-subject factors for the ANOVA (young vs. aged), post hoc tests for significance at each repeated measure were not appropriate; Student’s t tests for independent samples were performed.

Remaining comparisons between young and aged neurons were performed using Student’s t test for independent samples; two-tailed tests were used, unless prior published data from our research group justified use of a one-tailed test. The Bonferroni correction was used to control the family-wise error rate during multiple comparisons. Statistical significance was set at α = 0.05. Data are presented as mean ± standard error of the mean (S.E.M) in the figures and text.

3 Results

3.1 Population of neurons examined

Neurons that met the following electrophysiological criteria were included in the dataset: a resting membrane potential of ≤ −55 mV, stable access resistance throughout the duration of the recording (≤ 10% change), the presence of an AP overshoot (> 0 mV) and the ability to fire APs repetitively during depolarizing current steps. Neurons were selected that met both these electrophysiological criteria and the morphological criteria of an intact soma, bright and complete filling of spiny dendrites without varicosities or cut branches within the proximal twothirds of the primary dendritic branches. The selected neurons were then imaged with a confocal laser scanning microscope. A total of 6 pyramidal neurons from the young monkeys and 6 pyramidal neurons from the aged monkeys met the electrophysiological and morphological criteria for inclusion in this study. An additional 1 young and 1 aged neuron met electrophysiological criteria and morphological criteria for the apical tree, but for these cells basal arbors were not included in analyses due to the presence of varicosities on the dendritic branches.

3.2 Physiology of young vs. aged neurons

Based on our data, there was no evidence of an age-related difference in either the resting membrane potential (young: −64.3 ± 1.1 mV versus aged: −63.0 ± 0.9 mV, p = 0.36) or the membrane time constant (young: 20.5 ± 4.4 ms versus aged: 12.6 ± 1.8 ms, p = 0.11). However, the mean input resistance was higher in aged neurons at 109 ± 6 MΩ compared to 79 ± 9 MΩ in young neurons (p = 0.02; Fig. 1a). There was little evidence of age-related changes in measurements of single APs either: they did not differ in aged compared to young neurons with regard to threshold (−39.6 ± 1.5 mV vs. −40.5 ± 1.4 mV respectively, p = 0.68), amplitude (85.0 ± 3.1 mV vs. 91.8 ± 3.2 mV respectively, p = 0.15) or duration (1.6 ± 0.1 ms vs. 1.9 ± 0.1 ms respectively, p = 0.06). The decay time of single APs was faster in aged versus young neurons however (2.3 ± 0.2 ms vs. 3.5 ± 0.2 mV, p = 0.004). Physiological data are summarized in Table 1. These findings are largely consistent with our previous study of physiological firing properties in 35 young and 62 aged neurons (Chang et al. 2005), in which very few of the passive and single AP properties differed between the age groups.

Table 1.

Summary statistics for physiological data.

	Young	Aged	p
Input Resistance (MΩ)	79 ±9	109 ±6	0.02
Resting Membrane Potential (mV)	−64.3 ±1.1	−63.0 ±0.9	0.36
Membrane Time Constant (ms)	20.5 ±4.4	12.6 ±1.8	0.11
AP threshold (mV)	−40.5 ±1.4	−39.6 ±1.5	0.68
AP amplitude (mV)	91.8 ±3.2	85.0 ±3.1	0.15
AP half-width (ms)	1.9 ±0.1	1.6 ±0.1	0.06
AP rise time (ms)	1.1 ±0.1	0.9 ±0.1	0.33
AP decay time (ms)	3.5 ±0.2	2.3 ±0.2	0.004
Firing Rate, +80 pA (Hz)	0 ±0	0.6 ±0.4	0.16
Firing Rate, +130 pA (Hz)	0.3 ±0.2	5.9 ±1.9	0.03
Firing Rate, +180 pA (Hz)	1.6 ±0.8	12.6 ±1.8	< 0.001
Firing Rate, +230 pA (Hz)	4.3 ±1.3	16.9 ±1.6	< 0.001
Firing Rate, +280 pA (Hz)	6.6 ±1.6	19.1 ±1.9	< 0.001
Firing Rate, +330 pA (Hz)	7.6 ±1.7	19.9 ±2.4	0.002

Trains of APs were evoked by application of 2-s depolarizing current steps of increasing amplitude. All of the neurons in this study displayed slowly adapting, regular spiking AP firing characteristics, exemplified by the representative neurons in Figure 1b. Aged neurons had a lower rheobase (~100 pA) than did young neurons (~150 pA). All young neurons and all but one or two aged neurons seemed to exhibit Type I excitability (Hodgkin 1948; Rinzel and Ermentrout 1998), meaning they fired at arbitrarily low frequencies in response to small current injections. The remaining aged neurons seemed to exhibit Type II excitability (unable to generate arbitrarily slow firing), although this is difficult to assess empirically (Skinner 2013). The number of APs generated by a depolarizing current step of a given amplitude was significantly greater in the neurons from aged monkeys than it was in those from young monkeys at each stimulus amplitude, as shown by the firing rate versus current (f–I) plot in Figure 1c. Before using the mixed design ANOVA, the normality, and homogeneity of variance, and sphericity of the data at each level of current injection were tested. The null hypotheses of these tests were not rejected for firing rates at current injections of 180 pA and above (Shapiro-Wilk and Levene’s tests, p > 0.05 for each). The null hypothesis of sphericity was rejected (Mauchly’s test, p < 0.001), so the Greenhouse-Geisser correction was used. The ANOVA revealed that firing rates were significantly higher in aged than young neurons (F_(1.71,18.78) = 9.07, p = 0.003). These differences between age groups were present at current injections of 130 pA and above (p = 0.03 for 130 pA; p ≤ 0.002 for 180 pA and above).

Table 2.

Regressions of firing rate vs. R_N, age group, and both

Injected Current	Parameters Included in Regression
	RN only		age group only		age group and RN
	r2	p-value	r2	p-value	r2	p-value (adding RN)
180 pA	0.696	< 0.001	0.703	< 0.001	0.889	0.002
230 pA	0.583	0.002	0.771	< 0.001	0.871	0.02
280 pA	0.498	0.01	0.697	< 0.001	0.697	0.10
330 pA	0.400	0.02	0.591	0.002	0.591	0.24

Input resistance was significantly correlated with empirical firing rates at current injections of 130 pA and above across all neurons as a whole (Fig. 1d). However, age group was a better predictor than input resistance of empirical firing rates. As shown in Table 2, a higher percentage of variance in firing rate (as represented by r²) is explained by age group alone than by input resistance alone. Regressions of firing rate versus both age group and input resistance explained more variance in firing rate than either age group or input resistance alone, indicating that input resistance contributes to, but does not fully account for, increased firing rates in aged neurons, as we have previously suggested (Chang et al. 2005; Luebke et al. 2010).

3.3 Morphology of young vs. aged neurons

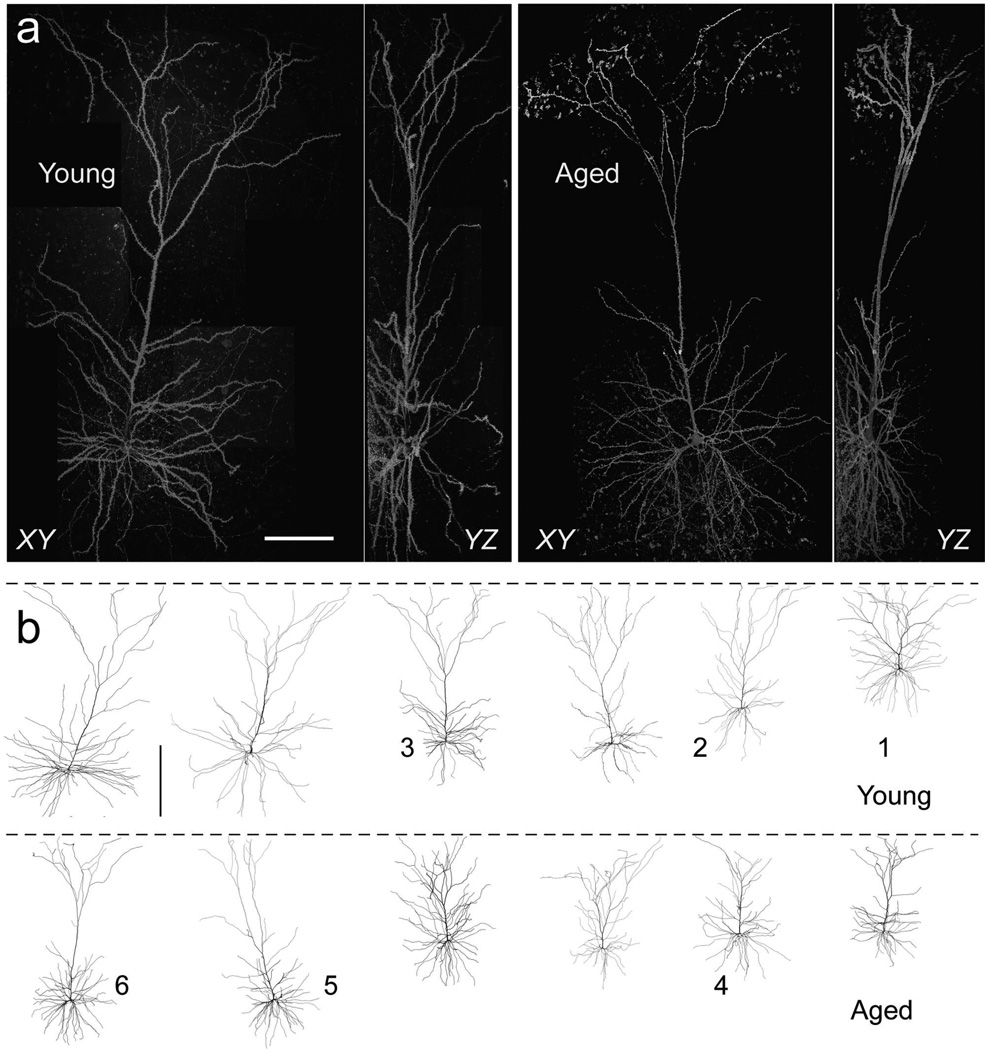
Figure 2a shows representative fully reconstructed dendrites and somata of young and aged L3 pyramidal neurons at high resolution, and Figure 2b shows 2D projections of the 3D reconstructed models for the 6 young and 6 aged pyramidal neurons analyzed in their entirety in this study. Summary statistics for 3D morphometric analyses of these neurons are provided in Table 3. The mean soma surface areas were not different in the aged compared to young neurons at 884 ± 120 and 800 ± 80 µm², respectively (p = 0.57). Similarly, neither the surface area nor the volume of the axon initial segment (assessed from the proximal 30 µm of axon in each neuron) differed in the two age groups (p = 0.68 and p = 0.81 respectively). Aged and young neurons were matched based on distance from the base of the soma to the pial surface in neurons from the young vs. aged monkeys (aged, 424 ± 41 µm; young, 463 ± 38 µm; p = 0.51); therefore, differences in dendritic trees were not due to differences in the depth within the cortex of the sampled neurons. The total apical dendritic length was significantly smaller in aged compared to young neurons at 3771 ± 459 µm vs. 5062 ± 425 (p = 0.046). The mean length of unbranched dendritic segments in the apical trees was also significantly lower in aged neurons relative to young (aged, 54.9 ± 4.0 µm; young, 71.6 ± 6.3 µm, p = 0.036). In the basal arbors, neither total dendritic length nor mean segment length differed in aged versus young neurons (p = 0.91 and p = 0.15, respectively.) The 3D Sholl analysis showed no significant differences between young and aged neurons for the number, area, or mean diameter of dendritic intersections within the Sholl spheres (mixed design one-tailed ANOVA with Greenhouse-Geisser correction: apical: p = 0.26, 0.28, 0.12, respectively; basal: p = 0.13, 0.32, 0.19, respectively).

Figure 2. Representative reconstructed L3 pyramidal neurons.

a) XY- and YZ- projections of tiled confocal image stacks of representative young and aged L3 pyramidal neurons. Scale bar, 100 µm. b) Reconstructed L3 pyramidal neurons from young and aged monkeys. Dashed line represents the pial surface. Modeling results for neurons labeled 1–6 are shown in Figure 6. Scale bar, 200 µm.

Table 3.

Summary statistics for morphometric data.

	Young	Aged	p
TOTAL ARBOR
Soma Surface Area (µm2)	880 ±80	884 ±120	0.57
Axon Initial Segment Surface Area (µm2)	71.9 ±4.3	74.9 ±6.0	0.68
Axon Initial Segment Volume (µm3)	14.3 ±1.7	15.0 ±2.5	0.81
Dendritic Surface Area (µm2)	20410 ±2421	20057 ±2650	0.92
Dendritic Volume (µm3)	4804 ±872	5141 ±915	0.80
Total Length (µm)	8777 ±549	7576 ±598	0.17
Number of Segments	130 ±10	147 ±16	0.38
Mean Segment Length (µm)	136 ±8	108 ±9	0.04
Spine Count	8169 ±1912	3703 ±459	0.07
Spine Volume (µm3)	1346 ±313	626 ±180	0.07
Spine Surface Area (µm2)	11954 ±2790	5499 ±696	0.07
Spine Density (#/µm)	1.81 ±0.37	0.96 ±0.08	0.07
Total Surface Area (Soma, Dendrites, Spines, µm2)	33160 ±5145	26440 ±3343	0.30
APICAL ARBOR
Surface Area (µm2)	11873 ±1381	10099 ±1469	0.40
Volume (µm3)	2941 ±477	2734 ± 506	0.77
Total Length (µm)	5062 ±394	3771 ±425	0.046
Number of Segments	72 ±6	68 ±5	0.59
Mean Segment Length (µm)	72 ±6	55 ±4	0.04
Spine Count	4835 ±1055	1915 ±288	0.03
Spine Volume (µm3)	656 ±143	260 ±39	0.03
Spine Surface Area (µm2)	6339 ±1383	2510 ±378	0.03
Spine Density (#/µm)	0.94 ±0.16	0.50 ±0.03	0.03
BASAL ARBOR
Surface Area (µm2)	7917 ±992	8905 ±1686	0.63
Volume (µm3)	1758 ±325	2099 ±534	0.60
Total Length (µm)	3405 ±321	3467 ±381	0.91
Number of Segments	55 ±5	76 ±15	0.21
Mean Segment Length (µm)	62 ±2	50 ±7	0.15
Spine Count	3087 ±707	1597 ±257	0.09
Spine Volume (µm3)	657 ±151	340 ±55	0.09
Spine Surface Area (µm2)	5292 ±1213	2738 ±440	0.09
Spine Density (#/µm)	0.89 ±0.18	0.45 ±0.05	0.06

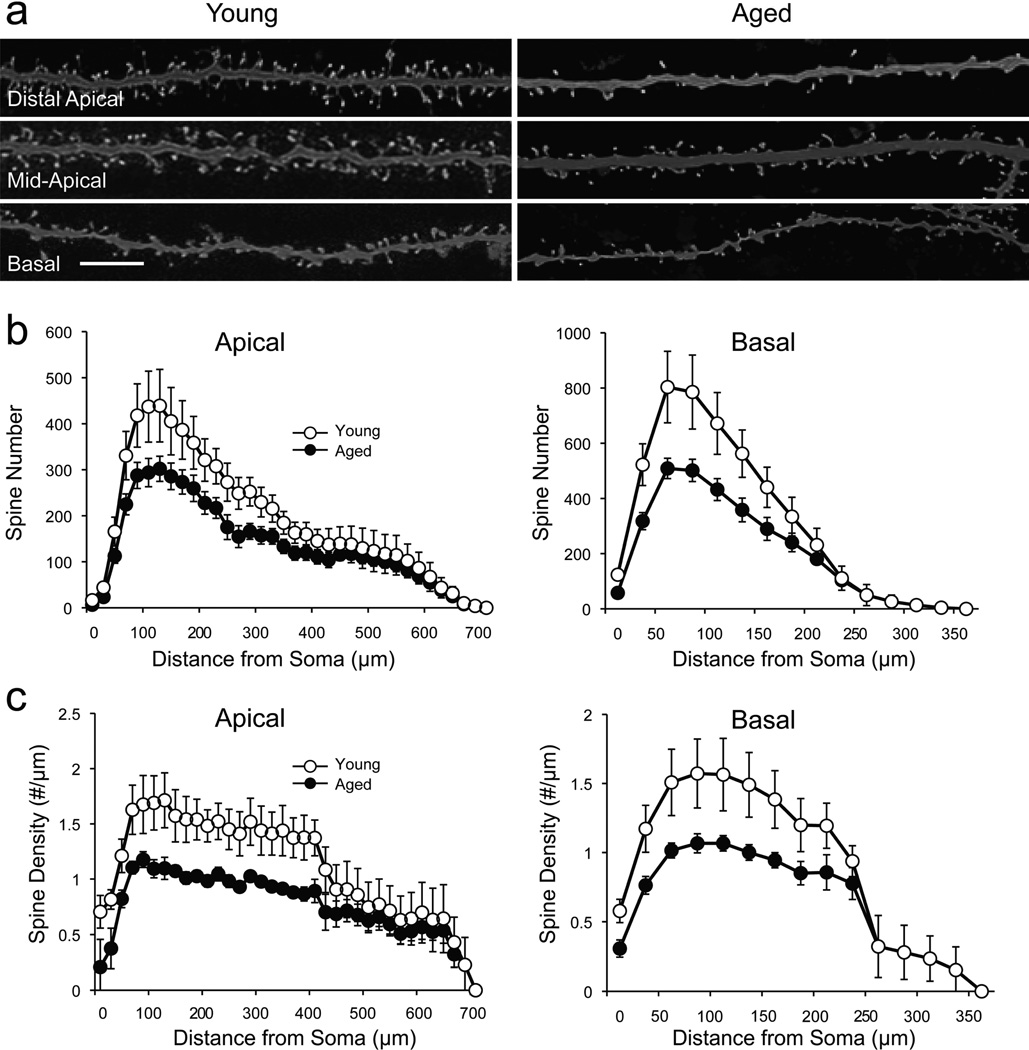
Apical dendrites of aged neurons possessed significantly fewer spines than those of young neurons (one-tailed t-test, p = 0.02; Table 3 and Fig. 3a–b), and basal dendrites also had significantly fewer spines (one-tailed t-test, p = 0.047). The mean spine density of both apical and basal dendrites of aged neurons was significantly less than the corresponding spine densities in young neurons (one-tailed t-tests; apical, p = 0.02 and basal, p = 0.04; Table 2 and Fig. 3). Sholl analyses revealed that significant reductions in spine number and density occurred uniformly across the proximal and middle regions of the apical dendritic tree, accompanied by significant reductions in spine density across the middle region of the basal tree (Fig. 3b–c; mixed design one-tailed ANOVA with Greenhouse-Geisser correction: apical: p = 0.02 for spine count and 0.03 for spine density; basal, p = 0.048 and 0.01, respectively).

Figure 3. The number and density of dendritic spines are significantly reduced in aged neurons.

a) Confocal images of representative dendritic segments from young and aged neurons demonstrating the loss of dendritic spines in distal apical, mid-apical and basal segments. Scale bar: 4 µm. b) Distribution of mean number of dendritic spines as a function of distance from the soma in apical (left) and basal (right) dendritic trees in young and aged dendritic trees (p < 0.05 where error bars do not overlap). c) Distribution of mean density of dendritic spines as a function of distance from the soma in apical (left) and basal (right) dendritic trees in young and aged dendritic trees. Density is reported as number of spines per unit of dendritic length (p < 0.05 where error bars do not overlap).

There were no significant correlations between morphological and physiological data. In particular, input resistance was correlated neither with soma surface area (p = 0.76 for all neurons; p = 0.78 and p = 0.61 for young and aged, respectively), nor with surface area of the soma and dendrites (with spine surface areas included: p = 0.43 for all neurons; p = 0.96 and p = 0.12 for young and aged neurons separately; likewise p-values with spine surface areas excluded were p = 0.58, p = 0.87, p = 0.09 respectively). Firing rate was also uncorrelated with these surface area measurements, either separated by age group or together as a whole (p > 0.05 for all current injections). Thus, while significant age-related changes in both morphology and physiology were observed, correlations shed little insight into any causal relationship between them. A limitation of the empirical methodology is that many additional variables contributing to structure-function relationships (e.g. membrane resistivity, channel composition and distribution, space clamp) cannot be controlled. Fortunately, such variables can be controlled in computational models, to which we turned next.

3.4 Dendritic voltage attenuation of model neurons

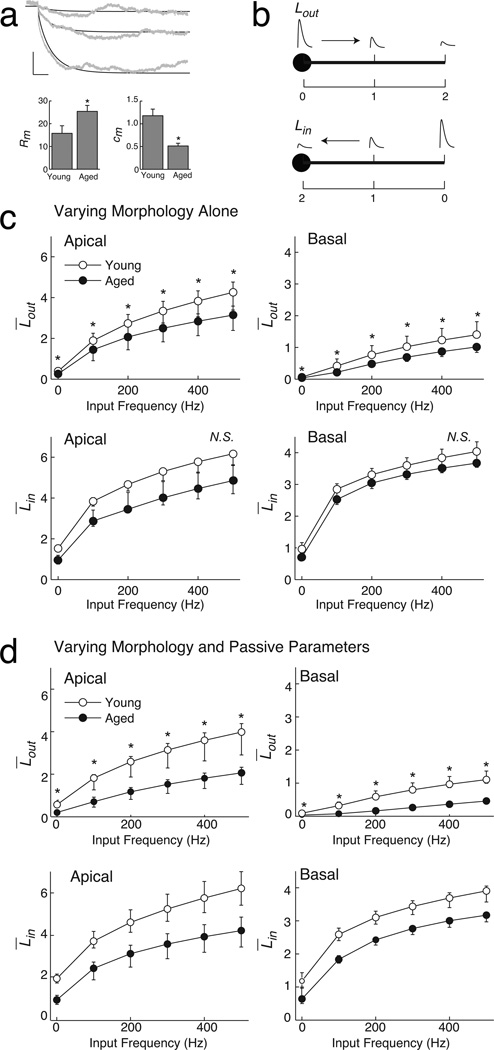
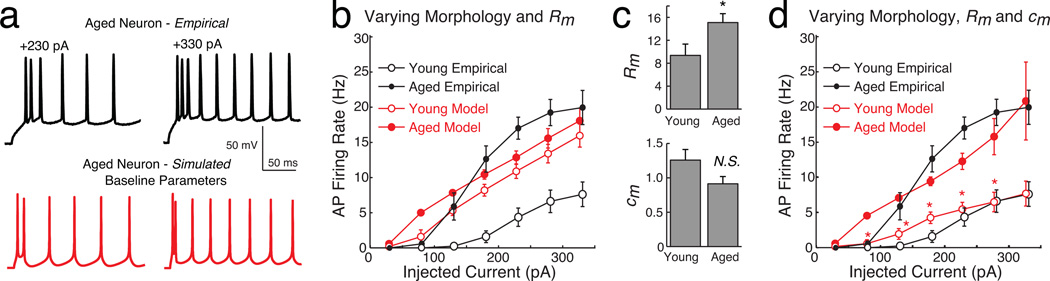
Using the same passive parameters from our recent simulations of LPFC neurons (Amatrudo et al. 2012) in all model cells, the simulated input resistance (R_N) of the young and aged model neurons did not differ significantly (young models: 112.74 ± 15.34 MΩ; aged models: 114.13 ± 13.10 MΩ, p = 0.95). This suggests that morphology alone is unlikely to account fully for the empirically observed difference in input resistance between young and aged neurons. Passive membrane parameters C_m, R_m, and E_L of each model neuron were then varied to fit the corresponding resting membrane potential, membrane time constant, and input resistance values measured empirically (Fig. 4a; R_a was held constant). After this parameter tuning R_m was higher in aged versus young model neurons (aged 25.4 ± 2.6 kΩ·cm²; young: 15.8 ± 3.3 kΩ·cm², p = 0.047) while C_m was lower (aged 0.51 ± 0.06 µF/cm²; young: 1.18 ± 0.14 µF/cm², p < 0.01). The leak reversal potential E_L did not differ between age groups (aged: −63 ± 1 mV vs young: −65 ± 1 mV, p = 0.18). Applying these customized parameter values, the simulated input resistance was higher in aged versus young model neurons (aged: 112 ± 7 MΩ vs. young: 75 ± 9 MΩ, p = 0.01). In some of the simulations below, passive parameters were held constant across all models to evaluate the extent to which age-related morphologic differences affected signal propagation and neuron firing properties. Otherwise, the simulations below use the passive parameters customized for each model neuron.

Figure 4. Voltage attenuates less in passive dendrites of aged versus young model neurons.

a) Top, Representative fit of a model to empirical data after tuning passive parameters. Scale bar: 2 mV and 20 ms. Bottom, tuning passive parameters for all models led to a significant difference in R_m and C_m in aged versus young models. b) Illustration of attenuation length. One unit equals a reduction in voltage by a factor of 1/e. Attenuation was measured either propagating outward from the soma (L̅_out, top), or inward towards the soma (L̅_in, bottom). c) Attenuation lengths when morphology varied but passive parameters were held constant. Top row: L̅_out versus input frequency of young and aged model neurons, for apical (left) and basal (right) dendrites. Bottom row: analogous layout, for L̅_in versus input frequency. d) Attenuation lengths when morphology and passive parameters were varied for all model neurons. Analogous layout to (c). Graphs show the median of each age group, with error bars equaling the first and third quartiles of the data..

Attenuation of dendritic voltage was assessed by four measurements: the mean inward and outward attenuation, L̅_in and L̅_out, computed for the apical and basal trees of each model neuron (Fig. 4a). Each computation was performed twice, once with spine surface area included and once without. Results with spines included are reported here, and except where noted below omitting spines did not affect the results.

Before using the mixed design ANOVA on these data, the normality, and homogeneity of variance, and sphericity at each input frequency were tested. There were two outliers in the data, for L̅_in attenuation in the apical dendrites. These outliers were not omitted from the analyses, because their inclusion did not violate the assumption of normality as assessed by Shapiro-Wilk’s test (p > 0.05 each for apical and basal L̅_out, and for apical and basal L̅_in). The null hypothesis of homogeneity of variances was not rejected for any of the four measurements (Levene’s test, p > 0.05 in each case). Because the null hypothesis of sphericity was rejected for each measurement (Mauchly’s test, p < 0.001), the Greenhouse-Geisser correction was applied to the ANOVA results. The outcomes of these tests were similar whether passive parameters were held constant or customized for each model.

First the mean inward and outward attenuation was calculated with passive parameters held constant across all models. Figure 4b summarizes the data at each input frequency as the median, with error bars marking the first and third quartiles of the data. Mean outward attenuation was significantly lower in aged versus young neurons, in both the apical and basal dendrites (apical: F_(1.03,12.38) = 6.18, p = 0.03; basal: F_{(1.01, 10.13)} = 12.11, p = 0.006). The difference between age groups appeared at every input frequency, for both apical and basal dendrites (p ≤ 0.03 for each). For mean inward attenuation, the null hypothesis of no difference in aged versus young neurons was not rejected (apical: F_{(1.07, 12.85)} = 3.29, p = 0.09; basal: F_{(1.68, 16.78)} = 1.45, p = 0.26). Excluding spines from the models changed the result of only one comparison: mean outward attenuation in the apical dendrites was not different in aged versus young neurons (apical: F_{(1.04, 12.42)} = 3.93, p = 0.07; basal: F_{(1.01, 10.11)} = 7.38, p = 0.02).

Next the mean inward and outward attenuation was recalculated after applying the customized passive parameter values to each model (Fig. 4d). Results were similar: mean outward attenuation was significantly lower in aged versus young neurons (apical: F_(1.01,4.75) = 7.29, p = 0.02; basal: F_{(1.02, 1.00)} = 12.88, p = 0.005), for every input frequency (p ≤ 0.02 for each). Also there was no evidence of a difference in mean inward attenuation (apical: F_(1.03,2.81) = 3.47, p = 0.09; basal: F_(1.05,0.18) = 1.02, p = 0.34).

To demonstrate the functional relevance of the L̅_out measure, the backpropagation of an empirically recorded AP into the dendrites was simulated for each model. The subsequent maximum membrane potential of each dendritic compartment was recorded in each young and aged model neuron, and then used to compute the mean NBPamp (Figure 5a_1–2). Figure 5a₂ shows the decrease of AP amplitude in the apical dendrites as distance from the soma increases (mean ± S.E.M. of young and aged model neurons in black and red respectively) when passive parameters were held constant and dendrites were assumed to be passive. Normalizing this attenuation over all dendrites yields the NBPamp of each model neuron (Fig. 5a₃). These simulations showed that age-related morphologic changes alone led to significantly increased passive backpropagation in aged neurons relative to young, in both the apical and basal dendrites (apical: aged, 21.9 ± 1.4 mV·µm; young, 16.6 ± 1.8 mV·µm; p = 0.04; basal: aged, 47.1 ± 1.4 mV·µm; young, 36.3 ± 2.3 mV·µm; p = 0.002).

Figure 5. AP backpropagation and EPSC properties differ in aged versus young model neurons.

a) Measurements of AP backpropagation. a₁, Maximum membrane potential in passive apical dendrites of a model neuron, from −50 mV (gray) to +20 mV (dark red); a₂, Maximum AP amplitude versus distance from the soma was used to compute NBPamp (gray solid, young models; red dashed, aged models). a₃, NBPamp was significantly higher in aged versus young model neurons. b) Simulation of somatic EPSCs. b₁, EPSCs evoked by activation of each individual synapse of the apical arbor of a typical young and typical aged model neuron. Individual EPSCs shown in black; mean EPSC traces shown in red. b₂, EPSC amplitude versus synaptic distance from the soma in the young (open circles) and aged (closed circles) model neurons from b₁. b₃, Bar graphs comparing mean EPSC amplitude and rise time in young versus aged model neurons.. In (a)–(b) passive parameters were held constant in all model neurons. c) AP backpropagation and EPSC properties when passive parameters were customized for each model, and active Hodgkin-Huxley channels were included in soma and dendrites as in Fig. 6 below. *: p < 0.05

Action potential backpropagation was also higher in aged compared to young neurons when customized passive parameters were applied to each model neuron. This was true for passive dendrites (not shown) and when voltage-gated ion channels were included in both the soma and dendrites as in Figure 6b (apical: aged, 24.0 ± 2.0 mV·µm; young, 13.7 ± 1.8 mV·µm; p = 0.003; basal: aged, 50.5 ± 2.3 mV·µm; young, 32.4 ± 2.2 mV·µm; p = 0.0002).

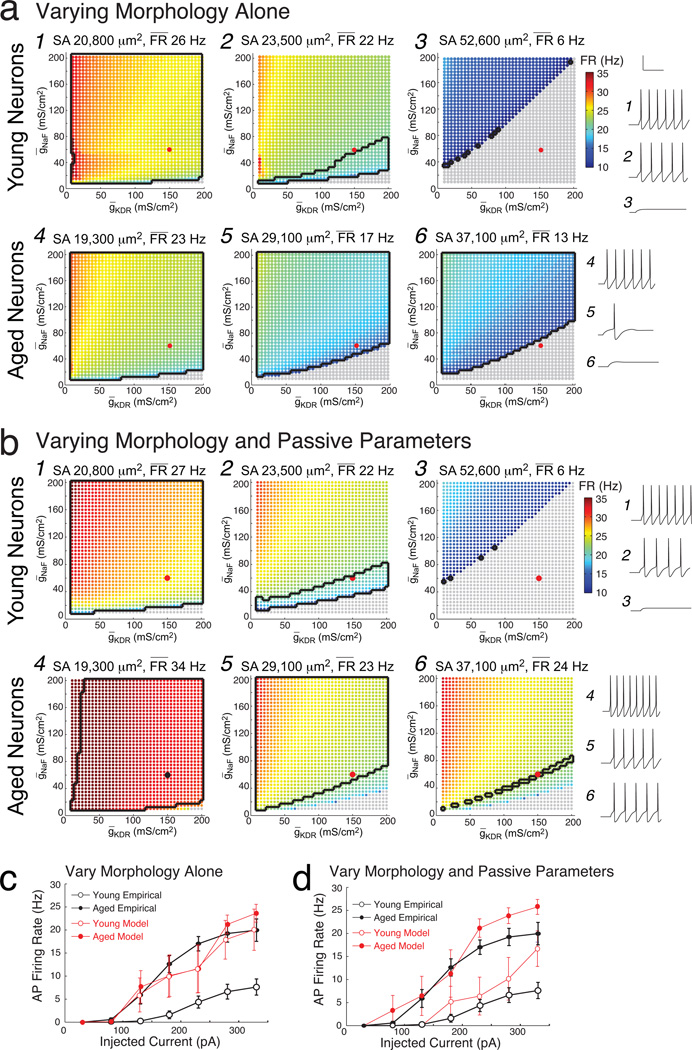
Figure 6. Influence of morphology, passive parameters, and ionic conductances on firing rates in young and aged Hodgkin-Huxley model neurons.

a) Results of the systematic searches with constant passive parameters for three young neuron models (labeled 1,2,3 here and in Fig. 2b) and three aged neuron models (labeled 4,5,6 here and in Fig. 2b). Surface area including spines and mean firing rate for each model neuron is noted above each graph. Colorscale indicates the firing rate in response to a +330 pA somatic current injection, from 10 (dark blue) to 35 Hz (red), as a function of varying values of ḡ_NaF and ḡ_KDR. Parameter combinations shown in gray fired no APs. Black contours enclose parameters whose output fit the neuron’s empirical data. Also shown are voltage traces from the model neurons, for the parameter combination (ḡ_NaF, ḡ_KDR) = (60, 150 mS/cm²) labeled as a large red dot. b) Similar graphs for the same six model neurons as in (a), with passive parameters customized for each. c) f–I curves of the mean firing rates of young and aged model neurons with constant passive parameters and (ḡ_NaF, ḡ_KDR) = (60, 150 mS/cm²), versus the mean firing rates measured empirically (in black). d) Analogous f–I curves as in (c), for models with customized passive parameters. In (c) and (d), young data are shown by open circles, which superimpose aged data indicated by closed circles.

As a functional analog of L̅_in, excitatory postsynaptic currents (EPSCs) were simulated in the dendrites of each model neuron, and their forward propagation to the soma was recorded. Figure 5b₁ overlays EPSCs recorded at the soma in response to synaptic inputs activated throughout the apical dendrites of one young and one aged neuron. The mean apical EPSC, shown in red, was clearly lower in amplitude in the young neuron. Substantial attenuation of signals originating in the distal dendrites can account for this (Fig. 5b₂). Repeating these simulations over apical and basal dendrites of all model neurons showed that EPSCs were greater in amplitude with a shorter rise time in aged than in young neurons (Fig. 5b₃; p < 0.001 for both apical and basal amplitude, and apical and basal rise time), even when passive parameters were held constant in all models. Moreover, EPSC decay times and half-widths were shorter in aged versus young neurons (apical decay time: aged, 7.47 ± 0.07 ms, young, 9.18 ± 0.06 ms; basal decay time: aged, 4.79 ± 0.01 ms; young, 5.23 ± 0.02 ms; apical half-width: aged, 9.6 ± 0.11 ms; young, 12.0 ± 0.10 ms; basal half-width: aged, 5.28 ± 0.03 ms; young, 6.04 ± 0.04 ms, p < 0.001 for all tests). Thus, while there was no evidence that L̅_in differed between the age groups here, the EPSC simulations suggested that morphological differences do contribute to reduced inward signal attenuation with aging. Results were similar when customized passive parameters were applied (Fig. 5c, p < 0.001 for all tests).

3.5 Firing rates of Hodgkin-Huxley model neurons

Our recently published study found that a model with Hodgkin-Huxley conductances (fast Na⁺ and delayed rectifier K⁺) was sufficient to demonstrate that morphologic differences largely account for higher firing rates in V1 as compared to LPFC neurons (Amatrudo et al. 2012). The question in the present study is whether morphologic differences alone—or morphologic plus predicted passive parameter changes—are sufficient to explain the empirically observed increase in firing rates with aging. Following Amatrudo et al. (2012), systematic sampling across 1,521 points in the (ḡ_NaF, ḡ_KDR) parameter space was conducted for each of the 12 model neurons. Firing rates in response to +230 and +330 pA somatic current injections were computed, and points whose output fit the empirically measured firing rates of each of the young and aged neurons were identified. As above, this was done first with passive parameters held constant for all models and then with passive parameters customized for each model.

Figure 6 shows the results of this systematic sampling for three young and three aged neurons that span the range of dendritic surface areas. Results for varying morphology alone (constant passive parameters) are shown in Figure 6a, and for varying morphology and passive parameters (customized for each model) in Figure 6b. Each (ḡ_NaF, ḡ_KDR) combination simulated for each model neuron is represented as a dot whose color indicates the firing rate of the model in response to a +330 pA somatic current injection. As expected with models, firing rates were inversely proportional to the neuron’s surface area (from highest to lowest firing rates in models across the three columns of Fig. 6a–d). Similarly, as expected from the Hodgkin-Huxley model, simulated firing rates were highest when ḡ_NaF was high and ḡ_KDR was low. Results from the +230 pA simulations were analogous.

The lowest nonzero firing rate of these models in response to this current injection was 6.6 Hz, greater than the empirically measured firing rates of half of the young neurons. Accordingly the ‘fit’ between empirical and simulated firing rates was defined broadly for both young and aged models (Methods). In Figure 6, points meeting the broad fitting criteria are outlined in black. In both age groups, some models had large regions of parameter space that fit both the corresponding empirical data (panels 1, 4, 5, 6 of Fig. 6a, and panels 1, 4, 5 of Fig. 6b). There was no single (ḡ_NaF, ḡ_KDR) point for which all models fit their respective firing rates, though points such as (ḡ_NaF, ḡ_KDR) = (60, 150 mS/cm²), shown on each panel of Figure 6a,b as a large red dot, fit for several of the models. Voltage traces at this point are also shown in Figure 6a,b, to the right of the systematic sampling results of each model neuron.

Using (ḡ_NaF, ḡ_KDR) = (60, 150 mS/cm²) as an example, we used a mixed design ANOVA to test the hypothesis that firing rates differed in aged versus young Hodgkin-Huxley model neurons, when passive parameters were either held constant or customized for each model. Before using the mixed design ANOVA on these data, the normality, and homogeneity of variance, and sphericity of the data at current injections above +130 pA were tested. There were no outliers in the data. However, due to several models with high rheobase, the assumption of normality as assessed by Shapiro-Wilk’s test was violated at +180 pA (constant R_m and C_m: p = 0.01 for young and p = 0.04 for aged; varied R_m and C_m: p = 0.03 young and p = 0.01 aged), +230 pA (constant R_m and C_m: p = 0.005 young; varied R_m and C_m: p = 0.03 young and 0.01 aged) and +280 pA (constant R_m and C_m, p = 0.04 young). Since the mixed-design ANOVA is somewhat robust to deviations from normality, the data were not transformed before the ANOVA was applied. The null hypothesis of equality of error variances was rejected by Levene’s test (p > 0.05) for injection levels below +330 pA when passive parameters were customized for each model (p = 0.02, p = 0.03 and p < 0001 for +180, +230 and +280 respectively), but not rejected otherwise (p > 0.05). The null hypothesis of sphericity was rejected when passive parameters were held constant (Mauchly’s test, p < 0.001) but not when passive parameters were customized for each measurement (p = 0.50). Therefore the Greenhouse-Geisser correction was applied in the former case but not the latter. All together, these tests indicate that the assumptions for using the mixed-design ANOVA were violated at several of the current injection levels, but in the interests of thoroughness we report the results here.

When all passive and active parameters were held constant across the young and aged model neurons, no difference was detected in the firing rates of young and aged model neurons (Fig. 6c red open versus closed circles; ANOVA F_{(1.64, 19.88)} = 0.48, p = 0.75). This is not surprising since morphologic differences alone did not account for the empirically observed differences in input resistance. With customized passive parameters the mean f–I curve of young models seemed to be lower than the mean f–I curve of aged models (Fig. 6d); yet again no difference in firing rates was detected at any of the current injection levels (mixed ANOVA with covariates R_m and C_m: F_{(3, 6.45)} = 0.26, p = 0.86).

The results from these Hodgkin-Huxley models support the idea that morphology alone cannot account for the increased input resistance and firing rates that are observed with aging. The results do suggest that passive membrane properties of LPFC neurons are changed with aging. However the extent to which these changes might contribute to firing rate differences is unclear. Yet also, while the Hodgkin-Huxley model was able to fit young and aged data on average, its ability to fit firing rates of individual neurons was limited. One explanation is that the Hodgkin-Huxley model only provides a mechanism to generate APs, not to modulate their frequency. These limitations motivated application of a model that contains additional ionic conductances capable of spike frequency modulation.

3.6 Model with additional conductances

The L3 neocortical pyramidal neuron model developed by Traub and colleagues (Traub et al. 2003) includes several ion channels capable of mediating spike frequency. Here, we modified the Traub et al. model by adding a slow AHP current, and then tuned parameters to fit firing rates in response to +230 and +330 pA somatic current injections of an aged neuron from the present study (Fig. 7a). (Other features such as time to first spike and firing rates at other injection levels were not the focus of the parameter tuning.) Those fitted parameters are hereafter called the ‘Baseline parameters’. Initially, all Baseline parameters (including passive parameters, maximal conductances, and channel kinetics) were applied identically to all young and aged model neurons, even though they led to lower input resistance values overall. As in the Hodgkin-Huxley models above, there was no difference in input resistance (young: 73.5 ± 7.5 MΩ versus aged: 69.9 ± 5.1 MΩ, p = 0.70) or mean firing rates among the two age groups when all parameters were held constant (F_{(1.01, 10.13)} = 0.06, p = 0.95; not shown).

Figure 7. Influence of morphology and passive parameters on firing rates in young and aged Traub model neurons.

a) Voltage traces recorded empirically in an aged neuron (black) in response to +230 pA and +330 pA somatic current injections, compared with the corresponding voltage responses of a model neuron tuned to fit these data (red, called ‘Baseline parameters’). Model neuron has the same morphology as the one shown in Fig. 6a₅ and labeled ‘5’ in Fig. 2b. b) f–I curves of the mean firing rates of young and aged model neurons with the Baseline parameters except scaled R_m (in red), versus the mean firing rates measured empirically (in black). Young models and data are shown as open circles, and aged models/data as closed circles. c) After adjusting passive parameters to restore firing in young neurons, R_m was higher in aged versus young models but C_m did not differ. d) Analogous f–I curves as in (b), for young and aged model neurons with the Baseline parameters except R_m and C_m customized as in (c). *: p < 0.05.

The effect of customized passive parameters on model firing rates was explored next. Passive parameters were not re-fit for each neuron with this modified Traub model. Instead the passive Baseline parameters were scaled proportionally according to the customized Hodgkin-Huxley fits above. First only R_m was scaled in each model with C_m held constant to test whether morphology plus the R_m change was sufficient to explain the higher firing rates of aged neurons. This led to significantly higher input resistance in aged versus young model neurons (aged: 62 ± 2 MΩ vs. young: 42 ± 4 MΩ, p = 0.003).

Firing rates of young versus aged neurons were compared at injection levels above +130 pA. Violations of the assumptions for using the mixed design ANOVA were far fewer than with the Hodgkin-Huxley models: both when C_m was held constant and when C_m was varied, the null hypotheses of normality and equality of error variances of firing rates were not rejected (p > 0.05 for all tests). In both cases the null hypothesis of sphericity was rejected (p < 0.001), but this violation was mitigated by using the Greenhouse-Geisser correction. As suggested by the red f–I curves shown in Figure 7b, there was no evidence of a difference in firing rate between young and aged models when morphology and R_m (but not C_m) varied across the model neurons (mixed ANOVA with covariate R_m: F_{(1.12, 11.04)} = 1.45, p = 0.26).

Scaling the baseline C_m value (0.83) of all neurons proportionally using the customized Hodgkin-Huxley fits worked well for the aged neurons, but led to very high values in the young neuron models (aged: 0.91 ± 0.11 µF/cm² versus young: 2.1 ± 0.3 µF/cm²). Combined with the lower R_m values, this led to unrealistic firing patterns in the young neurons: even injecting +330 pA led to firing rates below 2.5 Hz in five of six neurons, and to bursting behavior in the sixth (not shown). Accordingly we reduced the C_m scaling factor of all young neurons until the bursting behaviors went away (by 40%, down to 1.26 ± 0.16 µF/cm²; Fig. 7c), and then compared firing rates across the two age groups.

After this scaling there was no evidence to reject the null hypothesis that C_m values were equal in the populations of young and aged neurons (t-test p=0.10), consistent with the observed empirical result that membrane time constants did not differ. Yet interestingly, also consistent with experiments, firing rates were significantly higher in aged than in young model neurons for all but two levels of current injection (Fig. 7d; mixed ANOVA with covariates R_m and C_m: F_{(1.18, 67.14)} = 7.85, p = 0.02; post-hoc pairwise t-tests p < 0.02). Moreover, even though these Baseline parameter values were chosen by fitting simulated firing rates at two injection levels to data for a single neuron, the model f–I curve of both age groups matches the empirical one well overall. These results suggest that a significant increase of R_m in aged neurons together with subtle changes in morphology and C_m may be sufficient to explain the increased firing rates in aged versus young LPFC neurons.

4 Discussion

The present study was undertaken to use computational methods to evaluate the extent to which age-related morphological changes in L3 pyramidal neurons in the rhesus monkey LPFC contribute to functionally significant physiological changes, including increased excitability. This is the first time that both high-resolution morphology and physiology have been characterized simultaneously in young and aged neocortical pyramidal neurons of a primate. Empirical data were used to constrain computational models, which yielded insights into potential morphological and ionic underpinnings of increased excitability in aged neurons.

4.1 Relation to previous work

In a previous study we demonstrated that aged L3 pyramidal neurons in the monkey PFC exhibit both increased input resistance and significantly increased evoked action potential firing rates in vitro (Chang et al. 2005), but no change in resting membrane potential or membrane time constant. Correlation analyses demonstrated that the increase in input resistance was related to, but did not fully account for, the significant increase in excitability. The different set of L3 pyramidal neurons examined in the present study also exhibited a dramatic age-related increase in firing rates, and a higher input resistance. Taken together both studies provide evidence for increased in vitro firing rates in aged neurons and demonstrate that changes in input resistance alone do not account for this increase. Recently, Wang et al. (2011) found that in vivo firing rates in a population of rhesus monkey LPFC neurons were significantly reduced with aging. Our results are not necessarily inconsistent: the Wang et al. study was focused on neurons that fired during the delay phase of a delayed recognition task, a classification which is not possible with our in vitro studies. The present study also confirms and extends previous work on the effects of age on the morphological properties of L3 pyramidal neurons in the monkey (Page et al. 2002; Duan et al. 2003; Kabaso et al. 2009; Dumitriu et al. 2010; Hara et al. 2012). Accordingly, in the present study we observed dendritic regression in the apical arbors, and substantial reduction in spine density of up to 50% in the apical and basal arbors.

One of the goals of this study was to determine the functional consequences of morphological changes in aged neurons; interestingly, we found that none of the morphological and physiological changes were significantly correlated. This finding is consistent with the idea that age-related changes in structural and functional properties may be independent and unrelated, but may also be a reflection of the low degrees of freedom of the study. A powerful means of further interrogating potential consequences of morphological changes—and to make predictions about causes of increased excitability—is through computational neuron models constrained by morphologically realistic data, as undertaken here. It is important to interpret findings from such analyses conservatively, given that models are always simpler then actual neurons in terms of morphology and types and distribution of ion channels, and that in neurons assessed empirically space clamp and other technical limitations exist that are not present in the model cells. Nevertheless, the study of simplified model neurons often leads to important insights into mechanisms of normative and altered neuronal signaling that can be tested empirically.

In a previous modeling study with passive membrane properties, we demonstrated that reduced dendritic length and spine density led to significantly lower outward voltage attenuation (and stronger AP backpropagation) from the soma to the tips of apical dendrites in aged versus young LPFC neurons; inward voltage attenuation from the tips to the soma did not differ (Kabaso et al. 2009). Results were similar in the present study, both when dendrites were passive as well as when Hodgkin-Huxley conductances were included. One extension of this study over Kabaso et al. (2009) is the simulation of excitatory postsynaptic currents (EPSCs) as in Amatrudo et al. (2012), which were faster and greater in amplitude in aged versus young model neurons when membrane parameters were held constant. The Kabaso et al. (2009) study predicted that the observed morphologic changes would lead to higher input resistance in aged model neurons, and possibly to higher firing rates. The present study used computational models constrained by morphological and physiological data from young and aged neurons to test this hypothesis and to examine potential passive and ionic mechanisms of increased excitability in these neurons.

4.2 Computational modeling predicts altered passive membrane parameters in aging

The modeling work demonstrated that morphological changes alone cannot account for age-related increases in firing rate for broad regions of the parameter space of the two-conductance Hodgkin-Huxley model that were explored. This conclusion also held for the modified Traub model that included several currents such as I_M, I_h, and Ca²⁺-dependent K⁺ currents, which are thought to contribute to the firing rates of LPFC neurons (Traub et al. 2003; Wang et al. 2011; Luebke and Amatrudo 2012). While evoked firing rates were not different in young and aged models, the significant changes in spine density and dendritic morphology reported here were sufficient to reduce the attenuation of dendritic signals in aged neurons. This is consistent with previous computational studies showing that morphology can affect neuronal firing patterns and signal integration (Mainen and Sejnowski 1996; Vetter et al. 2001; Schaefer et al. 2003; Weaver and Wearne 2008; van Elburg and van Ooyen 2010). Morphologic changes in aging may ultimately affect firing rates of LPFC neurons by reducing attenuation of synaptic signals across the dendritic arbor that are summated at the soma; we will test this hypothesis in future studies which constrain synaptic inputs with empirical data (Luebke et al. 2004).

Collecting physiological and morphological data from the same neurons enabled basic fitting of passive and active membrane parameters of each model neuron separately. In two-conductance Hodgkin-Huxley models we tuned R_m, C_m, and E_L values to fit empirical measurements of input resistance, membrane time constant, and resting membrane potential. In these models R_m was higher and C_m lower in aged versus young neurons, while E_L did not differ. The significant difference in C_m values was surprising since no difference in membrane time constant was found empirically. Yet despite these significant differences—likely due in part to our limited sample size—there was not enough evidence to reject the null hypothesis that firing rates are equal in young and aged neurons. Simulations with the more complex Traub model showed that combining morphologic changes with a significant increase in R_m in aged neurons, together with subtle variations in C_m (below the level of detection by a t-test) was sufficient to reproduce the f–I curves observed empirically. As such our modeling predicts that passive membrane parameters (or other parameters with similar effects) are changed with aging in LPFC neurons. Membrane capacitance is difficult to assess empirically due to space clamp issues, but there is evidence that it varies in real neurons beyond the value of 1 µF/cm² often assumed by modelers (Norenberg et al. 2010; Thurbon et al. 1998).

Our findings do not preclude the possibility that differences in active channel conductances and/or kinetics, altered function of ion pumps, or different extracellular ion concentrations might contribute to the age-related increase in firing rates. Indeed, there is empirical evidence that several active channel conductances are altered with aging in L3 monkey LPFC neurons, including the Ca²⁺-dependent current that underlies the slow afterhyperpolarization, sI_AHP (Luebke and Amatrudo 2012), as well as HCN and KCNQ channels (Wang et al. 2011). In other brain areas, age-related reductions in a K⁺ conductance (Niesen et al. 1988) and delayed rectifier K⁺ current (Frolkis et al. 1989), increased calcium influx and amplitude of calcium-dependent sAHPs (for review: (Faber and Sah 2003; Foster 2007; Thibault et al. 2007)) and density of high-voltage activated L-type Ca²⁺ channels (Thibault and Landfield 1996; Porter et al. 1997; Blalock et al. 1999; Thibault et al. 2001; Oh et al. 2013) have all been described. The relationship between age-related changes in excitatory and inhibitory synaptic responses and firing rates also need further investigation: the present study showed that synaptic responses likely attenuate less in aged neurons, but a previous study established that the frequency of spontaneous EPSCs is reduced in these neurons with aging but the frequency of spontaneous inhibitory EPSCs is increased (Luebke et al. 2004).

Empirical and computational studies in several animal models, brain regions, and neuron types have shown that very similar firing patterns can be achieved by different combinations of active channel conductances (see (Marder and Goaillard 2006) for review). An in-depth study of the parameters contributing to the firing patterns of the modified Traub model is beyond the scope of the present paper. One area of our current research is to develop systematic approaches to optimize multiple parameters in complex models efficiently (Rumbell et al. 2014). This will allow us to identify and compare parameter sets fitting a variety of physiological features in multiple neurons from different age and treatment groups. Such technical advances are especially important given strong evidence that ion channel densities vary across the dendritic arbor (Magee 2000; Migliore and Shepherd 2002; Häusser and Mel 2003; London and Häusser 2005) and even from branch to branch (Losonczy et al. 2008; Branco and Hausser 2010).

Similarly, more work is needed to determine whether the age-related morphologic changes of LPFC neurons affect other kinds of dendritic physiology. Both Ca²⁺ waves and sparks (hotspots) can affect cell signaling cascades (reviewed in (Ross 2012)), but were not modeled here. Moreover, plateau potentials mediated by N-methyl-D-aspartate (NMDA) receptor currents are a mechanism by which thin dendritic branches can act as separate computational subunits (see (Antic et al. 2010) for review), but were beyond the scope of the present study. Age-related changes in dendritic branch lengths or spine distributions of these neurons may well affect their ability to create or sustain NMDA-dependent plateau potentials. Indeed, there is evidence that both the NR1 and NR2B NMDA receptor subunits are reduced with aging in cortical pyramidal neurons in the macaque (Hof et al. 2002; Bai et al. 2004).

4.3 Conclusion

The findings of the present study have important implications for understanding potential mechanisms of age-related changes in the function of neurons in other brain areas as well. As with the monkey LPFC, significantly increased spontaneous AP firing rates have been reported for cortical neurons in vivo in the visual cortex of the aged monkey (Schmolesky et al. 2000; Leventhal et al. 2003; Zhang et al. 2008; Fu et al. 2013), and for CA3 pyramidal neurons in the hippocampus of the aged rat (Wilson et al. 2005). In both the visual cortex and hippocampus, as with the LPFC, increased firing rates of neurons are associated with impaired function of these brain areas (Schmolesky et al. 2000; Leventhal et al. 2003; Wilson et al. 2005). Given the aging of the general population and the increasing prevalence of age-related amnestic mild cognitive impairment, it is vital to gain a detailed understanding of the age-related alterations to individual neurons that may lead to cognitive decline. This study contributes to that goal by providing novel and detailed information on both the structural and functional changes seen with normal aging in individual pyramidal neurons of the rhesus monkey LPFC, and demonstrating that the structural changes cannot fully account for altered function.