Significance
Understanding the molecular basis of energy conversion in F1-ATPase is of fundamental importance and requires a clear structure-based description of the system with particular emphasis on the conversion of ATP chemical energy to mechanical torque. Here we used our coarse-grained model of F1-ATPase and generated a structure-based rotary–chemical landscape that reproduced the observed torque for the wild-type enzyme without using phenomenological parameters. In doing so, we discovered the principles that determine whether free energy surfaces of specific shapes can lead to torque generation. Furthermore, by calculating the torque in several types of γ-deletion systems, we gained major insights into the molecular nature of the F1-ATPase rotary motor and established that electrostatics are important in generating the rotary–chemical coupling.
Keywords: molecular motors, rotary torque, bioenergetics, free energy surface, F0F1-ATPsynthase
Abstract
Unraveling the molecular nature of the conversion of chemical energy (ATP hydrolysis in the α/β-subunits) to mechanical energy and torque (rotation of the γ-subunit) in F1-ATPase is very challenging. A major part of the challenge involves understanding the rotary–chemical coupling by a nonphenomenological structure–energy description, while accounting for the observed torque generated on the γ-subunit and its change due to mutation of this unit. Here we extend our previous study that used a coarse-grained model of the F1-ATPase to generate a structure-based free energy landscape of the rotary–chemical process. Our quantitative analysis of the landscape reproduced the observed torque for the wild-type enzyme. In doing so, we found that there are several possibilities of torque generation from landscapes with various shapes and demonstrated that a downhill slope along the chemical coordinate could still result in negligible torque, due to ineffective coupling of the chemistry to the γ-subunit rotation. We then explored the relationship between the functionality and the underlying sequence through systematic examination of the effect of various parts of the γ-subunit on free energy surfaces of F1-ATPase. Furthermore, by constructing several types of γ-deletion systems and calculating the corresponding torque generation, we gained previously unknown insights into the molecular nature of the F1-ATPase rotary motor. Significantly, our results are in excellent agreement with recent experimental findings and indicate that the rotary–chemical coupling is primarily established through electrostatic effects, although specific contacts through γ-ionizable residue side chains are not essential for establishing the basic features of the coupling.
Gaining a detailed understanding of the biological conversion of ATP to ADP is crucial for understanding the nature of biological energy transduction and for practical understanding of the action of molecular motors (1, 2). At present it seems that some of the details of this process have remained a major puzzle (1–6). One of the main open questions is associated with the understanding of the way the chemical energy is converted to conformational changes and to work. This challenge become quite exciting in view of the remarkable progress made by single-molecule studies that directly visualized the unidirectional rotation of the γ-subunit (7–9). One of the intriguing findings of these studies has been the discovery of the catalytic dwells (7) where the γ-subunit rotation stops intermittently during the ligand binding and catalytic phases occurring in the α/β-subunits. Another recent discovery is the finding that the rotational process continues in the right direction even when major parts of the γ-subunit are removed (10, 11). These latest findings seem to present a problem for models that have postulated a steric mechanism as the driving force for torque generation.
Molecular dynamics simulations aimed at understanding the rotary–chemical coupling (12–15) have been instructive, but could not capture the relevant energetics or provide a structure-based quantitative understanding of the actual millisecond rotation and chemical/conformational coupling of the F1-ATPase motor. Attempts to understand the rotary mechanism by using coarse-grained models and targeted molecular dynamics (TMD) approaches (14, 15) forced the rotation of the γ-subunit rather than reproducing it from a structure-based landscape. In this respect, it seems to us that studies that do not produce the free energy surface of the whole biological process considering the complete F1-ATPase system cannot be used to relate the protein structure to the rotary–chemical action of this molecular motor. Furthermore, we are not aware of any computational study that was able to consistently produce the torque generated by the ATP hydrolysis process, although some works might have created the impression of producing the relevant torque and thus seem to lend support to the presumption that electrostatics might not play an important role in driving the F1-ATPase rotary–chemical coupling (detailed discussion in SI Text, Comparison with Other Studies of the Torque Generation).
At present it is unlikely that fully microscopic models with the current computer resources will be able to capture the overall free energy balance in molecular motors. The problem is the difficulty of obtaining converging free energies for the substantial conformational changes of large and highly charged systems. Alternatively, one can use coarse-grained (CG) models (reviews in refs. 16 and 17), realizing however, that using CG models without appropriate electrostatic terms (e.g., refs. 14 and 15) is also unlikely to reveal the electrostatic contribution to the free energy surfaces. Thus, we used in this work our CG model that focuses on a consistent description of the electrostatic energy of the system (16). Encouragingly, our recent computational study (18) that used the electrostatically enhanced CG model generated a free energy landscape that was able to show the functional stepwise coupling between the rotary γ-subunit and the catalytic α/β-subunits. In addition, we also elucidated the basic principle behind the position of the experimentally observed “catalytic dwell” that occurs after 80° rotation. This understanding was further reinforced by our Langevin dynamics (LD) simulations done over the rotary–chemical surface without any prior assumption on the position of the catalytic dwell (18).
Armed with our initial understanding of the rotary–chemical coupling in the F1-ATPase motor (18), we focus in this work on dissecting the role of the γ-subunit in shaping the basic free energy landscape. Especially, we show that the electrostatic landscape is preserved when the side chains of all γ-subunit residues are mutated to alanine, whereas the coupling between the γ-rotation and catalytic subunits is destroyed when the same residues are mutated to glycine. Moreover, we also show that truncating the γ-subunit progressively captures the region of the stalk that is required for a unidirectional stepwise rotation. In addition, we focused on careful exploration of the torque generation and analyzed the puzzling effect of different γ-deletion systems on the generated torque. Our result reproduces the trend of recent experimental findings on the F1-ATPase system. Especially, we reproduce the recent observation of rotation in the right direction even after truncation of most of the γ-subunit. Finally, the present study further emphasizes the problems associated with inconsistent attempts to obtain an agreement with experimental observations (see SI Text).
Background and Conceptual Issues
The Challenge of Reproducing Relevant Experiments by Simulation Studies.
The F1-ATPase system is composed of a stator ring (α/β-subunits) and an elongated rotor (γ-subunit), which is part of the complete F0F1complex. The rotor or the γ-subunit connects the cytoplasmic stator ring with the membrane-bound F0 portion of the enzyme. The γ-subunit is also responsible for the transmission of the rotary torque between the α/β-subunits and the F0 region during ATP hydrolysis or synthesis. The γ-rotation in F1-ATPase is observed to be a stepwise process with each step of 120° coupled to a single event of ATP hydrolysis. Each 120° step is further intercepted by at least two time dwells (known as the “ATP binding dwell” and the “catalytic dwell”). The catalytic dwell is found to consist of events in the milliseconds range, one of which is the actual chemical step and another event is most likely the phosphate release step (7).
The challenge is to reproduce the key observed facts (unidirectional rotation, dwell time, torque, and γ-truncation effects) by structure-based modeling approaches. Overcoming this challenge should help to elucidate the origin of the underlying physics of the rotary motor. At this stage, it is important to clarify what has been accomplished or overlooked in previous theoretical studies based on structural considerations. We already discussed in our previous work (18) the fact that the use of TMD to move between the initial and final structures (14) is not a justified way of reproducing the observed features of the catalytic dwell. Thus, we focus here on the problems of the implication that one can reproduce the experimental torque by using the TMD approach to rotate the γ-subunit. The rotation that has resulted from the TMD (14) has been accomplished in a much smaller timescale and also without considering the effect of chemical energy on the γ-rotation. The impact of such inconsistent implications of ref. 14 was unfortunately presumed in a recent work (19) that superimposed its experimental results on the simulated torque profile of ref. 14 (figure 5A of ref. 19 and the supporting information therein) in trying to interpret the physical basis of F1-ATPase functionality. Although the problems with this assertion are discussed in the SI Text, the most pertinent issue is the fact that the torque should reflect the chemical free energy coupled to the γ-rotation and having no such chemical gradient in the theoretical modeling methods should result in zero torque (next section). Thus, the argument of ref. 19 that that the simulation of ref. 14 reproduced the torque observed by experiments, even qualitatively, is problematic.
At this point we wish to clarify that our previous CG study (18), which is based on calculating the rotary–chemical free energy landscape, obtained a reasonable rotation time, which is one of the key experimental observations about the action of the system. Nevertheless, we have to address the challenge of evaluating the actual measured torque, which is discussed below in more detail. Furthermore, in addition to reproducing the observed torque in the wild-type F1-ATPase from the rotary–chemical surface, our next challenge is to reproduce the effects of several types of γ-truncation systems and to elucidate their significance in the rotation and chemical coupling.
Relation of the Average Torque to the Rotary–Chemical Landscape.
To elucidate the molecular origin of the rotary–chemical coupling, it seems to us that the torque and other rotational measurements must be related to the underlying molecular free energy landscape. Apparently, the motions are dictated by the landscape and not, as some may assume, the other way around. Now to clarify our point we present two schematic landscapes in Fig. 1 A and B, where Fig. 1A has a similar trend to that obtained in our previous study, with a least energy path along the diagonal. In this case the torque that rotates the γ-subunit reflects the fact that the lowest point in the landscape occurs where the γ-rotation and the chemical state are at 120° and ADP + Pi, respectively. Thus, the evolution of the system toward the 120° point rotates the γ-subunit in a unidirectional way. On the other hand, in Fig. 1B we have no net gradient for moving in the direction that rotates the γ from 0° to 120°. In this case, although the free energy decreases along the chemical coordinate, we still have no effective or average net torque. The relationship between the shapes of the landscape and the torque would guide us in the subsequent discussion and it will also serve to remind us that the torque cannot occur without proper coupling to the chemical energy.
Fig. 1.
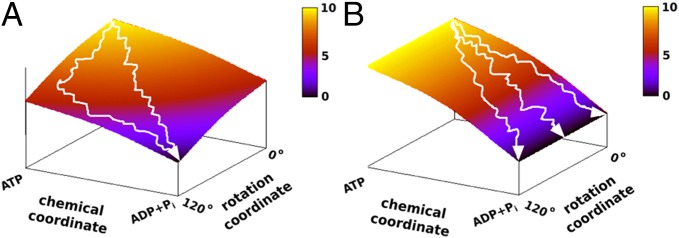
The relationship between the shape of the landscape and the generated torque is illustrated by the schematic landscapes for chemical and rotational coordinates (omitting the chemical or conformational barrier). Two extreme situations occur when the chemical free energy is (A) tightly coupled and (B) loosely coupled to the rotational coordinate. In A the chemical free energy decreases more when the rotational coordinate ϕ approaches 120° than when it approaches 0°. Hence the average trajectory ultimately moves from ϕ = 0° to ϕ = 120° and the system generates torque. In B due to loose coupling of the rotational and chemical coordinates, the system can move to different rotational angles over time so that we obtain zero torque in the ϕ direction.
Now, our task is to obtain the torque from the landscape and this can be done in several ways, including those discussed in refs. 6, 20, and 21. The first way is to consider the free energy released upon rotation of the γ-subunit (assuming that it is all transferred to the rotation of the magnetic beads). In this case we have
| [1] |
where is the angular torque and is the average angular torque.
The relevant free energy can be evaluated from the potential of mean force (PMF) along the rotation coordinate, , using a free energy perturbation-type expression,
| [2] |
where U is the free energy surface, X is the chemical coordinate, and the ΔG is accumulated to give the total torque free energy. The corresponding free energy can be evaluated by Monte Carlo (MC) simulations over the surface. The PMF can also be evaluated by standard umbrella sampling calculations on the corresponding surface that can be obtained from the LD simulations by using a mapping potential.
Another option is to adopt the approach used in several of the experimental works (e.g., refs. 20 and 21) with the formulation
| [3] |
where and are, respectively, the friction on the magnetic beads and the angular velocity. However, this approach is more applicable to experimental studies because the is frequently measured in conditions where it is much slower than the rotation of the stalk in a single cycle (22).
Another option is the use of the so-called “fluctuation theorem” (23) in the way suggested by Noji and coworkers (22) and elaborated by others (24). We can use this approach with the assumption of a constant torque and obtain
| [4] |
where , and is the corresponding probability distribution. However, obtaining a proper sampling for the appropriate from LD simulations and considering the proper boundary conditions require significant effort and extensive simulations, which are left to future studies. In this respect we note that the basic derivation of Eq. 4 has been based on LD formulation with a constant torque, and we already have a known surface with a known torque as well as LD simulation based on this torque. Thus, the torque can be more directly calculated from our free energy surface itself without facing the convergence problems of using Eq. 4, where overcoming the challenge of evaluating this equation by the LD simulations is mainly academic. Of course, trying to obtain the torque from experimental studies is a completely different issue (6, 20, 21).
Results and Discussion
The Rotary–Chemical Surface for the Wild-Type F1-ATPase.
Here we start by recalculating the F1-ATPase rotary–chemical surface (shown in SI Text) with the newer version of the CG model (16), using the same set of structures generated in ref. 18 (see Figs. S1 and S2 and SI Text for details). The electrostatic free energy surface plotted along the α/β-conformational coordinate and the γ-rotational coordinate shows a similar stepwise path, which highlights the coupled behavior of the catalytic subunits and the central stalk during ATP hydrolysis. In ref. 18, we further coupled the chemical coordinate with the least free energy path along the conformational surface to reveal the underlying guiding principle of the catalytic dwell occurring around 80° between each 120° rotation. This has been a significant advance in understanding the experimentally observed functional behavior of F1-ATPase, using structural and theoretical modeling approaches. The present work further explores the capability of the electrostatic free energy surface to quantitatively reproduce the relevant experimental observations, such as the average torque over the 120° rotations.
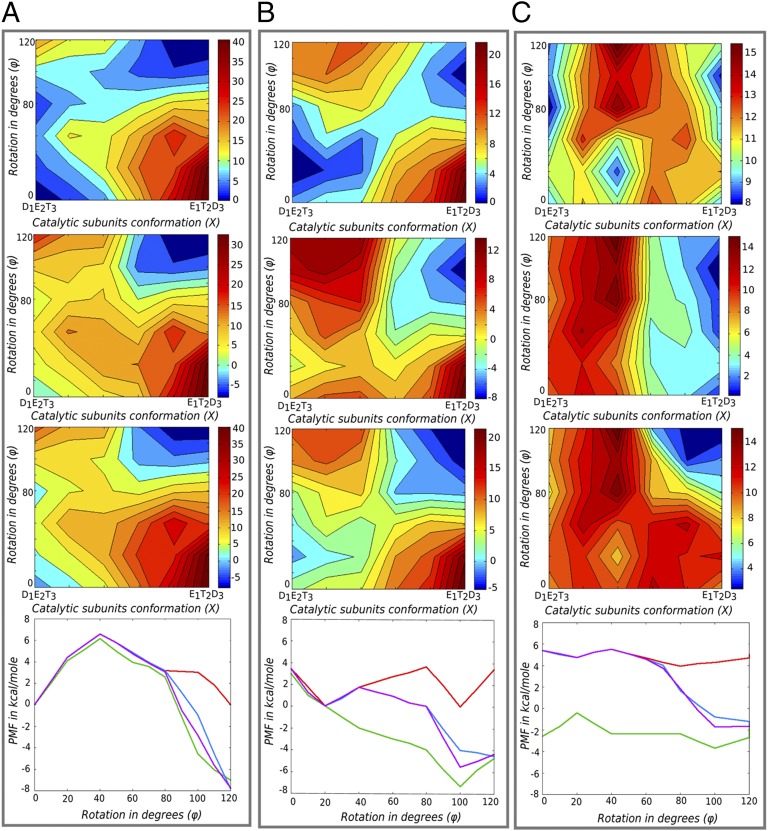
To explore the origin of the torque, we concentrate on a single event of ATP hydrolysis coupled to 120° γ-rotation. We use the 120° surface as shown in Fig. 2A (Top) and then add the chemical energy to it after the α/β-catalytic subunits have completed half of the conformational changes starting from D1E2T3 to E1T2D3 (Fig. 2A, Upper Middle and Lower Middle). Here E, T, and D represent the β-subunit in the “empty,” “ATP-bound,” and “ADP-bound” forms, and 1, 2, and 3 represent the catalytic subunit numbers. The α/β-conformational coordinate is designated as X and its value changes from 0 (representing D1E2T3) to 1.0 (representing E1T2D3). The chemical free energy of −8 kcal/mol has been added to the points on the CG surface in equal steps, starting from X = 0.6. This is a very reasonable option where we assumed that the chemical free energy release starts only after 50% of the net conformational changes have already been completed. The chemical energy has been added either to all ϕ values on the rotational coordinate (Fig. 2A, Upper Middle) or in a way that is consistent with the occurrence of the catalytic dwell at 80°. In the latter case, the chemical free energy has been added starting from X = 0.6 but only when γ has completed 80° rotations (Fig. 2A, Lower Middle). We have also considered other ways of distributing the chemical energy across ϕ, especially for cases where the coupling between X and ϕ is lost. The chemical barrier has not been considered in these calculations and it is also assumed that the chemical free energy release is completely coupled to the catalytic subunit changes (X).
Fig. 2.
Converting the conformational landscape to torque. A–C show 120° electrostatic free energy maps for (A) the WT system, (B) the all-alanine γ-system, and (C) the all-glycine γ-system. For each column, Top panels show the surfaces without the addition of the chemical energy, Upper Middle panels show the surfaces when the chemistry is added to all ϕ-values starting at X = 0.6, and Lower Middle panels show the surfaces when the chemistry was added at the catalytic dwell (assuming it occurs at ϕ = 80°) and at X = 0.6. Another third option of adding chemistry was also considered where half of the chemical energy was added to ϕ = 80° and X = 0.6 and then the rest was added in steps between [ϕ = 80° to ϕ = 120°] and [X = 0.6 to X = 1.0] (surfaces not shown). Bottom panels present the PMFs obtained by MC simulations over the surfaces without chemistry and the surfaces with three options of distributing the chemical energy as mentioned above. The PMFs in red are for surfaces without chemistry, those in green are for the surfaces in Upper Middle panels, and those in blue and magenta are for the surfaces of Lower Middle panels and the third option not shown in this figure.
Before considering the calculation of the torque from the surfaces in Fig. 2A, we present a very qualitative estimate based on the maximum free energy difference between 0° and 120°. A visualization of Fig. 2A, Upper Middle and Lower Middle shows that this difference is around 8 kcal/mol, when one adds the free energy of ATP hydrolysis at standard concentrations just after the catalytic subunits have completed more than half of the net conformational changes. Because the conformational free energy at 0° and 120° is almost the same, any average torque has to be generated by the addition of the chemical free energy to the conformational path. Using these values, the torque generated on the stalk surface can be as large as 56 pN nm. This lies close to the experimentally observed average torque range of 40–50 pN nm (6, 20). Note that our torque calculation is based on the maximum free energy difference between the initial and final states (0° and 120°) without considering the limiting factor of the effect of the viscous drag on the probe used to measure the experimental torque (6, 10, 20, 21). Hence, our values most likely represent the upper limit of the torque.
To obtain a more quantitative estimate of the torque from the rotary chemical surface of Fig. 2A (Lower Middle), we used Eq. 2 and obtained the PMF shown in Fig. 2A, Bottom. As seen from Fig. 2A, Bottom, we obtained a maximum free energy drop of around 7.6 kcal/mol between the 0° and 120° states in the direction of the rotational coordinate. This generates a maximum average torque of about 53 pN nm on the γ-surface. Whereas the above torque was obtained by adding the chemical energy after the catalytic dwell at 80°, it is important to consider other ways of adding the chemical energy. Thus, we calculated the PMF for the surface of Fig. 2A, Upper Middle, where the energy was added to all rotational stages of the γ but only after the chemical coordinate (α/β-subunits) has crossed its half point (i.e., starting at X = 0.6). As seen from Fig. 2A, Bottom, the free energy drop for this case was around 7 kcal, generating a maximum average torque of about 49 pN nm. Thus, we do not see a major difference in the generated torque for different ways of distributing the chemical energy in the wild-type F1-ATPase system. This point is further discussed below.
Exploring the Role of γ-Residues on the Rotary–Chemical Coupling and Torque Generation Process.
After establishing that our native surface reproduces a maximum average torque that corresponds well to the experimentally observed torque, we moved to the exploration of the observed effect of mutation of the γ-subunit. The mutations considered here were selected to dissect the process of torque generation in further detail and to validate our theoretical model. First, we studied the systems resulting from mutating all of the residues of the γ-subunit to either alanine or glycine.
The complete 360° free energy surfaces for the all-alanine and all-glycine γ-systems are shown in SI Text, whereas Fig. 2 B and C, Top shows the 120° surfaces without adding chemical free energy. The same different cases of adding the chemical energy that were considered in the wild type are also considered here. The PMFs calculated from these surfaces are shown in Fig. 2 B and C, Bottom. The electrostatic free energy maps in Fig. 2 B and C illustrate the overall role of γ-residues in shaping the coupling between the stalk and the α/β-subunit conformational changes during ATP hydrolysis. The results show that the all-alanine γ-system still retains the basic features of the coupled stepwise pathway that is important to channel the system along the 0°–120° rotational path. Thus, it appears that the residue-specific charge–charge interactions (salt bridges or side-chain–mediated hydrogen bonds) arising from the γ-subunit are not essential for shaping the rotary–chemical coupling inherent in the F1-ATPase system. Our result is in accordance with the recent experimental observations that infer the unimportance of any specific γ-residue guiding the torque generation in F1 (10). It may be tempting to infer directly from here that electrostatics is not the underlying driving force for the rotary–chemical coupling in F1-ATPase, which unfortunately is concluded by experimental and theoretical workers (10, 14, 19). However, one must be very careful in modeling the correct electrostatics in large macromolecules before coming to such conclusions. To model the short- and long-range behavior of charged residues, one must consider both columbic-type interactions and solvation effects arising from the polar and nonpolar groups surrounding the charged residues. The result in Fig. 2B merely shows that salt bridges or hydrogen bonds to the γ-subunit are not responsible in a major way for establishing the torque. At the same time, the result does not undermine the role of solvation effects provided by the γ-polar and nonpolar residues on the charged residues of the neighboring α/β-subunits. This fact is further clarified in Fig. 2C, where mutating all γ-residues to glycine destroys any solvation effect arising from the side chains of the F1 central stalk. Interestingly, Fig. 2C indeed shows that the coupled stepwise feature is completely lost, hence pointing to the importance of the γ-stalk in shaping the electrostatic free energy path. At this point we once more emphasize that the dominating electrostatic contribution to our free energy landscape is not simply the result of charge–charge interactions (pairwise columbic potential). In fact, it mainly reflects the self-energy term, which is the free energy associated with solvating charged residues with nonpolar and polar groups (discussion of the CG model in SI Text).
To quantify the role of γ-residues in shaping the electrostatic landscape that guides the rotary–chemical behavior of the F1-ATPase, we evaluated the average torque for the surfaces in Fig. 2 B and C. Running MC over the rotary–chemical surface of the all-alanine system we get a maximum average torque of about 44 pN nm from the 6.3-kcal free energy difference between the 0° and 120° rotational states. The efficiency of the all-alanine system was also explored with other ways of adding the chemical energy. For all ways, we end up with similar overall generated torque. The situation appeared to be different for the all-glycine system, where adding the chemistry at all rotational values (Fig. 2C, Upper Middle) generated a surface that is similar to that of the schematic surface in Fig. 1B. This implies that although the α/β-subunits could possibly perform the chemical step and release the chemical free energy as observed in a recent experimental study performed without the central stalk (11), the same free energy release is not coupled to any specific angle of the γ-subunit during the rotary process. If one were to perform LD simulations on such a surface where chemical free energy has the same probability of being released during any arbitrary rotational angles between 0° and 120°, the rotational coordinate would land anywhere between 0° and 120° during the relevant time period of the ADP or Pi release event (the major chemical step thought to release the chemical free energy of 8 kcal/mol). However, this large energy release will still not generate any significant torque as shown from the PMF calculation. We have also calculated PMFs by adding the chemical energy after 80° for the all-glycine system, but due to loss of proper coupling between the γ- and α/β-subunits, there is no justification to assume that the position of the catalytic dwell is at 80°. Thus, the surface depicted in Fig. 2C, Upper Middle that generated negligible torque seems to describe the all-glycine system better than other cases. On the contrary, note that the surfaces for the wild-type and the all-alanine systems show a clear coupled stepwise feature in the electrostatic surface (Fig. 2 A and B). This seems to be consistent with the addition of chemical energy after 80° γ-rotation, assuming that the chemistry is coupled at that step. However, it is important to note that the wild-type and all-alanine systems generated torque even when we add the chemical energy for all rotational values, highlighting the robustness of the F1-ATPase system and the role of the γ-subunit in shaping the rotary–chemical surface.
Overall, our results indicate that the chemical free energy must be tightly coupled to the rotational coordinate to generate any sizeable torque on the γ. The nature of the coupling between the chemical and rotational coordinates is shaped by the electrostatic free energy of the F1-ATPase system where the γ-residues specifically play the role of solvating the charged residues of the α/β-subunits.
Identifying the Minimal γ-Subunit Required for the Rotary–Chemical Coupling.
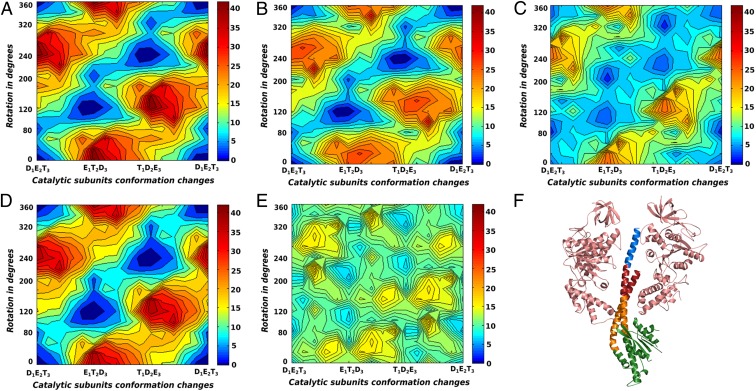
To determine the part of the stalk that is absolutely required for the unidirectional rotary–chemical coupling and the torque generation, we also considered deletions that gradually truncated parts of the γ-subunit, by converting the corresponding residues in the deleted region to glycine. The γ was truncated in four parts: γ1, the C-terminal end that is inserted into the α/β-cavity; γ2, the middle portion of the stalk that is inserted within the α/β-cavity; γ3, the portion of the stalk that surrounds the loop region of the α/β-subunits (known as the DELSEED) and also includes the bend on the N-terminal helix; and γ4, the rest of the stalk that mainly forms the globular part protruding from the α/β-cavity. The truncated regions of the γ-subunit are highlighted in different colors in Fig. 3F. The CG electrostatic free energy maps for the systems with any one of the γ1, γ2, γ3, and γ4 regions mutated to glycine are shown in Fig. 3 A, B, C, and D, respectively. For γ1 and γ4 truncated systems, the least free energy path and the relative barrier heights with respect to the highest points on the surface are very similar to the wild-type free energy map in Fig. 3A and Fig. S3A. This shows that both the C-terminal end embedded deep within the α/β-cavity and the part protruded from the α/β-cavity are nonessential for establishing the rotary–chemical coupling in F1-ATPase. This is in accordance with the recent experimental finding that the absence of these parts does not affect the unidirectional rotary movement of F1-ATPase (10). The map for the γ2 truncation system also retains the essential qualitative features of the least free energy path, although the higher barriers surrounding the stepwise path have now reduced. This reduction might lead to slippages of the rotating stalk without completing the chemical step, leading to lesser efficiency and reduced torque generation. The most drastic effect is seen for the γ3 truncation system, where the least free energy path has widened considerably, leading to loss of efficiency along the rotary path. Fig. 3E shows the free energy map for the system with combined γ2−γ3 truncation and the result highlights that loss of both these regions practically destroys the coupling between γ-rotation and -subunit conformational changes. We conclude from these studies that the most important region of the γ-subunit that confers the stepwise coupling feature to the F1-ATPase is the part around the α/β-DELSEED loop (γ3 region). The region of γ2 just above the DELSEED region is also important in establishing the overall functional free energy surface to some extent, whereas regions γ1 and γ4 are not essential for the rotary–chemical coupling.
Fig. 3.
The CG electrostatic free energy surfaces for the γ-truncation systems without the addition of chemical free energy are shown for (A) γ1, (B) γ2, (C) γ3, (D) γ4, and (E) combined γ2–γ3. (F) The γ-subunit with a pair of opposing β-subunits are shown [Protein Data Bank (PDB) ID: 1H8E], where γ1, γ2, γ3, and γ4 are colored in blue, red, orange, and green, respectively.
A recent experimental study conducted by replacing most of the γ-subunit with protein sequence from unrelated systems led to the conclusion that electrostatics are not important for the rotary–chemical coupling in F1-ATPase. Although corresponding experimental observations are important for understanding the system in detail, we do not agree with the general conclusion drawn from the observations (10) and in particular the assertion that the work of ref. 14 has actually produced any torque in a consistent way. In fact, our results corroborate the experimental findings (10) that the protruded part of the γ-stalk is not essential for unidirectional rotation, nor is the C-terminal part deeply embedded within the α/β-cavity. It is very hard to see how a steric nonelectrostatic model can produce such results. Overall, our results also support the general findings of the experimental study (10) that none of the γ-residues are forming specific contacts that are guiding the rotary–chemical coupling. Furthermore, our results show that despite the absence of torque contributions from any specific charged residues, the γ-subunit can still guide the rotary–chemical coupling of the system through electrostatic-mediated solvation effects. Combining the findings of Fig. 3 with those of Fig. 2, we find that specific charge–charge interactions through the γ-subunit are not essential for the coupling. However, the electrostatic solvation energy arising from the polar/nonpolar residues of the γ surrounding the α/β-subunits (especially the region around the nucleotide binding site) is important in shaping the functional free energy landscape. A detailed analysis of the α/β-subunits and the conformational free energy surface along the E (empty)-T (ATP bound)-D (ADP bound) path is left for future studies.
Concluding Remarks
Establishing a clear structure–function relationship of the F1-ATPAse rotary–chemical coupling should be based on well-defined physical principles that can actually reproduce the observed coupling rather than on phenomenological modeling. Here we are fortunate to have detailed and insightful experimental observations of the rotary–chemical behavior and torque generation for the F1-ATPase system, whose reproduction provides a powerful challenge for structure-based simulation approaches. In an effort to establish the experimental observations through theoretical simulations, it is important to clarify significant misunderstandings that have arisen. In particular, it is important to explain that the experimentally observed torque and related observations cannot be reproduced without proper coupling to the chemical energy that leads to the torque. Trying to force the γ-stalk rotation between different states of the enzyme can just reflect the applied force in the TMD that has been used to generate the rotation, rather than elucidating any inherent property of the system (stronger forces would simply lead to stronger response and faster rotation). The torque can be obtained from a structure-based simplified landscape of the entire system by several approaches, such as the one adopted in this study: calculating the PMF along the rotational degree of freedom by a free energy perturbation approach.
The present study examined the origin of the coupling between the chemical work and the rotation of the γ-subunit and showed that the torque is associated with the electrostatic coupling between the γ- and α/β-subunits. This conclusion has been strengthened by exploring the effects of major truncations of the γ-subunit. In this respect we note that the supposed support provided to the steric model (10, 19) from the simulations and torque calculations of ref. 14 is not valid, because as discussed here the reported torque reflects only the applied rotation force rather than the actual landscape and thus does not represent the rotary–chemical torque and hence actually cannot justify the steric or any other mechanism.
The relationships between the γ-dependent positioning of the catalytic dwell and the efficiency of the F1-ATPase rotary–chemical coupling have not been fully explored here. However, the qualitative picture that emerged from the MC PMF calculations indicated that in the wild type there is no major advantage in having the catalytic dwell at 80°. In the case of systems with reduced conformational coupling (e.g., for the all-glycine system) it will be more advantageous to have a release of the chemical energy at high values of ϕ. A more quantitative exploration of the issue of overall efficiency and the role of the catalytic dwell will require careful examination of the diffusional effects that can be done using our LD approach. However, we note that there are similar systems like V1V0 where the 80° catalytic dwell has not been observed (25).
Methods
The present work uses a CG model (16) that represents the side chains by a simplified united atom model (26) and the main chains by an explicit model, while focusing on a reliable electrostatic treatment. The details of our model are given elsewhere (16) and are also described in SI Text. It should be clarified that the CG conformational energy includes only the energy of the simplified side chains. The improvements of the CG model that were introduced recently (16) have yielded a similar landscape to that reported in ref. 18. The details of the structural modeling and generating the rotary–chemical surfaces for the wild-type and γ-truncation systems are discussed in SI Text.
Supplementary Material
Acknowledgments
We thank Dr. Kazuhiko Kinosita and Dr. Hiroyuki Noji for stimulating discussions. We also thank the University of Southern California High Performance Computing and Communication Center for computational resources. This work was supported by National Science Foundation Grant MCB-1243719 and National Institutes of Health Grant R01-AI055926.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1500979112/-/DCSupplemental.
References
- 1.Boyer PD. The ATP synthase—a splendid molecular machine. Annu Rev Biochem. 1997;66:717–749. doi: 10.1146/annurev.biochem.66.1.717. [DOI] [PubMed] [Google Scholar]
- 2.Weber J, Senior AE. Catalytic mechanism of F1-ATPase. Biochim Biophys Acta. 1997;1319(1):19–58. doi: 10.1016/s0005-2728(96)00121-1. [DOI] [PubMed] [Google Scholar]
- 3.Abrahams JP, Leslie AGW, Lutter R, Walker JE. Structure at 2.8 A resolution of F1-ATPase from bovine heart mitochondria. Nature. 1994;370(6491):621–628. doi: 10.1038/370621a0. [DOI] [PubMed] [Google Scholar]
- 4.Fersht A. Structure and Mechanism in Protein Science. A Guide to Enzyme Catalysis and Protein Folding. Freeman; New York: 1999. [Google Scholar]
- 5.Wang H, Oster G. Energy transduction in the F1 motor of ATP synthase. Nature. 1998;396(6708):279–282. doi: 10.1038/24409. [DOI] [PubMed] [Google Scholar]
- 6.Pänke O, Cherepanov DA, Gumbiowski K, Engelbrecht S, Junge W. Viscoelastic dynamics of actin filaments coupled to rotary F-ATPase: Angular torque profile of the enzyme. Biophys J. 2001;81(3):1220–1233. doi: 10.1016/S0006-3495(01)75780-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Adachi K, et al. Coupling of rotation and catalysis in F(1)-ATPase revealed by single-molecule imaging and manipulation. Cell. 2007;130(2):309–321. doi: 10.1016/j.cell.2007.05.020. [DOI] [PubMed] [Google Scholar]
- 8.Noji H, Yasuda R, Yoshida M, Kinosita K., Jr Direct observation of the rotation of F1-ATPase. Nature. 1997;386(6622):299–302. doi: 10.1038/386299a0. [DOI] [PubMed] [Google Scholar]
- 9.Watanabe R, et al. Mechanical modulation of catalytic power on F1-ATPase. Nat Chem Biol. 2012;8(1):86–92. doi: 10.1038/nchembio.715. [DOI] [PubMed] [Google Scholar]
- 10.Chiwata R, et al. None of the rotor residues of F1-ATPase are essential for torque generation. Biophys J. 2014;106(10):2166–2174. doi: 10.1016/j.bpj.2014.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Uchihashi T, Iino R, Ando T, Noji H. High-speed atomic force microscopy reveals rotary catalysis of rotorless F1-ATPase. Science. 2011;333(6043):755–758. doi: 10.1126/science.1205510. [DOI] [PubMed] [Google Scholar]
- 12.Czub J, Grubmüller H. Torsional elasticity and energetics of F1-ATPase. Proc Natl Acad Sci USA. 2011;108(18):7408–7413. doi: 10.1073/pnas.1018686108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Okazaki K, Hummer G. Phosphate release coupled to rotary motion of F1-ATPase. Proc Natl Acad Sci USA. 2013;110(41):16468–16473. doi: 10.1073/pnas.1305497110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pu J, Karplus M. How subunit coupling produces the gamma-subunit rotary motion in F1-ATPase. Proc Natl Acad Sci USA. 2008;105(4):1192–1197. doi: 10.1073/pnas.0708746105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Koga N, Takada S. Folding-based molecular simulations reveal mechanisms of the rotary motor F1-ATPase. Proc Natl Acad Sci USA. 2006;103(14):5367–5372. doi: 10.1073/pnas.0509642103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vicatos S, Rychkova A, Mukherjee S, Warshel A. An effective coarse-grained model for biological simulations: Recent refinements and validations. Proteins. 2014;82(7):1168–1185. doi: 10.1002/prot.24482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hyeon C, Thirumalai D. Capturing the essence of folding and functions of biomolecules using coarse-grained models. Nat Commun. 2011;2:487. doi: 10.1038/ncomms1481. [DOI] [PubMed] [Google Scholar]
- 18.Mukherjee S, Warshel A. Electrostatic origin of the mechanochemical rotary mechanism and the catalytic dwell of F1-ATPase. Proc Natl Acad Sci USA. 2011;108(51):20550–20555. doi: 10.1073/pnas.1117024108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Martin JL, Ishmukhametov R, Hornung T, Ahmad Z, Frasch WD. Anatomy of F1-ATPase powered rotation. Proc Natl Acad Sci USA. 2014;111(10):3715–3720. doi: 10.1073/pnas.1317784111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Arai HC, et al. Torque generation mechanism of F1-ATPase upon NTP binding. Biophys J. 2014;107(1):156–164. doi: 10.1016/j.bpj.2014.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sakaki N, et al. One rotary mechanism for F1-ATPase over ATP concentrations from millimolar down to nanomolar. Biophys J. 2005;88(3):2047–2056. doi: 10.1529/biophysj.104.054668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hayashi K, Ueno H, Iino R, Noji H. Fluctuation theorem applied to F1-ATPase. Phys Rev Lett. 2010;104(21):218103. doi: 10.1103/PhysRevLett.104.218103. [DOI] [PubMed] [Google Scholar]
- 23.Evans DJ, Searles DJ. The fluctuation theorem. Adv Phys. 2002;51(7):1529–1585. [Google Scholar]
- 24.Ciliberto S, Joubaud S, Petrosyan A. 2010. Fluctuations in out-of-equilibrium systems: From theory to experiment. J Stat Mech Theor Exp, 10.1088/1742-5468/2010/12/P12003.
- 25.Furuike S, et al. Resolving stepping rotation in Thermus thermophilus H(+)-ATPase/synthase with an essentially drag-free probe. Nat Commun. 2011;2:233. doi: 10.1038/ncomms1215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Levitt M, Warshel A. Computer simulation of protein folding. Nature. 1975;253(5494):694–698. doi: 10.1038/253694a0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.