Parameter-free methods distinguish Wnt pathway models and guide design of experiments

Significance

The canonical Wnt/β-catenin signaling pathway is important for essential cellular functions and is implicated in many diseases. We introduce a new mathematical model that focuses on β-catenin degradation and protein shuttling between cellular compartments. We compare our model to others and show that all fit to time-dependent experimental data. To evade this parameter problem, we use algebraic methods and characterize model features that are independent of the choice of parameter values. We find that multiple responses to Wnt are feasible under certain conditions for the new model, but not for the others; moreover, we provide dependencies between species (variables) that inform future experiments and model discrimination. We also highlight the wide applicability of these tools across problems in systems biology.

Abstract

The canonical Wnt signaling pathway, mediated by β-catenin, is crucially involved in development, adult stem cell tissue maintenance, and a host of diseases including cancer. We analyze existing mathematical models of Wnt and compare them to a new Wnt signaling model that targets spatial localization; our aim is to distinguish between the models and distill biological insight from them. Using Bayesian methods we infer parameters for each model from mammalian Wnt signaling data and find that all models can fit this time course. We appeal to algebraic methods (concepts from chemical reaction network theory and matroid theory) to analyze the models without recourse to specific parameter values. These approaches provide insight into aspects of Wnt regulation: the new model, via control of shuttling and degradation parameters, permits multiple stable steady states corresponding to stem-like vs. committed cell states in the differentiation hierarchy. Our analysis also identifies groups of variables that should be measured to fully characterize and discriminate between competing models, and thus serves as a guide for performing minimal experiments for model comparison.

The Wnt signaling pathway plays a key role in essential cellular processes ranging from proliferation and cell specification during development to adult stem cell maintenance and wound repair (1). Dysfunction of Wnt signaling is implicated in many pathological conditions, including degenerative diseases and cancer (2–4). Despite many molecular advances, the pathway dynamics are still not well understood. Theoretical investigations of the Wnt/β-catenin pathway serve as testbeds for working hypotheses (5–12).

We focus on models of canonical Wnt pathway processes with the aim of elucidating mechanisms, predicting function, and identifying key pathway components in adult tissues, such as colonic crypts. We compare four preexisting ordinary differential equation models (5–8) and find, using injectivity theory, that for any given conditions and parameter values, none of the models is capable of multiple cellular responses.

In many tissues Wnt plays a crucial role in cell fate specification (3). At the base of colonic crypts, cells exist in a stem-like, proliferative phenotype in the presence of Wnt. As these cells’ progeny move up the crypt axis they enter a Wnt-low environment and change fate (perhaps reversibly), becoming differentiated, specialized gut cells (13). In neuronal and endocrinal tissues, Wnt/β-catenin data suggest cell fate plasticity under different environmental conditions (14, 15). Here, we introduce a new model motivated by experimental findings not described in previous models (16–18) to investigate bistable switching in the Wnt pathway. We find the new model to be capable of multiple cellular responses; furthermore, our parameter-free techniques identify that molecular shuttling (between cytoplasm and nucleus) and degradation together may serve as a possible mechanism for governing bistability in the pathway, corresponding to, for example, a committed cell state and a stem-like cell state.

Comparison of models (and mechanisms) requires data; the type of comparison performed depends on the data at hand. If data show bistability (two distinct response states), then we could rule out all models that preclude bistability; however the converse is not true (a graded response may be compatible with all models). Experimental studies in Xenopus extracts have been performed to validate a model of Wnt signaling (5), with further pathway elucidation in refs. 19, 20; however, the parameters identified in these studies may differ markedly from those involved in mammalian Wnt signaling (21, 22). With the aim of discriminating between models, we present the five Wnt models under a unifying framework, with standardized notation to facilitate comparison. We fit parameters to recently published mammalian β-catenin signaling time-course data using Bayesian inference (22) and find that all of the studied models can describe the data well, demonstrating that additional data are required to compare models.

To determine which sets of protein species should be measured for carrying out a comparison between models and data, we introduce matroid theory to systems biology. A matroid is a combinatorial structure from mathematics, and in our case, it provides all of the steady-state invariants (23, 24) that have minimal sets of variables. The algebraic matroid associated with the steady-state ideal determines specific sets of species that should be measured to perform model discrimination without knowledge of parameter values. We demonstrate this parameter-free analysis with experimental data for two Wnt models.

In the next section, we introduce the previous models and new shuttle model. We perform injectivity–multistability analysis and classify the shuttle model as the only one capable of multistability. Next we infer the parameters of five competing models for time-course β-catenin data, revealing that all of the models fit the data. Finally we introduce algebraic matroids to inform experimental design for discriminating between models and data.

Models

Over the past decade, Lee et al.’s seminal model of canonical Wnt signaling (5) has spawned many variants. Briefly, the underlying biology of the pathway that these models describe is as follows (25): Wnt binds to cell-surface receptors that transduce a signal via a multistep process involving Dishevelled (Dsh) to the so-called destruction complex (DC), which contains forms of Axin, adenomatous polyposis coli (APC), and glycogen synthase kinase (3) (GSK-3). In the absence of a Wnt signal, the DC actively degrades β-catenin––which is being continually synthesized in the cell––by phosphorylating it and marking it for proteasomal degradation. Following Wnt stimulation, degradation of β-catenin is inhibited through phosphorylation of DC members, leading to accumulation in the cytoplasm of free β-catenin, which is able to translocate to the nucleus where it can form a complex with T-cell factor (TCF) and lymphoid-enhancing factor proteins and influence the transcription of target genes. These are cell-type specific, although genes controlling self-renewal and proliferation are commonly regulated across many cell types (1).

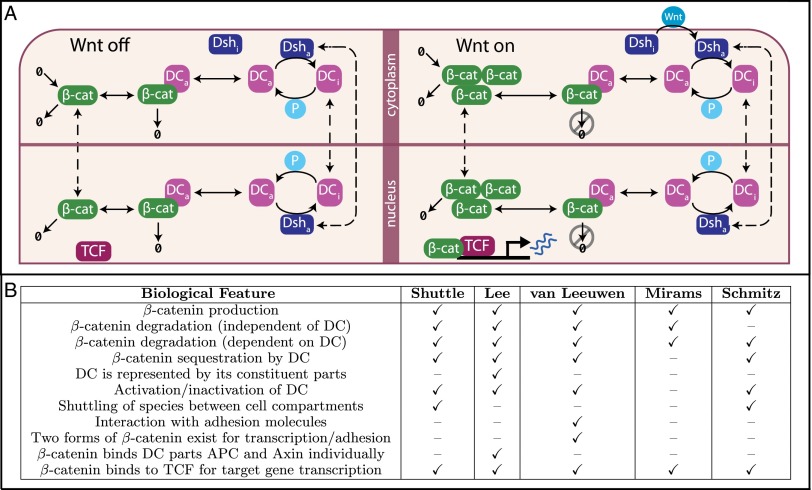
We include the core processes as well as the following in the proposed shuttle model (Fig. 1A and SI Appendix):

• i)spatial localization of shuttling components Axin, APC, GSK-3, and Dsh, the importance of which has been reported for each species (17, 26–30);
• ii)an alternative degradation mechanism whereby β-catenin is degraded while still bound to active DC and sequestered but not degraded by inactive DC (16);
• iii)catalysis of the reverse reaction by phosphatase (P) that converts DC from inactive to active form by dephosphorylating members of the DC (18, 31, 32).

Fig. 1.

Comparison of models of Wnt signaling. (A) Schematic of the new shuttle model in the absence (Left) and presence (Right) of a Wnt stimulus. DC and Dsh exist in inactive (i) and active (a) forms. P: phosphatase. For a full description of the reactions specifying this model, see SI Appendix. (B) Comparison of models: the shuttle model is compared with four others from literature (5–8) based on the features that are present–absent in each model.

The behavior of four other published models is analyzed and compared with that of the shuttle model (5–8). Fig. 1B summarizes the distinguishing qualitative features of each model; full model descriptions, using a standardized notation that differs from the authors’ originals, are summarized by a composite model in SI Appendix.

Results and Discussion

Wnt signaling interaction networks are polynomial systems whose steady-state solutions are defined by sets of algebraic equations for the species’ concentrations; this opens up avenues for parameter-free analysis, as we show here.

Parameter-Free Analysis of Wnt Models I: Multistability.

We are interested in determining whether or not a given model can produce multiple positive stable responses (states). Standard approaches from dynamical systems [e.g., bifurcation and singularity theory (33–35)] are useful for small systems or when we have knowledge of the parameters, however, for systems of more than a few free variables (the shuttle model has 19 species and 31 parameters), such approaches become infeasible. To overcome this, we apply theory developed for chemical reactions to Wnt pathway models; this is particularly helpful for determining whether multiple states are possible without the need for parameter values or sampling. There are various conventions in chemical reaction network theory (CRNT) for describing the number of positive steady states; we use the following terminology:

• i)injectivity implies at most one steady state;
• ii)multistationarity is the capacity for multiple steady states;
• iii)multistability is the capacity for multiple stable (accessible) steady states.

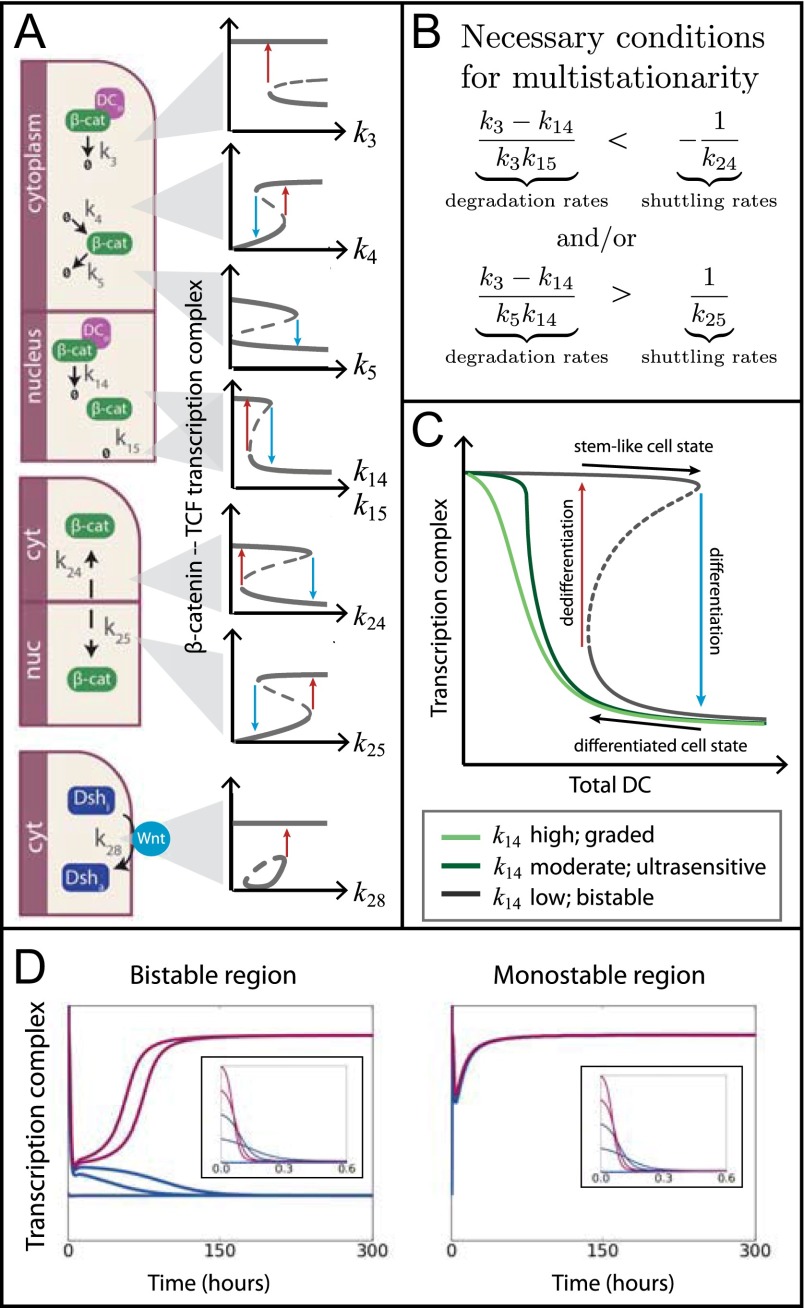
We test the injectivity of each model following graph-theoretic or Jacobian-based approaches used in CRNT (36–40). We find that only the Schmitz et al. (7) and the shuttle model fail injectivity and exhibit multistationarity. Further analysis reveals that the Schmitz et al. model is capable of at most two steady states, only one of which is stable (see SI Appendix for proofs). Whereas all of the previous models possess at most one positive stable steady state for any choice of the parameter values and conserved species’ concentrations, the shuttle model has the capacity for multistationarity and multistability. We find that when three species shuttle (e.g., Dsh, inactive DC, and β-catenin), the model exhibits two stable states; we proceed to analyze this version of the shuttle model. Previous mathematical studies have proven shuttling across compartments is a mechanism for multistability (41, 42).

For each model, we have a minimal collection $f_i$ of polynomial relations (including conservation laws) and $x_j$ of species. The model is injective if the determinant of the Jacobian matrix ($\partial f_i/\partial x_j$, which is polynomial in the parameters) has all positive or all negative coefficients: this ensures that the determinant is nonvanishing in the positive orthant where all feasible parameters lie. Although the shuttle model fails injectivity, we can find a set of eight sufficient conditions on the parameters (inequalities defining a semialgebraic set contained in the injective region of parameter space) that precludes multistationarity (SI Appendix). Negating these gives necessary, but not sufficient, conditions on the parameters for multistationarity, which depend explicitly on the degradation and shuttling rate constants (Fig. 2B). Because the parameter values are unknown, we compute an illustrative bifurcation diagram for a specific parameter set satisfying these necessary conditions. These diagrams are similar to dose–response curves in an experimental setting, and they demonstrate different behavior as the shuttling and degradation rate constants are varied (Fig. 2 A and C).

Fig. 2.

Bistability of shuttle model. (A) Bifurcations diagrams as a proof-of-concept for feasible shuttle model behavior. Reversible and irreversible behaviors are observed; however, this could change if parameter values are known. In each case the high state of target gene transcription corresponds to a stem-like state and the low state corresponds to a differentiated cell state. (B) Two of the eight necessary conditions for multistationarity of the shuttle model. (C) Model exhibits different behaviors as degradation parameter $k_{14}$ is varied: for low values, bistability; for moderate values, switch-like (ultrasensitive) response; and for high values, graded response. (D) Simulated trajectories for target gene transcription from five different initial conditions. In the bistable region we see two steady states reached; in the monostable region only the high (stem-like) state can be reached. Note that initial behavior in each region is similar: it is important to simulate for long enough to recover these differences in behavior.

Within a certain parameter region, we can either observe a graded response or switching and hysteresis behavior (Fig. 2C). The hysteresis loop shown by the black (stable state), blue (switch to committed state), and red (threshold switch to stem-like state) arrows enables switching at different thresholds between two stable steady states. Whereas over short timescales bi- and monostable behavior is indistinguishable (Fig. 2D), at steady state these differences emerge. In the bistable regime the low level of gene transcription is associated with a committed cell state and the high level with a stem-like phenotype over long time periods (Fig. 2D). As the value of a parameter, for example β-catenin shuttling into the cytoplasm $\left(k_{25}\right)$, decreases below a threshold, the bifurcation diagram predicts that cells will differentiate. If the shuttling rate was adequately increased, according to the diagram at these particular parameters, these cells would dedifferentiate to a stem-like state. If the parameter regime were known, bifurcation analysis and singularity analysis could also predict parameters governing reversible and irreversible behavior (e.g., $k_5$, irreversible in Fig. 2A).

If qualitative data showed a clear bistable switch, then the shuttle model would be the best model. However, given quantitative rather than qualitative data, how can we compare models?

Wnt Model Comparison via Parameter Inference.

Where competing models describe the same biological processes, one can perform parameter inference or model selection; such methods have been applied to a variety of problems in systems biology, ranging from cancer modeling to population genetics (43, 44).

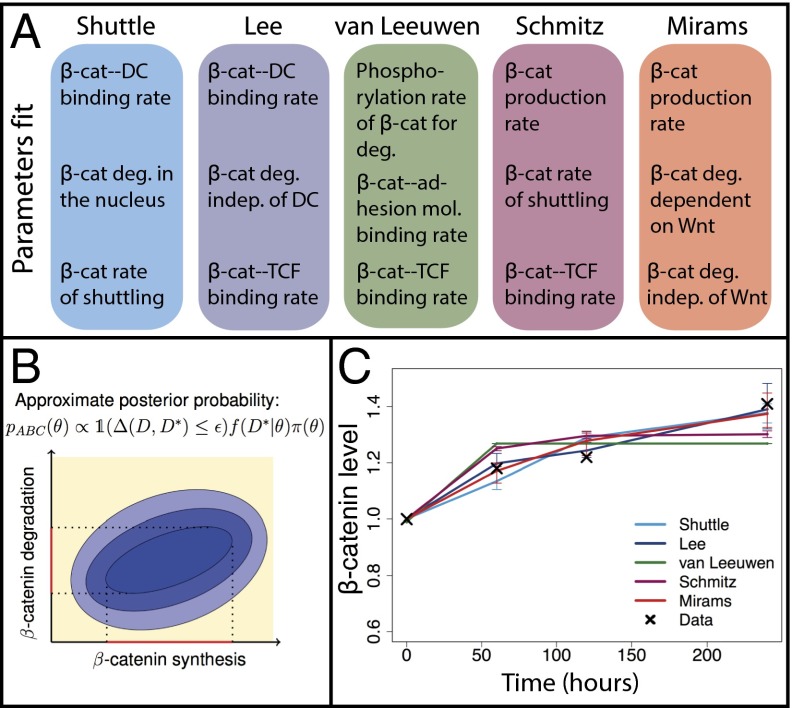
Inferring parameters from data via Bayesian analysis provides the posterior probability distribution over the parameters, from which more information can be gleaned than by point estimates alone. In Fig. 3B, we demonstrate the Bayesian inference procedure by considering a 2D subset of the parameter space (rates of β-catenin synthesis and β-catenin degradation). This panel shows how over successive iterations we can home in on the most probable region of parameter space given the data.

Fig. 3.

Bayesian parameter inference of Wnt signaling models. (A) Description of the parameters that are inferred for each of the models used to fit the data describing β-catenin dynamics following a Wnt stimulus. (B) Depiction of the posterior probability distribution used for approximate Bayesian computation. The sequentially decreasing region of probability (blue ovals) defines the joint space of two parameters. Here we show synthesis and degradation rates that are a subset of the full parameter space. This is applicable to any of the Wnt models considered. (C) Fits to the data simulated from the posterior distribution for each model (1,000 particles simulated). Bars represent the 5% and 95% intervals.

Each of the Wnt models has a different number of parameters. In an attempt to compare the models fairly and to reduce the size of the parameter space that we are searching, for each model we choose to fix all of the parameters (at estimated or arbitrary values) except for three. These three are allowed to vary and are used to fit the model to the Wnt/β-catenin time-course data recently published in ref. 22; see Materials and Methods for details. We chose the free parameters based on their point of influence on the pathway, targeting parameters with direct or near-direct influence on β-catenin dynamics (Fig. 3A); the fits we obtained after performing inference are shown in Fig. 3C. We see that even with only three degrees of freedom, good parameter fits are obtained for all of the models. Studying the posterior for each model reveals relationships between parameters: high β-catenin production and low β-catenin degradation rates are favored across models, but β-catenin-TCF binding rates vary considerably between models.

The disparity between model complexity and data availability prevents us from choosing between models based on model selection analysis. The problem could be addressed by simplifying models or collecting more data [additionally, experimental design influences Bayesian model selection results (45)]. Here, we proceed to use parameter-free methods to help guide experiments for model discrimination.

Parameter-Free Analysis of Wnt Models II: Matroids.

Instead of classifying the feasible behaviors of the whole system, we can use the finer structure of a model to derive relations in each part of the system, for example, the concentrations of species in a chemical reaction network at steady state. The matroid of a model is a list of

• i)the subsets of species that are related, and
• ii)the subsets of species whose concentrations are unrelated.

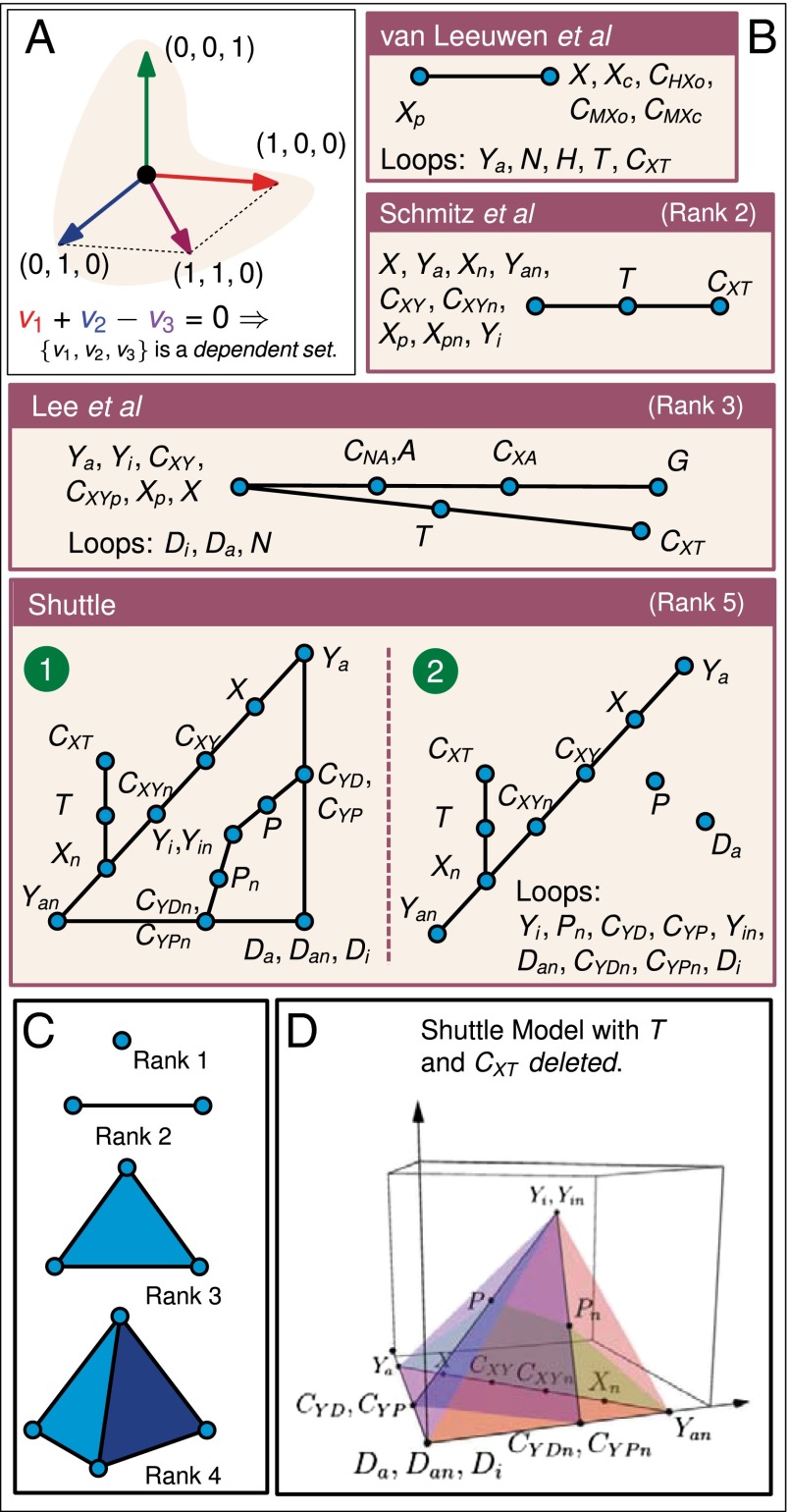
A matroid is a set with a notion of independence for its subsets. The classic example of a matroid is an arrangement of vectors. Suppose $v_1=\left(\mathrm{1,0,0}\right),v_2=\left(\mathrm{0,1,0}\right),v_3=\left(\mathrm{0,0,1}\right),v_4=\left(\mathrm{1,1,0}\right)$, as in Fig. 4A. A set of vectors is called “dependent” if it is linearly dependent, i.e., there is a set of scalars, not all zero, such that multiplying by the vectors and adding them together results in the zero vector. Here, $\left\{v_1,v_2,v_4\right\}$ is dependent because $v_1+v_2-v_4=\left(\mathrm{0,0,0}\right)$. If no such relation exists, the set is called “independent.” Any set of size 3 or smaller excluding 1-2-4 is independent (Fig. 4A). The matroid does not remember the coordinates of the vectors, only whether any subset is dependent or independent. The matroid construction in our discussion uses algebraic independence instead of linear independence. Explicitly, if there is a polynomial relationship that a collection of species satisfies at steady state, they are considered a dependent set. Note that this only considers relationships at steady state, where the possible species concentrations describe an algebraic variety. The independent and dependent sets of molecular players in each model may help compare models, guide experiments, and possibly reject models as described throughout this section.

Fig. 4.

Matroids allow for parameter-free model discrimination and prediction. (A) Depiction of linear dependence and independence in a vector space (see main text for additional information). (B) Schematic representation of the matroids for Wnt models. Each species represented by a loop is determined from the parameters alone; groups of species represented on a point can be determined by measurement of one of the species; groups of species represented on a line can be determined by measurement of two species. For notation used see SI Appendix, Table S1. (C) Schematic of rank, which corresponds to “what-to-measure.” So, for rank 1, measure 1 species to determine all of the others, for rank 2, measure 2, etc. (D) Deletion is a matroid-theoretic operation which removes a species x from the ground set of the matroid and only considers dependencies of the original model that excluded x. Deleting T and $C_{XT}$ gives a rank 4 matroid which can be visualized by planes in 3D space, as shown here.

We calculate the matroid of five Wnt signaling pathway models (four shown in Fig. 4B). Each model has a rank r, which dictates the number of species from the full set whose concentrations can be independently specified; taking measurements of r independent species determines (in terms of parameters) the values for all other species. Circuits are minimal dependent sets of species––they become important when we consider model discrimination. A matroid can be represented pictorially by point arrangements: the set of species labeling a point has rank 1, the set on a line has rank 2, the set on a two-dimensional plane has rank 3, and so on (Fig. 4C). Any two species labeling the same point are algebraically related, as are any three species on a line, any four species in a plane, etc.

We describe how the matroid of a model is computed in more detail in SI Appendix; the input is the polynomial ideal of steady-state relations and the output is a list of all circuits with their polynomial relations. Strictly speaking, a circuit is defined as a set of variables. However, in this application, we record the polynomial relations, because these are the support-minimal steady-state invariants. One approach involves computing a Gröbner basis for every elimination ordering, a feasible although lengthy computation for small systems. An alternative uses linear algebra to pinpoint the sets of variables appearing in invariants; then, it uses this information in conjunction with elimination or numerical algebraic geometry software to find polynomials (see ref. 46 for more detail). This approach is only now being implemented because algebraic matroids have only recently been adopted for applications, e.g., low-rank matrix completion (47).

The results of the matroid calculations (Fig. 4B) prompt biological insight; for illustration, we analyze the van Leeuwen et al. model (12). In this model, five species (called “loops”) can be determined from just the parameters. Among the others, any pair not including $X_p$ (β-catenin marked for ubiquitination) is dependent; therefore, an experiment measuring two of these concentrations could potentially reject the model if data are inconsistent with the relation. Assuming the model is consistent with data, measuring $X_p$ and any other nonloop is enough to determine all steady-state concentrations in terms of parameters.

Unlike the other models, the solution set for the shuttle model has two irreducible components (loosely, proper subsets that should be considered separately). The matroids for the two irreducible components both have rank 5. The number of components for a given model is determined by its algebraic structure; the number of components and real positive steady states are not analogous––multiple steady states may appear even when we have only one component. As described above, if we want to know all species concentrations in the shuttle model, five measurements must be made and these measurements should be chosen to be independent. For example, measuring TCF (T) and any four species not lying in the same plane in Fig. 4D would determine all species concentrations.

The minimal sets of species from the matroid can also be used to study part of the system. The partial information (relations on a subset of species) obtained from the matroid can be used as a self-consistency check between data and competing models and, in this way, serves as a method to rule out models. Model discrimination based on steady-state invariants has been performed for one specific ordering, so by including the matroid we can recover all possible steady-state invariants with different variables (full set of circuit polynomials, as defined in ref. 48), including conserved quantities. For example, Tan et al. (22) measured average β-catenin in the cytoplasm (X) and the nucleus $\left(X_n\right)$ after Wnt stimulation; we can investigate the relationship between these species. There are two models that include X and $X_n$ species: Schmitz et al. and shuttle. In the Schmitz et al. model, X and $X_n$ are encoded in the circuit polynomial

$$I=h_1\left(\delta \right)X^2+h_2\left(\delta \right)X_n^2+h_3\left(\delta \right)X{X}_n,$$

where $h_i,i\in \left(\mathrm{1,2,3}\right)$ are functions of the parameters (δ). From the data in ref. 22, we can test its compatibility with the model via a parameter-free method as described in ref. 24. Briefly, the method tests whether the data satisfy the Schmitz et al. circuit polynomial by checking whether there exist ${\tilde{h}}_i$, $i\in \left(\mathrm{1,2,3}\right)$ satisfying $I=0$, given these data. Clearly, if the circuit polynomial is satisfied then the coplanarity condition holds with ${\tilde{h}}_i=h_i$.

Model compatibility is determined by computing the coplanarity error $\left(\mathrm{\Delta }\right)$ via the singular value decomposition of the matrix

$$\left(\begin{array}{lll}{\widehat{X}}^2\hfill & {\widehat{X}}_n^2\hfill & \widehat{X}{\widehat{X}}_n\hfill \end{array}\right)\left(\begin{array}{c}{\tilde{h}}_1\\ {\tilde{h}}_2\\ {\tilde{h}}_3\end{array}\right)=0,$$

where $\widehat{X}$ denotes the observed value of species X. The null hypothesis that the model is compatible with the data can be rejected when the coplanarity error (normalized smallest singular value) is greater than a statistical bound as described in ref. 24 and SI Appendix, which is determined by the Gaussian measurement noise in the data and the invariant structure.

Before we test the models with data from ref. 22, we simulate data from both the shuttle and Schmitz et al. models. We draw random parameters from a lognormal distribution and then simulate 100 replicate measurements of $\left(X,X_n\right)$ with noise [we perturb the data with noise $\sim {10}^{-6}N\left(\mathrm{0,1}\right)$]. We test model compatibility at 5% significance level; results of the coplanarity test identify that the Schmitz et al. model is incompatible with data generated by the shuttle model (${\mathrm{\Delta }}_{Schmitz}=\mathrm{64,820}$, where the compatibility cutoff is 11.15). Unsurprisingly, the Schmitz et al. model is compatible with data generated by itself (${\mathrm{\Delta }}_{Schmitz}=3.768$, cutoff $=11.15$). We use the three replicates of X and $X_n$ from ref. 22 at $t=\mathrm{120,240}$ min, and assume the data are close to steady state. Because the noise in the data is unknown, we test different noise levels and are able to rule out the Schmitz et al. model up to noise $\sim {10}^{-4}N\left(\mathrm{0,1}\right)$ (SI Appendix). By consulting the matroid of the shuttle model, we find that X and $X_n$ are independent, thus no circuit polynomial exists and any data are compatible with the shuttle model (an additional species is required to form a circuit polynomial). Thus, as demonstrated, matroids guide experiment design to discriminate between models with minimal required measurements.

Conclusions

There is a wealth of mathematical and experimental research on Wnt signaling, aimed at understanding the pathway well enough to target Wnt-implicated diseases. There are two significant challenges to overcome. The disparity between models and data that we have highlighted via Bayesian inference prevents us from constraining parameter values in a manner that often helps to elucidate mechanisms and predict function. The second challenge is the gap between in vitro and in vivo studies, and the corresponding differences in parameter values. This is supported by evidence on the variation in parameter estimates between naive and crowded (physiological) in vitro molecular experiments (49, 50). To gain insight into these complex systems described by complicated models, we must evade this parameter problem.

Parameter-free approaches can provide additional information about the β-catenin/Wnt pathway. Based on injectivity–multistationarity analysis, we find that the shuttle model predicts the possibility of a regulatory switch, acting early in the cell fate determination pathway. Other systems have also reported early checkpoints in cell fate signaling in activation of apoptosis through receptor–ligand binding (51, 52). We identify the possibility of important roles for spatial localization and degradation in cell fate switching. In the Erk pathway, it is also seen that either localization (via shuttling) or degradation by apoptosis is crucial for bistable switching, both mathematically and experimentally (42, 53–55). We report for the first time, to our knowledge, that a combination of these processes governs the dynamical regime.

By computing the algebraic matroid of different Wnt models, we can characterize the dependencies between species. The matroid results enable us to guide experiments (which species to measure) to discriminate between models with data, all of the while not requiring parameter values. The mechanisms for bistability identified above are of course not exclusive and one could imagine many other models exhibiting bistability via different mechanisms. This scenario could prompt previously unidentified insight using our model discrimination framework, now with multiple bistable models.

Given the current (and growing) complexity of models across a wide range of topics, tools such as those demonstrated here offer strong potential for testing models and for predictions to be made. In addition, we provide possible directions for future experimentation to narrow the gap between data and models, and, through our predictions, help to unravel the workings of the intricate and essential Wnt pathway.

Materials and Methods

Bayesian Inference.

Model selection in systems biology can be performed using Bayesian inference (56). Here we perform parameter inference for model selection using approximate Bayesian computation, which forgoes evaluation of the likelihood function and instead calculates the (here Euclidean) distance between model and data (57), implemented in the ABC Sys-Bio package (58). For each model we compare the total free β-catenin level (in some cases addition of two species) with the data provided by ref. 22.

Multistability.

Determining whether a model is capable of multiple responses can be tested using injectivity. The injectivity of each model was determined using CRNT toolbox (59); for those that were not injective (Schmitz et al. and shuttle), we computed the determinant of the Jacobian following (42), and analyzed the sign of the coefficients in Mathematica (Version 9.0; Wolfram Research). Bifurcation diagrams were computed using Oscill8 (available at oscill8.sourceforge.net/doc) and visualized with MATLAB (R2013a; The MathWorks).

Matroids.

Matroid computation is performed by structured variable elimination on eligible polynomial systems. This is carried out using symbolic algebra software Macaulay2 (60) with the aid of packages presented in ref. 46. Code is available at math.berkeley.edu/∼zhrosen/matroids.html. When the set of steady-state solutions has multiple irreducible components, the matroid was computed for each to assess the independence structure in each regime. Isolated points in the solution set were not analyzed, as the matroid is trivial. Model discrimination was performed in Sage (available at cloud.sagemath.com) following the method presented in ref. 24.