The fingerprint of climate trends on European crop yields

Significance

Agriculture is one of the economic sectors most exposed to climate change impacts, but few studies have statistically connected long-term changes in temperature and rainfall with yields. Doing so in Europe is particularly important because yields of wheat and barley have plateaued since the early 1990s and climate change has been suggested as a cause of this stagnation. Here, we show that the impact of climate trends can be detected in the pattern of long-term yield trends in Europe. Although impacts have been large in some areas, the aggregate effect across the continent has been modest. Climate trends can explain 10% of the slowdown in wheat and barley yields, with changes in agriculture and environmental policies possibly responsible for the remainder.

Abstract

Europe has experienced a stagnation of some crop yields since the early 1990s as well as statistically significant warming during the growing season. Although it has been argued that these two are causally connected, no previous studies have formally attributed long-term yield trends to a changing climate. Here, we present two statistical tests based on the distinctive spatial pattern of climate change impacts and adaptation, and explore their power under a range of parameter values. We show that statistical power for the identification of climate change impacts is high in many settings, but that power for identifying adaptation is almost always low. Applying these tests to European agriculture, we find evidence that long-term temperature and precipitation trends since 1989 have reduced continent-wide wheat and barley yields by 2.5% and 3.8%, respectively, and have slightly increased maize and sugar beet yields. These averages disguise large heterogeneity across the continent, with regions around the Mediterranean experiencing significant adverse impacts on most crops. This result means that climate trends can account for ∼10% of the stagnation in European wheat and barley yields, with likely explanations for the remainder including changes in agriculture and environmental policies.

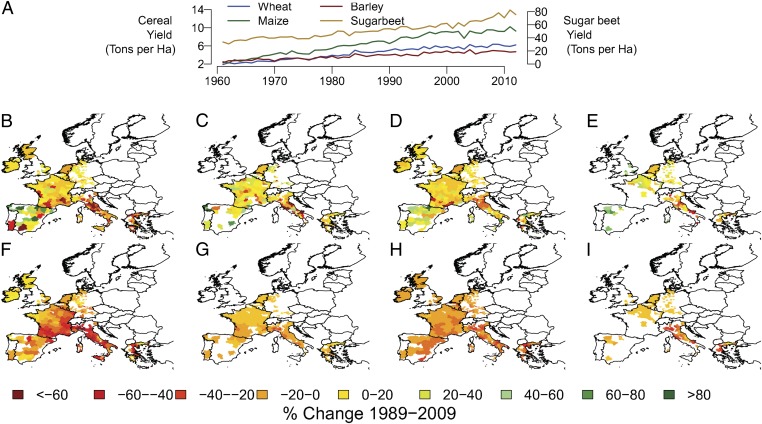
Europe has experienced a stagnation of yields for some crops, particularly wheat and barley, with a plateau since the early to mid-1990s (Fig. 1A) (1, 2). Explanations for this stagnation have focused on changing agricultural policy and, to a lesser extent, on shifting climate patterns (3, 4). Much of Europe saw the introduction of more stringent environmental policies during the 1990s, as well as the decoupling of subsidy payments from farm production in the European Union, both of which would be expected to lower the intensity of cereal production (5, 6). In addition, warming trends in the region have been large relative to natural variability and could be expected to negatively affect yields, particularly in southern Europe (SI Appendix, Fig. S1) (7, 8).

Fig. 1.

Patterns and time evolution of crop yields in Europe and the predicted impacts of climate trends. (A) Area-weighted yields of the four crops examined in this paper for the countries included in the study, 1960–2010 (SI Appendix, Table S1) (17). (B–E) Maps of the observed linear trend in yield in 1989–2009 for wheat (B), maize (C), barley (D), and sugar beet (E) (25). Maps of the expected change in yield based on growing-season temperature and precipitation trends in 1989–2009 (27, 28) and the yield response functions described by Moore and Lobell (8) (SI Appendix, Figs. S3 and S4) for wheat (F), maize (G), barley (H), and sugar beet (I). White shows areas not included in the study due to insufficient data.

Existing empirical evidence for either explanation is typically weak, taking the form of coincidence in the direction and timing of expected climate or policy effects with yield trends, so the relative importance of these mechanisms has not been rigorously demonstrated (3, 9). More persuasive detection and attribution studies instead identify impacts using a distinctive spatial pattern of trends associated with climate change forcing (10, 11). Because the spatial distribution of long-term trends is less likely to be correlated with other variables, these studies are better able to make a case for climate’s causal effect on the outcome of interest. Fig. 1 B–E shows the observed trends in yields of wheat, maize, barley, and sugar beet in Europe between 1989 and 2009. Fig. 1 F–I shows the trends in yield that would have been expected given observed changes in growing-season temperature and precipitation and the sensitivity of crops to those changes (8). Observed trends are both more positive and more spatially heterogeneous than the predicted trends, which would be expected given that the latter do not include the effects of technological improvements or of changing economic or policy conditions. Nevertheless, formal statistical tests can reveal whether or not the distinctive pattern, or fingerprint, of climate trend impacts is embedded within the observed pattern of long-term yield trends.

Formal detection of a climate change signal and the attribution of that signal to anthropogenic greenhouse gas emissions has been successful in many physical and some biological systems (10–12). However, few studies have attributed changing yield pattern to climate trends. This analysis is complicated by two factors. First, the expected response of agriculture to a given temperature or precipitation forcing is determined by an imperfectly known response function. This response uncertainty must be accounted for in determining whether or not climate change has had a statistically discernable impact. Second, farmers may or may not be adapting to the climate change they have experienced, creating additional uncertainty in the expected response of agriculture to climate forcing (13). This potential for adaptation means there are two response functions relevant to the detection (and prediction) of climate change impacts: the short-run response function that includes limited or no adaptation, and the long-run response function that includes full adaptation (8).

In this paper, we first develop two general statistical tests that can be applied to the detection of impacts and adaptation in any managed system affected by climate change and report the power of these tests under a range of parameter values. We then apply these tests to Europe to determine whether climate trends have affected yields and, if so, to what extent these impacts can explain the stagnation of European cereal yields.

Statistical Tests for Climate Change Impacts and Adaptation

Here, we present two formal statistical tests, the first designed to distinguish a system affected by climate trends from one not affected, and the second to distinguish a system adapting rapidly from one not adapting. Both tests rely on knowing the climate response function, namely how the outcome of interest $y$ should respond to changes in climate variables $w$, either including adaptation [the long-run response function, $y=f_{LR}\left(w\right)$] or not including adaptation [the short-run response function, $y=f_{SR}\left(w\right)$]. These response functions could be determined statistically (the approach in this paper), using a process-based model, or from known theoretical relationships. In many cases, the response functions may be nonlinear and in most cases will contain uncertain parameters.

As in other detection and attribution studies, these tests rely on comparing the spatial pattern of long-term trends in the variable of interest to what would be expected given the observed long-term trends in climate (14). Three linear time trends are calculated for each region $i$: the observed trend, the predicted long-run trend, and the predicted short-run trend:

$$y_{it}={\alpha }_0+Observed\text{\_}Tren{d}_i\ast t+{\epsilon }_{it},$$

$$f_{LR}\left(w_{it}\right)={\alpha }_1+Predicted\text{\_}Trend\text{\_}L{R}_i\ast t+{\epsilon }_{it},$$

$$f_{SR}\left(w_{it}\right)={\alpha }_2+Predicted\text{\_}Trend\text{\_}S{R}_i\ast t+{\epsilon }_{it}.$$

The region-specific trends $Predicted\text{\_}Trend\text{\_}L{R}_i$ and $Predicted\text{\_}Trend\text{\_}S{R}_i$ give a distinctive spatial pattern of the expected climate change impact that can be compared with the observed trends. The climate variables used in this paper ($w_{it}$) are the average growing season temperature and rainfall in subnational region $i$ in year $t$.

Our first test for the detection of climate change impacts (test 1) is based on the regression:

$$Observed\text{\_}Tren{d}_i={\beta }_0+{\beta }_{1}Predicted\text{\_}Tren{d}_i+{\epsilon }_i,$$ [1]

where $Predicted\text{\_}Tren{d}_i$ could be either from the short- or long-run response function. Here, we report results using the long-run response function because it includes fewer parameters, but results are robust to this decision. Because this specification includes the intercept term ${\beta }_0$, which demeans both the observed and predicted trends, the test relies on the spatial pattern of trends around the mean to estimate the climate signal, a characteristic “fingerprint,” rather than the absolute magnitude of change. Our statistical test is simply the following: H₀: climate trends have no explanatory power, ${\beta }_1=0$; H₁: climate trends have explanatory power, ${\beta }_1>0$.

This hypothesis is tested using the test statistic ${\tau }_1=\widehat{{\beta }_1}/\sqrt{\widehat{Var}\left(\widehat{{\beta }_1}\right)}$. In the standard regression model, ${\tau }_1$ would be normally distributed under the null hypothesis. However, in this case, uncertainty in the response function $f\left(w\right)$ means that we cannot rely on the standard normal approximation. Instead, we estimate the distribution of ${\tau }_1$ under the null using a bootstrap-t procedure that accounts for uncertainty in the parameters of the response function and therefore in the estimation of predicted trends (Methods). The 1-α quantile of this distribution then gives us the critical value for a test of size α. We compare ${\tau }_1$ against the critical value and reject the null if ${\tau }_1$ is larger, meaning it would be unlikely to occur if the null were true. The value of α is arbitrary, but is conventionally set at 5%, the value we use in this paper.

The second test (test 2) is designed to distinguish a system adapting rapidly from one adapting slowly to climate change impacts. It relies on two regressions:

$$Observed\text{\_}Tren{d}_i={\gamma }_0+{\gamma }_{1}Predicted\text{\_}Trend\text{\_}S{R}_i+{\epsilon }_i,$$ [2]

$$Observed\text{\_}Tren{d}_i={\gamma }_2+{\gamma }_{3}Predicted\text{\_}Trend\text{\_}S{R}_i+{\gamma }_4\left(Predicted\text{\_}Trend\text{\_}L{R}_i-Predicted\text{\_}Trend\text{\_}S{R}_i\right)+{\epsilon }_i.$$ [3]

If farmers have adapted quickly to the climate change experienced, then model 3 should be significantly better at explaining the variance in observed trends than model 2 and therefore should have significantly smaller residuals. We test this with the F statistic ${\tau }_2=\left(RS{S}_2-RS{S}_3\right)/\left(RS{S}_3/\left(n-3\right)\right)$, where $RS{S}_2$ is the residual sum of squares from model 2 and $RS{S}_3$ is the residual sum of squares from model 3. The hypotheses are as follows: H₀: farmers are not adapting, ${\tau }_2=0$; H₁: farmers are adapting, ${\tau }_2>0$.

We use the difference between the long- and short-run predicted trends rather than including them separately in the unrestricted model (model 3) because $Predicted\text{\_}Trend\text{\_}L{R}_i$ and $Predicted\text{\_}Trend\text{\_}S{R}_i$ are likely to be correlated. Under standard statistical assumptions, ${\tau }_2$ would have an F distribution, but in this case we again obtain the critical value by imposing the null hypothesis and using a multistage pairs bootstrap to give the distribution of ${\tau }_2$ under the null (Methods).

Before making statistical inferences, it is important to understand the power of the test to detect the signal of interest. If the test has low power, then the probability of a false negative is high and negative results cannot be interpreted either as evidence that climate change has had no impact (test 1) or that there has been no adaptation to climate change (test 2). SI Appendix, Table S3 and Figs. S5 and S6 show the results of a simulation analysis designed to determine the power of tests 1 and 2 under a range of reasonable conditions. These results suggest that test 1 should have high power under many conditions. Even if the magnitude of climate trends is small (as is the case in detection and attribution analyses performed today), power can be high if the noise (variation in yield trends from factors not included in the model) is low and variance in the climate trends and baseline climates is large, producing a distinctive signal. For larger climate trends, power is consistently high for most parameter combinations.

In contrast, the simulation suggests that power for test 2 is uniformly very low. Even given large climate trends and large differences in the short- and long-run response curves, power is frequently below 50% and only rarely exceeds 80%. Although arbitrary, the acceptable minimum test power is typically considered to be at least 80%. Thus, in most contexts, reliable statistical detection of climate change adaptation is likely to be challenging. Power may be higher if there is more variable adaptation potential across the landscape (i.e., if the adaptation “fingerprint” is more distinctive) or if specific adaptive changes are being examined. However, in general, these results suggest that studies finding no evidence for adaptation should, in the absence of a power analysis, be interpreted with caution because the probability of false negatives is likely high and a system adapting to climate change cannot be reliably distinguished from one not adapting.

Results

SI Appendix, Fig. S7 shows the simulated power of tests 1 and 2 using the actual climate trends, baseline climate, and noise observed for five European crop yields (Methods, SI Appendix, Table S4). The short- and long-run response functions were determined statistically using a combination of cross-sectional and interannual variation in yields and growing-season weather (Methods, SI Appendix, and ref. 8). Consistent with the results of the sensitivity analysis, the power of test 2 is uniformly low. The power of test 1 varies but exceeds 80% for wheat, maize, barley, and sugar beet yields. Power for oilseeds is lower largely because the parameters of the response function are imprecisely estimated (8). This simulation assumes 125 independent data points and therefore, because yields are in reality correlated over space and not independent, gives us an upper bound on test power for our data.

We therefore perform test 1, the detection of climate trend impacts, for wheat, maize, barley, and sugar beet yields. Table 1 shows the results of this statistical test, controlling for linear changes in farm-gate prices and coupled subsidy payments (Methods). We find that the climate change fingerprint is statistically detectable for all crops: the value of the test statistic ${\tau }_1$ is highly unlikely under the null hypothesis, and thus in all cases we are able to reject, at a test size of 5%, the hypothesis that long-term climate trends have not affected the development of crop yields in Europe. In other words, areas where temperature and precipitation changes realized between 1989 and 2009 would be expected to negatively impact yields have seen yields grow at slower rates compared with areas where climate trends would be expected to have had more positive impacts. The regression coefficients for maize and sugar beet are fairly close to 1, but the wheat and barley coefficients are less than 1, suggesting sensitivity to climate change may be overestimated in the response functions for these crops (15).

Table 1.

Results of test 1, the detection of the impact of long-term climate trends on European crop yields

Row name	Wheat yield	Maize yield	Barley yield	Sugar beet yield
Regression coefficient $\left({\beta }_1\right)$	0.41	1.39	0.50	0.82
SE	0.10	0.88	0.34	0.81
Test statistic (${\tau }_1$)	4.03	1.58	1.47	1.00
P(${\tau }_1|H_0$)	<0.002	0.002	0.012	0.02
Degrees of freedom	349	267	341	183
Adjusted R2	0.07	0.10	0.06	0.28

The null hypothesis is rejected for all crops at the test size of 5%. Significance levels are determined by a block-bootstrapping procedure that includes resampling the parameters of the climate-yield response function (Methods). Although centered on zero, this distribution is skewed to the left, meaning critical values are lower than under standard normality assumptions [critical values for a one-tailed test under the normal approximation are 1.64 (5%) or 1.28 (10%)].

SI Appendix, Table S5 gives results for two alternative specifications—one that includes country fixed effects and one that looks only at the impacts of temperature changes, controlling for precipitation change (Methods). Adding country fixed effects reduces the risk that results are being driven by unobserved differences in economic or policy conditions between countries (omitted-variable bias). However, because long-term temperature and precipitation trends vary smoothly across space, fixed effects can also remove a large component of the climate signal, exacerbating the effects of measurement error and causing a downward bias on the estimated coefficient (attenuation bias). SI Appendix, Table S5 shows that, as expected, country fixed effects reduce the magnitude of the estimated coefficient $\widehat{{\beta }_1}$, although all results are still significant at the 10% level. For wheat yield, adding country fixed effects substantially reduces the magnitude of the regression coefficient, suggesting that this result in particular is driven by intercountry rather than intracountry variation.

Looking at the effect of temperature alone ignores the impact of changing precipitation patterns on yields, but temperature trends are more likely related to anthropogenic climate change than rainfall changes. Although a formal attribution of warming trends to greenhouse gas emissions is outside the scope of this paper, temperature trends tend to be large relative to natural variability and positive across much of Europe (SI Appendix, Fig. S1). Power for temperature effects on maize yields is very low so this crop drops out of the analysis, but results for wheat, barley, and sugar beet are consistent with an effect of long-term temperature trends on yields, although the result for wheat is not statistically significant (P = 0.14; SI Appendix, Table S5).

Discussion

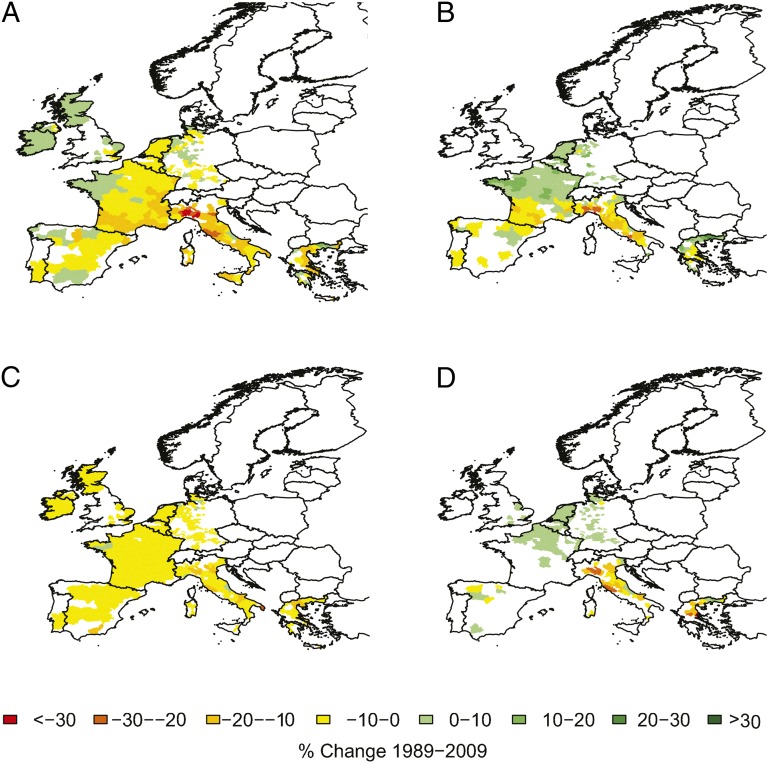
Temperature and precipitation changes in Europe have reduced average production-weighted continent-wide wheat and barley yields by 2.5% and 3.8% and have increased sugar beet and maize yields by 0.2% and 0.3% relative to what they would otherwise be (Fig. 2). These aggregate effects are fairly small, but the impacts have not been evenly distributed. Warmer regions in southern Europe have suffered most from warming, and in Italy this effect has been compounded by drying, leading to yield declines of 5% or more. In cooler regions such as the United Kingdom and Ireland, the more limited impacts of warming have been offset by benefits from increasing rainfall (Fig. 3). These results are consistent with previous work that has found long-term climate trends should have increased sugar beet yields in the United Kingdom, decreased wheat yields in France, and that the yield potential of wheat and barley has declined over much of Europe due to warming (3, 9, 16).

Fig. 2.

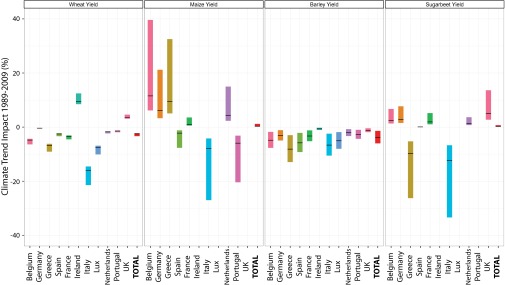
Impacts of growing-season temperature and precipitation trends in 1989–2009 on European crop yields by country and for the whole region (Total). Impacts are weighted by regional production of the relevant crop in 1989–1994 (Methods). The black line shows impacts calculated using the regression point estimate (Table 1), and the colored bars show the 90% confidence interval obtained by inverting a two-tailed hypothesis test of size 10% (Methods). This distribution is skewed for wheat, maize, and sugar beet yields, which is why the bars are asymmetric around the point estimate.

Fig. 3.

Spatial fingerprint of trends in growing-season temperature and precipitation in 1989–2009 on wheat (A), maize (B), barley (C), and sugar beet (D) yields. The maps show the predicted trends in crop yield due to temperature and precipitation changes (Fig. 1 F–I) corrected by the regression coefficient $\widehat{{\beta }_1}$(Table 1). White shows areas not included in the study due to insufficient data.

During the 1980s, yields of both wheat and barley were growing at ∼0.12 tons per ha per y (2, 17) (Fig. 1A). If they had continued growing at that rate after 1995, wheat and barley yields would be 30% and 37% higher today, respectively. This means that climate trends can account for ∼10% of the yield stagnation observed in Europe over the last two decades. Changes in agricultural subsidies and environmental policies, as well as proximity to possible biophysical yield limits, remain likely explanations for the major component of declining yield growth (2, 4, 5). Since 1989, Europe has seen major reforms to its agricultural subsidy policies. Although total support as a fraction of farm revenue has stayed essentially constant, the form of support shifted from price support to direct subsidy payments coupled to production following reforms in 1993, and to decoupled payments not dependent on production after 2004. This means that the fraction of farm support linked to commodity output declined steadily from 87% in 1989 to 27% in 2009 (18) (SI Appendix, Fig. S10). This change might be expected to reduce the incentive for intensive cultivation and therefore lower the rate of yield gains. In addition, changing environmental policies restricted the use of fertilizer application and may have limited yield growth (3, 19).

This paper is the first (to our knowledge) to present evidence for the distinctive fingerprint of long-term climate trends on European crop yields and to formally quantify the contribution of a changing climate to yield stagnation in Europe. We find evidence that trends in growing-season temperature and precipitation have affected wheat, maize, barley, and sugar beet yields but estimate that the mean effect across Europe has been relatively small, explaining ∼10% of the slowdown in wheat and barley yield gains since the early 1990s. Impacts have been larger in some regions: the combination of warming and drying trends in Italy has been particularly damaging, causing yields losses of 10% or more relative to baseline. Although the attribution of European climate trends to greenhouse gas emissions is beyond the scope of this paper, temperature trends are both large relative to natural variability and positive across much of Europe, suggesting they may more likely be linked to anthropogenic climate change than the weaker and more variable precipitation trends (SI Appendix, Fig. S1). We estimate that, in the absence of the warming experienced over Europe since 1989, wheat, barley, and sugar beet yields would be 3.5%, 3.8%, and 2.1% higher than they are today (SI Appendix, Fig. S9). Finally, this paper presents a formal statistical test for the detection of adaptation to climate change impacts using the difference in projected impacts made including and excluding adaptations. Our simulation analysis shows that the power of this test is likely to be very low in most contexts. Therefore, null results showing no evidence for adaptation to climate change should be interpreted with caution because the probability of false negatives is high, particularly given the relatively small amount of climate change experienced to date.

Methods

Response Function Estimation.

All variables were first detrended by fitting linear time trends at the subnational region level. Short- and long-run yield response functions to temperature and precipitation changes were then jointly estimated for each crop using balanced panel data from 1989 to 2009 (8). The long-run response function is a quadratic in both growing-season temperature and rainfall and is estimated using cross-sectional variation in long-term climate, therefore implicitly including substantial adaptation (20). The short-run response function includes an additional penalty term associated with weather that is different from the expected climate and is estimated using interannual variability. It therefore captures the effect of short-term weather variation that is only partly anticipated by farmers and so includes much less adaptation. The preferred model includes controls for soil quality, altitude, irrigation, subsidies, as well as country fixed effects that control for time constant variation between countries (21). Because the long-term linear trends in climate and yield for each region are removed before estimation, they do not influence the response function and therefore ensure the same data are not used to both train the response model and test for the impact of long-run changes in climate. The variance–covariance matrix of response function parameters are estimated using a parametric block-bootstrap at the country level. The estimating equation, response curves, and SEs are given in SI Appendix, with additional information in the study by Moore and Lobell (8).

Bootstrap of the Null Distribution.

Any detection and attribution study looking at the effect of climate on some outcome of interest (i.e., yields) must account for the fact that the response of that outcome to a given change in climate is uncertain. We account for this additional source of uncertainty by, as part of each bootstrap, creating a new response function by resampling the joint normal distribution of response function parameters and using this to recalculate the predicted trends in yields. Then these new data are resampled, as in a traditional bootstrap, to calculate the distribution of the test statistic under the null (22).

The bootstrap for test 1 uses a version of the bootstrap-t procedure (23). This involves first calculating the regression coefficient $\widehat{{\beta }_1}$ (Eq. 1), resampling the parameters of the response function and recalculating predicted trends in yields (to account for uncertainty in the yield response function), resampling the data by country (to account for spatial autocorrelation within countries), and calculating the bootstrapped coefficient $\widehat{{\beta }_{1\text{\_}b}}$. The variance of $\widehat{{\beta }_{1\text{\_}b}}$ is calculated by repeating the previous steps, using the bootstrapped sample, 500 times to give the bootstrapped test statistic ${\tau }_{1\text{\_}b}=\left(\widehat{{\beta }_{1\text{\_}b}}-\widehat{{\beta }_1}\right)/\left(\sqrt{\widehat{Var}}\left(\widehat{{\beta }_{1\text{\_}b}}\right)\right)$. Because $\widehat{{\beta }_1}$ is subtracted in calculating ${\tau }_{1\text{\_}b}$, this imposes the null hypothesis (i.e., that ${\tau }_{1\text{\_}b}$ is equal to zero, in expectation) and so gives the distribution of ${\tau }_1$ under the null (22). This procedure is repeated 500 times and the 1-α quantile of the resulting distribution used as the critical value of a one-tailed test of size α. Cameron et al. (23) show that this bootstrap-t procedure improves statistical inference in contexts with clustered data and a small number of clusters relative to the standard cluster-robust errors.

For test 2, each bootstrap is performed by first resampling the parameters of the response function from their joint distribution, recalculating the predicted yield trends using these parameters, and then resampling the data by country. Eq. 2 is then estimated using the bootstrap sample and $RS{S}_{2\text{\_}b}$ calculated as the residual sum of squares from that regression. The observed trends are then regressed on the short-run predicted trends and a random variable with the same mean and variance as the difference between the long- and short-run predicted trends and $RS{S}_{3\text{\_}b}$ calculated as the residual sum of squares from this regression. The bootstrapped test statistic is calculated as ${\tau }_{2\text{\_}b}=\left(RS{S}_{2\text{\_}b}-RS{S}_{3\text{\_}b}\right)/\left(RS{S}_{3\text{\_}b}/\left(n-3\right)\right)$. Because the random variable added in the second regression has no true explanatory power, this procedure imposes the null hypothesis in generating the bootstrap and therefore gives the distribution of ${\tau }_2$ under the null. This procedure is repeated 500 times and the 1-α quantile of the resulting distribution used as the critical value of a test of size α. Step-by-step versions of these procedures are given in SI Appendix for clarity.

Estimation of Climate Trend Impacts on Yields.

Power for tests 1 and 2 was determined using a simulation exercise parameterized using the European crop and climate data. Data were simulated by creating 125 predicted trends based on the distributions of baseline climates and long-term climate trends in the dataset, and the estimated long- and short-run response functions. White noise was then added with a variance determined by the actual unexplained variance in long-term yield trends in the data to simulate the observed yield trends. Tests 1 and 2 were performed using the simulated data and the bootstrapping procedure described above. This was repeated 500 times to determine the probability of rejecting the null hypothesis for each crop. SI Appendix, Table S4 shows the parameter values used for this simulation and additional details on the simulation analysis are given in SI Appendix. We also run a simulation to estimate the probability of rejecting a true null hypothesis using test 2 and find this is very close to the desired test size of 5% (SI Appendix, Fig. S8).

We conducted tests for which the power exceeds 80% (test 1 for wheat, maize, barley, and sugar beet yields). Linear trends in growing-season temperature and precipitation were estimated for the period 1989–2009 for each region in countries included in the yield response model (SI Appendix, Table S1) with at least 10 y of data. The growing season was defined using the observed planting and harvest dates in each region (24). These trends were combined with the baseline climate (1959–1988 mean) and the long-run response function to generate the predicted trends in yields using a local linear approximation of the nonlinear response function:

$$Predicted\text{\_}Trend\text{\_}Tem{p}_i={\theta }_{1,1}\left(\overline{T}+\mathrm{\Delta }T\right)+{\theta }_{2,1}{\left(\overline{T}+\mathrm{\Delta }T\right)}^2-\left({\theta }_{1,1}\overline{T}+{\theta }_{2,1}{\overline{T}}^2\right),$$

$$Predicted\text{\_}Trend\text{\_}Preci{p}_i={\theta }_{1,2}\left(\overline{P}+\mathrm{\Delta }P\right)+{\theta }_{2,2}{\left(\overline{P}+\mathrm{\Delta }P\right)}^2-\left({\theta }_{1,2}\overline{P}+{\theta }_{2,2}{\overline{P}}^2\right),$$

where ${\theta }_{i,j}$ are the parameters of the long-run response function (SI Appendix, Eq. S1), $\overline{T}$ and $\overline{P}$ are the baseline growing-season temperature and precipitation climatologies, and $\mathrm{\Delta }T$ and $\mathrm{\Delta }P$ are the linear change in growing-season weather between 1989 and 2009.

The observed linear trends in crop yields between 1989 and 2009 are used as the dependent variable. Trends in farm-gate prices between 1989 and 2009 and trends in coupled crop subsidies per hectare of cropland between 1993 and 2009 are included as controls (25). This subsidy control captures the change over this time period from subsidy payments coupled to production to decoupled payments (SI Appendix, Fig. S10). The preferred estimating equation is therefore the following:

$$Observed\text{\_}Tren{d}_i={\beta }_0+{\beta }_1\left(Predicted\text{\_}Trend\text{\_}Tem{p}_i+Predicted\text{\_}Trend\text{\_}Preci{p}_i\right)+{\beta }_{2}Price\text{\_}Tren{d}_i+{\beta }_{3}Subsidy\text{\_}Tren{d}_i,$$ [4]

where the coefficient of interest is ${\beta }_1$, the combined effect of temperature and precipitation changes on yields. SI Appendix, Table S5 also presents two alternative specifications, one that includes country fixed effects in Eq. 4 and one that examines only the effect of changing temperature, $Predicted\text{\_}Trend\text{\_}Tem{p}_i$, including $Predicted\text{\_}Trend\text{\_}Preci{p}_i$ as a control.

The corrected effect of climate trends on yield in region i is calculated as ${\widehat{\beta }}_1\ast \left(Predicted\text{\_}Trend\text{\_}Tem{p}_i+Predicted\text{\_}Trend\text{\_}Preci{p}_i\right)$ and is shown in Fig. 3. The mean effect in country j is a weighted average:

$$Impac{t}_j={\displaystyle \sum }_{i\in j}{\widehat{\beta }}_1\ast \left(Predicted\text{\_}Trend\text{\_}Tem{p}_i+Predicted\text{\_}Trend\text{\_}Preci{p}_i\right)\ast \frac{P_i}{P_j},$$

where $P_i$ is the mean production in region i over the 5 y at the start of the dataset (1989–1994) and $P_j$ is the same for country j. This assumes that the same climate response (${\widehat{\beta }}_1$) applies over the whole region because the data available does not allow for a more disaggregated analysis. Ninety percent confidence intervals for the aggregated effect in each country were obtained by inverting the 0.05 and 0.95 quantiles of the bootstrapped distribution of ${\tau }_1$ to obtain coefficients corresponding to the edges of the rejection region of a two-tailed hypothesis test of size 10% (26).