Abstract
The absorption and fluorescence spectra of poly(p-phenylenevinylene) (PPV) oligomers with up to seven repeat units were theoretically investigated using the algebraic diagrammatic construction method to second order, ADC(2), combined with the resolution-of-the-identity (RI) approach. The ground and first excited state geometries of the oligomers were fully optimized. Vertical excitation energies and oscillator strengths of the first four transitions were computed. The vibrational broadening of the absorption and fluorescence spectra was studied using a semiclassical nuclear ensemble method. After correcting for basis set and solvent effects, we achieved a balanced description of the absorption and fluorescence spectra by means of the ADC(2) approach. This fact is documented by the computed Stokes shift along the PPV series, which is in good agreement with the experimental values. The experimentally observed band width of the UV absorption and fluorescence spectra is well reproduced by the present simulations showing that the nuclear ensemble generated should be well suitable for consecutive surface hopping dynamics simulations.
1. Introduction
Organic π-conjugated polymers have several important applications. One of the most fascinating and challenging research frontiers in this field is the development of organic solar cells. In organic photovoltaic systems, exciton (electron–hole pair) transfer followed by population transfer of electrons occurring via charge transfer (CT) states to a donor/acceptor (D/A) boundary is crucial for the efficiency of the photovoltaic cell.1 Because of the structural flexibility of these chains, complex dynamical processes occur that need to be understood to control and improve the efficiency of the photovoltaic cell. The first step is the photoexcitation into a bright electronic state, which creates the initial conditions for the subsequent photodynamics. Therefore, the comprehensive investigation of the electronic spectra of polymers in particular with respect to vibrational broadening is an important prerequisite for studying the photodynamics.
Poly(p-phenylenevinylene) (PPV) (Scheme 1) is widely studied due to its relevance as a benchmark system for electroluminescent and photovoltaic materials design.2−7 Determining the mechanisms affecting its photophysical behavior is crucial for controlling and tuning the absorption and emission properties of PPV-derived materials. Experiments have shown interesting features of coherent PPV dynamics5 that have been rationalized in terms of the coupling of the electronic excitation to a vibrational mode.8 It has been established that the evolution of electronically excited states relates to the structural relaxation dynamics in these systems.1 This coupling involves multiple electronically excited states that can lead to strong nonadiabatic behavior.
Scheme 1. Structure of (PV)nP Oligomers.
Electronic structure calculations constitute an important tool for interpreting experimental data and providing working guidelines for design of new materials. However, there are considerable challenges concerning their use due to the large molecular sizes of the oligomers to be calculated and the difficulties in properly describing the relevant excited states. Calculations of PPV oligomers (Scheme 1) belong to this class of problems. Previous studies of PPV oligomers used several semiempirical methods for the description of the PPV spectra and photodynamics: the collective electronic oscillator (CEO) method combined with the semiempirical AM1 model9,10 and surface hopping dynamics based on the Pariser–Parr–Pople model Hamiltonian for π-electrons.11 Zerner’s intermediate neglect of differential overlap (ZINDO) semiempirical method was applied to the problem of the absorption spectra in PPV oligomers.12 Configuration interaction with single excitations (CIS) was also used to investigate the vibronic structure of optical transitions in PPV.13 The singlet–triplet splitting was investigated in a number of systems, including PPV, by means of the time dependent density functional theory (TDDFT).14 The dependence of the description of the electronic excitation character on the choice of correlation–exchange functionals was studied in detail.15
Because of the significantly larger computational demands, ab initio theory has been used primarily for the smaller oligomers. For instance, calculations of the electronic spectrum of stilbene used the complete active space with perturbation theory to second order (CASPT2)16 and the symmetry adapted cluster-configuration interaction (SAC-CI) spectra for oligomers with up to four PV units.17 The approximate coupled cluster method to second order (CC2)18 and the algebraic diagrammatic construction method to second order, ADC(2),19 combined with the resolution of identity (RI) approach,20 which allows efficient handling of the two-electron integrals, were employed successfully for examining vertical excitation energies of larger oligomers with up to seven phenylenevinylene (PV) units.21 The CC2 method has been proven useful in calculations of methylene-bridged oligofluorenes22 and oligo-p-phenylenes.23 Moreover, it should be mentioned that unlike CC2, the ADC(2) method has the advantage that the excited state energies are computed as eigenvalues of a Hermitian matrix resulting in an improved numeric stability.24 Furthermore, the resolution-of-the-identity approximation (RI) greatly reduces the computational time without affecting the quality of results significantly.20,25
Although theoretical information on the vertical excitation energies of PPV oligomers is available, few spectral simulations including vibrational broadening have been reported for these systems. Representative works of this type are the restricted configuration interactions with singles excitations (RCIS) calculations of Gierschner and co-workers,26 the AM1/CI calculations of Karabunarliev et al.,27 and the CEO simulations of Tretiak et al.9
To study the PPV oligomers at the ab initio level, it is necessary to deal with the sharp increase of computational cost upon increasing the size of the molecules along the series, especially when going beyond a calculation of vertical excitation energies. To this end, a careful balance between choices of methods, basis set size, and further time-reducing measures is required to not compromise the reliability of the description and to allow a controlled assessment of the introduced errors. For these reasons, it is necessary to devise strategies to use computationally demanding high-level theory and to assess the implications of the used approximations. This work is dedicated to this question, in which we present refined spectra simulations of PPV oligomers (PV)nP (n = 1–5) including vibrational broadening based on the above-mentioned ADC(2) method.
2. Computational Details
Geometry optimizations were carried out at the RI Møller–Plesset perturbation theory to second order (RI-MP2) level28 for the ground state and at the RI-ADC(2) level for the S1 state, with both the SV and the SV(P) Gaussian basis sets29 without any symmetry constraints. These basis sets offer a good qualitative description of the trends along the PPV oligomer series as shown before.21 Starting geometries were selected with the phenyl rings rotated by 10° relative to the vinylene plane, with consecutive rings being rotated in opposite directions. Geometry optimizations of the (PV)2P and (PV)3P oligomers were also performed with starting planar geometries for comparison purposes; geometries obtained this way are restricted to being planar and are not true minima. Convergence criteria for geometry optimizations include an energy threshold of 1 × 10–6 hartree and gradient component changes of less than 1 × 10–4 hartree/bohr. The vertical excitation energies, oscillator strengths, and simulated spectra were computed with the RI-ADC(2) method for the first four excited singlet states.
The vibrational broadening of the spectra was calculated with the nuclear-ensemble method.30,31 This method allows the simulation of the band envelope but averages out the vibrational fine structure; any such detail appearing on the simulated spectra is an artifact of the sampling procedure. To simulate the envelope broadening, it is necessary to sample the ground state configurational space for the absorption spectra simulation. The same procedure is performed for the S1 state when the fluorescence spectra are simulated. In the present case, we used a Wigner distribution along the molecular vibrational modes in the harmonic-oscillator approximation; 500 points were sampled in each case. Four excited states were included in the computation of the absorption spectrum and one excited state was considered in the florescence spectrum. Individual spectral lines were convoluted with Lorentzian line shapes using a phenomenological broadening of 0.05 eV. Due to the large computational effort involved in calculating frequencies for the larger molecules in the (PV)nP series, the ground state normal modes used for the photoabsorption calculations were obtained at the Hartree–Fock level and the S1 normal modes for the fluorescence spectra calculations were obtained at the TDDFT level with the BHandHBLYP functional. The latter was chosen due to findings that functionals including 50% Hartree–Fock exchange yield better descriptions of the exciton localization of the excited states in these systems.15 Band maxima were obtained from the spectra by fitting a Gaussian function to each band and determining their maxima and full width half-maximum (FWHM) values.
For the vertical excitations, both SV and SV(P) basis sets were used for all oligomers in the series, from n = 1 to n = 7. For the photoabsorption spectra simulations of (PV)1–3P, both the SV and the SV(P) basis sets were employed. For the larger (PV)4–5P oligomers, only the SV basis set was used. The fluorescence spectra simulations for (PV)2–4P employed the SV basis set. The Stokes shifts were computed by calculating the energy differences between the maxima in the absorption and fluorescence spectra. Radiative emission rates (krad) and the related lifetimes (τ0) for the S1 → S0 transition were calculated by two different approaches. The first is obtained directly from the vertical excitation energy (ΔE) and the oscillator strength of the transition and is given by32
| 1 |
where c is the speed of light and f is the oscillator strength. Though straightforward, this method relies on the Franck–Condon approximation and ignores the contribution from geometries close to equilibrium. The second procedure involves the integration of the differential emission rate (Γrad) in the energy domain, according to the equation31
| 2 |
This integrated lifetime is a step ahead of the simple Franck–Condon approximation procedure, and it is expected to provide more consistent results.
In all cases, a number of orbitals equal to twice the number of core orbitals were frozen during calculations. Geometry optimization and vertical excitation calculations were also carried out for stilbene with only the core obitals frozen to evaluate the effect of extended freezing.
All geometry optimizations, electronic structure, and normal mode calculations were done with the TURBOMOLE 6.5 program system.33 The spectra simulations were done with NEWTON-X34,35 package, version 1.4.
3. Results and Discussion
3.1. Assessment of Accuracy
The large computational effort involved arises especially because of the sampling of the Wigner distribution generating the nuclear ensemble (500 single-point calculations for each spectrum). Therefore, the theoretical approach used has to be computationally efficient. The RI-ADC(2) method is a good candidate for that purpose within the framework of ab initio theory. Nevertheless, the large size of the oligomers demands a number of measures to further reduce the computational effort. The consequences of these measures on the accuracy of the results were tested and are discussed in this subsection.
We first increased the number of frozen orbitals beyond the standard freezing scheme of freezing the 1s core orbitals. The number of frozen core orbitals were doubled, a procedure that was then tested for stilbene, (PV)1P. RI-MP2/SV(P) geometry optimization calculations were performed, freezing the 14 1s core orbitals or the 28 lowest-energy orbitals. The computed geometric parameters in the two cases are compared in Table S1 of the Supporting Information. It can be seen that bond distances are not significantly affected by increasing the number of frozen orbitals in the amount mentioned. The average absolute difference in the bond distances is 0.008 Å; the largest effects are observed in the length of C–H bonds, which decrease by 0.028 Å in the aromatic ring and by 0.020 Å in the vinylene unit. The CC bond lengths present significantly smaller changes, increasing only slightly (less than 0.003 Å) in most cases, except for the C–C single bonds, which increase by 0.016 Å. Changes in angles and dihedral angles are also quite small and should have no discernible effect on the electronic structure calculations.
We note that in both cases the calculated equilibrium geometry is nonplanar; the H2–C3–C4–C5 dihedral angle (for atomic numbering see Scheme S1, Supporting Information) corresponding to the out-of-the-plane ring torsion is about 20°. The issue of the planarity of stilbene has been addressed by Kwasniewski et al.,36 who showed by means of MP2 and coupled cluster calculations that the true torsional conformation in stilbene is planar; to obtain a planar ground state geometry at ab initio levels, relatively large basis sets with diffuse functions are necessary (at least of aug-cc-pVDZ quality). It is noted that in the present work converged nonplanar geometries persisted for the larger oligomers using the MP2/SV(P) approach with dihedral phenyl out-of-plane angles keeping values of around 20°, as found for stilbene (see also the discussion below).
The shallowness of the H2–C3–C4–C5 dihedral-angle potential well of stilbene makes zero-point energy (ZPE) contributions important in defining the correct geometry.37 Furthermore, the experimental data also point to a planar geometry as the correct one.38 Because the purpose of this work is to investigate significantly larger oligomers including geometry optimization of their first excited state, and due to the small energy differences involved, we did not make any attempt to correct for the nonplanarity of the PPV oligomers in the ground state by increasing the basis set. For these reasons, excited states and spectra of all the oligomers in this work were calculated from the nonplanar optimized ground state equilibrium geometries. However, a correction for the nonplanarity of the ground state will be introduced later.
The first four singlet excitation energies and the corresponding oscillator strengths computed at the RI-ADC(2)/SV(P) level for both frozen core and extended frozen core are presented in Table 1. The results show that the extended frozen core excitation energies are always larger by approximately 0.2 eV than those of the standard frozen core scheme. The dark S0 → S4 transition, the highest one, is most affected by freezing additional orbitals, being shifted by about 0.25 eV. As was discussed before for the poly(thieno[3,4-b]thiophene benzodithiophene/[6,6]-phenyl-C61-butyric acid methyl ester (PTB1/PCBM) system,39 the use of a carefully tested freezing scheme in the RI-ADC(2) approach allows the investigation of large molecular systems without compromising the accuracy of calculated transition energies.
Table 1. Stilbene Vertical Excitations Calculated at the RI-ADC(2)/SV(P) Level for Optimized RI-MP2/SV(P) Geometries26.
| frozen
corea |
frozen
(core +14)b |
|||
|---|---|---|---|---|
| excitation energy (eV) | oscillator strength | excitation energy (eV) | oscillator strength | |
| S1 | 4.715 | 1.033 | 4.937 | 0.934 |
| S2 | 4.909 | 0.000 | 5.085 | 0.000 |
| S3 | 4.935 | 0.150 | 5.123 | 0.253 |
| S4 | 6.134 | 0.005 | 6.389 | 0.004 |
Frozen core corresponds to calculations performed with 14 orbitals frozen.
Frozen (core+14) corresponds to the lowest 28 orbitals frozen.
Extensive basis set tests ranging from the split valence SV basis up to TZVPP29 containing two d functions and one f function on carbon were performed previously.21 It was found that the SV basis could be used with good success by observing that the relative energies of the first four excited states remained constant within ∼0.1 eV for the mentioned range of basis sets. In this work, we used the SV and SV(P) basis sets, considering the latter one for comparison purposes. The present calculations on the larger oligomers will be performed with the SV basis. The discussion of accuracy will be postponed until the comparison with experimental data in gas phase and in solution.
3.2. Geometry Optimization and Vertical Excitation Energies
The ground state geometries of PPV oligomers (PV)nP with up to six phenyl rings were optimized at the RI-MP2 level using both the SV and the SV(P) basis sets and the extended set of frozen core orbitals. The most important structural aspect is the phenyl ring torsional angle. All geometry optimizations were started from alternating twisted nonplanar geometries, which preserved this feature in the course of the optimization process. Table 2 collects for each structure the results for the outermost (θo) and the innermost (θi) phenyl ring angles. The other phenyl rings display torsional angles very similar to the innermost ring ones and, for this reason, they are not listed separately. Along the series (except n = 1), the θo torsional angles were found to be about 25.0° with the SV(P) basis and around 25.8° with the SV basis. The θi torsional angles are around 22° and do not change much along the series; the most pronounced difference is ∼0.35° between the (PV)2P oligomer and the larger oligomers in the series. The differences between the SV(P) and SV calculations are also quite small: the calculated SV θ2 torsional angles are larger than those computed with the SV(P) basis by no more than 0.75°.
Table 2. Selected Torsional Angles for Phenyl Ring Rotation Calculated at the RI-MP2 Level with the Extended Frozen Core Approach and with the SV(P) and SV Basis Sets for the (PV)nP (n = 1–7) Series in the Ground Statea.
| SV |
SV(P) |
|||
|---|---|---|---|---|
| θo (deg)b | θi (deg)c | θo (deg)b | θi (deg)c | |
| n = 1 | 25.52 | 24.29 | ||
| n = 2 | 25.87 | –23.22 | 25.01 | –22.49 |
| n = 3 | 25.78 | 22.87 | 24.83 | 22.17 |
| n = 4 | 25.80 | –22.87 | 24.98 | –22.15 |
| n = 5 | 25.80 | 22.86 | 24.95 | 22.21 |
| n = 6 | 25.81 | –22.84 | 25.00 | –22.12 |
| n = 7 | 25.81 | 22.89 | 24.99 | 22.22 |
Only symmetry unique angles in one half of the oligomer are listed.
Outermost ring rotation dihedral angle.
Innermost-ring rotation dihedral angle.
The RI-ADC(2)/SV geometry optimizations of the S1 state were also carried out for the (PV)1–5P series. Optimization of stilbene in S1 converged to a nonplanar geometry. This situation had been previously predicted by state-averaged complete active space self-consistent field (SA-CASSCF) calculations,40 which points to a twisted geometry (θo = 5° and the torsional angle around the ethylene bond ϕ = 167°). Because it turned out that this feature was special to stilbene, we did not follow it further. Starting with the (PV)2P oligomer in the series, the S1 minima were planar.
The vertical excitation energies are displayed in Table 3. Except for stilbene, (PV)1P in the SV basis, the largest oscillator strength was found for the S0 → S1 transition for both basis sets used here. Only stilbene in the SV basis shows an inversion of the character of excited states. For the SV(P) basis set, the first singlet excited state corresponds to the most intense absorption of the whole series, becoming stronger as the chain increases. The SV(P) basis set S0 → S3 transition also gets brighter further along the series. The SV excitation energies differ from the SV(P) energies by at most 0.2 eV.
Table 3. RI-ADC(2) Vertical Excitations for the S0 → S1 Transitions in the (PV)nP (n = 1–5) Oligomers Computed with the SV(P) and the SV Basis Sets.
| SV |
SV(P) |
|||
|---|---|---|---|---|
| excitation energy (eV) | oscillator strength | excitation energy (eV) | oscillator strength | |
| n = 1 | 5.023 | 0.275 | 4.937 | 0.934 |
| n = 2 | 4.461 | 2.087 | 4.281 | 2.063 |
| n = 3 | 4.164 | 3.071 | 3.973 | 2.957 |
| n = 4 | 4.012 | 3.986 | 3.822 | 3.821 |
| n = 5 | 3.925 | 4.897 | 3.734 | 4.689 |
The spectral simulations employed the nonplanar ground state equilibrium geometries. This approach could lead to systematic errors because the correct36−38 ground state planar geometries do not correspond to the minima structures except for very large basis sets.37 The potential energy surface in terms of torsional angles is very flat and the necessary large basis set sizes to obtain planar geometries make even ground state geometry optimizations costly for the larger oligomers along the series, not to mention for excited state optimizations. Spectra simulations and dynamics, which depend on a much larger number of energy calculations, would not be feasible. Even though the ground state energies for the nonplanar and planar geometries are located within a range of 0.05 eV, the vertical excitation energies show a larger sensitivity because the S1 energy surface does not possess the just-mentioned flatness of the ground state in terms of torsional angles. Therefore, to account for the true planar ground state geometry in the calculations using smaller basis sets, we also calculated the vertical excitation energies for geometries optimized with a planarity restriction. The results for the excitation energies of the first bright state in the (PV)2P and (PV)3P oligomers are displayed in Table 4. The vertical excitations for planar ground state geometries are smaller than those for nonplanar ones by ∼0.25 eV for (PV)2P and ∼0.27 eV for (PV)3P oligomers. For this reason, the absorption spectra calculated in this work on the basis of a nonplanar ground state reference geometry should be too high in energy by a similar amount. It is important to note that a corresponding correction is not necessary for the emission energies, because the equilibrium geometry for the S1 state does not show the torsional ambiguity of the ground state; it is already planar using our smallest basis, the SV set, and no further geometrical adjustments are necessary. These differences in the shapes of the S0 and S1 energy surfaces lead to different energy corrections for absorption and fluorescence energies. In the former case, an average value of 0.26 eV (see the (PV)2P and (PV)3P values just mentioned) will be deducted from the computed absorption energies based on nonplanar structures whereas for the fluorescence energies no corresponding correction is applied. Because the remaining corrections discussed below are the same for absorption and fluorescence, it is only this difference of 0.26 eV that affects the relative values of calculated absorption and fluorescence energies and thus also the computed Stokes shift.
Table 4. Comparison of RI-ADC(2)/SV and RI-ADC(2)/SV(P) S0–S1 Vertical Excitation Energies for (PV)nP (n = 2, 3) Calculated at Both the Nonplanar Equilibrium Geometry and at the Optimized Planar Geometry.
| basis set | SV |
SV(P) |
||
|---|---|---|---|---|
| planar | nonplanar | planar | nonplanar | |
| n = 2 | 4.205 | 4.461 | 4.039 | 4.281 |
| n = 3 | 3.882 | 4.164 | 3.712 | 3.973 |
It is clear that to have a meaningful comparison of excitation energies with experimental data, our approach needs to be corrected for all factors already mentioned, i.e., basis set effects, extended freezing of molecular orbitals, and the correction for the planarity of the ground state. A lower limit for the basis set correction when using the SV basis set was estimated in previous work21 and is taken as a lowering of the excitation energy by 0.45 eV. The freezing of an extended number of orbitals leads to an estimated reduction of 0.2 eV. On the basis of the arguments presented above, the error originating from using the nonplanar equilibrium geometry will be taken as a decrease of 0.26 eV. Thus, the overall total correction to be applied to the results computed with the SV basis equals −0.91 eV.
Because the experimental PPV spectra were obtained only in solution, the gas phase data reported in ref (26) were actually obtained by extrapolation from solvent data by plotting the band maxima for different solvents as a function of the solvent refraction indexes (nr) and then extrapolating the band values to the nr → 1 limit. The corrected (gas phase) ADC(2) values agree very well with the corresponding experimental gas phase data (Table 5). The former are only between 0.1 and 0.2 eV lower in energy. A bathochromic solvent shift of ∼0.18 eV is deduced from a comparison of the experimental gas phase and dioxane data of Table 5 (excluding the stilbene data). Comparing our solvent-shifted (“solv shifted” column in Table 5) results with the experimental data (“dioxane solv” column, Table 5) shows that this correction is not good for stilbene (n = 1) but improves as the oligomers get larger, with a difference between the theoretical and experimental data of ∼0.2 eV.
Table 5. Comparison of RI-ADC(2)/SV Vertical Excitation Energies for (PV)nP (n = 1–5) with Experimental Dataa.
| vertical
excitation (eV) |
exp
(eV) |
||||
|---|---|---|---|---|---|
| calculated gas phase | correctedb gas phase | solv shiftedc | gas phased | dioxane solve | |
| n = 1 | 5.023 | 4.11 | 3.93 | 4.19 | 4.17 (0.80) |
| n = 2 | 4.461 | 3.55 | 3.37 | 3.69 | 3.54 (0.58) |
| n = 3 | 4.164 | 3.25 | 3.07 | 3.47 | 3.28 (0.53) |
| n = 4 | 4.012 | 3.10 | 2.92 | 3.34 | 3.13 (0.53) |
| n = 5 | 3.925 | 3.01 | 2.84 | ||
Calculated values corrected for basis set deficiency, extended freezing of orbitals, and geometry are presented. Values including solvent shift for comparison with measurements in dioxane are also included. Experimental FWHM band width data are given in parentheses.
Corrections: basis set, −0.45 eV, orbital freezing, −0.2 eV, geometry, −0.26 eV. Total correction: −0.91 eV.
Corrected value + dioxane solvent shift (−0.18 eV, see text).
Values extrapolated from band maxima obtained for solvents with differing refraction indexes.26
Data taken directly from band maxima in experimental spectra obtained in dioxane.26
An analogous approach was used to compare the calculated emission energies with existing experimental fluorescence data (Table 6). The stilbene case is omitted because of the strong deviation from planarity in the S1 state, which classified this molecule as a special case not fitting into the PPV series. The computed solvent-shifted vertical emission energies shown in Table 6 are about 0.30–0.35 eV lower than the experimental data.
Table 6. Comparison of RI-ADC(2)/SV Emission Energies for (PV)nP (n = 2–4) with Experimental Dataa.
| vertical
emission energy (eV) |
exp (eV) | |||
|---|---|---|---|---|
| as calculated | correctedb gas phase | solv shiftedc | dioxaned solv | |
| n = 2 | 3.601 | 2.95 | 2.77 | 3.05 (0.51) |
| n = 3 | 3.291 | 2.64 | 2.46 | 2.79 (0.50) |
| n = 4 | 3.150 | 2.50 | 2.32 | 2.68 (0.51) |
Calculated values corrected for basis set deficiency and extended freezing of orbitals are presented. The value of the solvent shift for comparison with measurements in dioxane is included. Experimental full FWHM band width data are given in parentheses.
Corrections: basis set, −0.45 eV, orbital freezing, −0.2 eV. Total correction: −0.65 eV.
Corrected value + dioxane solvent shift (−0.18 eV).
Data taken directly from band maxima in experimental spectra obtained in dioxane.26
3.3. Simulated Spectra
The simulated absorption spectra comprise the first band of the (PV)nP oligomers that is composed exclusively of π–π* transitions. Both the SV(P) and SV calculations (Figure 1a,b, respectively) show an increase in the maximum of the photoabsorption cross section, along with a displacement of the band toward lower photon energies. Because the combination of basis set error, extended frozen core approximation, and ground state geometry effects increases the vertical excitation energies by about ∼0.9 eV for the SV results as shown before, the corresponding simulated spectra should be too high in energy by similar amounts and will be corrected below when comparing to the experimental spectrum.
Figure 1.
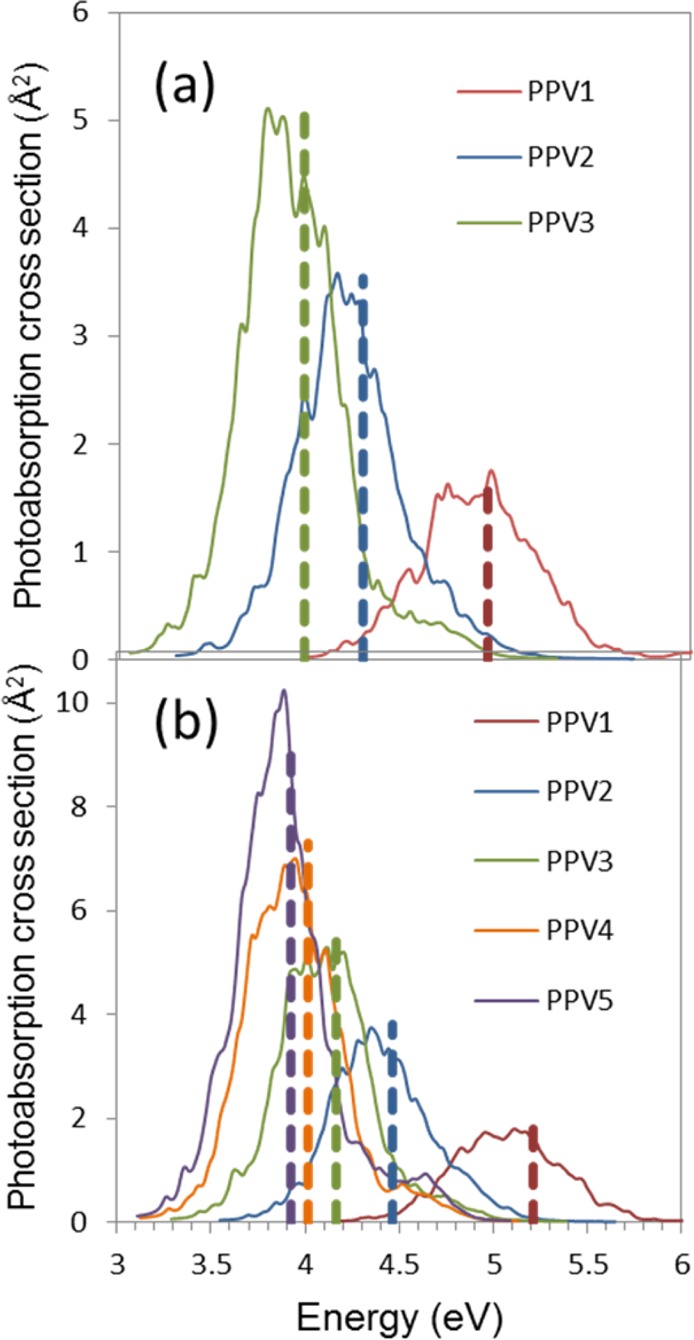
Simulated absorption spectra with vibrational broadening calculated at the RI-ADC(2) level for (PV)nP oligomers including the first four singlet states: (a) SV(P) spectra with n = 1–3; (b) SV spectra with n = 1–5. Dashed vertical lines mark the vertical excitation energies corresponding to the bright state in each oligomer. The relative heights of these lines are proportional to the corresponding calculated oscillator strength.
The spectra obtained with the SV basis for n = 1–3 are quite similar in shape to those obtained with the SV(P) basis. The spectra obtained with the SV basis suggest that the range of photon energies covered by the absorption band is already converged for the n = 5 oligomer, with absorption occurring between 3.0 eV (band onset) and 5.0 eV (band termination), which should not change much when advancing in the series. This feature indicates that a range of less than 2.0 eV of photon energies is necessary to excite this band for larger oligomers along the series. Moreover, the calculated absorption peak of the (PV)5P oligomer is located at ∼3.8 eV. Reducing this value by the estimated correction of 0.91 eV (Table 5) leads to a value for the (PV)5P first absorption band peak of ∼2.89 eV. This value should be an upper limit to the actual value of the PPV polymer band peak of a single ideal chain. Experimental data for the polymer suggest the existence of a defect band in the range of approximately 2.1–2.4 eV, a main band at 2.4–2.7 eV (peaking at ∼2.5 eV), and a vibronic band from 2.7 eV to higher energies.7 The 2.89 eV adjusted value for the (PV)5P peak differs by about 0.4 eV from that value measured in the PPV polymer.7
Characterization of the band widths by means of FWHM data obtained from our calculated spectra agree quite closely with those taken from experimental spectra, as seen by comparing values given in Table 7 to the experimental FWHM data in the “dioxane solv” columns in Tables 5 and 6. The calculated band maxima are quite close to the vertical excitation energies. Absorption spectra band maxima are always lower than the vertical excitation energies, the largest difference being found for n = 4 (0.10 eV), whereas for the fluorescence spectra the largest difference is found for n = 2 and n = 3, with a band maxima lower than the vertical excitation by 0.04 eV. The computed RI-ADC(2)/SV absorption spectra for (PV)n=2–4P (Figure 2) are not much broader than the corresponding fluorescence spectra (see FWHM values in Table 7). The intensity of the emission also increases along the series, together with a displacement of the band toward lower photon energies.
Table 7. Band Maxima (eV) from Simulated UV Absorption and Fluorescence Spectra and Computed FWHM Band Widths Using the RI-ADC(2)/SV.
Figure 2.
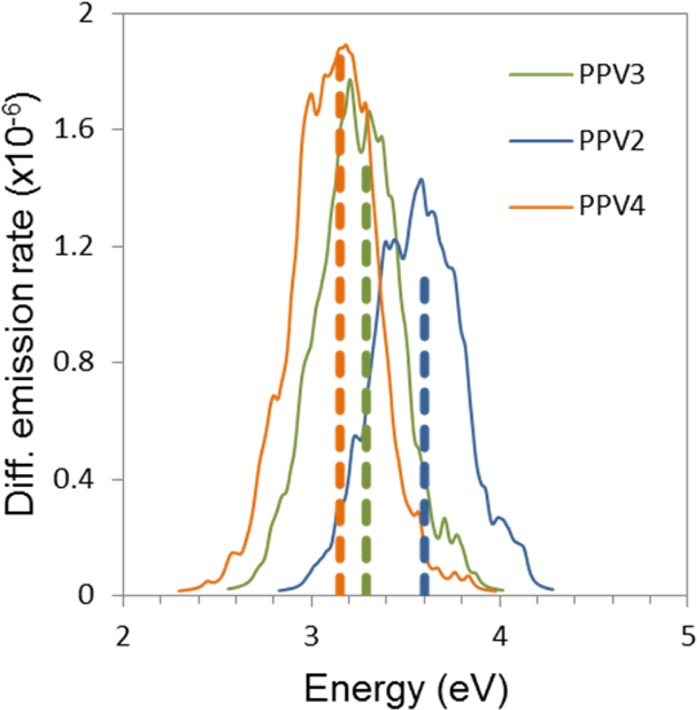
Simulated fluorescence spectra for the S1 → S0 transition with vibrational broadening calculated at the RI-ADC(2)/SV level for the (PV)nP (n = 2, 4) oligomers reported as a dimensionless differential emission rate. Dashed vertical lines mark the vertical excitation energies corresponding to the computed bright state in each oligomer. The relative heights of these lines are proportional to the corresponding calculated oscillator strength.
The radiative emission rates and lifetimes for the simulated fluorescence spectra were computed by two methods. One employed the Franck–Condon approximation (eq 1), and the other is obtained by integrating over the whole calculated band (eq 2); results are collected in Table 8. Two cases are presented. In the first one the uncorrected energy differences are used and in the second case corrected transition energies. Radiative emission rates are somewhat larger in the former case. They increase with the increasing oligomer length because the reduction of ΔE for larger oligomers is counterbalanced by the increase of the oscillator strength (f). Emission rates based on the integrated method are about 10% smaller than those obtained with using vertical excitations only; the former is expected to yield more consistent results because it includes information about the entire band. For n = 4, the lifetime is calculated to be 0.6–0.9 ns; it is expected to decrease even further when progressing along the series. To our knowledge, there are no experimental data for the lifetime of the S1 → S0 transition for the PPV oligomers. Therefore, these results are of particular interest.
Table 8. Radiative Emission Rates krad and Lifetimes τ0 for the S1 → S0 Transition, at the RI-ADC(2)/SV Level for (PV)nP (n = 2–4), Calculated Both by Integration of the Differential Radiative Rate (“Integrated” Method, Eq 2) and by Considering Only the Vertical Excitation Energy (“Vertical” Method, Eq 1).
| as calculated |
corrected
+ solv-shifteda |
||||
|---|---|---|---|---|---|
| method | krad (109 s–1) | τ0 (ns) | krad (109 s–1) | τ0 (ns) | |
| n = 2 | vertical | 1.40 | 0.72 | 0.80 | 1.25 |
| integrated | 1.25 | 0.80 | 0.71 | 1.41 | |
| n = 3 | vertical | 1.60 | 0.62 | 0.86 | 1.16 |
| integrated | 1.44 | 0.70 | 0.78 | 1.28 | |
| n = 4 | vertical | 1.82 | 0.55 | 0.95 | 1.06 |
| integrated | 1.64 | 0.61 | 0.85 | 0.85 | |
Corrected transition energies as listed in Table 6 were used.
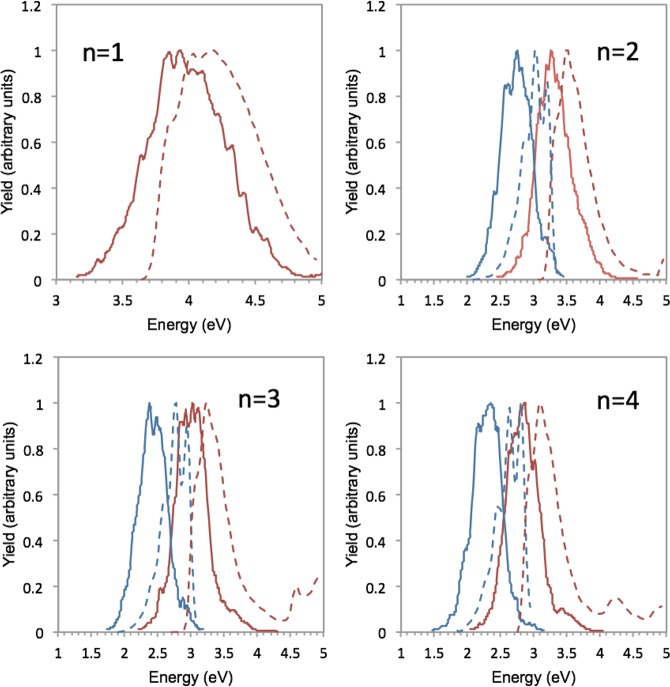
The calculated spectra can be compared with experimental absorption and fluorescence spectra obtained in dioxane at 293 K26 by superimposing the experimental data with the simulated spectra (Figure 3). The calculated spectra included in Figure 3 already take into account all the previously discussed corrections for calculated absorption and emission energies (Tables 5 and 6), including the solvent shift. The simulated absorption spectra have a shape quite close to the experimental one for all the examined spectra (Figure 3). The main difference in all cases is that the band tail at lower energies falls off more slowly in the simulated spectra than in the experimental spectra. A similar trend is present in the fluorescence band tails at higher energies. The vibrational fine structure of the fluorescence spectra is averaged out in the simulated spectra (Figure 3), because our semiclassical method for spectra simulation does not include vibrational resolution. As already mentioned above, the FWHM band width measure agrees quite nicely with the experimental ones.
Figure 3.
Comparison between experimental and simulated spectra for the n = 1–4 oligomers. Absorption spectra are red and fluorescence spectra are blue. Solid lines are for the RI-ADC(2)/SV spectra, and the dashed lines are for the experimental spectra obtained in dioxane at T = 293 K.26 All previously discussed corrections for calculated absorption and emission energies (Tables 5 and 6), including the solvent shift, are included in the calculated spectra. The simulated and the experimental absorption and fluorescence spectra were normalized to an arbitrary yield peaking at 1.
By taking the difference between maxima in the solvent corrected absorption and fluorescence spectra (Table 7), the Stokes shift is predicted to be ∼0.51 eV for n = 2 and n = 4, and ∼0.64 eV for n = 3. The results obtained from this procedure also compare quite well with the experimental values (0.45–0.46 eV), obtained by subtracting the experimental absorption and fluorescence band maxima listed in Tables 5 and 6.
4. Conclusion
The vibrational broadening of the first UV absorption and the fluorescence band in PPV oligomers was computed using the semiclassical nuclear ensemble method and the ab initio RI-ADC(2) approach for the electronic excitation energies. The ensemble of structures for simulating the vibrational broadening contained 500 geometries constructed from a Wigner distribution. To keep the calculations manageable in view of the large size of the PPV oligomers, relatively small basis sets and an extended scheme for freezing molecular orbitals had to be used. By comparison with previously obtained results using significantly larger basis sets21 and with more extended calculations, a thorough control of the influence of the different systematic factors on the computed excitation energies was achieved. In this way, it was possible to obtain quite accurate predictions using alternative methods to the computationally more efficient TDDFT methods, which have the issue that the exchange–correlation functional has to be selected carefully (see, e.g., ref (15)).
Overall, the absorption and fluorescence band shapes of the PPV oligomers were well-described. As the oligomer size increases, the π → π* photoabsorption and fluorescence bands show progressively larger peaks. The computed absorption and fluorescence bands were found to have a well-described shape and range of light absorption/emission spectra, displaying a Stokes shift of about 0.5 eV. We also could establish a correction of the S0 → S1 vertical transition energy due to the artificial nonplanar ground state of PPV oligomers found in MP2 and coupled cluster calculations using small- and medium-sized basis sets in the range of ∼0.25–0.28 eV.
Obtaining a reliable broadening of the electronic spectra of PPV is also an important asset for dynamics simulations because the nuclear ensembles used for describing the spectra also constitute the initial structures for surface hopping dynamics simulations34 of the oligomers that aim at the ab initio dynamics description of exciton and charge transfer processes.
Acknowledgments
I.B. thanks the Brazilian Agencies CNPq, Faperj, and CAPES, and the Brazilian Army, for support of this work. H.L., I.B., and T.M.C. acknowledge support from Capes in the framework of the Science without Borders Brazilian Program. H.L. is “Bolsista CAPES/Brasil”. This material is based upon work supported by the National Science Foundation under Project No. CHE-1213263 and by the Austrian Science Fund within the framework of the Special Research Program F41. Computer time at the Vienna Scientific Cluster (Project nos. 70019 and 70376) is gratefully acknowledged. Support was also provided by the Robert A. Welch Foundation under Grant No. D-0005.
Supporting Information Available
Stilbene geometry parameters and atom-labeling scheme for stilbene. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Supplementary Material
References
- Bredas J. L.; Norton J. E.; Cornil J.; Coropceanu V. Molecular Understanding of Organic Solar Cells: The Challenges. Acc. Chem. Res. 2009, 42, 1691–1699. [DOI] [PubMed] [Google Scholar]
- Bredas J. L.; Cornil J.; Beljonne D.; dos Santos D.; Shuai Z. G. Excited-State Electronic Structure of Conjugated Oligomers and Polymers: A Quantum-Chemical Approach to Optical Phenomena. Acc. Chem. Res. 1999, 32, 267–276. [Google Scholar]
- Peeters E.; Ramos A. M.; Meskers S. C. J.; Janssen R. A. J. Singlet and Triplet Excitations of Chiral Dialkoxy-P-Phenylene Vinylene Oligomers. J. Chem. Phys. 2000, 112, 9445–9454. [Google Scholar]
- Meier H.; Stalmach U.; Kolshorn H. Effective Conjugation Length and UV/Vis Spectra of Oligomers. Acta Polym. 1997, 48, 379–384. [Google Scholar]
- Kirova N. Understanding Excitons in Optically Active Polymers. Polym. Int. 2008, 57, 678–688. [Google Scholar]
- Collini E.; Scholes G. D. Coherent Intrachain Energy Migration in a Conjugated Polymer at Room Temperature. Science 2009, 323, 369–373. [DOI] [PubMed] [Google Scholar]
- Rauscher U.; Bässler H.; Bradley D. D. C.; Hennecke M. Exciton Versus Band Description of the Absorption and Luminescence Spectra in Poly(Para-Phenylenevinylene). Phys. Rev. B 1990, 42, 9830–9836. [DOI] [PubMed] [Google Scholar]
- Bredas J. L.; Silbey R. Excitons Surf Along Conjugated Polymer Chains. Science 2009, 323, 348–349. [DOI] [PubMed] [Google Scholar]
- Tretiak S.; Saxena A.; Martin R. L.; Bishop A. R. Conformational Dynamics of Photoexcited Conjugated Molecules. Phys. Rev. Lett. 2002, 89, 1–4. [DOI] [PubMed] [Google Scholar]
- Fernandez-Alberti S.; Kleiman V. D.; Tretiak S.; Roitberg A. E. Unidirectional Energy Transfer in Conjugated Molecules: The Crucial Role of High-Frequency C C Bonds. J. Phys. Chem. Lett. 2010, 1, 2699–2704. [Google Scholar]
- Sterpone F.; Rossky P. J. Molecular Modeling and Simulation of Conjugated Polymer Oligomers: Ground and Excited State Chain Dynamics of PPV in the Gas Phase. J. Phys. Chem. B 2008, 112, 4983–4993. [DOI] [PubMed] [Google Scholar]
- Lukes V.; Solc R.; Barbatti M.; Lischka H.; Kauffmann H. F. Torsional Potentials and Full-Dimensional Simulation of Electronic Absorption Spectra of Para-Phenylenevinylene Oligomers Using Semiempirical Hamiltonians. J. Theor. Comput. Chem. 2010, 9, 249–263. [Google Scholar]
- Karabunarliev S.; Bittner E. R. Polaron-Excitons and Electron-Vibrational Band Shapes in Conjugated Polymers. J. Chem. Phys. 2003, 118, 4291–4296. [Google Scholar]
- Pogantsch A.; Heimel G.; Zojer E. Quantitative Prediction of Optical Excitations in Conjugated Organic Oligomers: A Density Functional Theory Study. J. Chem. Phys. 2002, 117, 5921–5928. [Google Scholar]
- Nayyar I. H.; Batista E. R.; Tretiak S.; Saxena A.; Smith D. L.; Martin R. L. Localization of Electronic Excitations in Conjugated Polymers Studied by DFT. J. Phys. Chem. Lett. 2011, 2, 566–571. [Google Scholar]
- Molina V.; Merchan M.; Roos B. O. Theoretical Study of the Electronic Spectrum of Trans-Stilbene. J. Phys. Chem. A 1997, 101, 3478–3487. [Google Scholar]
- Saha B.; Ehara M.; Nakatsuji H. Investigation of the Electronic Spectra and Excited-State Geometries of Poly(Para-Phenylene Vinylene) (PPV) and Poly(Para-Phenylene) (PP) by the Symmetry-Adapted Cluster Configuration Interaction (SAC-CI) Method. J. Phys. Chem. A 2007, 111, 5473–5481. [DOI] [PubMed] [Google Scholar]
- Christiansen O.; Koch H.; Jorgensen P. The 2nd-Order Approximate Coupled-Cluster Singles and Doubles Model CC2. Chem. Phys. Lett. 1995, 243, 409–418. [Google Scholar]
- Trofimov A. B.; Schirmer J. An Efficient Polarization Propagator Approach to Valence Electron-Excitation Spectra. J. Phys. B 1995, 28, 2299–2324. [Google Scholar]
- Hättig C. Geometry Optimizations with the Coupled-Cluster Model CC2 Using the Resolution-of-the-Identity Approximation. J. Chem. Phys. 2003, 118, 7751–7761. [Google Scholar]
- Panda A. N.; Plasser F.; Aquino A. J. A.; Burghardt I.; Lischka H. Electronically Excited States in Poly(P-Phenylenevinylene): Vertical Excitations and Torsional Potentials from High-Level Ab Initio Calculations. J. Phys. Chem. A 2013, 117, 2181–2189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lukes V.; Aquino A. J. A.; Lischka H. Theoretical Study of Vibrational and Optical Spectra of Methylene-Bridged Oligofluorenes. J. Phys. Chem. A 2005, 109, 10232–10238. [DOI] [PubMed] [Google Scholar]
- Lukes V.; Aquino A. J. A.; Lischka H.; Kauffmann H. F. Dependence of Optical Properties of Oligo-Para-Phenylenes on Torsional Modes and Chain Length. J. Phys. Chem. B 2007, 111, 7954–7962. [DOI] [PubMed] [Google Scholar]
- Hättig C. Structure Optimizations for Excited States with Correlated Second-Order Methods: CC2 and Adc(2). Adv. Quantum Chem. 2005, 50, 37–60. [Google Scholar]
- Köhn A.; Hättig C. Analytic Gradients for Excited States in the Coupled-Cluster Model CC2 Employing the Resolution-of-the-Identity Approximation. J. Chem. Phys. 2003, 119, 5021–5036. [Google Scholar]
- Gierschner J.; Mack H. G.; Luer L.; Oelkrug D. Fluorescence and Absorption Spectra of Oligophenylenevinylenes: Vibronic Coupling, Band Shapes, and Solvatochromism. J. Chem. Phys. 2002, 116, 8596–8609. [Google Scholar]
- Karabunarliev S.; Baumgarten M.; Bittner E. R.; Mullen K. Rigorous Franck-Condon Absorption and Emission Spectra of Conjugated Oligomers from Quantum Chemistry. J. Chem. Phys. 2000, 113, 11372–11381. [Google Scholar]
- Møller C.; Plesset M. S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 0618–0622. [Google Scholar]
- Schäfer A.; Horn H.; Ahlrichs R. Fully Optimized Contracted Gaussian-Basis Sets for Atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar]
- Barbatti M.; Aquino A. J. A.; Lischka H. The UV Absorption of Nucleobases: Semi-Classical Ab Initio Spectra Simulations. Phys. Chem. Chem. Phys. 2010, 12, 4959–4967. [DOI] [PubMed] [Google Scholar]
- Crespo-Otero R.; Barbatti M.. Spectrum Simulation and Decomposition with Nuclear Ensemble: Formal Derivation and Application to Benzene, Furan and 2-Phenylfuran. Theor. Chem. Acc. 2012, 131. [Google Scholar]
- Brandsen B. H.; Jochain C. J.. Physics of Atoms and Molecules; Longman Group Limited: London, New York, 1983. [Google Scholar]
- Ahlrichs R.; Bär M.; Häser M.; Horn H.; Kölmel C. Electronic-Structure Calculations on Workstation Computers - the Program System Turbomole. Chem. Phys. Lett. 1989, 162, 165–169. [Google Scholar]
- Barbatti M.; Granucci G.; Persico M.; Ruckenbauer M.; Vazdar M.; Eckert-Maksic M.; Lischka H. The on-the-Fly Surface-Hopping Program System Newton-X: Application to Ab Initio Simulation of the Nonadiabatic Photodynamics of Benchmark Systems. J. Photochem. Photobiol., A 2007, 190, 228–240. [Google Scholar]
- Barbatti M.; Ruckenbauer M.; Plasser F.; Pittner J.; Granucci G.; Persico M.; Lischka H. Newton-X: A Surface-Hopping Program for Nonadiabatic Molecular Dynamics. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2014, 4, 26–33. [Google Scholar]
- Kwasniewski S. P.; Claes L.; Francois J. P.; Deleuze M. S. High Level Theoretical Study of the Structure and Rotational Barriers of Trans-Stilbene. J. Chem. Phys. 2003, 118, 7823–7836. [Google Scholar]
- Chowdary P. D.; Martinez T. J.; Gruebele M. The Vibrationally Adiabatic Torsional Potential Energy Surface of Trans-Stilbene. Chem. Phys. Lett. 2007, 440, 7–11. [Google Scholar]
- Champagne B. B.; Pfanstiel J. F.; Plusquellic D. F.; Pratt D. W.; Vanherpen W. M.; Meerts W. L. Trans-Stilbene - a Rigid, Planar Asymmetric-Top in the Zero-Point Vibrational Levels of Its S0 and S1 Electronic States. J. Phys. Chem. 1990, 94, 6–8. [Google Scholar]
- Borges I.; Aquino A. J. A.; Köhn A.; Nieman R.; Hase W. L.; Chen L. X.; Lischka H. Ab Initio Modeling of Excitonic and Charge-Transfer States in Organic Semiconductors: The PTB1/PCBM Low Band Gap System. J. Am. Chem. Soc. 2013, 135, 18252–18255. [DOI] [PubMed] [Google Scholar]
- Quenneville J.; Martinez T. J. Ab Initio Study of Cis-Trans Photoisomerization in Stilbene and Ethylene. J. Phys. Chem. A 2003, 107, 829–837. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.