Abstract
In the study of numeracy, some hypotheses have been based on response time (RT) as a dependent variable and some on accuracy, and considerable controversy has arisen about the presence or absence of correlations between RT and accuracy, between RT or accuracy and individual differences like IQ and math ability, and between various numeracy tasks. In this article, we show that an integration of the two dependent variables is required, which we accomplish with a theory-based model of decision making. We report data from four tasks: numerosity discrimination, number discrimination, memory for two-digit numbers, and memory for three-digit numbers. Accuracy correlated across tasks, as did RTs. However, the negative correlations that might be expected between RT and accuracy were not obtained; if a subject was accurate, it did not mean that they were fast (and vice versa). When the diffusion decision-making model was applied to the data (Ratcliff, 1978), we found significant correlations across the tasks between the quality of the numeracy information (drift rate) driving the decision process and between the speed/ accuracy criterion settings, suggesting that similar numeracy skills and similar speed-accuracy settings are involved in the four tasks. In the model, accuracy is related to drift rate and RT is related to speed-accuracy criteria, but drift rate and criteria are not related to each other across subjects. This provides a theoretical basis for understanding why negative correlations were not obtained between accuracy and RT. We also manipulated criteria by instructing subjects to maximize either speed or accuracy, but still found correlations between the criteria settings between and within tasks, suggesting that the settings may represent an individual trait that can be modulated but not equated across subjects. Our results demonstrate that a decision-making model may provide a way to reconcile inconsistent and sometimes contradictory results in numeracy research.
Keywords: Diffusion model, response time and accuracy, numeracy, number ability, individual differences
In decision-making tasks, several variables can be used to measure performance. In this article, we use a theory-based approach to investigate how dependent variables interact in decision tasks in the domain of numeracy research. We explain, first, how different dependent variables arise from the same underlying cognitive processes; second, why the value of a dependent measure may or may not be correlated between tasks; and third, why the value of one dependent variable may or may not be correlated with the value of another dependent variable. We show that an understanding of these issues is essential to the evaluation of data in numeracy research and the development of theories about numeracy. It is essential for answering questions such as how does the human mind represent numerical information? is there a common representation that is activated and used for all cognitive processes that make use of number? what are these cognitive processes? and what are the representations and processes that underlay children's abilities to learn arithmetic? It also may be essential for elucidating controversies in the numeracy literature. While we ourselves do not resolve any of these controversies, we do illustrate that a decision-making model is required.
When studies have examined correlations between tasks for some dependent measure that is thought to reflect numeracy processes, the results have been mixed. Sometimes correlations are found between symbolic tasks (“is 5 greater than 2“) and nonsymbolic tasks (“is the number of dots in one array greater than in another array”), and sometimes not (e.g., Price, Palmer, Battista, & Ansari, 2012; Gilmore, Attridge, & Inglis, 2011; Sasanguie, Defever, Van den Bussche, & Reynvoet, 2011; Maloney, Risko, Preston, Ansari, & Fugelsang, 2010; Holloway & Ansari, 2009; De Smedt, Verschaffel, & Ghesquiere, 2009). Sometimes correlations are found between non-symbolic number tasks and math ability, and sometimes not (e.g., Lyons & Beilock, 2011; Libertus, Feigenson, & Halberda, 2011; Gilmore, McCarthy, & Spelke, 2010; Halberda, Mazzocco, & Feigenson, 2008; Inglis, Attridge, Batchelor, & Gilmore, 2011; Holloway & Ansari, 2009; Mazzocco, Feigenson, & Halberda, 2011; Gilmore, McCarthy, & Spelke, 2010; Halberda, Mazzocco, & Feigenson, 2011; Mundy & Gilmore, 2009; Durand, Hulme, Larkin, & Snowling, 2005; De Smedt, et al., 2009; Price, et al., 2012).
The inconsistent use of dependent variables compounds these problems. Sometimes accuracy is used, sometimes mean response time (RT), and sometimes the slope of accuracy or RT as a function of the difficulty of a test item. When these variables are not correlated, they can give completely different pictures of number abilities. For example, Gilmore, Attridge, and Inglis (2011) found little correlation between all combinations of accuracy and RT across a range of symbolic and nonsymbolic tasks. A recent meta-analysis by Chen and Li (2014) reinforces the extent of the problem. For 36 recent studies, they found 21 that used overall accuracy, 9 that used mean RT, 17 that used the Weber fraction (an accuracy-based measure), and 8 that used a numerical distance effect based on RT.
Halberda et al. (2012, p. 11116) looked at correlations between two measures, as opposed to the same measure across tasks. One was the Weber fraction (w) and the other was RT. They state that “the Weber fraction and RT are largely uncorrelated ... suggesting they may index independent abilities.” Price et al. (2012, p. 54) concurred, saying that “the relationship between RT slope and w is not very strong, which might be explained by the fact that one is a measure of RT while the other is a measure of accuracy.”
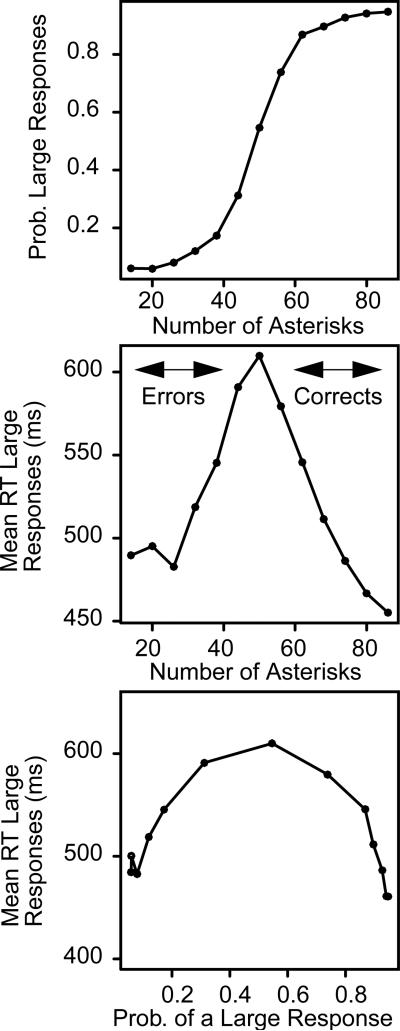
One of the main arguments we want to make is that accuracy and RT must be explained by the same mechanism, not independent mechanisms. Figure 1 shows why this is so. The data come from our first experiment: subjects were asked to decide whether the number of asterisks in a display was greater than 50 (“large”) or equal or less than 50 (“small”). The top panel shows the probability of responding “large.” Responses are highly accurate for the lowest numbers of asterisks and the highest numbers, but not with numbers in between (e.g., 40 asterisks).
Figure 1.
Plots of probability of a large response against number of asterisks (top panel), mean RT for “large” responses against number of asterisks (middle panel), and mean RT for a “large” response against the probability of a “large” response (bottom panel) in the numeracy discrimination task.
The middle panel shows mean RTs for “large” responses. When they are easy, RTs are short; when they are more difficult, RTs are longer. The right half of the plot shows correct responses and the left error responses (i.e., “large” responses to “small” stimuli). The RTs for correct and error responses mirror each other. The mean RTs for “small” responses show this same pattern.
The bottom panel shows the result that demands an explanation: when mean RTs are plotted against the probability of a “large “ response, the data sweep out a single function. When the probability of a “large” response is .80, RTs are short and when it is .60, RTs are longer. The right-hand side of the plot shows the latency-probability relation for correct responses, and the left-hand side shows it for errors (“large” responses to “small” stimuli). These plots show means across subjects. Each individual subject produces an inverted U-shaped function, but they differ in the amount of bowing (from fairly flat to quite bowed) and in location (lower or higher on the y-axis).
The latency-probability function in the bottom panel requires a theory-based explanation and sequential sampling models provide one.
In most number studies, like the ones we present in this article, the response required of a subject is a decision between two (or more) alternatives. Whatever the quality of a subject's numerosity information, a response must be chosen and the choice will take some amount of time. Accuracy and speed can trade off, and the trade-off is under a subject's control. A subject might decide to respond as quickly as possible, sacrificing accuracy, or as accurately as possible, sacrificing speed. If a subject adopts a speed emphasis, the slope of the function that relates RT to difficulty will be lower than if he or she adopts an accuracy emphasis. In consequence, differences among subjects in the quality of the numeracy information on which they base their decisions can be obscured by differences in their speed/accuracy settings. The only way to separate information quality from speed/accuracy settings is to understand how they interact. We do that with a sequential-sampling decision model, Ratcliff's (1978; Ratcliff & McKoon, 2008) diffusion model, which is described below.
In most if not all current theories about numeracy, it is assumed that a dependent measure directly assesses the quality of the numerosity information that determines decisions. If so, RTs and accuracy should correlate: subjects who have shorter RTs should also have better accuracy; subjects who have longer RTs should also have worse accuracy. When RTs and accuracy do not correlate, then other abilities have been invoked (e.g., Halberda et al., 2012; Price et al., 2012).
In contrast, in sequential sampling models in general and the diffusion model in particular, RT and accuracy do not directly assess the quality of the information on which decisions are based. These models separate out components of processing that jointly underlie decisions. The quality of the information available from a stimulus is one and the speed/accuracy criteria that a subject sets is another. Separating out these components allows explanations for the various patterns of relations among dependent variables that are observed empirically. Depending on the values of the components, RT and accuracy may not correlate even though they are based on the same, single representation of number.
In Ratcliff's diffusion model (Ratcliff, 1978; Ratcliff & McKoon, 2008), the central mechanism is the noisy accumulation of information over time. A response is made when the amount of accumulated information reaches one or the other of two boundaries, or criteria, one for each of the two possible choices (e.g., “is the number of asterisks large or small”). The rate of accumulation, called “drift rate,” is determined by the quality of the information that is available for a decision. For example, information about “is 9 greater than 1” would be stronger than information about “is 2 greater than 1” and the information available to a high-school student would likely be stronger than the information available to a second grader (e.g., Ratcliff, Love, Thompson, & Opfer, 2012).
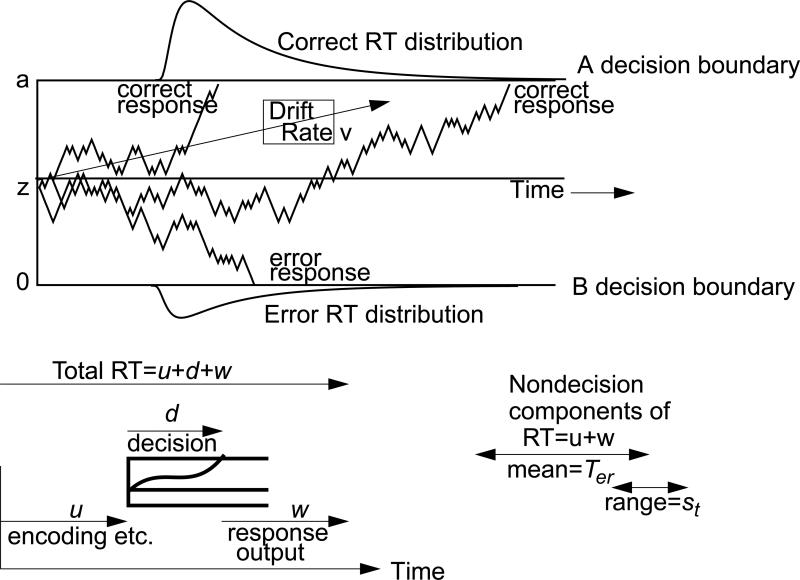
Figure 2 shows the operation of the model. Total RT is the time it takes to encode a stimulus, transform the stimulus representation to a decision-relevant representation, decide on a response, and execute a response. The transformation from the stimulus to a decision-relevant representation maps the many dimensions of a stimulus (e.g., size, color, shape, number) onto the task-relevant dimension-- the drift rate that drives the decision process. The accumulation of information begins at a starting point (z in the figure) and proceeds until one of the two boundaries is reached (a or 0 in the figure). Because the accumulation process is noisy, for a given value of drift rate, at each instant of time, there is some probability of moving toward the correct boundary and some smaller probability of moving toward the incorrect boundary. This variability means that accumulated information can hit the wrong boundary, producing errors, and that stimuli with the same values of drift rate will hit a boundary at different times. For application of the model, nondecision processes (e.g., stimulus encoding, transformation to task-relevant information, response execution) are combined into one parameter, Ter in the figure. As illustrated in the figure, the model predicts the skewed shapes of RT distributions that are observed empirically in two-choice tasks.
Figure 2.
An illustration of the diffusion model. The top panel shows three simulated paths with drift rate v, starting point z, and boundary separation a. Drift rate is normally distributed with SD η and starting point is uniformly distributed with range sz. Nondecision time is composed of encoding processes, processes that turn the stimulus representation into a decision-related representation, and response output processes. Nondecision time has mean Ter and a uniform distribution with range st.
The model decomposes accuracy and RTs into the three main components just described-drift rates, boundary settings, and nondecision processes. The values of these components vary from trial to trial because, it is assumed, subjects cannot accurately set identical values from trial to trial (e.g., Laming, 1968; Ratcliff, 1978). Across-trial variability in drift rate is assumed to be normally distributed with SD η, across-trial variability in the starting point (equivalent to across-trial variability in the boundary positions) is assumed to be uniformly distributed with range sz, and across-trial variability in the nondecision component is assumed to be uniformly distributed with range st. These distributional assumptions are the ones usually made, but they are not critical as long as they are within their usual ranges (Ratcliff, 2013).
Because the model decomposes accuracy and RTs into components and separates out variability in them, the power to observe effects of independent variables on performance can be substantially increased. For example, lexical decision experiments have been used to attempt to identify subjects with high anxiety by looking at their performance on “threat” words (e.g., anger, hostility, attack). Significant differences between high-anxiety and low-anxiety subjects did not appear with RTs or accuracy, but did appear with drift rates. The model analyses increased power by a factor of about two (White, Ratcliff, Vasey, & McKoon, 2010).
Current theories about numeracy are constrained only by mean RTs for correct responses or only by accuracy. The diffusion model is more tightly constrained. The most powerful constraint comes from the requirement that the model fit the right-skewed shape of RT distributions, as shown in Figure 2 (Ratcliff, 1978, 2002; Ratcliff & McKoon, 2008; Ratcliff, Van Zandt, & McKoon, 1999). In addition, across experimental conditions that vary in difficulty (and are randomly intermixed at test), changes in accuracy, RT distributions, and the relative speeds of correct and error responses must all be captured by changes in only one parameter of the model, drift rate. Across experimental conditions that vary in speed/accuracy criteria (e.g., speed versus accuracy instructions to subjects), all changes in accuracy, RT distributions, and the relative speeds of correct and error responses are usually captured by changes only in the settings of the boundaries. The boundaries cannot be adjusted as a function of difficulty because it would be necessary for the system to know which level of difficulty was being tested before boundary settings could be determined.
The diffusion model is highly falsifiable. Ratcliff (2002) generated simulated data for which RT distributions behaved across conditions in ways that are plausible but never obtained empirically. In all cases, the model failed to fit the data.
The model explains how drift rates and boundary settings interact to determine RTs and accuracy. For a given value of drift rate, a subject can adopt wider boundaries and so be more accurate but slower, and with narrower boundaries, a subject can be faster but less accurate. Across subjects, drift rates and boundary settings can differ independently. Subjects who have high drift rates will have good accuracy and fast responses when their boundaries are close together and good (perhaps slightly better) accuracy and slow responses when their boundaries are farther apart. Subjects who have low drift rates will have poor accuracy and fast responses when their boundaries are close together and (perhaps) somewhat better accuracy and slow responses when their boundaries are far apart. To put this another way, subjects with fast responses can be accurate or inaccurate and subjects with slow responses can be accurate or inaccurate (cf. Ratcliff, Thapar, & McKoon, 2006a, 2010, 2011). That boundary settings are under a subject's control has been demonstrated in past studies where subjects responded to instructions to maximize speed by decreasing the settings (Ratcliff, Thapar, & McKoon, 2001; 2003; 2004; Thapar, Ratcliff, & McKoon, 2003).
The model also solves a scaling problem for RT and accuracy. In the numeracy literature, when a task has high accuracy, the performance measure is typically RT (or a measure based on RT) and when a task has low accuracy, the measure is typically accuracy (or a measure based on accuracy). The two measures have different scales; accuracy varies from chance to ceiling and RTs vary from short to long. The diffusion model resolves this issue because the two measures come from the same underlying processes.
The model also helps to address problems with ceiling and floor effects. For some experiments, accuracy might be at chance for several of the most difficult conditions and it might be at ceiling for several of the easiest conditions. Despite chance or ceiling accuracy, the model can measure differences in drift rates when RTs vary across these conditions. For example, three conditions with perfect accuracy would have different drift rates if RTs among them differed. Similarly, if RTs were equally fast or equally slow for several conditions, the model can measure differences in drift rates when accuracy varies among them.
We tested a limited number of subjects in each experiment. The aim was to illustrate the utility of the approach by showing relationships among model parameters across tasks and across measures, rather than providing detailed analyses that would allow us to ask whether the correlation between a pair of model parameters was greater in one task than another. The correlations are large between pairs of tasks in many of the analyses which shows the model is extracting interpretable individual differences even with modest numbers of subjects. These also show that this modeling approach provides an explanation of individual differences in the various measures in common use.
Experiments 1-4
The aim of these experiments was to show how patterns of correlations in numeracy research can be interpreted by mapping accuracy and RTs to components of decision-making. Given that the diffusion model can explain accuracy and RT data and provide an account of decision-making in terms of model-based components of processing, the analysis can be used to test hypotheses about individual differences in numeracy using individual differences in model parameters.
We tested 32 subjects, each of whom participated in all four experiments. With 32 subjects, we could illustrate the utility of the diffusion model (and potentially models like it such as the leaky competing accumulator, Usher & McClelland, 2001; the linear ballistic accumulator, Brown & Heathcote, 2008) by showing relationships among the parameters across tasks and across measures. We found large correlations between pairs of tasks which shows that the model is extracting interpretable differences among subjects and that it provides an explanation of the patterns of individual differences in the relationships between accuracy and RT. However, we could not do more detailed analyses such as whether the correlation between a pair of model parameters is greater in one task than another.
In Experiment 1, numerosity discrimination, subjects were asked to decide whether the number of asterisks in an array was greater than 50. This task has been used in a number of applications including aging (Ratcliff et al., 2001, 2010), child development (Ratcliff, Love, et al., 2012), sleep deprivation (Ratcliff & Van Dongen, 2009) and hypoglycemia (Geddes et al., 2010). Experiment 2 was a symbolic version of the same task. Subjects decided whether a two-digit number was greater than 50.
For tasks like those in Experiments 1 and 2, the slope of the function relating RT and difficulty is often used as a dependent variable (e.g., Zebian & Ansari, 2012; Price et al., 2012). However, in Experiments 1 and 2, the functions were not linear and so, strictly speaking, it is not appropriate to fit linear functions to them and use the slopes of the functions as a measure of differences among individuals. Nevertheless, for generality, we examined the relations among slopes, RTs, accuracy, and components of the diffusion model.
The tasks used in Experiments 1 and 2 are “on-line” tasks, and they are typical of those that have been used in the literature on numeracy. To make a response, it is explicitly required that subjects determine the numerical difference between a test item and 50.
Experiments 3 and 4 used “off-line” tasks. In these experiments, subjects were given short lists of numbers to remember and each list was immediately followed by a series of test numbers. For each test number, subjects were to respond “old” if it had been among the studied numbers and “new” if it had not. In Experiment 3, the numbers ranged from 11 to 90 and in Experiment 4, they ranged from 101 to 900. The question for these experiments was whether the numeracy information used in off-line memory tasks is significantly correlated with the numeracy information used in on-line tasks. This has rarely been investigated (but see Brainerd & Gordon, 1994; Thompson & Siegler, 2010). For the memory experiments, we used two- and three-digit numbers because if single-digit numbers were mixed with two- or three-digit numbers, they would possibly be distinct from the two- or three- digit numbers and have higher accuracy.
Memory for number is a critical component of general mathematical achievement, it is essential for learning how to perform computations with numbers, and it is necessary for performing computations in real-life situations. This suggests that good memory for numbers is associated with high levels of numeracy skills. By examining the relationships between the on-line tasks and the memory tasks, we can begin to ask if the differences among individuals that are observed in the on-line tasks pinpoint a numeracy ability that is linked to a specific representation (the approximate number system, for example) or whether they are part of a larger cluster of skills that includes memory for numbers. In the latter case, they might be manifestations of a general use of number information or simply general intelligence.
Method
32 college students at the University of Oklahoma (mean age = 19.4) participated in the experiments in partial fulfillment of class requirements for an Introductory Psychology class. Each participated in two sessions of about 60 min. with the mean number of days between sessions 5.5 (SD = 2.25). Experiments 2 and 3 were tested in the first session and Experiments 1 and 4 in the second.
Prior to beginning each task, subjects were told that sometimes the decisions would be difficult to make, but they should nevertheless attempt to respond as quickly and accurately as possible. Between each block of trials, there was a break and subjects saw a progress bar that tracked their cumulative correct and error responses.
For all four tasks, the stimuli were displayed on the screen of a laptop computer and responses were collected from the laptop's keyboard, using the ?/ key for one choice and the Zz key for the other.
Experiment 1, nonsymbolic numerosity discrimination
On each trial, some number of white asterisks, between 11 and 90, was displayed against a black background. The asterisks occupied randomly selected positions in a 10x10 grid in the center of the laptop screen. The grid subtended a visual angle of 7.5 degrees horizontally and 7.0 degrees vertically. The asterisks remained on the screen until a response key was pressed. Then the screen was cleared, a smiling (correct response) or frowning (incorrect response) face was displayed for 500 ms, the screen was cleared, there was a 100 ms blank screen, and then the next trial. Subjects were instructed to respond “small” if the number of asterisks was between 11 and 49 and “large” if the number was between 51 and 90. There were 8 blocks of trials, 80 trials per block, with each of the possible numbers of asterisks tested once in each block in random order.
Experiment 2, number discrimination
On each trial, a white Arabic number between 10 and 90 was displayed on a black background in the middle of the laptop screen. The number remained on the screen until a response key was pressed. Then the screen was cleared, a smiling or frowning face was displayed for 500 ms, there was a 100 ms blank screen, and then the next trial. Subjects were instructed to respond “small” if the number was between 10 and 49 and “large” if it was between 51 and 90. There were 8 blocks of trials, 80 trials per block, with each of the possible numbers tested once in each block in random order.
Experiment 3, two-digit memory
The stimuli were white Arabic numbers displayed in the center of the laptop screen against a black background. There were 40 blocks in the experiment, with each block made up of a study list and a test list. For the study list, 6 numbers were chosen randomly (without replacement) from the range 11 to 90. Each was displayed for 1.5 s, in random order. The test list immediately followed. It was made up of 12 numbers in random order, the 6 that had appeared in the study list, for which subjects were instructed to respond “old,” and 6 that had not appeared in the study list, for which subjects were instructed to respond “new.” Each number was displayed until a response key was pressed. Then the screen was cleared, a smiling or frowning face was displayed for 500 ms, the screen was cleared for 100 ms, and then the next test number was displayed. Numbers were repeated no closer than four blocks apart and no more than eight blocks apart.
Experiment 4, three-digit memory
This task was the same as the two-digit task except that the numbers were chosen from the range 101-900 and no number appeared more than once in the 40 blocks.
Results
Responses shorter than 250 ms were eliminated from analyses, as were responses longer than 2000 ms for Experiments 1 and 2 and longer than 3500 ms for Experiments 3 and 4 (totaling 3.0%, 3.0%, 2.4%, and 5.6% of responses for the four experiments respectively).
For Experiments 1 and 2, the proportions of correct responses and mean RTs for correct responses are shown in Table 1. For Experiment 1, mean RTs for errors are also shown for the conditions for which all subjects made errors (the most difficult conditions). Stimuli were grouped into conditions as shown in the table in order to provide more observations per condition for application of the diffusion model (e.g., Ratcliff, Thapar, & McKoon, 2001). The number of groups (six for Experiment 1, eight for Experiment 2) was chosen to maximize the similarity of RTs and accuracy for the stimuli within each group (grouping “small” responses to large stimuli with “large” responses to small stimuli). For Experiment 1, subjects were slightly biased such that the chance level of accuracy for responding “large” and “small” was at about 47, not 50.
Table 1.
Response Proportion and Mean RTs for Experiments 1-4.
| Experiment | Condition | Proportion Correct | Mean Correct RT | Mean Error |
|---|---|---|---|---|
| Experiment 1: Numerosity Discrimination | 11-16/77-88 | 0.943 | 455.3 | |
| 17-22/71-76 | 0.934 | 479.4 | ||
| 23-28/65-70 | 0.908 | 491.7 | ||
| 29-34/59-64 | 0.874 | 527.2 | ||
| 35-40/53-58 | 0.783 | 558.3 | 583.7 | |
| 41-46/47-52 | 0.617 | 591.7 | 613.5 | |
| Experiment 2: Number Discrimination | 10-14/86-90 | 0.972 | 501.2 | |
| 15-19/81-85 | 0.963 | 512.1 | ||
| 20-24/76-80 | 0.968 | 510.7 | ||
| 25-29/71-75 | 0.952 | 529.4 | ||
| 30-34/66-70 | 0.956 | 534.7 | ||
| 35-39/61-65 | 0.943 | 563.5 | ||
| 40-44/56-60 | 0.904 | 590.0 | ||
| 45-49/51-55 | 0.879 | 632.0 | ||
| Experiment 3: Two-Digit Number Memory | Studied | 0.825 | 709.5 | 889.9 |
| Not Studied | 0.680 | 834.8 | 778.7 | |
| Experiment 4: Three-Digit Number Memory | Studied | 0.785 | 732.5 | 842.8 |
Note. Only two error RTs are shown for the numerosity discrimination task and none for the number discrimination task because in all the other conditions, at least one subject had no errors and so mean error RT cannot be computed. The divisions in the numerosity task were used because on average, subjects adopted 47 as the cutoff between large and small.
For both experiments, accuracy decreased and RTs increased with difficulty. For the three easiest conditions in Experiment 1 (those with the largest and smallest numbers of asterisks), accuracy was close to ceiling (above 90% correct) but RTs continued to decrease as the stimuli became easier. For Experiment 2, most of the conditions were above 90% correct but as conditions became easier, RTs decreased substantially, from 632 ms to 501 ms.
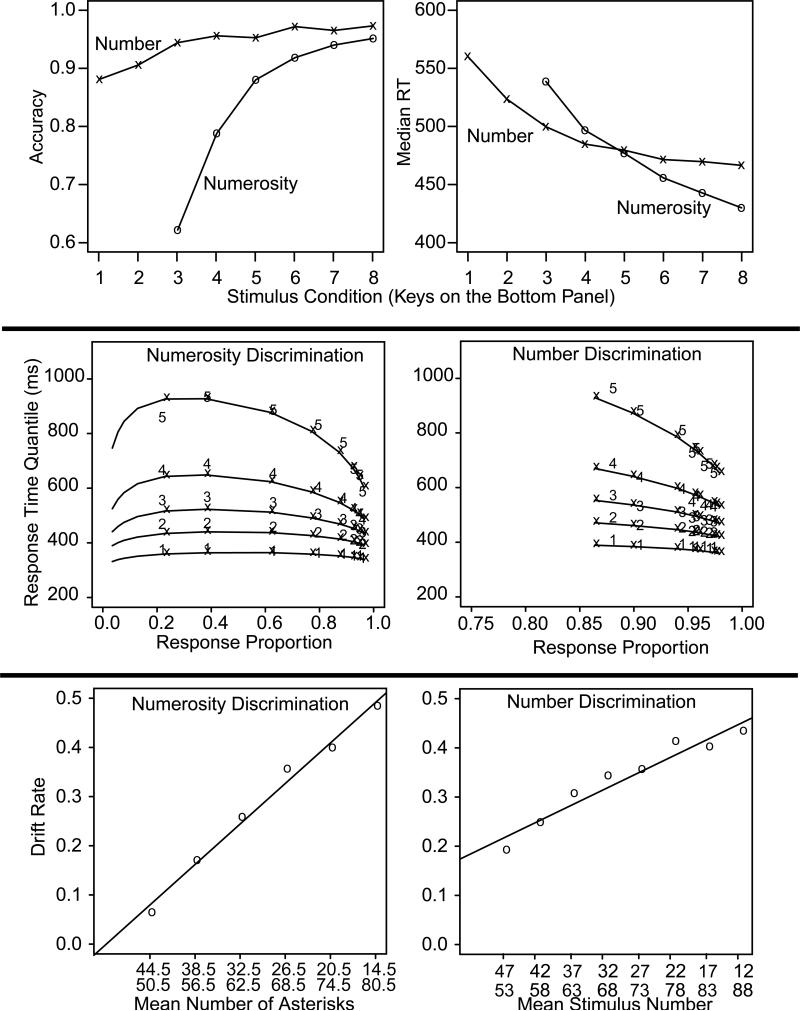
Plots of accuracy and median RT as a function of difficulty are shown in the top panel of Figure 3. For the numerosity task, the RT and accuracy functions are both nonlinear and for the number task, the RT function is nonlinear. The accuracy function for the number task appears linear because so many of the conditions are near ceiling.
Figure 3.
Top panel: plots of accuracy and median RT averaged over subjects for the numerosity and number discrimination tasks. Middle panel: quantile probability plots for Experiments 1 and 2. The x's represent the experimental data and the digits joined by lines are the model predictions. The conditions are shown on the x axis in terms of proportions of responses. Proportions on the right are for correct responses and proportions on the left for error responses (some of the error quantiles are missing because some of the subjects had zero responses for those conditions). The RT quantiles are, in order from bottom to top, the .1, .3, .5, .7, and .9 quantiles. Predictions were generated for each subject and then averaged over subjects. The data are averages over subjects. Bottom panel: drift rate plotted against number of asterisks in Experiment 1 and number in Experiment 2.
It is sometimes found in the numeracy literature that discriminability between small one-digit numbers (e.g., 1 versus 2) is better than between large one-digit numbers (e.g., 8 versus 9; Dehaene, Dupoux, & Mehler, 1990). For Experiments 1 and 2, the numbers tested were much larger, and we found no such differences (see also Ratcliff, 2014, Experiments 1 and 2). The accuracy values from these two experiments were symmetric around 47 (numerosity) and 50 (number).
Table 1 also shows the accuracy and RT data for Experiments 3 and 4. For both, accuracy shows reasonably good discrimination between studied and not-studied numbers.
For all four experiments, the model was fit to the data for each subject individually using the method we have most commonly used in applications of the model. The values of all of the components of processing identified by the model are estimated simultaneously from the data for all the conditions in an experiment. The fitting method uses quantiles of the RT distributions for correct and error responses for each condition (the .1, .3, .5, .7, and .9 quantile RTs). The model predicts the cumulative probability of a response at each RT quantile. Subtracting the cumulative probabilities for each successive quantile from the next higher quantile gives the proportion of responses between adjacent quantiles. For a chi-square computation, these are the expected values, to be compared to the observed proportions of responses between the quantiles (i.e., the proportions between .1, .3, .5, .7, and .9, are each .2, and the proportions below .1 and above .9 are both .1) multiplied by the number of observations. Summing over (Observed-Expected)2/Expected for correct and error responses for each condition gives a single chi-square value that is minimized with a general SIMPLEX minimization routine. The parameter values for the model are adjusted by SIMPLEX until the minimum chi-square value is obtained (see Ratcliff & Tuerlinckx, 2002, for a full description of the fitting method; see published packages for fitting the model by Vandekerckhove & Tuerlinckx, 2007; Voss & Voss, 2007, and Wiecki, Sofer, & Frank, 2013; see also evaluation of the fitting methods by Ratcliff & Childers, in press, and Voss, Nagler, & Lerche, 2013).
The RTs used for fitting the model, especially for Experiment 2, were slightly complicated by the fact that for many subjects for many conditions, there were fewer than five errors and so quantiles could not be computed. When this was the case, the RT distribution for a condition was divided at its median and the model was fit by predicting the cumulative probability of responses above and below the median. This reduced the number of degrees of freedom from 6 to 2 for that error condition. (To avoid very small or very large medians when there were only one or two responses, when these might be outliers, this division was used only when the median for errors was between the .3 and .7 median RTs for correct responses.) Mean chi-square values (Table 2) were lower than critical values. Because of the conditions with fewer than five errors, the average degrees of freedom were reduced from 55 to 50 for Experiment 1 and from 74 to 54 for Experiment 2.
Table 2.
Diffusion Model Parameters
| Experiment and Statistic | a | z | Ter | η | sz | st | χ 2 | vo | vn |
|---|---|---|---|---|---|---|---|---|---|
| 1: Numerosity, mean | 0.118 | 0.059 | 0.323 | 0.133 | 0.073 | 0.154 | 65.2 | ||
| 2: Number, mean | 0.129 | 0.064 | 0.336 | 0.099 | 0.072 | 0.140 | 64.2 | ||
| 3: Memory 2 digit, mean | 0.142 | 0.085 | 0.474 | 0.207 | 0.043 | 0.210 | 19.7 | 0.182 | −0.156 |
| 4: Memory 3 digit, mean | 0.135 | 0.075 | 0.461 | 0.178 | 0.055 | 0.240 | 23.2 | 0.161 | −0.109 |
| 1: Numerosity, SD | 0.023 | 0.011 | 0.025 | 0.094 | 0.029 | 0.041 | 17.1 | ||
| 2: Number, SD | 0.027 | 0.013 | 0.024 | 0.063 | 0.029 | 0.037 | 18.5 | ||
| 3: Memory 2 digit, SD | 0.034 | 0.019 | 0.049 | 0.097 | 0.041 | 0.073 | 10.6 | 0.086 | 0.084 |
| 4: Memory 3 digit, SD | 0.029 | 0.017 | 0.074 | 0.091 | 0.043 | 0.072 | 13.0 | 0.071 | 0.108 |
| 5: Numerosity normal, mean | 0.132 | 0.066 | 0.346 | 0.156 | 0.074 | 0.117 | 56.8 | ||
| 7: Numerosity speed, mean | 0.080 | 0.040 | 0.307 | 0.176 | 0.065 | 0.120 | 61.4 | ||
| 6: Number normal, mean | 0.128 | 0.064 | 0.351 | 0.099 | 0.073 | 0.124 | 81.1 | ||
| 8: Number speed, mean | 0.081 | 0.040 | 0.309 | 0.075 | 0.065 | 0.108 | 102.5 | ||
| 5: Numerosity normal, SD | 0.034 | 0.017 | 0.032 | 0.073 | 0.020 | 0.062 | 17.8 | ||
| 7: Numerosity speed, SD | 0.035 | 0.018 | 0.028 | 0.070 | 0.018 | 0.032 | 29.7 | ||
| 6: Number normal, SD | 0.011 | 0.005 | 0.023 | 0.125 | 0.018 | 0.038 | 17.6 | ||
| 8: Number speed, SD |
The parameters were: Boundary separation a, starting point z = a/2, mean nondecision component of response time, Ter, SD in drift across trials η, range of the distribution of starting point sz, range of the distribution of nondecision times, st, vo is the drift rate for “old” responses in the memory task and vn is the drift rate for new responses in the memory tasks. Critical values of chi-squares are 67.5 for 50 degrees of freedom for the numerosity discrimination task, 72.2 for 54 degrees of freedom for the number discrimination task, and 23.7 for 14 degrees of freedom for the two memory tasks.
For Experiments 1 and 2, the middle panel in Figure 3 demonstrates that the model accounted for the data well. The two plots in the middle panel show quantile probability plots. The x's and the lines between them are the predictions from the model and the digits are the data. The x-axis shows the conditions of the experiments indexed by the proportion of responses that occurs for each condition.
The conditions were constructed by collapsing over large and small stimuli. “Large” responses to large stimuli were combined with “small” responses to small stimuli, so correct responses are to the right of proportion 0.5. “Large” responses to small stimuli were combined with “small” responses to large stimuli, so incorrect responses are to the left of 0.5. For many of the conditions, some subjects had too few responses to construct quantiles and so these are not shown (on the extreme left of the plots).
Conditions for which accuracy was at ceiling are on the far right and, as conditions become more difficult, accuracy moves toward .5. On the left are the proportions of errors for those conditions that were not at ceiling. The quantile RTs for a condition are stacked vertically. They show the usual spread, with faster quantiles closer together and slower ones farther apart. For Experiment 1, the figure plots quantile probabilities for error responses for conditions with five or more errors, which were the two most difficult (farthest left) conditions in Experiment 1.
For Experiments 3 and 4, the fit of the model to the data was reasonably good with a mean chi-square value less than the critical value as for Experiments 1 and 2 (Table 2).
Model-based Interpretations of the Data
For all four experiments, Table 2 shows the values of the parameters that generated the best fit of the model to the data, averaged over subjects. Below we first discuss the values averaged over subjects and then differences in the values among individual subjects.
Values of Model Parameters Averaged Across Subjects
Drift rates
For Experiments 1 and 2, the panels in the bottom row of Figure 3 show the psychometric functions that relate drift rate to difficulty (Ratcliff, 2014). The lines in the figures are linear regressions for drift rate as a function of the independent variable (number of asterisks or number). Linear functions across all levels of difficulty provide a good fit for both experiments. For numerosity discrimination, performance is near chance for numbers of asterisks near 50 and so the intercept of the drift rate function is near zero. For number discrimination, the intercept is well above zero. The fact that the functions are linear is especially noteworthy because the functions based on accuracy and RT (Figure 3 top) are nonlinear. In other words, the drift rate functions provide a different picture of performance than do either the accuracy or RT functions.
For the memory tasks, drift rates were positive for studied items and negative for non-studied items (Table 1). The difference in drift rates between studied items and non-studied items (which represents discriminability between them) was higher with two digits than three, t=3.64, df=31, p<.05.
Boundaries
Subjects set the distance between the boundaries about the same for the two discrimination tasks and about the same for the two memory tasks. They set them wider apart for the memory than the discrimination tasks (F(3,93)=7.63, p<.05, MSE=0.000486).
Nondecision times were about the same for the two discrimination tasks and for the two memory tasks, but they were larger for the memory tasks (F(3,93)=92.11, p<.05, MSE=0.00194).
The difference, 121 ms, between the nondecision time for number discrimination and the nondecision time for two-digit memory is noteworthy because the stimuli were the same for the two tasks. Ratcliff, Thapar, and McKoon, (2006a, 2010) also found longer nondecision times for memory than numerosity. These differences suggest that the time to transform a stimulus to decision-relevant information is longer for memory tasks than perceptual tasks, perhaps because the memory tasks require retrieval of information from memory.
Variability parameters
The other parameters of the model are the range in nondecision times across trials, the standard deviation in drift rates across trials, and the range of starting points across trials. These were all significantly different across tasks (F's(3.93)=25.50, 11.03, and 8.42 respectively, p's<.05, MSE's= 0.00322, 0.00596, 0.000981). The larger across-trial variability in drift rate and the larger across-trial variability in nondecision times for the memory than the discrimination tasks may reflect more variability in encoding and accessing information from memory than discrimination, a reasonable but post hoc suggestion. For the increased variability in starting point for the discrimination tasks compared to the memory tasks, we see no obvious explanation.
Differences Among Individuals in Data and Model Parameters
By testing the same subjects on the four tasks, the correlations between the six possible pairings of the tasks can be examined. In order, we first examine correlations between measures from the data (accuracy, median RT, and the slope of the RT-difficulty function, which is sometimes used as a dependent measure), second, correlations between model parameters (drift rates, boundaries, and nondecision time), and third, correlations between model parameters and measures from the data (cf., Ratcliff, et al., 2006a, 2010, 2011).
Data
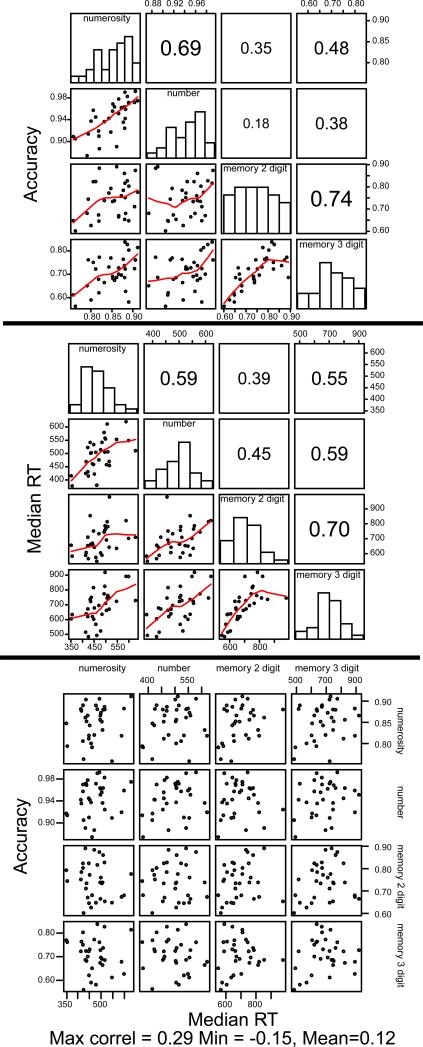
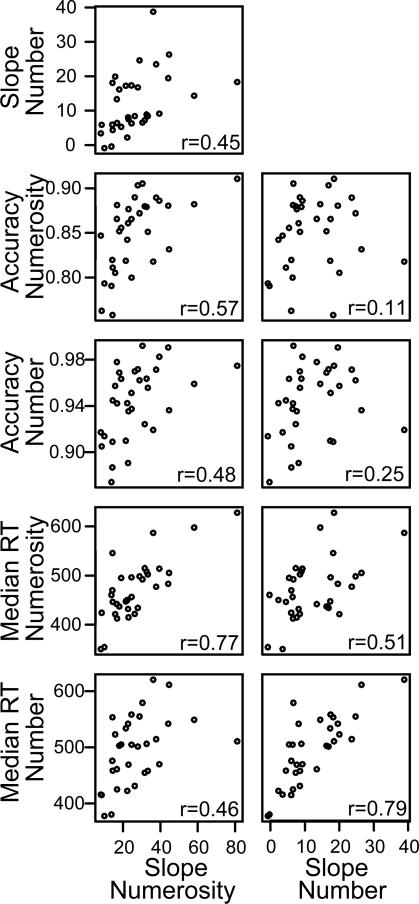
Not surprisingly, subjects who were accurate in one of the tasks were accurate in the others (mean correlation = .47) and subjects who were fast in one of the tasks were fast in the others (mean correlation = .55). Figure 4 shows the values of the correlations and their corresponding scatter plots (the critical value for significance with 30 degrees of freedom for a one-tailed test is .30). For accuracy, the correlations between the number discrimination task and the other tasks were smaller than other combinations because accuracy for number discrimination was near ceiling.
Figure 4.
Scatter plots, histograms, and correlations for accuracy (top panel) and for median RT (middle panel) for the four tasks. The bottom panel shows scatter plots for accuracy plotted against median RT for all combinations of tasks. Accuracy and median RTs are averaged over conditions. Each dot represents an individual subject. In the top two plots, the size of the number for the correlations represents the size of the correlation and the identity of the comparison in each off-diagonal plot or correlation is obtained from the task labels in the corresponding horizontal and vertical diagonal plots. The lines in the bottom left of the plots are lowess smoothers (from the R functions).
The most interesting result was that RTs were not significantly negatively correlated with accuracy. In other words, faster subjects were not necessarily more accurate subjects. The bottom panel of Figure 4 shows scatter plots for the 16 combinations of median RTs for one task with accuracy in that task and the other three tasks. The plots on the diagonal from top left to bottom right are the plots of accuracy against median RTs for the same task. The mean correlation for these four plots was 0.21, and the mean for all the others was 0.12 (ranging from −0.15 to 0.29). Not only were the correlations between RTs and accuracy not significant, they were in the wrong direction for the common-sense hypothesis that accurate subjects should be faster. These non-significant correlations replicate the lack of correlations found by Halberda et al. (2012) and Price et al. (2012) that were mentioned in the introduction.
The finding that accuracy-RT correlations were not significant calls into question interpretations of results from the many previous studies in the number literature for which only RTs or only accuracy were measured. The finding also puts a stringent constraint on theories about number processing: Whatever it is that determines a subject's overall accuracy is not directly related to whatever it is that determines his or her overall speed. Any theory about performance in numeracy tasks must explain why this is so. Later, we discuss how the diffusion model does this.
In addition to the median RT and accuracy correlations just described, we computed correlations for the slopes of RT-difficulty functions. The top panel of Figure 5 shows a scatter plot of slopes for the numerosity task plotted against slopes for the number task. The slopes were significantly correlated for the two tasks (.45).
Figure 5.
Scatter plots for accuracy and median RT plotted against slope of the RT-difficulty function for numerosity and number discrimination (within and across tasks) are shown. The top plot shows a plot of the slopes for numerosity and number discrimination.
The lower eight panels of Figure 5 show slopes plotted against median RTs and against accuracy within and between tasks. The slope for numerosity discrimination was significantly correlated with accuracy in the numerosity and number tasks, indicating that subjects who were more accurate had higher slopes relative to subjects who were less accurate. The correlations between the slope for number discrimination and accuracy for numerosity and number were not significant, possibly because accuracy was near ceiling for the number task. The correlations between median RTs and slopes were all significant.
Diffusion model parameters
Three sets of correlations were computed: 1) correlations between the main model parameters (drift rates, boundary settings, and nondecision times) for the six pairs of tasks; 2) correlations between drift rates and boundary settings, drift rates and nondecision times, and boundary settings and nondecision times for each of the four tasks; and 3) correlations between the slope of the psychometric drift rate-difficulty function and drift rate.
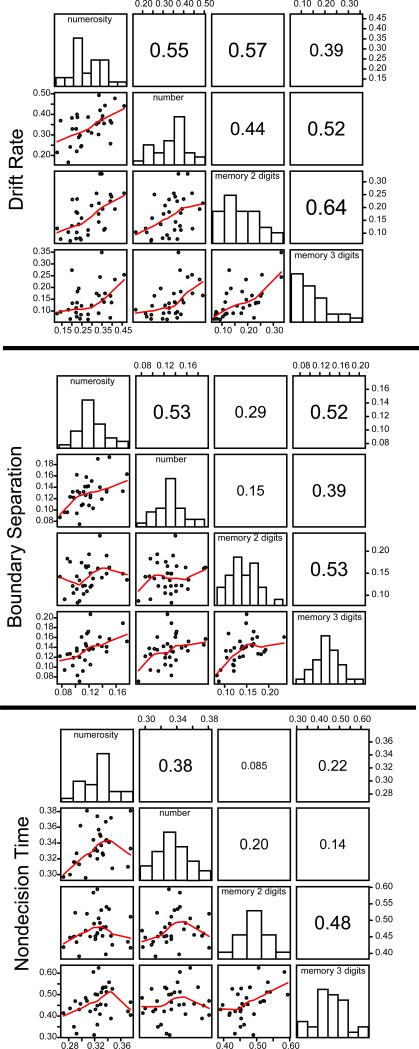
(1). Correlations and scatter plots for the diffusion model parameters are shown in Figure 6. Drift rates (averaged across the conditions in each experiment) were strongly correlated across the tasks (mean 0.52) and boundary settings were reasonably highly correlated (mean 0.40). For nondecision times, only two of the six combinations were significant (mean 0.25). As we have suggested before, the low correlations for nondecision times are likely a reflection of the differences between the tasks in the time taken to transform stimuli into representations that are appropriate for the task.
Figure 6.
Scatter plots, histograms, and correlations for boundary settings, nondecision time, and drift rate (averaged over conditions) are shown. Each dot represents an individual subject. The size of the number for the correlations represents the size of the correlation. The identity of the comparison in each off-diagonal plot or correlation is obtained from the task labels in the corresponding horizontal and vertical diagonal plots.
Parameters for the memory tasks should be the most highly correlated because the two tasks are so nearly the same. For this reason, the values of these correlations can be seen as an upper limit for all the others because the main differences between the two tasks are different random samples of data, differences in mathematical ability in dealing with 2-digit and 3-digit numbers (relative to other individuals, which should be minimal), and differences that might occur because the experiments were run on different days. For drift rates, boundary settings, and nondecision times, the correlations for the two memory tasks were between .48 and .64. These were larger than the correlations between any of the other pairs of tasks. Later, we use Monte Carlo simulations to further address power for the correlations in Figure 6 (also, Experiments 5-8 provide replications of some of the results).
(2). One of the more important results for these experiments is that the model parameters were not correlated with each other; this is true for all of the tasks (Table 3, bottom three rows). Drift rates were not significantly correlated with boundary settings or nondecision times and boundary settings were not significantly correlated with nondecision times. This shows that the model decomposes the dependent variables (accuracy and correct and error RT distributions) into components of processing that are orthogonal to each other, even though they all influence the dependent variables.
Table 3.
Correlations of model parameters and accuracy, median RT, and RT slope averaged over the tasks for Experiments 1-4.
| Data or parameter | a | Ter | v |
|---|---|---|---|
| accuracy | .36 | .10 | .46 |
| Median RT | .76 | .44 | −.39 |
| RT slope for numerosity and number | .69 | −.04 | −.34 |
| a | .05 | −.13 | |
| Ter |
(3). The bottom panels of Figure 3 show the psychometric functions that relate drift rates to levels of difficulty. For numerosity discrimination, drift rates for numbers of asterisks near 50 must be near zero. With the function anchored at zero, the slope must increase as mean drift rate increases, and so the correlation between slope and mean drift rate was high, .93.
In contrast, for number discrimination, accuracy was not close to chance even for numbers near 50, and so drift rate was not near zero. This means there are two possibilities for differences among individuals. One is that the drift rate-difficulty slope could be correlated with mean drift rate such that the slope is larger for subjects with higher overall drift rate. The other is that the functions for different subjects could be parallel, that is, as mean drift rate for a subject increases, the functions simply shift up. The first pattern is the one that was obtained; the correlation between slope and mean drift rate was .50.
Diffusion model parameters and data
Four sets of correlations were computed: 1), correlations between the parameters and accuracy and between the parameters and median RTs for each task; 2) correlations between the parameters and RT-difficulty slopes for each task; 3) correlations between the drift rate-difficulty slopes and accuracy, drift rate-difficulty slopes and median RTs, and drift rate-difficulty slopes and RT-difficulty slopes.
(1). Accuracy was significantly correlated with both boundary separation and drift rate (row 1, Table 3): the higher the drift rate, the more accurate the subject, and the wider the boundaries, the more accurate the subject. Median RT was significantly correlated with boundary separation, drift rate, and nondecision time (row 2, Table 3): subjects were slower with wider boundaries and longer nondecision times, and they were faster with higher drift rates. The correlations between accuracy and drift rate and between RT and boundary separation were much larger than the others; we explore why this is so in the next section.
(2). As would be expected, RT-difficulty slopes were correlated with boundary separation. Wider boundaries mean longer RTs and so increases in difficulty between conditions produce magnified increases in RT. RT-difficulty slopes did not correlate significantly with nondecision times. Because nondecision times do not change across levels of difficulty, variations in them simply shift the RT distributions. The correlation between RT-difficulty slopes and drift rates was marginal; higher drift rates produced lower slopes but only minimally so.
(3). For numerosity discrimination, the correlation between the slope of the drift rate-difficulty function and accuracy was .53. This follows from the high correlation of mean drift rate with slope of the drift rate-difficulty function. For number discrimination, the correlation was only .08 because accuracy values were near ceiling for many of the subjects and hence relatively less reliable than for numerosity discrimination.
The diffusion model can extract meaningful estimates of drift rates even when accuracy is near ceiling because drift rates are determined by RTs as well as accuracy. This explains why the correlation between mean drift rate and slope is higher (.53) than the correlation between accuracy and slope (.08).
For RTs, the correlations between median RT and the drift rate-difficulty slope were -.22 and -.44 for numerosity and number discrimination, respectively, which follows from the correlation of drift rate with RT. However, the correlations between drift rate-difficulty slope and RT-difficulty slope were -.01 and -.14 for numerosity and number discrimination, respectively. These low correlations came about because drift rates were a smaller determinant of RTs than boundary separation and nondecision time and estimates of slopes are less reliable than means.
How Model Parameters Influence Accuracy and RT
In the correlations reported above, two of the most relevant for understanding how the diffusion model predicts the data are, first, that accuracy was more highly correlated with drift rate than boundary separation, and second, that RT was more highly correlated with boundary separation than drift rate. In this section, we explore how the relative sizes of these correlations are related to the values of the model's parameters.
If there are large correlations between the parameters and individuals’ accuracy, RTs, and RT-difficulty slopes, then the differences among individuals in the parameters will have produced large effects on the dependent variables. The effects of some model parameters on dependent variables will be larger than the effects of others, and variability in the data will tend to wash out or reduce correlations so that the larger effects remain while the smaller effects disappear. Thus, to explain why some correlations are larger than others, we examined which parameters have the larger effects on dependent variables and which have the smaller effects.
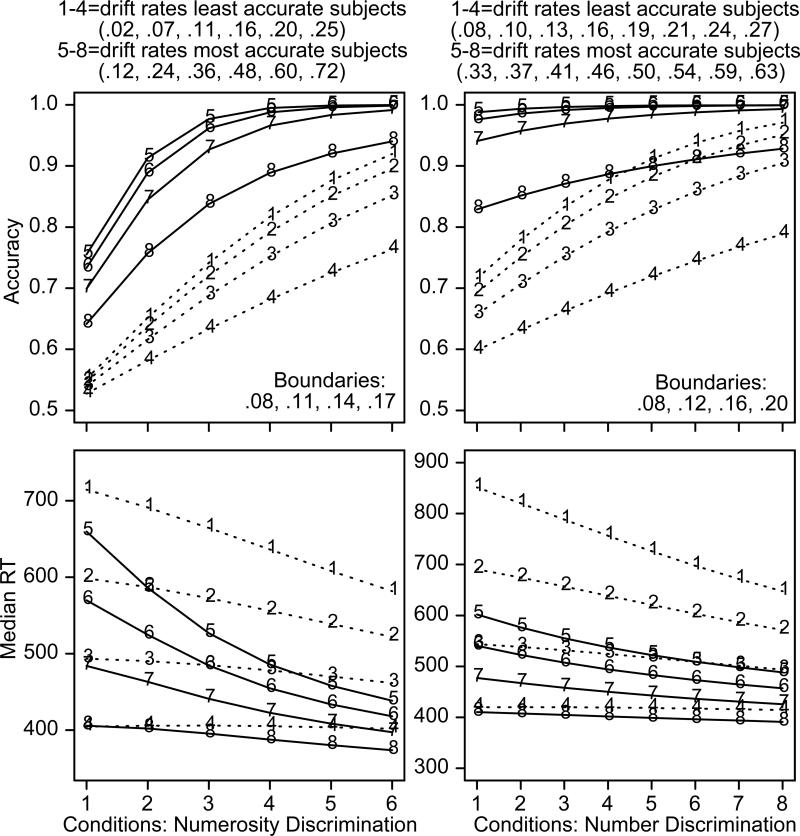
To do this, we generated predicted values of accuracy and median RT using values of drift rates and boundary settings that varied across the ranges found for them for Experiments 1 (numerosity discrimination) and 2 (number discrimination). For each experiment, we used the average of the drift rates for the two least accurate subjects and the average for the two most accurate subjects. For the six conditions for numerosity, the drift rates ranged from .02 to .25 for the least accurate subjects and from .12 to .72 for the most accurate subjects. For the eight conditions for number, the drift rates ranged from .08 to .27 for the least accurate subjects and from .33 to .63 for the most accurate subjects. (The drift rate values were smoothed to produce equal size differences across conditions.)
For boundary settings, we chose four values for each experiment that spanned the range from smallest to largest across subjects. The values varied from .08 to .17 for numerosity discrimination and from .08 to .20 for number discrimination. The other model parameters were the means across subjects for Experiments 1 and 2.
Figure 7 shows the accuracy and RT data predicted from the combinations of drift rates and boundary settings. The solid lines are for the subjects with high drift rates, one line for each boundary setting, and the dashed lines for the subjects with low drift rates, also one line for each boundary setting. The plots show that changes in drift rates produce larger changes in accuracy than do changes in boundary settings. In other words, the differences in accuracy between the high- and low-drift rate subjects are larger than the differences between the highest and lowest boundary settings; with various sources of variability, this leads to a larger correlation between accuracy and drift rates than between accuracy and boundary settings.
Figure 7.
Plots of predicted median RT and accuracy from parameter values from fits of the diffusion model to data for Experiments. All the parameters except drift rate and boundary separation were the mean values from Table 2. The values of drift rates and boundary separations are shown in the figure. There were four values of boundary separation that spanned the range from the narrowest to the widest from the fits to the individual subjects in each experiment. There were two sets of drift rates, one set from the lowest-performing subjects and another from the highest-performing subjects (the drift rate functions in the plots used equal size steps between adjacent conditions). For boundary separation, lines labeled 1 and 5 have the widest separation and 4 and 8 have the narrowest setting. For drift rates, 1-4 have the lowest drift rates and 5-8 have the highest drift rates.
Conversely, boundary settings had larger effects on RTs than did drift rates. The differences in RTs among the settings (lines 1 versus 4 and lines 5 versus 8) are larger than the differences in RTs between the high- and low-drift rate subjects (dotted versus solid lines). Median RTs for high- and low-drift rate subjects largely overlap with narrow boundary settings (4 and 8), but are well separated with wider settings (1 and 5).
The RT results in Figure 7 also illustrate that the slopes of RT-difficulty functions change much more with boundary settings than drift rates. The difference between the slopes for the high-and low-accuracy subjects (lines 1 through 4 versus 5 through 8) is less than the difference between the slopes for the wide and narrow boundary settings (e.g., lines 1 versus 4 and 5 versus 8). More specifically, for numerosity, the slope changes from 7 ms to 44 ms over boundary settings from 0.08 to 0.20 for high-drift rate subjects and from 1 ms to 27 ms for low-drift rate subjects. For number, the slope changes from 3 ms to 16 ms over boundary settings from 0.08 to 0.17 for the high-drift rate subjects and from 1 to 29 ms for the low-drift rate subjects.
The plots in Figure 7 show exact predictions from the drift rates and boundary settings that were used to generate the data. For real data, which might have at most only a few hundred observations, extra sampling variability would be introduced into accuracy and RTs, and therefore into the values of the diffusion model parameters derived from them. This variability obscures smaller differences (e.g., between high- and low-boundary settings in accuracy) to a greater degree than larger differences (e.g., between high- and low-drift rate subjects in accuracy), and this results in lower (or non-significant) correlations for the smaller differences than for the larger ones.
The plots in Figure 7 also illustrate scaling effects. For a constant difference between two conditions of an experiment in either drift rate or boundary settings, the size of the difference between the two conditions in RT and accuracy differs as a function of how near performance is to ceiling or floor, i.e., as a function of the values of drift rate or boundary separation. Also, variability in median RT increases as median RT increases (with lower drift rates and wider boundary settings), and variability in accuracy decreases as accuracy increases toward ceiling (with higher drift rates and wider boundary settings). Thus, longer RTs and higher accuracy are associated with larger variability than shorter RTs and lower accuracy.
It should be cautioned that the conclusions from the plots in Figure 7 depend on the values of the model parameters that were used to generate the data, that is, on the values that best predicted the real data from Experiments 1 and 2. Conclusions might be different for other tasks or other subject populations, which means that an analysis similar to that done to produce Figure 7 would need to be carried out.
We stress four overall points about the results of the experiments. First, if an individual had high accuracy and/or short RTs for one task, he or she tended to have high accuracy and/or short RTs for the other tasks. Second, if an individual had a high value for one of the components of the model for one task, then he or she tended to have a high value for the other tasks. Third, within a task, accuracy and RTs were highly correlated: as the difficulty of test items increased, accuracy fell and RTs increased. Fourth, in contrast to all of these, accuracy and RTs were not correlated with each other across subjects. In other words, a subject's accuracy did not provide any information about his or her RTs.
Power: Monte Carlo and Bootstrap Simulations
There are two sets of power analyses. The first addresses the power to find several significant correlations when each one is not particularly powerful. The second, presented in the general discussion, addresses the issue of not finding negative correlations between accuracy and RT.
First, we can examine the power for a single correlation. If the true correlation was .4, .45, .5, .55, or .6, there is a .72, .83, .91, .96, or .98 probability of getting a significant correlation, greater than the .3 critical value with 32 subjects (see also Cohen, 1992). This suggests that there is adequate power for most of the correlations of the size reported in Figures 4, 5, and 6.
However, there is more power because there were four tasks and therefore six pairs of correlations. If the population (true) correlations were equal across the six pairs at a moderately large value (e.g., those in Figure 6) then, by chance, some of them would not be significant. The analysis we present here examined the probabilities of finding combinations of significant values. The easiest way to do this is by simulation because the data are used in multiple comparisons, and so the six correlations are not independent.
For each simulation, 32 numbers were drawn randomly from normal distributions for each task, and then the correlations for the six pairs were computed. This was repeated 10,000 times to provide mean values of the correlations and the probabilities that all six would be significant.
First, if the true correlation between each of the six pairs was .6, .5, .4, .3, or .27, then at least one of them would not be significant (below .30) with probability .08, .32, .67, .92, or .95, respectively. The fact that for drift rates, all six are significant suggests that the correlation between all pairs (if it were the same) is quite high. Similarly, for boundary separation, it is likely that the population parameter is high. Second, the false positive rate is low. If the true correlation were zero, then for each pair, only .05 would be significant (greater than .30). The probability that all six would be significant would be .05 raised to the sixth power, which is less than 10-7. The probability that all six would be greater than zero would be only a .021 which suggests that the true correlation must be higher than zero for drift rates and boundary separation.
The results from the Monte Carlo simulations can be compared to the pairwise correlations shown in Figures 4 and 6. First, for the data from the experiments, all the correlations between pairs of experiments for median RTs and for drift rates were significant, which suggests that (if the true correlation was the same or similar across tasks) the population value was above .27 with probability .95. For accuracy and boundary separation, if the true correlation was the same across experiments, it would be lower. However, if the correlations were different among tasks it is likely that the values would be higher for similar tasks (discrimination tasks or memory tasks). Even if the correlations were different across tasks, it is unlikely that any of the true correlations are zero because the results replicate across Experiment 1-4 and 5-8.
For nondecision time, the correlations are lower than for the other model parameters, and Figure 6 bottom panel shows that the correlations between a discrimination task and a memory task are small and between .085 and .22. In contrast the correlation between the discrimination tasks is .38 and between the memory tasks .48. These values suggest that it is unlikely that the correlations for nondecision time are all the same, but there is not enough power to detect differences. For example, the difference between the .085 and .48 correlations is significant, but this difference was observed post hoc which means that the significance level should be corrected for (implicit) multiple comparisons. The differences among these correlations for nondecision time are interpretable in terms of differences in the encoding, transformation of the stimulus representation to the representation used in the decision process, and response output processes involved in the different tasks. For example, the two memory tasks share processing that involves accessing memory for the list of numbers which leads to the .48 correlation, but the number and numerosity discrimination tasks do not share this process with the memory tasks but they share a numerical size comparison.
There are limitations on the simulations. First, the correlations between each of the six pairs of experiments were assumed to be the same. If it were necessary to test hypotheses about differences among them, then many more than 32 subjects would be needed (because a difference between two correlations of about .4 is needed for a significance). Second, it was assumed that the values used to generate these correlations come from bivariate normal distributions. If the distributions were not normal then the conclusions might be different. However, it is likely that the distributions of parameters do not differ much from normality because in other experiments, the distributions of parameter values appear mostly symmetric and not that different from normal (e.g., Ratcliff et al., 2001, Figure 7). Third, sometimes large correlations can be obtained because of a few outlier values. However, the scatter plots in Figures 4 and 6 show that this is unlikely.
We also performed bootstrap analyses for Experiments 1-4. For each subject for each task, we generated 1000 bootstrap samples for each analysis and computed correlations between all pairs, namely, for accuracy, for median RT, and for each model parameter. For accuracy, median RT, and model parameters, there were six combinations, but for the correlations between accuracy and median RT for all the pairs of tasks, there were 16 combinations. For accuracy, the probability of a significant single correlation was 0.63, and for median RT it was 0.95. For all combinations of accuracy and median RT across tasks, the probability of a significant single correlation was 0.16. These results support the conclusion that the correlations we obtained in the experiments for accuracy and median RT were reliable, but the correlations between accuracy and median RT between pairs of tasks were small. For the model parameters (boundary separation, nondecision time, and mean drift rate), the probabilities that a single correlation was significant were 0.76, 0.47, and 0.90 respectively. All the bootstrap histograms were unimodal, as would be expected from the scatter plots in Figures 4 and 6. These results support the results of the Monte Carlo simulations that show strong relationships between RTs, between boundary separations, and between drift rates, but more modest relationships between accuracy values and between nondecision times. However, they show no evidence of any relationship between accuracy values and RTs.
Experiments 5-8
We interpreted the results from Experiments 1-4 in terms of the diffusion model: individual subjects’ boundary settings determined, in large part, their RTs, and their drift rates determined, in large part, their accuracy. Because boundary settings and drift rates were largely orthogonal, RTs and accuracy did not correlate significantly across subjects.
This result is not the result that might have been expected. Instead, as pointed out in the Introduction, common-sense might suggest that RTs and accuracy should correlate significantly, with better-performing subjects being both faster and more accurate than worse-performing subjects.
For Experiments 5-8, we conjectured that the expected correlation might appear if boundary settings were equated across subjects. We attempted to do this with speed instructions. With boundary settings equated, differences among subjects in accuracy would be due to differences among them in drift rates and so would differences among them in RTs (plus differences in the nondecision component).
Alternatively, it might be that a subject has some baseline setting for boundaries, and while speed instructions can modulate the setting, they do so only in proportion to the baseline. Under this hypothesis, speed instructions would not equate settings across subjects and so, as in Experiments 1 and 2, there would be no significant correlation between RTs and accuracy.
Experiments 5 and 6 were replications of Experiments 1 and 2 (numerosity discrimination and number discrimination). These experiments used standard instructions, that is, subjects were asked to respond as quickly and accurately as possible. Experiments 7 and 8 used speed instructions for the same tasks. Subjects were given instructions that strongly stressed speed, they were given feedback on RTs, and they were not given feedback on accuracy. Typically, speed instructions reduce boundary settings (e.g., Ratcliff & Rouder, 1998; Ratcliff et al., 2001, 2003, 2004).
Experiments 5-8 were also designed to examine the effects of speed instructions on drift rates. While subjects can adjust their boundary settings and perhaps the time taken for nondecision processes, they should not be able to adjust their drift rates. Subjects might “work harder” with standard instructions than speed instructions, or they might spend less time extracting information from the stimulus with speed instructions than standard instructions. But either way, differences in drift rates should be small.
Method
The subjects were 21 undergraduate students from The Ohio State University who took part in two 50-minute sessions for course credit. Experiments 5 and 6 were conducted in the first session and Experiments 7 and 8 in the second session. For each experiment, there were about 25 min. of data collection. Experiments 7 and 8 were conducted one or two days after Experiments 5 and 6.
For Experiments 7 and 8, subjects were instructed to respond as quickly as possible. For the first 10 trials of the experiments, RT feedback was given for every trial to allow subjects to calibrate themselves. On subsequent trials, whenever a RT was longer than 1200 ms, “Too slow” was displayed on the PC screen for 500 ms, followed by a blank screen for 100 ms, and then the next test item. (1200 ms was intended to occur very infrequently if a subject was responding as quickly as possible.) Whenever a RT was under 200 ms, “Too fast” was displayed for 1000 ms, then the 100 ms blank screen, and then the next test item. This feedback (and the long delay) was intended to keep fast guesses to a minimum. At the end of every block of trials, the mean RT for that block of trials was displayed for 2 sec.
Results
Responses shorter than 250 ms were eliminated from analyses, as were responses longer than 3000 ms for Experiments 5 and 6 and longer than 2000 ms for Experiments 7 and 8 (totaling 2.5%, 0.3%, 6.7%, and 5.9% of responses for the four experiments respectively). Most of the responses eliminated from Experiments 7 and 8 were shorter than 250 ms and had accuracy near chance. The data were analyzed in the same ways as for Experiments 1 and 2.
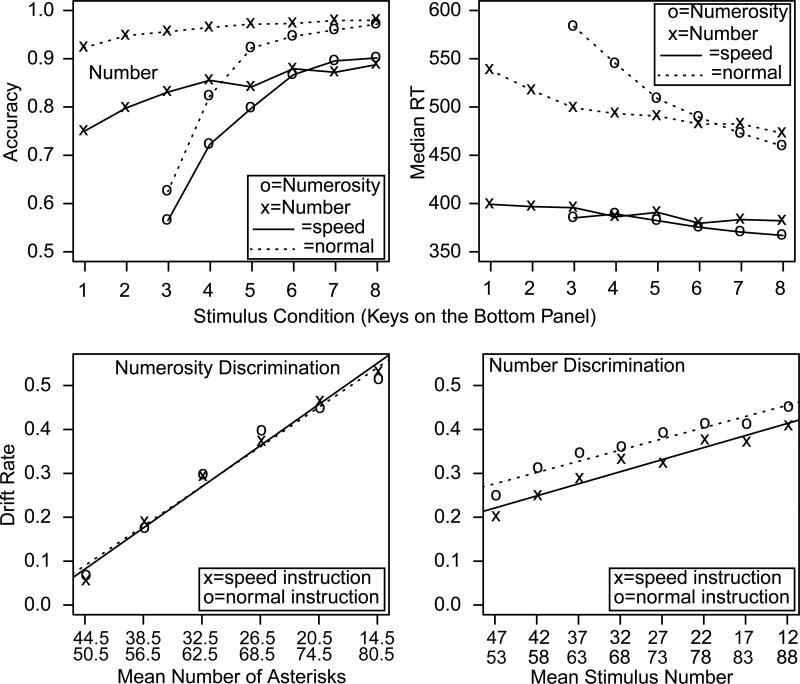
The top panels of Figure 8 show accuracy and median RTs for the four experiments. The results of Experiments 5 and 6 replicate those of Experiments 1 and 2. For Experiments 7 and 8, the speed instructions reduced accuracy by between 5 and 18% from Experiments 5 and 6 and median RTs were reduced by 100-200 ms. The slopes of the RT-difficulty functions were also reduced (as can be seen in Figure 8 top right panel). The slope for numerosity was reduced from 30.0 to 8.8, and for number it was reduced from 8.1 to 2.7.
Figure 8.
Top panel: plots of accuracy and median RT averaged over subjects for the numerosity and number discrimination tasks. Bottom panel: drift rate plotted against number of asterisks and number in Experiments 5-8.
Values of Model Parameters Averaged Across Subjects
Table 2 shows the parameters that produced the best fits to the data, averaged over subjects, the SD's in them, and chi-square goodness-of-fit values. The results of Experiments 5 and 6 differed little from those of Experiments 1 and 2. Mean goodness-of-fit chi-square values were a little larger than for Experiments 1 and 2, and a little larger for Experiments 7 and 8 than for Experiments 5 and 6.
Speed instructions had a large effect on boundary settings. The settings were reduced from about .13 for Experiments 5 and 6 to about .08 for Experiments 7 and 8. This reduction is similar to what has been obtained in other studies that have manipulated speed/accuracy instructions (Ratcliff et al., 2001; 2003; 2004). There was also a reduction in nondecision times, which might be due to a reduction in times for encoding and response execution, practice effects (because Experiments 7 and 8 always took place in the second session), or both (e.g., Ratcliff et al., 2006b; Petrov, Van Horn, & Ratcliff, 2011; see also Rinkenauer et al., 2004).
The bottom panels of Figure 8 show mean drift rates as a function of difficulty for numerosity discrimination and number discrimination. The first point is that all four drift rate-difficulty functions are approximately linear. Just as in Experiments 1 and 2, they do not exhibit nonlinearity like the accuracy and RT functions in the top panels of Figure 8.
Secondly, for numerosity discrimination, the drift rates with speed instructions were almost identical to the drift rates with standard instructions. For number discrimination, they were about 10% lower than with standard instructions. This reduction in drift rates might reflect subjects’ extracting a little more evidence from the stimuli with standard instructions either because of the instructions or because the standard instruction task always preceded the speed instruction task (or both). This result is not unique; for example, Starns, Ratcliff, and McKoon (2012) found that with extreme speed stress in a recognition memory task, drift rates were smaller than for accuracy stress along with decision boundaries.
The parameters representing across-trial variability in drift, starting point, and nondecision time were similar with speed and accuracy instructions despite the large standard deviations in these parameters due to sampling error (Ratcliff & Tuerlinckx, 2002).
Differences Among Individuals in Data and Model Parameters
The main result for individual differences was that Experiments 5-8 essentially replicate the results from Experiments 1-4. The largest correlations in both data and diffusion model parameters replicate, but some of the smaller correlations move from significant to non-significant, as might be expected from both variability and the lower numbers of subjects in Experiments 5-8.
Data
Table 4 shows correlations between speed and standard instructions for accuracy, median RTs, and the slopes of the RT-difficulty functions. The correlations were all significantly positive, except for accuracy for the number discrimination task which was not significant because accuracy in the standard-instruction conditions was near ceiling.
Table 4.
Correlations between measures for speed and normal conditions for Experiments 5-8.
| Measure | Normal vs. speed comparison | Other combinations of the 4 tasks | |
|---|---|---|---|
| Numerosity | Number | ||
| Accuracy | .77 | .30 | .54 |
| Median RT | .64 | .73 | .65 |
| Slope | .48 | .60 | .28 |
| a | .50 | .33 | .37 |
| Ter | .53 | .34 | .53 |
| v | |||
Note. “Other pairs” refers to mean correlations between speed numerosity and normal number, speed numerosity and speed number, normal numerosity and normal number, and normal numerosity and speed number. r=.43 is significant with 19 df. For boundary separation, the mean correlation for the other pairs without the normal instruction number discrimination values was .47.
The right hand column in Table 4 shows correlations for the other four combinations of instructions and tasks: speed and standard instructions for numerosity and number discrimination. These results show the same effects as for the correlations between Experiments 1 and 2. The only exception was for the RT-difficulty slopes because they were close to zero for Experiments 7 and 8.
The correlations for accuracy and median RT were computed for each experiment and Table 5 shows the means across experiments. Just as for Experiments 1 and 2, accuracy and RT were not correlated and, in fact, were in the wrong direction for the hypothesis that faster subjects are also more accurate.
Table 5.
Correlations between measures averaged over the four tasks for Experiments 5-8.
| within tasks | |
|---|---|
| Accuracy/Median RT | .18 |
| Median RT/Slope | .57 |
| Slope/Accuracy |
The slope of the RT-difficulty function was also correlated with accuracy and median RT for each experiment, and Table 5 shows the means over experiments. As in Experiments 1 and 2, the slopes were significantly correlated with accuracy and median RT.
Diffusion model parameters
The correlations in the diffusion model parameters for speed and standard instructions for each experiment are shown in Table 4 along with the mean correlation in the other four combinations of tasks.
For numerosity discrimination, between speed and standard instructions, boundary settings correlated, nondecision time correlated, and drift rates correlated (all were over .5). For number discrimination, the drift rate correlation was significant, but as in Figure 6, correlations were lower for boundary separation and nondecision time.
There were robust correlations between the other four combinations of Experiments 5-8 for drift rates and nondecision time. The correlations of boundary separation were lower but still positive (Table 4). The patterns of correlations from Experiments 5-8 match the patterns of correlations in model parameters from Experiments 1 and 2 that are shown in Figure 6. The mean value of the correlation in boundary separation across all the combinations of the four experiments was .39, suggesting that subjects set boundary settings consistently across experiments and across speed and standard instructions.
Table 6 shows correlations between drift rates and boundary settings, drift rates and nondecision times, and boundary settings and nondecision times, averaged over the four tasks. As for Experiments 1-4, the correlations were small and again show that the model decomposes accuracy and RTs into components of processing that are orthogonal to each other, even though they all influence the dependent variables.
Table 6.
Correlations of model parameters and accuracy, median RT, and RT slope averaged over the tasks for Experiments 5-8.
| Data or parameter | a | Ter | v |
|---|---|---|---|
| accuracy | .13 | .28 | .65 |
| Median RT | .63 | .58 | −.30 |
| RT slope | .63 | .10 | .01 |
| a | −.07 | −.15 | |
| Ter |
The correlation of a with accuracy is .40 for the normal conditions, −.13 for the speed conditions.
Table 6 shows correlations between each of boundary separation, nondecision time, and drift rate against each of accuracy, median RT, and slope of the RT-difficulty function. As for Experiments 1-4, the strongest correlations were for drift rate with accuracy, median RT with boundary separation and nondecision time, and RT-difficulty slope with boundary separation.
Power analyses
We can also examine power in the same way as for Experiments 1-4. The number of subjects was smaller (21 versus 32, so the critical value was .37), but there is still enough power because of the multiple comparisons.
For a single correlation, if the true correlation was .4, .45, .5, .55, or .6, there is a .50, .57, .70, .77, or .86 probability of getting a significant correlation (greater than the .37 critical value). Just as for Experiments 1-4, simulations examined the probability that all six pairs were significant as a function of the true correlation, where the true correlation was set at the same value across the pairs. If the true correlation between each of the six pairs was .6, .5, or .4, then at least one of them would not be significant (below .37) with probability .29, .60, or .85 respectively. Second, the false positive rate is low. As for Experiments 1-4, if the true correlation were zero, then only .05 of the six pairs would be significant (greater than .37). The probability that all six were significant would be .05 raised to the sixth power, which is less than 10−7. The probability that all six would be greater than zero would be only .021.
For the pairwise correlations for the data (Table 4), all were significant for median RTs and 3/6 for accuracy were significant (those that involved number tasks with accuracy values near ceiling were not significant). For boundary separation and nondecision time, three of six pairs were significant and for drift rate, five of six were significant. The Monte Carlo simulations showed that if the correlations had the value, then accuracy, boundary separation, and nondecision time would be consistent with a correlation of about .4, and drift rate and median RT with a correlation of about .5. The patterns of these results largely replicate those of Experiments 1-4.
We also performed bootstrap analyses as for Experiments 1-4. For accuracy and median RT (and model parameters), there were 6 combinations, but for the correlations between accuracy and median RT for all the pairs of tasks, there were 16 combinations. For accuracy, the probability of a significant single correlation was 0.62, for median RT, the probability of a significant single correlation 0.94. For all combinations of accuracy and mean RT across tasks, the probability of a significant single correlation was 0.10. These results support the conclusion that the correlations for accuracy and median RT were reliable, but there was little correlation between accuracy and median RT. For the model parameters, boundary separation, nondecision time, and mean drift rate, the probabilities that a single correlation was significant were 0.57, 0.68, and 0.78 respectively.
All the bootstrap histograms were unimodal as for Experiments 1-4. The results largely replicate those for Experiments 1-4 and support the results of the Monte Carlo simulations that show strong relationships between RTs and between drift rates, but more modest relationships between accuracy values, between boundary separations, and between nondecision times. However, they show no evidence of any relationship between accuracy values and RTs.
Summary
There are three important results from Experiments 5-8. The first is that accuracy and median RT are not correlated with each other, even with speed instructions in Experiments 7 and 8. The second result is that boundary separation is correlated between the standard- and speed-instruction conditions. This is consistent with a view that speed-accuracy boundary settings are not completely malleable and that individuals have some default setting (perhaps an individual trait) that can be modulated but not completely eliminated (as it would be if the correlation was zero). The third result is that the results from Experiments 5-8 closely replicate the results from Experiments 1 and 2.
General Discussion
The choice of what dependent variables to use to measure performance is often not discussed explicitly in empirical research in cognitive psychology. In the numeracy literature, RT is sometimes used and accuracy is sometimes used, but rarely are both used. We have shown here that the two dependent variables must be used jointly to interpret data and therefore to test theories about numeracy processes and representations. When a decision-making model identifies the components of processing that are responsible for performance, previous empirical conclusions may be invalidated. For example, some theories about numeracy have been targeted at explanations of how accuracy varies with the difficulty of stimuli, but a decision-making model changes the target to explanations about how components of processing, like drift rate, vary with difficulty. Furthermore, any model of decision-making and numerosity must explain the bow-shaped curve that relates RTs to accuracy (Figure 1). Theories that are addressed toward RTs only or accuracy only cannot do this.
Furthermore, one of our key findings is that accuracy and RT were not correlated across subjects. The fact that RTs and accuracy can behave in different ways across subjects means that if one of them were selected, one picture of differences among individuals might emerge, and if the other were selected, a different picture might emerge.
Below, we first review how, in the diffusion model, RT and accuracy are determined by the same components of processing. Second, we review the consequences of our findings for numeracy research.
Diffusion Model Interpretations of Differences among Individuals
Within subjects, when researchers look at speed and accuracy, they usually do so in terms of the effects of independent variables on them (for example, the number of asterisks in a numerosity task), and the relations between them usually are regular and lawful such that higher accuracy corresponds to shorter RTs (e.g., Figure 3, top panel). In this situation, RT and accuracy almost always tell similar stories. For example, we computed the correlations between median RT and accuracy over the conditions in Experiments 1 and 2 and found a mean over subjects for Experiment 1 of -.78 (numerosity discrimination) and a mean of -.59 for Experiment 2 (number discrimination).
Across subjects, the common-sense hypothesis, mentioned earlier, would be that higher accuracy goes with shorter RTs (if someone is better at a task, they will be faster). This predicts significant negative correlations between RT and accuracy, but in none of Experiments 1 - 8 did we find such correlations. Instead, the correlations were all positive, 0.22, 0.26, 0.21, 0.16, 0.11, 0.32, 0.10, and 0.20 from the eight experiments respectively. In the experiments in Ratcliff et al. (2010) for college-age subjects, there were also positive correlations, .29 for lexical decision, .13 for item recognition, and .22 for numerosity discrimination (similar to Experiment 1). Finding all 11 correlations positive is extremely unlikely if the true correlations were zero, much less if the correlations were truly negative. With a true correlation of zero, the probability of getting all 11 greater than zero is 0.00049, and the probability of getting all 11 greater than +0.1 is 0.0000016.
In terms of the diffusion model, the reason that there are no significant negative correlations across subjects between speed and accuracy is that drift rates and boundary settings, as well as nondecision times, are largely independent of each other. Accuracy is largely determined by drift rate and RT by boundary separation. For Experiments 1-8, the correlations between drift rates and accuracy averaged .56, the correlations between boundary settings and median RT averaged .70, and the correlations between nondecision time and median RT averaged .51. These correlations are particularly impressive because the groups of subjects in the experiments were relatively homogeneous (undergraduates at the University of Oklahoma and Ohio State) and because there were relatively few observations, only about 30 minutes of data collection on each task.
The trade-offs among the components of the model, accuracy, and RTs are illustrated by the functions in Figure 7. Overall, these functions provide the basis for an explanation of the pattern of correlations that we found (assuming that sampling variability reduces correlations for small differences relative to larger differences). Changes in accuracy are larger moving from a low-drift-rate subject to a high-drift-rate subject than when they are moving from a wide-boundary subject to a narrow-boundary subject, so accuracy correlates more strongly with drift rate. Conversely, changes in RTs are larger moving from a wide-boundary subject to a narrow-boundary subject than they are moving from a low-drift-subject to a high-drift-rate subject, so RT correlates more strongly with boundary separation.
Decision Criterion Settings
How subjects choose their boundary settings is something of a mystery (e.g., Starns & Ratcliff, 2010, 2012). In daily life, humans are constantly making decisions, with all kinds of decisions mixed together, and rarely do we make a long series of decisions with a single kind of stimulus, as subjects do in many psychology experiments. This suggests that boundary settings are not determined separately for different experimental tasks; rather they are set more globally through an individual's general experience. A subject who has relatively poor information in some tasks and so sets wider boundaries may generalize these wide settings across all tasks. For example, if this were the case, if a subject had relatively poor ability in some domain but strong numeracy abilities, then wide boundaries may be adopted across all tasks. Our results generally show consistent boundary settings across tasks: they were correlated positively from one task to another in Experiments 1-4 and in Experiments 5-8 (although two of the six pairings for Experiments 1-4 and two of the six pairings for Experiments 5-8 did not reach significance).
In Experiments 5-8, for both numerosity discrimination and number discrimination, boundary settings for standard instructions were significantly correlated with boundary settings for speed instructions for numerosity discrimination, and they were nearly significant for number discrimination. Similar correlations are obtained in experiments with letter discrimination (Thapar et al., 2003, correlation .44 for young adults similar to the subjects tested here) and brightness discrimination (Ratcliff et al., 2003, correlation .52 for young adults).
The speed instructions in Experiments 7 and 8 were an attempt to move all subjects to about the same boundary settings. If this were done, then accuracy and RTs would both be determined by drift rate, and so they would be significantly negatively correlated. However, while subjects did move their boundaries closer than with standard instructions, the relative differences in their boundaries were not eliminated. Again, this is consistent with the notion that boundary settings (and speed-accuracy criteria in general) have subject-determined base values. Subjects may have considerable flexibility in altering their settings, but the adjustments appear to be a function of their base values.
This lack of theory about criterion settings and their relationship to the quality of evidence used in decision making (e.g., drift rate) is not specific to numeracy; it is common across all two-choice tasks. For example, Bogacz et al. (2006) attempted to explain boundary settings within the framework of “reward-rate” analyses based on the animal literature. In that literature, animals deprived of water attempt to maximize the amount received. If they go too fast, they make errors and receive no water on those trials, whereas if they go too slow, they will get less water per unit time even if they are correct. Starns and Ratcliff (2010) examined criterion settings in several experiments and found that young adults, if given feedback and instructions, approached reward-rate optimality, but older adults and young adults without feedback did not. It should be noted, however, that generally speaking, reward-rate optimality represents the antithesis of academic training where the goal is to be as accurate as possible even if it takes more time (e.g., analyzing empirical data or taking an exam).
Numeracy
In the last two decades, a consensus had developed that the same abstract number system supports all (or most) operations with numeracy information. This hypothesis has recently come under attack because of the many failures to find significant correlations among tasks and measures. Inglis et al. (2011), Holloway and Ansari (2009), Mundy and Gilmore (2009), and Price et al. (2012) have all failed to find significant correlations between performance on nonsymbolic number comparison tasks and math ability. Holloway and Ansari (2009) failed to find a significant correlation between a symbolic number task and a nonsymbolic one, and Sasanguie et al. (2011) failed to find a significant correlation between a number priming task and three nonsymbolic tasks. Gilmore et al. (2011) failed to find any significant correlations among six symbolic and nonsymbolic number tasks, and Maloney et al. (2010) failed to find any significant correlations among seven tasks. These findings include efforts to detect correlations of the same measure across tasks and efforts to detect correlations between different measures.
The failures to find consistent correlations may have occurred because researchers have attempted to assess the quality of encoded stimulus information from RT or accuracy directly, some researchers choosing RT and some choosing accuracy. In contrast, with the diffusion model, drift rates provide a measure of quality and in doing so, they provide a meeting point between models that produce representations of numerical stimuli, on the one hand, and accuracy and RT data on the other. The representations must be such that when they are mapped through the decision process, they simultaneously account for accuracy and RTs. Theories about numeracy that predict only RTs or only accuracy are almost certainly incorrect.
Another contribution to the failures in previous research to find consistent correlations may be that accuracy or RTs approached ceiling or floor in some experiments or conditions (e.g., Figure 3 top panels for the number task). Ceiling and floor effects reduce the range across which the difficulty of independent variables can be measured, perhaps preventing the discovery of differences among conditions that would be essential to formulating a comprehensive model of numeracy performance. The diffusion model extends the range of psychometric functions because drift rates can be obtained when conditions that are at ceiling or floor in accuracy vary in their RTs, which happens frequently (e.g., Ratcliff, 2014).
The finding that drift rates and boundary settings are largely independent across subjects speaks to Halberda et al. (2012) and Price et al. (2012)'s suggestions that accuracy and RT stem from different abilities or processes. Whether decision-model analyses can always illuminate different patterns of accuracy and RT data is a subject for further research.
The successful application of the diffusion decision-making model to the results of the eight experiments illustrates the benefits and information that comes from these analyses. The model's success provides some benchmarks for the integration of a theory about numeracy and decision models.
-
1)
A decision-making model that is successful in simultaneously explaining RT, accuracy, and the relations between them, as the diffusion model did in Experiments 1 - 8.
-
2)
An estimate of the quality of the information that a subject encodes from a stimulus or memory (often the main hypothesis for an experiment), which also requires a decision-making model.
-
3)
Within a task, if a variable is manipulated that changes the difficulty of the task, correlations between accuracy and RTs are significantly negative.
-
4)
Across subjects, correlations between RTs and accuracy are slightly positive, not negative as might be expected.
-
5)
An account of the relations between speed and accuracy that subjects adopt; with the diffusion model, the relation cannot be predicted for individual subjects, but the model does provide an account of it in terms of drift rates versus boundary settings and nondecision times.
-
6)
The functions of RT and accuracy against difficulty are bowed; the functions of drift rates are linear (in the tasks and ranges of conditions that we studied).
-
7)
Manipulations like speed versus accuracy instructions and the difficulty of stimuli both affect RT and accuracy, yet the effects are accommodated by changes in only a single parameter of the diffusion model.
-
8)
Performance on on-line tasks that ask for immediate judgments about stimuli (e.g., the numerosity and number two-choice tasks used in the experiments here) is correlated positively with performance on off-line tasks that address subjects’ memory for numbers.
Summary
The research reported in this article does not resolve controversies among numeracy theories about how number information is represented or processed. Instead, we lay the groundwork for new or revised approaches that can be empirically evaluated and competitively tested against each other. Decision-model analyses can potentially relate many numeracy tasks to each other, tasks that might operate at quite different performance levels (e.g., symbolic, nonsymbolic, memory for number). Model-based analyses can potentially give insights into the correlations that are and are not obtained from one task to another task or to a subject variable such as IQ or math ability. They may also give insights into memory for numerical information and how it relates to immediate judgments. To our knowledge, these possibilities are new to numeracy research.
The same caveats apply to our research as to most previous studies of numeracy. The numeracy abilities tapped by on-line and off-line tasks may be more elementary or primitive than those that determine scores on math achievement tests, and achievement tests may themselves measure a large variety of different sorts of skills. The degree to which achievement tests tap into unidimensional constructs may (partially) explain why correlations between performance on simple tasks like those we used and performance on achievement tests are sometimes significant and sometimes not. It is also the case that achievement tests may measure a range of factors, only some of which are what cognitive psychologists mean by numeracy or number skills. What is needed is a detailed analysis of achievement tests and then the design of cognitive tasks that relate to the processes involved in the skills that are being tested. Then deficits in the cognitive tasks might provide pointers to processes that are not fully functional, and more interesting, patterns of deficits in cognitive tasks might point to constellations of deficits.
Overall, the findings from our eight experiments show that accuracy and RTs can be successfully decomposed into separate components of processing-- drift rates, speed/accuracy settings, and nondecision processes-- and these components are largely uncorrelated with each other. It is our hope that such decompositions will find further applications in studies of numerosity and help to resolve the conflicts that have been observed among previous studies.
Supplementary Material
Acknowledgments
Preparation of this article was supported by NIA grant R01-AG041176, AFOSR grant FA9550-11-1-0130, and DOE/IES grant R305A120189. We would like to thank Sarah Wiatrek, Brian Pickens, and Mollie Rischard for their help with data collection.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bogacz R, Brown E, Moehlis J, Holmes P, Cohen JD. The physics of optimal decision making: A formal analysis of models of performance in two-alternative forced choice tasks. Psychological Review. 2006;113:700–765. doi: 10.1037/0033-295X.113.4.700. [DOI] [PubMed] [Google Scholar]
- Brainerd CJ, Gordon LL. Development of verbatim and gist memory for numbers. Developmental Psychology. 1994;30:163–177. [Google Scholar]
- Brown SD, Heathcote AJ. The simplest complete model of choice response time: Linear ballistic accumulation. Cognitive Psychology. 2008;57:153–178. doi: 10.1016/j.cogpsych.2007.12.002. [DOI] [PubMed] [Google Scholar]
- Chen Q, Li J. Association between individual differences in non-symbolic number acuity and math performance: A meta-analysis. Acta Psychologica. 2014;148:163–172. doi: 10.1016/j.actpsy.2014.01.016. [DOI] [PubMed] [Google Scholar]
- Cohen J. A power primer. Psychological Bulletin. 1992;112:155–159. doi: 10.1037//0033-2909.112.1.155. [DOI] [PubMed] [Google Scholar]
- Dehaene S. The number sense: How the mind creates mathematics. Oxford University Press; New York: 1997. [Google Scholar]
- Dehaene S, Dehaene-Lambertz G, Cohen L. Abstract representations of numbers in the animal and human brain. Trends in Neuroscience. 1998;21:355–361. doi: 10.1016/s0166-2236(98)01263-6. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Dupoux E, Mehler J. Is numerical comparison digital? Analogical and symbolic effects in two-digit number comparison. Journal of Experimental Psychology: Human Perception and Performance. 1990;16:626–641. doi: 10.1037//0096-1523.16.3.626. [DOI] [PubMed] [Google Scholar]
- De Smedt B, Verschaffel L, Ghesquiere P. The predictive value of numerical magnitude comparison for individual differences in mathematics achievement. Journal of Experimental Child Psychology. 2009;103:469–479. doi: 10.1016/j.jecp.2009.01.010. [DOI] [PubMed] [Google Scholar]
- Durand M, Hulme C, Larkin R, Snowling M. The cognitive foundations of reading and arithmetic skills in 7- to 10-year old children. Journal of Experimental Child Psychology. 2005;91:113–136. doi: 10.1016/j.jecp.2005.01.003. [DOI] [PubMed] [Google Scholar]
- Gilmore C, Attridge N, Inglis M. Measuring the approximate number system. Quarterly Journal Of Experimental Psychology. 2011;64:2099–2109. doi: 10.1080/17470218.2011.574710. [DOI] [PubMed] [Google Scholar]
- Gilmore CK, McCarthy SW, Spelke ES. Non-symbolic arithmetic abilities and mathematics achievement in the first year of formal schooling. Cognition. 2010;115:394–406. doi: 10.1016/j.cognition.2010.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halberda J, Mazzocco MMM, Feigenson L. Individual differences in nonverbal number acuity predict maths achievement. Nature. 2008;455:665–668. doi: 10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
- Holloway ID, Ansari D. Mapping numerical magnitudes onto symbols: The numerical distance effect and individual differences in children's math achievement. Journal of Experimental Child Psychology. 2009;103:17–29. doi: 10.1016/j.jecp.2008.04.001. [DOI] [PubMed] [Google Scholar]
- Inglis M, Attridge N, Batchelor S, Gilmore CK. Non-verbal number acuity correlates with symbolic mathematics achievement: but only in children. Psychonomic Bulletin and Review. 2011;18:1222–1229. doi: 10.3758/s13423-011-0154-1. [DOI] [PubMed] [Google Scholar]
- Laming DRJ. Information theory of choice reaction time. Wiley; New York: 1968. [Google Scholar]
- Libertus ME, Feigenson L, Halberda J. Preschool acuity of the approximate number system correlates with school math ability. Developmental Science. 2011;14:1292–1300. doi: 10.1111/j.1467-7687.2011.01080.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyons IM, Beilock SL. Mathematics anxiety: Separating the math from the anxiety. Cerebral Cortex. 2011 doi: 10.1093/cercor/bhr289. first published online October 20, 2011 doi:10.1093/cercor/bhr289. [DOI] [PubMed] [Google Scholar]
- Maloney E, Risko E, Preston F, Ansari D, Fugelsang J. Challenging the reliability and validity of cognitive measures: The case of the numerical distance effect. Acta Pyschologica. 2010;134:154–161. doi: 10.1016/j.actpsy.2010.01.006. [DOI] [PubMed] [Google Scholar]
- Mazzocco MMM, Feigenson L, Halberda J. Impaired acuity of the approximate number system underlies mathematical learning disability (dyscalcula). Child Development. 2011;82:1224–1237. doi: 10.1111/j.1467-8624.2011.01608.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mundy E, Gilmore C. Children's mapping between symbolic and nonsymbolic representation of number. Journal of Experimental Child Psychology. 2009;103:490–502. doi: 10.1016/j.jecp.2009.02.003. [DOI] [PubMed] [Google Scholar]
- Petrov AA, Van Horn NM, Ratcliff R. Dissociable perceptual learning mechanisms revealed by diffusion-model analysis. Psychonomic Bulletin and Review. 2011;18:490–497. doi: 10.3758/s13423-011-0079-8. [DOI] [PubMed] [Google Scholar]
- Price GR, Palmer D, Battista C, Ansari D. Nonsymbolic numerical magnitude comparison: Reliability and validity of different of different task variants and outcome measures, and their relationship to arithmetic achievement in adults. Acta Psychologica. 2012;140:50–57. doi: 10.1016/j.actpsy.2012.02.008. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychological Review. 1978;85:59–108. [Google Scholar]
- Ratcliff R. A diffusion model account of reaction time and accuracy in a two choice brightness discrimination task: Fitting real data and failing to fit fake but plausible data. Psychonomic Bulletin and Review. 2002;9:278–291. doi: 10.3758/bf03196283. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. Parameter variability and distributional assumptions in the diffusion model. Psychological Review. 2013;120:281–292. doi: 10.1037/a0030775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R. Measuring psychometric functions with the diffusion model. Journal of Experimental Psychology: Human Perception and Performance. 2014;40:870–888. doi: 10.1037/a0034954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Childers R. Individual Differences and Fitting Methods for the Two-Choice Diffusion. Decision. doi: 10.1037/dec0000030. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Love J, Thompson CA, Opfer J. Children are not like older adults: A diffusion model analysis of developmental changes in speeded responses. Child Development. 2012;83:367–381. doi: 10.1111/j.1467-8624.2011.01683.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, McKoon G. The diffusion decision model: Theory and data for two-choice decision tasks. Neural Computation. 2008;20:873–922. doi: 10.1162/neco.2008.12-06-420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. The effects of aging on reaction time in a signal detection task. Psychology and Aging. 2001;16:323–341. [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. Aging and individual differences in rapid two-choice decisions. Psychonomic Bulletin and Review. 2006a;13:626–635. doi: 10.3758/bf03193973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. Aging, practice, and perceptual tasks: A diffusion model analysis. Psychology and Aging. 2006b;21:353–371. doi: 10.1037/0882-7974.21.2.353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. Individual differences, aging, and IQ in two-choice tasks. Cognitive Psychology. 2010;60:127–157. doi: 10.1016/j.cogpsych.2009.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. Effects of aging and IQ on item and associative memory. Journal of Experimental Psychology: General. 2011;140:46–487. doi: 10.1037/a0023810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Tuerlinckx F. Estimating the parameters of the diffusion model: Approaches to dealing with contaminant reaction times and parameter variability. Psychonomic Bulletin and Review. 2002;9:438–481. doi: 10.3758/bf03196302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Van Zandt T, McKoon G. Connectionist and diffusion models of reaction time. Psychological Review. 1999;106:261–300. doi: 10.1037/0033-295x.106.2.261. [DOI] [PubMed] [Google Scholar]
- Rinkenauer G, Osman A, Ulrich R, Muller-Gethmann H, Mattes S. On the locus of speed-accuracy tradeoff in reaction time: inferences from the lateralized readiness potential. Journal of Experimental Psychology: General. 2004;133:261–282. doi: 10.1037/0096-3445.133.2.261. [DOI] [PubMed] [Google Scholar]
- Sasanguie D, Defever E, Van den Bussche E, Reynvoet B. The reliability of and the relation between non-symbolic numerical distance effects in comparison, same-different judgments and priming. Acta Psychologica. 2011;136:73–80. doi: 10.1016/j.actpsy.2010.10.004. [DOI] [PubMed] [Google Scholar]
- Starns JJ, Ratcliff R. The effects of aging on the speed-accuracy compromise: Boundary optimality in the diffusion model. Psychology and Aging. 2010;5:377–390. doi: 10.1037/a0018022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starns JJ, Ratcliff R. Age-related differences in diffusion model boundary optimality with both trial-limited and time-limited tasks. Psychonomic Bulletin and Review. 2012;19:139–145. doi: 10.3758/s13423-011-0189-3. [DOI] [PubMed] [Google Scholar]
- Starns JJ, Ratcliff R, McKoon G. Evaluating the unequal-variability and dual-process explanations of zROC slopes with response time data and the diffusion model. Cognitive Psychology. 2012;64:1–34. doi: 10.1016/j.cogpsych.2011.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson CA, Siegler RS. Linear numerical magnitude representations aid children's memory for numbers. Psychological Science. 2010;21:1274–1281. doi: 10.1177/0956797610378309. [DOI] [PubMed] [Google Scholar]
- Usher M, McClelland JL. The time course of perceptual choice: The leaky, competing accumulator model. Psychological Review. 2001;108:550–592. doi: 10.1037/0033-295x.108.3.550. [DOI] [PubMed] [Google Scholar]
- Vandekerckhove J, Tuerlinckx F. Fitting the Ratcliff diffusion model to experimental data. Psychonomic Bulletin & Review. 2007;14:1011–1026. doi: 10.3758/bf03193087. [DOI] [PubMed] [Google Scholar]
- Voss A, Nagler M, Lerche V. Diffusion Models in Experimental Psychology: A Practical Introduction. Experimental Psychology. 2013;60:385–402. doi: 10.1027/1618-3169/a000218. [DOI] [PubMed] [Google Scholar]
- Voss A, Voss J. Fast-dm: A free program for efficient diffusion model analysis. Behavior Research Methods. 2007;39:767–775. doi: 10.3758/bf03192967. [DOI] [PubMed] [Google Scholar]
- White CN, Ratcliff R, Vasey MW, McKoon G. Using diffusion models to understand clinical disorders. Journal of Mathematical Psychology. 2010;54:39–52. doi: 10.1016/j.jmp.2010.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiecki TV, Sofer I, Frank MJ. HDDM: Hierarchical Bayesian estimation of the Drift-Diffusion Model in Python. Frontiers in Neuroinformatics. 2013;7:1–10. doi: 10.3389/fninf.2013.00014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zebain. S, Ansari D. Differences between literates and illiterates on symbolic but not nonsymbolic numerical magnitude processing. Psychonomic Bulletin and Review. 2012;19:93–100. doi: 10.3758/s13423-011-0175-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.