Distinguishing Emotional Co-Regulation From Co-Dysregulation: An Investigation of Emotional Dynamics and Body-Weight in Romantic Couples

Abstract

Well-regulated emotions, both within people and between relationship partners, play a key role in facilitating health and well-being. The present study examined 39 heterosexual couples’ joint weight status (both partners are healthy-weight, both overweight, one healthy-weight and one overweight) as a predictor of two interpersonal emotional patterns during a discussion of their shared lifestyle choices. The first pattern, co-regulation, is one in which partners’ coupled emotions show a dampening pattern over time and ultimately return to homeostatic levels. The second, co-dysregulation, is one in which partners’ coupled emotions are amplified away from homeostatic balance. We demonstrate how a coupled linear oscillator (CLO) model (Butner, Amazeen, & Mulvey, 2005) can be used to distinguish co-regulation from co-dysregulation. As predicted, healthy-weight couples and mixed-weight couples in which the man was heavier than the woman displayed co-regulation, but overweight couples and mixed-weight couples in which the woman was heavier showed co-dysregulation. These results suggest that heterosexual couples in which the woman is overweight may face formidable co-regulatory challenges that could undermine both partners’ well-being. The results also demonstrate the importance of distinguishing between various interpersonal emotional dynamics for understanding connections between interpersonal emotions and health.

The emotions of partners in close relationships become interconnected in numerous ways (Butler, 2011). Two potentially health-relevant interpersonal emotional patterns are co-regulation and co-dysregulation. Co-regulation refers to a process in which partners’ emotions are bi-directionally linked and mutually dampening (Boker & Laurenceau, 2007; Butler & Randall, 2013; Chow, Ram, Boker, Fujita, & Clore, 2005; Sbarra & Hazan, 2008). In other words, the effect of each partner’s emotions on the other takes the form of negative feedback, such that as Partner-1’s emotions begin to deviate from his or her habitual baseline, the effect of Partner-2’s emotions is to push or pull Partner-1 back towards that baseline, thereby ultimately contributing to emotional stability, or homeostasis for both partners (Boker & Laurenceau, 2006, 2007; Butler & Randall, 2013; Sbarra & Hazan, 2008). Co-dysregulation, on the other hand, has not been defined systematically in the literature. To do so, we extend the co-regulation model to include its obvious complement: if negative feedback creates co-regulation, then positive feedback could create co-dysregulation. Co-dysregulation therefore refers to a process in which partners’ emotions are bi-directionally linked and mutually amplifying, away from emotional stability.

Relationship scientists have well-developed theory suggesting that co-regulation and co-dysregulation should have different associations with relationship functioning and health. For example, co-regulation has been described as a form of interpersonal regulation contributing to psychological and physiological balance across the lifespan (Sbarra & Hazan, 2008). This reciprocal homeostatic regulation of emotion is believed to be a critical feature of secure attachment relationships, including parent-child dyads and adult romantic relationships (Butler & Randall, 2013; Sbarra & Hazan, 2008). In contrast, amplified, excessive emotionality, such as may occur in co-dysregulation, is often described as a central feature of hostile or conflictual interactions (Coleman, Vallacher, Nowak, & Bui-Wrzosinska, 2007; Kiecolt-Glaser et al., 2005; Kiecolt-Glaser et al., 1993; Nealey-Moore, Smith, Uchino, Hawkins, & Olson-Cerny, 2007). Co-dysregulation may arise during conflict, particularly if negative feedback control mechanisms are not engaged to terminate the conflict, thus leading to destructive rather than constructive interactions (Coleman et al., 2007). In addition, co-dysregulation could occur when partners attempt to regulate or control their emotions, but ultimately are overwhelmed and experience a depletion of regulatory abilities, resulting in emotion regulatory failure (Baumeister, Vohs, & Tice, 2007; Muraven & Baumeister, 2000). Importantly, over time, continuous emotional co-dysregulation may contribute to chronically heightened neuroendocrine or cardiovascular responses (also known as heighted allostatic load), which is associated with a variety of health conditions, including atherosclerosis, obesity, and cardiovascular disease (Logan & Barksdale, 2008; McEwen, 1998, 2004).

Despite widespread interest in the theory of co-regulation (e.g., (Butler & Randall, 2013; Saxbe & Repetti, 2010; Sbarra & Hazan, 2008), testing the theory has been hindered because the statistical approach to distinguish between co-regulation and other emotional patterns has not been clearly identified. To address this issue, we demonstrate how coupled linear oscillator (CLO) models can be used to differentiate between co-regulation and co-dysregulation. We apply these distinctions to test several hypotheses regarding differences in emotion dynamics between couples in which one or both partners are – or are not – overweight.

Emotion Dynamics in Individuals and Couples

Before discussing the use of CLO models, we first discuss several assumptions about emotions. The first assumption is that emotions are oscillatory (Boker & Nesselroade, 2002; Butner, Diamond, & Hicks, 2007; Chow et al., 2005; Pettersson, Boker, Watson, Clark, & Tellegen, 2013). Like a thermostat, people have their own individual emotional set points that they tend to return to after being perturbed (Chow et al., 2005; Pettersson et al., 2013). External stimulation, such as experiences in daily life, bump emotions up and down, but well-functioning people adapt to these experiences, both automatically and via purposeful emotion regulation, and stabilize back to their homeostatic set-point (Lehrer & Eddie, 2013). This combination of perturbations and self-regulation results in an oscillating pattern of emotions (Bisconti, Bergeman, & Boker, 2004; Chow et al., 2005; Pettersson et al., 2013).

Evidence in support of emotions being oscillatory includes research showing significant oscillations of daily positive and negative emotions in a sample of recently bereaved widows (Bisconti et al., 2004), as well as in samples of college students (Chow et al., 2005; Pettersson et al., 2013). Significant oscillations have also been shown for couples’ daily relationship-specific affect (Steele & Ferrer, 2011) and daily feelings of intimacy (Boker & Laurenceau, 2006). Furthermore, significant oscillations have also been reported for second-by-second physiological responses such as heart rate and respiration, which are responsive to interpersonal interactions and react to shifts in emotional states (Helm, Sbarra, & Ferrer, 2012). Therefore, an optimal model for emotional dynamics should allow for oscillatory processes.

A second assumption is that emotions may dampen or amplify over time. Regulating emotions involves both negative feedback loops (e.g., A produces B, which in turn, inhibits A), and positive feedback loops (e.g., A produces B, which produces more of A) (Lehrer & Eddie, 2013). Negative feedback would dampen emotional oscillations, while positive feedback would amplify them. Importantly, dampening and amplification are most relevant when examined in the context of a single regulatory process evolving over time. For example, we may be more likely to observe dampening or amplification in laboratory-based studies that focus on specific regulatory tasks (e.g., resolving a conflict with a partner), as opposed to daily diary studies that likely assess numerous regulatory events over time. Thus, a dynamic model of emotions designed to capture regulatory processes should allow for dampening back to a homeostatic set point, or amplification away from it.

A third assumption is that partners’ emotions typically become interconnected, due to both automatic and conscious mechanisms (Butler, 2011). For example, partners may influence each other’s emotions via contagion, whereby observing a partner’s emotional display results in mimicry and empathy, which leads to feeling similar emotions (Levenson & Ruef, 1992; Parkinson, 2011). Partners’ emotions may also become interconnected due to experiencing a shared stimulus (e.g., watching a scary movie together), or by being a stimulus for each other (Parkinson & Simons, 2012). The latter is often referred to as reactivity, whereby one partner’s emotional behavior provokes an experiential response in the other partner (Lorber & Smith Slep, 2005). Additionally, partners may explicitly attempt to regulate each other’s emotions, whereby one partner is motivated to change the other’s affective state (Diamond & Aspinwall, 2003; Zaki & Williams, 2013). Therefore, partners’ oscillating emotions can become coupled, meaning that some aspect of one partner’s emotional dynamics is influencing some aspect of the other partner’s dynamics. For example, partners may pulled into, or out of, synchrony with each other, or have mutually dampening or amplifying effects (Boker & Laurenceau, 2006; Butner et al., 2005; Butner et al., 2007; Helm et al., 2012; Steele & Ferrer, 2011). Thus a dynamic model of emotions in interpersonal contexts should allow for coupling to exist between social partners.

Modeling Interpersonal Emotional Dynamics With Coupled Linear Oscillator Models

One central requirement for studying emotional dynamics is the availability of time-series data with an appropriate temporal resolution (Boker & Nesselroade, 2002). With too few observations it is impossible to model faster frequency oscillations, but with too many observations it is easy to mistake random noise for systematic fast oscillations. Second, if emotional oscillations are relevant to the research question, then classic approaches, such as repeated measures regression, temporal multilevel models, growth modeling, or sequential analyses are inadequate (Boker & Nesselroade, 2002; Butner et al., 2005; Hessler, Finan, & Amazeen, 2013). These methods can assess the general emotional tone of an interaction, trajectories of change across time, or within- and between-person concurrent associations (synchrony) and time-lagged associations (transmission), as well as moderators of these associations (Butler, 2011; Randall, Post, Reed, & Butler, 2013; Reed, Randall, Post, & Butler, 2013). However, these methods do not allow for an oscillatory pattern, or the assessment of dampening or amplification, that may arise due to regulatory dynamics. In contrast, coupled linear oscillator (CLO) models explicitly represent oscillatory behavior.

Co-regulation and co-dysregulation are complex dynamics and cannot be assessed solely by one aspect of emotional responding. Rather, a complete representation requires indicators of both intra- and inter-personal emotional characteristics and regulatory processes, including the frequency of each partner’s emotional oscillations, the dampening or amplification of their oscillations, and the coupling between interacting partners’ emotional oscillations (Butler & Randall, 2013; Butner et al., 2005; Butner et al., 2007). Thus CLO models are ideal for the study of co-regulation and co-dysregulation (Boker & Laurenceau, 2006; Butner et al., 2005; Butner et al., 2007; Ferrer & Helm, 2013; Helm et al., 2012; Steele & Ferrer, 2011). Co-regulation is indicated by systematically oscillating emotions that are coupled between partners and are dampening over time. In contrast, co-dysregulation is similar, but with the presence of amplification of emotion rather than dampening.

Previous studies have employed the CLO model to examine a variety of interpersonal constructs, but they have not distinguished between co-regulation and co-dysregulation. Instead, any evidence of coupling, dampening, or amplification, has been referred to as co-regulation. Studies on couples’ self-disclosure and intimacy (Boker & Laurenceau, 2006), and daily emotions (Butner et al., 2007), showed between-partner coupling, but found no evidence of dampening or amplification, which would suggest a lack of both co-regulation and co-dysregulation as we have defined them. In another study, however, women’s daily positive emotions were influenced by their partner’s positive emotions, such that the partner’s effect was to slow the women’s frequency and dampen their oscillations (Steele & Ferrer, 2011). Men showed a similar frequency effect, but no dampening due to their partner. These findings suggest that dampening may occur, at least for women’s positive emotions, but it is unclear how these findings relate to co-regulation because dampening is more clearly related to co-regulation in the context of negative emotions, rather than positive ones.

Another issue to consider with some of these previous studies is their focus on co-regulation of daily emotions across relatively long periods of time (anywhere from two weeks to three months, for example). Such methods likely capture multiple regulatory processes (e.g., minor conflicts over daily hassles, interactions involving intimacy building or capitalization). Although we would still expect to see an oscillatory pattern of emotions, as well as potential coupling of partners’ emotions, it is not clear what dampening or amplification would mean across these longer time frames, since it would be averaging across distinct regulatory episodes. As such, the CLO method may be best suited for methods and time-frames that reflect a single regulatory process, such as a single conversation or a laboratory interaction task. One study did just this and examined attachment processes and partners’ physiologies during a series of structured interaction tasks (Helm et al., 2012). Interestingly, men with higher levels of avoidance had an amplifying effect on their female partners’ heart rate, suggesting that high levels of men’s avoidance may be associated with co-dysregulatory physiological processes. Clearly, however, more research is needed that employs methods that capture a single regulatory process to examine co-regulatory and co-dysregulatory emotion dynamics.

Although the findings from CLO models, as applied to dyadic emotional data, have been exclusively referred to as co-regulation (e.g., Butner et al., 2005; Helm et al., 2012), these models can capture other emotional patterns as well, including co-dysregulation. CLO models are an extension of the damped linear oscillator model (Boker, 2001; Boker & Nesselroade, 2002; Chow et al., 2005), which uses the first (dx/dt) and second (d2x/dt2) derivatives of a focal variable (e.g., repeated measures of emotional experience or physiology) to model a process that fluctuates around a homeostatic set point. The univariate expression of a damped linear oscillator model is:

$$(d^2{x}_{\left(t\right)}/{\mathit{dt}}^2)=\mathrm{\eta }{x}_{(t)}+\zeta (d{x}_{\left(t\right)}/dt)+{\mathrm{e}}_{(\mathrm{t})}$$ (1)

where, in the context of intra-personal emotion dynamics, (d²x_(t)/dt²), x_(t), and (dx_(t)/dt), represent the acceleration, position, and velocity of some emotion variable x at a given time t. More specifically, (d²x_(t)/dt²) represents acceleration in some aspect of emotion x at time t (i.e., how fast a person’s emotion trajectory x is speeding up or slowing down at time t); x_(t) represents the position of a person’s emotion measure x at time t (usually estimated as the observed measure at time t minus the person’s mean for that measure across time), and (dx_(t)/dt) represents the velocity in a person’s emotion x at time t (i.e., whether a person’s emotion trajectory x is speeding up or slowing down at time t) (Boker & Nesselroade, 2002; Chow et al., 2005). In other words, velocity is the rate of change in emotions over time and acceleration is the rate of change in velocity over time.

The univariate damped linear oscillator model can be extended into a bivariate CLO model by taking into account two interconnected oscillating emotion systems (Butner et al., 2005; Helm et al., 2012). There are many possible versions of CLO models, two of which have been used in the context of interpersonal emotional processes. Both extend the univariate case by including a model for each partner, along with between-partner influences. One version represents between-partner influences by allowing Partner-1’s position and velocity to influence Partner-2’s acceleration, as well as vice versa (Helm et al., 2012). In contrast, in the second version, between-partner influences are represented using a coupling term, which is calculated as the partner’s position minus one’s own position (Butner et al., 2005). We fit the data using both versions of the CLO model and got a similar pattern of results either way. For simplicity we focus on the model with fewer terms (i.e., the second version; Butner et al., 2005). The expression for the coupled version of the CLO model we used is:

$$\begin{array}{l}(d^2{x}_{(t)}/{\mathit{dt}}^2)=\eta x_{(t)}+\zeta (d{x}_{(t)}/dt)+\kappa (y_{(t)}-x_{(t)})+e_{(t)}\\ (d^2{y}_{(t)}/{\mathit{dt}}^2)=\eta y_{(t)}+\zeta (d{y}_{(t)}/dt)+\kappa (x_{(t)}-y_{(t)})+e_{(t)},\end{array}$$ (2)

where, x and y correspond to repeated emotional ratings from the man (x) and woman (y) in a couple. In the first equation, the man’s acceleration (d²x_(t)/dt²) in emotions at time t is predicted from his own position (x_(t)), own velocity (dx_(t)/dt), and coupling between his partner’s and his own emotion ratings (y_(t) – x_(t)) at time t. The second equation is symmetric, predicting the woman’s acceleration from her own position, own velocity, and coupling with her partner. Below we provide an overview of the interpretation of the parameters η, ζ, and κ and Figure 1 provides a graphical representation of them (for additional discussion see: Butner et al., 2005, Helm et al., 2012, Steele & Ferrer, 2011):

1. The parameter (η) is associated with the observed emotion ratings (position). It is often referred to as frequency in the literature on emotional dynamics. This parameter represents how quickly the emotional process oscillates. However, values for η are not interpretable until transformed into frequency (cycles per time), or its reciprocal, period (time for one cycle). Estimates for the parameter η also need to be negative in order to be interpretable. Assuming a negative estimate, η < 0, the time for one complete cycle (period) is estimated by ((2π) / (sqrt(-[η]))). Larger absolute values of η are indicative of more rapid oscillations.

2. The parameter (ζ) is associated with the first derivative of the emotion ratings (velocity). Negative values of ζ represent dampening, or a tendency for emotional responses to converge back to homeostatic levels. Positive values of ζ represent amplification, or the tendency of emotional responses to increasingly deviate away from homeostatic levels (Steele & Ferrer, 2011). A dampening parameter of zero (ζ = 0) represents a continuously oscillating process of constant amplitude (i.e., neither dampening nor amplifying).

3. Lastly, the parameter (κ) represents coupling. In the present study, coupling is defined as the between-partner difference score, (i.e., partner emotion rating – own emotion rating). A coupling parameter of zero (κ = 0) indicates that the partners behave independently; when κ is nonzero, there is coupling between the partners (Hessler et al., 2013). Partners will be pulled into phase (as pictured in Figure 1) if the signs of their coupling terms are opposite (i.e., the man has a negative coupling parameter and the woman has a positive one, or vice versa). The mathematics that explain why this occurs is beyond the scope of the article; however, intuitively, when partners have opposite coupling signs (Partner 1 = +κ; Partner 2 =-κ), Partner 1 speeds up to catch up with Partner 2, and Partner 2 slows down to allow Partner 1 to catch up. Ultimately, this produces an in phase pattern. When partners have the same coupling signs, the effect is that both Partners are slowing down (Partner 1 =-κ; Partner 2 =-κ), or both Partners are speeding up (Partner 1 = +κ; Partner 2 = +κ), and neither partner ever catches up to the other. Ultimately, they will remain in whatever relative phase relationship they started out with at the beginning of the interaction.

Figure 1.

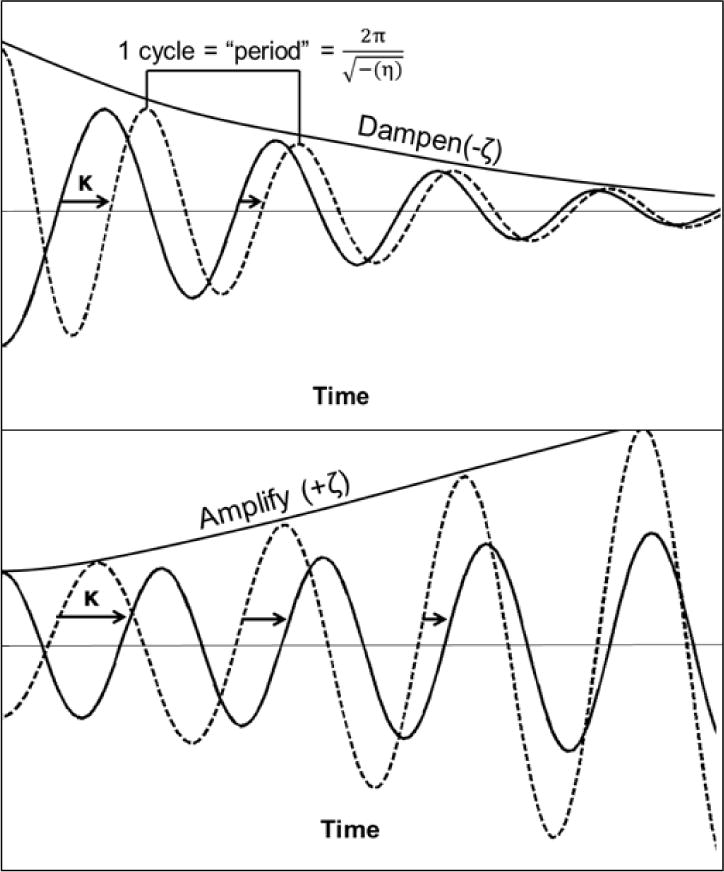
An illustration of the parameters of the coupled linear oscillator model. The solid line refers to Partner 1 and the dotted line refers to Partner 2. Frequency (η) = the number of cycles per time (period = the time it takes to complete 1 cycle); to be interpretable, frequency (η < 0) should be translated using the equation provided. Dampening (-ζ) = the tendency of emotional responses to converge back to homeostatic levels. Amplification (+ζ) = the tendency for emotional responses to increasingly deviate away from homeostatic levels. Coupling (κ) = partners’ emotions can be pulled into phase (as pictured in both panels above), or out of phase.

We can begin to distinguish between co-regulation and co-dysregulation by interpreting parameter estimates obtained from fitting the CLO model to data. Evidence of co-regulation is provided by the presence of coupling plus dampening, while evidence of co-dysregulation is provided by coupling plus amplification. Conclusions cannot be drawn solely by looking at individual parameter estimates, however, because emotion dynamics are dependent on the set of parameters as a whole (i.e., the frequency, dampening, and coupling parameters for both partners), as well as the initial starting values for each partner (i.e., their emotional rating at the beginning of the observation period). There are an infinite number of possible combinations of parameters and start values, given that each of those could be anywhere on a continuum. Because of this, it is challenging to intuit emotion dynamics based solely on the partners’ parameter estimates. For example, both partners’ dampening parameters may be non-significant, but their combined effect, along with the other parameters, may result in notably dampened system behavior. Therefore, to adequately understand which emotional pattern is occurring, we need to graph the emotional trajectories estimated from the model to see a visual representation of system dynamics. As such, for the present study, we present the parameter estimates from the CLO model, the starting values of emotional levels, and figures of the estimated bivariate emotional trajectories. This set of information allows us to infer the presence of different interpersonal emotional dynamics for couples with differing body-weight combinations.

Interpersonal Emotional Dynamics and Body-Weight

Overweight and obesity are critical public health issues (Ogden et al., 2006). Although genetics and environment are important, a person’s weight status (e.g., healthy weight, overweight, obese) is also related to socio-emotional factors (Burke, Randall, Corkery, Young, & Butler, 2012; Meltzer, McNulty, Novak, Butler, & Karney, 2011; Wickrama & Bryant, 2012). Specifically, weight status can be thought of as both a cause and a consequence of interpersonal emotional processes. For example, partners’ relative weight status (e.g., whether or not one partner has a higher body mass index [BMI] than the other) can predict arguing, conflict, and relationship dissatisfaction (Burke et al., 2012; Meltzer et al., 2011). Going the other direction, relationship dissatisfaction and marital discord can predict unhealthy behaviors, such as emotional eating, which can ultimately contribute to weight gain (Markey, Markey, & Birch, 2001). Clearly this could become a vicious circle, with hurtful emotional dynamics contributing to weight gain, which in turn exacerbates undesirable interpersonal emotional patterns (Meltzer, Novak, McNulty, Butler, & Karney, 2013).

In the present study we focus on weight status as a predictor of interpersonal emotion dynamics. Previous research has studied weight and global interpersonal emotional states such as conflict (Burke et al., 2012), relationship dissatisfaction (Meltzer et al., 2011), closeness (Wickrama & Bryant, 2012), relationship quality (Boyes & Latner, 2009), or intimacy and sexual satisfaction (Ledyard & Morrison, 2008). Although these emergent socio-emotional states are important, they tell us little about the interpersonal dynamics that give rise to them. The present study addresses this issue by investigating couples’ joint weight statuses as a predictor of co-regulation and co-dysregulation in the context of couples discussing their shared health behaviors and lifestyle choices.

It is important to clarify that existing research on weight, emotion, and relationships is largely a-theoretical, but based on previous empirical findings we hypothesized that healthy weight couples, and mixed-weight couples in which the man is the overweight partner, would be able to achieve co-regulation when discussing their shared lifestyle choices, but that mixed-weight couples in which the woman is the heavier partner would show co-dysregulation. We base these predictions on a growing body of literature that suggests that mixed-weight couples in which the woman is heavier than the man may experience emotional difficulties related to weight, but that this is not true when the man is the heavier partner. As an example, couples in which the women were heavier than their male partners reported more habitual conflict and daily arguing than couples of other joint weight statuses (Burke et al., 2012). In addition, newly married husbands and wives were both less satisfied to the extent that the wives had higher body mass indices (BMIs) than the husbands (Meltzer et al., 2011). Others have found that it is particularly important to men that their female partner has an attractive body (e.g., (Chen & Brown, 2005). The reason for this may be explained by evolutionary theory in that men perceive women’s attractiveness to be an indicator of reproductive fitness (Buss & Schmitt, 1993). Furthermore, overweight women may be aware that their partner would be more attracted to them if they were thinner and therefore feel insecure or critical about their bodies, which could contribute to poor regulation of negative emotions experienced during a conversation about living a healthy lifestyle (Burke et al., 2012).

In contrast, social weight stigma tends to be less for overweight men than overweight women (Cossrow, Jeffery, & McGuire, 2001; Sobal, 2005). As such, being overweight may not contribute to the same intrapersonal (and ultimately, interpersonal) emotional difficulties for men as for women. In addition, women place less emphasis on their partners’ thinness than do men (Chen & Brown, 2005; Sheets & Ajmere, 2005), suggesting that when discussing health issues, healthy-weight women with overweight male partners may be less negative and better able to regulate emotions. Thus, although mixed-weight couples with a heavier man may find discussions about their lifestyle choices to be emotionally relevant, potentially challenging, and demanding of some degree of emotion regulation, we expected these couples to be able to achieve a co-regulatory state.

Research on couples in which both partners are overweight is contradictory with respect to its impact on interpersonal emotional processes. On the one hand, such couples may be resilient against emotional instability because their shared, potentially “unhealthy” lifestyle may bring them closer together and facilitate more effective interpersonal emotion dynamics. The System-Symptom Fit theory reflects this perspective and suggests that shared unhealthy behaviors, such as eating out or watching television together, may help to preserve relationship well-being by increasing positive emotion or couple closeness (Rohrbaugh, Shoham, Butler, Hasler, & Berman, 2009; Shoham, Butler, Rohrbaugh, & Trost, 2007). As an example of this, when asked what role weight played in their relationships, partners who both had high BMIs reported that their shared weight status facilitated higher levels of comfort, closeness, and trust between them (Ledyard & Morrison, 2008). In contrast, however, other research suggests that couples in which both partners are battling weight issues may experience emotional difficulties in their relationship due to the effects of being overweight on their sexual intimacy and closeness (Kolotkin et al., 2006; Kolotkin, Zunker, & Østbye, 2012; Ledyard & Morrison, 2008). In sum, it is unclear based on prior research whether shared overweight status will predict emotional co-regulation or co-dysregulation when discussing shared lifestyle issues.

Hypotheses

Based on the literature reviewed above, we proposed the following hypotheses:

1. For healthy weight couples we expected to see co-regulation of relatively weak emotions when discussing lifestyle choices, due to them not having significant concerns about weight or health. As such, we expected these couples to show a weak co-regulatory pattern characterized by coupling of low amplitude, dampened emotional oscillations (i.e., a lack of emotional extremes converging towards stability).

2. For mixed-weight couples in which the man had a higher BMI than the woman (M > W), we expected that discussing lifestyle choices could be an emotional topic, given mutual concerns about his health, but prior research suggests that relationship functioning is not impaired for these couples. Thus we expected that they would show a state of co-regulation, characterized by coupled, higher amplitude, but dampened, emotional oscillations (i.e., less and less extreme emotional highs and lows, converging towards stability).

3. For mixed-weight couples in which the woman had a higher BMI than the man (W > M), prior evidence suggests these couples experience more conflict, arguing, and lower relationship satisfaction and so we expected to see co-dysregulation, characterized by strongly coupled, amplified emotional oscillations (i.e., increasingly extreme emotional highs and lows).

4. For overweight couples, prior research is contradictory, suggesting either that shared high BMI may bring these couples closer together, or that it may contribute to problems surrounding sexual intimacy. While the former could contribute to co-regulation, the latter could contribute to co-dysregulation; thus we did not propose an a-prior hypothesis for these couples.

Method

Participants

Participants were 39 heterosexual couples (78 individuals), ranging in age from 18 to 69 years (M = 31.6, SD = 12.5). Approximately 45% of the sample was married and 55% of the sample was in a cohabitating relationship. Participants’ relationship length ranged from four months to 30 years, with a mean of 5.5 years (SD = 5.3). The sample was 72% European American, 2.6% African American, 2.6% Asian American, and 15% other (7.8% of the sample had missing ethnicity data). In terms of highest level of education obtained by the participants, the majority of the sample reported some college (41%) or reported completion of an undergraduate degree (29%).

Design and Procedure

Data for this study were collected as a part of a larger study on relationships, eating, and emotions that included a baseline questionnaire, a laboratory portion, and a seven-day diary. Only data from the laboratory portion was used in the present analyses (for other analyses of this data set see: (Burke et al., 2012; Randall et al., 2013; Reed et al., 2013). Participants were recruited from online advertisements posted on Craig’s List. Participating couples had to meet the following criteria: (1) both individuals were over the age of 18, (2) both individuals were willing to participate, and (3) the individuals had been in a romantic relationship with each other for at least six weeks. Participants that completed all portions of the study received US$90.

At the laboratory, couples engaged in a video-recorded 20 minute conversation with their partner about the importance of a healthy lifestyle, and the positive and negative impact they have on each other’s health behaviors. The specific topics were: (1) How important do you think it is to live a healthy lifestyle? (2) How willing are each of you to make sacrifices (e.g. spend more money, take time out from other activities) in order to live a more healthy lifestyle? (3) What are some of the things you do that have a negative impact on each other’s lifestyle or on each other’s attempts to be healthy? and, (4) What are some of the things you do that have a positive impact on each other’s lifestyle or on each other’s attempts to be healthy? These conversation topics were introduced one at a time during the interaction and participants indicated when they had completed one topic and were ready to move to the next. Following the conversation, a privacy screen was placed between the partners so they could not see each other. The partners were asked to watch the video-recording of their interaction and rate how they remembered feeling (second-by-second) during the conversation using a rating dial (see below). Finally, height and weight measurements were taken, and the participants were debriefed.

Measures

Body-mass index (BMI)

Participants’ height and weight were measured and used to calculate BMI, using the standard equation of [weight(lbs)/(height(in)²)] * 703. Dyadic-level indices were created to indicate couple average BMI ((man’s BMI + woman’s BMI)/2) and the partner’s difference in BMI (woman’s BMI – man’s BMI). We describe the purpose of these variables in the data analysis section.

Emotional experience

We assessed recalled emotional experience during the conversation using a bipolar rating dial (Levenson & Gottman, 1983). Each partner was given a rating dial, which turned through 180° and was clearly labeled with anchors of frowning versus smiling faces and the corresponding labels of “negative” and “positive”. The middle position corresponded to “neutral” experienced emotion, and served as a reference point. Prior to the rating dial task, a member of the research team demonstrated how to use the dial and informed the participants to continuously rate how they remembered feeling during their conversation. Participants were asked to use the full range of the dial and to rate their emotions relative to the conversation (not their entire lifetime). Although this method entails retrospective ratings of recalled emotions, which are subject to self-report bias, previous research has demonstrated that these cued-recall ratings are comparable to ratings made in the moment, suggesting they are a valuable method for validly and accurately measuring emotion experience across time (Mauss, Levenson, McCarter, Wilhelm, & Gross, 2005). The rating dial provided a continuous measure of emotional experience (positive to negative) in second-by-second increments and was calibrated so that it ranged from a signal of 0 = “very negative” to 5 = “very positive”. Data was recorded for the duration of the conversation in 1-second increments and was later averaged across 10-second segments to reduce random noise.

Data Analysis¹

Appropriateness of a CLO Model

To investigate whether a CLO model was appropriate for the present study, we first visually inspected the raw data for evidence of systematic emotional oscillations, amplification/dampening, and coupling. To demonstrate, Figure 2 presents twelve representative plots (~26% of the data) of couples’ raw emotion ratings over time; some couples demonstrate a large amount of emotionality in the form of rapid high amplitude oscillations (Panel G), whereas others appear to be much less emotional (Panel A). Additionally, most of the panels (except for A and D) demonstrate clearly oscillating patterns with roughly three or more oscillations per conversation length. There is also some evidence of dampening in panels in Panels D – F and of amplification in Panels G – L. Lastly, there is evidence of varying patterns of coupling, including in phase (Panel H) and out of phase (Panel I). Thus we concluded that the CLO model was a reasonable representation of the couples’ raw emotion data obtained in this study.

Figure 2.

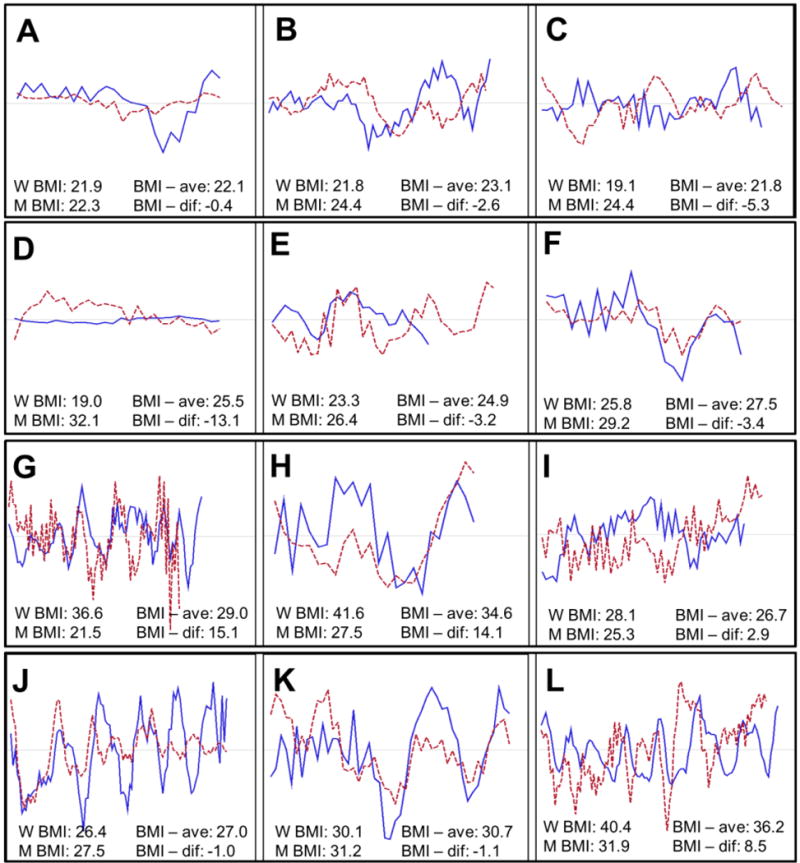
Representative plots of couples’ raw emotion ratings (y-axis) over time (x-axis). The solid line refers to the female partner and the dotted line refers to the male partner. BMI = body mass index; BMI – ave = couple average BMI (female + male / 2); BMI – dif = couple difference in BMI (female – male). Panels A, B, and C are representative of healthy-weight couples; Panels D, E, and F are representative of mixed-weight couples with a heavier man (M > W); Panels G, H, and I are representative of mixed-weight couples with a heavier woman (W > M); Panels J, K, and L are representative of overweight couples. Because couples’ conversation lengths were allowed to differ, the time scales for the panels are different, ranging from ~7 to ~17 minutes.

Estimating derivatives

First and second derivatives of an observed measure, along with the observed measure itself, form the core of CLO models. In keeping with most research on interpersonal emotions, we used a two-step procedure in which we first estimated the derivatives from the data using Generalized Local Linear Approximation (GLLA) and then used those estimates as input data for a multilevel model estimating the CLO parameters (Boker, Deboeck, Edler, & Keel, 2010; Boker & Laurenceau, 2006; Butner et al., 2005; Butner et al., 2007). GLLA requires that decisions be made about two parameters: the number of embedding dimensions (d), and Tau (τ) (Boker et al., 2010; Steele & Ferrer, 2011). The d parameter indicates the number of points to include during derivative approximation and functions as a smoothing process (Steele & Ferrer, 2011). Selection of an appropriate value for d should be based on how the construct of interest is expected to behave and the sampling frequency of the data (Steele & Ferrer, 2011). Based on these considerations, and the possibility of high-frequency noise due to frequent emotion ratings (every 10 seconds), we chose a d parameter of 5, which corresponds to 5 data points being included to estimate derivative approximation. The value of this d parameter is also in line with previous emotion research (Steel & Ferrer, 2011).

The τ parameter indicates how far apart successive observations will be when performing the GLLA (e.g., τ = 1 indicates that each successive observation will be used, τ = 2 indicates that every other observation will be used). As suggested by Boker and colleagues (Boker et al., 2010; Boker & Nesselroade, 2002), one way to determine an adequate τ value is to plot the variance explained (R²) by a univariate oscillator model based on different τ values; the optimal value of τ is the first value at which the variance explained begins to asymptote (i.e., the first value at which the variance explained seems to become maximal). This method employs a within-person multilevel model (time nested in person) that models each person’s data as a damped oscillator. This yields grand average estimates for frequency and for dampening/amplification, as well as random, person-specific components for each term. Based on this model, we found different values of R² for different combinations of τ and d. Ultimately, we chose the combination of τ = 2 and d = 5 (R² = .57), which produced an estimate of the grand-average emotional frequency as one cycle every 3 minutes. The relatively large R² suggests fairly good model fit and the frequency estimate fits well with the theoretical justification that emotion cycles should be in the range of a few minutes, as well as with visual inspection of the raw data. Using these parameters, we computed the estimates of the first and second derivatives using R syntax available at S. Boker’s website (URL: http://people.virginia.edu/~smb3u/), which then became the input data for the multilevel CLO models.

Baseline CLO model

Multilevel modeling is required for CLO models due to the nested nature of the data. Specifically, the outcome variable (acceleration at each time point) is a repeated measure nested within each person, who is in turn nested in a dyad. This results in non-independent residuals, thus invalidating regular regression models (Kenny, Kashy, & Cook, 2006; Singer & Willett, 2003). All models were estimated using the PROC MIXED procedure in SAS version 9.2 (SASInstitute, 2004), using empirical errors and maximum likelihood. First, we started with an empty model (i.e., one with no moderators of the CLO parameters) to check for random between-person variation in the parameters. The Level 1 equation for this model was:

$${\mathrm{d}}^2{\mathrm{Dial}}_{\mathrm{time} \mathrm{i}, \mathrm{couple} \mathrm{j}}=(\mathrm{male})\ast [{\mathrm{\pi }}_{1\mathrm{j}}({\mathrm{Dial}}_{\mathrm{i}})+{\mathrm{\pi }}_{2\mathrm{j}}({\mathrm{d}}^1{\mathrm{Dial}}_{\mathrm{i}})+{\mathrm{\pi }}_{3\mathrm{j}}(\mathrm{Partner}{\mathrm{Dial}}_{\mathrm{i}}-{\mathrm{OwnDial}}_{\mathrm{i}})]+(\mathrm{female})\ast [{\mathrm{\pi }}_{4\mathrm{j}}({\mathrm{Dial}}_{\mathrm{i}})+{\mathrm{\pi }}_{5\mathrm{j}}({\mathrm{d}}^1{\mathrm{Dial}}_{\mathrm{i}})+{\mathrm{\pi }}_{6\mathrm{j}}(\mathrm{Partner}{\mathrm{Dial}}_{\mathrm{i}}- {\mathrm{OwnDial}}_{\mathrm{i}})]+{\mathrm{e}}_{\mathrm{ij}},$$ (3)

where “d² Dial” is the second derivative of the observed dial ratings, “Dial” is the observed dial ratings (the associated parameters represent frequency), “d¹ Dial” is the first derivative of the observed dial ratings (the associated parameters represent dampening/amplification), and “PartnerDial – OwnDial” is the difference in the two partners’ observed dial ratings (the associated parameters represent coupling). Finally, “male” and “female” represent indicator variables, set to 0 or 1 to indicate whether an observation came from a man or woman. Note that this model does not have the usual intercept term. We specified the e_ij to have separate variance components for men and women, allowed those to covary between partners, and allowed auto-correlation over time within people (Laurenceau & Bolger, 2005). Women’s dampening did not show any random variability, and the model would not converge if the remaining random parameters were allowed to covary, and so the Level 2 equation for this model was:

$$(\mathit{male})\ast \left[\begin{array}{l}{\mathrm{\pi }}_{1j}={\Upsilon }_{10}+{\zeta }_{1j}\\ {\mathrm{\pi }}_{2j}={\Upsilon }_{20}+{\zeta }_{2j}\\ {\mathrm{\pi }}_{3j}={\Upsilon }_{30}+{\zeta }_{3j}\end{array}\right]+(\mathit{female})\ast \left[\begin{array}{l}{\mathrm{\pi }}_{4j}={\Upsilon }_{40}+{\zeta }_{4j}\\ {\mathrm{\pi }}_{5j}={\Upsilon }_{50}\\ {\mathrm{\pi }}_{6j}={\Upsilon }_{60}+{\zeta }_{6j}\end{array}\right],$$ (4)

where the represent the population average of the level-1 parameters, the represent between-person residual variance in the level-1 parameters (i.e., random parameters), and we assume the between-person residual variances are independent of each other.

Adding moderators to the CLO Model

To examine emotion dynamics predicted by the couples’ combined weight statuses, we made use of a dyadic “average-difference” version of the CLO model (Kenny et al., 2006) and estimated parameters of the model centered at four theoretically meaningful combinations of BMI averages (i.e., the combined average of the two partners’ BMI) and differences (the difference between the partners’ BMIs; for an explanation of centering and its use in interpreting regression-type models, see (Aiken & West, 1991). We used the 10^th, 50^th, and 90^th percentiles as our centering values, which resulted in a low BMI-average = 21.2, a medium BMI-average = 25.4, a high BMI-average = 31.5, a low BMI-difference =-7.4 (the woman’s BMI was 7.4 points lower than the man’s), a medium BMI-difference = 0, and a high BMI-difference = 8.5 (the woman’s BMI was 8.5 points higher than the man’s). The four combinations were: (1) Healthy-weight couples, indicated by a BMI difference of zero and a low BMI average. (2) Mixed-weight couples where the man was heavier than the woman (M > W), indicated by a low BMI difference and a medium BMI average. (3) Mixed-weight couples where the woman was heavier than the man (W > M), indicated by a high BMI difference and a medium BMI average. (4) Overweight couples where both partners were overweight, indicated by a BMI difference of zero and a high BMI average. Because the BMI variables vary only between dyads (not within dyads or within people), the Level 1 model remains the same as described above and the BMI terms were treated as fixed effects. In addition, after adding the BMI fixed predictors there was no longer any random variation in either men’s or women’s dampening or coupling, so the final Level 2 model was:

$$\begin{array}{l}(\mathit{male})\ast \left[\begin{array}{c}{\mathrm{\pi }}_{1j}={\Upsilon }_{10}+{\Upsilon }_{11}(\text{BMIave})+{\Upsilon }_{12}(\text{BMIdif})+{\zeta }_{1j}\\ {\mathrm{\pi }}_{2j}={\Upsilon }_{20}+{\Upsilon }_{21}(\text{BMIave})+{\Upsilon }_{22}(\text{BMIdif})\\ {\mathrm{\pi }}_{3j}={\Upsilon }_{30}+{\Upsilon }_{31}(\text{BMIave})+{\Upsilon }_{32}(\text{BMIdif})\end{array}\right]\\ +(\mathit{female})\ast \left[\begin{array}{c}{\mathrm{\pi }}_{4j}={\Upsilon }_{40}+{\Upsilon }_{41}(\text{BMIave})+{\Upsilon }_{42}(\text{BMIdif})+{\zeta }_{4j}\\ {\mathrm{\pi }}_{5j}={\Upsilon }_{50}+{\Upsilon }_{51}(\text{BMIave})+{\Upsilon }_{52}(\text{BMIdif})\\ {\mathrm{\pi }}_{6j}={\Upsilon }_{60}+{\Upsilon }_{61}(\text{BMIave})+{\Upsilon }_{62}(\text{BMIdif})\end{array}\right],\end{array}$$ (5)

The BMI terms in equation 5 refer to the non-centered, continuous BMI averages and BMI differences variables (i.e., parameters of this model are estimated at zero BMI-average and zero BMI-difference). To interpret the significant interactions between the BMI variables and the CLO parameters (e.g., dampening, coupling), we re-ran the model and replaced the non-centered “BMIave” and “BMIdif” variables in Equation 5 with the four different combinations of centered BMI-average and BMI-difference variables described above.

Model Fit

To support the validity of the BMI variables as moderators, we examined nested model comparisons using the log-likelihood (-2LL) deviance statistic to compare model fits of the baseline and moderated CLO models. The difference between the-2LL for the two models was 31.9 and the difference in degrees of freedom was 9; a chi square test indicates that the moderated model significantly improves the model fit at the p = .01 level. Additionally, the AIC statistic also improved with the moderated model (difference of 13.9). The BIC statistic stayed relatively the same.

We also estimated the overall R² of the moderated model and found that it was about the same as the estimate we obtained for the univariate model (reported above with respect to derivatives), with 55% of the variance being explained. One explanation as to why the univariate and CLO models fit about the same, despite substantially different models, is that variance that was explained in the univariate model by the random dampening parameter, and its covariance with the random frequency parameter, is explained in the moderated CLO model by the inclusion of coupling and BMI effects. Thus the moderated CLO model appears to systematically account for what was random variability in the univariate model and overall fits the data adequately.

Graphing the model estimated bivariate time-series

To fully understand the emotion dynamics at each of the different combinations of BMI, we graphed the model-estimated bivariate time series. Doing so requires first estimating the starting values of the emotion ratings for men and women at each of the combinations of BMI. We used a standard dyadic growth model centered at time 1 to obtain these estimates. The parameter estimates from the CLO model and the start values from the dyadic growth model were then used to produce four figures in Matlab (version R2012b), one for each of the meaningful combinations of BMI averages and difference.

Results

Descriptive Analyses

Based on national guidelines (“Centers for Disease Control and Prevention,” 2013), participants included the full range of weight status from slightly underweight to obese. For descriptive purposes, the number and percentage of participants in each weight category is provided in Table 1. Women’s BMI ranged from 18.7 to 41.61 (M = 25.08, SD = 6.00); Men’s BMI ranged from 18.13 to 38.74 (M = 26.04, SD = 4.21). All analyses were conducted using the continuous measures of BMI.²

Table 1.

Number and Percentage of Participants in Each Weight Category

	Women (%)	Men (%)
Underweight (BMI < 18.5)	0 (0)	1 (2.6)
Healthy weight (18.5 to 24.9)	24 (61.5)	18 (46.2)
Overweight (25 to 29.9)	8 (20.5)	12 (30.8)
Obese (BMI > = 30)	7 (17.9)	8 (20.5)

Baseline CLO Parameters

Frequency estimates from the baseline model indicated that both men and women showed significant emotional oscillations. Men’s estimated η was −0.17, corresponding to a period of one cycle approximately every 2.5 minutes, (t(4014) = −28.80, p. < .0001), and women’s was very similar at −0.18 (t(4014) = −28.00, p. < .0001). None of the other parameters were significant, indicating that on average couples did not show dampening/amplification or coupling.

Effects of BMI Averages and Differences on CLO Parameters

Table 2 presents the overall F-tests for the average frequency, dampening, and coupling parameters for men and women at zero BMI-average and BMI-difference, as well as the moderating effects of BMI averages and differences on the CLO model parameters. In contrast to the baseline model, once BMI was accounted for in the model there were not only main effects of frequency for men and women, but also coupling for men, and dampening for women. As predicted, however, these main effects were qualified by several interactions. BMI averages significantly moderated women’s dampening and had a marginal effect on men’s coupling. In addition, BMI differences moderated men’s dampening and both partner’s coupling.

Table 2.

Overall F-Tests for the Predictors in the CLO Model

	F value	P value
Male * frequency	39.22	0.00
Male * dampening	2.76	0.10
Male * coupling	4.20	0.04
Male * frequency * BMIave	0.49	0.48
Male * dampening * BMIave	2.50	0.11
Male * coupling * BMIave	3.17	0.08
Male * frequency * BMIdiff	0.81	0.37
Male * dampening * BMIdiff	3.81	0.05
Male * coupling * BMIdiff	23.42	0.00
Female * frequency	14.20	0.00
Female * dampening	4.87	0.03
Female * coupling	0.64	0.42
Female * frequency * BMIave	0.26	0.61
Female * dampening * BMIave	5.08	0.02
Female * coupling * BMIave	0.49	0.48
Female * frequency * BMIdiff	0.05	0.83
Female * dampening * BMIdiff	1.15	0.28
Female *coupling * BMIdiff	28.21	0.00

Note. “BMIave” refers to BMI couple average; “BMIdiff” refers to BMI couple difference.

In order to interpret the moderating effects of BMI, we estimated the parameters at meaningful combinations of BMI (as detailed in data analysis section above). The resulting parameter estimates are presented in Table 3. Note that unlike the usual decomposition of interaction effects, we are interested in the values of the parameters, not the value of the outcome variable, which in this case is acceleration and does not have an interesting interpretation in this context. In other words, in the context of CLO models, acceleration (the second derivative of the observed variable) is simply what needs to be the outcome variable mathematically in order for the CLO model to provide estimates of frequency and dampening/amplification. Despite the different focus, the decomposition process is identical and involves centering the predictors at meaningful values and observing the resulting model estimates (see Aiken & West, 1991). As expected, all frequency estimates were negative and significant, indicating an oscillating pattern for both partners’ emotion ratings. We also see preliminary evidence of varying interpersonal emotional dynamics. For example, healthy weight and mixed-weight couples (M > W) had negative dampening parameters for both partners, while mixed-weight (W > M) and overweight couples showed positive dampening parameters, or amplification. In addition, healthy weight partners show equivalent coupling parameters, mixed-weight partners show opposing coupling parameters, and overweight couples show no evidence of coupling. Nevertheless, fully understanding the dynamic patterns arising from these combinations of parameters demands visualization (see below).

Table 3.

CLO Model Unstandardized Parameter Estimates at Combinations of BMI Averages and Differences

	Both Healthy Weight	Mixed-Weight		Both Overweight
		(M > W)	(W > M)
BMI difference BMI average	0 10th percentile	10th percentile 50th percentile	90th percentile 50th percentile	0 90h percentile
Men’s Frequency	−0.17*	−0.18*	−0.16*	−0.17*
Women’s Frequency	−0.18*	−0.18*	−0.18*	−0.19*
Men’s Dampening	−0.03	−0.05*	0.02	0.01
Women’s Dampening	−0.02	−0.03*	0.002	0.02
Men’s Coupling	−0.005	0.01*	−0.015*	0.002
Women’s Coupling	−0.004	−0.01*	0.005	0.000

Note.

^*indicates the parameter estimate differs from zero with p < .05. Positive dampening values correspond to amplification.

Average Levels of Emotions

To highlight the value of the CLO model approach, as compared to a traditional means-based approach, we also present the average emotion levels for men and women at meaningful combinations of BMI. The unstandardized average parameter estimates are presented in Table 4. These estimates show that in healthy weight and mixed-weight couples in which the W > M, men’s average emotion ratings were significantly negative. In overweight and mixed-weight couples in which the M >W, men’s emotion ratings were significantly positive. In other words, healthy weight men were more negative on average, while overweight men were more positive on average, especially if paired with an overweight woman.

Table 4.

Unstandardized Parameter Estimates (Averages) for Emotional Experience at Combinations of BMI Averages and Differences

	Both Healthy Weight	Mixed-Weight		Both Overweight
		(M > W)	(W > M)
BMI difference BMI average	0 10th percentile	10th percentile 50th percentile	90th percentile 50th percentile	0 90th percentile
Men’s Average Emotion	−0.04*	0.04*	−0.06*	0.22*
Women’s Average Emotion	0.003	0.01	0.01	0.03

Note.

^*indicates the parameter estimate differs from zero with p < .05.

Start Values of Emotion Ratings

In order to obtain starting values to graph the estimated bivariate time series, we used a dyadic growth model predicting the dial ratings for men and women from time, BMI averages, and BMI differences. The overall F tests are presented in Table 5 and show that men’s intercepts and slopes were not impacted by BMI, but women’s were, such that both BMI averages and differences moderated women’s start values and slopes over time. In order to interpret these moderating effects, and to obtain start values, we again estimated the model at the meaningful combinations of BMI. The unstandardized intercept and slope (i.e., effect of time) estimates are presented in Table 6. These estimates show that women with overweight partners, regardless of whether they were healthy-weight or overweight themselves, started the conversations in a significantly negative state and became progressively more neutral over time. This trend may have arisen due to the conversations starting with discussion of negative interpersonal influences and ending with discussion of positive influences.

Table 5.

Overall F-Tests for the Predictors in the Dyadic Growth Model

	F value	P value
Male * Intercept	0.15	0.69
Male * Time	0.95	0.33
Male * BMIave	0.06	0.81
Male * Time * BMIave	0.95	0.33
Male * BMIdif	1.18	0.28
Male * Time * BMIdif	0.29	0.59
Female * Intercept	5.59	0.02
Female * Time	13.03	0.00
Female * BMIave	4.45	0.03
Female * Time * BMIave	5.25	0.02
Female * BMIdif	7.46	0.00
Female * Time * BMIdif	7.39	0.00

Note. “BMIave” refers to BMI couple average; “BMIdiff” refers to BMI couple difference.

Table 6.

Dyadic Growth Model Unstandardized Parameter Estimates (Intercepts and Slopes) at Combinations of BMI Averages and Differences

	Both Healthy Weight	Mixed-Weight		Both Overweight
		(M > W)	(W > M)
BMI difference BMI average	0 10th percentile	10th percentile 50th percentile	90th percentile 50th percentile	0 90th percentile
Men’s Intercept	−0.004	0.05	−0.08	−0.04
Women’s Intercept	0.026	−0.15*	0.08	−0.12*
Men’s Slope	0.000	−0.001	0.001	0.002
Women’s Slope	0.000	0.004*	0.000	0.004*

Note. Intercepts represent start values and slopes represent linear changes over time,

^*indicates the parameter estimate differs from zero with p < .05.

Graphing the CLO Model-Estimated Bivariate Time Series

Figures 3 – 6 show the predicted emotional dynamics at the various combinations of BMI averages and differences, based on the parameter estimates obtained from the CLO model (see Table 3), in combination with the estimated start values obtained from the dyadic growth model (see Table 6). These model-predicted trajectories are idealized versions of the raw data; therefore, we also provide three prototypical examples of raw data for each couple type in Figure 2. As predicted, Figures 3 – 6 show co-regulatory and co-dysregulatory emotion dynamics. We next discuss these figures as they relate to our hypotheses.

Figure 3.

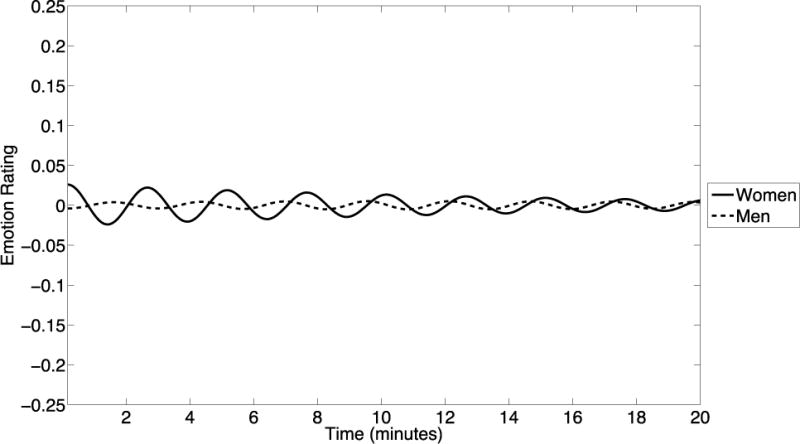
CLO-model estimated bivariate time-series of emotion ratings for couples in which both partners are healthy weight (BMI-dif = 0, BMI-ave = 21.2).

Figure 6.

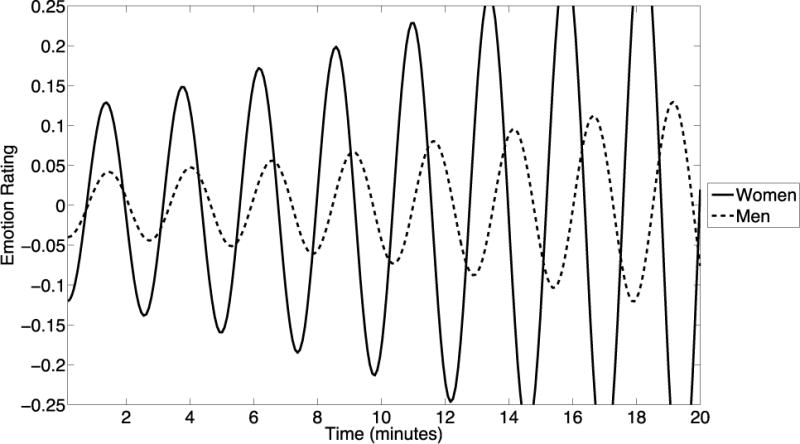
CLO-model estimated bivariate time-series of emotion ratings for couples in which both partners are overweight (BMI-dif = 0, BMI-ave = 31.5).

Hypothesis 1: Healthy Weight Couples

We hypothesized that for couples in which both partners were healthy weight (BMI difference = zero, BMI average = 10^th percentile), we would see a relatively weak co-regulatory pattern characterized by coupling of low-amplitude, dampened oscillations. Figure 3 supports this hypothesis and shows the partners starting in a weakly oscillating, anti-phase pattern, but moving towards a more in phase pattern (i.e., there is some evidence of coupling). It also shows that their oscillations begin at relatively low amplitude and trail off to an even less emotional state over time. Overall, the pattern could be described as fairly non-emotional, with some evidence of weak co-regulation bringing the couple to a steady, completely neutral state.

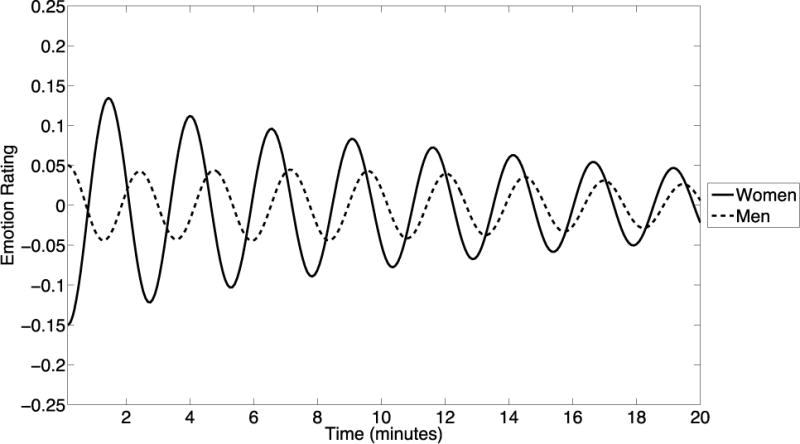
Hypothesis 2: Mixed-Weight Couples (M > W)

We hypothesized that we would see co-regulation in mixed-weight couples in which the man had a higher BMI than the woman (M > W; BMI difference = 10^th percentile, BMI average = 50^th percentile). Figure 5 provides support for this hypothesis. Although these couples begin with fairly high amplitude emotional oscillations, especially for the women, both partners show dampening over time. In addition, the partners begin out of phase with each other, but are pulled into phase over time. Thus this pattern matches our theoretical definition of co-regulation, where partners’ emotions are coupled together and mutually dampening, such that over time their emotions jointly return to a stable level.

Figure 5.

CLO-model estimated bivariate time-series of emotion ratings for couples in which the woman is heavier than the man (W > M; BMI-dif = 8.5, BMI-ave = 25.4).

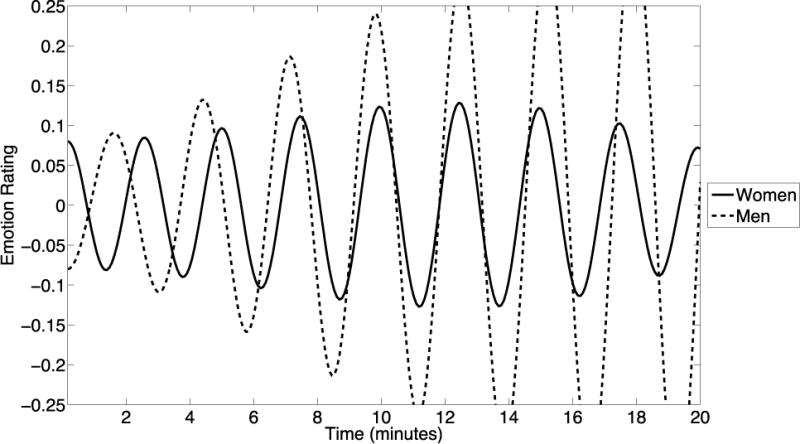
Hypothesis 3: Mixed-Weight Couples (W > M)

We hypothesized that we would see co-dysregulation in mixed-weight couples in which the woman had a higher BMI than the man (W > M; BMI difference = 90^th percentile, BMI average = 50^th percentile). Figure 4 supports this hypothesis. These couples begin with higher amplitude oscillations than the healthy weight couples, and those oscillations are amplified over time, especially for the men. In addition, the partners begin in an anti-phase pattern but are pulled into phase with each other over time. Thus this pattern can be summarized as one in which the partners become interconnected emotionally over time, but in an amplified and volatile way. Interestingly, towards the end of the time period the model predicts that the women will begin to dampen and move out of phase with the male partner, perhaps suggesting that they are disconnecting from the volatile interaction or attempting to draw the system back into balance.

Figure 4.

CLO-model estimated bivariate time-series of emotion ratings for couples in which the man is heavier than the woman (M > W; BMI-dif = −7.4, BMI-ave = 25.4).

Hypothesis 4: Overweight Couples

Based on contradictory prior literature, we were unsure what pattern overweight couples would show (BMI difference = zero, BMI average = 90^th percentile). However, Figure 6 clearly shows a co-dysregulatory pattern. Both partners show high amplitude oscillations right from the beginning, and these are further amplified as the conversation progresses, especially for women. Furthermore, unlike the other 3 types of couples who all showed some evidence of being pulled into phase with each other, the overweight couples begin in phase but then appear to become un-coupled over time. The general picture is of a highly emotional and increasingly volatile interpersonal system.

Discussion

The quality of people’s social relationships predicts mortality (Holt-Lunstad, Smith, & Layton, 2010; House, Landis, & Umberson, 1988). Such a dramatic effect is likely driven by multiple mechanisms, and understanding them will require fine-grained distinctions between the many interpersonal processes that occur (and co-occur) in close relationships. In the present work we demonstrate how to distinguish between two interpersonal emotional patterns that have divergent implications for emotional well-being, and as a result, for general health. Our findings indicate that the coupled linear oscillator model can be used to distinguish between co-regulation, where partners’ emotions have dampening, homeostatic influences on each other, and co-dysregulation, where the reverse is true. Furthermore, we show that these patterns are associated with an important health indicator, specifically partners’ joint body weight. Our findings suggest that some couples are able to co-regulate when dealing with weight issues, which could help them to achieve coordinated emotions surrounding weight maintenance, and ultimately, coordinated healthy lifestyles. Unfortunately, for other couples, weight issues may contribute to co-dysregulation, which could present a barrier to maintaining stable health behaviors.

Couples’ Weight and Emotions

As hypothesized, healthy weight couples showed co-regulation of relatively weak emotions when discussing shared lifestyle choices, likely because neither partner had significant weight concerns. Although these couples showed a weak form of co-regulation, in that there was some evidence of dampening and coupling, the overall impression is one of mild emotion subsiding to a completely neutral state. This finding highlights an important caveat for future studies: when studying co-regulation it will be important to employ dyadic interaction tasks that are salient enough to both partners to perturb their emotional system adequately to require regulation in the first place (Butler & Randall, 2013).

Also as hypothesized, mixed-weight couples with a heavier man (M >W) showed co-regulation, but those with a heavier woman (W > M) showed co-dysregulation. These findings fit with prior research suggesting that mixed-weight status is particularly problematic when it is the woman who has the higher BMI (Boyes & Latner, 2009; Burke et al., 2012; Butler, Young, & Randall, 2010; Meltzer et al., 2011). In contrast, couples with a heavier male partner do not appear to have such difficulties (Chen & Brown, 2005; Sheets & Ajmere, 2005). Thus, although these couples seemed to find the topic of lifestyle choices an emotionally provocative one, perhaps due to shared concerns about his health and physical fitness, they were able to co-regulate as the conversation evolved and move towards a more stable, less emotional state.

Lastly, couples in which both partners were overweight showed a clear pattern of co-dysregulation, with both partners showing high amplitude oscillations that became more extreme over time. This finding contradicts the idea that both partners being overweight (and likely sharing in unhealthy behaviors) may preserve relationship well-being by facilitating positive interpersonal relationship processes, as suggested by the System-Symptom Fit perspective (Rohrbaugh et al., 2009; Shoham et al., 2007). Rather, it seems that weight issues arising from both partners having high BMIs, such as decreased sexual satisfaction and intimacy, may contribute to volatile, destabilizing emotional processes. However, given prior contradictory findings regarding relationship quality for overweight couples, with some studies finding shared overweight status acting as a bonding factor (Ledyard & Morrison, 2008), but others suggesting it is problematic (Kolotkin et al., 2006; Kolotkin et al., 2012), an important direction for future research is to explore whether there are moderating variables such that some overweight couples are able to co-regulate, while others experience co-dysregulation.

One strength of the present study is that the CLO model allowed us to examine fluctuations in partners’ emotions, rather than just average emotions or linear trajectories over time. Our results show that the various approaches provide distinct and potentially complementary information. We found that on average, healthy weight men reported more negative emotional experience, regardless of their partner’s weight status, while overweight men reported more positive experience, especially when paired with an overweight partner. This information needs to be considered within the context of the CLO results, however. Healthy weight men with healthy weight partners were somewhat negative on average, but this was in the context of mild oscillations showing dampening over time. In contrast, those with overweight partners were also more negative on average, but they experienced increasingly volatile fluctuations, suggesting a regulatory attempt that was failing. Similarly, overweight men with overweight partners experienced relatively high average levels of positive experience, but it was in the context of dramatic oscillations, suggesting that it was a fairly unstable form of positivity. Thus our results suggest that weight status can influence both how distressing an interaction is overall (average level effects) and how a couple regulates that experience (co-regulatory effects apparent in the oscillatory pattern).

In sum, our findings demonstrate the important role that weight may play in interpersonal emotion systems and highlight the potentially vicious cycle that may emerge in which high BMIs negatively influence intra- and inter-personal emotions, which may then feed back into weight gain or unhealthy behaviors, potentiating high BMIs. As such, these findings suggest that weight maintenance and loss interventions may need to consider relational dynamics and the relative weight status of partners to be successful. Furthermore, the finding that many couples experienced co-dysregulation suggests that an important direction for future research is to better understand whether co-dysregulation is arising due to a lack of regulatory effort, thus allowing a dysregulated state to emerge, or regulatory failure subsequent to extensive effort, or some other process. Clearly, designing interventions demands an answer to this question.

Methodological Considerations and Limitations

The present study expands on previous research on interpersonal emotional dynamics (Boker & Laurenceau, 2006; Butner et al., 2007; Steele & Ferrer, 2011) by using the CLO model to examine both co-regulation and co-dysregulation. Prior research has referred to any evidence of between-partner regulatory influences as co-regulation, but our findings demonstrate that qualitatively distinct patterns can emerge, depending on the combination of within- and between-person influences and the initial state of both partners. We have demonstrated how a combination of start values and CLO parameter estimates can be used to generate visual representations of emotional dynamics at meaningful levels of a set of predictors (e.g., weight status). We believe this provides the missing piece in the co-regulation literature, that being the ability to go from statistical results to a meaningful interpretation in terms of interpersonal emotional dynamics.

One of the strengths of the present study is that we used model estimated start values of partners’ emotions for each weight combination when representing the patterns of emotion dynamics. Both versions of the CLO model presented in the introduction (Butner et al., 2005; Helm et al., 2012) are very sensitive to start values, which needs to be taken into account in any empirical investigation. Future analyses could go even further and explore the use of person-specific start values (rather than group estimates) to allow for more specificity. Similarly, when estimating the derivatives we did not use different Tau and embedding parameter estimates for each couple, or for each person, which would contribute to noisy derivative estimates if some individuals have faster or slower rates than others (Deboeck, Boker, & Bergeman, 2008; Ferrer & Helm, 2013). It is important to note, however, that when deciding on the values of parameters to use for derivative estimation we used a multilevel approach to fit a univariate damped linear oscillator model, and allowed each person to have his or her own frequency (i.e., frequency was treated as random). Therefore, at every step of the way, including choosing parameters for derivative estimation and testing the final models, we allowed individuals to have their own cycle frequencies. A related limitation is that we estimated derivatives directly from the observed data (Boker, 2001; Boker & Ghisletta, 2001; Boker & Nesselroade, 2002). Although the approach we employed is simpler than methods that combine derivative estimation and model fitting, it does have the disadvantage that biased parameter estimates may arise due to noise in the observed data (Boker et al., 2010; Boker, Neale, & Rausch, 2004; Boker & Nesselroade, 2002).

An additional limitation is our use of a bipolar rating dial, which prevents us from distinguishing between dampening of negative versus positive emotions. Although dampening of negative emotions is typically considered a beneficial intra- and inter-personal process, the effect of dampening positive emotions may depend more on the context. For example, sometimes dampening of positive emotions may have undesirable effects, such as when one individual fails to share in the excitement or happiness of their partner, thereby pulling their partner into a more neutral state. Other times, it may be beneficial, such as when partners need to unwind after an exciting day, or to prevent manic tendencies. Therefore, future research may benefit from having participants make two passes when rating their emotions – one pass to rate their negative emotions, and another pass to rate their positive emotions.

Another consideration is that our models included cross-level interaction terms (i.e., interactions that involve predictors that vary at different levels). Typically, cross-level interaction terms (and related effects) require relatively large samples for sufficient statistical power. The power to detect cross-level interactions is determined primarily by the magnitude of the cross-level interaction effect, the variance of the level-1 (L1) slopes across level-2 (L2) units, and by L1 and L2 sample sizes (Mathieu, Aguinis, Culpepper, & Chen, 2012). Researchers do not usually have control over the size of the cross-level interaction effect or the variance of the L1 slopes across L2 units; however, researchers can increase the L1 and L2 sample sizes to increase power (Mathieu et al., 2012). As such, due to our repeated measures of emotion (average number of time points per person was 53) and the sufficient number of couples (N= 39), our data set was sufficient to detect cross-level effects, but this issue should be considered when designing research intended to test for cross-level interactions.

One final consideration is that the conversation topics we used, or the rating dial technique, could have influenced the oscillatory pattern of emotions we found. It is true that the conversation topics included both ‘negative’ and ‘positive’ ones, but it was also the case that individuals rated feeling positive during the negative topics, and vice versa, and people showed a fair bit of variability in oscillatory frequency that cannot be explained by the fixed order of topics. Thus, we cannot assume that the observed oscillations are simply due to the conversation topics. Additionally, the rating dial may have contributed to the oscillatory pattern of emotions because it was relatively easy to move from positive to negative when using it. However, the rating dial cannot explain the different frequencies, dampening/amplification, or coupling that we also found across partners’ emotion ratings. For example – individuals could not have been influenced by the dial to couple their emotion ratings with their partner’s because a privacy screen was placed between them at the time.

Conclusion and Future Directions

Social scientists have increasingly sophisticated theories about interpersonal emotion systems, but we are limited by a lack of statistical modeling tools adequate for addressing those dynamic theories (Ferrer & Helm, 2013; Ferrer, Steele, & Hsieh, 2013; Helm et al., 2012). The coupled linear oscillator model is a first step in the right direction to distinguish between, and address the complexities of, emotional co-regulation versus co-dysregulation. There are, however, new areas of modeling still to pursue. For example, to provide a comprehensive understanding of interpersonal emotions, we should explore all components of emotion (including experience, behavior, and physiology) simultaneously, rather than separately. Additionally, although the coupled linear oscillator model may be able to differentiate between co-regulation and co-dysregulation, there are other emotion dynamics, such as co-escalation and co-deescalation (i.e., coupled emotion channels escalating above or de-escalating below a homeostatic level along a linear trajectory), which also need to be considered and modeled. Lastly, regime switching models, or CLO models with stochastic drift, need to be developed that can account for changing patterns or “regimes” of emotion dynamics within couples’ interactions. For example, a couple may start off in a co-escalation state, then move into a co-dysregulated state, and then end in a co-regulatory state. In the standard CLO model, such as we present here, the oscillations are treated as having uniform dampening or amplification effects on all data points (Hessler et al., 2013). A regime switching model, however, could more accurately represent the complexity of reality by allowing for sequences of different dynamic patterns to emerge across the duration of one interaction. Thus, an important research direction for social and health psychologists is to collaborate with computational and mathematical scientists in order to take socio-emotional theories and model them accurately, thereby disentangling the complexities of dynamic, interpersonal emotional systems.