A Deformable Atlas of the Laboratory Mouse

Abstract

Purpose

This paper presents a deformable mouse atlas of the laboratory mouse anatomy. This atlas is fully articulated and can be positioned into arbitrary body poses. The atlas can also adapt body weight by changing body length and fat amount.

Procedures

A training set of 103 micro-CT images was used to construct the atlas. A cage-based deformation method was applied to realize the articulated pose change. The weight-related body deformation was learned from the training set using a linear regression method. A conditional Gaussian model and thin-plate spline mapping were used to deform the internal organs following the changes of pose and weight.

Results

The atlas was deformed into different body poses and weights, and the deformation results were more realistic compared to the results achieved with other mouse atlases. The organ weights of this atlas matched well with the measurements of real mouse organ weights. This atlas can also be converted into voxelized images with labeled organs, pseudo CT images and tetrahedral mesh for phantom studies.

Conclusions

With the unique ability of articulated pose and weight changes, the deformable laboratory mouse atlas can become a valuable tool for preclinical image analysis.

Introduction

In the last decade, digital atlases of the mouse anatomy have become useful tools for preclinical research and data analysis. Various types of mouse atlases have been developed focusing on different aspects of mouse studies. Some atlases aim at providing whole-body-scale gross anatomy, such as the Digimouse atlas [1], the MOBY phantom [2], the MR visible mouse [3], and the Virtual Population mouse models [4]. Some atlases focus more on specific organs like the skeleton [5], heart [6], liver [7], skull [8], limbs [9], and trunk organs [10]. Among all the organs, the brain attracted the most attention, and many atlases have been constructed for the mouse brain based on different imaging modalities, such as MR [11–14], histological gene expression images [15–20], light microscopy tomography [21], and fused MR/histology images [22, 23]. In the research field of mouse embryonic development, atlases of different embryo stages were also developed, for example the Edinburgh mouse embryo atlas [24] which incorporates gene expression database [25], the Caltech μMR atlas of mouse development [26], and the embryo atlas based on micro-CT [27].

The atlas proposed in this paper belongs to the whole-body category. Whole-body atlases are generally used as anatomical references to be registered with preclinical images [28–33] or as digital phantoms for computerized simulation [34–37]. However, most of the existing whole-body atlases are based on a single reference subject positioned in a static body pose. It is challenging to use such atlases to register/simulate real word subjects with posture and anatomic variations. Efforts have been made to compensate for such limitations. The MOBY phantom was scaled to simulate different body weights [36], but simple scaling does not account for the nonlinear anatomical changes caused by weight differences. The Virtual Population mouse models have incorporated body articulation [38] for pose-related thermal or electromagnetic simulations; however, such articulation is not designed for atlas registration. The articulated skeleton atlas [5, 28, 30, 39, 40] was specially designed to be registered with articulated subjects, but this atlas only contains the skeleton without soft organs and thus is not suitable for simulation usage or data analysis. Overall, the problem of whole-body-scale posture and anatomic variance has not been fully resolved, leaving a major obstacle in automated analysis of preclinical images [41].

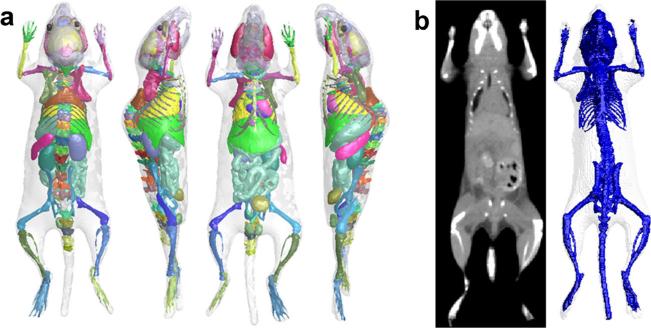
To tackle the above problem, a deformable mouse atlas is proposed in this work. Compared to the existing mouse atlases, this new atlas is fully articulated and can be freely deformed into arbitrary body poses. It can also adapt its organ anatomy according to changes of body weight. The atlas is constructed based on multiple training subjects. Cage-based deformation and statistical learning methods were used to realize body articulation and weight change. Fig. 1a demonstrates 3D rendering of the deformable mouse atlas. Details of atlas construction and test results are described in the following sections.

Fig. 1.

a The 3D surface rendering of the deformable mouse atlas, viewed from four different angles. b The reference subject of the atlas, shown as the CT image (left) and the surface rendering of the skin and skeleton (right).

Materials and Methods

Preparation of Training Subjects

To construct the deformable mouse atlas, 103 mouse micro-CT images (including 94 contrast-enhanced and 9 non-contrast images) were used as the training set. These images were selected from the preclinical image database of the Crump Institute for Molecular Imaging, University of California, Los Angeles (UCLA) [42]. The contrast agents were Fenestra™ LC (liver contrast agent) for 93 of the images and Fenestra™ VC (vascular contrast agent) for one image. For all the training images, healthy subjects of different strains, weights, sex, and postures were acquired in vivo. Three of the most frequently used strains in preclinical studies (nude, C57, and severe-combined immunodeficient (SCID)) were included. The body weights ranged from 15 to 45 g. The subjects were imaged at prone positions inside a multimodality chamber that provided anesthesia and heating [43]. Postures of the subjects were not strictly regularized; random body bending towards left, right, and back directions was acquired. The imaging system was a microCAT II small animal CT (Siemens Preclinical Solutions, Knoxville, TN, USA). The exposure settings were 70 kVp, 0.5 mA, 0.5 s, and 360 ° rotation in 1 ° steps with 2.0-mm aluminum filtration. Images were reconstructed using a modified Feldkamp process to isotropic voxel size 0.20 mm and matrix size 256×256×496.

From the training set, an 18-g C57 mouse with Fenestra™ LC contrast was selected as the reference subject of the atlas (as shown in Fig. 1b). The criteria of selection are that the reference subject should have an average body pose and the least amount of fat, so that it can be used as a starting shape of the pose and weight change.

Organ structures were segmented from the training micro-CT images by a human expert. For all the 103 images, skin, skeleton, and lungs were segmented. From the 93 Fenestra™ LC-enhanced images, the pericardium, liver, spleen, and kidneys were segmented. From the Fenestra™ VC-enhanced image, detailed cardiac vascular structures including the left and right ventricles and atria, aorta, and vena cava were segmented. The neck brown adipose tissue, stomach, intestine, bladder, and abdominal cavity were segmented from the image of the reference subject. Labels of skull, limbs, and thoracic bones were obtained by registering the articulated mouse skeleton atlas [28] to the reference subject. This articulated skeleton atlas was constructed by Baiker et al.[28, 40] based on the skeleton of the Digimouse atlas. However, the spinal structures, scapulas, and clavicles were not labeled in Baiker's articulated atlas. We added the missing labels of 35 vertebrae, the spinal cord, scapulas, and clavicles by segmenting them from the original CT image of the Digimouse atlas. Brain structures, eyes, masseter muscles, and lachrymal glands were directly adopted from the Digimouse atlas [1]. All structures taken from the Digimouse atlas were mapped into the reference subject using the thin-plate spline (TPS) transform. Overall, 89 organ labels were included in the atlas, as listed in Table 1.

Table 1.

List of organ structures included in the atlas

Organ system	Included structures/organs
Nervous	Brain structures (medulla, cerebellum, olfactory bulbs, external cerebrum, striatum, lachrymal glands); spinal cord
Musculoskeletal	Skin, muscle surface, masseter muscles; individual bones (skull, 35 vertebrae, ribs, clavicles, scapulas, sternum, pelvis, forepaws, distal forelimbs, proximal forelimbs, proximal hindlimbs, distal hindlimbs, hindpaws)
Cardiovascular	Heart (pericardium, left and right ventricles, left and right atriums); main aorta and vena cava
Respiratory	Lungs; nasal cavity
Digestive	Liver, gallbladder, stomach, and intestines
Immune	Spleen, thymus
Renal/urinary	Kidneys and bladder
Reproductive	Testis
Vision	Eyes
Adipose	Neck brown fat, subcutaneous fat, abdominal fat

All the segmented organs were converted to triangular surface meshes. The vertex correspondences between the training subjects were obtained by registering the organ meshes of the reference subject to other subjects using the point set registration method [44]. For the skeleton, the point set registration method does not work well due to the skeleton's articulated nature; therefore, the articulated skeleton atlas [28] was used and registered to each training subject to obtain skeleton vertex correspondences. After the vertex correspondences of the soft organs and the bones were established, the cardiac vascular structures taken from the Fenestra™ VC-enhanced image were mapped into the reference subject via TPS transform, using the corresponding vertices of the pericardium and spine as TPS control landmarks.

Articulated Deformation of Skeleton and Skin

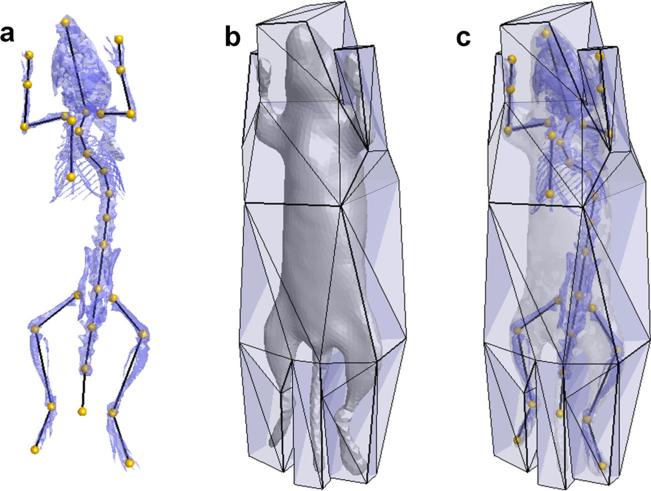
Articulated deformation of the atlas is driven by a skeleton graph defined on the reference subject, as shown in Fig. 2a. In total, 30 graph vertices were manually located at the skeleton joints. To simplify spine articulation, only 11 graph vertices were defined at the vertebrae where significant spine bending occurs. The graph serves as a kinematics chain controlling the articulated skeleton deformation based on the skeletal subspace deformation (SSD) method [45]

$$P_i^{\prime }=\left(\sum _j{\omega }_{i,j}{T}_j\right)p_i,$$ (1)

where p_i is the four-element homogeneous coordinate (x_i, y_i, z_i, and 1) of the ith skeleton vertex, and $p_i^{\prime }$ is the homogeneous coordinate after deformation. T_j is a 4×4 matrix of the jth graph edge, representing the rigid transform starting from the reference pose. ω_i,j is the weighting coefficient (also named the rigging factor) of graph edge j on skeleton vertex i, and ω_i,j is defined as

$${\omega }_{i,j}=\{\begin{array}{cc}\exp (-D_{i,j})\hfill & (\text{if}J\in S_i)\hfill \\ 0\hfill & (\text{if}j\notin S_i),\hfill \end{array}\phantom{\}}$$ (2)

where D_i,j is the closest distance from vertex i to graph edge j. S_i is the set of graph edges that have an anatomical control of vertex i. If vertex i belongs to the skull, limbs, paws, or sternum, S_i is a single graph edge of the bone that vertex i belongs to; otherwise, if vertex i belongs to the spine, ribs, scapulas, or clavicles, S_i contains multiple graph edges with ω_i,j>0. To satisfy the normalization constraint, the weighting coefficient ω_i,j is further normalized as ${\omega }_{i,j}∕\sum {\omega }_{i,j}$, so that $\sum {\omega }_{i,j}=1$.

Fig. 2.

a Definition of the skeleton graph. b The deformation cage enclosing the mouse body. c Overlaid display of the skeleton graph, deformation cage, skeleton, and skin meshes.

For the skeleton, SSD is fast and effective for modeling articulated motion. However, for the skin, this method generates skin folding artifacts near the joints, namely the “joint collapse” and “candy-wrapper” defects [46]. This problem has been solved for human skin via various approaches [47–49] but was not well addressed for small mammals like mice. Specifically, in small-sized mammals, significant skin sliding happens at the shoulder and waist area during large rotations of the humerus and femur. One successful approach to model this sliding effect is to construct a spring mesh of the skin and conduct physical simulation based on spring tension and mesh collision [50]. This solution sacrifices computation speed, and is time-consuming for atlas registration applications. To efficiently model the smooth skin deformation caused by this sliding effect, we developed a cage-based skin deformation method based on the harmonic coordinate technique [51]. An enclosing cage was manually constructed, surrounding the reference subject (Fig. 2b, c). The cage is a closed triangular mesh with only 52 vertices depicting the rough mouse shape. The cage vertices are used as control landmarks to deform any point inside the cage, i.e.,

$$v_i^{\mathrm{S}}=\sum _j\left(h_{i,j}{v}_j^{\mathrm{C}}\right),$$ (3)

where $v_j^{\mathrm{C}}$ is the 3D displacement vector of the jth cage vertex, and $v_i^{\mathrm{S}}$ is the displacement vector of the ith skin vertex. h_i,j is the harmonic coordinates serving as the control weight of the jth cage vertex to the ith skin vertex. h_i,j can be calculated using the harmonic coordinate method [51].

Equation (3) implies that the sparseness of the cage vertices determines the smoothness of the skin deformation, i.e., sparser cage will yield smoother skin deformation. Therefore, the cage is designed to be sparse at the shoulder and waist areas. The effect of this design is that when large bone rotations happen at the shoulder or hip, the skin mesh will smoothly deform without folding, mimicking the sliding of the skin over the underlying bones.

To synchronize the cage deformation with the skeleton articulation, the automatic rigging method [52] is applied to calculate the rigging factors (ω_i,j in Eq. (1)) between the cage vertices and the skeleton graph. As a result, the skeleton graph drives the cage movement and then the cage movement leads to skin deformation. However, since the skeleton and the skin are deformed via different approaches, they might intersect with each other when large limb rotations occur. To overcome this problem, we only use the cage for the skin deformations caused by shoulder and hip joints. For other joints, the skin is still deformed using the SSD method, and the rigging factors between the skin vertices and the skeleton graph are also calculated with the automatic rigging method [52].

Weight-Related Deformation of the Skin and Skeleton

For mice, there are two major factors that contribute to body weight change: body size and fat amount. These two factors are decoupled for the deformable mouse atlas, based on the assumption that the change of fat amount does not significantly alter the anatomy of other organs [53, 54]. The change of body size is simplified as linear scaling of the skin and skeleton,

$$P=S(l,P_0)=\frac{l}{l_0}(P_0-O)+O,$$ (4)

where P is a 3×n array representing the vertex coordinates of the deformed atlas, and n is the total number of vertices. P₀ are the vertex coordinates of the reference subject. O is a 3×n array where every column is the same 3×1 vector of the centroid of P₀. l₀ is the spine length of the reference subject, and l is the spine length of the target body size. The spine length is defined as the curved length of the spinal cord center line, starting from the neck top to the middle of pelvis.

The change of fat amount is modeled as a 3D deformation of the skin. Fig. 3 demonstrates the modeling process. As a prenormalization step, intersubject differences of body pose and bone sizes are removed from the training set. This is achieved by applying the Laplacian mesh deformation method [55] to the bones and skins of each subject, so that the body size and pose of the whole training set is uniform. After the prenormalization, the remaining skin shape differences are primarily caused by fat amount differences.

Fig. 3.

Modeling body weight change. The selected training subjects of different weights are first normalized into the same pose and size, and then, a linear regression method is used to calculate the deformation vectors related to fat amount changing. The deformation vectors are shown at the right end of this figure. The red color intensity of the skin represents the magnitude of the vectors.

Based on the normalized training set, the linear regression method [49] is applied to extract the skin deformation vectors corresponding to fat amount change. The inputs to the linear regression are the skin vertices and the body weight of each normalized subject, while the output is the skin deformation vector V_f corresponding to unit weight difference. Since the training subjects are normalized, the input weight should be the normalized value, i.e., $\frac{w_k}{{(l_k∕l_0)}^3}$, where w_k and l_k are body weight and spine length of the kth training subject. Based on V_f, the skin vertices of body weight w are calculated as

$$P=\mathit{W}(w,P_0)=P_0+\left(\frac{w}{{(l∕l_0)}^3}-w_0\right)\cdot V_f,$$ (5)

where w₀ is the body weight of the reference subject. Equation (5) assumes P and P₀ have the same spine length. To account for spine length difference, Eqs. (4) and (5) are combined as

$$P=\mathit{S}(l,\mathit{W}(w,P_0)).$$ (6)

In Eq. (6), l and w are decoupled as two separated inputs. However, for normal mice housed in typical conditions, the body weight and spine length always change simultaneously by aging. To model this combined changing, we fit a polygonal function l= g(w) based on the training set and use g(w) to calculate the spine length for any given body weight; thus, Eq. (6) can be modified as

$$P=\mathit{S}(\mathrm{g}\left(w\right),\mathit{W}(w,P_0))$$ (7)

To distinguish the two different ways of weight changing, we call Eq. (6) the decoupled mode and Eq. (7) the combined mode.

Deformation of the Entire Atlas

Based on the above pose and weight changing models, the entire atlas is deformed as follows. First, Eq. (6) or (7) is applied to deform the skin and skeleton into the required body weight. The choice of Eq. (6) or (7) is subject to the user, i.e., depending on whether the user wants to change the fat amount and body length separately or simultaneously. Next, internal organs are mapped based on the conditional Gaussian model (CGM) [10] and TPS interpolation. Finally, articulated deformation is applied to all the organs to obtain the final deformation result.

For internal organ mapping, two different methods (CGM and TPS) are used. CGM is a mathematical tool for modeling the conditional distribution between two multivariate Gaussian variables. In our case, it is used to estimate the shapes and positions of internal organs, given the known skin and skeleton. As revealed by our previous studies [10, 56], CGM is more accurate than TPS for estimating the organs that have near-Gaussian shape distributions across the population, such as the heart, lungs, liver, spleen, and kidneys. For the organs that have near-random shape distributions (such as the intestines, bladder, and stomach) and the organs that do not have enough training samples (such as the detailed brain structures, cardiovascular structures, spinal cord, and testis), the TPS interpolation is used.

For details of the CGM, we refer the readers to our previous work [10]. Briefly, the CGM is constructed based on the 93 Fenestra™ LC-enhanced training subjects. The organs of the training subjects are divided into two groups: one for the skin and skeleton and the other for the heart, lungs, liver, spleen, and kidneys. The conditional distribution of organ vertices between the two groups is learned from the training set. When the vertices of one group are known, the vertices of the other group can be estimated based on the conditional distribution. After the CGM-based mapping, the rest of the internal organs (the intestines, bladder, stomach, detailed brain structures, cardiovascular structures, spinal cord, and testis) are all mapped via the TPS interpolation, using the control points from nearby organs.

The final step is to apply the pose deformation to all the atlas organs, based on the same articulated deformation method that was used for the skin. As a prerequisite, harmonic coordinates (h_i,j in Eq. (3)) and rigging factors (ω_i,j in Eq. (1)) need to be computed for all the organs. The harmonic coordinates are computed using the same method for the skin, and the rigging factors are computed by diffusing the rigging factors of the skin and skeleton to all the other organs using the Laplacian diffusion method [51].

Results

To test the deformation performance, the atlas was deformed into different body poses and weights. The deformation algorithm was programmed using IDL 7.1 (ITT Visual Information Solutions, Boulder, CO, USA). For the decoupled mode, the required inputs of the program were body weight, spine length, and spatial transform matrices of skeleton graph edges (as defined in Eq. (1)). For the combined mode, only the body weight and transform matrices were required. On a laptop PC with 1.7 GHz CPU and 4 GB RAM, the entire run time for combined pose and weight deformation was 0.98 s, divided in 0.05 s for weight deformation, 0.12 s for CGM-based organ mapping, 0.61 s for TPS-based organ mapping, and 0.2 s for pose deformation. A user interface was constructed for a manual control of the atlas deformation. The user can adjust the slide bars to change body weight and spine length. To adjust body pose, the keyboard was used to rotate each bone about its root joint, and the rotations were converted to transform matrices as the inputs of the deformation program. The operation based on the user interface is demonstrated in the supplementary video. More detailed results of the pose and weight changes are presented in the following sections.

Pose Change

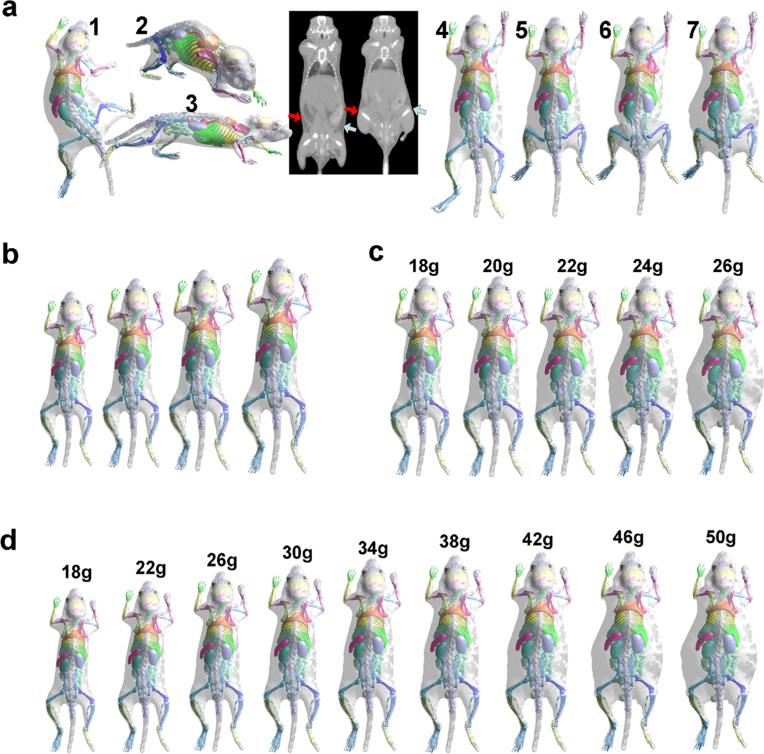
The results of pose changes are shown in Fig. 4a. In results 1~3, the limbs, head, and spine were rotated in different directions, showing the full range of articulation possible with the atlas. The two CT images in the middle were acquired for the same test subject with different femur positions in order to illustrate the skin sliding effect at the waist area. Note the smooth skin and lack of folding artifacts when the underlying femurs are rotated almost 90 °. Results 4 and 5 demonstrate that the atlas can realistically simulate this skin sliding effect, thanks to the cage-based deformation method. In comparison, Savinaud et al. [57] used the SSD method to realize mouse skin articulation, and we demonstrate by result 6 that this method can generate skin folding with large limb rotations. Finally, result 7 has the same pose but a different fat amount from result 5, showing that the atlas can make superimposed pose and weight changes.

Fig. 4.

Test results of the pose and weight changes. a Results 1~3 are atlases of different poses. The two CT images in the middle show the skin sliding effect at the waist area when large femur rotation happens. The arrows point to the area where the muscles slide under the skin, and different arrow colors are used for different body sides. Results 4 and 5 show that the atlas realistically replicates the skin sliding effect. In comparison, the SSD method yields a skin folding artifact, as shown by result 6. Result 7 shows that the atlas can perform superimposed pose and weight change. b Results of only changing the body size. c Results of only changing the fat amount. d Results of combined body size and fat amount changes. For c and d, the body weight is marked on top of each image.

Weight Change

As mentioned in the “Materials and Methods” section, the atlas has two modes of weight change: one for decoupled changes of size and fat and the other for combined changes of size and fat. Both these modes are tested in this experiment. The results of the decoupled mode are shown in Fig. 4b, c, where Fig. 4b demonstrates changing spine length while maintaining the fat ratio, and Fig. 4c demonstrates changing the fat ratio while maintaining the spine length. For Fig. 4c, the spine length was kept at 74.0 mm, while the body weight was increased evenly from 18 to 26 g. It is clear that the linear regression strategy results in skin deformation pattern related to subcutaneous fat accumulation, whereas most of the deformation happens at the lateral sides of the abdomen and thorax. It is worth noting that when the skin deforms, the internal organs remain relatively stable, because the CGM realistically captures the shape relationship between the skin and the internal organs for various body weights.

The results of the combined mode described by Eq. (7) are shown in Fig. 4d. For this mode, the body weight is the only input to the model. The results show that when the body weight increases, the body size and fat ratio increase simultaneously. It is interesting to see that below a certain growth point (~38 g in the figure), weight increases mainly by growth in length, while above this point, weight increases primarily by fat accumulation. This finding coincides with the fact that when mice get old, their musculoskeletal growth slows down, and they start to accumulate fat [58]. Finally, as a comparison, Xie and Zaidi [36] uses simple linear scaling of the MOBY phantom to simulate different body weights, which is similar to what we do for decoupled body size changing (Fig. 4b). It is expected that our combined size and fat change are more realistic than simple scaling.

Organ Weight Validation

Although Fig. 4 shows realistic results of pose and weight changes, it is not clear how well the atlas quantitatively matches with real world subjects. Therefore, we compared the organ weights from the atlas with the organ weights of real mouse subjects. The organs involved in this test were the heart, lungs, liver, spleen, kidneys, and fat. The atlas was set into combined mode and deformed into eight different body weights ranging from 15 to 50 g with an interval of 5 g. The weights of atlas organs were calculated by multiplying the organ volume with the mouse organ densities from Xie and Zaide [36]. For experimental mouse data, organ dissections were conducted for 36 mice between 16 and 45 g at the UCLA Crump Institute for Molecular Imaging. Before dissection, as much as possible, the blood was removed by cardiac puncture. The organs were harvested right after euthanasia and measured using an electronic scale with a precision of 0.001 g. For fat tissue, it is impossible to extract whole-body fat via dissection; thus, we borrowed reference data from the literature [59] where the fat mass of different body weights were obtained using chemical analysis for 790 mice of 40 strains.

Fig. 5 demonstrates the comparison between the atlas organ weights (pink curve) and the experimentally measured real organ weights (blue dots). Each chart is for one organ, the abscissa axis is for body weight, and the vertical axis is for organ weight. The relative error (RE) between the atlas curve and the measured data is defined as (w_a−w_m)/w_m, where w_a and w_m are the organ weights of the atlas and the measured data for the same body weight, respectively. For each organ, the mean and standard deviation of RE across all the 36 subjects are computed and shown in Fig. 5. It can be seen for both the atlas and the measured data that the organ weights increase as the body weight grows, and the atlas curves of all the organs fall into the distribution range of the measured data. The mean RE for all the organs is within the range of ±0.3, and the standard deviation is between 0.17 and 0.47. The best fit is for the liver (RE, −0.06±0.17), which is the largest soft organ. Note that there are four outliers of the spleen (red triangles) between 20 and 25 g body weights. These four outliers are from tumor-bearing mice with shoulder xenografts, and the presence of tumor stimulated the immune response, making the spleen much larger than normal [60]. This result implies that the atlas does not match well with diseased subjects, and that is expected because the training set was composed of healthy subjects. The RE of the spleen was calculated excluding these diseased outliers.

Fig. 5.

Comparison between atlas organ weights and measured organ weights from subjects. Each chart stands for one organ. For each chart, the abscissa axis is for the body weight and the vertical axis is for the organ weight. The pink curve fits the organ weights generated by the atlas, the blue dots are the measurements of the real organs, and the red triangles in the spleen chart are the four tumor-baring subjects with enlarged spleen. The mean value±standard deviation of the relative error (RE) is also shown for each organ.

For fat tissue, according to statistics obtained from reference data [59], mice between 10.1±0.9 and 46.8± 0.9 g have body fat between 2.0±0.5 and 20.1±0.5 g. For comparison, the atlas was also deformed into 10.1 and 46.8 g, and the resultant fat weights were 0.90 and 19.49 g, respectively. It seems that the atlas fat is slightly lighter than the reference data, but the difference is within 0.6~1.6 g, which can be considered as a reasonably good match.

Atlas Voxelization and Tetrahedralization

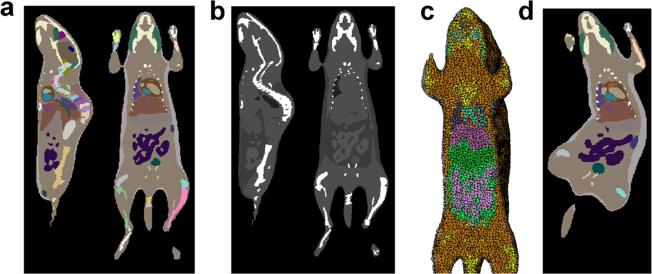
In this paper, all organs of the atlas are represented by triangular meshes. However, there are many applications that require voxelized or tetrahedralized atlases, such as phantom-based simulations, image registration, volume rendering, etc. To meet these requirements, we filled the triangular meshes into a voxelized image and labeled the 89 organs with different voxel values. Theoretically, the atlas can be filled with arbitrarily small voxels; however, smaller voxels than those of the training CT images do not offer any additional anatomical detail. Therefore, the smallest meaningful voxel size is 0.2 mm. Fig. 6a shows the filled label image with a voxel size of 0.2 mm. Based on the labeled image, we can also assign different organs with appropriate Hounsfield values to generate pseudo CT images, as shown in Fig. 6b. The voxelized label image can be further converted into tetrahedral mesh (Fig. 6c) using the iso2mesh software [61], enabling finite element analysis based on the atlas. Of course, the atlas can also be deformed into arbitrary pose and weight and then voxelized into a labeled image, as shown in Fig. 6d.

Fig. 6.

Voxelization and tetrahedralization of the atlas. a The atlas is voxelized into a labeled image with a 0.2-mm resolution. The labeled image is shown in sagittal and coronal slices with pseudo color. b The labeled image is converted into pseudo CT by assigning different organs with appropriate Hounsfield values. c The labeled image is converted into tetrahedral mesh. d A voxelized label image of an arbitrary body pose and weight.

Discussion and Conclusions

As revealed by the experimental results, the deformable atlas demonstrates more realistic body deformation than could be achieved with other mouse atlases, thanks to the use of state-of-art techniques like cage-based harmonic coordinates, linear shape regression, and conditional Gaussian model. Besides the deformation ability, there are several other features that distinguish this atlas from existing whole-body mouse atlases. First, this atlas is constructed based on multiple training subjects rather than only one reference subject. It is the training set size that enables the extraction of anatomical variability related to weight change. By learning from the training set, the atlas gains the ability to deform into any feasible pose and weight. The key advantage of the deformable atlas is that it is not a simple collection of the training subjects, it is a deformation model learned from them. Second, all the training subjects of this atlas were imaged in vivo, in contrast to atlases obtained via cryosectioning or ex vivo imaging. The use of in vivo data avoids deformities inherent with ex vivo imaging. Last but not least, this atlas includes more detailed anatomical structures than the existing mouse atlases, such as individual vertebrae, spinal cord, and neck brown fat, and therefore provides more anatomical details for atlas-based simulation.

For the first time, we use multiple training subjects to construct a whole-body-scale mouse atlas. However, the concept of multiple training subjects is not novel for mouse brain atlases. Multiple brain MR images were used to calculate the average, variance, and label probability of the image voxels [12]. Unlike the brain atlases, we represent the organs as surface meshes and learn surface deformation patterns from the training set. As the training subjects and the test subjects all belong to the weight range of 15~45 g, the atlas is not designed to match with a subject far beyond this range, for example a body weight of 70 g. Nevertheless, the weight modeling method in this paper can be directly applied to much heavier training sets. Given a proper training set of extremely heavy subjects, a deformable atlas of obese subjects can be similarly constructed.

The training subjects of this atlas were all imaged in the prone positions inside an animal chamber specially developed for multimodality imaging [43]; therefore, the atlas best mimics the subject acquired using prone positions, which is the most common position used when imaging small animals. It is unclear how well the atlas can match subjects in supine or other positions; however, with the ability to freely change the pose within the atlas, potentially reasonable results can be obtained for any position. For subjects positioned in narrow holders that squeeze the animals, such as conical tubes, the atlas does not have the ability to compensate for the deformation caused by soft tissue squeezing; thus, more complicated tissue deformation schemes would need to be investigated to evaluate and match this type of data.

It is worthwhile to compare this deformable mouse atlas with other mouse atlases that also have deformation ability. The well-known articulated mouse skeleton atlas [5] was the first one to incorporate pose change function. It has been successfully used for the automated analysis of preclinical images with posture differences [28–30, 39, 40] and is also used for the construction of our atlas. However, the articulation ability of this atlas is limited to the bones, not including soft organs. This atlas is mainly designed for registration purposes; thus, the soft organs can only be mapped during the registration. The Virtual Population mice models [38] are also posable, but no special treatment was applied to deal with the skin sliding effect, and the deformation speed is not fast enough for practical registration use. The MOBY phantom is not articulated, although it includes unique features of respiratory and cardiac motions. Moreover, none of the existing whole-body mouse atlases have incorporated the weight changing function, which is a novel contribution of our atlas.

With the weight changing ability, the atlas realistically models the body deformation pattern caused by differences in fat content. However, according to Fig. 5, the organ weights generated by the atlas only roughly match with the real measurements. There are several potential reasons for the imperfect matching accuracy. First, the atlas is constructed based on different genders and strains which have inherent variations of organ weights [54, 59]; it might be helpful to construct specialized atlas for each gender and strain to improve the modeling accuracy. Second, our decoupled weight modeling scheme assumes the organ size scales linearly with body size (spine length), but this assumption only roughly holds since the organs do not strictly grow in proportion with each other [54]. Third, the organ densities used for calculating atlas organ weights were taken from the literature and thus may be inconsistent with the real subjects of our measurements. Last, the precision of the measured data could also be affected by subjective operational factors during organ dissection. Despite these possible influencing factors, this atlas has demonstrated an improved method for matching real subjects in many positions and is also illustrating where future development can make further improvements.

Like all existing mouse atlases, this deformable atlas is constructed based on healthy subjects. No disease model was specifically included in the atlas. As a result, this work only represents healthy anatomy and does not match well with diseased subjects. This has been revealed by the results of Fig. 5, where the atlas spleen weights do not agree well with the diseased subjects. There are two main reasons for not including disease models: firstly, that the atlas is considered as a reference of normal anatomy, and secondly, disease types are too various to model. However, for future investigation, it is rather important to model anatomical changes caused by diseases. A dedicated study is required to survey the disease-induced anatomical abnormalities, and special techniques must be developed to model organ deformations caused by the presence of tumors.

With the unique features of pose and weight change, this atlas will have potential applications in the field of preclinical imaging and phantom simulation. For example, it can be registered with preclinical mouse images of different poses and weights. The subsecond deformation speed enables fast atlas registration, and the deformation speed can be further accelerated by converting the IDL codes into C language or using parallel programming. The atlas can also be registered with a video sequence of freely moving mice, offering a useful tool for studying animal motion. Moreover, when used as a digital phantom, the atlas's ability of changing fat amount without altering body length is ideal for diabetes or obesity research, and the pseudo CT image generated from the atlas could be registered to individual PET images to provide attenuation correction. In future research, we will focus on investigating these applications. The atlas will also be published to the research community, so that worldwide researchers can use this new tool.